多元线性回归与多元逐步回归
回归分析的回归方法

回归分析的回归方法
回归分析是一种统计分析方法,用于探索和建立自变量与因变量之间的关系。
在回归分析中,有多种回归方法可以使用,其中常见的包括线性回归、多项式回归、多元线性回归、逐步回归、岭回归和Lasso回归等。
1. 线性回归:最简单也是最常用的回归方法,假设自变量和因变量之间存在线性关系,通过最小化残差平方和来估计模型参数。
2. 多项式回归:在线性回归的基础上,将自变量的高阶项添加进模型,以更好地拟合非线性关系。
3. 多元线性回归:包含多个自变量和一个因变量的回归方法,考虑多个因素对因变量的影响。
4. 逐步回归:通过逐步选择自变量,不断添加或删除变量,以找出最合适的自变量集合。
5. 岭回归:一种通过引入正则化项来控制模型复杂度的回归方法,可以有效应对高维数据和共线性问题。
6. Lasso回归:与岭回归类似,也是一种使用正则化项来约束模型复杂度的方法,与岭回归不同的是,Lasso回归可以自动进行变量选择,倾向于将某些系数设为
零。
这些回归方法各有特点,选择合适的方法取决于具体问题的特点和数据的性质。
逐步回归的方法原理是

逐步回归的方法原理是
逐步回归(Stepwise Regression)是一种常见的统计分析方法,用于选择与目标变量之间具有显著影响的自变量。
其原理是基于多元线性回归模型,通过逐步加入或剔除自变量,最终获得具有最佳预测性能的模型。
逐步回归可以分为前向选择(Forward Selection)和后向删除(Backward Elimination)两种方式。
前向选择的过程是从空模型开始,每次选择与目标变量相关性最高(即对解释因变量的能力最强)的自变量加入模型,直到添加新自变量不能显著提高模型的解释效果或达到预设的停止准则。
后向删除的过程则是从包含所有自变量的完全模型开始,逐步剔除对目标变量贡献最小(即对解释因变量的能力最弱)的自变量,直到删除自变量导致的模型解释力显著下降或达到预设的停止准则。
逐步回归方法的优势在于它能够在大量的自变量中找到最佳的子集,从而避免了过度拟合问题。
通过逐渐加入或剔除自变量,可以减少模型的复杂性,提高模型的预测性能和解释力。
此外,逐步回归还能够检验变量的显著性和建立预测模型。
然而,需要注意的是,逐步回归方法在模型选择过程中往往会导致选择出与样本特征相关的变量,而不一定具有普适性和可解释性。
同时,逐步回归方法也受到
自变量之间多重共线性的影响,可能产生不稳定的结果。
因此,在使用逐步回归方法时需要谨慎地选择合适的停止准则,并对最终得到的模型进行验证和评估。
总而言之,逐步回归方法通过逐步选择或删除自变量来构建最佳预测模型,是一种常用的统计方法。
它能够避免过度拟合,提高模型的预测性能和解释力,但在选择自变量和解释结果时需要慎重考虑。
冲刺高考数学多元线性回归分析与逐步回归法

冲刺高考数学多元线性回归分析与逐步回归法在高考数学的广袤领域中,多元线性回归分析与逐步回归法犹如两颗璀璨的明珠,闪耀着智慧的光芒。
对于即将踏上高考战场的学子们来说,深入理解和掌握这两个重要的数学工具,无疑是在数学高分征途上迈出的坚实一步。
首先,让我们来揭开多元线性回归分析的神秘面纱。
多元线性回归分析,简单来说,就是研究一个因变量与多个自变量之间线性关系的一种统计方法。
想象一下,我们在生活中常常会遇到这样的情况:比如,想要预测一个地区的房价,我们可能会考虑到房屋的面积、房龄、地理位置等多个因素;又或者,预测学生的考试成绩,可能会关联到学习时间、参加课外辅导的次数、家庭学习氛围等多种变量。
在这些场景中,多元线性回归分析就派上了用场。
它的基本原理是通过建立一个数学模型,来描述因变量与多个自变量之间的线性关系。
这个模型通常可以表示为:Y = b₀+ b₁X₁+b₂X₂++ bₙXₙ +ε,其中 Y 是因变量,X₁、X₂、、Xₙ 是自变量,b₀是截距,b₁、b₂、、bₙ 是回归系数,而ε 则是随机误差。
那么,如何求解这些回归系数呢?这就需要运用到最小二乘法。
最小二乘法的核心思想是使得实际观测值与模型预测值之间的误差平方和最小。
通过一系列复杂的数学运算,我们可以得到回归系数的估计值,从而确定回归方程。
但是,在实际应用中,并不是所有的自变量都对因变量有显著的影响。
这时候,逐步回归法就登场了。
逐步回归法就像是一个精明的筛选者,它能够从众多的自变量中挑选出那些对因变量影响最为显著的变量,从而建立一个更加简洁、有效的回归模型。
逐步回归法主要分为向前逐步回归、向后逐步回归和双向逐步回归三种。
向前逐步回归是从没有自变量开始,逐步引入对因变量影响显著的自变量;向后逐步回归则是先将所有的自变量纳入模型,然后逐步剔除不显著的自变量;双向逐步回归则是结合了前两种方法的特点,既可以引入新的自变量,也可以剔除已有的自变量。
在高考中,多元线性回归分析与逐步回归法可能会以多种形式出现。
多重线性回归与多元逐步回归统计学

第一节 多重线性回归
概念
• 多重线性回归(multiple linear regression)
• 因变量: 一个, Y • 自变量: 多个, X1, X2, X3, … , Xp
方程:
Y ˆ b 0 b 1X 1 b 2X 2 .. b .pX p
• 多元线性回归(multi- variate linear regression) • 简称多元回归(multi- variate regression):
回
表13-2 方差分析表
变
异
来 DF
SS
源
回 归
p
SS回归 ( yˆi y)2
误
差 n- p -1
SS误差
( yi yˆi )2
总 n-1
n
SS总 ( yi y)2 i 1
MS
MS回归 SS回归 / p MS误差 SS误差 /(n p 1)
MS总 SS总/(n 1)
F
P
MS回归/ MS误差
Yn
前提条件(LINE)
多重线性回归模型应满足以下条件:
(1) Y 与 X1 , X 2 , X m 之间具有线性关系;
(2)各观测值Yj j 1,2,,n 之间相互独立; (3)残差 服从均数为 0、方差为 2 的正态分布,
它等价于对于任意一组自变量 X1 , X 2 , X m ,应
变量Y 均服从正态分布且方差齐。
• Adj R2 =1-MS残/MS总,
• 0<AdjR2≤1, 越接近于1, 说明回归方程效果 越好。
调整的确定系数(adjusted
R , 2
R
2 ad
)
R a 2 d 1 M M 残 总 1 S 差 S S 残 S 总 S / / n S n 差 p 1 1 1 1 R 2n n p 1 1
回归分析方法总结全面

回归分析方法总结全面回归分析是一种常用的统计分析方法,用于建立一个或多个自变量与因变量之间的关系模型,并进行预测和解释。
在许多研究领域和实际应用中,回归分析被广泛使用。
下面是对回归分析方法的全面总结。
1.简单线性回归分析:简单线性回归分析是最基本的回归分析方法之一,用于建立一个自变量和一个因变量之间的线性关系模型。
它的方程为Y=a+bX,其中Y是因变量,X是自变量,a是截距,b是斜率。
通过最小二乘法估计参数a和b,可以用于预测因变量的值。
2. 多元线性回归分析:多元线性回归分析是在简单线性回归的基础上扩展的方法,用于建立多个自变量和一个因变量之间的线性关系模型。
它的方程为Y = a + b1X1 + b2X2 + ... + bnXn,其中n是自变量的个数。
通过最小二乘法估计参数a和bi,可以用于预测因变量的值。
3.对数线性回归分析:对数线性回归分析是在简单线性回归或多元线性回归的基础上,将自变量或因变量取对数后建立的模型。
这种方法适用于因变量和自变量之间呈现指数关系的情况。
对数线性回归分析可以通过最小二乘法进行参数估计,并用于预测因变量的对数。
4.多项式回归分析:多项式回归分析是在多元线性回归的基础上,将自变量进行多项式变换后建立的模型。
它可以用于捕捉自变量和因变量之间的非线性关系。
多项式回归分析可以通过最小二乘法估计参数,并进行预测。
5.非线性回归分析:非线性回归分析是一种更一般的回归分析方法,用于建立自变量和因变量之间的非线性关系模型。
这种方法可以适用于任意形式的非线性关系。
非线性回归分析可以通过最小二乘法或其他拟合方法进行参数估计,用于预测因变量的值。
6.逐步回归分析:逐步回归分析是一种变量选择方法,用于确定最重要的自变量对因变量的解释程度。
它可以帮助选择最佳的自变量组合,建立最合适的回归模型。
逐步回归分析可以根据其中一种准则(如逐步回归F检验、最大似然比等)逐步添加或删除自变量,直到最佳模型被找到为止。
多元线性回归分析与逐步回归分析的比较研究

多元线性回归分析与逐步回归分析的比较研究陈正江;蒲西安【摘要】文章用多元线性回归分析与逐步回归分析方法的应用进行对比研究,其结果为:一是多元回归分析和逐步回归分析两种方法对方程的检验方法和步骤都相同,均可用相关性检验和方差分析两种方法中的任何一种.二是多元回归方程方差分析模型只有一种,而逐步回规方程方差分析模型可有两种或两种以上.三多元回归分析,它将假定从方程中去掉一个自变量xi后,减少的回归平方和称为该自变量的偏回归平方和pi,并对其进行显著性检验;逐步回归则是对所有自变量进行检验,依次对作用不大、无意义的变量进行剔除,并选入有效的、对因变量Y影响较大的自变量进入方程,使其得到最佳方程.【期刊名称】《牡丹江教育学院学报》【年(卷),期】2016(000)005【总页数】3页(P131-133)【关键词】多元线性回归;逐步回归;回归系数;复相关系数【作者】陈正江;蒲西安【作者单位】四川民族学院,四川康定 626001;四川民族学院,四川康定 626001【正文语种】中文【中图分类】G80-3多元线性回归分析与逐步回归分析是科学研究领域最常用的也是最重要的两种统计方法。
在各研究领域中,一个应变量往往受到许多因素的影响,而多元线性回归分析与逐步回归分析可以解决一个应变量与多个自变量之间的数量依存关系。
那么,如何正确使用统计方法,使研究结果更加科学合理,显得尤其重要。
用多元线性回归分析和逐步回归分析方法,对同一数据统计分析,将其结果进行比较研究。
1.多元线性回归分析与逐步回归分析概述(1)多元线性回归分析。
当所有研究问题中有一组自变量x1,x2,x3……xp对一个因变量Y共同发生作用时,可以利用多元回归建立Y与诸多xi之间的关系。
如果选用的函数模型为线性模型,那么,这种回归就称为多元线性回归[1]。
它们的数据较复杂,一般不考虑变量间的因果关系,不必区分应变量与因变量,也就是说,它可以任何一变量作为因变量。
回归分析

回归分析摘要回归分析是应用极其广泛的数据分析方法之一。
它基于观测数据建立变量间适当的相关关系,以分析数据的内在规律,并用于预报、控制等问题。
本次我们选取27名糖尿病人的四种血液成分测量值,依次选用线性回归模型、逐步回归模型和线性Logistic 回归模型来进行数据分析。
关键字:多元线性回归 逐步回归 Logistic 回归题目:27名糖尿病人的血清总胆固醇、甘油三酯、空腹胰岛素、糖化血红蛋白、空腹血糖的测量值于表1中,建立三种回归模型进行分析血糖和其他指标的关系。
表1序 号 总胆 固醇 甘油 三酯 胰岛 素 糖化血 红蛋白 血糖 序 号 总胆 固醇 甘油 三酯 胰岛 素 糖化血 红蛋白 血糖X1 X2 X3 X4 Y X1 X2 X3 X4 Y5 1 5.68 1.90 4.53 8.2 11.2 15 6.13 2.06 10.35 10.5 10.9 2 3.79 1.64 7.32 6.9 8.8 16 5.71 1.78 8.53 8.0 10.1 3 6.02 3.56 6.95 10.8 12.3 17 6.4 2.4 4.53 10.3 14.8 4 4.85 1.07 5.88 8.3 11.6 18 6.06 3.67 12.79 7.1 9.1 5 4.60 2.32 4.05 7.5 13.4 19 5.09 1.03 2.53 8.9 10.8 6 6.05 0.64 1.42 13.6 18.3 20 6.13 1.71 5.28 9.9 10.2 7 4.90 8.50 12.60 8.5 11.1 21 5.78 3.36 2.96 8.0 13.6 8 7.08 3.00 6.75 11.5 12.1 22 5.43 1.13 4.31 11.3 14.9 9 3.85 2.11 16.28 7.9 9.6 23 6.50 6.21 3.47 12.3 16.0 10 4.65 0.63 6.59 7.1 8.4 24 7.98 7.92 3.37 9.8 13.2 11 4.59 1.97 3.61 8.7 9.3 25 11.54 10.89 1.20 10.5 20.0 12 4.29 1.97 6.61 7.8 10.6 26 5.84 0.92 8.61 6.4 13.3 13 7.79 1.93 7.87 9.9 8.4 27 3.84 1.20 6.45 9.6 10.4 14 6.19 1.18 1.42 6.9 9.6一.多元线性回归分析解:设Y 与 1X ,2X ,3X 和4X 的观测值之间满足关系i i i i i i x x x x y εβββββ+++++=443322110 27,...,2,1=i ,其中)27,...,2,1(=i i ε相互独立,均服从正态分布).,0(2σN 利用SAS 系统中的PROC REG 过程可得如下分析结果。
多元线性回归与逐步回归
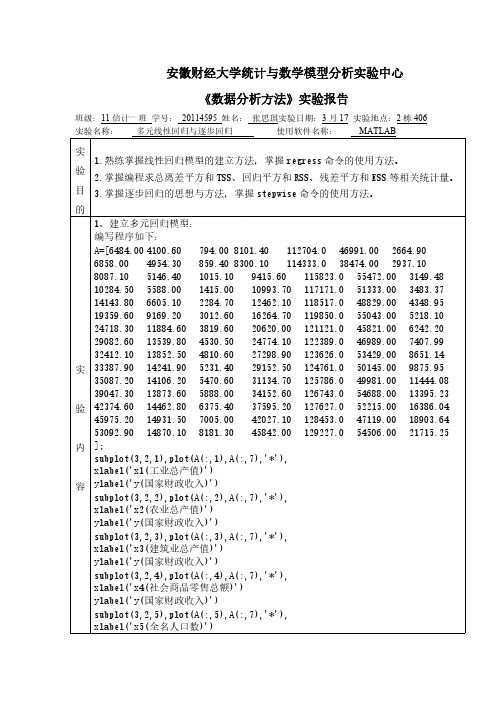
实 1.熟练掌握线性回归模型的建立方法,掌握 regress 命令的使用方法。
验 2.掌握编程求总离差平方和 TSS、回归平方和 RSS、残差平方和 ESS 等相关统计量。
目 3.掌握逐步回归的思想与方法,掌握 stepwise 命令的使用方法。
的 1、建立多元回归模型: 编写程序如下:
A=[6484.00 4100.60 794.00 8101.40 112704.0 46991.00 2664.90 6858.00 4954.30 859.40 8300.10 114333.0 38474.00 2937.10 8087.10 5146.40 1015.10 9415.60 115823.0 55472.00 3149.48 10284.50 5588.00 1415.00 10993.70 117171.0 51333.00 3483.37 14143.80 6605.10 2284.70 12462.10 118517.0 48829.00 4348.95 19359.60 9169.20 3012.60 16264.70 119850.0 55043.00 5218.10 24718.30 11884.60 3819.60 20620.00 121121.0 45821.00 6242.20 29082.60 13539.80 4530.50 24774.10 122389.0 46989.00 7407.99 32412.10 13852.50 4810.60 27298.90 123626.0 53429.00 8651.14 实 33387.90 14241.90 5231.40 29152.50 124761.0 50145.00 9875.95 35087.20 14106.20 5470.60 31134.70 125786.0 49981.00 11444.08 39047.30 13873.60 5888.00 34152.60 126743.0 54688.00 13395.23 验 42374.60 14462.80 6375.40 37595.20 127627.0 52215.00 16386.04 45975.20 14931.50 7005.00 42027.10 128453.0 47119.00 18903.64 53092.90 14870.10 8181.30 45842.00 129227.0 54506.00 21715.25 内 ]; subplot(3,2,1),plot(A(:,1),A(:,7),'*'), xlabel('x1(工业总产值)') 容 ylabel('y(国家财政收入)') subplot(3,2,2),plot(A(:,2),A(:,7),'*'), xlabel('x2(农业总产值)') ylabel('y(国家财政收入)')
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
例子
儿童身高与年龄、性别的关系
肺活量与年龄、性别、身高、体重 以及胸围的呼吸差等因素的关系
多元线性回归
一个应变量与多个自变量间的关系
第一节 多元线性回归 第二节 多元逐步回归 第三节 多元线性回归的注意事项
第一节 多元线性回归
(multiple linear regression )
多元线性回归的数据格式
表 11-1 多元线性回归原始观察数据
例号 i
X1
X2
……
Xk
Y
1
X11
X21
……
Xk1
Y1
2
X12
X22
……
Xk2
Y2
3
X13
X23
……
Xk3
Y3
……
……
n
X1n
X2n
……
Xkn
之中,U 为Xj 的偏回归平方和, 即U= SS回归-SS回归(-j)
表11-5 例11.1数据的偏回归系数F检验表
方程内 自变量
X1,X2 X2 X1
平方和
SS回归
SS回归-SS回归(-j)
116.626
66.275
50.352
114.703
1.924
SS残差 46.025
F
18.598 0.710
Yn
Yˆ
一 、多元线性回归方程 (multiple linear regression equation)
Y ˆ b 0 b 1 X 1 b 2 X 2 b k X k
bj为偏回归系数(partial regression coefficient)
常数项,表示当所有自变量为0时 应变量Y的总体平均值的估计值
胰岛素( x1, mu / L )
生长素( x2 , g / L )
1
12.21
15.2
2
14.54
16.7
3
12.27
11.9
4
12.04
14.0
5
7.88
19.8
6
11.10
16.2
7
10.43
17.0
8
13.32
10.3
9
19.59
5.9
10
9.05
18.7
11
6.44
25.1
12
9.49
16.4
自由度为 总=n-1, 回归=k, 剩余=n-k-1
N
SSTotal (Yi Y)2
i1
SSmodel N(Yi Y)2
i1
SSerror N(Yi Yi)2
i1
Y X2
X1
Total SS Model SS Residual SS
对于例11.1的模型检验
P 0.000
由表11-4可知,F=21.54,P<0.05。从而,拒绝H0,可以认为β1 和β2不全为0,即所求回归方程有统计学意义。
2.偏回归系数的检验
(1)F 检验 H 0:j 0 ; H 1:j 0 j=1,2,…,k
Fj=
U /1 SS残差 ( / n
k
1)
Fj服从F(1 ,n - k - 1)分布
Yi Yˆi 2
i1
得到bj
b 0y (b 1x 1 b 2x 2… … b pxp)
2.例 子
例11.1 20名糖尿病人的血糖、胰岛素及生长素的测定值列于下表 中,试建立血糖对于胰岛素及生长素的二元线性回归方程。
病例号 i
表 11-2 糖尿病人的血糖、胰岛素及生长素的测定值
血糖 y ( mmol / L )
二、回归方程的假设检验
1.模型检验
F=
SS回归 / k
MS回归
SS残差 /(n k 1) MS残差
其中:
SS 总=
n
n
Yi2 ( Yi ) 2 / n
i 1
i 1
n
n
SS = 回归 (Yˆi Y )2 bi LiY
i 1
i 1
n
SS = 残差 (Yi Yˆi )2 SS总 SS回归 i1
表11-3的主要结果。
表 11-3 偏回归系数估计结果
偏回归系
变量
标准误
t
P
数
常数项 17.011 2.472 6.880 0.000
X1
-0.406 0.094 -4.313 0.000
X2
0.098
0.116 0.843 0.411
由此得到回归方程为
Y ˆ 1 7 .0 1 1 0 .4 0 6 X 1 0 .0 9 8 X 2
P
<0.05 >0.05
在=0.05水平上,可以认为胰岛素对血糖的线性回归关系有统计学意义, 而生长素对血糖的线性回归关系无统计学意义。所以应剔除X2,只建立X1与Y
的线性回归方程。
(2) t 检验
H 0:j 0 ; H 1:j 0 j=1,2,…,k
tb j
bjBiblioteka Sbjtb1 4.31 ,P=0.0005; tb2 0.84
表示除以外的其它自变量固定不变 的情况下,每改变一个测量单位时
所引起的应变量Y的平均改变量
两个自变量与应变量的散点图
两个自变量与应变量的拟合面
bj 为 xj方向的斜率
1. 求偏回归系数bj及b0
• 根据最小二乘法(method of least square)原理求出bj ,
即
n
SS残差
,P=0.4110。
在α =0.05水平下,认为血糖与胰岛素的线性回归关系
有统计学意义,而与生长素的线性回归关系无统计学意义。
对于本例有:
n
S S 残 差
Y i Y ˆi 2nY i (b 0 b 1 x 1 b 2 x 2 )2
i 1
i 1
采用最小二乘法即可求出常数项b0和偏回归系数b1、b2。
其中
b0Y(b1x1b2x2)
对表11-2的数据资料由SAS统计软件可得到如下
H0: β 1=β 2=0
=0.05
H1:β 1和β 2不全为0
对表11-3的数据资料,由SAS统计软件可得到如下表11-4
的模型检验结果。
变异来 源 回归 残差
总变异
表 11-4 回归方程的方差分析表
SS
MS
F
116.626
2
46.025
17
162.651 19
58.313 21.539 2.707
13
10.16
22.0
14
8.38
23.1
15
8.49
23.2
16
7.71
25.0
17
11.38
16.8
18
10.82
11.2
19
12.49
13.7
20
9.21
24.4
9.51 11.43 7.53 12.17 2.33 13.52 10.07 18.89 13.14 9.63 5.10 4.53 2.16 4.26 3.42 7.34 12.75 10.88 11.06 9.16
