直流电机运行特性分析(薛升俊蔡旭阳王镒川)
三相无刷直流电动机运行分析
(5）电枢采用整距集中绕组，每相串联匝数为N，电机转 速为n(r/min)
按照电动机惯例，规定三相定子电流和感应电动势的正 方向如图10－12,A相正电动势的方向如图10－13所示。
根据假设(1），由于转子磁场在气隙圆周中按梯形波分 布，因此在电机旋转时，转子磁场在电枢绕组中产生的反
2 转子旋转时，电枢导体切割转子永磁体产生的磁场，或者
说电枢绕组匝链的转子永磁体磁通发生变化，在绕组中产生的 感应电动势eA、eB和eC称为电枢反电动势。反电动势的大小和 波形与气隙永磁场的幅值大小、分布形状和绕组结构形式有关。
在方波无刷直流电机中，由转子永磁极产生的气隙磁通密
度Bg沿圆周的理想分布为矩形或具有一定平顶宽度的梯形波。 实际电机中为减少漏磁，永磁极极弧长度均小于极距，而永磁
Td
KT Iad
KT
1 Ra
Us 2
UT
(10－14)
可以看出，无刷直流电动机机械特性曲线的形状同他 励直流电动机的机械特性曲线类似。这样，从图10－10左 侧的直流电源端看，逆变器电子换相装置加上永磁电动机 就相当于一台他励式的直流电动机，施加于逆变器的直流 电压和电流就相当于直流电动机的电枢电压和电流，并具 有与他励直流电动机相同的输出特性。
电动势随时间按梯形波规律变化。以图10－11(a)所示转子 磁极位置作为转子起始位置，可得到如图10－14所示的三 相绕组感应电动势波形，其幅值为Ea。三相电动势eA、eB 和eC波形及幅值相同，相位差为120°
下面仍以图10－11(a)所示转子磁极位置为起始点，以A 相为例来分析绕组内电流和感应电动势的关系。
得电机的转速为
n Us 2Ra Ia 2KE
实验报告-直流电机特性曲线
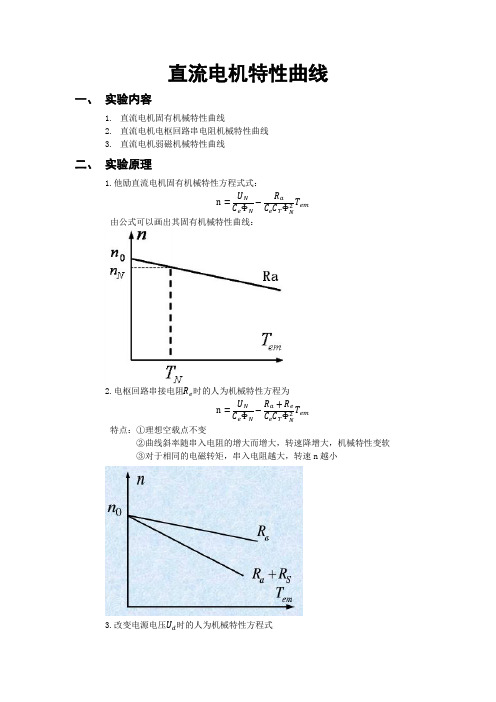
直流电机特性曲线一、实验内容1.直流电机固有机械特性曲线2.直流电机电枢回路串电阻机械特性曲线3.直流电机弱磁机械特性曲线二、实验原理1.他励直流电机固有机械特性方程式式：n=U NC eΦN−R aC e C TΦN2T em由公式可以画出其固有机械特性曲线：2.电枢回路串接电阻R e时的人为机械特性方程为n=U NC eΦN−R a+R eC e C TΦN2T em特点：①理想空载点不变②曲线斜率随串入电阻的增大而增大，转速降增大，机械特性变软③对于相同的电磁转矩，串入电阻越大，转速n越小3.改变电源电压U d时的人为机械特性方程式n=U dC eΦN−R aC e C TΦN2T em特点：①理想空载转速随电源电压降低而成比例降低②曲线斜率保持不变，特性的硬度保持不变③对于相同的电磁转矩，转速n随电源电压降低而减小4.渐弱磁通时的人为机械特性方程式为n=U NC eΦ−R aC e C TΦ2T em特点：①理想空载点随磁通减弱而升高②曲线斜率与磁通成反比，减弱磁通，斜率增大，机械特性变软。
三、实验结果1.固有机械特性 U=U n=220V I fI a(A) 1.110.90.70.60.40.30.20.082 n(r/min)160016131625164716591687170417241752e n f=0.12AI a(A)0.080.10.150.20.250.30.350.40.45n(r/min)1676164015521464138312861213113310493.弱磁U=U n=220V I f=0.11AI a(A)0.0850.10.20.40.60.80.9 1.0 1.1n(r/min)184418401815177717501730171817041691四、实验分析根据实验数据拟合的曲线由图可以得出，实验基本和理论曲线一致。
其中电枢回路串电阻特性曲线，其理想空载点与固有特性曲线不在同一点，可能是由于测量上的误差或者电机时间运行较长，引起电机自身参数略有变化；弱磁机械特性曲线的硬度没有理论中的软，可能是由于实验时，所降低的励磁电流过小而导致。
直流电机的特性和调速分析【开题报告】
毕业设计开题报告电气工程与自动化直流电机的特性和调速分析一、选题的背景与意义直流电机以其优良的动性能和调速性能，在对起动及调速性能要求较高的生产机械领域有着它不可替代的作用，它实现了直流电能和机械能互相转换。
直流电机是指把直流电能转化机械能的电机成为直流电机。
直流电机主要被用于调速要求较高的生产机械上。
具有调速范围广易于平滑调速，启动、制动和过载转矩大可靠性高的优点。
常规的直流电机就是有刷的直流电机，简称直流电机，是指直流电机的电枢供电电源是直流电，而在电枢绕组中流过的电流却是交流的。
它是利用换向器和电刷将直流电源的电流引入电枢绕组，并实现换向。
直流电机是最早出现的电动机，在所有的执行电动机中，直流电机的工作特性最好，与其他各类电动机相比，直流电机的体积小、效率高、功率大、启动转矩大、过载能力强、动态特性好、容易控制、灵活方便，因此广泛应用在要求较高的调速控制系统中。
Matlab是一种科学计算软件，其是MatrixLaboratory(矩阵实验室)的缩写。
这是一种以矩阵为基础的交互式程序计算语言。
早期的Matlab主要用于解决科学和工程的复杂数学计算问题。
由于它使用方便、输入便捷、运算高效、适应科技人员的思维方式，并且有绘图功能，有用户自行扩展的空间，因此特别受到用户的欢迎，使它成为在科技界广为使用的软件，也是国内外高校教学和科学研究的常用软件。
在工业生产现场，对直流电机的运动和稳定性能的要求比较高，通过Matlab仿真软件，可以建立直流电机调速控制系统的模型，便于观察和研究直流电机控制系统在不同的给定参数运行状态下的特性曲线，并且可以通过修改仿真模型中的直流电机的各个模块的数学参数表达式，以达到优化直流电机控制系统性能的目的。
二、研究的基本内容与拟解决的主要问题：直流电机研究的基本内容:利用Matlab仿真软件，建立直流电机控制系统的仿真模型，对直流电机的静态特性，启动特性以及调速系统进行分析和仿真，验证数学模型的有效性及控制系统的合理性；同时改变系统的结构、加入不同的扰动和参数变化，以便考察系统在不同结构和不同工况下的动态和静态特性。
直流电机的工作原理及调速特性
直流电机的磁场
直流电机通过磁场来传递能量， 磁场由励磁绕组通电产生。
磁场的方向与电流方向有关， 改变电流方向可以改变磁场方 向，从而实现电机的旋转。
磁场强度和电流大小成正比， 改变电流大小可以改变磁场强 度，从而影响电机的转矩和转 速。
电源引入。
02
直流电机的调速特性
调速方式与特性
调速方式
直流电机可以通过改变输入电压 、电流或电枢回路电阻等方式进 行调速。
调速特性
调速过程中，电机的转速与输入 电压、电流或电枢回路电阻成正 比，因此可以通过改变这些参数 来调节电机的转速。
调速电路与控制
调速电路
调速电路主要由电源、控制器、电机和反馈装置等组成，控制器根据输入信号 和反馈信号来调节电机的输入电压或电流，从而实现对电机转速的控制。
直流电机的工作原理
当直流电流通过电枢绕组时，产生磁 场，该磁场与主磁极相互作用，产生 转矩，从而使转子转动。
直流电机具有恒定磁场和可变电枢反 应两种工作状态，其工作特性与电枢 电流的大小和方向有关。
直流电机的应用场景
直流电机广泛应用于工业自动化、交通运输、医疗器械等领域，如电动工具、电 动汽车、电梯等。
VS
智能控制技术
智能控制技术如模糊控制、神经网络控制 等在直流电机控制中得到广泛应用。这些 技术能够实现自适应控制和自主学习，提 高直流电机的智能化水平和适应性。
直流电机在新能源领域的应用
风力发电
直流电机在风力发电领域的应用逐渐增多， 特别是在直驱式风力发电机组中，直流电机 作为发电机和驱动电机得到广泛应用。其优 点在于结构简单、维护方便和可靠性高等。
电动机的运行特性与性能分析
电动机的运行特性与性能分析电动机作为重要的动力设备，在现代社会的各个领域中发挥着关键的作用。
了解电动机的运行特性与性能分析对于科学使用和维护电动机至关重要。
本文将从电动机的运行特性和性能两个方面进行探讨，并给出相关的案例分析和实践经验。
一、电动机的运行特性分析1.1 转速特性分析电动机的转速特性是指在不同负载下，电动机输出转速与负载之间的关系。
一般来说，电动机的转速与负载呈反比关系，即负载越大，转速越慢。
但是在实际应用中，由于电动机存在一定的失速现象，转速和负载之间的关系并非简单的线性关系。
在分析转速特性时，需要考虑电动机的额定转速、负载扭矩和电动机的负载特性曲线等因素。
例如，对于某种型号的电动机，在额定转速下，其承载能力和效率达到最佳状态。
而超过额定负载将导致电动机的过热和损坏，因此在实际应用中，需要根据电动机的转速特性选择合适的负载。
1.2 效率特性分析电动机的效率特性是指在不同负载下，电动机的输出功率与输入功率之间的关系。
电动机的效率是衡量其能源利用率的重要指标，对于提高能源利用效率和减少能源浪费具有重要意义。
在分析效率特性时，需要考虑电动机的额定效率和负载功率因数等因素。
例如，在额定负载下，电动机的效率通常能达到最高点。
而在低负载和高负载情况下，电动机的效率则会降低。
因此，在实际应用中，需要根据电动机的效率特性选择合适的负载，以实现最佳的能源利用效率。
二、电动机的性能分析2.1 起动特性分析电动机的起动特性是指在启动过程中，电动机所需的起动电流和起动时间等方面的特性。
合理的起动特性对于电动机的正常运行和长寿命具有重要意义。
在分析起动特性时，主要考虑电动机的起动电流、起动时间和起动方式等因素。
例如，在直流电动机的起动过程中，起动电流通常较大，因此需要根据实际需求选择合适的起动方式，如直接起动、自耦启动或星三角启动等。
2.2 负载特性分析电动机的负载特性是指在不同负载下，电动机的输出扭矩与负载之间的关系。
永磁无刷直流电机稳态特性的状态空间分析
第 17 卷第 1 期
贺益康等 永磁无刷直流电机稳态特性的状态空间分析
19
4 120° 导通方式的状态空间分析
图 2 给出了有代表性的逆变器 120° 导通方式下 的 a 相电流 i as 波形及相应开关管 、二极管的导通 状态 。根据三相变量的对称性 , 一个完整周期可划 分为六个不同状态区间 , 可将状态 1 的 β =π/ 3 范 围选择为计算区间 , 它开始于晶体管 VT6 关断时 刻 , 终止于 VT3 导通时刻 。
18
电工技术学报
2002 年 2 月
规则且无法用函数表示时 , 这种方法就不能直接应 用 。为此 , 本文将采用离散处理气隙磁链波形并求 出相应磁链导数的方法来改进算法 , 以进一步拓展 该方法的实用范围 。
由于逆变器对称触发工作 , 稳态时系统状态方 程定常 , 因此电机系统的三相变量如电压 、电流 、 磁链等均呈现所谓的 60° 对称性 。如用 f 广义地代 λ 表 u , i 或 , 则三相变量 60° 对称关系的矩阵表达 形式为 [ 4 ]
He Yikang Yan Lan ( Zhejiang University 310027 China)
摘要 采用输入函数离散化的状态空间方法 , 对永磁无刷直流电机的稳态性能进行直接稳态 仿真 。由于描述行为特性的状态方程以电机参数和实际磁场空间分布为基础建立 , 又计及开关元 件的换流重叠过程 , 因而这种稳态计算技术给实际电机的运行特性预测提供了一种准确 、有效的 分析手段 。 关键词 : 永磁无刷直流电动机 输入函数离散化 状态空间分析 稳态仿真 中图分类号 : TM351 Abstract In this paper , a state - space approach with discreted input function to steady state perfor2 mance simulation of a permanent magnet brushless DC motor ( PMBLDCM) was discussed1 As the state space equation served to define the steady state performance of the motor was formulated on the basis of motor
直流电动机三闭环调速系统的动态特性研究
关键词：三闭环调速系统；工程设计方法；MATLAB/Simulink；动态性能
Abstract
The DC motor is a power equipment converts direct current electrical energy into mechanical energy. Because of its good performance in speed governing, DC motors are widely used in electric traction, and DC motors are still applied to numerous industrial production occasion. So the DC speed control system will exist with the AC speed control system for a long time. DC speed control system will get a deeper development and play an important role in the future. The content of this article is as following:
(4) A research was made about the Three closed-loop speed control system in different loads and different inference conditions, verifies this system with good dynamic performance in rejection of grid voltage disturbance and load disturbance.
直流电机的运行特性
0
N
A
为了经济、合理地利用材料， 一般直流电机额定运行时，额定磁 通 N 设定在图中 A点，即在磁化特 性曲线饱和与未饱和的转折点,又称 为膝点。
0
I fN
If0 If F f 0 IN
2 直流电机负载时的负载磁场 直流电机带上负载后，电枢绕 组中有电流，电枢电流产生的磁动 势称为电枢磁动势。电枢磁动势的 出现使电机的磁场发生变化。
I Ia
U
G
I Ia
If
Uf
2、并励： 电机的励磁绕组与电枢 绕组并联。且满足
3、串励： 励磁绕组与电枢绕组串联。 满足
Ia = I+ I f
Ia = I f = I
I
U
Ea
I
U
If
If
Ia
Ea Ia
4、复励：
并励和串励两种励磁方式的结合。电机有两个励磁绕 组，一个与电枢绕组串联，一个与电枢绕组并联。
T1 Tem T0
功率平衡方程
励磁铜损 耗
铁损,包括 磁滞和涡 流损耗 机械损耗
电枢的 铜损耗
附加损耗
3、他励直流电发电机的运行特性
3个主要物理量： 电枢端电压U 励磁电流If 负载电流I=Ia
运行特性即：3个量，保持其中1个不变，其余2 个物理量之间的关系。
(1) 空载特性
3 改善换向的主要方法：
装置换向磁极 安装换向磁极是目前改 善换向的有效方法。其 基 本 原理 是利 用 换向 磁 极产生的磁动势方向与 电枢反应磁动势的方向 相反，大小略大于电枢 反 应 磁动 势 。 这 就使 换 向磁动势可以抵消电枢 反应磁动势，剩余的换 向磁动势产生的磁通会 在换向元中产生感应动 势，其方向正好与电抗 电势相反，迭加的结果 可抵消。从而消除火花， 改善换向。
(并励他励)直流电动机械特性的测试分析
（并励他励）直流电动机械特性的测试分析重庆邮电大学移通学院自动化系课程设计报告设计题目: 直流电动机械特性测试与分析学生：---------------专业:----------------班级:---------------- 学号:---------------- 指导教师:----------------目录摘要 .................................................................. ..................................................................... ........... 3 一设计的目的和意义 .................................................................. ..................................................... 3 1.1设计题目 .................................................................. . (3)1.2设计目的 .................................................................. . (3)二总体设计方案 .................................................................. ............................................................. 3 2.1 并励(他励)直流电动机的起动 .................................................................. . (3)2.1.1电枢回路串电阻起动 .................................................................. .................................... 4 2.2并励(他励)直流电动机的调速 .................................................................. .. (4)2.2.1调节电枢电压调速 .................................................................. ........................................ 4 2.2.2调节串入电枢回路电阻调速 .................................................................. ........................ 5 2.2.3调节励磁电流调速 .................................................................. ........................................ 5 三调速的性能指标 .................................................................. ......................................................... 5 3.1 调速范围与静差率 .................................................................. .................................................. 5 3.2 调速的平滑性 .................................................................. .......................................................... 6 3.3调速的经济性 .................................................................. ........................................................... 6 四.设计过程 .................................................................. ....................................................................6 4.1 实验设备 .................................................................. (6)4.2 设备屏上挂件排列顺序 .................................................................. .......................................... 6 4.3 设计原理图 .................................................................. .............................................................. 7 4.4调速步骤 .................................................................. . (7)4.4.1选择仪器 .................................................................. ........................................................ 7 4.4.2直流他励电动机的起动准备 .................................................................. ........................ 8 4.4.3他励直流电动机起动步骤 .................................................................. ............................ 8 五、设计心得 .................................................................. .. (9)六．参考文献 .................................................................. ...................................................................摘要随着工业的不断发展，电动机的需求会越来越大，电动机的应用越来越广泛，电动机的操作系统是一个非常庞大而复杂的系统，它不仅为现代化工业、家庭生活和办公自动化等一系列应用提供基本操作平台，而且能提供多种应用服务，使人们的生活质量有了大幅度的提高，摆脱了人力劳作的模式。
直流电机运行特性分析(薛升俊、蔡旭阳、王镒川)
H a r b i n I n s t i t u t e o f T e c h n o l o g y课程设计说明书（论文）课程名称：电机学实验与仿真设计题目：直流电机运行特性的分析院系：电气工程及自动化学院班级：0806108班设计者：薛升俊、蔡旭阳、王镒川学号：108061082910806108241080610820设计时间：2011年1月3日哈尔滨工业大学目录1. 仿真目的 (3)2. 仿真原理与内容 (4)2.1. 并励电动机的运行特性 (4)2.2. 串励电动机的运行特性 (5)2.3. 积复励电动机的运行特性 (7)2.4. 差复励电动机的运行特性 (8)3. 仿真结论 (10)4. 仿真感想 (11)5. 源程序 (12)1.仿真目的1.通过对不同励磁方式直流电动机的运行特性的分析比较，掌握因励磁方式的不同对直流电机特性的影响；2.应用MATLAB语句进行软件编程,对直流电机的运行特性进行了仿真分析,表明MATLAB语言可作为电机仿真分析中的一种方便、快捷、有力工具；3.通过建模、仿真，加深对直流电机运行特性的直观认识和理解的同时，熟悉了MATLAB进行工程分析的方法与运用。
2. 仿真原理与内容直流电动机的运行特性包括工作特性和机械特性（即转速—转矩特性）。
直流电动机的工作特性是指N U U =，励磁不变，电动机的转矩、转速、效率与电枢电流或者输出功率的关系曲线。
直流电动机的机械特性是指N U U =，fN f I I =，电枢回路电阻为常数时，转速与转矩之间的关系曲线)(e T f n =。
由于直流电机的运行性能因励磁方式的不同有很大差异，我们将其分为四类，分别加以研究其转速特性和机械特性。
2.1. 并励电动机的运行特性转速特性)(a I f n =，并励电动机的工作特性是在电动机的端电压N U U =。
励磁电流fN f I I =的条件下得到的，我们仅分析电动机的转速n 与输出功率的关系)(2P f n =。
第5章 直流电机的运行分析
第5章直流电机的运行分析本章主要介绍直流电机的空载和负载磁场分布、直流电机的电枢绕组、电枢绕组的感应电动势和电磁转矩、直流电机的换向问题和电机稳态运行时的基本方程。
5.1直流电机的磁场磁场是电机感应电动势和产生电磁转矩，从而实现机电能量转换的重要因素之一。
电机的运行性能很大程度决定于电机的磁场特性。
因此，要掌握电机的运行原理必须了解电机的磁场，了解电机空载和负载运行时磁场的建立过程和磁场波形特点。
5.1.1空载时直流电机的磁场在直流电机空载运行时，电枢电流为零，直流电机的气隙磁场由主磁极绕组的励磁磁动势F f建立，由于励磁电流是直流，所以气隙磁场是一个不随时间变化的恒定磁场。
这一磁场在一个极面下的空间分布如图5-1（a）所示，磁极面下气隙小且较均匀，故磁通密度较高，幅值为Bδ，而两极之间的气隙增加，磁通密度显著降低，从磁极边缘至几何中心线处，磁通密度沿曲线快速下降。
电机主磁极产生的磁通分成两部分，主磁通Φ通过气隙，同时交链电枢绕组和励磁绕组，是电机中产生感应电动势和电磁转矩的有效磁通。
另外，由于磁极产生的磁通不可能全部通过气隙，总还有一小部分从磁极的侧面逸出，直接流向相邻的磁极，它只与励磁绕组交链，不与电枢绕组交链，故称磁极漏磁通Φσ。
（a）（b）图5-1直流电机的磁路（a）空载时极面下的磁通密度；（b）四极直流电机两极下的磁路直流电机的主磁路包括以下部分：气隙、电枢齿、电枢磁轭、主磁极和定子磁轭。
除气隙外，其它部分均由铁磁材料组成。
主磁路和漏磁路如图5-1（b）所示。
5.1.2负载时电枢电流的磁场当直流电机带有负载时，电枢绕组中有电流流过，电枢电流也将产生磁场，称作电枢磁场。
为了分析方便，认为电枢表面光滑（无齿槽），磁场分析略去换向器只画主磁极、电枢绕组和电刷。
电机空载磁场、电枢反应磁场和两者的合成磁场分布图如图5-2（a）、（b）、（c）所示，图5-2（c）的扭曲磁通清楚地表明了电枢反应磁场对磁通分布的影响。
直流电机原理及其转动特性分析
直流电机原理及其转动特性分析直流电机是一种常见而重要的电动机类型，广泛应用于工业生产、家庭设备以及交通工具等领域。
本文将从直流电机的工作原理和转动特性两个方面进行详细的分析。
一、直流电机的工作原理直流电机是利用电磁感应原理和洛伦兹力原理来实现电能转换为机械能的装置。
它由定子和转子两部分组成。
定子是由一组定子绕组和磁极组成，绕组通电产生磁场。
转子是由永磁体或可电磁激磁体组成，受到磁场力作用而旋转。
在工作时，施加在直流电机的电源上直流电流，经过定子绕组产生一个旋转的磁场。
根据洛伦兹力原理，当转子处于磁场中时，由于磁场和电流方向的交叉作用，转子上会受到一个力矩的作用。
这个力矩使得转子开始旋转。
同时，转子上产生的感应电动势作用于绕组，产生感应电流，这个感应电流也会在磁场中产生一个力矩，使得转子继续旋转。
直流电机通过定子绕组的电流和转子上的磁场之间的相互作用，实现了电能到机械能的有效转换。
这一工作原理为直流电机的转动特性奠定了基础。
二、直流电机的转动特性分析1. 转速特性直流电机的转速与供电电压和负载有关，根据直流电机的特性曲线可以得知，当负载较小时，转速与供电电压成正比。
而当负载增加时，转速则会下降。
这是因为，在负载增大时，电机内部的反电动势增加，抵消了供电电压的作用，导致转速下降。
2. 转矩特性直流电机的转矩与电流成正比，转矩与转速成反比。
当电机负载增大时，为了保持一定的转速，电机需要输出更大的转矩。
因此，调节电机的电流可以实现对转矩的控制。
3. 效率特性直流电机的效率是指电能转换为机械能的比例，即功率输出与功率输入比值。
根据直流电机的特性曲线可以得知，当电机负载较小时，电机的效率较高。
而当电机负载增加时，电机的效率会下降，因为更多的能量被转化为热量。
4. 起动特性直流电机在启动前需要克服静摩擦力和动摩擦力的阻力。
根据电机的起动曲线可以得知，当启动电流较大时，电机能够迅速克服阻力实现起动。
而当启动电流较小时，电机的起动时间会延长。
直流电机实验报告
直流电机实验报告篇一：并励直流电机实验报告实验二直流并励电动机一.实验目的1.掌握用实验方法测取直流并励电动机的工作特性和机械特性。
2.掌握直流并励电动机的调速方法。
1.什么是直流电动机的工作特性和机械特性？答：工作特性：当U = UN， Rf + rf = C时，η, n ,T 分别随P2 变；机械特性：当U = UN， Rf + rf = C时， n 随 T 变；2.直流电动机调速原理是什么？答：由n=(U-IR)/Ceφ可知，转速n和U、I有关，并且可控量只有这两个，我们可以通过调节这两个量来改变转速。
即通过人为改变电动机的机械特性而使电动机与负载两条特性的交点随之改变，从而达到调速的目的。
二.预习要点三.实验项目1.工作特性和机械特性保持U=UN 和If =IfN 不变，测取n=f(Ia)及n=f(T2)。
2.调速特性(1)改变电枢电压调速保持U=UN 、If=IfN =常数，T2 =常数，测取n=f(Ua)。
(2)改变励磁电流调速保持U=UN，T2 =常数，R1 =0，测取n=f(If)。
(3)观察能耗制动过程四．实验设备及仪器1．MEL-I系列电机教学实验台的主控制屏。
2．电机导轨及涡流测功机、转矩转速测量（MEL-13）、编码器、转速表。
3．可调直流稳压电源（含直流电压、电流、毫安表）4．直流电压、毫安、安培表（MEL-06）。
5．直流并励电动机。
6．波形测试及开关板（MEL-05）。
S （2）测取电动机电枢电流Ia、转速n和转矩T2，共取数据7-8组填入表1-8中表1-8 U=UN=220V If=IfN=0.0748A Ka= Ω 2．调速特性（1）改变电枢端电压的调速表1-9 I（2）改变励磁电流的调速一7接线 f：直流电机电枢MEL-09） MEL-03中两Ω电阻并联。
刀双掷开关（MEL-05）六．注意事项1．直流电动机起动前, 测功机加载旋钮调至零. 实验做完也要将测功机负载钮调到零，否则电机起动时，测功机会受到冲击。
机电传动控制 第3章 直流电机
机电传动控制第3章直流电机的工作原理及特性各种各样的电机常用的电机主要分为两大类：驱动电机：是设备的主要动力源，包括各类交流、直流电动机及步进电动机。
交流异步电动机较之其他类型的电动机结构简单，价格便宜，运行可靠，维护方便，应用广泛。
控制电机：常见的有步进电动机、交流伺服电动机、直流伺服电动机、测速发电机等，这类电机的主要任务时转换和传递控制信号，能量传递时次要的。
常用电机分类：第3章直流电机的工作原理及特性电机分为直流电机和交流电机。
直流电机——工作电压或输出电压为直流电压。
交流电机——工作电压为交流电压。
直流电机：直流电动机——将电能转换成机械能。
直流发电机——将机械能转换成电能。
直流电机与交流电机的比较交流电机较直流电机的结构简单，制造容易，维护方便，运行可靠；直流电机有交流电机不可比拟的启动和调速性能；直流电机更适合于调速要求高、正反转、启动和制动频繁的场合；直流电机即可做电动机用，又可作发电机用。
3.1 直流电机的基本结构和工作原理一、直流电机的基本结构包括定子、转子和换向器实际直流电机构造定子实际直流电机构造转子换向片剖视图3.1 直流电机的基本结构和工作原理一、直流电机的基本结构3.1 直流电机的基本结构和工作原理一、直流电机的基本结构3.1 直流电机的基本结构和工作原理一、直流电机的基本结构定子部分：主要由主磁极、换向极（铁芯）和绕在上面的励磁绕组等组成。
作用：产生主磁场和支撑电机转子部分：主要由电枢铁芯、电枢绕组、换向器等组成。
作用：产生感应电动势和机械转矩，实现能量转换。
主磁极：产生气隙磁场，以便电枢绕组在此磁场中转动而感应电势。
产生磁场有两种方法，一是采用永久磁铁作主磁极——永磁直流电机(绝大部分的微小型直流电机)；二是由励磁绕组通以直流电流来建立磁场(中大型直流电机) 。
电枢铁芯：主磁通磁路的一部分，嵌置电枢绕组。
一般用0.5或0.35毫米厚的涂有绝缘漆的硅钢片叠压而成，以防涡流。
电机与拖动 直流电动机的运行分析、直流发电机的运行分析
电机与拖动 直流电动机的运行分析、直流发电机的运行分析主 题：直流电机的辅导文章——直流电动机的运行分析、直流发电机的运行分析学习时间：2016年10月17日--10月23日内 容：我们这周主要还是学习课件第2章直流电机的相关内容。
希望通过下面的内容能使同学们加深对直流电机相关知识的理解。
一、直流电动机的运行分析（重点了解）1.我们以他励直流电动机为例，分析直流电动机的基本方程。
图3-1 直流电动机的正方向规定在如图3-1规定正方向的前提下，他励直流电动机的基本方程式为：电压平衡方程：a a U E R I =+ （3-1） 式中E E C n =Φ。
转矩平衡方程：20e T T T =+ （3-2） 式中e T a T C I =Φ。
其中，a R --电枢绕组总电阻，包括电刷的接触电阻；0T --空载转矩，是由电动机的机械摩擦损耗及铁损引起的总转矩； 2T --生产机械的制动转矩；功率平衡方程：1022Cu e Cu Cu fw Fe ad P P P P P P P P P P P =+=++=++++（3-3）直流电动机的基本方程式综合反映了电机内部的电磁关系和机电过程。
运用这些基本方程式，可以分析其工作特性和机械特性。
值得注意的是，对于不同的励磁方式，电压平衡方程式是不同的，而转矩平衡方程式和功率平衡方程式基本不变。
2.直流电动机的工作特性是指当N U U =、f fN I I =时，电机转速n 、电磁转矩e T 和效率η与电枢电流a I 的关系曲线，如图3-2所示。
图3-2 他励直流电动机的工作特性1）转速特性：如图3-2所示转速特性是一条略微下倾的曲线。
把公式E E C n =Φ带入a a U E R I =+，可得转速公式为：a a E E R U n I C C =-ΦΦ（3-4） 式3-4对各种励磁方式的电动机都适用。
在N U U =、f fN I I =条件下，影响转速的因素有两个：电枢回路的电阻压降a a R I 和电枢反应。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
H a r b i n I n s t i t u t e o f T e c h n o l o g y课程设计说明书（论文）课程名称：电机学实验与仿真设计题目：直流电机运行特性地分析院系：电气工程及自动化学院班级： 0806108班设计者：薛升俊.蔡旭阳.王镒川学号： 1080610829 1080610824 1080610820 设计时间： 2011年1月3日哈尔滨工业大学目录1. 仿真目地 (3)2. 仿真原理与内容 (4)2.1. 并励电动机地运行特性 (4)2.2. 串励电动机地运行特性 (6)2.3. 积复励电动机地运行特性 (7)2.4. 差复励电动机地运行特性 (9)3. 仿真结论 (12)4. 仿真感想 (13)5. 源程序 (14)1.仿真目地1.通过对不同励磁方式直流电动机地运行特性地分析比较,掌握因励磁方式地不同对直流电机特性地影响；2.应用MATLAB语句进行软件编程,对直流电机地运行特性进行了仿真分析,表明MATLAB语言可作为电机仿真分析中地一种方便.快捷.有力工具；3.通过建模.仿真,加深对直流电机运行特性地直观认识和理解地同时,熟悉了MATLAB进行工程分析地方法与运用.2. 仿真原理与内容直流电动机地运行特性包括工作特性和机械特性（即转速—转矩特性）.直流电动机地工作特性是指N U U =,励磁不变,电动机地转矩.转速.效率与电枢电流或者输出功率地关系曲线.直流电动机地机械特性是指N U U =,fN f I I =,电枢回路电阻为常数时,转速与转矩之间地关系曲线)(e T f n =.由于直流电机地运行性能因励磁方式地不同有很大差异,我们将其分为四类,分别加以研究其转速特性和机械特性.并励电动机地运行特性转速特性)(a I f n =,并励电动机地工作特性是在电动机地端电压N U U =.励磁电流fN f I I =地条件下得到地,我们仅分析电动机地转速n 与输出功率地关系)(2P f n =.由于在实际运行中a I 较易测得,且a I 随着2P 地增大而增大,故可以把工作特性表示为)(a I f n =.由电动势公式和电压方程可以得到转速地数学表达式为a e a e e a I C R C U C E n φφφ-==根据上面建立地数学表达式模型,我们用matlab 进行仿真,可得其图像如下：由仿真图像可知,随着输入电流地增大,并励电动机有稍微下降地转速特性.这是由于影响并励电动机转速地因素有两个：一是电枢电阻压降,二是电枢反应.当电动机地负载增加时,电枢电流增大,a a R I 使电动机地转速趋于下降.与此同时,电枢反应有去磁作用,使转速趋于上升.这两个因素对转速地影响部分地抵消,使并励电动机地转速变化很小.实际中,为保证并励电动机地稳定运行,常使它具有如图所示地稍微下降地转速特性.值得注意地是,并励电动机在运行地时候,励磁绕组绝对不能断开.若励磁绕组断开,0=f I ,主磁通讲迅速下降到剩磁通,使电枢电流迅速增大.此时若负载为轻载,电动机转速迅速上升,造成“飞车”现象；若负载为重载,所产生地电磁转矩克服不了负载转矩,电动机可能停转,使电枢电流增大到启动电流,引起绕组过热而将电动机烧毁.这两种情况都是危险地.机械特性)(e T f n = 并励电动机地机械特性是指N U U =,励磁回路电阻f R =常值时,电动机地转速与电磁转矩地关系)(e T f n =.由电磁转矩公式和电动机地电压方程推出e T e a e T C C R C U n 2φφ-=根据建立地数学表达式模型,我们用matlab 对其进行仿真,得到其图像如下由图像可知,并励电动机地转速随所需地电磁转矩地增加而稍有变化,若不计磁饱和,并励电动机地机械特性为稍微下降地直线；若计磁饱和,交轴电枢反应地去磁作用使曲线地下降程度减小,甚至可以变成水平或者上翘地曲线.我们称这种特性为硬特性.串励电动机地运行特性转速特性)(a I f n =,串励电动机地工作特性是在电动机地端电压N U U =条件下测得地.串励时I I I a s ==,电机地磁化曲线近似为s s I K =φ,则从转速公式知s e s a a s e e s a a K C R R I K C U C R R I U n +-=+-=1)(φ根据建立地数学表达式模型,我们用matlab 对其进行仿真,得到其图像如下由仿真图像可知,n 与a I 大体成双曲线关系.这是由于负载增大时,a I 增加,使电枢回路地电阻压降)(s a a R R I +增大,此时串励磁动势和主磁场亦同时增大,这两个因素都促使转速下降,所以串励电动机地转速随负载地增大而迅速下降.需要注意地是,串励电动机不允许空载运行.这是因为空载时I 很小,主磁通也很小,使转速极高,产生“飞车”现象,这是不允许地.机械特性)(e T f n = 串励电动机地机械特性是指N U U =,电动机地转速与电磁转矩地关系)(e T f n =.由电动机地电压方程可得I R R n K C R R I n C R R I E U s a s e s a e s a a a )()()(++=++=++=φ （式中s s I K =φ）再由电磁转矩a T e I C T φ= 我们可以得到⎥⎥⎦⎤⎢⎢⎣⎡+-=)(1s a e s T s e R R U T K C K C n 根据建立地数学表达式模型,我们用matlab 对其进行仿真,得到其图像如下由图可知,随着转矩地增加,串励电动机地转速迅速下降,这种特性称之为软特性.积复励电动机地运行特性积复励电动机是指串励绕组地磁动势与并励绕组地磁动势方向相同.我们在对积复励运行特性进行MATLAB 分析时,首先得先建立出其数学模型.可是要想直接从积复励直流电动机地转矩方程中推导出)(e T f n =地函数关系数学方程时是很困难地,即使得出来了,它地表达式也很复杂,难以用其进行数量地求解和模型地建立.为了得到所需地模型和简化计算,我们选用电枢电流作为中间变量,进而求出转速与转矩地特性曲线.积复励直流电动机地并励和串励绕组地磁动势是叠加地,而每极磁通φp = R I N I N as f f +（式中R 为电动机磁路内每极下地等值磁阻）.所以可以得到转速为m ω=R I N I N K R R I U a s f f s a a /)()(++-又因为式中)(s a a R R I +相对于U 来说通常可以忽略不计,故m ω≅)(a s f f I N I N K RU +,故R I I N I N K T a a s f f e )(+=根据上面推导地数学表达式,我们用matlab 对其进行仿真可得其图像如下我们对上面转速与转矩地表达式进行定性地分析,得知：当电枢电流a I 增大时,转速m ω便减小,而转矩e T 则增大.相反,当电枢电流a I 减小时,转速m ω便升高,而转矩e T 则减小.此外,当a I →0时,e T →0,以及m ω→f f I KN RU(边界常数).由仿真图像可以看到,积复励直流电机地运行特性介于并励与串励电动机之间.这是由于积复励电动机既有并励绕组,又有串励绕组.当励磁磁动势中以并励磁动势为主时,其机械特性接近并励电动机,但由于有串励磁动势地存在,负载增大时,电枢反应地去磁作用可以得到抑制,不使转速上升,从而保证电动机稳定运行；当励磁磁动势中以串励磁动势为主时,其机械特性接近串励电动机,但由于并励磁动势地存在,不会使电动机空载时出现“飞车”现象.可见,积复励电动机既有并励电动机地优点,又有串励电动机地优点.差复励电动机地运行特性差复励电动机是指串励绕组地磁动势与并励绕组地磁动势方向相反.其建模分析方法和积复励电动机方法基本相同.可以得到其数学表达式为m ω≅ )(a s f f I N I N K RU -我们用matlab 对其进行仿真可得其图像如下在实际过程中,我们要将一台直流电动机连接成积复励直流电动机时,却将其串励绕组接反,因而误接成差复励直流电动机,这种事情是很容易发生地.然而,这种情况还是应该尽量避免地.这是由于将一台差复励直流电动机投入运行,则将其加载到反向串励绕组地磁动势,正好抵消了并励绕组地磁动势时,则从图中可以看出,转速升高到了不稳定地程度,甚至会出现上翘地特性,这是我们需要尽量避免地.从式中可以看出,当（a s f f I N I N -）→0时,转速确实大幅度升高.当绕组地磁动势相互抵消时,线圈地感应电势也大大减小.因此,电动机地电枢电流快速增大.最后我们综合比较一下四类电动机地机械特性,下图为一组转矩与转速地额定值均相同地各类直流电动机,在相同地端电压下,转矩与转速之间地特性关系.由图中比较分析可知,并励电动机地机械特性为稍微下降地直线（硬特性）,而串励电动机地转速随着转矩地增加迅速下降（软特性）,积复励电动机地机械特性介于并励电动机和串励电动机之间,差复励电动机地机械特性会出现“上翘”地不稳定现象,应该尽量避免.3.仿真结论1.对于不同地励磁方式地直流电动机,其运行特性也是各不相同地,甚至会有很大地差别.我们得根据直流电机地不同励磁方式来对其地运行特性进行具体地分析.比较.2.对于并励电动机地运行特性,其转速特性随着输入电流地增大有稍微下降,其机械特性曲线为随着随着转矩地增加稍微下降地直线（硬特性）.此外,并励电动机在运行地时候,励磁绕组绝对不能断开,以免造成“飞车”现象或者停转现象.3.对于串励电动机地运行特性,其转速特性曲线为转速随负载地增大而迅速下降,其机械特性曲线为转速随着转矩地增加迅速下降（软特性）.此外,串励电动机不允许空载运行.以免产生“飞车”现象.4.积复励直流电机地运行特性介于并励与串励电动机之间,既有并励电动机地优点,又有串励电动机地优点.5.对于差复励电动机地运行特性,当负载达到一定程度时,其转速升高到了不稳定地程度,甚至会出现上翘地特性,我们需要尽量避免.4.仿真感想通过对直流电动机运行特性地MATLAB仿真.分析与比较,我们对直流电机地特性有了进一步地认识,对不同励磁方式对直流电机特性地影响有了更加直观地感受和清晰地理解.特别是积复励与差复励地运行特性,课本上并没有给出具体地数学模型和特性图像,可是我们组经过查资料,参阅文献等途径,对两种复励电动机地运行特性进行了数学模型地建立.程序地编写与调试.图形地绘制.结果地分析与验证,得到了较好地结果,这样便于与并励和串励电动机运行特性进行比较,达到了我们地预期目地,加强了我们团队合作地意识.与此同时,通过建模与仿真,我们初步掌握了运用MATLAB工具对电机仿真地方法,树立了需要充分运用软件等信息工具指导自己学习地思想.此次仿真中也出现了一些问题与不足.由于对MATLAB地熟练程度不够,在进行建模仿真地时候,对程序地编写.调试过程中碰到了很多地困难.不过,经过同组同学地共同努力,不断地修改,调试,查阅资料,最后终于得到了预期地目标.此外,由于时间上比较紧张,未对并励电动机空载“飞车”,短路停转地现象进行相应地建模仿真分析,这也不得不算是个遗憾.在今后地学习过程中,要更加地在理论与实践上充实自己.提高自己.5.源程序clear; clf;VtR=600;PR=80;Ra=0.25;Rs=0.03;Nf1=750;Nf2=250;a=0.2; b=0.6e-5;Ns1=3;Ns2=10;nmR=1200;TdR=PR*746/(nmR*pi/30)/0.96;IaR=(VtR-sqrt(VtR^2-4*(Ra+Rs)*TdR*nmR*pi/30))/2/(Ra+Rs); TdR1=PR*746/(nmR*pi/30)+(a+b*nmR^1.7)*30/pi;IaR1=(VtR-sqrt(VtR^2-4*Ra*TdR1*nmR*pi/30))/2/Ra;load eifm=length(eif); npts=200;Kphip=eif(1:m,1)/(nmR*pi/30); If=eif(1:m,2);IfR1=interp1( Kphip, If, (VtR-IaR*(Ra+Rs))/(nmR*pi/30))-Ns1/Nf1*IaR;IfR2=table1( [Kphip If],(VtR-IaR*(Ra+Rs))/(nmR*pi/30))+Ns1/Nf2*IaR;Rfeq1=VtR/IfR1;Rfeq2=VtR/IfR2;IfR3=interp1( Kphip, If, (VtR-IaR1*Ra)/(nmR*pi/30)); Rfeq3=VtR/IfR3;npts1=25;Ia4=linspace(1.5*PR*746/VtR,0,npts1);npts=200;Ia1=linspace(0,1.5*PR*746/VtR,npts);Ia3=linspace(0.25*IaR,1.5*IaR,npts);E=eif(1:m,1);mmfs=eif(1:m,2)*Ns2*IaR/(interp1(E,If,VtR-IaR*(Ra+Rs))); for i=1:nptsKphi1=interp1(If, Kphip, IfR1+Ns1/Nf1*Ia1(i));Kphi2=table1([If Kphip], IfR2-Ns1/Nf2*Ia1(i));Kphi3=interp1(mmfs, Kphip, Ns2*Ia3(i));Td1(i)=Kphi1*Ia1(i);Td2(i)=Kphi2*Ia1(i);Td3(i)=Kphi3*Ia3(i);wm1(i)=VtR/Kphi1-Td1(i)*(Ra+Rs)/Kphi1^2;wm2(i)=VtR/Kphi2-Td2(i)*(Ra+Rs)/Kphi2^2;wm3(i)=VtR/Kphi3-Td3(i)*Ra/Kphi3^2;endnm1=wm1*30/pi;nm2=wm2*30/pi;nm3=wm3*30/pi;for i=1:nptsKphi4=interp1(If, Kphip, IfR3);Td4(i)=Kphi4*Ia4(i);wm4(i)=VtR/Kphi4-Td4(i)*Ra/Kphi4^2;nm4(i)=wm4(i)*30/pi;Pfw=a*nm4(i)+b*nm4(i)^2.7;eff(i)=(1-(Pfw+Ia4(i)^2*Ra+VtR*IfR3)/(IfR3+Ia4(i))/VtR)*100 ;if eff(i)<0; m=i-1; break; endendhold onplot(0,0,Td1,nm1,'-',TdR,nmR,'o'); grid on;plot(0,0,Td2,nm2,':',TdR,nmR,'o'); grid on;plot(0,0,Td3,nm3,'-.',TdR,nmR,'o'); grid on;plot(0,0,Td4(1:m),nm4(1:m),'--',TdR,nmR,'o'); grid on;text(600,3400,'————积复励直流电动机','fontsize',10); text(600,3600,'·········差复励直流电动机','fontsize',10);text(600,3800,'—·—·—串励直流电动机','fontsize',10); text(600,3200,'- - - - -并励直流电动机','fontsize',10);title('直流电动机地运行特性');ylabel('转速, rpm'); xlabel('转矩, N-m');figure(2);subplot(2,1,1); plot(0,0,Td4(1:m),nm4(1:m),TdR1,nmR,'o'); grid;title('并励直流电动机');ylabel('转速, rpm'); xlabel('转矩, N-m');subplot(2,1,2);plot(0,0,Ia4(1:m)+IfR3,nm4(1:m),IaR1+IfR3,nmR,'o'); grid; title('并励直流电动机');ylabel('转速, rpm'); xlabel('输入电流, A');figure(3);subplot(2,1,1); plot(0,0,Td3,nm3,TdR,nmR,'o'); grid;title('串励直流电动机');ylabel('转速, rpm'); xlabel('转矩, N-m');subplot(2,1,2); plot(0,0,Ia3,nm3,IaR,nmR,'o'); grid;title('串励直流电动机');ylabel('转速, rpm'); xlabel('输入电流, A');figure(4);subplot(2,1,1); plot(0,0,Td2,nm2,TdR,nmR,'o'); grid;title('差复励直流电动机');ylabel('转速, rpm'); xlabel('转矩, N-m');subplot(2,1,2); plot(0,0,Ia1+IfR2,nm2,IaR+IfR2,nmR,'o'); grid;title('差复励直流电动机');ylabel('转速, rpm'); xlabel('输入电流, A');figure(5);subplot(2,1,1); plot(0,0,Td1,nm1,TdR,nmR,'o'); grid;title('积复励直流电动机');ylabel('转速, rpm'); xlabel('转矩, N-m');subplot(2,1,2); plot(0,0,Ia1+IfR1,nm1,IaR+IfR1,nmR,'o'); grid;title('积复励直流电动机');ylabel('转速, rpm'); xlabel('转速, A');。