§4.06 系统方框图和信号流图
合集下载
结构图与信号流图

1 ( Cs
1 R1
XI’AN UNIVERSITY OF POSTS & TELECOMUNICATION
西安邮电学院自动化学院 18
第四节 结构图与信号流图
2 引出点和比较点的移动变换
原则:保持移动前后封闭域输入输出关系不变。
X ( s)
1
G (s)
X ( s)
2
X ( s)
1
G (s)
XI’AN UNIVERSITY OF POSTS & TELECOMUNICATION
西安邮电学院自动化学院
5
第四节 结构图与信号流图
比较点(综合点、相加点):
表示对两个以上的信号进行加减运算,加号常省略,负号必 须标出;进行相加减的量,必须具有相同的量纲。
引出点: 表示信号引出或测量的位置,同一位置引出的信号大小和性 质完全相同。
G (s)
比较点前移
西安邮电学院自动化学院 20
移动的支路上乘以它所扫过方框内的传函的倒数。
XI’AN UNIVERSITY OF POSTS & TELECOMUNICATION
第四节 结构图与信号流图
3 相邻引出点可互换位置、可合并
a b
b
a
4 相邻比较点可互换位置、可合并
a
b
XI’AN UNIVERSITY OF POSTS & TELECOMUNICATION
XI’AN UNIVERSITY OF POSTS & TELECOMUNICATION
西安邮电学院自动化学院
3
例2 引入闭环控制后的直流电机转速控制系统
+Vcc
ur
uf
第四节信号流图

∴ ∆ = 1 − ∑ La = 1 + G1G2G3Gu G f , ∆1 = 1
G1G2G3Gu Ω( s ) 1 1 P= = ∑ Pk ∆ k = u g ( s ) ∆ k =1 1 + G1G2G3Gu G f
Wednesday, March 16, 2011
11
梅逊公式||例2-13 梅逊公式 例
1
G4
1
G1
C
有四个回路,分别是:
G8 − H2 − H1
− G2 H 2 ,−G1G2G3G4 H1 ,−G1G2G7G4 H1 ,−G1G2G8G4 H1
它们都是互相接触的。 ∴ ∆ = 1 + G2 H 2 + G1G2G3G4 H1 + G1G2G7G4 H1 + G1G2G8G4 H1 有九条前向通道,分别是:
Wednesday, March 16, 2011
∆1 = 1
(因为三个回路都与前向通道接触。)
13
梅逊公式||例2-13 梅逊公式 例
1
1 R1
−1
1
1 C1s
ui
ue
I1
−1
I
a 1 b u
1 R2
1 C2 s
I2
−1
uo
讨论:信号流图中,a点和b点之间的传输为1,是否可以将该两 点合并。使得将两个不接触回路变为接触回路?如果可以的话, 总传输将不一样。 不能合并。因为a、b物理上不是相同的信号,信号值不一样。
Wednesday, March 16, 2011
16
梅逊公式||例 梅逊公式 例2-14
E (s) 求 : R(s)
∆ 不变。
结构图与信号流图ppt课件

精选ppt
11
绘图:U(s)为输入,画在最左边。
这个例子不是由微分方程组——代数方程组— —结构图,而是直接列写s域中的代数方程, 画出了结构图。
精选ppt
12
如果在这两极R-C 网络之间接入一个 输入阻抗很大而输 出阻抗很小的隔离 放大器,如图2-22 所示。则此电路的
方块图如图(b)所示。
R1
直接对应 图形编程
无对应关系
精选ppt
3
一、结构图的基本单元和等效规则 1、结构图的基本单元
(1)信号线
u(t),U(s)
•带箭头的直线 •箭头表示信号的流向 •在直线旁标注信号的时间函数或象函数
(2)引出点 (或测量点)
u(t),U(s) u(t),U(s)
•信号引出或测量位置
精选ppt
4
•同一位置引出的信号在数值和性质方面完全相同
E(s)=R(s) ±B(s) 整理有:
C (s)R (s)F (s)R (s)1G G (s (s )H )精(选s)ppt
结论:闭环传递函数
“+”正反馈
“-” 负反馈
16
(4) 比较点的移动
(1) 比较点前移
R(s)
G(s)
C(s) Q(s)
(2) 比较点后移
R(s) Q(s)
G(s)
C(s)
2-3 结构图与信号流图
引言 一、结构图的基本单元和等效规则 二、信号流图的组成和性质 三、信号流图的绘制 四、Mason公式 五、闭环系统的传递函数
精选ppt
1
引言
何谓结构图
由单向运算框图和信号流向线组成的描写一般系统中信 号传递关系的定量分析图形。
何谓信号流图 由单向增益支路和节点运算框图和信号流向线组成的描
控制系统的结构图与信号流图
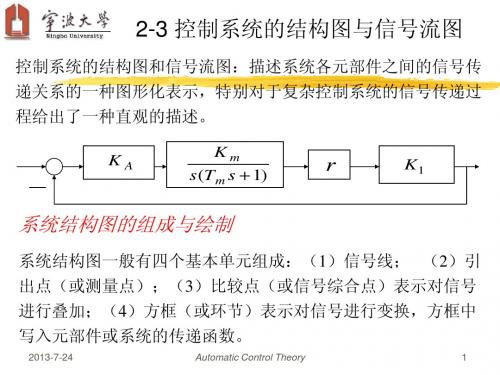
2-3 控制系统的结构图与信号流图
控制系统的结构图和信号流图:描述系统各元部件之间的信号传 递关系的一种图形化表示,特别对于复杂控制系统的信号传递过 程给出了一种直观的描述。
KA
Km s (T m s 1)
r
K1
系统结构图的组成与绘制
系统结构图一般有四个基本单元组成:(1)信号线; (2)引 出点(或测量点);(3)比较点(或信号综合点)表示对信号
Automatic Control Theory 2
M s C M U a (s )
2013-7-24
绳轮传动机构: L( s ) r m ( s )
测量电位器:
E (s)
E 2 ( s ) K 1 L( s )
M s (s)
CM
U a (s )
E1 ( s )
m (s) L (s )
2013-7-24 Automatic Control Theory 14
•回路 起点和终点同在一个节点上,而且信号通过每个节点不多 于一次的闭合通路(单独回路)。 •不接触回路 回路之间没有公共节点时,该回路称为不接触回路。
信号流图的绘制
(1)由微分方程绘制信号流图: RC串联电路的信号流图
u r (t ) i1 (t ) R1 u c (t ) u c (t ) i (t ) R2 1 i2 (t ) dt i1 (t ) R1 u1 (t ) C i1 (t ) i2 (t ) i (t )
之间的所有传递函数之乘积,记为 H(s)
开环传递函数:反馈引入点断开时,输入端对应比较器输出 E(s)
到输入端对应的比较器的反馈信号 B(s) 之间所有传递函数的乘 积,记为GK(s), GK(s)=G(s)H(s) E (s) C (s)
控制系统的结构图和信号流图:描述系统各元部件之间的信号传 递关系的一种图形化表示,特别对于复杂控制系统的信号传递过 程给出了一种直观的描述。
KA
Km s (T m s 1)
r
K1
系统结构图的组成与绘制
系统结构图一般有四个基本单元组成:(1)信号线; (2)引 出点(或测量点);(3)比较点(或信号综合点)表示对信号
Automatic Control Theory 2
M s C M U a (s )
2013-7-24
绳轮传动机构: L( s ) r m ( s )
测量电位器:
E (s)
E 2 ( s ) K 1 L( s )
M s (s)
CM
U a (s )
E1 ( s )
m (s) L (s )
2013-7-24 Automatic Control Theory 14
•回路 起点和终点同在一个节点上,而且信号通过每个节点不多 于一次的闭合通路(单独回路)。 •不接触回路 回路之间没有公共节点时,该回路称为不接触回路。
信号流图的绘制
(1)由微分方程绘制信号流图: RC串联电路的信号流图
u r (t ) i1 (t ) R1 u c (t ) u c (t ) i (t ) R2 1 i2 (t ) dt i1 (t ) R1 u1 (t ) C i1 (t ) i2 (t ) i (t )
之间的所有传递函数之乘积,记为 H(s)
开环传递函数:反馈引入点断开时,输入端对应比较器输出 E(s)
到输入端对应的比较器的反馈信号 B(s) 之间所有传递函数的乘 积,记为GK(s), GK(s)=G(s)H(s) E (s) C (s)
方框图的等效转换和信号流图解析

[ui (s) u(s)]
1 R1
I1(s)
I1(s) I (s) I2 (s)
R1
ui
i1
i, u
R2
i2
C1 C2
i2 uo
I(s) 1 u(s) C1s
[u(s) uo (s)]
1 R2
I 2 (s)
I 2 (s)
1 C2s
uo (s)
ui (s) -
1 I1(s) - 1 u(s)
2019
自动控制原理
5
环节的合并
(一)环节的合并:有串联、并联和反馈三种形式。
环节的串联:
X (s) G1(s) …
Y (s) Gn (s)
G(s)
Y (s) X (s)
n i 1
Gi (s)
环节的并联:
G1 ( s ) X (s)
Y (s)
Gn (s)
G(s)
Y (s) X (s)
G(s)
Sunday, October 20, 2019
自动控制原理
G(s) Y (s)
12
信号分支点的移动和互换
②信号分支点的移动: 分支点从环节的输入端移到输出端
X1(s) G(s) Y (s)
X1(s)
X1(s) G(s)
Y (s)
N(s) X1(s)
N(s) ?
X1(s)G(s)N (s)
-1
R1
方框图等效变换例子
R1C2 s
1
u(s)
C1s
1 R2C2s 1
uo (s) ②
ui (s) -
1
-
控制系统的方块图及其基本组成

Υ Υ
1
3
-
Υ 1-Υ 2+Υ 3
-
Υ2
R2 (s)
图2-15比较点示意图
Υ2
注意:进行相加减的量,必须具有相同的量刚。 (3)分支点(引出点、测量点)Branch Point 表示信号测量或引出的位置 C(s) 注意:同一位置引出的信号 R(s) P(s) G1 (s) G2 (s) 大小和性质完全一样。
注意:由于N(s)极性的随机性,因而在求E(s)时,不能认
为利用N(s)产生的误差可抵消R(s)产生的误差。 2.4.3 方块图的绘制 (1)考虑负载效应分别列写系统各元部件的微分方程或传递 函数,并将它们用方框(块)表示。 (2)根据各元部件的信号流向,用信号线依次将各方块连接 起来,便可得到系统的方块图。 系统方块图-也是系统数学模型的一种。
**
R(s)
+ -
E(s)
G1 (s)
+
+
G2 (s)
C(s)
B(s)
H(s)
打开反馈
N(s)
G1 (s)
G2 (s)
C(s)
H(s)
图2-18 输出对扰动的结构图 利用公式**,直接可得:
M N ( s) G2 ( s ) C ( s) N ( s) 1 G( s) H ( s)
(7)误差对扰动的传递函数 假设R(s)=0
(4)闭环传递函数 Closed-loop Transfer Function 假设N(s)=0 输出信号C(s)与输入信号R(s)之比。
G1 ( s)G2 ( s) C ( s) G( s) R( s) 1 H ( s)G( s) 1 H ( s)G( s)
系统的信号流图分解课件

与电路图的关系
电路图是用于描述电子系统中的电路连接和元件功能的图 表,而信号流图则关注信号在系统中的传递和处理过程。 尽管两者有所不同,但它们在某些方面具有相似性,如都 强调信号或电流的传递。
在分析电子系统时,将电路图和信号流图结合起来使用, 有助于更全面地理解系统中信号的传递和处理过程,以及 元件之间的相互关系。
在此添加您的文本16字
总结词:基本操作
在此添加您的文本16字
详细描述:在简单系统中,主要涉及基本的信号流图操作 ,如节点和边的添加、删除和修改等。
复杂系统的信号流图分解
总结词
复杂度增加
01
总结词
模块化设计
03
总结词
优化与重构
05
02
详细描述
对于复杂系统,信号流图可能变得庞大而复 杂,需要采用有效的分解策略来降低分析难 度。
信号线
连接节点和边的媒介,表示信号传递的具体 内容。
信号流图的表示方法
可以采用图形绘制软件或手绘方式进行绘制 ,要求清晰、准确、规范。
02
信号流图的分解方法
分解的目的与原则
目的
将复杂的信号流图分解为更易于理解和分析的子图,提高系统的可维护性和可扩展性。
原则
保持系统功能和性能的完整性,遵循模块化设计思想,便于后续的修改、扩展和维护。
系统的信号流图分解课件
目录
• 信号流图概述 • 信号流图的分解方法 • 信号流图分解实例 • 信号流图分解的优缺点 • 信号流图与其他系统的关系 • 总结与展望
01
信号流图概述
定义与特点
定义
信号流图是一种图形化工具,用于描 述系统的动态行为和信号传递过程。
特点
能够直观地展示系统中信号的传递、 处理和转换过程,便于对系统进行定 性和定量分析。
信号与系统-系统函数与信号流图_图文_图文

(3)反馈 等效系统函数为
对于负反馈,总有
二.信号流图
系统的信号流图是用一些点和有向线段来描述系统。变成信号流图形式 就是用线段端点代表信号,称为节点。有向线段表示信号传输的路径和方 向,一般称为支路,每一条支路上有增益,所以每一条支路相当于乘法器 。
信号流图中的节点可以有很多信号输入,它们是相加的关系, 而且可以有不同方向输出。
对于连续时间动态LTI系统的模拟,通常由加法器、标量乘 法器和积分器三种部件构成。
系统模拟可以理解为就是用这三种部件画出系统的信号流图 或是系统的方框图,使得流图或方框图实现了指定的系统函数。
四.系统模拟
例: 用加法器、标量乘法器和积分器三种部件模拟下面微分方程描
述的系统
解:首先考虑下面的系统
由线性时不变系统的性质知道存在下面关系
节点:
三.Mason公式
表示系统中的变量或信号的点称为节点。
支路:
连接两节点间的有向线段称为支路。 支路增益就是两节点间的增益。
输入节点(源点): 仅有输出支路的节点, 一 般为系统的输入。
输出节点(阱点): 仅有输入支路的节点,一般为系统的输出
混合节点:
既有输入支路又有输出支路的节点
三.Mason公式
四.系统模拟
方程两边积分三次得到
说明
是某信号积分三次得到,可以画出部分框图。
四.系统模拟
第一个积分器的输入信号实际是 可以画出部分系统框图
四.系统模拟
可以画出完整的系统框图
四.系统模拟
对应的信号流图为
其中
若 则
表示积分器(拉普拉斯变换的性质)
通路: 从任一节点出发沿着支路箭头方向连续地穿过 各相连支路到达另一节点的路径称为通路。
对于负反馈,总有
二.信号流图
系统的信号流图是用一些点和有向线段来描述系统。变成信号流图形式 就是用线段端点代表信号,称为节点。有向线段表示信号传输的路径和方 向,一般称为支路,每一条支路上有增益,所以每一条支路相当于乘法器 。
信号流图中的节点可以有很多信号输入,它们是相加的关系, 而且可以有不同方向输出。
对于连续时间动态LTI系统的模拟,通常由加法器、标量乘 法器和积分器三种部件构成。
系统模拟可以理解为就是用这三种部件画出系统的信号流图 或是系统的方框图,使得流图或方框图实现了指定的系统函数。
四.系统模拟
例: 用加法器、标量乘法器和积分器三种部件模拟下面微分方程描
述的系统
解:首先考虑下面的系统
由线性时不变系统的性质知道存在下面关系
节点:
三.Mason公式
表示系统中的变量或信号的点称为节点。
支路:
连接两节点间的有向线段称为支路。 支路增益就是两节点间的增益。
输入节点(源点): 仅有输出支路的节点, 一 般为系统的输入。
输出节点(阱点): 仅有输入支路的节点,一般为系统的输出
混合节点:
既有输入支路又有输出支路的节点
三.Mason公式
四.系统模拟
方程两边积分三次得到
说明
是某信号积分三次得到,可以画出部分框图。
四.系统模拟
第一个积分器的输入信号实际是 可以画出部分系统框图
四.系统模拟
可以画出完整的系统框图
四.系统模拟
对应的信号流图为
其中
若 则
表示积分器(拉普拉斯变换的性质)
通路: 从任一节点出发沿着支路箭头方向连续地穿过 各相连支路到达另一节点的路径称为通路。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
a0q
(t )
x (t )
方程两边积分三次得到
q(t)
a2
d 2q(t) dt2
a1
dq(t) dt
a0q(t)
x(t)dt
说明 q(t) 是某信号积分三次得到,可以画出部分框图。
q'''(t) q''(t) q'(t) q(t)
信号与系统
四.系统模拟
第一个积分器的输入信号实际是
q
不接触环路: 环路之间没有公共节点。
信号与系统
三.Mason公式
Mason公式为
M
H (s)
Y (s)
Pk (s)k (s)
k1
X (s)
(s)
其中 H (s) (s) Pk(s) k (s)
从输入节点到输出节点之间的系统函数
特征式 (s) 1 Li LiLj LiLj Lk
从输入节点到输出节点的第k条前向通路增益
X 4 X1H14 X 2 H 24 X 3H 34
信号与系统
三.Mason公式
节点: 支路:
表示系统中的变量或信号的点称为节点。
连接两节点间的有向线段称为支路。 支路增益就是两节点间的增益。
输入节点(源点): 仅有输出支路的节点, 一 般为系统的输入。
输出节点(阱点): 仅有输入支路的节点,一般为系统的输出
信号与系统
信号与系统
一.系统方框图
一个系统的方框图可由许多子系统的框图作适当联接组成。
子系统的基本联接方式有级联、并联和反馈三种。
(1)级联
(2)并联
等效系统函数为
H (s) H1(s)H2 (s)
等效系统函数为
H (s) H1(s) H2 (s)
信号与系统
一.系统方框图
(3)反馈
等效系统函数为
y(s)
X (s)
a
y(s)
信号与系统
复习:laplace变换的积分性质(page.180)
f (t) F(s)
t
f ()d
0 t
f ()d
F(s) s
F(s) 1 0
s s f ()d
信号与系统
积分器
零状态
t
y(t) x(t)dt 0
时域
x(t)
y(t)
非零状态
y(t) t x(t)dt x(1) (0) 0
混合节点:
既有输入支路又有输出支路的节点
信号与系统
三.Mason公式
通路: 从任一节点出发沿着支路箭头方向连续地穿过 各相连支路到达另一节点的路径称为通路。
前向通路: 从输入节点到输出节点的通路。
前向通路中通过任何节点不多于一次。
开通路: 如果通路与任一节点相遇不多于一次,则称为开通路。
闭通路: 如果通路的终点就是通路的起点,而且与其余节点相遇不 多于一次,则称为闭通 路、回路、环路或简称为环。
d3q(t) dt3
a2
d2q(t) dt2
a1
dq(t) dt
a0
q(t)
x(t)
由线性时不变系统的性质知道存在下面关系
d2q(t) dq(t) y(t) b2 dt2 b1 dt b0q(t)
信号与系统
信号与系统
信号与系统
四.系统模拟
d
3q(t) dt3
a2
d
2q(t) dt2
a1
dq(t) dt
H(s)1Fra bibliotekH1(s) H1(s)H2
(s)
对于负反馈,总有
H(s)
H1(s)
1 H1(s)H2(s)
对于负反馈,总有
H(s)
H1(s)
1 H1(s)H2(s)
信号与系统
一.系统方框图
基本运算器模型
加法器
x1(t) x2 (t)
标量乘 法器
x(t)
a
y(t)
t域
y(t)
X1(s) s 域 X2 (s)
其中L1、L2,L1、L3是两两不接触的回路,没有三三不接触的回路。
信号与系统
三.Mason公式
所以流图的特征式为
1 (H2G2 H4G4 H5G5 H2 H3 H4 H5G1) (H2 H4G2G4 H2G2 H5G5 )
前向通路只有一条,即
X X 1 X 2 X 3 X 4 Y
四.系统模拟
对应的信号流图为
1 其中 s 表示积分器(拉普拉斯变换的性质)
信号与系统
二.信号流图
系统的信号流图是用一些点和有向线段来描述系统。变成信号流图形式 就是用线段端点代表信号,称为节点。有向线段表示信号传输的路径和方
向,一般称为支路,所以每一条支路相当于乘法器。
信号流图中的节点可以有很多信号输入,它们是相加的 关系,而且可以有不同方向输出。
三条前向通路之(2)
X X1 X4 Y
P2 H1H 5H 6
2 1
信号与系统
三.Mason公式
三条前向通路之(3)
X X 1 X2 Y
P3 H1 H 2 H 7
所以系统函数为
3 1 H4G1
H
H1H 2 H 3H 4 H5 H1H5 H 6 H1H 2 H 7 1 H 4G1
信号与系统
三.Mason公式
例: 用Mason公式求图所示系统的系统函数
解:先求环路,一共有4个环路,即 L1 ( X 3 X 4 X 3 ) H4G1
L2 ( X1 X 2 X 3 X 4 Y X1 ) H2 H3 H4 H5G2 L3 ( X1 X 4 Y X1 ) H5 H6G2 L4 ( X1 X 2 Y X1 ) H2 H7G2
'(t)
x(t)
a2
d 2q(t) dt2
a1
dq(t dt
)
a0q
(t
)
可以画出部分系统框图
q dq q
信号与系统
四.系统模拟
d 2q(t) dq(t) y(t) b2 dt2 b1 dt b0q(t)
可以画出完整的系统框图
b2
b1
x(t)
yq1t
b0
y(t)
a2 a1 a0
信号与系统
信号与系统
信号与系统
四.系统模拟
例: 用加法器、标量乘法器和积分器三种部件模拟下面微分方程描
述的系统,即画出该系统的时域和s域模拟图,并求解系统函数。
d3 y(t) dt3
a2
d2 y(t) dt2
a1
dy(t) dt
a0
y(t )
b2
d2 x(t) dt2
b1
dx(t) dt
b0 x(t)
解:首先考虑下面的系统
k1
X (s)
(s)
Ø 系统模拟(t s )
x(1) (0)
x(t)
y(t)
x(1) (0)
s域 X (s) 1 Y (s)
s
s
X (s)
1 s
Y (s)
信号与系统
四.系统模拟
系统模拟指用一些标准的部件通过一定的连接方式实 现同样的系统函数。 对于连续时间动态LTI系统的模拟,通常由加法器、 标量乘法器和积分器三种部件构成。 系统模拟可以理解为就是用这三种部件画出系统的信 号流图或是系统的方框图,使得流图或方框图实现了 同样的系统函数。
其中L1、L4是两两不接触的回路
信号与系统
三.Mason公式
可以求得流图的特征式
1 H4G1 H 2 H 3H 4 H 5G2 H 5H 6G2 H 2 H 7G2 H 2 H 4 H 7G1G2
三条前向通路之(1)
P1 H1H 2 H 3H 4 H5
X X1 X 2 X 3 X 4 Y 1 1 0 0 1
所有回路都和这条前向通路接触,所以
P1 H1H 2 H3H 4H5 1 1 0 0 1
信号与系统
三.Mason公式
系统函数为
H
H1H 2H3H4H5
1 H2G2 H 4G4 H 5G5 H 2 H 3H 4 H 5G1 H 2 H 4G2G4 H 2 G2H 5G 5
1 H4G1 H 2 H 3H 4 H 5G2 H 5H 6G2 H 2 H 7G2 H 2 H 4 H 7G 1G2
信号与系统
课程小结
Ø 系统方框图
级联、并联、反馈
Ø 信号流图
节点、支路、增益、通路、环路......
Ø Mason公式
M
H (s)
Y (s)
Pk (s)k (s)
在 (s) 中,将与第k条前向通路相接触
的回路所在项去掉后余下的部分
Li
所有不同回路增益之和
Li Lj 所有两两互不接触回路增益乘积之和
Li Lj Lk 所有三个互不接触回路增益乘积之和
信号与系统
三.Mason公式
例:用Mason公式求图所示系统的系统函数
解:先求环路,一共有4个环路,即 L1 H 2G2 L2 H 4G4 L3 H 5G5 L4 H 2 H 3H 4 H5G1
