统计模式识别方法
统计模式识别 统计分类方法

统计模式识别统计分类方法
统计模式识别是一种常见的机器学习算法,用于对未知模式和统
计模式进行学习。
它可以使用模式的历史记录和观察结果来预测未来
模式的行为。
该技术也被称为统计分类,用于解决分类和分组问题,
其目的是根据现有的统计数据来评估一个特定的类别的可能性。
统计模式识别基于概率统计理论,可对数据进行分析并扩展到传
统模式识别范围之外,以解决复杂问题。
它可以用于分类多维数据,
识别新类别或模式,并帮助训练机器学习模型,使用有效的特征提取
和结构学习算法。
它提供一种新的方法,通过有效的表示和分类模型,来表示实体和相关的对象。
与其他分类算法相比,统计模式识别的有点是它'数据挖掘'的概念,在这种类型的模式识别中,模式数据是根据观察数据一直进行改
变的,没有预先定义模式及其功能,它根据具有可利用自学能力的方
法逐渐改善。
统计模式识别非常重要,因为它可以帮助我们找到自动化解决方
案来实现更多基于数据的智能分析和决策,从而增强分析模型的能力,例如,可以使用该技术识别股票市场及其他金融市场的模式变化,以
便于能够更高效地进行投资决定。
它也可以应用于诊断和分析少量样
本事件,进而对学习和决策进行调节和优化。
什么是模式识别模式识别的方法与应用

什么是模式识别模式识别的方法与应用模式识别是通过计算机用数学技术方法来研究模式的自动处理和判读。
那么你对模式识别了解多少呢?以下是由店铺整理关于什么是模式识别的内容,希望大家喜欢!模式识别的简介模式识别(英语:Pattern Recognition),就是通过计算机用数学技术方法来研究模式的自动处理和判读。
我们把环境与客体统称为“模式”。
随着计算机技术的发展,人类有可能研究复杂的信息处理过程。
信息处理过程的一个重要形式是生命体对环境及客体的识别。
对人类来说,特别重要的是对光学信息(通过视觉器官来获得)和声学信息(通过听觉器官来获得)的识别。
这是模式识别的两个重要方面。
市场上可见到的代表性产品有光学字符识别、语音识别系统。
人们在观察事物或现象的时候,常常要寻找它与其他事物或现象的不同之处,并根据一定的目的把各个相似的但又不完全相同的事物或现象组成一类。
字符识别就是一个典型的例子。
例如数字“4”可以有各种写法,但都属于同一类别。
更为重要的是,即使对于某种写法的“4”,以前虽未见过,也能把它分到“4”所属的这一类别。
人脑的这种思维能力就构成了“模式”的概念。
在上述例子中,模式和集合的概念是分未弄的,只要认识这个集合中的有限数量的事物或现象,就可以识别属于这个集合的任意多的事物或现象。
为了强调从一些个别的事物或现象推断出事物或现象的总体,我们把这样一些个别的事物或现象叫作各个模式。
也有的学者认为应该把整个的类别叫作模去,这样的“模式”是一种抽象化的概念,如“房屋”等都是“模式”,而把具体的对象,如人民大会堂,叫作“房屋”这类模式中的一个样本。
这种名词上的不同含义是容易从上下文中弄淸楚的。
模式识别是人类的一项基本智能,在日常生活中,人们经常在进行“模式识别”。
随着20世纪40年代计算机的出现以及50年代人工智能的兴起,人们当然也希望能用计算机来代替或扩展人类的部分脑力劳动。
(计算机)模式识别在20世纪60年代初迅速发展并成为一门新学科。
[数学]模式识别方法总结
![[数学]模式识别方法总结](https://img.taocdn.com/s3/m/9bfe35a6a0116c175f0e484a.png)
假定有m个类别ω1, ω2, …, ωm的模式识别问题,
每类有Ni(i=1, 2, …, m)个样本, 规定类ωi的判别函数
为
gi (x) min x xik
i
k 1, 2,
, Ni
其中, xki表示第i类的第k个元素。 判决准则: gi (x) ,则x∈ω 若 g j (x) i min j 1,2, , m
定义Fisher线性判决函数为
( 1 2 )2 J F (w ) S1 S2
分子反映了映射后两类中心的距离平方,
该值越大, 类间可
分性越好;
分母反映了两类的类内离散度,
从总体上来讲,
其值越小越好;
JF(w)的值越大越好。 使JF(w)达到最大值的w即为最
在这种可分性评价标准下,
如果P(ω1|x)<P(ω2|x), 则判决x属于ω2;
如果P(ω1|x)=P(ω2|x), 则判决x属于ω1或属于ω2。
这种决策称为最大后验概率判决准则, 也称为贝叶斯 (Bayes)判决准则。 假设已知P(ωi)和p(x|ωi)(i=1, 2, …, m), 最大后验概率判 决准则就是把样本x归入后验概率最大的类别中, 也就是,
0
Sigmoid (a) 取值在(0, 1)内; (b) 取值在(-1, 1)内
神经网络结构 神经网络是由大量的人工神经元广泛互连而成 的网络。 根据网络的拓扑结构不同, 神经网络可分
R( j | x) ( j , i ) P(i | x)
i 1 m
最小风险贝叶斯判决准则: 如果
R( k | x) min R( j | x)
j 1, 2 ,, m
使用人工智能开发技术进行模式识别的方法

使用人工智能开发技术进行模式识别的方法引言:随着人工智能技术的迅猛发展,机器学习和模式识别成为了研究热点。
人们意识到,通过使用人工智能开发技术,可以帮助从大量的数据中提取有用的信息和模式。
本文就将介绍一些使用人工智能进行模式识别的方法。
一、传统模式识别方法在了解使用人工智能进行模式识别的方法之前,我们可以先了解一下传统的模式识别方法。
传统模式识别方法主要包括统计模式识别和基于特征的模式识别。
1. 统计模式识别统计模式识别是通过对样本数据的统计分析,来确定模式的类别和属性。
其中,常用的方法包括贝叶斯分类器、最近邻分类器和聚类算法等。
然而,传统的统计模式识别方法存在着参数设定困难、效率低下和对样本数据要求较高等问题。
2. 基于特征的模式识别基于特征的模式识别方法是通过对样本数据的特征进行提取和选择,来确定模式的类别和属性。
其中,常用的方法包括主成分分析、线性判别分析和支持向量机等。
尽管基于特征的模式识别方法在一定程度上解决了参数设定困难的问题,但它们仍然面临着特征提取和选择的复杂性。
二、深度学习在模式识别中的应用深度学习作为一种人工智能技术,近年来在模式识别中得到广泛应用。
它通过模拟人脑神经网络的工作原理,学习和提取数据中的高级特征,从而实现更准确的模式识别。
深度学习的核心是神经网络模型(Neural Network Model)。
神经网络包括输入层、隐藏层和输出层,每个神经元将输入的信号传递给下一层。
通过调整神经网络中的连接权值,使得网络能够从输入数据中提取更高级的特征。
深度学习中的常用模型包括卷积神经网络(Convolutional Neural Network,CNN)和循环神经网络(Recurrent Neural Network,RNN)。
CNN主要用于图像、语音等具有拓扑结构的数据的模式识别,而RNN主要用于序列型数据(如时间序列)的模式识别。
三、人工神经网络的训练方法人工神经网络的训练是指通过调整神经网络中的连接权值,使得网络能够准确地识别模式。
模式识别在工业自动化中的应用

模式识别在工业自动化中的应用工业自动化是指通过自动化设备和技术手段实现对工业生产过程中各种物理、化学、生物过程的自动控制。
近年来,随着计算机技术和人工智能的迅速发展,模式识别在工业自动化领域中的应用日益广泛。
本文将探讨模式识别在工业自动化中的应用背景、主要方法和前景展望。
一、应用背景工业自动化生产过程中常涉及大量的数据,包括传感器采集的物理量、生产线上的图像和视频等等。
这些数据通常非常复杂,很难通过传统的手动分析方法进行有效处理。
而模式识别作为一种强大的数据处理工具,可以帮助工业自动化系统实现高效的数据分析和异常检测。
二、主要方法1. 统计模式识别:统计模式识别是一种基于概率统计原理的模式识别方法。
通过分析和建模数据的概率分布,可以对未知数据进行分类、聚类和异常检测等操作。
在工业自动化中,统计模式识别常用于故障检测和质量控制等领域。
2. 机器学习:机器学习是一种通过训练数据来学习和建立模型,并通过已学习的模型对新数据进行分类、预测和决策的方法。
在工业自动化中,机器学习被广泛应用于生产线上的监测和控制、生产计划优化等方面。
例如,利用机器学习算法可以构建预测模型,准确预测材料消耗和产品质量等指标,帮助企业进行生产计划的优化和资源的合理配置。
3. 深度学习:深度学习是机器学习的一种分支,通过构建深层神经网络模型,实现对复杂非线性问题的高效处理。
在工业自动化中,深度学习被广泛应用于图像和视频处理、声音识别等方面。
例如,利用深度学习算法可以实现图像识别技术,对生产过程中的缺陷进行自动检测和分类,大大提高了产品质量的稳定性和生产线的效率。
三、前景展望随着工业自动化技术的不断发展和深化,模式识别在工业自动化中的应用前景非常广阔。
首先,工业生产过程中的数据量和复杂度会不断增加,对高效的数据处理和分析提出更高要求,而模式识别技术正好可以满足这一需求。
其次,随着人工智能技术的进一步突破,模式识别算法和模型的性能将大幅提升,对更广泛的工业场景进行应用也将变得更加可行和有效。
3.3识别与解释
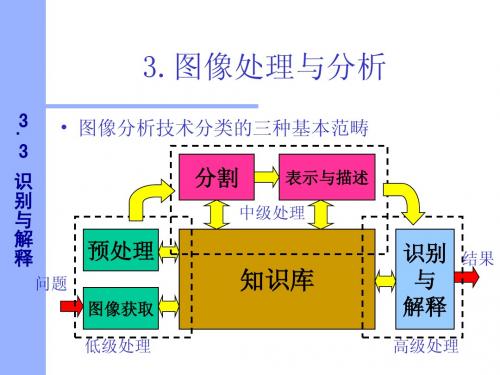
x2 花瓣宽 3.0 2.5 2.0 1.5 1.0 0.5 1 2 3 4 5 6 7 x1 花瓣长 多毛的 维吉尼亚 多色的
3.3.1 模式与模式类
3 . . . . 3 识 别 与 解 释 –模式特征向量举例:分析 模式特征向量举例: 模式特征向量举例
一般特征向量的选择方法
– 尽量不选择带噪声和相关度高的特征 – 先选择一组直觉上合理的特征,然后逐渐减少到最佳 先选择一组直觉上合理的特征,
3.3.1 模式与模式类
3 . . . . 3 识 别 与 解 释 2)模式串 2)模式串 用于以对象特征的结构或空间关系作为 模式的识别 –模式串举例:梯状的模式 模式串举例: 模式串举例
3.3.2统计模式识别 统计模式识别
3 3 识 别 与 解 释
3. 分类器
–最小距离分类器 最小距离分类器 以蝴蝶花的例子为例: 以蝴蝶花的例子为例:
为多色( 和多毛( 的两种蝴蝶花, (1)为多色(w1)和多毛(w2 )的两种蝴蝶花, 确定两个原形 或称模板) 原形( 确定两个原形(或称模板)m1和m2 对于一个未知模式向量x 判断x (2 ) 对于一个未知模式向量x , 判断 x与 m1 和m2 的 距离, 如果与m 的距离小于与m 的距离, 距离 , 如果与 m1 的距离小于与 m2 的距离 , 则 x 属 否则属于w 于w1,否则属于w2 。
a
S(1) S->aA A(2) A->bS A(3) A->b
a b
b
a b a b
3.3.1 模式与模式类
3 3 识 别 与 解 释 3)模式树 3)模式树
以分层目录结构排序的模式类, 以分层目录结构排序的模式类,一般多采用树结构
统计模式识别简介

监督参数统计法
• KNN法( K最近邻法) • Fisher判别分析法
K最近邻法
• KNN法,也称K最近邻法,是模式识别的标准算法之一。 • 其基本原理是先将已经分好类别的训练样本点“记入” 多维空间中,然后将待分类的未知样本也记入空间。考 察未知样本的K个近邻,若近邻中某一类样本最多,则 可以将未知样本也判为该类。在多维空间中,各点间的 距离通常规定为欧几里得空间距离。KNN法的好处是它 对数据结构没有特定的要求,只要用每个未知点的近邻 属性类来判别就行了;KNN法也不需要训练过程。KNN 法的一个缺点就是它没有对训练点作信息压缩,因此每 判断一个新的未知点都要将所有对已知点的距离全部算 一遍,计算工作量较大。一种简化的算法称为类重心法, 即将训练中每类样本点的重心求出,然后判别未知样本 点与各类的重心的距离;未知样本与哪一类重心距离最 近,
最小风险贝叶斯判别准则
• • 在实际工作中,有时仅考虑错误率最小是 不够的。要引入比错误率更广泛的概念— 风险、损失。 • 如果在采取每一决策时,其条件风险都最 小,则对所有的x作决策时,其平均(期望 风险)也最小。称为最小风险的贝叶斯决 策。
• 在决策理论中,称所采取的决定为决策或 行动。每个决策或行动都会带来一定的损 失。该损失用λ表示,它是与本该属于wi但 采取的决策为αj所造成的损失有关。由此定 义损失函数为λ(αj| wi)=λij(i,j=1,2, …,R)。 对样本X属于wi,有贝叶斯公式已知后验概率 为P(wi|X)
• 假使在特征空间中规定某种距离度量,从直观 上看,两点之间的距离越小,它们所对应的模 式就越相似。在理想的情况下,不同类的两个 模式之间的距离要大于同一类的两个模式之间 的距离,同一类的两点间连接线上各点所对应 的模式应属于同一类。一个畸变不大的模式所 对应的点应紧邻没有畸变时该模式所对应的点。 在这些条件下,可以准确地把特征空间划分为 同各个类别相对应的区域。在不满足上述条件 时,可以对每个特征向量估计其属于某一类的 概率,而把有最大概率值的那一类作为该点所 属的类别。
几种统计模式识别方案的比较

几种统计模式识别方案的比较摘要:模式识别是对表征事物或现象的各种形式的(数值的,文字的和逻辑关系的)信息进行处理和分析,以达到对事物或现象进行描述、辨认、分类和解释的目的,是信息科学和人工智能的重要组成部分。
而统计决策理论是处理模式分类问题的基本理论之一,它对模式分析和分类器的设计有着实际的指导意义。
本文归纳总结了统计模式识别的不同方案的详细性能,比较了它们的原理、算法、属性、应用场合、错误率等。
关键词:统计模式识别贝叶斯决策方法几何分类法监督参数统计法非监督参数统计法聚类分析法Comparison of Several Kinds of Statistical Pattern Recognit ion SchemesAbstract: Pattern recognition deals with and analyses the i nformation which signify all kinds of things and phenomena (number values, Characters and logic relation), in order to describe, recognize, classify and interpret them. It is on e of the important parts of information science and artific ial intelligence. While statistical pattern recognition is one of the basics theory of classifying and is real directi ve significance in analyzing and classifying of pattern. Wesum up the detailed performance of summarizing different s chemes which counts the pattern recognition in this text, C ompare their principle, algorithm, attribute, using occasio n, etc.1引言模式识别诞生于20世纪20年代,随着40年代计算机的出现,50年代人工智能的兴起,模式识别在60年代初迅速发展成为一门学科。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
统计模式识别方法
在嗅觉模拟技术领域中,模式识别问题就是由气敏传感器阵列的测量空间向被测对象的的分类或分级空间转化的问题。
由于这种模式空间的变化对识别或鉴别结果有着较大的影响,因此模式识别算法的研究和讨论始终较为活跃,各种模式识别方法层出不穷,有力推动了嗅觉模拟技术的应用进程。
下面介绍几种常用的统计模式识别方法。
1统计模式识别概述
统计方法,是发展较早也比较成熟的一种方法。
被识别对象首先数字化,变换为适于计算机处理的数字信息。
一个模式常常要用很大的信息量来表示。
许多模式识别系统在数字化环节之后还进行预处理,用于除去混入的干扰信息并减少某些变形和失真。
随后是进行特征抽取,即从数字化后或预处理后的输入模式中抽取一组特征。
所谓特征是选定的一种度量,它对于一般的变形和失真保持不变或几乎不变,并且只含尽可能少的冗余信息。
特征抽取过程将输入模式从对象空间映射到特征空间。
这时,模式可用特征空间中的一个点或一个特征矢量表示。
这种映射不仅压缩了信息量,而且易于分类。
在决策理论方法中,特征抽取占有重要的地位,但尚无通用的理论指导,只能通过分析具体识别对象决定选取何种特征。
特征抽取后可进行分类,即从特征空间再映射到决策空间。
为此而引入鉴别函数,由特征矢量计算出相应于各类别的鉴别函数值,通过鉴别函数值的比较实行分类。
统计模式识别的技术理论较完善,方法也很多,通常较为有效,现已形成了一个完整的体系。
尽管方法很多,但从根本上讲,都是利用各类的分布特征,即直接利用各类的概率密度函数、后验概率等,或隐含地利用上述概念进行识别。
其中基本的技术为聚类分析法、判别类域代数界面法、统计决策法、最邻近法等。
在聚类分析中,利用待分类模式之间的“相似性”进行分类,较相似的作为一类,较不相似的作为另外一类。
在分类过程中不断地计算所划分的各类的中心,一个待分类模式与各类中心的距离作为对其分类的依据。
这实际上在某些设定下隐含地利用了概率分布概念,因常见的概率密度函数中,距期望值较近的点概密值较大。
该类方法的另一种技术是根据待分类模式和已指判出类别的模式的距离来确定其判别,这实际上也是在一定程度上利用了有关的概念。
判别类域界面法中,用已知类别的训练样本产生判别函数,这相当于学习或训练。
根据待分类模式
代入判别函数后所得值的正负来确定其类别。
判别函数提供了相邻两类判别域的界面,其也相应于在一些设定下两类概密函数之差。
在统计判决中,在一些分类识别准则下严格地按照概率统计理论导出各种判决规则,这些判决规则可以产生某种意义上的最优分类识别结果。
这些判决规则要用到各类的概率密度函数、先验概率或后验概率。
这可以通过训练样本对未知概率密度函数中的参数进行估计,或对未知的概密函数等进行逼近而估计他们。
在最邻近法中,是根据待分类模式的一个或k 个近邻样本的类别而确定其类别。
2 主成分分析方法
主成分分析是一种掌握事物主要矛盾的统计分析方法,也是一种古老的多元统计分析技术。
它可以从多元事物中解析出主要影响因素,揭示事物的本质,简化复杂的问题。
计算主成分的目的是将高维数据投影到较低维空间。
给定 n 个变量的m 个观察值,形成一个 n x m 的数据矩阵,n 通常比较大。
对于一个由多个变量描述的复杂事物,人们难以认识,那么是否可以抓住事物主要方面进行重点分析呢?如果事物的主要方面刚好体现在几个主要变量上,我们只需要将这几个变量分离出来,进行详细分析。
但是,在一般情况下,并不能直接找出这样的关键变量。
这时我们可以用原有变量的线性组合来表示事物的主要方面,PCA 就是这样一种分析方法。
PCA 的目标是寻找 r (r<n )个新变量,使它们反映事物的主要特征,压缩原有数据矩阵的规模。
每个新变量是原有变量的线性组合,体现原有变量的综合效果,具有一定的实际含义。
这r 个新变量称为“主成分”,它们可以在很大程度上反映原来n 个变量的影响,并且这些新变量是互不相关的,也是正交的。
通过主成分分析,压缩数据空间,将多元数据的特征在低维空间里直观地表示出来。
例如,将多个时间点、多个实验条件下的基因表达谱数据(N 维)表示为3维空间中的一个点,即将数据的维数从 N R 降到 3R 。
PCA 的算法步骤
设相关矩阵为Rp×p ,求特征方程0=-i R λ,其解为特征根λi 将解由小到大进行排序为:
1. 求样本数据矩阵X 的协方差矩阵。
2. 求协方差矩阵
的特征值,并按降序排列, 如 3. 求对应于各特征值的单位特征向量 , ,…, 并作相应的主
轴。
120
p λλλ≥≥≥>∑∑120p λλλ≥≥≥>2u 1u
4. 按下式计算某个特征值的贡献率 :
5. 根据各特征值贡献率的大小,依次选取所需要的第一主轴,第二主轴,
直至第m 主轴。
6. 利用下式计算样本数据矩阵X 的第i 主成分Yi :
在应用时,一般取累计贡献率为80%以上比较好。
3 近邻法
KNN 法也称K 最近邻法,是模式识别的标准算法之一,属于有监督(或称有导师)的模式识别方法。
其基本思想是,先将已知类别或等级的样本点在多维空间中描述出来,然后将待分类的未知样本点也用同样的多维空间加以描述。
考察未知样本点的K 个近邻(K 为奇正数,如1,3,5,7等)。
若近邻中某一类或某一等级的样本点最多,则可将未知样本点判为此类获此等级中的点。
在多维空间中,各样本点的距离通常用欧氏距离来描述: 21
12
)(),(∑=-=n i i i y x
y x d 式中,),(y x d 是未知类别(或等级)样本点x 到已知类别(或等级)样本点y 的欧氏距离;n 是多维空间的维数;i x 是x 的第i 维分量;i y 是y 的第i 维分量。
有时为了计算方便,也采用绝对距离来描述:
∑=-=n i i i y x
y x d 1),(
当然,也可用其他距离或度量来描述多维空间中两样本点的距离(如马氏距离等)。
KNN 法的好处是,它对数据结构没有特定的要求,如不要求线性可分性,只需用每个每个未知样本点的近邻类别或等级属性来判别即可。
这种方法的缺点是没有对样本点进行信息压缩。
因此,每当判别一个新样本点时都要对已知样本点的距离全部计算一遍,计算量较大。
一种简化的算法称为类重心法:将已知类别或等级的样本点重心求出,然后判别未知样本点与各重心点的距离。
未知样本点与哪一个重心距离最近,即可将未知样本点归属于哪一类或哪一等级。
i ν1100%i p
j
j λλ=⨯∑m i X u i T i ,...,2,1,Y ==。
