最新奥数巧求面积
四年级下册数学奥数思维训练(第5讲)巧求面积
第5讲 巧求面积
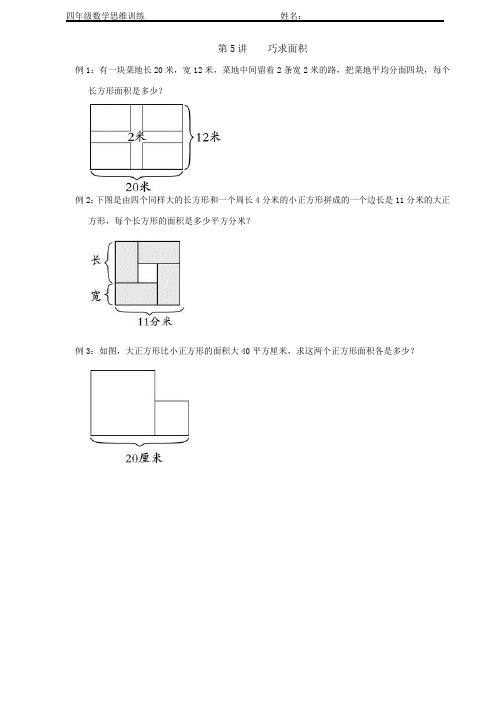
例1:有一块菜地长20米,宽12米,菜地中间留着2条宽2米的路,把菜地平均分面四块,每个长方形面积是多少?
例2:下图是由四个同样大的长方形和一个周长4分米的小正方形拼成的一个边长是11分米的大正方形,每个长方形的面积是多少平方分米?
例3:如图,大正方形比小正方形的面积大40平方厘米,求这两个正方形面积各是多少?
四年级数学思维训练
姓名:
练习
1、有一块长方形的土地,长是宽的2倍,中间有一座雕塑,这个雕塑的底面是一个正方形,周围
是草坪,这个草坪的面积是多少平方米?
2、求图中正方形中阴影部份的面积?
3、四个一样的长方形和一个小正方形拼成一个大正方形,小正方形的边长是2厘米,大正方形边
长是小正方形边长的4倍。
求每个长方形的面积分别是多少平方厘米?
4、两个正方形的边长和为18分米,它们的面积差为36平方分米,求这两个正方形面积各是多少?
5、求下图中阴影部份的面积是多少?。
六年级奥数——巧求面积(附习题及解答)

第五讲 巧求面积本讲主要介绍平面图形面积的一些巧妙算法,首先看一个例子.如图,BC=CE,AD=CD,求三角形ABC的面积是三角形CDE面积的几倍?解:连结BD,在△ABD与△BCD中,因为AD=DC,又因为这两个三角形的高是同一条高,所以S△ABD=S△BCD.在△BCD与△DCE中,因为BC=CE,又因为这两个三角形也具有同一条高,所以有S△BCD=S△CDE.因此,S△ABC=S△ABD+S△BCD=2S△CDE. 从以上的推导中看一看这两个三角形面积之比与这两个三角形的边有什么关系.CE于M,如右图,在△ACM与△DCN中,有AC∶CD=AM∶DN.因此,即,当两个三角形各有一个角,它们的和是180°时,这两个三角形的面积之比等于分别夹这两个角的两条边的长度乘积之比.类似可知,当两个三角形各有一个角,它们相等时,这个结论也成立.解:在△ABC与△CDE中,因为AD=DC,所以 AC=2CD,又因为BC=CE,所以S△ABC=2×1×S△CDE=2S△CDE.答:△ABC的面积是△CDE面积的2倍.下面我们就应用上面这个结论来看几个具体例子.例1 如图,三角形ABC的面积为1,并且AE=3AB,BD=2BC,那么△BDE的面积是多少?解:在△BDE与△ABC中,∠DBE+∠ABC=180°.因为AE=3AB,所以BE=2AB.又因为BD=2BC,所以S△BDE=2×2×S△ABC=4×1=4.答:△BDE的面积是4.例2 如图,在△ABC中,AB是AD的6倍,AC是AE的3倍.如果△ADE的面积等于1平方厘米,那么△ABC的面积是多少?解:在△ABC与△ADE中,∠BAC=∠DAE.因为AB=6AD,AC=3AE,所以S△ABC=6×3×S△ADE=18×1=18(平方厘米).答:△ABC的面积为 18平方厘米.例3 如图,将△ABC的各边都延长一倍至 A′、 B′、 C′,连接这些点,得到一个新的三角形A′B′C′.若△ABC的面积为1,求△A′B′C′的面积.解:在△A′B′B与△ABC中,∠A′BB′+∠ABC=180°.因为 AB=AA′,所以A′B=2AB,又因为B′B=BC,所以S△A′B′B=1×2×S△ABC=2S△ABC=2.同理S△B′C′C=2×1×S△ABC=2.S△A′C′A=2×1×S△ABC=2.所以S△A′B′C′=S△A′B′B+S△B′C′C+S△A′C′A+S△ABC=2+2+2+1=7答:△A′B′C′的面积为7.例4 如下图,将凸四边形ABCD的各边都延长一倍至 A′、B′、 C′、D′,连接这些点得到一个新的四边形A′B′C′D′,若四边形A′B′C′D′的面积为30平方厘米,那么四边形ABCD的面积是多少?分析 要求四边形ABCD的面积,必须求出四边形ABCD与四边形A′B′C′D′的关系,因而就要求出△A′B′B、△B′C′C、△C′D′D、△A′D′A与四边形ABCD的关系.解:连结AC、BD.在△A′B′B与△ABC中,∠A′BB′+∠ABC=180°.因为A′A=AB,所以A′B=2AB,又因为 B′B=BC,所以有S△A′B′B=2×1×S△ABC=2S△ABC.同理 有S△B′C′C=2×1×S△BCD=2S△BCDS△C′D′D=2×1×S△ADC=2S△ADCS△A′D′A=2×1×S△ABD=2S△ABD.所以 S四边形A′B′C′D′=S△A′B′B+S△B′C′C+S△C′D′D+S△A′D′A+S四边形ABCD =2S△ABC+2S△BCD+2S△ADC+2S△ABD+S四边形ABCD=2(S△ABC+S△ADC)+2(S△BCD+S△ABD)+S四边形ABCD=2S四边形ABCD+2S四边形ABCD+S四边形ABCD=5S四边形ABCD则S四边形ABCD=30÷5=6(平方厘米).答:四边形ABCD的面积为6平方厘米.B1C1=C1C,△A1B1C1的面积为1平方厘米,则△ABC的面积为多少平方厘米?解:连接A1C.如上图在△BB1C与△A1B1C1中,∠BB1C+∠A1B1C1=180°,因为A1B1=所以有S△BB1C=2×2×S△A1B1C1=4×1=4(平方厘米).在△A1C1C与△A1B1C1中,∠A1C1C+∠A1C1B1=180°,因为CC1=C1B1,A1C1=A1C1,所以有S△A1C1C=1×1×S△A1B1C1=1×1=1(平方厘米).在△ABD与△ADC中,∠ADB+∠ADC=180°.因为BD=DC,在△ABA1与△ABD中,∠BAA1=∠BAD.因为AB=AB,AA1=答:三角形ABC的面积为9平方厘米.习 题 五四边形DBCE的面积.(下图)2.下图中的三角形被分成了甲(阴影部分)、乙两部分,图中的数字是相应线段的长度,求两部分的面积之比.GA,求阴影部分面积占三角形ABC面积的几分之几?厘米,AE=11厘米,三角形DAE的面积是多少?的面积与三角形ABC 的面积之比.(下图)与三角形DEF的面积之比.7.如下图所示,把△ABC的BA边延长1倍到D点,AC边延长3倍到F点,CB边延长2倍到E点,连接DE、EF、FD,得到△DEF.已知三角形DEF的面积为54平方厘米,求△ABC的面积.的面积.9.在△ABC中,CD、AE、BF分别为BC、AC、AB长10.把边长为40厘米的正方形ABCD沿对角线AC截成两个三角形,在两个三角形内按图示剪下两个内接正方形M、N.这两个正方形中面积较大的是哪一个?它比较小的正方形面积大多少平方厘米?习题五解答因为CD=1,DB=3,所以BC=1+3=4=4CD.所以S乙=S△ABC-S甲=6S甲-S甲=5S甲.所以S甲∶S乙=S甲∶5S甲=1∶5.答:甲乙两部分的面积之比为1∶5.3.解:利用正文中的结论容易求得:答:△ADE的面积为22平方厘米.所以S△DEF∶S△ABC=61∶120.答:△DEF与△ABC的面积之比为61∶120.S△ABE∶S△EDF=3∶4.答:三角形ABE与三角形EDF的面积之比为3∶4.7.解:S△ADF=4×1×S△ABC=4S△ABC,S△BED=2×2×S△ABC=4S△ABC,S△ECF=3×3×S△ABC=9S△ABC.所以S△DEF=S△ADF+S△EBD+S△ECF+S△ABC=4S△ABC+4S△ABC+9S△ABC+S△ABC=18S△ABC答:三角形ABC的面积为3平方厘米.8.解:连DF.因为AE=ED,所以有S△ABE=S△BED,S△AEF=S△DEF.所以S△BEA+S△AEF=S△BED+S△DEF=S△BDF=S阴影所以S△ABC=S△ABF+S△BDF+S△CDF9.解:记S1=S△AEN2,S2=S△BFN3,S3=S△CDN1,S=S△N1N2N3.由下图知S△ABE+S△BCF+S△CAD+S=S△ABC+S1+S2+S3但是S△ABE=S△BCF所以 S=S1+S2+S3.连结CN2,则即S△N1N2N3∶S△ABC=1∶7.答:S△N1N2N3与S△ABC之比为1∶7.10.解:为了方便,在下图中标上字母E、F、G、H、M1、N1、K,连结DK.页码,5/5习题五解答2011-10-28 ada99:11240_SR.HTM。
巧奥数巧算面积(课堂PPT)

12÷4=3(平方米)。
因为水泥路宽1米,所以小长方形的长是:
3÷1=3(米)。
中间花坛的面积是:(3+1)×(3+1) -4×3=4(平方米)
12
做一做 5
问题 如下图,有一个正方形水池(图中阴影部分), 在它的周围修一个宽是8米的草地,草地的面 积为480平方米。 求水池的边长。
答案
13
如下图①,正方形的边长为12厘米。
小
奥
学
数
巧算面积
1
四年级奥数- 基础点睛 巧算面积
解答比较复杂的关于长方形、正方形的周长和面积的计算问题时,不能生搬硬 套公式,需要运用移位、合并、分解、转化等解题技巧。因此,敏锐的观察力 和灵活的思维在解题中至关重要。
2
例题1
下图①是一块长方形草地,长方形长255米,宽的,一条是平行四边形的。
问有草部分的面积是多少?
答案
将上图①中的四块阴影部分平移,拼在一起,组成 一个长、宽各少5米的长方形(如上图②阴影部 分)。 (255-5)×(105-5)=25000(平方米)
3
如下图所示,一块长方形草地,长100米,宽80米,中间 有条宽4米的道路,求草地(阴影部分)的面积。
做一做 1
问题
4
求下图的面积。(单位:厘米)
10
做一做 4
问题 有9个小长方形,它们的长和宽分别相等,用这9个小长形拼成的 大长方形(如下图)的周长是29厘米,求这个大长方形的面积。
答案
11
例题5
一个正方形的花坛,四周有1米宽的水泥路 (如右图①), 问题 如果水泥路的总面积是12平方米, 问中间花坛的面积是多少平方米?
答案
把水泥路的部分分成四个同样大小的长 方形(如右图②)。每个长方形的面积是:
奥数-巧求面积
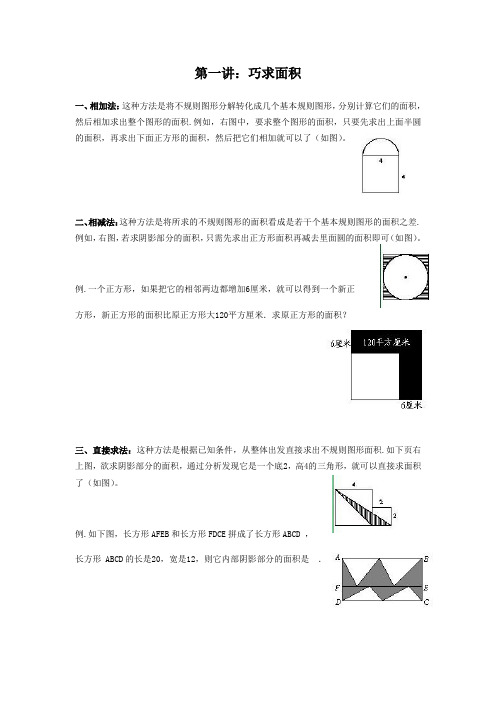
第一讲:巧求面积一、相加法:这种方法是将不规则图形分解转化成几个基本规则图形,分别计算它们的面积,然后相加求出整个图形的面积.例如,右图中,要求整个图形的面积,只要先求出上面半圆的面积,再求出下面正方形的面积,然后把它们相加就可以了(如图)。
二、相减法:这种方法是将所求的不规则图形的面积看成是若干个基本规则图形的面积之差.例如,右图,若求阴影部分的面积,只需先求出正方形面积再减去里面圆的面积即可(如图)。
例.一个正方形,如果把它的相邻两边都增加6厘米,就可以得到一个新正方形,新正方形的面积比原正方形大120平方厘米.求原正方形的面积?三、直接求法:这种方法是根据已知条件,从整体出发直接求出不规则图形面积.如下页右上图,欲求阴影部分的面积,通过分析发现它是一个底2,高4的三角形,就可以直接求面积了(如图)。
例.如下图,长方形AFEB和长方形FDCE拼成了长方形ABCD ,长方形 ABCD的长是20,宽是12,则它内部阴影部分的面积是.四、重新组合法:这种方法是将不规则图形拆开,根据具体情况和计算上的需要,重新组合成一个新的图形,设法求出这个新图形面积即可.例如,欲求右图中阴影部分面积,可以把它拆开使阴影部分分布在正方形的4个角处,这时采用相减法就可求出其面积了(如图)。
例.已知大正方形边长是7厘米,小正方形边长5厘米,求阴影部分的面积。
五、辅助线法:这种方法是根据具体情况在图形中添一条或若干条辅助线,使不规则图形转化成若干个基本规则图形,然后再采用相加、相减法解决即可.如右图,求两个正方形中阴影部分的面积.此题虽然可以用相减法解决,但不如添加一条辅助线后用直接法作更简便(如图)。
六、割补法:这种方法是把原图形的一部分切割下来补在图形中的另一部分使之成为基本规则图形,从而使问题得到解决.例如,如右图,欲求阴影部分的面积,只需把右边弓形切割下来补在左边,这样整个阴影部分面积恰是正方形面积的一半(如图).例.求阴影部分的面积。
巧奥数4年级第13讲巧算面积

进阶练习题
总结词
提升解题能力
详细描述
进阶练习题在基础练习题的基础上,增加了难度和复杂度,需要学生灵活运用面积计算公式解决实际问题,培养 他们的思维能力和解题技巧。
挑战练习题
总结词:挑战自我
详细描述:挑战练习题是难度最大的题目,需要学生综合运用多个知识点,解决一些较为复杂的问题。这类题目旨在激发学 生的挑战精神,培养他们解决问题的能力。
提高数学能力
掌握面积计算方法有助于 提高学生的数学思维能力、 空间想象力和解决问题的 能力。
数学考试重点
在小学数学考试中,面积 计算是常考的知识点之一, 学生需要熟练掌握各种图 形的面积计算公式。
02 巧算面积的方法
公式法
总结词
公式法是计算面积最常用的方法,适用于各种规则的几何图 形。
详细描述
公式法是通过使用几何图形的面积公式来计算面积。对于矩 形、三角形、圆形等规则图形,都有相应的面积公式可以直 接使用。使用公式法时,需要注意公式的适用范围和单位换 算。
THANKS FOR WATCHING
感谢您的观看
拼凑法是将多个几何图形拼凑在一起,形成一个简单的几何图形,然后计算总面 积。
详细描述
拼凑法适用于一些不规则或难以直接计算的几何图形。通过将图形与其他图形拼 凑,形成易于计算的组合图形,可以简化计算过程。拼凑法需要一定的组合和创 新能力,以找到合适的拼凑方式。
03 面积计算的实例矩Fra bibliotek面积的计算矩形面积计算公式
约成本。
购物预算
在购买家具或电器时,需要根据房 间面积来选择合适的大小,并计算 所需的总面积来制定购物预算。
空间规划
在规划家庭空间时,需要根据家庭 成员的活动需求和习惯来计算各个 功能区的面积,以确保空间的有效 利用和舒适度。
三年级奥数第11讲:巧求面积-教案

师:这确实是一种方法,老师刚刚在下面还看到有同学有不同做法,请你来说下你的思路。
生2:我是用大长方形的面积减去蓝色正方形的面积,再减去绿色正方形的面积,剩下的就是红色长方形的面积。
师:非常好,这也是一种很好的方法,你能具体说说具体的算法吗?生2: 大长方形的面积是6×10=60(平方厘米),蓝色正方形的面积是6×6=36 (平方厘米),绿色正方形的面积是4×4=16(平方厘米)师:那红色长方形的面积是多少呢?生2:60-36-16=8(平方厘米)。
师:这样求出来的答案也是8平方厘米。
这样做的同学举手示意一下。
师:看来也有很多同学是这么想的。
其实两种方法都是可以的。
同学们的思维真是活跃啊。
我们一起看下答案算对了吗。
板书:方法一:(10-6)×(6-4)=8(平方厘米)方法二:6×10-6×6-4×4=8(平方厘米)答:红色部分面积是8平方厘米。
师:刚刚我们解决了例题3,两种方法大家都会了吗?生:会了。
师:很好,很多题目我们可以从不同角度去思考。
我相信下面的练习3肯定也难不倒同学们。
大家自己动手做一做吧。
练习3:(5分)由两个完全相同的图形组成的图形(如图),计算下列图的面积。
分析:将图形进行平移、剪拼后可以发现这个图形的面积是一个边长为6厘米的大正方形减去一个边长为2厘米的小正方形的面积。
板书:6×6-2×2=32(平方厘米)答:这个图的面积是32平方厘米。
(二)例题4:(12分)一块长方形草地,长是38米,宽是28米,中间有两条宽2米的小路可以通过,这块草地的绿化面积是多少平方米?讲解重点:这个题目有2中方法,一个是用平移法,将两条小路移到一边,求空白小长方形的面积,就是绿化面积;或者可以求出两条小路的面积之和,要注意的是中间有一块2×2的地被重复计算了一次,要减掉。
再用草地面积减去小路面积,师:题目中要我们求这块草地的绿化面积是多少平方米,你们会怎么思考?生1:像上一个题目一样,我们可以用平移法把两条小路移到一边,中间就是绿化面积。
(完整版)三年级奥数面积计算

三年级奥数 巧求图形面积思维聚焦求正方形和长方形面积的公式是:正方形的面积二a x a (a 为边长), 长方形的面积=a x b (a 为长,b 为宽)。
利用这两个公式可以计算出各种各样的直角多边形的面积。
对一些图,我 们无法直接求出它的面积,但是通过将它分割或切补成几块,其中每一块都是 正方形或长方形,分别计算出各块面积再求和或差,就得出整个图形的面积。
形的面积等于多少平方米?n .5 _分析:我们不能直接求出它的面积,但是可以将此图形分割成若 -------------------- 习3 干个长方形。
下面两种较简单的方法,图形都被分割成三个长方 3 4形。
根据这两种不同的分割方法,都可以计算出图形的的面积。
__________________解: 5X 2+ (5 + 3) X 3+ (5 + 3 + 4) X 2=58(米 2);2或 5X (2 + 3+ 2) + 3X (2 + 3) + 4X 2 = 58(米)。
上面的方法是通过将图形分割成若干个长方形,然后求图形面积的。
实际上,我们也可以将图形“添补”成一个大长方形 (见下图),然 后利用大长方形与两个小长方形的面积之差,求出图形的面积 (5 + 3+ 4) X (2 + 3+ 2)-2 X 3-(2 + 3) X 4 = 58(米 2); 或(5 + 3+ 4) X (2 + 3 + 2)-2 X (3 + 4)-3 X 4= 58(米2)。
由例1看出,计算直角多边形面积,主要是利用“分割”和“添补”的方法,将图形演 变为多个长方形的和或差,然后计算出图形的面积。
其中“分割”是最基本、最常用的方法。
例1、下图中的每个数字分别表示所对应的线段的长度 (单位:米)。
这个图E_555+3+45+3M练习:1、右图是一幢楼房的平面图形,它的面积是_______________ 平方米.(单位:米)2、求下面图形的面积。
(单位:厘米)434 34'33、求下面图形的面积。
四年级《巧求面积》奥数教案

师:今天的知识,都比较有挑战性。
消磨光你们的耐心了吗?生:没有。
师:看来大家意志都很坚定嘛。
那我们接着看一下更难理解的例题四吧。
给你们两分钟时间读题,然后跟同桌之间讨论讨论,思考一下如何解决这个问题。
师:想好了吗?生:想好了。
师:那哪组派个代表来说说自己的发现。
生1:长方形游泳池的面积是50乘以25等于1250平方米。
师:对吗?生:对。
师:没错,因为由题意我们可以知道游泳池的长和宽分别是50米和25米。
所以就很容易求出游泳池的面积。
师:那还有那个小组愿意说说自己的成果?生2:可以把白瓷砖的部分分成4个小长方形。
师:那可以怎么分呢?生:横着分也可以,竖着分也可以。
师:很好,那我们就先横着分。
【课件演示分割动画。
】师:这样的话,我们可以发现红色的这两个长方形面积怎么求?生2:50乘以2。
师:这样求出来的是几个小长方形的面积?生2:一个。
师:所以要再……生2:乘以2 。
师:没错,请坐。
这样我们就求出了红色的两个小长方形的面积,还剩两个小长方形呢。
怎么办?生:25加上4在乘以2。
师:为什么25要加上4?生:因为这两个长方形的两头都比游泳池的宽长2米,就是总共长4米了。
师:听懂了吗?生:听懂了。
师:没错,解释得非常到位。
【课件演示竖向的两个长方形的面积求解过程。
】师:刚刚我们是纵向的分割白瓷砖,先在我们还可以……生:横向的分割。
师:没错,现在请你们自己写在课堂练习本上吧。
【教师下台巡视。
然后讲解解题过程。
】师:我们刚刚了解两种分割方法,如果我们不分割的话,该怎么求?生:用大的减去小的。
师:大的指什么?小的指什么?生:大的指白瓷砖包括游泳池的面积。
师:这个大的长宽分别是多少?生:50加4和25加4。
师:没错,所以我们就可以求出大的长方形面积是1566平方米。
师:那刚刚说的小的面积是指什么?生:是指游泳池的面积。
【课件演示方法三的解题动画。
】师:没错,所以,我们只要把大的面积减去小的面积,就可以得到白色瓷砖的面积了。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
巧求面积问题
一.知识点回顾
在解答比较复杂的关于长方形、正方形的面积计算的问题时,生搬硬套公式往往不能奏效,可以添加辅助线或运用割补、转化等解题技巧。
因此,敏锐的观察力和灵活的思维在解题中十分重要。
长方形面积公式:a b =⨯=⨯长方形长方形面积长宽,记作:S
正方形面积公式:2a a a =⨯=⨯=正方形正方形面积边长边长,记作:S 二.习题训练
1.用不同的方法计算下图的面积
2.计算图形的面积:
40
203030
3. 把一张长为4米,宽为3米的长方形木板,剪成一个面积最大的正方形。
这个正方形木板的面积是多少平方米?
4.将一张长10厘米、宽8厘米的长方形纸片剪成一个面积最大的正方形,那么剪下的另一个小长方形的面积是多少?
5.学校里有一个正方形花坛,四周种了一圈绿篱,绿篱总长20米。
花坛的面积是多少平方米?
6. 有两个相同的长方形,长是8厘米,宽是3厘米。
如果把它们按下图叠放,
这个图形的面积是多少?
7.两张边长8厘米的正方形纸,一部分叠在一起放在桌上(如下图),桌面被盖住的面积是多少?
8
884
48
8.求下图中阴影部分的面积。
(单位:分米)
5
2
27
9.一个长方形与一个正方形部分重合,求没有重合的阴影部分面积相差多少?(单位:厘米)5
56
9
10.右图为一个长50米、宽25米的标准游泳池。
它的四周铺设了宽2米的白瓷地砖(阴影部分)。
求游泳池面积和地砖面积。
11.有一块菜地长16米,宽8米,菜地中间留了宽2米的路,把菜地平均分成四块,每一块地的面积是多少?
12.有一个长方形,如果宽不变,长增加4米,面积就增加24平方米,如果长不变,宽增加3米,面积就增加36平方米,求原来长方形的面积。
13.一个长方形若长增加2厘米,面积就增加10平方厘米,若宽减少3厘米,面积就减少18平方厘米。
求原来长方形的面积。
14.如图,在一块长24米,宽16米的绿地上,有一条宽2米的小路。
请你列式计算出这条小路的面积。
15.如图所示,两个长方形拼成了一个正方形,如果正方形的周长比两个长方形的周长的和少6厘米,则正方形的面积是多少平方厘米?
初中历史大事年表(完整版)
中国古代史大事年表古代部分
距今约170万年元谋人生活在云南元谋一带
距今约70万~20万年北京人生活在北京周口店一带
距今约30000年山顶洞人生活在北京周口店一带
距今约7000~5000年河姆渡、半坡原始居民生活的时代
距今约5000~4000年传说中的炎帝、黄帝和尧、舜、禹时期夏(约前2070~约前1600年)
约公元前2070年禹建立夏朝
商(约前1600~前1046年)
约公元前1600年,汤朝灭夏,商朝建立
西周(前1046~前771年)
公元前1046年周武王灭商,西周开始
公元前771年戎族攻入镐京,西周结束
春秋(前770~前476年)
公元前770年,周平王迁都洛邑,东周开始
战国(前475~前221年)
公元前356年商鞅开始变法
秦(前221~前207年)
公元前221年秦统一六国
公元前209年陈胜、吴广起义爆发
公元前207年巨鹿之战
刘邦攻入咸阳秦亡
西汉(前202~9年)
公元前202年西汉建立
公元前138年张骞第一次出使西域
公元9年西汉灭亡
东汉(25~220年)
公元25年东汉建立
200年官渡之战
208年赤壁之战
三国(220~280年)
220年魏国建立。
东汉灭亡。
221年蜀国建立
222年吴国建立。
