2019年中考数学总复习第三单元函数课时训练12反比例函数练习
浙江省2019年中考数学 第三单元 函数及其图象 课时训练12 反比例函数练习 (新版)浙教版
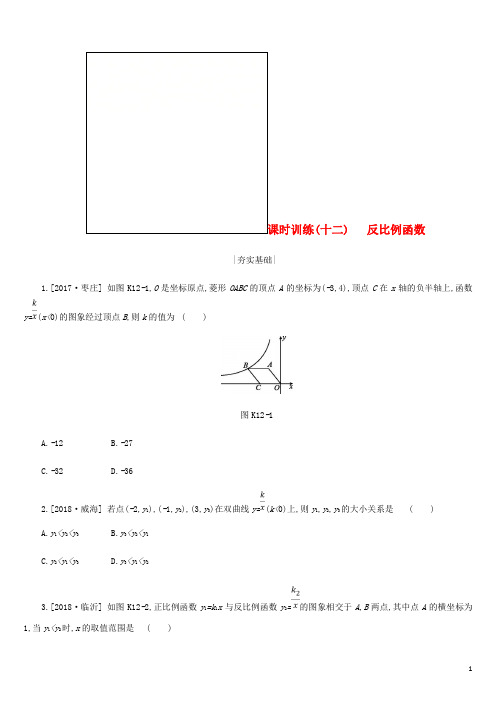
(十二) 反比例函数|夯实基础|1.[2017·枣庄] 如图K12-1,O是坐标原点,菱形OABC的顶点A的坐标为(-3,4),顶点C在x轴的负半轴上,函数y=(x<0)的图象经过顶点B,则k的值为()图K12-1A.-12B.-27C.-32D.-362.[2018·威海] 若点(-2,y1),(-1,y2),(3,y3)在双曲线y=(k<0)上,则y1,y2,y3的大小关系是()A.y1<y2<y3B.y3<y2<y1C.y2<y1<y3D.y3<y1<y23.[2018·临沂] 如图K12-2,正比例函数y1=k1x与反比例函数y2=的图象相交于A,B两点,其中点A的横坐标为1,当y1<y2时,x的取值范围是()图K12-2A.x<-1或x>1B.-1<x<0或x>1C.-1<x<0或0<x<1D.x<-1或0<x<14.[2018·广州] 一次函数y=ax+b和反比例函数y=在同一直角坐标系中大致图象是()K12-35.[2018·重庆A卷] 如图K12-4,在平面直角坐标系中,菱形ABCD的顶点A,B在反比例函数y=(k>0,x>0)的图象上,横坐标分别为1,4,对角线BD∥x轴.若菱形ABCD的面积为,则k的值为()图K12-4A.B.C.4 D.56.[2018·温州] 如图K12-5,点A,B在反比例函数y=(x>0)的图象上,点C,D在反比例函数y=(x>0)的图象上,AC∥BD∥y轴,已知点A,B的横坐标分别为1,2,△OAC与△ABD的面积之和为,则k的值为()图K12-5A.4B.3C.2D.7.[2017·泰州] 如图K12-6,P为反比例函数y=(k>0)在第一象限内图象上的一点,过点P分别作x轴,y轴的垂线交一次函数y=-x-4的图象于点A,B,若∠AOB=135°,则k的值是()图K12-6A.2B.4C.6D.88.已知点P(3,-2)在反比例函数y=(k≠0)的图象上,则k= ;在第四象限中,函数值y随x的增大而.9.[2017·连云港] 设函数y=与y=-2x-6的图象的交点坐标为(a,b),则+的值是.10.[2018·盐城] 如图K12-7,点D为矩形OABC的边AB的中点,反比例函数y=(x>0)的图象经过点D,交BC边于点E.若△BDE的面积为1,则k= .图K12-711.[2017·温州] 如图K12-8,矩形OABC的边OA,OC分别在x轴、y轴上,点B在第一象限,点D在边BC上,且∠AOD=30°,四边形OA'B'D与四边形OABD关于直线OD对称(点A'和A,B和B'分别对应),若AB=1,反比例函数y=(k≠0)的图象恰好经过点A',B,则k的值为.图K12-812.[2018·衢州] 如图K12-9,点A,B是反比例函数y=(x>0)图象上的两点,过点A,B分别作AC⊥x轴于点C,BD⊥x轴于点D,连结OA,BC,已知点C(2,0),BD=2,S△BCD=3,则S△AOC= .图K12-913.[2018·杭州] 已知一艘轮船上装有100吨货物,轮船到达目的地后开始卸货,设平均卸货速度为v(单位:吨/时),卸完这批货物所需的时间为t(单位:时).(1)求v关于t的函数表达式;(2)若要求不超过5小时卸完船上的这批货物,那么平均每小时至少要卸货多少吨?14.[2018·南充] 如图K12-10,直线y=kx+b(k≠0)与双曲线y=(m≠0)交于点A-,2,B(n,-1).(1)求直线与双曲线的解析式;(2)点P在x轴上,如果S△ABP=3,求点P的坐标.图K12-1015.[2018·天水] 如图K12-11所示,在平面直角坐标系中,直线y=x-1与y轴相交于点A,与反比例函数y=(k≠0)的图象在第一象限内相交于点B(m,1).(1)求反比例函数的解析式;(2)将直线y=x-1向上平行移动后与反比例函数的图象在第一象限内相交于点C,且△ABC的面积为4,求平行移动后的直线的解析式.图K12-11|拓展提升|16.[2018·宁波] 如图K12-12,平行于x轴的直线与函数y=(k1>0,x>0),y=(k2>0,x>0)的图象分别相交于A,B 两点,点A在点B的右侧,C为x轴上的一个动点.若△ABC的面积为4,则k1-k2的值为()图K12-12A.8B.-8C.4D.-417.[2017·湖州] 如图K12-13,在平面直角坐标系xOy中,已知直线y=kx(k>0)分别交反比例函数y=和y=在第一象限的图象于点A,B,过点B作BD⊥x轴于点D,交函数y=的图象于点C,连结AC.若△ABC是等腰三角形,则k的值是.图K12-1318.[2017·金华] 如图K12-14,已知点A(2,3)和点B(0,2),点A在反比例函数y=的图象上.作射线AB,再将射线AB绕点A按逆时针方向旋转45°,交反比例函数图象于点C,则点C的坐标为.图K12-1419.[2017·德州] 有这样一个问题:探究同一平面直角坐标系中系数互为倒数的正、反比例函数y=x与y=(k≠0)的图象性质.小明根据学习函数的经验,对函数y=x与y=,当k>0时的图象性质进行了探究.下面是小明的探究过程:(1)如图K12-15所示,设函数y=x与y=图象的交点为A,B.已知A点的坐标为(-k,-1),则B点的坐标为.图K12-15(2)若点P为第一象限内双曲线上不同于点B的任意一点.①设直线PA交x轴于点M,直线PB交x轴于点N.求证:PM=PN.证明过程如下:设P m,,直线PA的解析式为y=ax+b(a≠0).则解得∴直线PA的解析式为.请你把上面的解答过程补充完整,并完成剩余的证明.②当P点坐标为(1,k)(k≠0)时,判断△PAB的形状,并用k表示出△PAB的面积.参考答案1.C[解析] ∵A(-3,4),∴OA==5,∵四边形OABC是菱形,∴AO=CB=OC=AB=5,则点B的横坐标为-3-5=-8,故B的坐标为(-8,4),将点B的坐标代入y=得,=4,解得k=-32.故选C.2.D3.D[解析] 由正比例函数图象、反比例函数图象的中心对称性,以及正比例函数y1=k1x与反比例函数y2=的图象交点A的横坐标为1,可得另一个交点B的横坐标为-1,结合图象知,当y1<y2时,x的取值范围是x<-1或0<x<1,故选D.4.A[解析] 由选项A,B中直线的位置,可知a>0,b>0,而当x=-1时,y=-a+b<0,从而a-b>0,故反比例函数y=的图象应该在第一,三象限,故选项B错误;由选项C,D中直线的位置,可知a<0,b>0,而当x=-1时,y=-a+b>0,从而a-b<0,反比例函数y=的图象应该在第二,四象限,故选项C,D错误.故答案为A.5.D[解析] 设点A(1,k),则由点A,B均在双曲线y=上,得B(4,),由菱形ABCD的面积为,得AC·BD=×2(k-)×6=,解得k=5,故选D.6.B[解析] 因为点A,B在反比例函数y=上,所以A(1,1),B(2,),又因为AC∥BD∥y轴,平行于y轴的直线上的点的横坐标相等,所以利用A点的横坐标是1求出C点的横坐标是1,同理,B点的横坐标是2,所以D点的横坐标是2.则得到C(1,k),D(2,),所以AC=k-1,BD=-,因为△OAC和△ABD中,AC和BD上的高都是1,所以△OAC的面积=(k-1),△ABD 的面积=(-),所以△OAC与△ABD的面积之和=(k-1)+(-)=,解得k=3.故选B.7.D[解析] 如图,设直线AB与x轴交于点G,与y轴交于点K,则G(-4,0),K(0,-4).∴OG=OK=4,在Rt△GOK中,∠OGK=∠OKG=45°,∴∠OBG+∠BOG=45°,∠OGB=∠OKA=135°.又∵∠BOA=135°,∠GOK=90°,∴∠BOG+∠AOK=45°,∴∠OBG=∠AOK ,∴△BOG ∽△OAK ,∴=,设P 点坐标为(x ,y ),则BG=y ,AK=x ,故=,∴2xy=16,xy=8,∴k=xy=8.8.-6 增大 [解析]∵点P (3,-2)在反比例函数y=(k ≠0)的图象上,∴k=3×(-2)=-6. ∵k=-6<0,∴反比例函数y=的图象在第二、四象限,且在每个象限内y 随x 的增大而增大,∴在第四象限中,函数值y 随x 的增大而增大.9.-2 [解析] 根据函数图象的交点为(a ,b ),可代入两个函数的解析式得ab=3,b=-2a-6,即b+2a=-6,所以+===-2.10.4 [解析] 设D (a ,),∵点D 为矩形OABC 的AB 边的中点,∴B (2a ,),∴E (2a ,),∵△BDE 的面积为1,∴·a ·(-)=1,解得k=4.11. [解析] 由点B 在反比例函数图象上且AB=1,可得OA=k ,由对称性可知OA'=OA=k ,∠AOA'=2∠AOD=60°,∴点A'的坐标为(k ,k ),由点A'在反比例函数图象上,得k×k=k,∴k=.12.5[解析] ∵△BCD的面积=3,BD=2,∴CD=3, 又∵点C坐标为(2,0),∴OD=5,连结OB,则△BOD的面积=OD·BD=5,根据反比例函数的性质可得:△AOC的面积也是5.13.解:(1)v=(t>0).(2)由题意得0<t≤5,当t=5时,v=20,∵k=100>0,∴v≥20,∴平均每小时至少要卸货20吨.14.解:(1)∵点A-,2在双曲线y=上,∴2=,∴m=-1,∴y=-.∴B(1,-1).又∵直线y=kx+b经过A,B两点,∴解得∴y=-2x+1.(2)直线y=-2x+1与x轴交点为C(,0),S△ABP=S△ACP+S△BCP=×2·CP+×1·CP=3,解得CP=2.∴P的坐标为(,0)或(-,0).15.解:(1)∵点B(m,1)在直线y=x-1上,∴1=m-1,解得m=2,∴点B(2,1).∵点B(2,1)在反比例函数y=的图象上,∴k=2,∴反比例函数的解析式为y=.(2)如图标注各点,设平移后直线与y轴交于点D,过点D作DE⊥直线AB,交AB于点E.对于直线y=x-1,当x=0时,y=-1,当y=0时,x=1,∴点A(0,-1),点F(1,0),∴AO=FO.∵∠AOF=90°,∴∠FAO=45°.∵点B(2,1),点A(0,-1),∴AB=2.由S△ABC=AB·DE=4,AB=2,可知DE=2.在Rt△ADE中,∠DAE=45°,DE=2,∴AD=4,则点D的坐标为(0,3).将直线AB平移得直线CD,设直线CD的关系式为y=x+a,∵点D在直线y=x+a上,∴a=3,则平移后的直线的解析式为y=x+3.16.A[解析] 设点A的坐标为(x A,y A),点B的坐标为(x B,y B),点C的坐标为(x C,0).∵AB∥x轴,∴y A=y B.过点C作CD⊥AB交AB的延长线于点D(x D,y D).∵AB=x A-x B,CD=y D-y C=y A-y C,∴S△ABC=AB·CD=(x A-x B)(y A-y C)=(x A-x B)y A=(x A y A-x B y B)=(|k1|-|k2|)=(k1-k2), 即4=(k1-k2),∴k1-k2=8.17.或[解析] 设出B,A两点的坐标,并表示出C点坐标,得到BC的长度,然后分三种情况讨论k值.设B(a,),A(b,),∴C(a,),∵A,B在直线y=kx上,∴ka=,kb=.∴a2=,b2=.又∵BD⊥x轴,∴BC=.分类一:当AB=BC时,∵AB=,∴(a-b)=,∴(-)=,∴k=.分类二:当AC=BC时,∵AC=,∴(1+)(-)2=,∴k=.分类三:当AB=AC时,1+=1+k2,∴k=0(舍去).综上所述k=或.18.(-1,-6)[解析] 设AC与x轴交于点D.如图,过点A作HA⊥AB交x轴于点H,过点D分别作DE⊥AB,DF⊥AH,垂足分别为E,F,AB与x轴交点为G.设直线AB的解析式为y=kx+b,把点A(2,3)和点B(0,2)的坐标分别代入,得解得∴y=x+2.令y=0,则x+2=0,得x=-4.∴G(-4,0).∴OG=4,OB=2.∵点A(2,3),OG=4,可得AG=3.∵∠BGO=∠HGA,∠GOB=∠GAH=90°,∴△BOG∽△HAG,∴=,即=,∴AH=.由△AGH的面积,可得×3GH=AG·AH,即3GH=3×,得GH=,∴OH=GH-OG=.∵AH⊥AB,∠GAC=45°,∴AD平分∠GAH.∵DE⊥AB,DF⊥AH,∴DE=DF=AF.由△AGH的面积,可得DE·AG+DF·AH=AG·AH,即(3+)DF=×3×,∴DF=,∴AF=,FH=-=,∴DH==,∴OD=OH-DH=-=1,∴D(1,0).设直线AD的解析式为y=mx+n,把点A(2,3),D(1,0)的坐标代入,得解得∴y=3x-3.把点A(2,3)的坐标代入y=,得y=.由得或∴点C的坐标为(-1,-6).19.[解析] (1)根据正比例函数图象与反比例函数图象的对称性可知点A与点B关于原点O对称,据此可求B点的坐标;(2)①利用加减消元法易求a,b的值(用含m,k的式子表示);利用直线PA的解析式,确定点M的坐标,过点P作PH⊥x轴于H,可得MH=NH,继而可得结论PM=PN.②当P点坐标为(1,k)(k≠0)时,有MH=HN=PH,从而可求∠APB=90°,故△PAB为直角三角形.分k>1,0<k<1两种情况,利用相关三角形的面积和差计算△PAB的面积.解:(1)B点的坐标为(k,1).(2)①证明过程如下:设P(m,),直线PA的解析式为y=ax+b(a≠0),则解得∴直线PA的解析式为y=x+-1.令y=0,得x=m-k,∴M点的坐标为(m-k,0).过点P作PH⊥x轴于H,∴点H的坐标为(m,0).∴MH=x H-x M=m-(m-k)=k.同理可得HN=k.∴PM=PN.②由①知,在△PMN中,PM=PN,△PMN为等腰三角形,且MH=HN=k,当P点坐标为(1,k)时,PH=k,∴MH=HN=PH,∴∠PMH=∠MPH=45°,∠PNH=∠NPH=45°,∴∠MPN=90°,即∠APB=90°,∴△PAB为直角三角形.当k>1时,如图①,S△PAB=S△PMN-S△OBN+S△OAM=MN·PH-ON·y B+OM·|y A|=×2k×k-(k+1)·1+(k-1)·1=k2-1.当0<k<1时,如图②,S△PAB=S△OBN-S△PMN+S△OAM=ON·y B-k2+OM·|y A|=(k+1)·1-k2+(1-k)·1=1-k2.。
(河北专版)中考数学复习 第三单元 函数 课时训练12 反比例函数及其应用-人教版初中九年级全册数学

课时训练(十二)反比例函数及其应用(限时:45分钟)|夯实基础|1.[2019·某某]如果反比例函数y=a-2a(a是常数)的图象在第一、三象限,那么a的取值X围是()A.a<0B.a>0C.a<2D.a>22.[2019·贺州]已知ab<0,一次函数y=ax-b与反比例函数y=aa在同一直角坐标系中的图象可能是()图K12-13.[2019·某某路北区一模]已知点P(m,n)是反比例函数y=-3a图象上一点,当-3≤n<-1时,m的取值X围是()A.1≤m<3B.-3≤m<-1C.1<m≤3D.-3<m≤-14.[2019·某某]如图K12-2,一次函数y1=ax+b和反比例函数y2=aa的图象相交于A,B两点,则使y1>y2成立的x 的取值X围是()图K12-2A.-2<x<0或0<x<4B.x<-2或0<x<4C.x<-2或x>4D.-2<x<0或x>45.[2019·某某]验光师测得一组关于近视眼镜的度数y(度)与镜片焦距x(米)的对应数据如下表.根据表中数据,可得y关于x的函数表达式为()近视眼镜的度数y(度) 200 250 400 500 1000 镜片焦距x(米) 0.50 0.40 0.25 0.20 0.10A.y=100a B.y=a100C.y=400aD.y=a4006.如图K12-3,已知动点A,B分别在x轴,y轴正半轴上,动点P在反比例函数y=6a(x>0)的图象上,PA⊥x轴,△PAB是以PA为底边的等腰三角形.当点A的横坐标逐渐增大时,△PAB的面积将会 ()图K12-3A.越来越小B.越来越大C.不变D.先变大后变小7.[2019·某某质检]如图K12-4,点A在反比例函数y=aa(x>0,k>0)的图象上,AB⊥x轴于点B,点C在x轴的负半轴上,且BO=2CO.若△ABC的面积为18,则k的值为()图K12-4A.12B.18C.20D.248.[2019·]在平面直角坐标系xOy中,点A(a,b)(a>0,b>0)在双曲线y=a1a上.点A关于x轴的对称点B在双曲线y=a2a上,则k1+k2的值为.9.[2019·某某]如图K12-5,点A,C分别是正比例函数y=x的图象与反比例函数y=4a的图象的交点,过A点作AD⊥x轴于点D,过C点作CB⊥x轴于点B,则四边形ABCD的面积为.图K12-510.如图K12-6,平行于x轴的直线与函数y=a1a (k1>0,x>0),y=a2a(k2>0,x>0)的图象分别相交于A,B两点,点A在点B的右侧,C为x轴上的一个动点.若△ABC的面积为4,则k1-k2的值为.图K12-611.某超市销售进价为2元的雪糕,在销售中发现,此雪糕的销售单价x(元)与日销售量y(根)之间有如下关系:销售单价x/元 3 4 5 6日销售量y/根40 30 24 20(1)猜测并确定y与x之间的函数关系;(2)设此雪糕的日销售利润为W元,求W关于x的函数解析式.若物价局规定此雪糕的最高售价为10元/根,请求出此雪糕的日销售最大利润.12.[2019·某某]如图K12-7,在平面直角坐标系xOy中,一次函数y=kx+b的图象与反比例函数y=a的图象在第a.二象限交于点B,与x轴交于点C,点A在y轴上,满足条件:CA⊥CB,且CA=CB,点C的坐标为(-3,0),cos∠ACO=√55 (1)求反比例函数的表达式;的解集.(2)直接写出当x<0时,kx+b<aa图K12-7|拓展提升|13.[2019·威海]如图K12-8,在平面直角坐标系中,点A,B在反比例函数y=a(k≠0)的图象上运动,且始终保持a线段AB=4√2的长度不变,M为线段AB的中点,连接OM.则线段OM的长度的最小值是(用含k的代数式表示).图K12-8(k>0,x>0)的图象与等边三角形OAB的边OA,AB 14.[2019·某某]如图K12-9,在平面直角坐标系中,函数y=aa分别交于点M,N,且OM=2MA.若AB=3,则点N的横坐标为.图K12-915.[2019·呼和浩特]如图K12-10,在平面直角坐标系中,矩形OCAB(OC>OB)的对角线长为5,周长为14,若反比的图象经过矩形顶点A.例函数y=aa(1)求反比例函数的解析式;若点(-a,y1)和(a+1,y2)在反比例函数的图象上,试比较y1与y2的大小.<0成立(2)若一次函数y=kx+b的图象过点A并与x轴交于点(-1,0),求出一次函数解析式,并直接写出kx+b-aa时,对应x的取值X围.图K12-10【参考答案】1.D2.A图象上一点,∴n=-3时,m=1,n=-1时,m=3,3.A[解析]∵点P(m,n)是反比例函数y=-3a则m的取值X围是1≤m<3.故选A.4.B5.A6.C[解析]如图,过点B 作BC ⊥PA 于点C ,则BC=OA.设点P x ,6a ,则S △PAB =12PA ·BC=12·6a ·x=3,所以当点A 的横坐标逐渐增大时,△PAB 的面积不变,始终等于3. 7.D[解析]设点A 的坐标为a ,a a,则OB=a ,AB=a a.∵BO=2CO , ∴CB=32a ,∴12·32a ·aa =18,解得k=24.故选D . 8.09.8[解析]解{a =a ,a =4a,得{a =2,a =2或{a =-2,a =-2,∴A 的坐标为(2,2),C 的坐标为(-2,-2). 又AD ⊥x 轴,CB ⊥x 轴, ∴B (-2,0),D (2,0), ∴BD=4,AD=2,∴四边形 ABCD 的面积=AD ·BD=8.10.8[解析]如图,过点B 作BE ⊥x 轴,垂足为点E ,过点A 作AF ⊥x 轴,垂足为点F ,直线AB 交y 轴于点D.因为△ABC 与△ABE 同底等高, 所以S △ABE =S △ABC =4. 因为四边形ABEF 为矩形, 所以S 矩形ABEF =2S △ABE =8, 因为k 1=S 矩形OFAD ,k 2=S 矩形OEBD ,所以k 1-k 2=S 矩形OFAD -S 矩形OEBD =S 矩形ABEF =8.11.解:(1)通过观察表中数据,可以发现x 与y 的乘积是相同的,∴y 与x 成反比例.设反比例函数的解析式为y=aa . ∵当x=3时,y=40,∴k=3×40=120. ∴y=120a .(2)W=(x -2)y=(x -2)·120a=120-240a . ∵x ≤10,∴当x=10时,W 最大=120-24=96. ∴当x=10时,日销售最大利润为96元. 12.解:(1)如图,过点B 作BH ⊥x 轴于点H ,则∠BHC=∠BCA=∠COA=90°, ∴∠BCH=∠CAO. ∵点C 的坐标为(-3,0), ∴OC=3. ∵cos∠ACO=√55, ∴AC=3√5,AO=6. 在△BHC 和△COA 中,{∠aaa =∠aaa =90°,∠aaa =∠aaa ,aa =aa ,∴△BHC ≌△COA (AAS). ∴BH=CO=3,CH=AO=6. ∴OH=9,即B (-9,3). ∴m=-9×3=-27,∴反比例函数的表达式为y=-27a .(2)∵在第二象限中,B 点右侧一次函数的图象在反比例函数图象的下方,∴当x<0时,kx+b<aa 的解集为-9<x<0. 13.√2a +8[解析]过点A 作AC ⊥x 轴,过点B 作BD ⊥y 轴,垂足分别为C ,D ,AC 与BD 相交于点F ,连接OF.当点O ,F ,M 在同一直线上时OM 最短,即OM 垂直平分AB.设点A 的坐标为(a ,a+4),则点B 坐标为(a+4,a ),点F 的坐标为(a ,a ).由题意可知△AFB 为等腰直角三角形.∵AB=4√2,∴AF=BF=4.∵点A 在反比例函数y=aa (k ≠0)的图象上,∴a (a+4)=k ,解得a=√a +4-2,在Rt△OCF中,OF=√aa 2+aa 2=√2a=√2(√a +4-2)=√2a +8-2√2,∴OM=OF+FM=√2a +8-2√2+2√2=√2a +8.14.3+√52[解析]如图,过点A ,M 分别作AC ⊥OB ,MD ⊥OB ,垂足分别为C ,D.∵△AOB 是等边三角形,∴AB=OA=OB=3,∠AOB=60°.又∵OM=2MA ,∴OM=2,MA=1,在Rt△MOD 中,OD=12OM=1,MD=√22-12=√3,∴M (1,√3),∴反比例函数的解析式为y=√3a.在Rt△AOC 中,OC=12OA=32,AC=√32-(32) 2=3√32,∴A32,3√32.设直线AB 的解析式为y=kx+b ,把A 32,3√32,B (3,0)分别代入得:{3a +a =0,32a +a =3√32,解得{a =-√3,a =3√3,∴y=-√3x+3√3.由题意得,{a =-√3a +3√3,a =√3a,解得x=3±√52.∵x>32, ∴x=3+√52.故点N 的横坐标为3+√52.15.解:(1)根据题意得OB+OC=7,OB 2+OC 2=52. ∵OC>OB ,∴OB=3,OC=4, ∴A (3,4),把A (3,4)的坐标代入反比例函数y=aa中,得m=3×4=12, ∴反比例函数的解析式为y=12a .∵点(-a ,y 1)和(a+1,y 2)在反比例函数的图象上, ∴-a ≠0,且a+1≠0,∴a ≠-1,且a ≠0, ∴当a<-1时,-a>0,a+1<0,则点(-a ,y 1)和(a+1,y 2)分别在第一象限和第三象限的反比例函数的图象上,于是有y 1>y 2; 当-1<a<0时,-a>0,a+1>0, 若-a>a+1,即-1<a<-12时,y 1<y 2;若-a=a+1,即a=-12时,y 1=y 2;若-a<a+1,即-12<a<0时,y 1>y 2.当a>0时,-a<0,a+1>0,则点(-a ,y 1)和(a+1,y 2)分别在第三象限和第一象限的反比例函数的图象上,于是有y 1<y 2.综上,当a<-1时,y 1>y 2; 当-1<a<-12时,y 1<y 2;当a=-12时,y 1=y 2; 当-12<a<0时,y 1>y 2; 当a>0时,y 1<y 2.(2)∵一次函数y=kx+b 的图象过点A (3,4),并与x 轴交于点(-1,0), ∴{3a +a =4,-a +a =0,解得{a =1,a =1, ∴一次函数的解析式为y=x+1.解方程组{a =a +1,a =12a 得{a 1=-4,a 1=-3,{a 2=3,a 2=4,∴一次函数y=kx+b 的图象与反比例函数y=a a的图象相交于两点(-4,-3)和(3,4), 当一次函数y=kx+b 的图象在反比例函数y=a a 的图象下方时,x<-4或0<x<3, ∴kx+b -a a<0成立时,对应x 的取值X 围为x<-4或0<x<3.。
江苏专版中考数学复习第三单元函数课时训练12反比例函数

江苏专版中考数学复习第三单元函数课时训练12反比例函数(限时:30分钟)|夯实基础|的图象上,则k的值是()1.[2018·淮安]若点A(-2,3)在反比例函数y=kkA.-6B.-2C.2D.62.[2019·淮安] 当矩形面积一定时,下列图象中能表示它的长y和宽x之间函数关系的是()图K12-13.[2019·江西]已知正比例函数y1的图象与反比例函数y2的图象相交于点A(2,4),下列说法正确的是()A.反比例函数y2的解析式是y2=-8kB.两个函数图象的另一个交点坐标为(2,-4)C.当x<-2或0<x<2时,y1<y2D.正比例函数y1与反比例函数y2都随x的增大而增大(k≠0)在同一坐标系内的图象可能是 ()4.[2018·怀化]函数y=kx-3与y=kk图K12-2的图象上,则x1,x2,x3的大小关系是() 5.[2018·天津]若点A(x1,-6),B(x2,-2),C(x3,2)在反比例函数y=12kA.x1<x2<x3B.x2<x1<x3C.x2<x3<x1D.x3<x2<x1的图象位于第二、四象限,则k的取值范围是.6.[2018·益阳]若反比例函数y=2-kk7.[2018·天水]若点A(a,b)在反比例函数y=3的图象上,则代数式ab-1的值为.k8.[2018·镇江]反比例函数y=k(k≠0)的图象经过点A(-2,4),则在每一个象限内,y随x的增大k而.(填“增大”或“减小”)9.[2019·无锡] 某个函数具有性质:当x>0时,y随x的增大而增大,这个函数的表达式可以是(只要写出一个符合题意的答案即可).10.如图K12-3,矩形ABCD的边AB与x轴平行,顶点A的坐标为(2,1),点B与点D都在反比例函数y=6k(x>0)的图象上,则矩形ABCD的周长为.图K12-311.如图K12-4,点A是反比例函数y=2k (x>0)的图象上任意一点,AB∥x轴交反比例函数y=-3k的图象于点B,以AB为边作□ABCD,其中C,D在x轴上,则□ABCD的面积是.图K12-412.[2019·盐城大丰区一模] 一定质量的二氧化碳,它的体积V(m3)与它的密度ρ(kg/m3)之间成反比例函数关系,其图象如图K12-5所示.(1)试确定V与ρ之间的函数表达式;(2)当ρ=2.5 kg/m3时,求V的值.图K12-513.[2019·常州]如图K12-6,在□ABCO中,OA=2√2,∠AOC=45°,点C在y轴上,点D是BC的中点,反比例函数y=kk(x>0)的图象经过点A,D.(1)求k的值;(2)求点D的坐标.图K12-614.[2019·大庆] 如图K12-7,反比例函数y=2k和一次函数y=kx-1的图象相交于A(m,2m),B两点.k(1)求一次函数的表达式;<kx-1的x的取值范围.(2)求出点B的坐标,并根据图象直接写出满足不等式2kk图K12-7|拓展提升|(x>0)的图象上,过点C的直线与x轴,y轴分别交于点A,B, 15.[2018·嘉兴]如图K12-8,点C在反比例函数y=kk且AB=BC,△AOB的面积为1.则k的值为()图K12-8A.1B.2C.3D.416.[2019·淄博] 如图K12-9,△OA1B1,△A1A2B2,△A2A3B3,…是分别以A1,A2,A3,…为直角顶点,一条直角边在x(x>0)的图轴正半轴上的等腰直角三角形,其斜边的中点C1(x1,y1),C2(x2,y2),C3(x3,y3),…均在反比例函数y=4k象上.则y1+y2+…+y10的值为()图K12-9A.2√10B.6C.4√2D.2√717.[2019·孝感] 如图K12-10,双曲线y=9k (x>0)经过矩形OABC的顶点B,双曲线y=kk(x>0)交AB,BC于点E,F,且与矩形的对角线OB交于点D,连接EF.若OD∶OB=2∶3,则△BEF的面积为.图K12-10【参考答案】1.A2.B3.C4.B[解析]因为当k>0时,直线y=kx-3过一、三、四象限,反比例函数y=kk的图象在一、三象限内,当k<0时,直线y=kx-3过二、三、四象限,反比例函数y=kk的图象在二、四象限内.所以B正确,故选B.5.B[解析]把点A(x1,-6),B(x2,-2),C(x3,2)的坐标分别代入y=12k可得x1,x2,x3的值,即可得x2<x1<x3,故选B.6.k>2[解析]∵反比例函数y=2-kk的图象位于第二、四象限,∴2-k<0,解得:k>2.7.2[解析]∵点A(a,b)在反比例函数y=3k的图象上,∴ab=3.则代数式ab-1=3-1=2.8.增大[解析]∵反比例函数y=kk(k≠0)的图象经过点A(-2,4),∴k=(-2)×4=-8<0.∴反比例函数y=kk(k≠0)的图象在每一个象限内,y随x的增大而增大.9.y=-2k(答案不唯一)10.12[解析]∵四边形ABCD是矩形,顶点A的坐标为(2,1),∴设B,D两点的坐标分别为(x,1),(2,y).∵点B与点D都在反比例函数y=6k(x>0)的图象上,∴x=6,y=3.∴B,D两点的坐标分别为(6,1),(2,3).∴AB=6-2=4,AD=3-1=2.∴矩形ABCD的周长为12.11.512.解:(1)设V与ρ之间的函数表达式为:V=kk ,把(1.5,4)代入V=kk,得k=6,故V与ρ之间的函数表达式为:V=6k(ρ>0).(2)当ρ=2.5 kg/m3时,V=62.5=2.4(m3).13.解:(1)如图,延长BA交x轴于点F,取OA的中点E,连接DE,则AF⊥x轴于点F.在Rt△AOF中,OA=2√2,∠AOC=45°,可得OF=AF=2,从而A(2,2).∵反比例函数y=kk(x>0)的图象经过点A,D,∴k=2×2=4.(2)∵O(0,0),A(2,2),∴线段OA 的中点E 的坐标为(1,1). ∵在y=kk 中,当x=1时,y=4, ∴点D 的坐标为(1,4).14.解:(1)∵A (m ,2m )在反比例函数图象上, ∴2m=2kk , ∴m=1,∴反比例函数的表达式为y=2k ,A (1,2). 又∵A (1,2)在一次函数y=kx -1的图象上, ∴2=k -1,即k=3,∴一次函数的表达式为:y=3x -1.(2)由{k =2k ,k =3k -1解得{k =1,k =2或{k =-23,k =-3,∴B -23,-3,∴由图象知满足不等式2k k <kx -1的x 的取值范围为-23<x<0或x>1.15.D [解析]过点C 作CD ⊥x 轴于点D ,连接OC.由CD ∥OB ,得△ABO ∽△ACD ,∴kk kk =kkkk ,∵AB=BC ,∴AO=OD ,∵AB=BC ,∴S △ABO =S △BOC =1,而AO=OD ,∴S △AOC =S △COD =2,根据S △COD =k2,可得k=4,故正确答案为D .16.A [解析]过C 1,C 2,C 3,…分别作x 轴的垂线,垂足分别为D 1,D 2,D 3,…∵点C 1在反比例函数y=4k 的图象上, ∴C 1(2,2),y 1=2, ∴OD 1=D 1A 1=2,设A 1D 2=a ,则C 2D 2=a ,此时C 2点坐标为(4+a ,a ),代入y=4k 得:a (4+a )=4,解得:a=2√2-2(负值已舍),即:y 2=2√2-2, 同理:y 3=2√3-2√2,y 4=2√4-2√3,……∴y 1+y 2+…+y 10=2+2√2-2+2√3-2√2+…+2√10-2√9=2√10.故选A .17.2518 [解析]设D (2m ,2n ), ∵OD ∶OB=2∶3,∴A (3m ,0),C (0,3n ),B (3m ,3n ).∵双曲线y=9k (x>0)经过矩形OABC 的顶点B ,∴9=3m ·3n , ∴mn=1.∵双曲线y=k k(x>0)经过点D , ∴k=4mn , ∴双曲线y=4kkk(x>0),∴E 3m ,43n ,F43m ,3n ,∴BE=3n -43n=53n ,BF=3m -43m=53m , ∴S △BEF =12BE ·BF=2518mn=2518.。
河北省2019年中考数学总复习第三单元函数课时训练12反比例函数练习
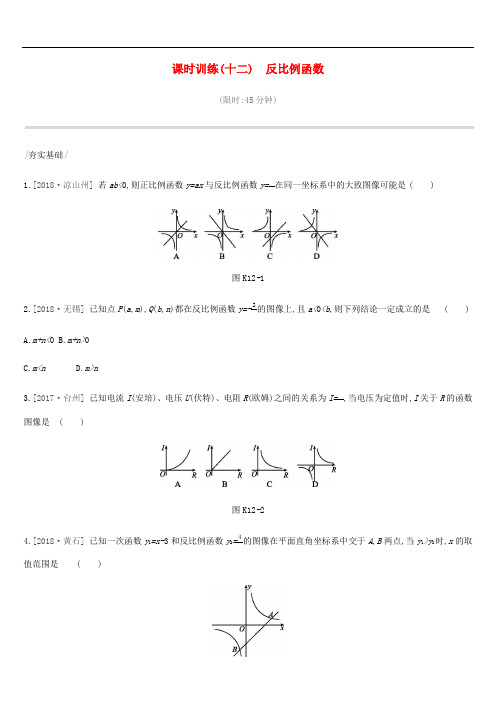
课时训练(十二)反比例函数(限时:45分钟)|夯实基础|在同一坐标系中的大致图像可能是()1.[2018·凉山州]若ab<0,则正比例函数y=ax与反比例函数y=bb图K12-12.[2018·无锡]已知点P(a,m),Q(b,n)都在反比例函数y=-2的图像上,且a<0<b,则下列结论一定成立的是()bA.m+n<0B.m+n>0C.m<nD.m>n3.[2017·台州]已知电流I(安培)、电压U(伏特)、电阻R(欧姆)之间的关系为I=b,当电压为定值时,I关于R的函数b图像是()图K12-24.[2018·黄石]已知一次函数y1=x-3和反比例函数y2=4的图像在平面直角坐标系中交于A,B两点,当y1>y2时,x的取b值范围是()A.x<-1或x>4B.-1<x<0或x>4C.-1<x<0或0<x<4D.x<-1或0<x<4(x>0)的图像上,PA⊥x轴,△PAB是以5.如图K12-4,已知动点A,B分别在x轴,y轴正半轴上,动点P在反比例函数y=6bPA为底边的等腰三角形.当点A的横坐标逐渐增大时,△PAB的面积将会()图K12-4A.越来越小B.越来越大C.不变D.先变大后变小6.[2018·莱芜]在平面直角坐标系中,已知△ABC为等腰直角三角形,CB=CA=5,点C(0,3),点B在x轴正半轴上,点A在的图像上,则k=()第三象限,且在反比例函数y=bbA.3B.4C.6D.12(k是常数,k≠1)的图像有一支在第二象限,那么k的取值范围是. 7.[2018·上海]已知反比例函数y=b-1b上,则m2+n2的值为.8.[2018·宜宾]已知:点P(m,n)在直线y=-x+2上,也在双曲线y=-1b9.[2018·张家界]如图K12-5,矩形ABCD的边AB与x轴平行,顶点A的坐标为(2,1),点B与点D都在反比例函数y=6(x>0)的图像上,则矩形ABCD的周长为.b10.[2018·唐山丰润区一模]如图K12-6,△OAC和△BAD都是等腰直角三角形,∠ACO=∠ADB=90°,反比例函数y=b在第b一象限的图像经过点B.图K12-6①若OC=3,BD=2,则k= ;②若OA2-AB2=18.则k= .11.[2018·泰安]如图K12-7,矩形ABCD的两边AD,AB的长分别为3,8,E是DC的中点,反比例函数y=b(x<0)的图像经b过点E,与AB交于点F.图K12-7(1)若点B坐标为(-6,0),求m的值及图像经过A,E两点的一次函数的表达式;(2)若AF-AE=2,求反比例函数的表达式.12.为了筹款支持希望工程,某“爱心”小组决定利用暑假销售一批进价为10元的小商品,为寻求合适的销售价格,他们进行了试销,试销情况如下表:第1天第2天第3天第4天…日单价x(元) 20 30 40 50 …日销量y(个) 30 20 15 12 …(1)若y是x的反比例函数,请求出这个函数关系式;(2)若该小组计划每天的销售利润为450元,则其单价应为多少元?|拓展提升|13.如图K12-8,双曲线y=bb (k≠0)与y=-3b中的一支分别位于第一、四象限,A是y轴上任意一点,B是双曲线y=-3b上的点,C是双曲线y=bb (k≠0)上的点,线段BC⊥x轴于点D,且4BD=3CD,则下列说法:①双曲线y=bb(k≠0)在每个象限内,y随x的增大而减小;②若点B的横坐标为3,则点C的坐标为(3,-43);③k=4;④△ABC的面积为定值7.正确的有()图K12-8A.1个B.2个C.3个D.4个(x>0)的图像经过点C, 14.[2018·唐山丰润区一模]如图K12-9,在△ABC中,AC=BC,AB⊥x轴,垂足为A.反比例函数y=bb.交AB于点D.已知AB=4,BC=52图K12-9(1)若OA=4,求k的值;(2)连接OC,若BD=BC,求OC的长.参考答案1.B2.D [解析] ∵a<0<b ,∴x=a 时,m=y=-2b>0,x=b 时,n=y=-2b<0,∴m>n.3.C4.B5.C [解析] 如图,过点B 作BC ⊥PA 于点C ,则BC=OA ,设点P x ,6b ,则S △PAB =12PA ·BC=12·6b ·x=3,当点A 的横坐标逐渐增大时,△PAB 的面积不变,始终等于3. 6.A [解析] 如图,作AH ⊥y 轴于H.∵CA=CB ,∠AHC=∠BOC ,∠ACH=∠CBO , ∴△ACH ≌△CBO , ∴AH=OC ,CH=OB , ∵C (0,3),BC=5, ∴OC=3,OB=√52-32=4, ∴CH=OB=4,AH=OC=3, ∴OH=1, ∴A (-3,-1),∵点A 在y=bb 的图像上, ∴k=3.7.k<18.6 [解析] ∵点P (m ,n )在直线y=-x+2上,∴n+m=2,∵点P (m ,n )在双曲线y=-1b 上, ∴mn=-1,∴m 2+n 2=(n+m )2-2mn=4+2=6.9.12 [解析] 由矩形ABCD 的边AB 与x 轴平行,顶点A 的坐标为(2,1),可知点B 的纵坐标为1,点D 的横坐标为2,因为点B 与点D 都在反比例函数y=6b (x>0)的图像上,所以当x=2时,y=3;当y=1时,x=6.即点D 与点B 的坐标分别是(2,3),(6,1).则AB=4,AD=2,则矩形ABCD 的周长为12. 10.5 9 [解析] ①∵△OAC 和△BAD 都是等腰直角三角形,∴OC=AC=3,BD=AD=2, ∴OC+BD=5,CD=3-2=1,即B (5,1),∵反比例函数y=b b在第一象限的图像经过点B ,∴k=5×1=5.②设点B (a ,b ),∵△OAC 和△BAD 都是等腰直角三角形, ∴OA=√2AC ,AB=√2AD ,OC=AC ,AD=BD , ∵OA 2-AB 2=18, ∴2AC 2-2AD 2=18,即AC 2-AD 2=9,∴(AC+AD )(AC-AD )=9, ∴(OC+BD )·CD=9, ∴ab=9,∴k=9.11.解:(1)∵B (-6,0),AD=3,AB=8,E 为CD 的中点,∴E (-3,4),A (-6,8).∵反比例函数图像过点E (-3,4), ∴m=-3×4=-12.设图像经过A ,E 两点的一次函数表达式为:y=kx+b , ∴{-6b +b =8,-3b +b =4,解得{b =-43,b =0,∴y=-43x.(2)连接AE ,∵AD=3,DE=4,∴AE=5.∵AF-AE=2,∴AF=7,∴BF=1.设点E 横坐标为a ,则E 点坐标为(a ,4),点F 坐标为(a-3,1),∵E ,F 两点在y=bb 的图像上, ∴4a=a-3,解得a=-1, ∴E (-1,4), ∴m=-4, ∴y=-4b .12.解:(1)由表中数据得:xy=600,∴y=600b ,∴所求函数关系式为y=600b .(2)由题意得(x-10)y=450, 把y=600b代入得:(x-10)·600b=450,解得x=40,经检验,x=40是原方程的根,且符合题意.所以若该小组计划每天的销售利润为450元,则其单价应为40元.13.B [解析] ①∵双曲线y=bb 的一支在第一象限,∴k>0,∴在每个象限内,y 随x 的增大而减小,故①正确;②∵点B 的横坐标为3,∴y=-33=-1,∴BD=1.∵4BD=3CD ,∴CD=43,∴点C 的坐标为3,43,故②错误;③设点B 的坐标为x ,-3b .∵4BD=3CD ,BD=3b ,则CD=4b ,∴点C 的坐标为x ,4b,∴k=x ·4b=4,故③正确;④设点B 的横坐标为x ,则其纵坐标为-3b,故点C 的纵坐标为4b,则BC=4b +3b =7b,则△ABC 的面积为12·x ·7b=3.5,故④错误.14.解:(1)作CE ⊥AB ,垂足为E ,∵AC=BC ,AB=4,∴AE=BE=2.在Rt △BCE 中,BC=52,BE=2,∴CE=32,∵OA=4,∴C 点的坐标为52,2, ∵点C 在y=bb 的图像上,∴k=5.(2)设A 点的坐标为(m ,0),∵BD=BC=52,∴AD=32,∴D ,C 两点的坐标分别为m ,32,m-32,2. ∵点C ,D 都在y=bb 的图像上,∴32m=2m-32,∴m=6,∴C 点的坐标为92,2,作CF ⊥x 轴,垂足为F ,∴OF=92,CF=2,在Rt △OFC 中,OC 2=OF 2+CF 2,∴OC=√972.。
福建省福州市2019年中考数学复习第三章函数第三节反比例函数及其应用同步训练

第三节 反比例函数及其应用姓名:________ 班级:________ 限时:______分钟1.(2018·徐州)如果点(3,-4)在反比例函数y =kx 的图象上,那么下列各点中,在此图象上的点是( ) A .(3,4)B .(-2,-6)C .(-2,6)D .(-3,-4)2.(2017·镇江)a 、b 是实数,点A(2,a)、B(3,b)在反比例函数y =-2x 的图象上,则( )A .a<b<0B .b<a<0C .a<0<bD .b<0<a3.(2018·龙岩质检)在同一直角坐标系中,函数y =kx和y =kx +1的大致图象可能是( )4.(2018·临沂)如图,正比例函数y 1=k 1x 与反比例函数y 2=k 2x 的图象相交于A 、B 两点,其中点A的横坐标为1,当y 1<y 2时,x 的取值范围是( )A .x <1或x >1B .-1<x <0或x >1C .-1<x <0或0<x <1D .x <-1或0<x <15.(2018·天津)若点A(x 1,-6),B(x 2,-2),C(x 3,2)在反比例函数y =12x 的图象上,则x 1,x 2,x 3的大小关系是( ) A .x 1<x 2<x 3B .x 2<x 1<x 3C .x 2<x 3<x 1D .x 3<x 2<x 16.(2018·嘉兴)如图,点C 在反比例函数y =kx(x >0)的图象上,过点C 的直线与x 轴,y 轴分别交于点A ,B ,且AB =BC ,△AOB 的面积为1,则k 的值为( )A .1B .2C .3D .47.(2018·莆田质检)如图,点A ,B 分别在反比例函数y =1x (x >0),y =ax (x <0)的图象上,若OA⊥OB,OBOA=2,则a 的值为( )A .-4B .4C .-2D .28.(2018·郴州)如图,A ,B 是反比例函数y =4x 在第一象限内的图象上的两点,且A ,B 两点的横坐标分别是2和4,则△AOB 的面积是( )A .4B .3C .2D .19.(2018·重庆B 卷)如图,菱形ABCD 的边AD⊥y 轴,垂足为点E ,顶点A 在第二象限,顶点B 在y 轴的正半轴上,反比例函数y =kx (k≠0,x >0)的图象同时经过顶点C ,D.若点C 的横坐标为5,BE =3DE ,则k 的值为( )A.52B .3C.154D .510.(2018·云南省卷)已知点P(a ,b)在反比例函数y =2x 的图象上,则ab =________.11.(2018·宜宾)已知:点P(m ,n)在直线y =-x +2上,也在双曲线y =-1x 上,则m 2+n 2的值为________.12.(2018·陕西)若一个反比例函数的图象经过点A(m ,m)和B(2m ,-1),则这个反比例函数的表达式为________.13.(2018·随州)如图,一次函数y =x -2的图象与反比例函数y =kx (k >0)的图象相交于A 、B 两点,与x 轴交于点C ,若tan ∠AOC=13,则k 的值为________.14.(2018·衢州)如图,点A ,B 是反比例函数y =kx (x >0)图象上的两点,过点A ,B 分别作AC⊥x轴于点C ,BD⊥x 轴于点D ,连接OA ,BC ,已知点C(2,0),BD =2,S △BCD =3,则S △AOC =________.15.(2018·漳州质检)如图,双曲线y =k x (x >0)经过A ,B 两点,若点A 的横坐标为1,∠OAB=90°,且OA =AB ,则k 的值为________.16 .(2018·盐城)如图,点D 为矩形OABC 的AB 边的中点,反比例函数y =kx (x >0)的图象经过点D ,交BC 边于点E.若△BDE 的面积为1,则k =________.17.(2018·南平质检)如图,反比例函数y =kx (k≠0)与一次函数y =ax +b (b≠0)相交于点A(1,3),B(c ,-1).(Ⅰ)求反比例函数与一次函数的解析式;(Ⅱ)在反比例函数图象上存在点C ,使△AOC 为等腰三角形,这样的点有几个,请直接写出一个以AC 为底边的等腰三角形顶点C 的坐标.18.(2018·山西)如图,一次函数y 1=k 1x +b(k 1≠0)的图象分别与x 轴、y 轴相交于点A 、B ,与反比例函数y 2=k 2x (k 2≠0)的图象相交于点C(-4,-2),D(2,4).(1)求一次函数和反比例函数的表达式; (2)当x 为何值时,y 1>0;(3)当x 为何值时,y 1<y 2,请直接写出x 的取值范围.19.(2018·泰安)如图,矩形ABCD 的两边AD 、AB 的长分别为3、8,E 是DC 的中点,反比例函数y =mx的图象经过点E ,与AB 交于点F. (1)若点B 的坐标为(-6,0),求m 的值及图象经过A 、E 两点的一次函数的表达式; (2)若AF -AE =2,求反比例函数的表达式.20.(2018·杭州)设一次函数y=kx+b(k,b 是常数,k≠0)的图象过A(1,3),B(-1,-1)两点.(1)求该一次函数的表达式;(2)若点(2a+2,a2)在一次函数图象上,求a的值;(3)已知点C(x1,y1),D(x2,y2)在该一次函数图象上,设m=(x1-x2)(y1-y2),判断反比例函数y=m+1x的图象所在的象限,说明理由.21.(2018·凉州区)如图,一次函数y =x +4的图象与反比例函数y =kx (k 为常数且k≠0)的图象交于A(-1,a),B 两点,与x 轴交于点C. (1)求此反比例函数的表达式;(2)若点P 在x 轴上,且S △ACP =32S △BOC ,求点P 的坐标.22.(2018·湘潭)如图,点M 在函数y =3x (x >0)的图象上,过点M 分别作x 轴和y 轴的平行线交函数y =1x (x >0)的图象于点B 、C.(1)若点M 的坐标为(1,3). ①求B 、C 两点的坐标; ②求直线BC 对应的函数解析式; (2)求△BMC 的面积.23.(2018·江西)如图,反比例函数y =kx (k≠0)的图象与正比例函数y =2x 的图象相交于A(1,a),B 两点,点C 在第四象限,CA ∥y 轴,∠ABC=90°.(1)求k 的值及点B 的坐标; (2)求tan C 的值.1.(2018·泉州质检)如图,反比例函数y =kx 的图象经过正方形ABCD 的顶点A 和中心E ,若点D 的坐标为(-1,0),则k 的值为( )A .2B .-2 C.12D .-122.(2018·福州质检)如图,直线y 1=-43x 与双曲线y 2=kx 交于A ,B 两点,点C 在x 轴上,连接AC ,BC ,若∠ACB=90°,△ABC 的面积为10,则k 的值是______.3.(2018·宁德质检)如图,点A ,D 在反比例函数y =mx (m <0)的图象上,点B ,C 在反比例函数y=nx(n >0)的图象上,若AB∥CD∥x 轴,AC∥y 轴,且AB =4,AC =3,CD =2,则n =________.4.(2018·荆门)如图,在平面直角坐标系xOy 中,函数y =kx (k >0,x >0)的图象经过菱形OACD 的顶点D 和边AC 的中点E ,若菱形OACD 的边长为3,则k 的值为______.5.(2018·安徽)如图,正比例函数y =kx 与反比例函数y =6x 的图象有一个交点A(2,m),AB⊥x轴于点B ,平移直线y =kx ,使其经过点B ,得到直线l .则直线l 对应的函数表达式是________.6. (2018·厦门质检)已知点A ,B 在反比例函数y =6x (x >0)的图象上,且横坐标分别为m ,n ,过点A ,B 分别向y 轴、x 轴作垂线段,两条垂线段交于点C ,过点A ,B 分别作AD⊥x 轴于D ,BE⊥y轴于E.(1)若m=6,n=1,求点C的坐标;(2)若m(n-2)=3,当点C在直线DE上时,求n的值.7.(2018·北京)在平面直角坐标系xOy中,函数y=kx(x>0)的图象G经过点A(4,1),直线l:y=14x+b与图象G交于点B,与y轴交于点C.(1)求k的值;(2)横、纵坐标都是整数的点叫做整点,记图象G在点A,B之间的部分与线段OA,OC,BC围成的区域(不含边界)为W.①当b=-1时,直接写出区域W内的整点个数;②若区域W内恰有4个整点,结合函数图象,求b的取值范围.参考答案【基础训练】1.C 2.A 3.A 4.D 5.B 6.D 7.A 8.B 9.C 10.2 11.6 12.y =4x 13.3 14.5 15.1+5216.417.解: (Ⅰ)把A(1,3)代入y =kx (k≠0)中得,k =3×1=3,∴反比例函数的解析式为y =3x ,把B(c ,-1)代入y =3x 中,得c =-3,把A(1,3),B(-3,-1)代入y =ax +b 中,得⎩⎪⎨⎪⎧a +b =3,-3a +b =-1,∴⎩⎪⎨⎪⎧a =1,b =2. ∴一次函数的解析式为y =x +2.(Ⅱ)如解图,这样的点有4个,以AC 为底边的有C 1(1,3),C 2(3,1)或C 3(-3,-1)或C 4(-1,-3).18.解: ∵一次函数y 1=k 1x +b(k≠0)的图象经过点C(-4,-2),D(2,4),∴⎩⎪⎨⎪⎧-4k 1+b =-22k 1+b =4,解得⎩⎪⎨⎪⎧k 1=1,b =2, ∴一次函数的表达式为y 1=x +2;∵反比例函数y 2=k 2x (k≠0)的图象经过点D(2,4),∴4=k 22,∴k 2=8,∴反比例函数的表达式为y 2=8x.(2)由y 1>0,得x +2>0, ∴x>-2,∴当x >-2时,y 1>0. (3)x <-4或0<x <2.19.解: (1)∵B(-6,0),AD =3,AB =8,E 为CD 的中点,∴E(-3,4),A(-6,8). ∵反比例函数图象过点E(-3,4),∴m=-3×4=-12. 设图象经过A 、E 两点的一次函数表达式为:y =kx +b(k≠0),∴⎩⎪⎨⎪⎧-6k +b =8,-3k +b =4, 解得⎩⎪⎨⎪⎧k =-43,b =0.∴y=-43x.(2)∵AD=3,DE =4,∴AE=5. ∵AF-AE =2,∴AF=7,∴BF=1.设E 点坐标为(a ,4),则F 点坐标为(a -3,1). ∵E,F 两点在y =mx 的图象上,∴4a =a -3,解得a =-1,∴E(-1,4),∴m=-4,∴y=-4x.20.解: (1)将A(1,3),B(-1,-1)代入y =kx +b 中,得出⎩⎪⎨⎪⎧k +b =3,-k +b =-1, ,解得⎩⎪⎨⎪⎧k =2,b =1.∴一次函数的表达式为y =2x +1. (2)∵点(2a +2,a 2)在该一次函数图象上, ∴ a 2=2(2a +2)+1,∴a 2-4a -5=0, 解得a 1=5,a 2=-1.(3)由题意知, y 1-y 2=(2x 1+1)-(2x 2+1)=2(x 1-x 2), ∴m=(x 1-x 2)(y 1-y 2)=2(x 1-x 2)2≥0, ∴m+1≥1>0,∴反比例函数y =m +1x 的图象在第一、三象限.21.解: (1)把点A(-1,a)代入y =x +4,得a =3, ∴A(-1,3).把A(-1,3)代入反比例函数y =kx ,得k =-3.∴反比例函数的表达式为y =-3x .(2)联立两个函数表达式:⎩⎪⎨⎪⎧y =x +4,y =-3x ,解得⎩⎪⎨⎪⎧x =-1,y =3,或⎩⎪⎨⎪⎧x =-3,y =1.∴点B 的坐标为(-3,1).当y =x +4=0时,得x =-4, ∴点C(-4,0). 设点P 的坐标为(x ,0). ∵S △ACP =32S △BOC ,∴12×3×|x-(-4)|=32×12×4×1, 解得x 1=-6,x 2=-2. ∴点P(-6,0)或(-2,0).22.解: (1)①∵点M 的坐标为(1,3), 且B 、C 在函数y =1x (x >0)的图象上,∴点C 横坐标为1,纵坐标为1, 点B 纵坐标为3,横坐标为13,即点C 坐标为(1,1),点B 坐标为(13,3).②设直线BC 对应函数解析式为y =kx +b(k≠0), 把B 、C 点坐标分别代入得⎩⎪⎨⎪⎧1=k +b ,3=13k +b ,解得⎩⎪⎨⎪⎧k =-3,b =4.∴直线BC 对应的函数解析式为:y =-3x +4. (2)设点M 的坐标为(a ,b), ∵点M 在函数y =3x (x >0)的图象上,∴ab=3.易知点C 坐标为(a ,1a ),B 点坐标为(1b ,b),∴BM=a -1b =ab -1b ,MC =b -1a =ab -1a ,∴S △BMC =12·ab -1b ·ab -1a =12×(ab -1)2ab =23.23.解: (1)把A(1,a)代入y =2x ,得a =2,则A(1,2), 把A(1,2)代入y =kx ,得k =1×2=2,∴反比例函数的解析式为y =2x ,联立方程⎩⎪⎨⎪⎧y =2x ,y =2x,得⎩⎪⎨⎪⎧x =1,y =2,或⎩⎪⎨⎪⎧x =-1,y =-2,, ∴B 点坐标为(-1,-2); (2)设AC 与x 轴交于点D ,Rt △ABC 中,∠ABC=90°, ∴∠C+∠A=90°Rt △AOD 中,∠A+∠AOD=90°,∴∠C=∠AOD, ∴tan C =ADOD =2.【拔高训练】1.B 2.-6 3.83 4.2 5 5.y =32x -36.解: (1)∵当m =6时,y =66=1,又∵n=1,∴C(1,1).(2)∵点A ,B 的横坐标分别为m ,n , ∴A(m,6m ),B(n ,6n )(m >0,n >0).∴D(m,0),E(0,6n ),C(n ,6m).设直线DE 对应的函数表达式为y =kx +b(k≠0), 把D(m ,0),E(0,6n )分别代入表达式,可得y =-6mn x +6n .∵点C 在直线DE 上,∴把C(n ,6m )代入y =-6mn x +6n,化简得m =2n.把m =2n 代入m(n -2)=3,得2n(n -2)=3. 解得n =2±102.∵n>0,∴n=2+102.7.(1)解:∵点A(4,1)在y =kx (x>0)的图象上.∴k4=1, ∴k=4.(2)① 3个.(1,0),(2,0),(3,0).②a .当直线过(4,0)时:14×4+b =0,解得b =-1,b .当直线过(5,0)时:14×5+b =0,解得b =-54,第7题解图①c .当直线过(1,2)时:14×1+b =2,解得b =74, d .当直线过(1,3)时:14×1+b =3,解得b =114第7题解图②∴综上所述:-54≤b<-1或74<b≤114.。
中考数学总复习《反比例函数的性质》练习题及答案

中考数学总复习《反比例函数的性质》练习题及答案班级:___________姓名:___________考号:_____________一、单选题1.对于反比例函数y=2x,下列说法正确是()A.图象经过点(2,﹣1)B.图象位于第二、四象限C.图象是中心对称图形D.当x<0时,y随x的增大而增大2.对于反比例函数y=2x,下列说法不正确的是()A.当x<0时,y随x的增大而减小B.点(-2,-1)在它的图象上C.它的图象在第一、三象限D.当x>0时,y随x的增大而增大3.如图,过y轴上任意一点P,作x轴的平行线,分别与反比例函数y=4x和y=2x的图象交于A点和B点,若C为x轴上任意一点,连接AC,BC,则△ABC的面积为()A.3B.4C.5D.64.已知反比例函数y=k x的图象如图所示,则一次函数y=kx+k的图象经过()A.第一、二、三象限B.第二、三、四象限C.第一、二、四象限D.第一、三、四象限5.若点M(﹣3,a),N(4,﹣6)在同一个反比例函数的图象上,则a的值为()A.8B.﹣8C.﹣7D.56.函数y=1x+√x的图象在()A.第一象限B.第一、三象限C.第二象限D.第二、四象限7.图所示矩形ABCD中,BC=x,CD=y,y与x满足的反比例函数关系如图2所示,等腰直角三角形AEF的斜边EF过C点,M为EF的中点,则下列结论正确的是A.当x=3时,EC<EM B.当y=9时,EC>EMC.当x增大时,EC·CF的值增大。
D.当y增大时,BE·DF的值不变。
8.已知函数y=−k 2+1x的图象经过点P1(x1,y1),P2(x2,y2),如果x2<0<x1,那么()A.0<y2<y1B.y1>0>y2C.y2<y1<0D.y1<0<y29.已知双曲线y=k−1x向右平移2个单位后经过点(4,1),则k的值等于()A.1B.2C.3D.510.对于反比例函数y=k x(k≠0),下列说法正确的是()A.当k>0时,y随x增大而增大B.当k<0时,y随x增大而增大C.当k>0时,该函数图象在二、四象限D.若点(1,2)在该函数图象上,则点(2,1)也必在该函数图象上11.下列关于反比例函数y=8x的描述,正确的是()A.它的图象经过点(12,4)B.图象的两支分别在第二、四象限C.当x>2时,0<y<4D.x>0时,y随x的增大而增大12.反比例函数y= 1x的图象的两个分支分别位于()象限.A.一、二B.一、三C.二、四D.一、四二、填空题13.如图,已知点A、B在双曲线y= k x(x>0)上,AC△x轴于点C,BD△y轴于点D,AC与BD 交于点P,P是AC的中点,若△ABP的面积为3,则k=.14.如图,矩形ABCD的顶点A和对称中心在反比例函数y=k x(k≠0,x>0)的图象上,若矩形ABCD的面积为16,则k的值为.15.已知反比例函数y= k x(k为常数,k≠0)的图象位于第一、第三象限,写出一个符合条件的k的值为.16.若反比例函数y=﹣mx的图象经过点(﹣3,﹣2),则当x<0时,y随x的增大而.17.若点(4,m)与点(5,n)都在反比例函数y=8x(x≠0)的图象上,则m n(填>,<或=).18.如图,A(1,1),B(2,2),双曲线y= k x与线段AB有公共点,则k的取值范围是。
中考数学考点12反比例函数的图像与性质及实际应用总复习(原卷版)
反比例函数的图像与性质及实际应用【命题趋势】在中考中.反比例函数的图像与性质常以选择题和填空形式考查;反比例函数解析式主要在反比例函数综合题中与一次函数、几何图形结合考查。
【中考考查重点】一、结合具体情境体会反比例函数的意义.能根据已知条件确定反比例函数的表达式;二、能画出反比例函数的图像.根据图像和表达式探索并理解k>0和k<0时.图像的变化情况;三、结合具体情境体会反比例函数的意义四、能用反比例函数解决简单实际问题考点一:反比例函数的概念一般地.形如.叫做反比例函数.自变量x的取值概念范围是≠0的一切实数【提分要点】反比例函数图像上的点的横纵坐标之积是定值k1.(2021秋•南召县期末)下列函数是y关于x的反比例函数的是()A.y=B.y=C.y=﹣D.y=﹣2.(2021•门头沟区一模)在物理实验室实验中.为了研究杠杆的平衡条件.设计了如下实验.如图.铁架台左侧钩码的个数与位置都不变.在保证杠杆水平平衡的条件下.右侧采取变动钩码数量即改变力F.或调整钩码位置即改变力臂L.确保杠杆水平平衡.则力F与力臂L满足的函数关系是()A.正比例函数关系B.反比例函数关系C.一次函数关系D.二次函数关系3.(2021秋•越秀区校级期末)函数y=(m﹣1)x|m|﹣2是反比例函数.则m的值为.考点二:反比例函数的图像与性质概念kk >0k <0图像所在象限一、三二、四增减性 在每个象限内.y 随x 的增大而减少在每个象限内.y 随x 的增大而增大图像特征图像无限接近于坐标轴.但不与坐标轴相交;关于直线y=±x 成轴对称;关于原点成中心对称4.(2021秋•南开区期末)若反比例函数y =的图象在其所在的每一象限内.y 随x的增大而减小.则k 的取值范围是( ) A .k <﹣2B .k >﹣2C .k <2D .k >25.(2021秋•揭阳期末)点(x 1.y 1)、(x 2.y 2)、(x 3.y 3)在反比例函数y =﹣的图象上.且x 1<0<x 2<x 3.则有( ) A .y 1<y 2<y 3B .y 2<y 3<y 1C .y 1<y 3<y 2D .y 3<y 2<y 16.(2020秋•浦东新区校级期末)已知函数y =kx .y 随x 的增大而减小.另有函数.两个函数在同一平面直角坐标系内的大致图象可能是( )A .B .C .D .7.(2020秋•孝义市期末)近视眼镜的度数y (度)与镜片焦距x (米)之间具有如图所示的反比例函数关系.若要配制一副度数小于400度的近视眼镜.则镜片焦距x 的取值范围是( )A .0米<x <0.25米B .x >0.25米C .0米<x <0.2米D .x >0.2米考点三:反比例函数系数k 的几何意义8.(2021秋•铁西区期末)如图.A 是反比例函数y =的图象上一点.过点A 作AB ⊥y 轴于点B .点C 在x 轴上.且S △ABC =2.则k 的值为( )K 的几何意义在反比例函数上任取一点P(x.y),过这个点分别作x 轴.y 轴的垂线PM 、PN.于坐标轴围成的矩形PMON 的面积S=PM ·PN===k基本图形面积基本图形面积A .4B .﹣4C .﹣2D .29.(2021•铜仁市)如图.矩形ABOC 的顶点A 在反比例函数y =的图象上.矩形ABOC 的面积为3.则k= .考点四:反比例函数解析式的确定10.2021秋•房山区期末)若反比例函数的图象经过点(3.﹣2).则该反比例函数的表达式为( ) A .y = B .y =﹣C .y =D .y =﹣11.(2021秋•泰山区期中)如果等腰三角形的面积为6.底边长为x .底边上的高为y .则y 与x 的函数关系式为( ) A .y =B .y =C .y =D .y =12.(2021•江西模拟)小明学习了物理中的杠杆平衡原理发现:阻力×阻力臂=动力待定系数法 1. 设所求反比例函数解析式为:2. 找出反比例函数图像上一点P (a,b ).并将其代入解析式得k=ab ;3. 确定反比例函数解析式利用k 得几何意义 题中已知面积时.考虑利用k 得几何意义.由面积得.再综合图像所在象限判段k 得正负.从而得出k 的值.代入解析式即可×动力臂.现已知某一杠杆的阻力和阻力臂分别为2400N和1m.则动力F(单位:N)关于动力臂l(单位:m)的函数图象大致是()A.B.C.D.1.(2021秋•隆回县期中)下面的函数是反比例函数的是()A.y=B.y=C.y=D.y=2.(2021秋•大东区期末)如果反比例函数的图象经过点P(﹣3.﹣1).那么这个反比例函数的表达式为()A.y=B.y=﹣C.y=x D.y=﹣x 3.(2021春•海淀区校级月考)某物体对地面的压力为定值.物体对地面的压强p(Pa)与受力面积S(m2)之间的函数关系如图所示.这一函数表达式为()A.B.C.D.4.(2020秋•瓜州县期末)如图.在某温度不变的条件下.通过一次又一次地对气缸顶部的活塞加压.测出每一次加压后气缸内气体的体积V(mL)与气体对气缸壁产生的压强p(kPa)的关系可以用如图所示的反比例函数图象进行表示.下列说法错误的是()A.气压p与体积V表达式为p=.则k>0B.当气压p=70时.体积V的取值范围为70<V<80C.当体积V变为原来的时.对应的气压p变为原来的D.当60≤V≤100时.气压p随着体积V的增大而减小5.(2020秋•东莞市校级期末)已知点(3.y1).(﹣2.y2).(2.y3)都在反比例函数的图象上.那么y1.y2与y3的大小关系是()A.y3<y1<y2B.y3<y2<y1C.y1<y2<y3D.y1<y3<y2 6.(2021秋•西湖区期中)已知y1和y2均是以x为自变量的函数.当x=m时.函数值分别是M1和M2.若存在实数m.使得M1+M2=1.则称函数y1和y2具有性质P.以下函数y1和y2不具有性质P的是()A.y1=x2+2x和y2=﹣x﹣1B.y1=x2+2x和y2=﹣x+1C.y1=﹣和y2=﹣x﹣1D.y1=﹣和y2=﹣x+17.(2021秋•会宁县期末)如图.A.B是反比例函数的图象上关于原点对称的两点.BC ∥x轴.AC∥y轴.若△ABC的面积为6.则k的值是.8.(2021春•沙坪坝区校级期末)已知函数y=(m﹣1)是反比例函数.则m的值为.1.(2018•柳州)已知反比例函数的解析式为y=.则a的取值范围是()A.a≠2B.a≠﹣2C.a≠±2D.a=±2 2.(2020•上海)已知反比例函数的图象经过点(2.﹣4).那么这个反比例函数的解析式是()A.y=B.y=﹣C.y=D.y=﹣3.(2021•黔西南州)对于反比例函数y=.下列说法错误的是()A.图象经过点(1.﹣5)B.图象位于第二、第四象限C.当x<0时.y随x的增大而减小D.当x>0时.y随x的增大而增大4.(2021•济南)反比例函数y=(k≠0)图象的两个分支分别位于第一、三象限.则一次函数y=kx﹣k的图象大致是()A.B.C.D.5.(2021•宜昌)某气球内充满了一定质量m的气体.当温度不变时.气球内气体的气压p(单位:kPa)是气体体积V(单位:m3)的反比例函数:p=.能够反映两个变量p和V函数关系的图象是()A.B.C.D.6.(2021•沈阳)如图.平面直角坐标系中.O是坐标原点.点A是反比例函数y=(k≠0)图象上的一点.过点A分别作AM⊥x轴于点M.AN⊥y轴于点N.若四边形AMON 的面积为12.则k的值是.7.(2021•阜新)已知点A(x1.y1).B(x2.y2)都在反比例函数y=﹣的图象上.且x1<0<x2.则y1.y2的关系一定成立的是()A.y1>y2B.y1<y2C.y1+y2=0D.y1﹣y2=0 8.(2020•大庆)已知正比例函数y=k1x和反比例函数y=.在同一平面直角坐标系下的图象如图所示.其中符合k1•k2>0的是()A.①②B.①④C.②③D.③④9.(2021•自贡)已知蓄电池的电压为定值.使用蓄电池时.电流I(单位:A)与电阻R (单位:Ω)是反比例函数关系.它的图象如图所示.下列说法正确的是()A.函数解析式为I=B.蓄电池的电压是18VC.当I≤10A时.R≥3.6ΩD.当R=6Ω时.I=4A10.(2020•河北)如图是8个台阶的示意图.每个台阶的高和宽分别是1和2.每个台阶凸出的角的顶点记作T m(m为1~8的整数).函数y=(x<0)的图象为曲线L.(1)若L过点T1.则k=;(2)若L过点T4.则它必定还过另一点T m.则m=;(3)若曲线L使得T1~T8这些点分布在它的两侧.每侧各4个点.则k的整数值有个.1.(2021•抚顺模拟)下列函数中.y是x的反比例函数的是()A.B.C.D.2.(2021•卧龙区二模)已知反比例函数.在下列结论中.不正确的是()A.图象必经过点(﹣1.﹣2)B.图象在第一、三象限C.若x<﹣1.则y<﹣2D.点A(x1.y1).B(x2.y2)图象上的两点.且x1<0<x2.则y1<y23.(2021•富阳区二模)已知反比例函数y=.当﹣2<x<﹣1.则下列结论正确的是()A.﹣3<y<0B.﹣2<y<﹣1C.﹣10<y<﹣5D.y>﹣104.(2021•武陟县模拟)某气球内充满了一定质量的气体.当温度不变时.气球内气体的气压P(kpa)是气体体积V(m3)的反比例函数其图象如图所示.当气体体积为1m3时.气压为()kPa.A.150B.120C.96D.84 5.(2021•云岩区模拟)阿基米德说:“给我一个支点.我就能撬动整个地球”这句话精辟地阐明了一个重要的物理学知识﹣﹣杠杆原理.即“阻力×阻力臂=动力×动力臂”.若已知某一杠杆的阻力和阻力臂分别为1200N和0.5m.则这一杠杆的动力F和动力臂l之间的函数图象大致是()A.B.C.D.6.(2021•昆明模拟)如图.点P在双曲线第一象限的图象上.P A⊥x轴于点A.则△OP A的面积为()A .2B .3C .4D .67.(2021•乐陵市一模)为预防新冠病毒.某学校每周末用药熏消毒法对教室进行消毒.已知药物释放过程中.教室内每立方米空气中含药量y (mg )与时间t (h )成正比例;药物释放完毕后.y 与t 成反比例.如图所示.根据图象信息.下列选项错误的是( )A .药物释放过程需要小时B .药物释放过程中.y 与t 的函数表达式是y =tC .空气中含药量大于等于0.5mg /m 3的时间为hD .若当空气中含药量降低到0.25mg /m 3以下时对身体无害.那么从消毒开始.至少需要经过4.5小时学生才能进入教室8.(2021•山西模拟)已知.A (﹣3.n ).C (3n ﹣6.2)是反比例函数y =(x <0)图象上的两点.则反比例函数的解析式为 .9.(2021•雁塔区校级模拟)已知同一象限内的两点A (3.n ).B (n ﹣4.n +3)均在反比例函数y =的图象上.则该反比例函数关系式为 .10.(2021•昭通模拟)若函数y =是关于x 的反比例函数.则a 满足的条件是 .。
【教育资料精选】2019年中考数学第三单元函数及其图象课时训练12反比例函数练习(新版)浙教版
课时训练(十二) 反比例函数|夯实基础|1.[2017·枣庄] 如图K12-1,O是坐标原点,菱形OABC的顶点A的坐标为(-3,4),顶点C在x轴的负半轴上,函数y=(x<0)的图象经过顶点B,则k的值为()图K12-1A.-12B.-27C.-32D.-362.[2018·威海] 若点(-2,y1),(-1,y2),(3,y3)在双曲线y=(k<0)上,则y1,y2,y3的大小关系是()A.y1<y2<y3B.y3<y2<y1C.y2<y1<y3D.y3<y1<y23.[2018·临沂] 如图K12-2,正比例函数y1=k1x与反比例函数y2=的图象相交于A,B两点,其中点A的横坐标为1,当y1<y2时,x的取值范围是()图K12-2A.x<-1或x>1B.-1<x<0或x>1C.-1<x<0或0<x<1D.x<-1或0<x<14.[2018·广州] 一次函数y=ax+b和反比例函数y=在同一直角坐标系中大致图象是()K12-35.[2018·重庆A卷] 如图K12-4,在平面直角坐标系中,菱形ABCD的顶点A,B在反比例函数y=(k>0,x>0)的图象上,横坐标分别为1,4,对角线BD∥x轴.若菱形ABCD的面积为,则k的值为()图K12-4A.B.C.4D.56.[2018·温州] 如图K12-5,点A,B在反比例函数y=(x>0)的图象上,点C,D在反比例函数y=(x>0)的图象上,AC∥BD∥y轴,已知点A,B的横坐标分别为1,2,△OAC与△ABD的面积之和为,则k的值为()图K12-5A.4B.3C.2D.7.[2017·泰州] 如图K12-6,P为反比例函数y=(k>0)在第一象限内图象上的一点,过点P分别作x轴,y轴的垂线交一次函数y=-x-4的图象于点A,B,若∠AOB=135°,则k的值是()图K12-6A.2B.4C.6D.88.已知点P(3,-2)在反比例函数y=(k≠0)的图象上,则k=;在第四象限中,函数值y随x的增大而.9.[2017·连云港] 设函数y=与y=-2x-6的图象的交点坐标为(a,b),则+的值是.10.[2018·盐城] 如图K12-7,点D为矩形OABC的边AB的中点,反比例函数y=(x>0)的图象经过点D,交BC边于点E.若△BDE的面积为1,则k=.图K12-711.[2017·温州] 如图K12-8,矩形OABC的边OA,OC分别在x轴、y轴上,点B在第一象限,点D在边BC上,且∠AOD=30°,四边形OA'B'D与四边形OABD关于直线OD对称(点A'和A,B和B'分别对应),若AB=1,反比例函数y=(k≠0)的图象恰好经过点A',B,则k的值为.图K12-812.[2018·衢州] 如图K12-9,点A,B是反比例函数y=(x>0)图象上的两点,过点A,B分别作AC⊥x轴于点C,BD⊥x轴于点D,连结OA,BC,已知点C(2,0),BD=2,S△BCD=3,则S△AOC=.图K12-913.[2018·杭州] 已知一艘轮船上装有100吨货物,轮船到达目的地后开始卸货,设平均卸货速度为v(单位:吨/时),卸完这批货物所需的时间为t(单位:时).(1)求v关于t的函数表达式;(2)若要求不超过5小时卸完船上的这批货物,那么平均每小时至少要卸货多少吨?14.[2018·南充] 如图K12-10,直线y=kx+b(k≠0)与双曲线y=(m≠0)交于点A-,2,B(n,-1).(1)求直线与双曲线的解析式;(2)点P在x轴上,如果S△ABP=3,求点P的坐标.图K12-10。
中考数学复习----反比例函数之定义、图像与性质知识点总结与练习题(含答案解析)
中考数学复习----反比例函数之定义、图像与性质知识点总结与练习题(含答案解析)知识点总结1. 反比例函数的定义:形如()0≠=k xky 的函数叫做反比例函数。
有时也用k xy =或1−=kx y 表示。
2. 反比例函数的图像:反比例函数的图像是双曲线。
3. 反比例函数的性质与图像:反比例函数()0≠=k xky k 的符号0>k0<k所在象限一、三象限二、四象限大致图像增减性在一个支上(每一个象限内),y 随x 的增大而减小。
在一个支上(每一个象限内),y 随x 的增大而增大。
对称性图像关于原点对称练习题1.(2022•黔西南州)在平面直角坐标系中,反比例函数y =xk(k ≠0)的图像如图所示,则一次函数y =kx +2的图像经过的象限是( ) A .一、二、三 B .一、二、四C .一、三、四D .二、三、四【分析】先根据反比例函数的图像位于二,四象限,可得k <0,由一次函数y =kx +2中,k <0,2>0,可知它的图像经过的象限. 【解答】解:由图可知:k <0,∴一次函数y =kx +2的图像经过的象限是一、二、四. 故选:B .2.(2022•上海)已知反比例函数y =xk(k ≠0),且在各自象限内,y 随x 的增大而增大,则下列点可能在这个函数图像上的为( ) A .(2,3)B .(﹣2,3)C .(3,0)D .(﹣3,0)【分析】根据反比例函数的性质判断即可.【解答】解:因为反比例函数y =(k ≠0),且在各自象限内,y 随x 的增大而增大, 所以k <0,A .2×3=6>0,故本选项不符合题意;B .﹣2×3=﹣6<0,故本选项符合题意;C .3×0=0,故本选项不符合题意;D .﹣3×0=0,故本选项不符合题意; 故选:B .3.(2022•广东)点(1,y 1),(2,y 2),(3,y 3),(4,y 4)在反比例函数y =x4图像上,则y 1,y 2,y 3,y 4中最小的是( ) A .y 1B .y 2C .y 3D .y 4【分析】根据k >0可知增减性:在每一象限内,y 随x 的增大而减小,根据横坐标的大小关系可作判断. 【解答】解:∵k =4>0,∴在第一象限内,y 随x 的增大而减小,∵(1,y 1),(2,y 2),(3,y 3),(4,y 4)在反比例函数y =图像上,且1<2<3<4, ∴y 4最小. 故选:D .4.(2022•云南)反比例函数y =x6的图像分别位于( ) A .第一、第三象限 B .第一、第四象限 C .第二、第三象限D .第二、第四象限【分析】根据反比例函数的性质,可以得到该函数图像位于哪几个象限,本题得以解决.【解答】解:反比例函数y =,k =6>0, ∴该反比例函数图像位于第一、三象限, 故选:A .5.(2022•镇江)反比例函数y =xk(k ≠0)的图像经过A (x 1,y 1)、B (x 2,y 2)两点,当x 1<0<x 2时,y 1>y 2,写出符合条件的k 的值 (答案不唯一,写出一个即可). 【分析】先根据已知条件判断出函数图像所在的象限,再根据系数k 与函数图像的关系解答即可.【解答】解:∵反比例函数y =(k ≠0)的图像经过A (x 1,y 1)、B (x 2,y 2)两点,当x 1<0<x 2时,y 1>y 2,∴此反比例函数的图像在二、四象限, ∴k <0,∴k 可为小于0的任意实数,例如,k =﹣1等. 故答案为:﹣1.6.(2022•福建)已知反比例函数y =xk的图像分别位于第二、第四象限,则实数k 的值可以是 .(只需写出一个符合条件的实数)【分析】根据图像位于第二、四象限,易知k <0,写一个负数即可. 【解答】解:∵该反比例图像位于第二、四象限, ∴k <0,∴k 取值不唯一,可取﹣3, 故答案为:﹣3(答案不唯一).7.(2022•成都)在平面直角坐标系xOy 中,若反比例函数y =xk 2−的图像位于第二、四象限,则k 的取值范围是 .【分析】根据反比例函数的性质列不等式即可解得答案. 【解答】解:∵反比例函数y =的图像位于第二、四象限,∴k ﹣2<0, 解得k <2, 故答案为:k <2.8.(2022•襄阳)二次函数y =ax 2+bx +c 的图像如图所示,则一次函数y =bx +c 和反比例函数y =xa在同一平面直角坐标系中的图像可能是( ) A . B .C .D .【分析】根据二次函数图像开口向下得到a <0,再根据对称轴确定出b ,根据与y 轴的交点确定出c <0,然后确定出一次函数图像与反比例函数图像的情况,即可得解. 【解答】解:∵二次函数图像开口方向向下, ∴a <0,∵对称轴为直线x =﹣>0,∴b >0,∵与y 轴的负半轴相交, ∴c <0,∴y =bx +c 的图像经过第一、三、四象限, 反比例函数y =图像在第二四象限, 只有D 选项图像符合. 故选:D .9.(2022•菏泽)根据如图所示的二次函数y =ax 2+bx +c 的图像,判断反比例函数y =xa与一次函数y =bx +c 的图像大致是( )A .B .C .D .【分析】先根据二次函数的图像,确定a 、b 、c 的符号,再根据a 、b 、c 的符号判断反比例函数y =与一次函数y =bx +c 的图像经过的象限即可. 【解答】解:由二次函数图像可知a >0,c <0, 由对称轴x =﹣>0,可知b <0,所以反比例函数y =的图像在一、三象限,一次函数y =bx +c 图像经过二、三、四象限. 故选:A .10.(2022•安顺)二次函数y =ax 2+bx +c (a ≠0)的图像如图所示,则一次函数y =ax +b 和反比例函数y =xc(c ≠0)在同一直角坐标系中的图像可能是( ) A . B .C .D .【分析】直接利用二次函数图像经过的象限得出a ,b ,c 的取值范围,进而利用一次函数与反比例函数的性质得出答案.【解答】解:∵二次函数y =ax 2+bx +c 的图像开口向上, ∴a >0,∵该抛物线对称轴位于y 轴的右侧, ∴a 、b 异号,即b <0. ∵抛物线交y 轴的负半轴,∴c <0,∴一次函数y =ax +b 的图像经过第一、三、四象限,反比例函数y =(c ≠0)在二、四象限. 故选:A .11.(2022•西藏)在同一平面直角坐标系中,函数y =ax +b 与y =axb(其中a ,b 是常数,ab ≠0)的大致图像是( )A .B .C .D .【分析】根据a 、b 的取值,分别判断出两个函数图像所过的象限,要注意分类讨论. 【解答】解:若a >0,b >0,则y =ax +b 经过一、二、三象限,反比例函数y =(ab ≠0)位于一、三象限,若a >0,b <0,则y =ax +b 经过一、三、四象限,反比例函数数y =(ab ≠0)位于二、四象限, 若a <0,b >0,则y =ax +b 经过一、二、四象限,反比例函数y =(ab ≠0)位于二、四象限, 若a <0,b <0,则y =ax +b 经过二、三、四象限,反比例函数y =(ab ≠0)位于一、三象限, 故选:A .12.(2022•张家界)在同一平面直角坐标系中,函数y =kx +1(k ≠0)和y =xk(k ≠0)的图像大致是( )A.B.C.D.【分析】分k>0或k<0,根据一次函数与反比例函数的性质即可得出答案.【解答】解:当k>0时,一次函数y=kx+1经过第一、二、三象限,反比例函数y=位于第一、三象限;当k<0时,一次函数y=kx+1经过第一、二、四象限,反比例函数y=位于第二、四象限;故选:D.13.(2022•绥化)已知二次函数y=ax2+bx+c的部分函数图像如图所示,则一次函数y=ax+b2﹣4ac与反比例函数y=xc ba++24在同一平面直角坐标系中的图像大致是()A.B.C.D.【分析】由二次函数y=ax2+bx+c的部分函数图像判断a,b2﹣4ac及4a+2b+c的符号,即可得到答案.【解答】解:∵二次函数y=ax2+bx+c的部分函数图像开口向上,∴a>0,∵二次函数y =ax 2+bx +c 的部分函数图像顶点在x 轴下方,开口向上, ∴二次函数y =ax 2+bx +c 的图像与x 轴有两个交点,b 2﹣4ac >0, ∴一次函数y =ax +b 2﹣4ac 的图像位于第一,二,三象限,由二次函数y =ax 2+bx +c 的部分函数图像可知,点(2,4a +2b +c )在x 轴上方, ∴4a +2b +c >0, ∴y =的图像位于第一,三象限,据此可知,符合题意的是B , 故选:B .14.(2022•贺州)已知一次函数y =kx +b 的图像如图所示,则y =﹣kx +b 与y =xb的图像为( )A .B .C .D .【分析】本题形数结合,根据一次函数y =kx +b 的图像位置,可判断k 、b 的符号;再由一次函数y =﹣kx +b ,反比例函数y =中的系数符号,判断图像的位置.经历:图像位置﹣系数符号﹣图像位置.【解答】解:根据一次函数y =kx +b 的图像位置,可判断k >0、b >0. 所以﹣k <0.再根据一次函数和反比例函数的图像和性质, 故选:A .15.(2022•广西)已知反比例函数y =xb(b ≠0)的图像如图所示,则一次函数y =cx ﹣a (c ≠0)和二次函数y =ax 2+bx +c (a ≠0)在同一平面直角坐标系中的图像可能是( )A .B .C .D .【分析】本题形数结合,根据反比例函数y =(b ≠0)的图像位置,可判断b >0;再由二次函数y =ax 2+bx +c (a ≠0)的图像性质,排除A ,B ,再根据一次函数y =cx ﹣a (c ≠0)的图像和性质,排除C .【解答】解:∵反比例函数y =(b ≠0)的图像位于一、三象限, ∴b >0;∵A 、B 的抛物线都是开口向下,∴a <0,根据同左异右,对称轴应该在y 轴的右侧, 故A 、B 都是错误的.∵C 、D 的抛物线都是开口向上,∴a >0,根据同左异右,对称轴应该在y 轴的左侧, ∵抛物线与y 轴交于负半轴, ∴c <0由a >0,c <0,排除C . 故选:D .16.(2022•滨州)在同一平面直角坐标系中,函数y =kx +1与y =﹣xk(k 为常数且k ≠0)的图像大致是( )A .B .C .D .【分析】根据一次函数和反比例函数的性质即可判断.【解答】解:当k >0时,则﹣k <0,一次函数y =kx +1图像经过第一、二、三象限,反比例函数图像在第二、四象限,所以A 选项正确,C 选项错误;当k <0时,一次函数y =kx +1图像经过第一、二,四象限,所以B 、D 选项错误. 故选:A .17.(2022•德阳)一次函数y =ax +1与反比例函数y =﹣xa在同一坐标系中的大致图像是( )A .B .C .D .【分析】根据一次函数与反比例函数图像的特点,可以从a >0,和a <0,两方面分类讨论得出答案.【解答】解:分两种情况:(1)当a >0,时,一次函数y =ax +1的图像过第一、二、三象限,反比例函数y =﹣图像在第二、四象限,无选项符合;(2)当a <0,时,一次函数y =ax +1的图像过第一、二、四象限,反比例函数y =﹣图像在第一、三象限,故B 选项正确. 故选:B .18.(2022•阜新)已知反比例函数y =x k (k ≠0)的图像经过点(﹣2,4),那么该反比例函数图像也一定经过点( )A .(4,2)B .(1,8)C .(﹣1,8)D .(﹣1,﹣8)【分析】先把点(﹣2,4)代入反比例函数的解析式求出k 的值,再对各选项进行逐一判断即可.【解答】解:∵反比例函数y =(k ≠0)的图像经过点(﹣2,4),∴k =﹣2×4=﹣8,A 、∵4×2=8≠﹣8,∴此点不在反比例函数的图像上,故本选项错误;B 、∵1×8=8≠﹣8,∴此点不在反比例函数的图像上,故本选项错误;C 、﹣1×8=﹣8,∴此点在反比例函数的图像上,故本选项正确;D 、(﹣1)×(﹣8)=8≠﹣8,∴此点不在反比例函数的图像上,故本选项错误. 故选:C .19.(2022•襄阳)若点A (﹣2,y 1),B (﹣1,y 2)都在反比例函数y =x2的图像上,则y 1,y 2的大小关系是( )A .y 1<y 2B .y 1=y 2C .y 1>y 2D .不能确定 【分析】根据反比例函数图像上点的坐标特征即可求解.【解答】解:∵点A (﹣2,y 1),B (﹣1,y 2)都在反比例函数y =的图像上,k =2>0,∴在每个象限内y 随x 的增大而减小,∵﹣2<﹣1,∴y 1>y 2,故选:C .20.(2022•海南)若反比例函数y =xk (k ≠0)的图像经过点(2,﹣3),则它的图像也一定经过的点是( )A .(﹣2,﹣3)B .(﹣3,﹣2)C .(1,﹣6)D .(6,1) 【分析】将(2,﹣3)代入y =(k ≠0)即可求出k 的值,再根据k =xy 解答即可.【解答】解:∵反比例函数y =(k ≠0)的图像经过点(2,﹣3),∴k =2×(﹣3)=﹣6,A 、﹣2×(﹣3)=6≠﹣6,故A 不正确,不符合题意;B 、(﹣3)×(﹣2)=6≠﹣6,故B 不正确,不符合题意;C 、1×(﹣6)=﹣6,故C 正确,符合题意,D 、6×1=6≠﹣6,故D 不正确,不符合题意.故选:C .21.(2022•武汉)已知点A (x 1,y 1),B (x 2,y 2)在反比例函数y =x6的图像上,且x 1<0<x 2,则下列结论一定正确的是( )A .y 1+y 2<0B .y 1+y 2>0C .y 1<y 2D .y 1>y 2 【分析】先根据反比例函数y =判断此函数图像所在的象限,再根据x 1<0<x 2判断出A (x 1,y 1)、B (x 2,y 2)所在的象限即可得到答案.【解答】解:∵反比例函数y =中的6>0,∴该双曲线位于第一、三象限,且在每一象限内y 随x 的增大而减小,∵点A (x 1,y 1),B (x 2,y 2)在反比例函数y =的图像上,且x 1<0<x 2,∴点A 位于第三象限,点B 位于第一象限,∴y 1<y 2.故选:C .22.(2022•天津)若点A (x 1,2),B (x 2,﹣1),C (x 3,4)都在反比例函数y =x8的图像上,则x 1,x 2,x 3的大小关系是( )A .x 1<x 2<x 3B .x 2<x 3<x 1C .x 1<x 3<x 2D .x 2<x 1<x 3 【分析】根据函数解析式算出三个点的横坐标,再比较大小.【解答】解:点A (x 1,2),B (x 2,﹣1),C (x 3,4)都在反比例函数y =的图像上, ∴x 1==4,x 2==﹣8,x 3==2. ∴x 2<x 3<x 1,故选:B .23.(2022•淮安)在平面直角坐标系中,将点A (2,3)向下平移5个单位长度得到点B ,若点B 恰好在反比例函数y =xk 的图像上,则k 的值是 .【分析】点A (2,3)向下平移5个单位长度得到点B (2,﹣2),代入y =利用待定系数法即可求得k 的值.【解答】解:将点A (2,3)向下平移5个单位长度得到点B ,则B (2,﹣2), ∵点B 恰好在反比例函数y =的图像上,∴k =2×(﹣2)=﹣4,故答案为:﹣4.24.(2022•北京)在平面直角坐标系xOy 中,若点A (2,y 1),B (5,y 2)在反比例函数y =xk (k >0)的图像上,则y 1 y 2(填“>”“=”或“<”). 【分析】先根据函数解析式中的比例系数k 确定函数图像所在的象限,再根据各象限内点的坐标特征及函数的增减性解答.【解答】解:∵k >0,∴反比例函数y =(k >0)的图像在一、三象限,∵5>2>0,∴点A (2,y 1),B (5,y 2)在第一象限,y 随x 的增大而减小,∴y 1>y 2,故答案为:>.。
中考数学总复习《反比例函数》练习题(附答案)
中考数学总复习《反比例函数》练习题(附答案)班级:___________姓名:___________考号:_____________一、单选题1.一次函数y1=k1x+b(k1≠0)与反比例函数y2=k2x(k2≠0)的图象交于点A(−1,−2),点B(2,1).当y1<y2时,x的取值范围是()A.x<−1B.−1<x<0或x>2 C.0<x<2D.0<x<2或x<−12.关于函数y=−2x,下列说法中正确的是()A.图像位于第一、三象限B.图像与坐标轴没有交点C.图像是一条直线D.y的值随x的值增大而减小3.如图,在直角坐标系中,点A是双曲线y= 3x(x>0)上的一个动点,点B是x轴正半轴上的一个定点,当点A的横坐标逐渐增大时,△OAB的面积将会()A.逐渐减小B.不变C.逐渐增大D.先减小后增大4.在同一平面直角坐标系中,反比例函数y=-8x与一次函数y=-x+2交于A,B两点,O为坐标原点,则△AOB的面积为()A.2B.6C.10D.85.如图,△ABC的三个顶点分别为A(1,2),B(4,2),C(4,4).若反比例函数y= k x在第一象限内的图象与△ABC有交点,则k的取值范围是()A.1≤k≤4B.2≤k≤8C.2≤k≤16D.8≤k≤166.如图,过反比例函数y= 1x(x>0)的图象上任意两点A、B分别作x轴的垂线,垂足分别为C、D,连接OA、OB,设AC与OB的交点为E,△AOE与梯形ECDB的面积分别为S1、S2,比较它们的大小,可得()A.S1>S2B.S1=S2C.S l<S2D.大小关系不能确定7.某村耕地总面积为50公顷,且该村人均耕地面积y(单位:公顷/人)与总人口x(单位:人)的函数图象如图所示,则下列说法正确的是()A.该村人均耕地面积随总人口的增多而增多B.该村人均耕地面积y与总人口x成正比例C.若该村人均耕地面积为2公顷,则总人口有100人D.当该村总人口为50人时,人均耕地面积为1公顷8.在同一直角坐标系中,函数y=kx+1与y=−k x(k≠0)的图象大致是()A.B.C.D.9.如图,在平面直角坐标系xOy中,函数y=kx+b(k≠0)与y= mx(m≠0)的图象相交于点A(-2,3),B(6,-1),则不等式kx+b>mx的解集为()A.x<−2B.−2<x<0或x>6 C.x<6D.0<x<6或x<−210.已知两个函数y1=k1x+b与y2= k2x的图象如图所示,其中A(-1,2),B(2,-1),则不等式k1x+b>k2x的解集为()A.x<−1或x>2B.x<−1或0<x<2 C.−1<x<2D.−1<x<0或0<x<211.在反比例函数y=−3x图象上有三个点A(x1,y1)、B(x2,y2)、C(x3,y3),若x1<0<x2<x3,则下列结论正确的是()A.y3<y2<y1B.y1<y3<y2C.y2<y3<y1D.y3<y1<y2 12.图所示矩形ABCD中,BC=x,CD=y,y与x满足的反比例函数关系如图2所示,等腰直角三角形AEF的斜边EF过C点,M为EF的中点,则下列结论正确的是A.当x=3时,EC<EM B.当y=9时,EC>EMC.当x增大时,EC·CF的值增大。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
课时训练(十二)反比例函数
(限时:45分钟)
|夯实基础|
1.[2018·凉山州]若ab<0,则正比例函数y=ax与反比例函数y=在同一坐标系中的大致图像可能是
()
图K12-1
2.[2018·无锡]已知点P(a,m),Q(b,n)都在反比例函数y=-的图像上,且a<0<b,则下列结论一定成立的是()
A.m+n<0
B.m+n>0
C.m<n
D.m>n
3.[2017·台州]已知电流I(安培)、电压U(伏特)、电阻R(欧姆)之间的关系为I=,当电压为定值时,I 关于R的函数图像是()
图K12-2
4.[2018·黄石]已知一次函数y1=x-3和反比例函数y2=的图像在平面直角坐标系中交于A,B两点,当y1>y2时,x的取值范围是()
图K12-3
A.x<-1或x>4
B.-1<x<0或x>4
C.-1<x<0或0<x<4
D.x<-1或0<x<4
5.如图K12-4,已知动点A,B分别在x轴,y轴正半轴上,动点P在反比例函数y=(x>0)的图像上,PA⊥x 轴,△PAB是以PA为底边的等腰三角形.当点A的横坐标逐渐增大时,△PAB的面积将会 ()
图K12-4
A.越来越小
B.越来越大
C.不变
D.先变大后变小
6.[2018·莱芜]在平面直角坐标系中,已知△ABC为等腰直角三角形,CB=CA=5,点C(0,3),点B在x轴正半轴上,点A在第三象限,且在反比例函数y=的图像上,则k=()
A.3
B.4
C.6
D.12
7.[2018·上海]已知反比例函数y=(k是常数,k≠1)的图像有一支在第二象限,那么k的取值范围是.
8.[2018·宜宾]已知:点P(m,n)在直线y=-x+2上,也在双曲线y=-上,则m2+n2的值为.
9.[2018·张家界]如图K12-5,矩形ABCD的边AB与x轴平行,顶点A的坐标为(2,1),点B与点D都在反比例函数y=(x>0)的图像上,则矩形ABCD的周长为.
图K12-5
10.[2018·唐山丰润区一模]如图K12-6,△OAC和△BAD都是等腰直角三角形,∠ACO=∠ADB=90°,反比例函数y=在第一象限的图像经过点B.
图K12-6
①若OC=3,BD=2,则k= ;
②若OA2-AB2=18.则k= .
11.[2018·泰安]如图K12-7,矩形ABCD的两边AD,AB的长分别为3,8,E是DC的中点,反比例函数y=(x<0)的图像经过点E,与AB交于点F.
图K12-7
(1)若点B坐标为(-6,0),求m的值及图像经过A,E两点的一次函数的表达式;
(2)若AF-AE=2,求反比例函数的表达式.
12.为了筹款支持希望工程,某“爱心”小组决定利用暑假销售一批进价为10元的小商品,为寻求合适的销售价格,他们进行了试销,试销情况如下表:
(1)若y是x的反比例函数,请求出这个函数关系式;
(2)若该小组计划每天的销售利润为450元,则其单价应为多少元?
|拓展提升|
13.如图K12-8,双曲线y=(k≠0)与y=-中的一支分别位于第一、四象限,A是y轴上任意一点,B是双曲线y=-上的点,C是双曲线y=(k≠0)上的点,线段BC⊥x轴于点D,且4BD=3CD,则下列说法:①双曲线y=(k≠0)在每个象限内,y随x的增大而减小;②若点B的横坐标为3,则点C的坐标为;③k=4;④△ABC 的面积为定值7.正确的有()
图K12-8
A.1个
B.2个
C.3个
D.4个
14.[2018·唐山丰润区一模]如图K12-9,在△ABC中,AC=BC,AB⊥x轴,垂足为A.反比例函数y=(x>0)的图像经过点C,交AB于点D.已知AB=4,BC=.
图K12-9
(1)若OA=4,求k的值;
(2)连接OC,若BD=BC,求OC的长.
参考答案
1.B
2.D[解析] ∵a<0<b,∴x=a时,m=y=->0,x=b时,n=y=-<0,∴m>n.
3.C
4.B
5.C[解析] 如图,过点B作BC⊥PA于点C,则BC=OA,
设点P x,,则S△PAB=PA·BC=··x=3,
当点A的横坐标逐渐增大时,△PAB的面积不变,始终等于3.
6.A[解析] 如图,作AH⊥y轴于H.
∵CA=CB,∠AHC=∠BOC,∠ACH=∠CBO,
∴△ACH≌△CBO,
∴AH=OC,CH=OB,
∵C(0,3),BC=5,
∴OC=3,OB==4,
∴CH=OB=4,AH=OC=3,
∴OH=1,
∴A(-3,-1),
∵点A在y=的图像上,
∴k=3.
7.k<1
8.6[解析] ∵点P(m,n)在直线y=-x+2上,
∴n+m=2,∵点P(m,n)在双曲线y=-上,
∴mn=-1,∴m2+n2=(n+m)2-2mn=4+2=6.
9.12[解析] 由矩形ABCD的边AB与x轴平行,顶点A的坐标为(2,1),可知点B的纵坐标为1,点D的横坐标为2,因为点B与点D都在反比例函数y=(x>0)的图像上,所以当x=2时,y=3;当y=1时,x=6.即点D与点B的坐标分别是(2,3),(6,1).则AB=4,AD=2,则矩形ABCD的周长为12.
10.59[解析] ①∵△OAC和△BAD都是等腰直角三角形,
∴OC=AC=3,BD=AD=2,
∴OC+BD=5,CD=3-2=1,
即B(5,1),∵反比例函数y=在第一象限的图像经过点B,∴k=5×1=5.
②设点B(a,b),
∵△OAC和△BAD都是等腰直角三角形,
∴OA=AC,AB=AD,OC=AC,AD=BD,
∵OA2-AB2=18,
∴2AC2-2AD2=18,
即AC2-AD2=9,
∴(AC+AD)(AC-AD)=9,
∴(OC+BD)·CD=9,
∴ab=9,∴k=9.
11.解:(1)∵B(-6,0),AD=3,AB=8,E为CD的中点,
∴E(-3,4),A(-6,8).
∵反比例函数图像过点E(-3,4),
∴m=-3×4=-12.
设图像经过A,E两点的一次函数表达式为:y=kx+b,
∴解得
∴y=-x.
(2)连接AE,∵AD=3,DE=4,∴AE=5.
∵AF-AE=2,∴AF=7,∴BF=1.
设点E横坐标为a,则E点坐标为(a,4),点F坐标为(a-3,1),
∵E,F两点在y=的图像上,
∴4a=a-3,解得a=-1,
∴E(-1,4),
∴m=-4,
∴y=-.
12.解:(1)由表中数据得:xy=600,
∴y=,
∴所求函数关系式为y=.
(2)由题意得(x-10)y=450,
把y=代入得:(x-10)·=450,
解得x=40,
经检验,x=40是原方程的根,且符合题意.
所以若该小组计划每天的销售利润为450元,则其单价应为40元.
13.B[解析] ①∵双曲线y=的一支在第一象限,∴k>0,∴在每个象限内,y随x的增大而减小,故①正确;
②∵点B的横坐标为3,∴y=-=-1,∴BD=1.
∵4BD=3CD,∴CD=,∴点C的坐标为3,,故②错误;③设点B的坐标为x,-.∵4BD=3CD,BD=,则CD=,
∴点C的坐标为x,,∴k=x·=4,故③正确;④设点B的横坐标为x,则其纵坐标为-,故点C的纵坐标为,则BC=+=,则△ABC的面积为·x·=3.5,故④错误.
14.解:(1)作CE⊥AB,垂足为E,
∵AC=BC,AB=4,∴AE=BE=2.
在Rt△BCE中,BC=,BE=2,∴CE=,
∵OA=4,∴C点的坐标为,2,
∵点C在y=的图像上,∴k=5.
(2)设A点的坐标为(m,0),
∵BD=BC=,∴AD=,
∴D,C两点的坐标分别为m,,m-,2.∵点C,D都在y=的图像上,
∴m=2m-,
∴m=6,∴C点的坐标为,2,
作CF⊥x轴,垂足为F,
∴OF=,CF=2,
在Rt△OFC中,OC2=OF2+CF2,
∴OC=.。
