思维导图图解初中数学知识ppt课件
合集下载
思维导图数学篇ppt课件

8
三 同化记忆
思维导图具有极大的可伸缩性,它顺应了我们大 脑的自然思维模式。从而,可以使我们的主观意 图自然地在图上表达出来。它能够将新旧知识结 合起来。学习的过程是一个由浅入深的过程,在 这个过程中,将新旧知识结合起来是一件很重要 的事情,因为人总是在已有知识的基础上学习新 的知识,在学习新知识时,要把新知识与原有认 知结构相结合,改变原有认知结构,把新知识同 化到自己的知识结构中,能否具有建立新旧知识 之间的联系是学习的关键。
25
解题思维导图
26
解题过程
27
函数的单调性
课堂练习:
用定义证明
f
(x)
x x2
1
在[1,)上是减函数.
28
用定义证明
判号
定论
变形
作差
设元
f ( x1 ) f ( x2 )
任取 x 1, x 2 假设 x
[1,x12 1 x2 2 1
34
例子
35
四、思维导图在小组合作学习中的应用
运用思维导图进行小组合作学习,可以在很大程度 上改变传统合作学习表面上热热闹闹,实质上糊里 糊涂,不能取得实质进展的面貌。独立完成思维导 图,让每个成员依据自己的水平与能力,踏实地思 考解决问题的方法,运用思维导图记录观点;在组 长组织下有序讨论,每个成员看到了别人的思维过 程;教师也可以对讨论进行有效的监控和引导,通 过交流、对比与决策,最终寻求到更为有效的解决 办法,使合作学习真正落实到实处。
在数学教学中运用思维导图,重要的一点是在 思维导图的帮助下,通过教师引导、学生独立思考, 逐渐培养学生运用知识解决问题的能力,达到提高 数学能力、学会学习的目标。思维导图还是一个新 事物,如何更好地运用它改善教师的教,促进学生 的学,还有很长的路要走。
三 同化记忆
思维导图具有极大的可伸缩性,它顺应了我们大 脑的自然思维模式。从而,可以使我们的主观意 图自然地在图上表达出来。它能够将新旧知识结 合起来。学习的过程是一个由浅入深的过程,在 这个过程中,将新旧知识结合起来是一件很重要 的事情,因为人总是在已有知识的基础上学习新 的知识,在学习新知识时,要把新知识与原有认 知结构相结合,改变原有认知结构,把新知识同 化到自己的知识结构中,能否具有建立新旧知识 之间的联系是学习的关键。
25
解题思维导图
26
解题过程
27
函数的单调性
课堂练习:
用定义证明
f
(x)
x x2
1
在[1,)上是减函数.
28
用定义证明
判号
定论
变形
作差
设元
f ( x1 ) f ( x2 )
任取 x 1, x 2 假设 x
[1,x12 1 x2 2 1
34
例子
35
四、思维导图在小组合作学习中的应用
运用思维导图进行小组合作学习,可以在很大程度 上改变传统合作学习表面上热热闹闹,实质上糊里 糊涂,不能取得实质进展的面貌。独立完成思维导 图,让每个成员依据自己的水平与能力,踏实地思 考解决问题的方法,运用思维导图记录观点;在组 长组织下有序讨论,每个成员看到了别人的思维过 程;教师也可以对讨论进行有效的监控和引导,通 过交流、对比与决策,最终寻求到更为有效的解决 办法,使合作学习真正落实到实处。
在数学教学中运用思维导图,重要的一点是在 思维导图的帮助下,通过教师引导、学生独立思考, 逐渐培养学生运用知识解决问题的能力,达到提高 数学能力、学会学习的目标。思维导图还是一个新 事物,如何更好地运用它改善教师的教,促进学生 的学,还有很长的路要走。
初中数学思维导图精选幻灯片

字
不改变 分式的值
公因式
通分
通分化 成同分
母
数与代数3-1
分母不变 分子相加
减
注:分子、 分母为多 子积为子 项式时先 母积为母 分解因式
基本性质
分式
代 数 式
化除法为
乘法
运算
乘除 乘方
a b
n
an bn
n为整数
分式方程 应用
an
1 an
n为整数
去分母 整式方程
解法
解方程
突出重点 精简整合
内在逻辑关系
如:代数式“先分散,后集 中”,预备知识与方程问题 有机整合,整式中归纳提高
内
知识横向联系
在
逻
辑
有弹性保基础供发展
关
系
螺旋上升的概念思想
如:加强数形,用坐标的方 法处理更多内容(二元一次 方程组.平移.对称.函数等)
如:按照“说点儿理”“说理”“推 理”“符号表示推理”等不同层次,分阶 段培养推理能力,内容注重基础,留有发
6
三、教材内容
y
y
b>0,图象在
Y
一二三象限 o
x
随
o
b>0,图象在 x 一二四象限
Y
随
x 的
y
y
x 的
增 大
b=0,图象在 一三象限
o 注意x:过原点o
b=0,图象在 x 二四象限
增 大
而 增
y
y
而 减
大 b<0,图象在
一三四象限
o
x
o
b<0,图象在 x 二三四象限
小
一条直线
=kx+b,k≠0, k,b为常数
初中数学知识结构图思维导图(与“性质”相关文档)共10张PPT
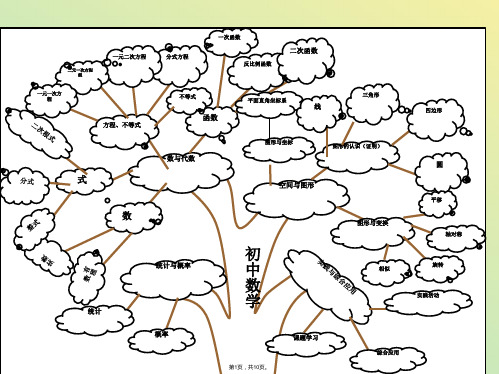
法
公式
法
配方
法
直接
有一交点
( b,0)
2a
Δ=0
有两个等根
b x1= x2 = 2a
开平 方法
无交
Δ<0点Βιβλιοθήκη 关系 二次函数无实 根
解法
一元二次方程
应用
传播问题 行程问题 效率问题
与y轴交点位置 c>0.在正
开向口上方向a<. 0.向a>下0.对置称轴在左y同轴右的异位半负轴半轴c=0.在原点
c<0.在
余角.补角
性质
等角的余角相等 等角的补角相等
和 为1800
相
定义 性质
等
一“放”二“靠” 三“推”四“画”
角的比较
角的比较与运算
对邻
垂
顶补
直
角角
画法
同位角相等
角的度量
借助角研究平面内两条直 线的位置关系
相交线
图形认识初步
关系
相交线.平行线
判定
条件
内错角相等 同旁内角互补
平行线
平行公理.推论
性质
同位角相等 内错角相等
特
对应点与旋转中心所连线段的夹角=
征
旋转角
图形的 全等变 换
旋转角=1800
中心对称图形
旋转
中心对称
旋转1800后与 其自身 重合
对称中心是对称点连线的中 点
对应线段 平行且相等
动
应用
利用平移制作图 案
平移过程 对应点坐标 的变化规律
( x,y ) 平 移 后 (x±a,y±b)
右加左减
上加下减
图案设计
直线.射线.线段
同旁内角互补
初中数学知识结构图思维导图 精品优选公开课件

动
应用
性质
特征
对应角相等, 周长的比=相似比 方
对应边成比例, 面积的比=相似比的平
适合判定 所有三角 形 全等
AAS ASA SAS
角平分线
条件
全等三角形
SSS
对应边、角、周长 面积、中线、高线、
角平分线相等
性质 表示方法
定义
两个三角形 用符号≌连接
完全重合 两个三角形
关系
位似变换
性质
两角对应 相等
度.分.秒互化
定义.表示 进位.计算 尺规作角
直线公理 表示与画法 寻找射线方法
表示与画法 计算与比较
性质
直线 射线 线段
角的比较
角的比较与运算
对邻
垂
顶补
直
角角
画法
同位角相等
角的度量
借助角研究平面内两条直 线的位置关系
相交线
图形认识初步
关系
相交线.平行线
判定
条件
内错角相等 同旁内角互补
平行线
平行公理.推论
征
旋转角
图形的 全等变 换
旋转角=1800
中心对称图形
旋转
中心对称
旋转1800后与 其自身 重合
对称中心是对称点连线的中 点
对应线段 平行且相等
动
应用
利用平移制作图 案
平移过程 对应点坐标 的变化规律
( x,y ) 平 移 后 (x±a,y±b)
右加左减
上加下减
图案设计
用平移.轴对称和旋转的组合设计图 案
关于中心对称
两图形全等
关于原点对称
旋转1800后与 另一图形 重合
用坐标表示 旋转
应用
性质
特征
对应角相等, 周长的比=相似比 方
对应边成比例, 面积的比=相似比的平
适合判定 所有三角 形 全等
AAS ASA SAS
角平分线
条件
全等三角形
SSS
对应边、角、周长 面积、中线、高线、
角平分线相等
性质 表示方法
定义
两个三角形 用符号≌连接
完全重合 两个三角形
关系
位似变换
性质
两角对应 相等
度.分.秒互化
定义.表示 进位.计算 尺规作角
直线公理 表示与画法 寻找射线方法
表示与画法 计算与比较
性质
直线 射线 线段
角的比较
角的比较与运算
对邻
垂
顶补
直
角角
画法
同位角相等
角的度量
借助角研究平面内两条直 线的位置关系
相交线
图形认识初步
关系
相交线.平行线
判定
条件
内错角相等 同旁内角互补
平行线
平行公理.推论
征
旋转角
图形的 全等变 换
旋转角=1800
中心对称图形
旋转
中心对称
旋转1800后与 其自身 重合
对称中心是对称点连线的中 点
对应线段 平行且相等
动
应用
利用平移制作图 案
平移过程 对应点坐标 的变化规律
( x,y ) 平 移 后 (x±a,y±b)
右加左减
上加下减
图案设计
用平移.轴对称和旋转的组合设计图 案
关于中心对称
两图形全等
关于原点对称
旋转1800后与 另一图形 重合
用坐标表示 旋转
中考数学总复习--初中数学各章节知识图解思维导图82页PPT

中考数学总复习--初中数学各章节知 识图解思维导图
1、纪律是管理关系的形式。——阿法 纳西耶 夫 2、改革如果不讲纪律,就难以成功。
3、道德行为训练,不是通过语言影响 ,而是 让儿童 练习良 好道德 行为, 克服懒 惰、轻 率、不 守纪律 、颓废 等不良 行为。 4、学校没有纪律便如磨房里没有水。 ——夸理、服从集体,养 成儿童 自觉的 纪律性 ,这是 儿童道 德教育 最重要 的部分 。—— 陈鹤琴
16、业余生活要有意义,不要越轨。——华盛顿 17、一个人即使已登上顶峰,也仍要自强不息。——罗素·贝克 18、最大的挑战和突破在于用人,而用人最大的突破在于信任人。——马云 19、自己活着,就是为了使别人过得更美好。——雷锋 20、要掌握书,莫被书掌握;要为生而读,莫为读而生。——布尔沃
1、纪律是管理关系的形式。——阿法 纳西耶 夫 2、改革如果不讲纪律,就难以成功。
3、道德行为训练,不是通过语言影响 ,而是 让儿童 练习良 好道德 行为, 克服懒 惰、轻 率、不 守纪律 、颓废 等不良 行为。 4、学校没有纪律便如磨房里没有水。 ——夸理、服从集体,养 成儿童 自觉的 纪律性 ,这是 儿童道 德教育 最重要 的部分 。—— 陈鹤琴
16、业余生活要有意义,不要越轨。——华盛顿 17、一个人即使已登上顶峰,也仍要自强不息。——罗素·贝克 18、最大的挑战和突破在于用人,而用人最大的突破在于信任人。——马云 19、自己活着,就是为了使别人过得更美好。——雷锋 20、要掌握书,莫被书掌握;要为生而读,莫为读而生。——布尔沃
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
性质 HL
判定
应用
( x,y ) 平 移 后 (x±a,y±b)
右加左减
上加下减
图案设计
用平移.轴对称和旋转的组合设计图 案
关于中心对称
两图形全等
关于原点对称
旋转1800后与 另一图形 重合
用坐标表示 旋转
对称点的坐标符号 相反
8
到角两边距离相等的 点
对应点的坐标比为k或-k
适用于 直角三角形
点到角两边 的距离相 等
看式
子类
型能
口述
性质 ① y ax2 ② y ax2 k
③ y ax h2 ④ y ax h2 k
⑤ y ax2 质
类型 应用
与y轴交点位置 c>0.在正
开口上方a向<. 0.向a>下0.向对置称轴在左y同轴右的异位半 在轴 负半c=轴0.在原点
o
b=0,图象在 二四象限
x
y
y
b<0,图象在
二三四象限
o
x 一条直线 o
x
Y随 x的 增 大 而 减 小
Y随 x的 增大 每象一限而小减 内
图象在 一三象限
y
图象在 二四象限
y
Y随 x的 增大 而增 每一大 象限 内
o
x
双曲线
o
x
k>0
k<0
k>0
k<0
图象
性质
一次函数
最优方案
应用
解析式
形如y=kx+b (k.b为常数,k≠0)
当b=0时,是 正比例函数
关系
K同号时, 有两交点。 K异号时, 有两个、一个 或无交点
图象 性质
一次函 数与反 比例函 数
反比例函数
应用
柱形储藏室轮船卸货 力学问题 电学问题
解析式
形如y k x
(k为常数,k 0)
实际问题,图象在第 一象限
4
看图 象能 口述 性质
y
y
ox
o
1.开口方向 2.顶点坐标 3.对称轴 4.增减性 5.极值
思维导图-分析初中数学的 知识
1
二元一次方程组
一元二次方程
分式方程
知识 一次函数
反比例函数
二次函数
一元一次方 程
方程、不等式
不等式
函数
数与代数
式
数
统计
统计与概率 概率
平面直角坐标系
线
三角形
四边形
图形与坐标
图形的认识(证明)
空间与图形
圆
平移
初 中 数 学
图形与变换
轴对称
相似
旋转
实践活动
课题学习
综合应用
分母 不为零
系数 相加 字母 不变
合并 同类项
加减 同类项
每个单项式 升降幂排列
项 次数
多项式
整式
最高项的次 数
意义
单项式
知识 基本性质 运算
分式
分式方程
乘除 乘方
化除法为乘法
a b
n
an bn
n为整数
an
1 an
n为整数
解法
应用
二次根式
运算 加减
代
数
性质
乘除
定义
字母指数和
一元二次方程
应用
传播问题 行程问题 效率问题
解析
二次函数 与 一元二
次方程
定义
面积问题
y=ax2+bx+c (a.b.c为常数a≠0)
y ax h2 k y ax x1x x2
(a 0)
a 0
ax2+bx+c=0 (a≠0)
5
角平分线
余角.补角
性质
等角的余角相等 等角的补角相等
和 为1800
相
定义 性质
等
一“放”二“靠” 三“推”四“画”
度.分.秒互化
直线公理 表示与画法 寻找射线方法
表示与画法 计算与比较
性质
叠合法 度量法
定义.表示 进位.计算 尺规作角 直线 射线 线段
角的比较
角的比较与运算
对邻
垂
顶补
直
角角
画法
同位角相等
角的度量
借助角研究平面内两条直 线的位置关系
相交线
高.中线.角平分线 三边关系
等
表
边
示
对
定 义
方 法
要 素
等 角
三 线 合 一
等 角 对 等 边
概念
性质
判定
多边形 及其
内角和
等腰三角形
有关的角
三角形
等
已知两边求第三
边
边
三
角 形
弦图 毕达哥拉 斯苏菲尔德
应用
特例
定理
勾股定理
证明 内容
文字.符号图形
互逆命题
内容
文字.符号图形
直角三角形
逆定理
全等
证明
应用
次数
系数
数字因 数
式
a a 0
(1) a a 0双非负
2
(2) a a(a 0) (3) a2 a
3
Y随 x的 增 大 而 增 大
b>0,图象在 一二三象限
y
o
x
y
b>0,图象在
o
x 一二四象限
b=0,图象在 一三象限
b<0,图象在 一三四象限
y
y
注意:过原点
o
x
知三边定形状
锐角三角函数
有关线段
定义
三角 形
解直角三角形
锐角三角函数
定义
计算
三边关系锐角关 系边角关系
应用
坡度 仰.俯角 方位角
正弦
余弦
符号.几何意义. 特殊角的值
特殊值的运算
正切
7
作对称轴 作一点到两点距离相等 离相等(外心)
作等腰三角形 作一点到三点距
翻折后与 另一图形重 合
到两点距离相等的 点
2
逆用公式
不改变 分式的值
通分化成同分 母
平方 差、
公式 提公 法 因式 法
公因式
分母不变 分子相 加减
完全
平方
多项式除以单项式
注:分子、
分母为多
思维导图-分析初中数学的 单项式除以单项式
通分
子积为子母积为母
项式时先 分解因式
同底数幂相除
除法
乘法公式
单项式与多项式 幂的乘法
乘法
运算
分母中 含字母、
旋转中心
旋转方向 旋转角 对应点到旋转中心的距离相等
轴对称
图形的 全等变 换
图形的旋转
旋转前.后的图形全等
特
对应点与旋转中心所连线段的夹角=
征
旋转角
旋转角=1800
中心对称图形
旋转
中心对称
旋转1800后与 其自身 重合
对称中心是对称点连线的中 点
对应线段 平行且相等
动
应用
利用平移制作图 案
平移过程 对应点坐标 的变化规律
c<0.
十字
抛物线与x轴的交点
一元二次方程的根
相乘
x
法 万能
公式
化为
直接
开方
应用
平方
有两交点
Δ >0
有两个不等根
提公 因式
根
(x1,0)( x2,0 )
X1, x2
法
公式
法
配方
法
直接
有一交点
(
b,0)
2a
Δ =0
有两个等根
b x1= x2 = 2a
开平 方法
无交
Δ <0
点
关系
二次函数
无实 根
解法
点到两点 的距离 相等
性质
判定
应用
垂直平分线
定义
对称点
关于轴对称
基本 图形
对称 轴
特征
要素
利用轴对称制作图案
用
坐
作:关于x轴、
标
y轴的对称点
表
示
轴
对
解决几何中的
称
极值问题
基本图形
一条直线
翻折后与 两部分 重合
对称轴 定义
轴对称图形 静
基本图形 方向 距离
前.后图形全等
要素 特征
平移
轴对称变换
静
要
动
素
图形认识初步
关系
相交线.平行线
判定
条件
内错角相等 同旁内角互补
平行线
平行公理.推论
性质
同位角相等 内错角相等
直线.射线.线段
同旁内角互补
多姿多彩的图形
立体图形
平面图形
图形认识初 步 相交线
平行线
命题
分类 结构
辨认 展开图
确定有标记的相对图
点与直线位置关系
6
条件
定义
镶嵌
外角和
内角和 定义
内角和
外角的性质
