信号与系统自测题(第2章 参考答案)
信号与系统第二章习题

rt et ht
sin tut ut 1ut ut 1
t
0
sin
d
τ
u
t
ut
2
1
t 1
sin
τ
d
τut
u
t
2
1 1 costut ut 2
X
20
第
例2-4 计算卷积 f1(t) f2(t),并画出波形。
页
f1 t
f2 t
2
1
1 e t1u t 1
则得
A1 A2 3 3A1 2A2 2
解得
A1 A2
4 7
代入(1)得
ht 4e2t 7e3t ut X
18
例2-3
第
页
已知线性时不变系统的一对激励和响应波形如下图所示,
求该系统对激励的 et sin tut ut 1零状态响应。
et
r t
1
1
O 12
t
对激励和响应分别微分一次,得
t0
因为特解为3,所以 强迫响应是3,自由响应是 4 et e2t
X
12
方法二
第
页
零状态响应rzs t是方程
d2 r dt
t
2
3
dr d
t
t
2r
t
2
t
6ut
且满足rzs 0 rzs0 0的解
(5)
由于上式等号右边有 t项 ,故rzst应含有冲激函数,
从而rzs t 将发生跳变,即 rzs 0 rzs 0
d2 rt 3 d rt 2rt 0
dt2
dt
信号与系统课后题答案

《信号与系统》课程习题与解答第二章习题(教材上册第二章p81-p87)2-1,2-4~2-10,2-12~2-15,2-17~2-21,2-23,2-24第二章习题解答2-1 对下图所示电路图分别列写求电压的微分方程表示。
图(a):微分方程:11222012()2()1()()()2()()()()2()()()c cc di t i t u t e t dtdi t i t u t dtdi t u t dt du t i t i t dt ⎧+*+=⎪⎪⎪+=⎪⇒⎨⎪=⎪⎪⎪=-⎩图(b ):微分方程:⎪⎪⎪⎩⎪⎪⎪⎨⎧-==+++=+++⎰⎰2021'2'21'2'11)(01)(1Ri t v Ri Mi Li dt i Ct e Ri Mi Li dt i C)()(1)(2)()2()(2)()(33020022203304422t e dtd MR t v C t v dt d C R t v dt d C L R t v dt d RL t v dt d M L =+++++-⇒ 图(c)微分方程:dt i C i L t v ⎰==211'101)(⎪⎪⎪⎩⎪⎪⎪⎨⎧===⇒⎰dt t v L i t v L i dtdt v L i dt d)(1)(1)(10110'1122011∵ )(122111213t i dt d L C i i i i +=+=)(0(1]1[][101011022110331t e dt dR t v RL v dt d RR L C v dt d R C R C v dt d CC μ=+++++⇒图(d)微分方程:⎪⎩⎪⎨⎧+-=++=⎰)()()()()(1)()(11111t e t Ri t v t v dt t i C t Ri t e μRC v dt d 1)1(1+-⇒μ)(11t e V CR = ∵)()(10t v t v μ=)()(1)1(0'0t e R v t v R Cv v =+-⇒2-4 已知系统相应的其次方程及其对应的0+状态条件,求系统的零输入响应。
信号与系统课后习题参考答案

1试分别指出以下波形是属于哪种信号?题图1-11-2试写出题1-1图中信号的函数表达式。
1-3已知信号)(1t x 与)(2t x 波形如题图1-3中所示,试作出下列各信号的波形图,并加以标注。
题图1-3⑴)2(1-t x ⑵)1(1t x -⑶)22(1+t x⑷)3(2+t x ⑸)22(2-t x ⑹)21(2t x - ⑺)(1t x )(2t x -⑻)1(1t x -)1(2-t x ⑼)22(1t x -)4(2+t x 1-4已知信号)(1n x 与)(2n x 波形如题图1-4中所示,试作出下列各信号的波形图,并加以标注。
题图1-4⑴)12(1+n x ⑵)4(1n x -⑶)2(1n x ⑷)2(2n x -⑸)2(2+n x ⑹)1()2(22--++n x n x⑺)2(1+n x )21(2n x -⑻)1(1n x -)4(2+n x ⑼)1(1-n x )3(2-n x1-5已知信号)25(t x -的波形如题图1-5所示,试作出信号)(t x 的波形图,并加以标注。
题图1-51-6试画出下列信号的波形图:⑴)8sin()sin()(t t t x ΩΩ=⑵)8sin()]sin(211[)(t t t x ΩΩ+= ⑶)8sin()]sin(1[)(t t t x ΩΩ+=⑷)2sin(1)(t tt x = 1-7试画出下列信号的波形图:⑴)(1)(t u e t x t -+=⑵)]2()1([10cos )(---=-t u t u t e t x t π⑶)()2()(t u e t x t --=⑷)()()1(t u e t x t --=⑸)9()(2-=t u t x ⑹)4()(2-=t t x δ1-8试求出以下复变函数的模与幅角,并画出模与幅角的波形图。
⑴)1(1)(2Ω-Ω=Ωj e j X ⑵)(1)(Ω-Ω-Ω=Ωj j e e j X ⑶Ω-Ω---=Ωj j e e j X 11)(4⑷21)(+Ω=Ωj j X 1-9已知信号)]()([sin )(π--=t u t u t t x ,求出下列信号,并画出它们的波形图。
信号与系统课后习题与解答第二章
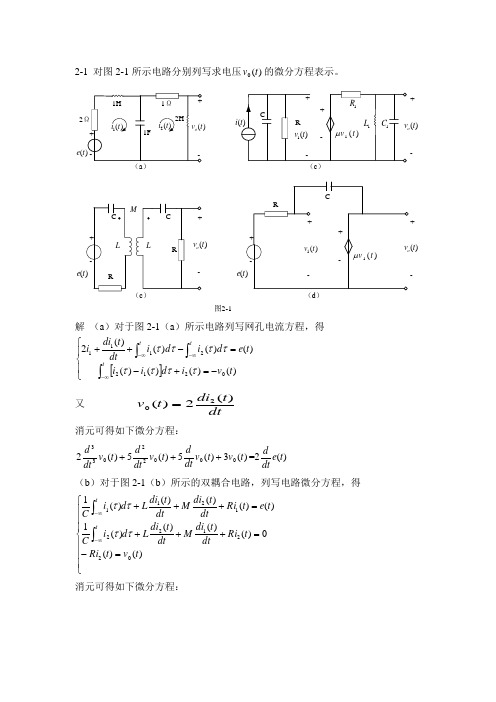
2-1 对图2-1所示电路分别列写求电压)(0t v 的微分方程表示。
2(t ei )(t +-(e )(e )(t +-图2-1解 (a )对于图2-1(a )所示电路列写网孔电流方程,得[]⎪⎩⎪⎨⎧-=+-=-++⎰⎰⎰∞-∞-∞-t t t t v i d i i t e d i d i dt t di i )()()()()()()()(202122111ττττττττ 又 dtt di t v )(2)(20= 消元可得如下微分方程:)(3)(5)(5)(200022033t v t v dt dt v dtd t v dt d +++=2)(te dt d(b )对于图2-1(b )所示的双耦合电路,列写电路微分方程,得⎪⎪⎪⎩⎪⎪⎪⎨⎧=-=+++=+++⎰⎰∞-∞-)()(0)()()()(1)()()()()(10221221211t v t Ri t Ri dt t di M dt t di L d i Ct e t Ri dtt di M dt t di L d i C ttττττ 消元可得如下微分方程:)()(1)(2)(2)(2)()(22020022203304422t e dtd MR t v C t v dt d C R t v dtd R R L t v dtd RL t v dt d M L =++⎪⎭⎫ ⎝⎛+++- (c )对于图2-1(c )所示电路列写电路方程,得⎪⎪⎩⎪⎪⎨⎧=⎥⎦⎤⎢⎣⎡+++=⎰∞-)()()(1)()()()(10101011t v t v dt d C dt t v L R t v R t v t v dt d C t i t μ 消元可得如下微分方程:)()(1)(1)()(101011022110331t i dt dR t v RL t v dt d R R L C t v dt d R C R C t v dt d CC μ=+⎪⎪⎭⎫ ⎝⎛++⎪⎪⎭⎫ ⎝⎛++ (d )对图2-1(d )所示电路列写电路方程,电流)(t i 如图2-2所示,得⎪⎪⎩⎪⎪⎨⎧==+=++⎰∞-)()()()()()()()(1)(1011t v t v t e t v t Ri t e t v d i C t Ri t μμττ 消元可得如下微分方程:(t e )(t +-图2-2)()(1)()1(00t e Rt v R t v dt d Cμμ=+-2-2 图2-3所示为理想火箭推动器模型。
信号系统第3版课后习题答案第二章
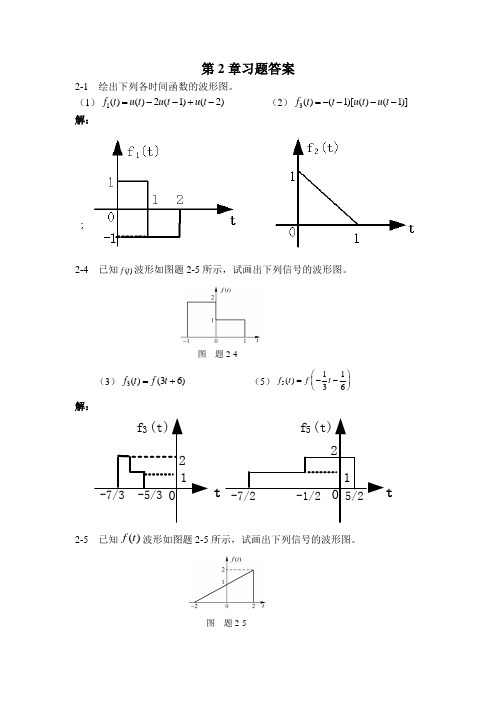
第2章习题答案2-1 绘出下列各时间函数的波形图。
(1)1()()2(1)(2)f t u t u t u t =--+- (2)3()(1)[()(1)]f t t u t u t =----解:2-4 已知()f t 波形如图题2-5所示,试画出下列信号的波形图。
图 题2-4(3)3()(36)f t f t =+ (5)511()36f t f t ⎛⎫=-- ⎪⎝⎭解:tt2-5 已知()ft 波形如图题2-5所示,试画出下列信号的波形图。
图 题2-5(4)4()(2)(2)f t f t u t =-- (6)6()(1)[()(2)]f t f t u t u t =--- 解:2-6 计算下列各式。
(1)0()()f t t t δ+ (2)24e (3)d tt t δ-+⎰(3)e sin (1)d t t t t δ∞-+⎰(4)d [e ()]d tt t δ- (5)00()(2)d t t u t t t δ∞-∞--⎰(6)j 0e [()()]d t t t t t Ωδδ∞--∞--⎰(7)'e [()()]d t t t t δδ∞--∞+⎰(8)(1cos )()(/2)d t u t t t δπ∞-∞--⎰解:(1) 原式0()()f t t δ=(2)原式2334(3)e t dt e δ---=+=⎰(3)原式1sin(1)(1)0(()1)e t t dt δδ+∞-=-++=⎰不在积分区间内 (4)原式)()](['0t t e dtd δδ==(5)原式⎩⎨⎧<>=-=--=⎰∞+∞-0100)()2()(000000t t t u dt t t u t t δ(6)原式000[()()]1j t j t e t e t t dt e δδ+∞-Ω-Ω-∞=--=-⎰ (7)原式'00()()2tt t tt t de e t dt e t dt e dtδδ-+∞+∞---=-∞-∞==+=-=⎰⎰(8)原式/2(1cos )()1t t u t π==-=2-8 已知()f t 的波形如图题2-13所示,求()f t '和()f t '',并分别画出()f t '和()f t ''的波形图。
智慧树答案信号与系统(西安交通大学)知到课后答案章节测试2022年

绪论1.图像增强属于系统综合。
答案:对2.这门课程中研究的信号是确定性信号。
答案:对第一章1.ω0越大,离散时间序列sin(ω0n)的频率越高。
答案:错2.离散时间信号在n1≦n≦n2区间的平均功率为答案:错3.一切物理可实现的连续时间系统都是因果的。
答案:错4.对任意的线性系统,当输入为零时输出也一定为零。
答案:对5.已知信号x当n<—2或n>4时等于零,则x当()时一定等于零。
答案:n<-7和n>-16.某系统的输入输出关系为y=,则该系统是一个()系统。
答案:因果不稳定7.离散时间信号的基波频率是()。
答案:8.在信号与系统这门课程中,信号和系统的主要研究对象分别是()。
答案:一维确定性信号,线性时不变系统9.关于单位冲激函数的取样性质,表达正确的是()。
答案:10.下面关于和的表达式中,正确的有()。
答案:;第二章1.由两个因果的LTI系统的级联构成的系统一定是因果系统。
答案:对2.一切连续时间线性系统都可以用它的单位脉冲响应来表征。
答案:错3.具有零附加条件的线性常系数微分方程所描述的系统是线性的。
答案:对4.两个单位冲激响应分别为,的LTI系统级联构成的系统,其总的单位冲激响应是。
答案:错5.若和,则。
答案:对6.线性时不变系统的单位脉冲响应为,该系统稳定的充要条件为()。
答案:7.由离散时间差分方程所描述的系统为()。
答案:FIR(有限长脉冲响应)系统8.LTI系统的单位脉冲响应为,输入为,求时系统的输出时,输入的加权系数是()。
答案:9.信号通过单位冲激响应为的LTI系统,输出等于()。
答案:10.离散时间LTI系统的单位脉冲响应,则该系统是。
答案:因果稳定系统第三章1.对一个信号进行尺度变换,其傅里叶级数系数及傅里叶级数表示均不会改变。
答案:错2.令是一个基波周期为T、傅里叶级数系数为的周期信号,则的傅里叶级数系数是:()答案:3.令是一个基波周期为T、傅里叶级数系数为的实值周期信号,则下列说法正确的是:()答案:若是偶信号,则它的傅里叶级数系数一定为实偶函数4.对于一个周期信号,如果一次谐波分量相移了,为了使合成后的波形只是原始信号的一个简单的时移,那么k次谐波应该相移。
(完整版)信号与系统课后题答案
《信号与系统》课程习题与解答第二章习题(教材上册第二章p81-p87)2-1,2-4~2-10,2-12~2-15,2-17~2-21,2-23,2-24第二章习题解答2-1 对下图所示电路图分别列写求电压的微分方程表示。
图(a):微分方程:11222012()2()1()()()2()()()()2()()()c cc di t i t u t e t dtdi t i t u t dtdi t u t dt du t i t i t dt ⎧+*+=⎪⎪⎪+=⎪⇒⎨⎪=⎪⎪⎪=-⎩图(b ):微分方程:⎪⎪⎪⎩⎪⎪⎪⎨⎧-==+++=+++⎰⎰2021'2'21'2'11)(01)(1Ri t v Ri Mi Li dt i Ct e Ri Mi Li dt i C)()(1)(2)()2()(2)()(33020022203304422t e dtd MR t v C t v dt d C R t v dt d C L R t v dt d RL t v dt d M L =+++++-⇒ 图(c)微分方程:dt i C i L t v ⎰==211'101)(⎪⎪⎪⎩⎪⎪⎪⎨⎧===⇒⎰dt t v L i t v L i dtdt v L i dt d)(1)(1)(10110'1122011∵ )(122111213t i dt d L C i i i i +=+=)(0(1]1[][101011022110331t e dt dR t v RL v dt d RR L C v dt d R C R C v dt d CC μ=+++++⇒图(d)微分方程:⎪⎩⎪⎨⎧+-=++=⎰)()()()()(1)()(11111t e t Ri t v t v dt t i C t Ri t e μRC v dt d 1)1(1+-⇒μ)(11t e V CR = ∵)()(10t v t v μ=)()(1)1(0'0t e R v t v R Cv v =+-⇒2-4 已知系统相应的其次方程及其对应的0+状态条件,求系统的零输入响应。
信号与系统-第2章例题
解得A=2,因此,系统的冲激响应为
d
[
f
h(t) 2e3tu(t)
(t) g(t)] f (t)
g(t)
f
(t)
g(t)
dt
求导后,对含有δ(t)的项利用冲激信号δ(t)的取样特性进行化简,即
f (t) g(t) f (0) (t)
零输入响应
例: 求系统的零输入响应
d2
d
dt 2
y(t) 3 dt
A
d
r(t) dt
10r(t
)
5
Ae(t)
t 0 (2)
(1),(2)两式矛盾。故此系统不满足均匀性
例: 判断下列两个系统是否为非时变系统。
系统1: r(t) cose(t) t 0
系统2: r(t) e(t) cos t t 0
解: 系统1的作用是对输入信号作余弦运算。
时移 t0
经过系统
dy(t) 3y(t) 2 f (t) dt
试求系统的冲激响应h(t)。
(t 0)
解 根据系统冲激响应h(t)的定义,当f(t)=δ(t)时,即为h(t),即原动 态方程式为
dh(t) 3h(t) 2 (t) (t 0)
dt
由于动态方程式右侧存在冲激信号δ(t),为了保持动态方程式的左 右平衡,等式左侧也必须含有δ(t)。这样冲激响应h(t)必为Aeλtu(t)
iL v(t)
例:列写 iL (t)与 v1 (t) 的微分方程。 is (t)
解:
Lp
R2
iL
uC
u1
(
1 R1Cp
1)u1
u1
R1
iS
iL
用消元法求得。
信号与系统习题2附答案
习题二一、基本题1.()()u t u t *=[][]u n u n *=2.已知信号f (t )= sin (100t )* cos (200t ),其最高频率分量为 f m = ,奈奎斯特取样率f s = 3.已知F )()]([ωj F t f =,则F j3[()e ]tf t =F()(2)n f t t n δ∞=-∞⎡⎤-⎢⎥⎣⎦∑= 4.设某因果离散系统的系统函数为az zz H +=)(,要使系统稳定,则a 应满足 5.已知某系统的频率响应为j3()4e H j ωω-=,则该系统的单位阶跃响应为6.已知某系统的系统函数为2()1H s s =+,激励信号为)(e )(2t t f t ε-=,则该系统的零状态响应为 7.已知)2)(21()(--=z z z z X ,收敛域为221<<z , 其逆变换为 8.已知一个因果序列的z 变换X(z)的表达式为:)5.01)(5.01(1)(11--+-=z z z X ,则此序列的初值x(0) = ,终值=∞)(x 。
二、已知)]1()([)(--=t u t u t t f ,求)(*)()(t f t f t s =。
三、给定系统微分方程)(3)(d d)(2)(d d 3)(d d 22t f t f tt y t y t t y t +=++,若激励信号和初始状态分别为)()(t t f ε=,10=-)y(,20=-)(y ',试求该系统的完全响应。
四、求()f t =F []{}1cos (1)(1)u u ωωω-⋅+--。
五、已知系统如题图所示,其中输入信号sin(π)()πt f t t =,∑∞-∞=-=n s T nT t t ),()(δδ T s =0.5秒,Ty (t )f (t )1.求信号()A f t 的频谱函数()A F j ω,并画出()A F j ω的频谱图; 2.求输出信号()y t 的频谱函数()Y j ω,并画出()Y j ω的频谱图; 3.能否从输出信号()y t 恢复信号()A f t ?若能恢复,请详细说明恢复过程;若不能恢复,则说明理由。
《信号与系统》课程习题与解答
《信号与系统》课程习题与解答第二章习题(教材上册第二章p81-p87)2-1,2-4~2-10,2-12~2-15,2-17~2-21,2-23,2-24第二章习题解答2-1 对下图所示电路图分别列写求电压的微分方程表示。
图(a):微分方程:11222012()2()1()()()2()()()()2()()()c cc di t i t u t e t dtdi t i t u t dtdi t u t dt du t i t i t dt ⎧+*+=⎪⎪⎪+=⎪⇒⎨⎪=⎪⎪⎪=-⎩图(b ):微分方程:⎪⎪⎪⎩⎪⎪⎪⎨⎧-==+++=+++⎰⎰2021'2'21'2'11)(01)(1Ri t v Ri Mi Li dt i Ct e Ri Mi Li dt i C)()(1)(2)()2()(2)()(33020022203304422t e dtd MR t v C t v dt d C R t v dt d C L R t v dt d RL t v dt d M L =+++++-⇒ 图(c)微分方程:dt i C i L t v ⎰==211'101)(⎪⎪⎪⎩⎪⎪⎪⎨⎧===⇒⎰dt t v L i t v L i dtdt v L i dt d)(1)(1)(10110'1122011∵ )(122111213t i dt d L C i i i i +=+=)(0(1]1[][101011022110331t e dt dR t v RL v dt d RR L C v dt d R C R C v dt d CC μ=+++++⇒图(d)微分方程:⎪⎩⎪⎨⎧+-=++=⎰)()()()()(1)()(11111t e t Ri t v t v dt t i C t Ri t e μRC v dt d 1)1(1+-⇒μ)(11t e V CR = ∵)()(10t v t v μ=)()(1)1(0'0t e R v t v R Cv v =+-⇒2-4 已知系统相应的其次方程及其对应的0+状态条件,求系统的零输入响应。
