Boost变换器系统建模及其控制.ppt
14、boost变换器DCM小信号建模
I1
I2
+ -
Vg
V1
R1
V2
V
图4
二端口网络的输入功率等于输出功率,所以有 Vg 2 V 2 ,于是 Re R
V Vg
R Re
R
2L D 2TS
V *
Vg V
R
2L D 2TS
* (1
1 V
)
Vg
经化简得: M V 1 RD2TS 1
Vg 2
2L 4
2、DCM 方式 boost 变换器的小信号交流模型 已知
|dˆ (s)0
g2
*(R
||
r2
||
1 sC
)
)
i2 (t) Ts I2 i2 (t)
式中,D、V1、I1、V2、I
2
为静态工作点;d (t
)、v1
(t
)、i1
(t
)、v2
(t
)、i2
(t
)
为扰动量,
平均模型的输入端口方程为非线性方程
i1 (t )
TS
d12Ts 2L
*
v2 (t) TS v2 (t) TS
* v1(t) TS v1(t) TS
VD
i2
+ -
Vg(t)
v1
VT
v2
C
V
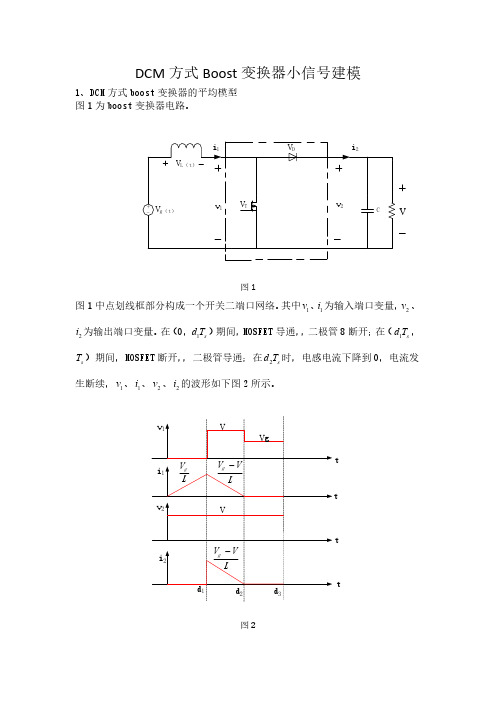
图1
图 1 中点划线框部分构成一个开关二端口网络。其中 v1 、i1 为输入端口变量,v2 、 i2 为输出端口变量。在(0,d1Ts )期间,MOSFET 导通,,二极管 8 断开;在( d1Ts , Ts )期间,MOSFET 断开,,二极管导通;在 d2Ts 时,电感电流下降到 0,电流发 生断续, v1 、 i1 、 v2 、 i2 的波形如下图 2 所示。
Boost变换器工作原理与设计

选择磁芯材料
根据工作频率和电感值, 选择合适的磁芯材料,以 确保电感的性能和效率。
确定线圈匝数
根据电感值、线圈直径和 磁芯材料,计算线圈匝数, 以获得所需的电感性能。
二极管选择
1 2
选择合适的二极管类型
根据工作电压、电流和开关频率,选择合适的二 极管类型。
确定额定电流和电压
根据最大输出电流和电压,选择二极管的额定电 流和电压。
重要性
Boost变换器在许多应用中都非 常重要,如分布式电源系统、电 动汽车和可再生能源系统等。
Boost变换器的历史与发展
历史
Boost变换器最初在20世纪80年代 被提出,随着电力电子技术和控制理 论的不断发展,其性能和效率得到了 不断提高。
发展
目前,Boost变换器已经广泛应用于 各种领域,并且随着新能源和电动汽 车的快速发展,其需求和应用前景仍 然非常广阔。
当开关管关断时,电感释放所 储存的能量,通过二极管和输 出电容向负载提供电流,同时 输出电压逐渐升高。
通过控制开关管的通断时间, 可以调节输出电压的大小。
电感的作用
电感在开关管导通时 储存能量,在开关管 关断时释放能量。
电感的值决定了输出 电压的大小和开关频 率。
电感的作用是调节电 流和维持输出电压的 稳定。
小型化
随着电子设备的小型化和集成化,减小Boost变换器的体积成为 未来的重要发展方向。
智能化
随着人工智能和物联网技术的发展,实现Boost变换器的智能化 控制和远程监控成为未来的重要发展方向。
THANKS
感谢观看
02
Boost变换器的工作原理
工作原理概述
Boost变换器是一种DC-DC转换 器,用于提高直流电压。
DCM Buck-Boost变换器的建模与控制设计

DCM Buck-Boost变换器的建模与控制设计方露;党幼云;康朋飞【摘要】DC converter has the characteristics of nonlinear and multimodal .The model building of Buck-Boost converter is the key to design its closed-loop control system. The reliable output voltage and perfect dynamic characteristic of the Buck-Boost converter was greatly influenced by it. The AC small signal model is build on the basis of Buck-Boost converter's average switch model. Then get the transfer function of system. The voltage loop was also designed based on it. The design details for voltage loop were given and zero-pole compensation method from classic control theory was applied to the field of power electronics. The design of closed-loop control system and the model were verified through the analysis of the result of simulation in MATLAB software.%直流变换器一般具有非线性、多模态等特点。
14、boost变换器DCM小信号建模

f1( v1(t) TS , v2 (t) TS , d (t))
将该式在静态工作点附近作泰勒级数展开得到:
I1 iˆ1
f1(V1,V2, D) vˆ1
f1 (v1 ,V2 dv1
,
D)
|v1 V1
vˆ2
f1(V1, v2 , dv2
D)
|v2
V2
dˆ (t )
f1 (V1 ,V2 dd
,
D)
|v2 V2
(M
1 1)2
Re
j1
df1(V1,V2, d ) dd
|d D
2MV1 D(M 1)2 Re
类似的,对输出端口作同样处理,输出端口方程为:
i2 (t)
TS
d12Ts 2L
*
v1(t) v2 (t) TS
2 TS
v1(t)
TS
f2 ( v1(t) TS , v2 (t) TS , d (t))
i1 (t )
TS
d12Ts 2L
*
v2 (t) TS v2 (t) TS
* v1(t) TS v1(t) TS
i2 (t)
TS
d12Ts 2L
*
v1(t) v2 (t) TS
2 TS
v1(t)
TS
首先引入扰动,即令
d (t) D d (t)
v1
(t
)
Ts
V1
v1
(t
)
iv12((tt))TTs sIV1 2i1v(t2)(t
j2
df2 (V1,V2 , d ) dd
|d D
2V1 D(M 1)Re
根据上式,DCM 方式下 boost 变换器的小信号模型如图 5 所示
双向直流变换器建模ppt课件

① Buck 方向时, K2断开,电源V1提供负载R2能量:
VBuck V1 d
I Buck
V1 R2
d
② Boost 方向时,K1断开,电源V2提供负载R1能量:
VBoost V1 d
I Boost
V1 R1 D 2
d
③ 稳态时,电压之间的关系满足下式:V1 :V2 1: D
34
3 双向 Buck-Boost 变换器的小信号模型
1 iL
0
uc
27
2、 Boost 方向小信号模型的建立
(2)dTs ≤ t ≤ Ts(时间段记为dTs),状态空间 方程:
•
iL
0
• uc
1 C1
1 L
1 R1C1
iL uc
1 L 0
v2
v1
i2
0 1
1 iL
0
uc
28
2、 Boost 方向小信号模型的建立
L
iL
+
D1
+
V1
Q2
D2
V2
-
-
图1 双向Buck-Boost DC/DC变换器
3
1、 Buck 方向小信号模型的建立
1.1 列出状态方程
Buck 方向时电路结构如图2所示,忽略电感、
电容的寄生电路,开关管、二极管均假定为理想器
件。
i1
+
Q1
L
iL
+
V1
D2
C2 R2
V2
-
-
图2 Buck 方向在连续状态下的等效电路
基本建模法
建模方法
状态空间平均法 开关元件平均模型法 开关网络平均模型法
Boost和Buck变换器

7.3.1电流模式控制Boost 变换器在DC-DC 开关变换器的混沌状态研究中,电流模式控制Boost 变换器是一重要研究对象[90,122,123],其基本电路框图如图7-1所示,根据开关管G 的状态不同,Boost 变换器的电路拓扑也发生变化,假定变换器工作于连续导通模式,则有两种电路拓扑分别对应开关管G 的两个状态,其微分方程描述为:⎩⎨⎧+=+=截止导通G E B x A x G E B x A x off off on on (7-5) 其中x 为状态矢量,即x=[I L ,V o ]T ,系数矩阵分别为:⎥⎥⎦⎤⎢⎢⎣⎡=⎥⎥⎦⎤⎢⎢⎣⎡--=⎥⎥⎦⎤⎢⎢⎣⎡=⎥⎥⎦⎤⎢⎢⎣⎡-=01,111001,1000L B RC C L A L B RC A off off on on (7-6) 设时钟脉冲开始后开关管G 是导通的,则电感电流I L 线性增加,当I L 增加至峰值参考电流I ref *时,触发器复位,开关管G 截止,这期间到来的时钟脉冲均被忽略,然后电感L 与Boost 变换器的RC 输出部分产生谐振,电感电流I L 谐振下降,直至下一个时钟脉冲到来后再次使开关管G 导通,图7-2就是电感电流I L 的一种典型波形。
微分方程式(7-5)的解可由解析的方法得到,也可由数值仿真的方法得到,在本文中则选择数值仿真的方法,即以式(7-5)来构造Matlab 下的分段开关模型,并用龙格-库塔(Runge-Kutta )算法来进行仿真。
根据文献[90,122,123],电路参数取为:E =10V ,L =1mH ,C =12μF ,R =20Ω,I ref *=0.6A ~5.5A ,驱动时钟是频率f s 为10kHz 的脉冲波。
以精确电路模型(7-5)式进行仿真,基于§5.2频闪映射的概念,取每个开关周期初始时的电路状态变量构成庞加莱截面,可得Boost 变换器在峰值参考电流I ref *的变化区间上的分叉图,如图7-3所示,可见这是一个典型的倍周期分叉过程,而在I ref *≈4.79A 之后,出现了以3周期为起始的倍周期分叉。
Boost变换器系统建模及其控制.

概要» 2•设计要求• 2.LC参数的设计» 3•小信号模型的建立拿4.串联超前滞后补偿网络的设计♦ PSIM中对电路波形的仿真oost变换器电路参数设计要求♦ 1. 1技术指标*输入电压:V=500v 输出电压:V= 700v*开关频率:50kHz«额定功率:10.5kw亿”2 G •心心Boost 变换器系统电路图结构Boost 变换器的负反馈控制系统传递函数图其中4(、为占空比至输出的传递函数,6(•为PWM 脉宽调制器的传递函数. 表希反備通路的传递函数, 为补偿网络的传递函数。
其中 为未加补偿网络时的回路增益函数,称之为原始回路增益函数Q3为待设计的补偿网络函数LC 参数的选取*田已知可得:输岀额定电流:/<)= A =j°lr 10 =i54% --* 占空比:D=1-^ =2.857 &严伫= 46.6670 ♦求解临界电感 ° *♦当变换器工作在临界状态时,其电感电流波形如图所示:V -匕VV」_■- 7)7;=』(1 一 /刀 7; =2/° = 2」LLRI =匕 Q(1 — OF c _ ~~27^.计算得 Q= 0.068mH 选取 厶竝选L=0.08mH电容值的选取•二极管关闭时,电容向负载提供直流电流,7(X)*田此,得出临界电感值如下:•二极管开通,同时向电容以及负载提供 ・电流,电容充放电荷量相同。
AV =也==比。
7,° C C RC取纹波z\V ;)vl2V •临界电容由公式得1)X1。
A X AV0,2857x1550x10*12= 7」“F•在此选U >£・C = 9pF2Boost 变涣殊临界状态电感电流波形• Boost变换器的平均开关网络模型首先对开关元件的电压或电流变星在一个开关周期内求平均.得到等效的平均参数电路。
从而消除了开关波纹的影响,但此时仍然是一个非线性电路,这样的电路由于同时包含了直流分量与交流分量的作用, 成为大信号等效电路:其次将各平均变量表达为对应的直流分量与交流小信号分量之和,消去直流分量后即可得到只含有小倍号分量的表达式,达到分离小佶号的目的;最后对只含小信号分量的表达式作线性化处理,从而将非线性系统在直流工作点附近近似为线性系统.为线性系统的各种分析与设计方法的应用做好准备"开关周期平均算子的定义:1 r $乜<x(t) >T s = —[ X{T\1T_ |•式中・X (『是DC/DC 变换器中某电®:7;为开关周期。
电流控制二次型Boost变换器的建模与设计

成果。文献[7]运用非线性动力学理论建立了它 的分段光滑迭代映射模型,但因所建模型不属于 小信号模型,无法直接指导控制环路的设计。文 献[8]采用状态空间平均法建立了功率级交流小 信号模型,但缺乏对控制级进行建模,使得模型 不够完整。文献[9]基于时间平均等效原理建立 了包含控制级与功率级的交流小信号模型,但所 建模型不够直观。鉴于此,本文在文献[7-9]的基 础 上 ,通 过 引 入 脉 冲 波 形 积 分 法[10],最 终 建 立 了 峰值电流控制 CCM 下二次型 Boost 变换器系统
Abstract: In order to broaden the input voltage variation range of DC-DC converters,quadratic Boost converters have received extensive attention in new energy generation systems,whose mathematical modeling is very important for system design and application. Therefore,the power level small-signal model based on ideal transformer was established with pulse waveform integration method for quadratic Boost converter worked in CCM (continuous conduction mode),mathematical expressions of output voltage and inductance current were obtained, and the complete AC small signal model of quadratic Boost converter worked in CCM with peak current control was derived. Based on this model,the control loop was designed and verified by experiments.
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
压,这里将它们定义为开关网络的输入变量。
为开关网络的
输出变量。用受控源等效网络子电路,如v图1(t)3和 所i2示(t)
图3 用受控源等效的网络子电路
为保证图3中受控源两端口与图2中的开关网络完全等效,受控源两端 口网络的两个端口必须与开关网络的两个端口波形相同,将图3中的 二端口网络作开关周期平均运算之后,有:
Boost变换器的平均开关网络模型 首先对开关元件的电压或电流变量在一个开关周期内求平均,得到
等效的平均参数电路。从而消除了开关波纹的影响,但此时仍然是一 个非线性电路。这样的电路由于同时包含了直流分量与交流分量的作 用,成为大信号等效电路。
其次将各平均变量表达为对应的直流分量与交流小信号分量之和, 消去直流分量后即可得到只含有小信号分量的表达式,达到分离小信 号的目的;
vg (t)
i1(t) L
v1 (t )
D i2 (t)
ic(t)
v2 (t) C R v(t)
图1 Boost变换器开关网络
i1 (t)
D i2 (t)
v1 (t )
v2 (t)
图2 Boost变换器开关网络子电路
i1(t)和v2(t)
在Boost变换器中,端口变量
刚好分别为电感电流和电容电
Boost变换器的负反馈控制系统传递函数图
Vref (s) 参考信号
误差信号 E(s) Gc (s)
Vc (s) Gm (s)
d (s) Gvd (s) Vo (s)
B(s) 反馈信号
H (s)
其中Gvd (s) 为占空比至输出的传递函G数m (,s) 为PWM 脉宽调制器的传 递函H数(s), 表示反馈通路的传递Gc函(s)数, 为补偿网络的传递函数。
若省略二阶交流项,可得到经线性化处理后的受控电压、电流源如图6
概要
1.设计要求 2.LC参数的设计 3.小信号模型的建立 4.串联超前滞后补偿网络的设计 PSIM中对电路波形的仿真
Boost变换器电路参数设计要求
1.1技术指标 输入电压:V=500v 开关频率:50kHz 额定功率:10.5kw
输出电压:V= 700vLeabharlann Boost变换器系统电路图结构
最后对只含小信号分量的表达式作线性化处理,从而将非线性系统 在直流工作点附近近似为线性系统,为线性系统的各种分析与设计方 法的应用做好准备。
开关周期平均算子的定义:
1
x(t)Ts
Ts
tTs x()d
t
式 流中等,电x 量( t 进) 行是开D关C/周DC变期平换均器运中算某,电将量T 保;s 留原为信开号关的周低期频。部对分电,压而、滤电除
开关频率分量、开关频率谐波分量。
可以证明:经过开关周期平均算子作用后,电感的电流和电感两端的 电压仍然满足法拉第电磁感应定律,即电感元件特性方程中的电压、 电流分别用他们各自的开关周期平均值代替后,方程仍然成立。
类似的,电容元件的特性方程中的电压电流被代替后,方程仍然成立
图1与图2分别为Boost变换器电路和它的开关网络子电路,其开关网络 子电路可用两端口网络表示,端口变量为 v 1(t)、 i1(t)、 v2(t)和 i2(t)
其中
为未加补偿网络时的回路增益函数,称之为原始
回路增Gc(益s) 函数, 为待设计的补偿网络函数.
G o (s) G v( d s)G m (s)H (s)
LC参数的选取
由已知可得:输出额定电流:I0
P0 U0
10.5103 700
15A
占空比: D=1- Vg =2.857
V0
求解临界电感
V0
Q Q
V0
在此选C CC,取 C9F
DTS
DTS
t
ID I0 t
t
小信号模型的建立
占空比D(t)经低频 调制后, Dc/Dc变 换器的输出电压也 被低频调制,即输出 低频调制频率电压分 量的幅度与Dm成正比,频率与占 空比扰动信号调制频率相 同,这就是线性电路的特征, 实际上, DC/DC变换器的输出电压中除直流和低频调制频率电压分量外,还包含 开关频率及其边频带、开关频率谐波及其边频带。
P2
R0
0 U0
46.667
当变换器工作在临界状态时,其电感电流波形如图所示:
iL V gL V 0D T s V L 0(1 D )T s 2 I0 2 V R 0
iL
IL
由此,得出临界电感值如下:
1 I0 2 IL
计算得
LC
VoD(1D)2
2I O
fs
LC0.068mH
Boost变换器临界状态电感电流波形
图5 加入扰动后的电路模型 其受控电压源的电压:
[ D d ˆ ( t ) V ] v ˆ ( t ) [ D ] [ V v ˆ ( t ) V ] d ˆ ( t ) v ˆ ( t ) d ˆ ( t )
同样,受控电流源的电流:
[ D d ˆ ( t )I ] i ˆ ( t ) [ D ] [ I i ˆ ( t ) I ] d ˆ ( t ) i ˆ ( t ) d ˆ ( t )
受控电压源的开关周期平均值为:
v 1 (t) T s d (t) v 2 (t) T s
同理,受控电流源的开关周期平均值为:
i2 (t) T s d (t) i1 (t) T s
经过开关周期平均变换后Boost变换器的等效电路如图4所示:
图4 经开关周期平均后的等效电路 对电路作小信号扰动,即令:
选取 L LC ,在此选L=0.08mH
电容值的选取
二极管关闭时,电容向负载提供直流电流, 二极管开通,同时向电容以及负载提供 VD
电流,电容充放电荷量相同。
Vo C QI0D C 1Ts R V0 D C 1Ts
V0 iD
取纹波 V0 12V
临界电容由公式得
C CfD s IV 0 5 0 0 .2 8 1 5 0 7 3 1 1 5 27.1F
vg(t) T sV gv ˆg(t) d(t)Ddˆ(t) d(t)Ddˆ(t) i(t) T si1 (t) T s I iˆ(t) v( t) T sv 2 ( t) T sV v ˆ ( t)
v1(t) T sV 1v ˆ1(t) i2(t) TsI2iˆ2(t)
将扰动引入电路,得到作小信号扰动后的电路,如图5 所示:
