初二上数学 ppt课件

合集下载

浙教版八上数学一次函数复习PPT课件

所以一次函数的解析式为y＝x＋2或y＝－x＋2.
2.一慢车和一快车沿相同路线从A地到B地，所行的路程与时间之间的函数图象如图所示，试根据图象，回答下列问题：
（1）慢车比快车早出发____2___小时，快车追上慢车时行驶了_2_7__6千米，快车比慢车早___4__小时到达B地；
（2）在下列3个问题中任选一题求解:①快车追上慢车需几小时？②求慢车，快车的速度；③求A，B两地之间的距离．
(1)正比例函数与一次函数的图象
正比例函正比例函数 y＝kx(k≠0)的图象是经过点
数的图象
(0,0)和点(1，k)的一条直线
一次函数 y＝kx＋b(k≠0)的图象是经过点
一次函数的图象
(0，b)和－bk，0的一条直线
一次函数 y＝kx＋b 的图象可由正比例函数
图象关系 y＝kx 的图象平移得到，b>0，向上平移 b
利用一次函数解决分段函数问题
为响应国家节能减排的号召，鼓励市民节约用电，我市从2012年7月1日起，居民用电实行“一户一表”的阶梯电价，分三个档次收费，第一档是用电量不超过180千瓦时实行“基本电价”，第二、三档实行“提高电价”，具体收费情况如折线图，请根据图象回答下列问题：
(1)当用电量是180千瓦时时，电费是___1_0__8__元； (2)第二档的用电量范围是1_8__0_＜__x_≤_ 45；0 (3)“基本电价”是______0_._6__元/千瓦时； (4)小明家8月份的电费是328.5元，这个月他家用电多少千瓦时？
置关系
相交
__k_1_≠_k_2__⇔l1和l2相交
平行 k1＝k_2_，__b_1_≠_b_⇔2 l1和l2平行
两直线的交点坐标及一次函数的图象与坐标轴围成的三角形的面积

初中数学青岛版八年级上2.4《线段的垂直平分线》课件(16张PPT)

D. CD平分∠ACB
ＣＢ
Ｄ
2.（1）用尺规作线段AB、BC的
垂直平分线；
A
(2) 若AB与BC的垂直平分线交于
点P，PA与PC相等吗？
B
C
PA=PC
回归生活
1.在公路CD同侧有A、B
两个村庄，现要在公路上建
A
一车站，使车站到两村距离
相等，如何确定车站的位置？
连接AB，作AB的垂直平分线ＥＦ交CD于P，
• You have to believe in yourself. That's the secret of success. 人必须相信自己，这是成功的秘诀。
•
线段垂直平分线的性质定理：
M P
A
O
B
N
提出新问题
•如果一个点到线段两端点的距离相等，那么这个点是否在线段的垂直平分线上？
•如图,PA=PB，
• 试比较PA，PB的大小，并说明理由。
连接MB，因为MN垂直平分AB，所以MB=ＭＡ，所以PA=PM+MA=PM+MB， △ＰＭＢ中，PM+MB＞PB，所以PA＞PB。
P M
A
N
B
颗粒归仓－－－你学会了吗？
•1.线段的轴对称性 •２.线段的垂直平分线定义 •３.线段的垂直平分线的性质与判定 • 4.尺规作线段的垂直平分线
2.如图，BC=40CM，DE是线段AB
A
的垂直平分线，与BC相交于E，AC=24CM，
求 △ACE的周长。
D
C AC＋CE＋ＡＥ＝ＡＣ＋ＣＥ＋ＥＢ＝６４ＣＭ
E
B
当堂过关检测－－－大显身手
1.如图，AC=AD，BC=BD，则有（ A）

人教版八年级数学上册《12-2 三角形全等的判定(第1课时)》教学课件PPT初二优秀公开课

例2 已知：如图，AB＝AC，AD＝AE，BD＝CE. 求证：∠BAC＝∠DAE.
分析：要证∠BAC＝∠DAE，而这两个角所在三角形显然不全等，我们可以利用等式的性质将它转化为证∠BAD＝∠CAE；由已知的三组相等线段可证明 △ABD≌ △ACE，根据全等三角形的性质可得∠BAD＝∠CAE.
探究新知
这说明有三个角对应相等的两个三角形不一定全等.
探究新知
②三条边
已知两个三角形的三条边都分别为3cm、4cm、6cm .它们一定全等吗？
3cm
4cm
6cm
6cm 4cm
4cm 6cm
3cm
3cm
探究新知
做一做先任意画出一个△ABC，再画出一个△A′B′C′,使A′B′= AB ,B′C′
=BC, A′ C′ =AC.把画好的△A′B′C′剪下，放到△ABC上，它们全
D HC
课堂小结
边边边
内容
有三边对应相等的两个三角形全等（简写成 “SSS”)
应用
思路分析书写步骤
结合图形找隐含条件和现有条件，找准备条件
四步骤
注意
1.说明两三角形全等所需的条件应按对应边的顺序书写 2.结论中所出现的边必须在所证明的两个三角形中
课后作业
作业内容
教材作业
从课后习题中选取自主安排配套练习册练习
3.已知△ABC ≌ △DEF，找出其中相等的边与角.
A
D
B
①AB=DE
④ ∠A=∠D
C
E
② BC=EF
⑤ ∠B=∠E
F
③ CA=FD
⑥ ∠C=∠F
即：三条边分别相等，三个角分别相等的两个三角形全等．

八年级上数学课件 PPT

2022/8/22
三角形得内角与就是 180°
拓展
四边形内角与就是360° 五边形内角与就是？六边形内角与就是？ …… n边形内角与就是？
2022/8/22
例1:已知三角形各角度数之比就是1:3:5,求各角度数。例2:等腰三角形一腰上得高与另一腰得夹角为30°,则顶角度数为( )°
A、30 B、60 C、90 D、120 或60 例3:如图,在△ABC中,AB=AC,点D、E、F分别在BC、AB、AC边上,且 BE=CF,AD+EC=AB。 (1)求证:△DEF就是等腰三角形; (2)当∠A=40°时,求∠DEF得度数。
P,作射线OP,由作法得△OCP≌△ODP得根据就是( )
A、SAS B、ASA C、AAS D、SSS
2022/8/22
4、等腰三角形:有两条边相等得三角形,叫做等腰三角形。相等得两条边叫做腰,另一条边叫做底边,两腰所夹得角叫做顶角,底边
与腰得夹角叫做底角。
等腰三角形得性质 (1)等腰三角形得两个底角相等(简称“等边对等角”) (2)等腰三角形得顶角平分线、底边上得中线、底边上得高相互重合。 (3)等腰三角形就是轴对称图形,底边上得中线(顶角平分线、底边上得高)所在直线就就是它得对称轴。 (4)等腰三角形两腰上得高、中线分别相等,两底角得平分线也相等。 (5)等腰三角形一腰上得高与底边得夹角就是顶角得一半。 (6)等腰三角形顶角得外角平分线平行于这个三角形得底边。
2022/8/22 ;AC=DF ②AB=DE ;∠B=∠E ;BC=EF ③ ∠ B= ∠ E;BC=EF; ∠ C= ∠ F ④AB=DE;AC=DF; ∠ B= ∠ E
其中,能使△ABC≌△DEF得条件共有( )
A、1组 B、2组 C、3组 D、4组

初二数学《一次函数》课件

进阶习题
01
A. (4,4) 或 (-4,-4)
02
B. (4,-4) 或 (-4,4)
03
C. (-4,8) 或 (4,-8)
04
D. (-4,-8) 或 (4,8)
高阶习题
1
高阶习题1：已知一次函数 y = kx + b（k≠0）经过点 (0,2)，且与坐标轴围成的三角形的面积为 4，求这个一次函数的解析式．
2
A. y = x + 2 或 y = -x + 2
3
B. y = x - 2 或 y = -x + 2
高阶习题
01
C. y = x + 2 或 y = -x - 2
02
D. 以上都不对
03
高阶习题2：已知一次函数 y = kx + b（k≠0）的图象经过点 P(3,4)，它与 x、 y 轴的正半轴分别相交于 A、B 两点，且 OA+OB=15，求此一次函数的解析式．
详细描述
斜截式为 $y = mx + b$，其中 $m$ 是斜率，$b$ 是截距。这种形式简洁地表示了直线方程的斜率和截距，便于理解和计算。
一次函数的点斜式
总结词
点斜式是一次函数的另一种表达方式，用于描述通过某一点的直线方程。
详细描述
点斜式为 $y - y_1 = m(x - x_1)$，其中 $(x_1, y_1)$ 是直线上的一个点，$m$ 是斜率。该形式通过一个已知点和斜率来表示直线方程，具有更强的实际应用价值。
注重理解而非死记硬背
函数的性质和特点应通过理解来掌握，而不是简单地记忆公式。
多做练习
通过大量的练习，可以更好地掌握一次函数的运用，提高解题能力。

初二上数学课件(人教版)-等边三角形的性质与判定

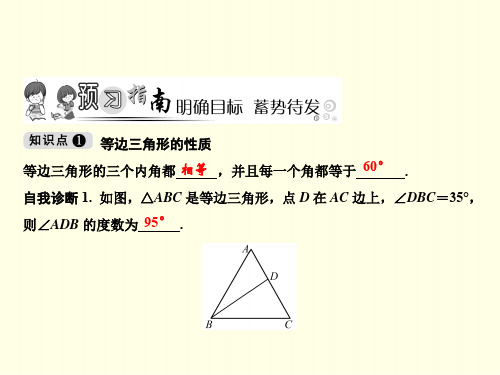
12．(恩施中考)如图，△ABC、△CDE 均为等边三角形，连接 BD、AE 交于点 O，BC 与 AE 交于点 P．求证：∠AOB＝60°.
证明：∵△ABC 和△ECD 都是等边三角形， ∴AC＝BC，CD＝CE，∠ACB ＝∠DCE＝60°，∴∠ACB＋∠BCE＝∠DCE＋∠BCE, 即∠ACE＝∠BCD,
6．如图所示，等边△ABC 中，D 是 AC 的中点，E 是 BC 延长线上的一点，且 CE＝CD，DF⊥BE，垂足是 F. 求证：BF＝EF.
证明：∵△ABC 是等边三角形，D 是 AC 中点，∴∠DBC＝12∠ABC＝30°， ∵DC＝CE，∴∠E＝12∠ACB＝12∠ABC＝30°，∴∠DBE＝∠E，∴BD＝ DE，∵DF⊥BE，∴BF＝FE.
在△ACE 和△BCD 中，A∠CA＝CBEC＝∠BCD CD＝ቤተ መጻሕፍቲ ባይዱE
， ∴△ACE≌△BCD(SAS), ∴
∠CAE＝∠CBD, ∵∠APC＝∠BPO, ∴∠AOB＝∠ACP＝60°，即∠AOB ＝60°.
13．已知：如图，B 是 AC 上一点，△ABD 和△DCE 都是等边三角形． (1)求证：AC＝BE； (2)若 BE⊥DC，求∠BDC 的度数． (1)证明：∵△ABD 和△DCE 是等边三角形，∴∠ADB＝∠CDE＝60°，AD ＝BD，DE＝DC，∴∠ADB＋∠BDC＝∠EDC＋∠BDC，∴∠ADC＝∠EDB， ∴△EDB≌△CDA(SAS)，∴AC＝BE； (2)解：∵BE⊥DC，∴∠DEB＝90°－∠EDC＝30°，由△EDB≌△CDA 知 ∠ACD＝∠DEB＝30°，∵∠ABD＝60°，∴∠BDC＝60°－30°＝30°.
自我诊断 2. 等腰三角形补充下列条件后，仍不一定成为等边三角形的是

北师大版数学八上3.2 平面直角坐标系(第2课时)特殊点的横纵坐标关系课件(共14张PPT)

1.已知点P(m+3,m+1)在平面直角坐标系X轴上，则m=________.
2.已知线段MN平行于Y轴，且M，N的坐标分别为(3，-5) 和(x，2)，那么x=_________.
3.平面直角坐标系中，已知点P(1-2a,a-2) 在第三象限角平分线上，求a的值和该点坐标。
ห้องสมุดไป่ตู้
课后作业：
1.已知A(0，2m)和点B(-1，m+1)，且直线AB//X 轴，则m=_________.
2.在直角坐标系XOY中，点P坐标为 (2，2)，点Q 在Y轴上，Δ PQO是等腰三角形，则满足条件的Q点有______个。
3.在直角坐标系XOY中，已知点A(0，8)和点B(6，8)。 ①尺规作图：求作一个点P，使点P到A、B两点的距离相等，同时使P到两坐标轴的距离也相等。 ②写出点P的坐标。
1.若P（x,y）满足x+y<0,xy>0,则点P在第______象限；若P（x,y）满足xy<0,则点P在第______象限；若P（x,y）满足xy=0,则点P在_________位置.
2.直角坐标系中，（1）点M(a,b)在第二象限且点M到X轴和Y轴的距离分别为3和5，则点M的坐标为_____________; （2）若点M到X轴和Y轴的距离分别为3和5，则点M的坐标为_____________.
北师大版八年级数学上册第三章第二节
平面直角坐标系中特殊点的横纵坐标关系
同学们，你们了解自己的家乡吗？知道自己的学校是在抚州的什么位置吗？
你还知道学校周边的景点在哪儿吗？
人民公园
拟砚台
金巢实验学校
名人雕塑园
革命纪念馆
M

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

2020/9/21
直角三角形的两个锐角______ 三角形的外角等于与它不相邻的__________ 三角形的外角和是______ 多边形的外角和为______
n边形的每个外角都为24°，则n=______
* 一个三角形中，最多有___个直角；
一个三角形中，最多有___个钝角；一个三角形中，最少有___个锐角；任意一个三角形中，最大的一个角的度数至少为___。
例3：如图点A、D、C、E在同一条直线上，AB∥EF，AB=EF，
∠B=∠F， AE=10，AC=7，则CD的长为______。
A．5.5
2020/9/21
B．4 C．4.5
D．3
1.3稳定性
三角形具有稳定性，四边形具有不稳定性。
例1：大桥钢架、索道支架、人字梁等为了坚固，都采用三角形结构，这是根据_________。例2：生活中的活动铁门是利用平行四边形的______。例3：如图，在△ABC中，D为BC边上一点，∠1＝∠2，G为AD的中点，延长 BG交AC于E，F为AB上一点，CF⊥AD于H．下面判断：①AD是△ABE的角平分线；②BE是△ABD的边AD上的中线；③CH是△ACD的边AD上的高；④ AH是△ACF的角平分线和高．其中正确的有________。
例2：用一根18厘米的细铁丝围成一个等腰三角形。（1）若腰是底边的两倍，求出各边长。（2）能围成有一条边是4厘米的等腰三角形吗？
总结：只要选取两条较短的线段，求出和并与第三边进行比较即可。
2020/9/21
1、中线
1.2线的性质
连结三角形的一个顶点和它所对边的中点，所得的线段叫三角形的中线。
三角形中线的相关定理：直角三角形斜边的中线等于斜边的一半等腰三角形底边的中线三线合一(底边的中线、顶角的角平分线、底边的高重合)
2020/9/21
角平分线是天然的、涉及对称的模型，一般情况下，有三种作辅助线的方式： 1．由角平分线上的一点向角的两边作垂线， 2．过角平分线上的一点作角平分线的垂线，从而形成等腰三角形，
3. OA=OB，这种对称的图形应用得也较为普遍，
2、全等三角形的性质（1）全等三角形对应边相等；（2）全等三角形对应角相等；
3、全等三角形的判定方法（1）三边对应相等的两个三角形全等（SSS）。（2）两角和它们的夹边对应相等的两个三角形全等（ASA）。（3）两角和其中一角的对边对应相等的两个三角形全等（AAS）。（4）两边和它们的夹角对应相等的两个三角形全等（SAS）。（5）斜边和一条直角边对应相等的两个直角三角形全等（HL）。
初二数学上
2020/9/21
第一章三角形
1.1 三角形的边 1.2 三角形的高、中线与角平分线 1.3 三角形的稳定性 1.4 三角形的内角
2020/9/21
由不在同一条直线上的三条线段首尾顺次连结所组成的图形，叫三角形。
A
B
C
2020/9/21
直角三角形按角锐角三角形分
钝角三角形
例1：如图，点D为码头，A，B两个灯塔与码头的距离相等，DA，DB为海岸线。一轮船离开码头，计划沿∠ADB的角平分线航行，在航行途中C 点处，测得轮船与灯塔A和灯塔 B的距离相等。试问：轮船航行是否偏离指定航线？请说明理由。
第5题
例2：在△ABC中，∠C=90°，DE垂直平分斜边AB，分别交AB、BC于D、 E．若∠CAB=∠B+30°，CE=2cm. 求: (1)∠AE B 度数．（2）BC的长。
三角形中位线定义：连结三角形两边中点的线段叫做三角形的中位线．
三角形中位线定理：三角形的中位线平行于第三边并且等于它的一半．
中位线判定定理：经过三角形一边中点且平行于另一边的直线必平分第三边．
2020/9/21
2、高
从三角形的一个顶点向它所对的边所在直线作垂线，三角形顶点和垂足之间的线段，叫三角形的高。
斜三角形
ቤተ መጻሕፍቲ ባይዱ
等边三角形（正三角形）
按
等腰三角形
边
底边和腰不相等的三角形
分
不等边三角形（不规则三角形）
2020/9/21
三角形两边之和大于第三边，任意两边之和都大于第三边，两边之差小于第三边。
例1：下列长度的三条线段能组成三角形的是（） A．6， 8 ，10 B．4, 5，9 C．1，2, 4 D．5, 15, 8
2020/9/21
2020/9/21
第二章全等三角形
2.1 全等三角形 2.2 全等三角形的判定 2.3 角平分线的性质
2020/9/21
2.1
2020/9/21
1、全等的图形必须满足：（1）形状相同的图形；（2）大小相等的图形；即能够完全重合的两个图形叫全等形。同样我们把能够完全重合的两个三角形叫做全等三角形。
2020/9/21
2020/9/21
2020/9/21
例：如图，AC∥DE，BC∥EF，AC=DE．求证：AF=BD．
2020/9/21
4、角平分线的性质及判定性质：角平分线上的点到这个角的两边的距离相等判定：到一个角的两边距离相等的点在这个角平分线上
它们具有互逆性。
2.2
角平分线的性质： 1.角平分线可以得到两个相等的角。 2.角平分线上的点到角两边的距离相等。 3. 三角形的内心到三角形三边的距离相等。
3、角平分线
三角形一个内角的平分线与它的对边相交，这个内角的顶点与交点之间的线段，叫三角形的角平分线。
2020/9/21
三角形的外心是三角形三边的垂直平分线的交点。三角形的内心是三角形三条内角平分线的交点。三角形的垂心是三角形三边上的高的交点。三角形的重心是三角形三条中线的交点。
2020/9/21
2020/9/21
1.4 内角三角形的内角和是180°
拓展
四边形内角和是360° 五边形内角和是？六边形内角和是？ …… n边形内角和是？
2020/9/21
例1：已知三角形各角度数之比是1:3:5，求各角度数。例2：等腰三角形一腰上的高与另一腰的夹角为30°，则顶角度数为（）°
A.30 B.60 C.90 D.120 或60 例3：如图，在△ABC中，AB=AC，点D、E、F分别在BC、AB、AC边上，且BE=CF，AD+EC=AB。（1）求证：△DEF是等腰三角形；（2）当∠A=40°时，求∠DEF的度数。