江苏省南通市2020届高三下学期5月阶段性练习数学试题

合集下载

南通市达标名校2020年高考五月大联考数学试卷含解析

南通市达标名校2020年高考五月大联考数学试卷一、选择题：本题共12小题，每小题5分，共60分。

在每小题给出的四个选项中，只有一项是符合题目要求的。

1．1777年，法国科学家蒲丰在宴请客人时，在地上铺了一张白纸，上面画着一条条等距离的平行线，而他给每个客人发许多等质量的，长度等于相邻两平行线距离的一半的针，让他们随意投放.事后，蒲丰对针落地的位置进行统计，发现共投针2212枚，与直线相交的有704枚.根据这次统计数据，若客人随意向这张白纸上投放一根这样的针，则针落地后与直线相交的概率约为（） A ．12πB ．3πC ．2πD ．1π2．已知函数()2sin()(0,0)3f x x A ωωπ=->>，将函数()f x 的图象向左平移3π个单位长度，得到函数()g x 的图象，若函数()g x 的图象的一条对称轴是6x π=，则ω的最小值为A ．16B ．23C ．53D ．563．已知函数()f x 的图象如图所示，则()f x 可以为（）A ．3()3x f x x =-B ．e e ()x xf x x --= C ．2()f x x x =-D ．||e ()xf x x=4．已知集合{}2,1,0,1A =--，{}22*|,B x x a a N=≤∈，若A B ⊆，则a 的最小值为（）A ．1B ．2C ．3D ．45．函数()xf x e ax =+（0a <）的图像可以是（）A ．B ．C ．D ．6．下图所示函数图象经过何种变换可以得到sin 2y x =的图象（）A ．向左平移3π个单位 B ．向右平移3π个单位 C ．向左平移6π个单位 D ．向右平移6π个单位 7．复数z 的共轭复数记作z ，已知复数1z 对应复平面上的点()1,1--，复数2z :满足122z z ⋅=-.则2z 等于（） A 2B ．2C 10D ．108．若将函数()2sin 16f x x π⎛⎫=+- ⎪⎝⎭的图象上各点横坐标缩短到原来的12(纵坐标不变)得到函数()g x 的图象，则下列说法正确的是（） A ．函数()g x 在0 6π⎛⎫⎪⎝⎭，上单调递增 B ．函数()g x 的周期是2π C ．函数()g x 的图象关于点 012π⎛⎫- ⎪⎝⎭，对称 D ．函数()g x 在0 6π⎛⎫⎪⎝⎭，上最大值是1 9．若集合}{}{2,33A x y x B x x ==-=-≤≤，则A B =（）A ．[]3,2-B ．{}23x x ≤≤ C ．()2,3D ．{}32x x -≤<10．已知实数,x y 满足约束条件30202x y x y x -+≥⎧⎪+≥⎨⎪≤⎩，则3z x y =+的最小值为（）A ．-5B ．2C ．7D ．1111．若函数32()39f x x ax x =++-在3x =-时取得极值，则a =（） A ．2B ．3C ．4D ．512．设全集U =R ，集合{|(1)(3)0}A x x x =--≥，11|24xB x ⎧⎫⎪⎪⎛⎫=>⎨⎬ ⎪⎝⎭⎪⎪⎩⎭.则集合()U A B 等于（）A ．(1,2)B ．(2,3]C ．(1,3)D ．(2,3)二、填空题：本题共4小题，每小题5分，共20分。

2020年5月江苏省百校高三数学第五次统测联考卷附答案解析

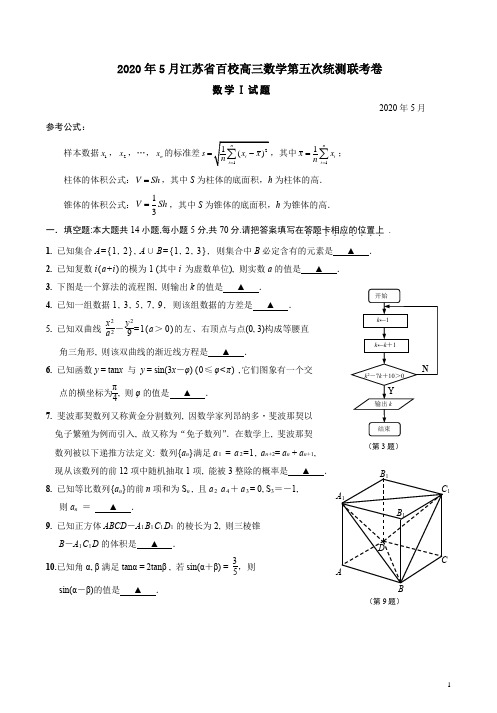
2020年5月江苏省百校高三数学第五次统测联考卷数学Ⅰ试题2020年5月参考公式：样本数据1x ，2x ，…，n x 的标准差211()ni i s x x n ==-∑，其中11ni i x x n ==∑；柱体的体积公式：V Sh =，其中S 为柱体的底面积，h 为柱体的高．锥体的体积公式：13V Sh =，其中S 为锥体的底面积，h 为锥体的高．一．填空题:本大题共14小题,每小题5分,共70分.请把答案填写在答题卡相应的位置上．．．．．．．．．。

1. 已知集合A ={1, 2}, A ∪B ={1, 2, 3}, 则集合中B 必定含有的元素是 ▲ ．2. 已知复数i (a +i )的模为1 (其中i 为虚数单位), 则实数a 的值是 ▲ ．3. 下图是一个算法的流程图, 则输出k 的值是 ▲ ．4. 已知一组数据1, 3, 5, 7, 9, 则该组数据的方差是 ▲ ．5. 已知双曲线 x 2a 2－y 29=1(a ＞0)的左、右顶点与点(0, 3)构成等腰直角三角形, 则该双曲线的渐近线方程是 ▲ ．6. 已知函数y = tan x 与 y = sin(3x －φ) (0≤φ<π) ,它们图象有一个交点的横坐标为π4, 则φ的值是 ▲ ．7. 斐波那契数列又称黄金分割数列, 因数学家列昂纳多・斐波那契以兔子繁殖为例而引入, 故又称为“免子数列”．在数学上, 斐波那契数列被以下递推方法定义: 数列{a n }满足a 1 = a 2=1, a n+2= a n + a n+1, 现从该数列的前12项中随机抽取1项, 能被3整除的概率是 ▲ ． 8. 已知等比数列{a n }的前n 项和为S n , 且a 2 a 4＋a 3= 0, S 3＝－1, 则a n ＝ ▲ ．9. 已知正方体ABCD －A 1B 1C 1D 1的棱长为2, 则三棱锥 B －A 1C 1D 的体积是 ▲ ．10.已知角α, β满足tanα = 2tanβ , 若sin(α＋β) = 35，则sin(α－β)的值是 ▲ ．开始k ←1k ←k ＋1k 2－7k ＋10＞0Y输出kN结束（第3题）（第9题）ABCDC 1B 1A 1B 111.若函数f (x )=(x －a )・x (其中a ＞0)在区间[1，9]上的最小值为18, 则a 的值是 ▲ ．12.如图, 已知A 为椭圆x 2a 2＋y 2b 2=1 (a >b >0)上一点, 它关于原点的对称点为B , 点F 为圆的右焦点,且以AB 为直径的圆过点F , 当 ∠ABF = π6时, 该椭圆的离心率是 ▲ ．13.已知x , y 均为正实数, 且x ＋1y ＝1, 则 yx＋8y 的最小值是 ▲ ．14.已知当x >0时, 函数f (x )=a ln x (a >0),且f (x )=f (-x ).若g (x )=2x 2-m (m >0)的图象与f (x )的图象在第二象限有公共点, 且在该点处的切线相同, 当实数m 变化时,实数a 的取值范围是 ▲ ．二、解答题:本大题共6小题,共计90分,请在答题卡指定区域内．．．．．．．．．作答解答时应写出文字说明、证明过程或演算步驟． 15. (本小题满分14分)在△ABC 中,角A ,B ,C 的对边分别是a ,b ,c .已知C =π6, m =(sin A ,－1), n =(cos B ,1),且m ∥n ．(1) 求A 的值;(2) 若点D 为边BC 上靠近B 的四等分点, 且AD = 21, 求△ABC 的面积．16. (本小题满分14分)在三棱柱A －BCD 中,E ,F 分别为AD , DC 的中点,且BA =BD ,平面ABD ⊥平面ADC ． (1) 证明: EF ∥平面ABC ． (2) 证明: CD ⊥BE ．（第12题）xy A oF BFABCDE （第16题）一胸针图样由等腰三角形OAB 及圆心C 在中轴线上的圆弧AB 构成, 已知OA =OB =1, ∠ACB =2π3. 为了增加胸针的美观程度,设计师准备焊接三条金丝线CO ,CA ,CB ,且AC 长度不小于OC 长度．设∠AOC =θ．(1) 试求出金丝线的总长度L (θ), 并求出的取值范围;(2) 当θ为何值时,金丝线的总长度L (θ)最小, 并求出L (θ)的最小．18. (本小题满分16分)已知椭圆C : x 2a 2＋y 2b 2=1 (a >b >0)右集点F 的盤标为(1,0), 点P (1, 32)为椭圆C 上一点．(1) 求椭圆C 的方程;(2) 过椭圆C 的右焦点F 作斜率为－3的直线l 交椭圆C 于M , N 两点, 且OM →＋ON →＋OH →＝0, 求△MNH 的面积．19. (本小题满分16分)已知函数f (x )=x 3＋x 2－a x (a ∈R ), g (x )=x l n x ． (1) 求曲线在x ＝1处的切线方程；(2) 对任意x ∈(0, a ], f (x )＞g (x )恒成立，求实数a 的取值范围； (3) 当x ∈(0, a ]时, 试求方程f (x )=g (x )的根的个数．A θ MCO（第17题）己知数列{a n }满足a 1＝12，a n +1＝λa n1+ a λn ，n ∈N *．(1) 若λ＝1,(ⅰ) 求数列{a n }的通项公式；(ⅱ) 证明: 对∀n ∈N *，a 1 a 2 a 3＋a 2 a 3 a 4＋…＋a n a n +1 a n +2＝ n （n +5）12（n +2）(n +3)．(2) 若λ＝2, 且对∀n ∈N *，有0＜a n ＜l, 证明: a n +1－a n ＜2＋18．数学Ⅱ（附加题）21A.[选修4－2:矩阵与变换] (本小题满分10分) 已知矩阵A ＝⎣⎢⎡⎦⎥⎤1 k 0 1 ，A 2＝⎣⎢⎡⎦⎥⎤1 20 1 ，求A -1.22B.[选修4－4:坐标系与参数方程] (本小题满分10分)在直角坐标系xOy 中, 直线l 的参数方程为⎩⎨⎧x ＝12t ，y ＝1＋32t ，(t 为参数) .若以直角坐标系xOy 的O 点为极点，Ox 为极轴,且长度单位相同,建立极坐标系, 得曲线C 的极坐标方程为ρ=2cos ⎝⎛⎭⎫α－π3. (1) 求直线l 的倾斜角；(2) 若直线l 与曲线C 交于A , B 两点, 求AB 的长度.如图,在四棱锥P －ABCD 中, 底面ABCD 为梯形,AB ∥CD .若棱AB , AD ,AP 两两垂直,长度分别为1,2,2,且向量PC →与BD →夹角的余弦值为1515.(1) 求CD 的长度(2) 求直线PC 与平面PBD 所成角的正弦值.24D .(本小题满分10分)记f (α)为(ax ＋1)n 二项展开式中的x 3项的系数, 其中a ∈{1,2,3,…,n },n ≥3. (1) 求f (1), f (2), f (3)；(2) 证明: a =1nf (α) = C n n+1(n 3＋n 2)（第23C 题）A BCPD11。

2020年江苏省南通市5月06日联考高三2.5模数学卷逐题解析文字稿

Read xIf x < 0 Then m ← 2x +1 Elsem ←23x - End If Print m（第4题）南通市2020届高三阶段性练习数学 2020.05.06一、填空题：本大题共14小题，每小题5分，共计70分．1．已知集合{}2101M =--，，，，{}20N x x x =+≤，则M N =I ▲ ．【答案】{}10-，2．已知复数i 2ia ++为纯虚数，其中i 为虚数单位，则实数a 的值是 ▲ ．【答案】12-3．某同学5次数学练习的得分依次为114，116，114，114，117，则这5次得分的方差是 ▲ ．【答案】854．根据如图所示的伪代码，当输入的x 为1-时，最后输出的m 的值是 ▲ ．【答案】325．在平面直角坐标系xOy 中，若双曲线22221y x a b-=(00)a b >>，，则该双曲线的渐近线的方程是 ▲ ．【答案】2y x =±6．某同学参加“新冠肺炎防疫知识”答题竞赛活动，需从4道题中随机抽取2道作答．若该同学会其中的3道题，则抽到的2道题他都会的概率是 ▲ ．【答案】127．将函数()π()sin 23f x x =+的图象向右平移ϕ个单位得到函数()g x 的图象．若()g x 为奇函数，则ϕ的最小正值是 ▲ ．【答案】π68．已知非零向量b 与a 的夹角为120︒，且||2=a ，|2+|4=a b ，则||=b ▲ ．【答案】49．已知等比数列{}n a 的各项均为正数，且18a ，3a ，26a 成等差数列，则785622a a a a ++的值是 ▲ ．【答案】1610．在平面直角坐标系xOy 中，已知过点(100)-，的圆M 与圆22660x y x y +--=相切于原点，则圆M 的半径是 ▲ ．【答案】5211．唐朝的狩猎景象浮雕银杯如图1所示，其浮雕临摹了国画、漆绘和墓室壁画，体现了古人的智慧与工艺．它的盛酒部分可以近似地看作是半球与圆柱的组合体（假设内壁表面光滑，忽略杯壁厚度），如图2所示．已知球的半径为R ，酒杯内壁表面积为214π3R ．设酒杯上部分（圆柱）的体积为1V ，下部分（半球）的体积为2V ，则12V V 的值是 ▲ ．【答案】212．已知函数()log (1)a f x x a =>的图象与直线(1)y k x =-()k ∈R 相交．若其中一个交点的纵坐标为1，则k a +的最小值是 ▲ ．【答案】313．已知函数22401()(2)0x x x f x x x +⎧⎪+=⎨⎪+<⎩，≥，，．若关于x 的不等式()10()f x mx m m ---<∈R 的解集是 123()()x x x +∞U ，，，123x x x <<，则m 的取值范围是 ▲ ．【答案】(02)(23)U ，， 14．如图，在ABC △中，32AC BC =，点M N ，分别在AC BC ，上，且13AM AC =，12BN BC =．若BM 与AN 相交于点P ，则CP AB的取值范围是 ▲ ．【答案】1(2)5，二、解答题：本大题共6小题，共计90分． 15．（本小题满分14分）在斜三角形ABC 中，角A B C ，，的对边分别为a b c ，，．（1）若2cos a C b =，且2sin sin sin C A B =，求B 的值；（2）若cos(2)3cos 0A B B ++=，求tan tan A C 的值．（第14题）PNMCB A （第11题图1）（第11题图2）【解】（1）在△ABC 中，由余弦定理得22222a b c a b ab+-⋅=，化简得22a c =，即a c =．…… 2分因为2sin sin sin C A B =，且2sin sin sin a b c R A B C ===（R 为ABC △外接圆半径），所以2c ab =，…… 4分所以c a b ==，所以ABC △为正三角形，所以3B π=．…… 6分（2）因为cos(2)3cos 0A B B ++=，且π()B A C =-+，所以[][]cos π()3cos π()0A C A C +-+-+=， …… 8分所以cos()3cos()A C A C -=-+，…… 10分即cos cos sin sin 3cos cos 3sin sin A C A C A C A C +=-+，所以2cos cos sin sin A C A C =，…… 12分因为斜三角形ABC 中，π2A ≠，π2C ≠，所以cos 0A ≠，cos 0C ≠，所以tan tan 2A C =．…… 14分 16．（本小题满分14分）如图，在三棱柱111ABC A B C -中，平面11ACC A ⊥平面11BCC B ，侧面11BCC B 是矩形，点E F ，分别为11BC A B ，的中点．求证：（1）1BC AC ⊥；（2）EF ∥平面11ACC A ．【证】（1）因为侧面11BCC B 是矩形，所以1BC CC ⊥，因为平面11ACC A ⊥平面11BCC B ，平面11ACC A I 平面111BCC B C C =，BC ⊂平面11BCC B ，所以BC ⊥平面11ACC A ． …… 4分因为1AC ⊂平面11ACC A ，ACA 1C 1 BB 1EGF所以1BC AC ⊥． …… 6分（2）取11A C 的中点G ，连结FG ，CG ．在111A B C △中，F ，G 分别是11A B ，11A C 的中点，所以11FG B C ∥，且1112FG B C =．…… 8分在矩形11BCC B 中，E 是BC 的中点，所以11EC B C ∥，且1112EC B C =．所以EC FG ∥，且EC FG =． …… 10分所以四边形EFGC 为平行四边形，所以EF GC ∥．…… 12分又因为EF ⊄平面11ACC A ，GC ⊂平面11ACC A ，所以EF ∥平面11ACC A ． …… 14分 17. (本小题满分14分)如图，某森林公园内有一条宽为100米的笔直的河道（假设河道足够长），现拟在河道内围出一块直角三角形区域养殖观赏鱼．三角形区域记为ABC △，A 到河两岸的距离AE AD ，相等，B C ，分别在两岸上，AB AC ⊥．为方便游客观赏，拟围绕ABC △区域在水面搭建景观桥．为了使桥的总长度l （即ABC △的周长）最短，工程师设计了以下两种方案：方案1：设ABD α∠=，求出l 关于α的函数解析式()f α，并求出()f α的最小值．方案2：设EC x =米，求出l 关于x 的函数解析式()g x ，并求出()g x 的最小值．请从以上两种方案中自选一种解答．（注：如果选用了两种方案解答，则按第一种解答计分）【解】方案1：（1）因为AB AC ⊥，所以90EAC BAD ∠+∠=︒，在Rt ABD △中，90ABD BAD ∠+∠=︒，所以EAC ABD α∠=∠=，(0)2απ∈，．… 2分因为50AD AE ==，在Rt ADB △和Rt AEC △中，AB =50sin α，AC =50cos α，…… 4分（第17题）BCDEαA所以BC ==50sin cos αα=，所以()11150()sin cos sin cos f ααααα=++sin cos 150()sin cos αααα++=，其中(0)2απ∈，． …… 7分（2）方法一：设sin cos t αα=+，则sin cos )4t αααπ=++，因为(0)2απ∈，，所以(1t ∈， …… 9分因为212sin cos t αα=+，所以21sin cos 2t αα-=．所以250(1)100112t y t t +==--， …… 12分所以当t =min ()100f α==+答：景观桥总长的最小值为(100+米． …… 14分方法二：250(cos sin )(1sin cos sin cos )()(sin cos )f ααααααααα-----'=， …… 10分因为(0)2απ∈，，所以1sin cos sin cos 0αααα----<，2(sin cos )0αα>，当(0)4απ∈，时，cos sin 0αα->，()0f α'<，()f α单调递减，当()42αππ∈，时，cos sin 0αα-<，()0f α'>，()f α单调递增． …… 12分所以当4απ=时，()f α取得最小值，最小值为(100+米．答：景观桥总长度的最小值为(100+米．…… 14分【解】方案2：（1）因为AB AC ⊥，所以90EAC BAD ∠+∠=︒，在Rt ABD △中，90ABD BAD ∠+∠=︒，所以EAC ABD ∠=∠．所以Rt CAE △∽Rt ABD △，所以AC EC AB AD=．…… 2分因为EC x =，AC =50AD =，所以AB．……4分2500BC xx=+，所以2500()()g x xx+=，0x>．……7分（2）因为0x>，所以()gx+≥……10分100=100100=≥． (12)分2500xx=，即50x=时取“=”．所以min()100g x=+答：景观桥总长的最小值为(100+米．……14分18．（本小题满分16分）在平面直角坐标系xOy中，已知椭圆2222:1yxCa b+=(00)a b>>，短轴的两个顶点与右焦点（1）求椭圆C的标准方程；（2）直线:l y kx m=+(00)k m>≠，与椭圆C交于P Q，两点，设直线OP OQ，的斜率分别为12k k，．已知212k k k=⋅．①求k的值；②当OPQ△的面积最大时，求直线PQ的方程．【解】（1）设椭圆的焦距为2c，则222=c a b-．因为短轴的两个顶点与右焦点的连线构成等边三角形，所以c=．（第18题图）22a c =所以21a b ==，，所以椭圆C 的标准方程为2214x y +=． …… 3分（2）①设11()P x y ，，22()Q x y ，，联立2214y kx m x y =+⎧⎪⎨+=⎪⎩，，消去y 得222(41)8440k x kmx m +++-=， 2222644(41)(44)0k m k m ∆=-+->，化简得2241m k <+，所以122841km x x k -+=+，21224441m x x k -⋅=+，又OP 的斜率111y k x =，OQ 的斜率222yk x =，所以2221212121212121212()()()y y kx m kx m k x x km x x m k k k x x x x x x +++++=⋅===， …… 6分化简得212()0km x x m ++=，所以228041km km m k -⋅+=+．又因为0m ≠，即241k =，又0k >，所以12k =．…… 8分②由①得12k =，直线PQ 的方程为12y x m =+，且122x x m +=-，21222x x m ⋅=-，22m <．又0m ≠，所以0m <<所以PQ12x =-==，…… 10分点O 到直线PQ 的距离d =，…… 12分所以22(2)1122OPQm m S PQ d +-=⋅==△当且仅当222m m =-，即1m =±时，OPQ △的面积最大，所以，直线PQ 的方程为112y x =±．…… 16分19．（本小题满分16分）已知数列{}n a 的前n 项和为n S ，11a =，2121n n n n a S S S λ++++⋅=，n λ*∈∈N R ，．（1）若3λ=-，21a =-，求3a 的值；（2）若数列{}n a 的前k 项成公差不为0的等差数列，求k 的最大值；（3）若20a >，是否存在λ∈R ，使{}n a 为等比数列？若存在，求出所有符合题意的λ的值；若不存在，请说明理由．【解】记2121n n n n a S S S λ++++⋅=为（*）式．（1）当3λ=-时，（*）式为21213n n n n a S S S +++-+⋅=，令1n =得，221323a S S S -+⋅=，即221123123()()a a a a a a a -+⋅++=+，由已知11a =，21a =-，解得33a =-．…… 2分（2）因为前k 项成等差数列，设公差为d ，则21a d =+，312a d =+，若3k =，则22S d =+，333S d =+．在（*）式中，令1n =得，22132a S S S λ+⋅=，所以2(1)33(2)d d d λ+++=+，化简得21(1)d d d λ++=+，① …… 4分若4k =，则446S d =+，在（*）式中，令2n =得，23243a S S S λ+⋅=，所以2(12)(2)(46)(33)d d d d λ++++=+，化简得2321(12)d d d λ++=+，②②-①得，22d d d λ+=，因为公差不为0，所以0d ≠，所以21d λ+=，代入①得，220d d +=，所以2d =-，3λ=-．所以4k =符合题意．…… 6分若5k =，则1234511357a a a a a ==-=-=-=-，，，，，3453815S S S =-=-=-，，, 在（*）式中，令3n =得，43533(5)(3)(15)60a S S -+=-⨯-+-⨯-=，224(8)64S =-=，所以243543a S S S -+≠，所以k 的最大值为4． …… 8分（3）假设存在λ∈R ，使{}n a 为等比数列，设前3项分别为21q q ，，，则2123111S S q S q q ==+=++，，，（*）式中，令1n =得，22(1)(1)q q q q λ+++=+，化简得(1)0q λ-=，因为20q a =>，所以1λ=，…… 10分此时（*）式为2121()n n n n n S S S S S +++-+⋅=，即112(1)(1)n n n n S S S S +++-=-（**），由11S =，2211S a =+>，得31S >，由231S S >，得41S >L ，，依次类推，10n S >≥，所以（**）等价于21111n n n nS S S S +++--=，所以数列11n n S S +-⎧⎫⎨⎬⎩⎭为常数列，所以122111n n S S a S S +--==，…… 14分于是2n ≥时，122111n n n n S a S S a S +--=⎧⎨-=⎩，，两式相减得12n n a a a +=⋅，因为221a a a =⋅，所以12n n a a a +=⋅()n *∈N ，又120a a ≠，，所以12n na a a +=（非零常数），所以存在1λ=，使{}n a 为等比数列．…… 16分20．（本小题满分16分）对于定义在D 上的函数()f x ，若存在k ∈R ，使()f x kx <恒成立，则称()f x 为“()m k 型函数”；若存在k ∈R ，使()f x kx ≥恒成立，则称()f x 为“()M k 型函数”．已知函数()(12)ln f x ax x =-()a ∈R ．（1）设函数1()()1h x f x =+(1)x ≥．若0a =，且1()h x 为“()m k 型函数”，求k 的取值范围；（2）设函数21()()h x f x x =+．证明：当12a =-时，2()h x 为“(1)M 型函数”；（3）若a ∈Z ，证明存在唯一整数a ，使得()f x 为“()14m 型函数”．【解】（1）0a =时，1()ln 1h x x =+．因为1()h x 为“()m k 型函数”，所以1()h x kx <恒成立，即ln 1x k x+>恒成立．设ln 1()x g x x +=(1)x ≥，则2ln ()0x g x x-'=≤恒成立，所以()g x 在[1)+∞，上单调递减，所以()(1)1g x g =≤，所以k 的取值范围是(1)+∞，． …… 3分（2）当12a =-时，要证2()h x 为“(1)M 型函数”，即证1(1)ln x x x x ++≥，即证1(1)ln 0x x x x++-≥．方法一：令1()(1)ln R x x x x x=++-，则22211111()ln (1)1ln ln x R x x x x x x x x x x -'=++⋅--=+-=+，当1x >时，ln 0x >，210x x->，则()0R x '>；当01x <<时，ln 0x <，210x x-<，则()0R x '<；所以()R x 在(01)，上单调递减，在(1+)∞，上单调递增， …… 6分则()(1)R x R ≥，又(1)0R =，所以()0R x ≥，所以2()h x 为“(1)M 型函数”．…… 8分方法二：令211()ln F x x x x =+-，则22331122()0x x F x x x x x -+'=-+=>，所以函数()F x 在(0+)∞，上单调递增，又(1)0F =，所以当01x <<时，()0R x '<，当1x >时，()0R x '>，所以()R x 在(01)，上单调递减，在(1+)∞，上单调递增， …… 6分以下同方法一．（3）函数()f x 为“()14m 型函数”等价于1()(12)ln 04p x ax x x =--<恒成立，当0a ≤时，e e (e)(12e)1044p a =--->≥，不合题意；当2a ≥时，12111()1(4e )0e e 4e e 4a p =---->≥，不合题意；…… 10分当1a =时，方法一：1()(12)ln 4p x x x x =--，① 当1x ≥或102x <≤时，1()004p x x -<≤． …… 12分② 当112x <<时，120x -<，由（2）知1ln x x x ->，所以2(12)(1)11()(32)044x x p x x x x x---<-=-≤，综上，存在唯一整数1a =，使得()f x 为“()14m 型函数”．…… 16分方法二：1()(12)ln 4p x x x x =--，12119()2ln 2ln 44x p x x x x x -'=-+-=-+-，记19()2ln 4x x x ϕ=-+-，则221()0x x xϕ-'=-<，所以()()x p x ϕ'=在(0+)∞，上单调递减．易得ln 1x x -≤，所以99171)0444p '=-==≤；又因为()1992ln 22120244p '=+->+->，所以存在唯一零点(012x ∈，使得019()2ln 04p x x x '=-+-=，且0x 为()p x 的最大值点，…… 12分所以()00000000019(12)411117()(12)ln 242428x x p x x x x x x x --=--=-=+-，注意到117228y x x =+-在(12上单调递增，所以()017117()0824p x p<-=<，所以()0p x <．综上，存在唯一整数1a =，使得()f x 为“()14m 型函数”． …… 16分21．【选做题】本题包括A 、B 、C 三小题，请选定其中两题，并在．．．．．．．．．答题卡．．．相应的答题区域内作答．．．．．．．．．．．若多做，则按作答的前两题评分．解答时应写出文字说明、证明过程或演算步骤．A ．[选修4-2：矩阵与变换]（本小题满分10分）已知矩阵A 的逆矩阵132=21-⎡⎤⎢⎥⎣⎦A ．（1）求矩阵A ；（2）若向量21⎡⎤=⎢⎥⎣⎦α，计算2A α．【解】（1）设矩阵=a b c d ⎡⎤⎢⎥⎣⎦A ，则113232322122100a b a c b d c d a c b d -⎡⎤⎡⎤⎡⎤⎡⎤==⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦⎣⎦⎣=+⎦+++A A ，故3212032021a c a c b d b d +=⎧⎪+=⎪⎨+=⎪⎪+=⎩，，，，解得1223a b c d =-⎧⎪=⎪⎨=⎪⎪=-⎩，，，，则矩阵12=23⎡⎤⎢⎥⎣--⎦A ． …… 5分（2）由矩阵12=23⎡⎤⎢⎥⎣--⎦A ，得2121258=2323813⎡⎤⎡⎤⎡⎤=⎢⎥⎢⎥-----⎢⎥⎣⎦⎣⎦⎣-⎦A ． …… 8分所以2582281313⎡⎤⎡⎤⎡⎤=⎢⎥⎢⎥-⎢⎥⎣⎦⎣=-⎦⎣⎦-A α． …… 10分 B ．[选修4-4：坐标系与参数方程]（本小题满分10分）在平面直角坐标系xOy 中，已知直线l的参数方程112x y t ⎧=+⎪⎨⎪=⎩，（t 为参数）．在以坐标原点为极点，x 轴正半轴为极轴的极坐标系中，曲线C 的极坐标方程为()4cos 3ρθπ=+．设P 为曲线C 上动点，求点P 到直线l 距离的最大值．【解】由()4cos 3ρθπ=+得()24cos =2cos sin 3ρρθρθθπ=+-，所以曲线C的直角坐标方程为2220x y x +-+=，即22(1)(4x y -+=，圆心(1,，半径2r =．…… 3分由直线l的参数方程112x y t ⎧=+⎪⎨⎪=⎩，得1x =+，所以直线l的普通方程为10x --=． …… 6分所以圆心(1,到直线l 的距离32d =，…… 8分所以点P 到直线l 距离的最大值为37222+=． …… 10分C ．[选修4-5：不等式选讲]（本小题满分10分）若实数x y z ，，满足231x y z ++=，求222xy z ++的最小值．【解】由柯西不等式，得2222222(23)(123)()x y z x y z ++++⋅++≤，…… 5分即23x y z ++ 因为231x y z ++=，所以222114x y z ++≥，当且仅当123yx z ==，即11314714x y z ===，，时取等号．综上，222x y z ++的最小值为114．…… 10分【必做题】第22、23题，每小题10分，共计20分．请在答题卡指定区域．．．．．．．内作答，解答时应写出文字说明、证明过程或演算步骤． 22．(本小题满分10分)如图，在平面直角坐标系xOy 中，已知抛物线22(0)y px p =>，过点(40)M p ，的直线l 交抛物线于1122()()A x y B x y ，，，两点．当AB 垂直于x 轴时，OAB △的面积为（1）求抛物线的方程；（2）设线段AB 的垂直平分线交x 轴于点T ．① 证明：12y y 为定值；② 若OA TB ∥，求直线l 的斜率．【解】（1）当AB 垂直于x 轴时，(4)A p ，(4)B p -，所以OAB △的面积为211422AB OM p ⋅⋅=⋅⋅==，因为0p >，所以12p =，所以抛物线的方程为2y x =．（2）① 由题意可知直线l 与x 轴不垂直．由（1）知(20)M ，，设211()A y y ，，222()B y y ，，则122212121AB y y k y y y y -==+-．（第22题）由A M B ，，三点共线，得12221222y yy y =--，因为12y y ≠，化简得122y y =-． …… 5分② 因为122y y =-，所以21142()B y y -，．因为线段AB 垂直平分线的方程为22121212()()22y y y y y y y x ++-=-+-，令0y =，得22122121114(1)22T y y x y y ++==++． …… 7分因为OA TB ∥，所以OA TB k k =，即1211221121144(1)2y y y y y =++-，整理得2211(1)(4)0y y +-=，解得12y =±，故(42)A ±，．所以1AM k =±，即直线l 的斜率为1±． …… 10分23．(本小题满分10分)设n k n k *∈∈N N ，，≥．（1）化简：11112C C C C k k n n k k n n +++++⋅⋅；（2）已知2220122(1)nnn x a a x a x a x -=++++L ，记21()(1)nkk k F n n a ==+∑．证明：()F n 能被21n +整除．【证】（1）证明：11112(1)!(1)!C C!(1)!(1)!()!(2)!C C!!()!(1)!(1)!k k n n k k n n n n k n k k n k n n k n k k n k +++++++⋅⋅+-+-=+⋅⋅-++-(1)!(1)!1!(2)(1)!2n n n n n n n n +⋅⋅++==+⋅++．…… 3分（2）证明：由（1）得，11211111111C C +C 11122C C C C C k k k n n n k k k k k n n n n n n n n n +++++++++++++=⋅=⋅++⋅⋅ ()1111112C C k kn n n n ++++=⋅++． …… 6分因为122121(1)(1)(1)2122C C C k k k k k k k n n n k k k k n a n +++⎡⎤---+==⋅+⎢⎥+⎣⎦，所以221112121(1)(1)21()(1)2C C k k nnk k k k k n n k k k n F n n a +==++⎡⎤--+=+=⋅+⎢⎥⎣⎦∑∑，因为2112121(1)(1)C C k k nk k k n n k k +=++⎡⎤--+⎢⎥⎣⎦∑122122322121212121212121211221212212()()C C C C C C C C n n n n n n n n n n n n n n n n -+++++++++--+--+=+++++++++L L 12222212121212121211212212()()C C C C C C n n n n n n n n n n n n +++++++---+=++++++L1221221212121212111112()2C C C C C n n n n n n n n n n -++++++--=+++++=L ．所以2121()(1)2(21)2nk k k n F n n n n n a =+=+=⋅=+∑能被21n +整除．…… 10分（第22题）。

江苏省南通市2019-2020学年高考数学五月模拟试卷含解析

江苏省南通市2019-2020学年高考数学五月模拟试卷一、选择题：本题共12小题，每小题5分，共60分。

在每小题给出的四个选项中，只有一项是符合题目要求的。

1．从5名学生中选出4名分别参加数学，物理，化学，生物四科竞赛，其中甲不能参加生物竞赛，则不同的参赛方案种数为A ．48B ．72C ．90D ．96 【答案】D【解析】因甲不参加生物竞赛，则安排甲参加另外3场比赛或甲学生不参加任何比赛①当甲参加另外3场比赛时，共有13C •34A =72种选择方案；②当甲学生不参加任何比赛时，共有44A =24种选择方案．综上所述，所有参赛方案有72+24=96种故答案为：96点睛：本题以选择学生参加比赛为载体，考查了分类计数原理、排列数与组合数公式等知识，属于基础题．2．已知命题p ：“a b >”是“22a b >”的充要条件；:q x ∃∈R ，|1|x x +≤，则（）A ．()p q ⌝∨为真命题B ．p q ∨为真命题C ．p q ∧为真命题D ．()p q ∧⌝为假命题【答案】B【解析】【分析】由2x y =的单调性，可判断p 是真命题；分类讨论打开绝对值，可得q 是假命题，依次分析即得解【详解】由函数2x y =是R 上的增函数，知命题p 是真命题．对于命题q ，当10x +≥，即1x ≥-时，11x x x +=+>；当10x +<，即1x <-时，11x x +=--，由1x x --≤，得12x =-，无解，因此命题q 是假命题．所以()p q ⌝∨为假命题，A 错误；p q ∨为真命题，B 正确；p q ∧为假命题，C 错误；()p q ∧⌝为真命题，D 错误．故选：B【点睛】本题考查了命题的逻辑连接词，考查了学生逻辑推理，分类讨论，数学运算的能力，属于中档题.3．已知101 1M dxx=+⎰，2cosN xdxπ=⎰，由程序框图输出的S为（）A．1 B．0 C．2πD．ln2【答案】D【解析】试题分析：111ln(1)|ln21M dx xx==+=+⎰，2cos sin|12N xdx xππ===⎰，所以M N<，所以由程序框图输出的S为ln2.故选D．考点：1、程序框图；2、定积分．4．已知不重合的平面,,αβγ和直线l，则“//αβ”的充分不必要条件是（）A．α内有无数条直线与β平行B．lα⊥且lβ⊥C．αγ⊥且γβ⊥D．α内的任何直线都与β平行【答案】B【解析】【分析】根据充分不必要条件和直线和平面，平面和平面的位置关系，依次判断每个选项得到答案.【详解】A. α内有无数条直线与β平行，则,αβ相交或//αβ，排除；B. lα⊥且lβ⊥，故//αβ，当//αβ，不能得到lα⊥且lβ⊥，满足；C. αγ⊥且γβ⊥，//αβ，则,αβ相交或//αβ，排除；D. α内的任何直线都与β平行，故//αβ，若//αβ，则α内的任何直线都与β平行，充要条件，排除.故选：B .【点睛】本题考查了充分不必要条件和直线和平面，平面和平面的位置关系，意在考查学生的综合应用能力. 5．下列四个图象可能是函数35log |1|1x y x +=+图象的是（） A ． B ． C ．D ．【答案】C【解析】【分析】首先求出函数的定义域，其函数图象可由35log ||x y x=的图象沿x 轴向左平移1个单位而得到，因为35log ||x y x=为奇函数，即可得到函数图象关于(1,0)-对称，即可排除A 、D ，再根据0x >时函数值，排除B ，即可得解.【详解】∵35log |1|1x y x +=+的定义域为{}|1x x ≠-，其图象可由35log ||x y x =的图象沿x 轴向左平移1个单位而得到， ∵35log ||x y x=为奇函数，图象关于原点对称， ∴35log |1|1x y x +=+的图象关于点(1,0)-成中心对称. 可排除A 、D 项.当0x >时，35log |1|01x y x +=>+，∴B 项不正确. 故选：C【点睛】本题考查函数的性质与识图能力，一般根据四个选择项来判断对应的函数性质，即可排除三个不符的选项，属于中档题.6．已知双曲线22221x y a b-= (a>0，b>0)的右焦点为F ，若过点F 且倾斜角为60°的直线l 与双曲线的右支有且只有一个交点，则此双曲线的离心率e 的取值范围是（）A ．[2,)+∞B ．(1,2),C ．(2,)+∞D ．(1,2] 【答案】A【解析】【分析】若过点F 且倾斜角为3π的直线与双曲线的右支有且只有一个交点，则该直线的斜率的绝对值小于等于渐近线的斜率．根据这个结论可以求出双曲线离心率的取值范围．【详解】已知双曲线22221(0,0)x y a b a b-=>>的右焦点为F ，若过点F 且倾斜角为3π的直线与双曲线的右支有且只有一个交点，则该直线的斜率的绝对值小于等于渐近线的斜率b a，∴b a 22224a b e a +=…， 2e ∴…，故选：A ．【点睛】本题考查双曲线的性质及其应用，解题时要注意挖掘隐含条件．7．若双曲线222:14x y C m-=的焦距为C 的一个焦点到一条渐近线的距离为（）A ．2B ．4CD ．【答案】B【解析】【分析】根据焦距即可求得参数m ，再根据点到直线的距离公式即可求得结果.【详解】因为双曲线222:14x y C m-=的焦距为故可得(224m +=，解得216m =，不妨取4m =；又焦点()F ，其中一条渐近线为2y x =-，由点到直线的距离公式即可求的4545d ==.故选：B.【点睛】本题考查由双曲线的焦距求方程，以及双曲线的几何性质，属综合基础题.8．已知抛物线2:4C y x =和点(2,0)D ，直线2x ty =-与抛物线C 交于不同两点A ，B ，直线BD 与抛物线C 交于另一点E ．给出以下判断：①以BE 为直径的圆与抛物线准线相离；②直线OB 与直线OE 的斜率乘积为2-；③设过点A ，B ，E 的圆的圆心坐标为(,)a b ，半径为r ，则224a r -=．其中，所有正确判断的序号是（）A ．①②B ．①③C ．②③D ．①②③ 【答案】D【解析】【分析】对于①，利用抛物线的定义，利用12||||||222d d BF EF BE d R ++==>=可判断；对于②，设直线DE 的方程为2x my =+，与抛物线联立，用坐标表示直线OB 与直线OE 的斜率乘积，即可判断；对于③，将2x ty =-代入抛物线C 的方程可得，18A y y =，从而，2A y y =-，利用韦达定理可得242||164832BE m m =++，再由222||||2BE r MN ⎛⎫=+ ⎪⎝⎭，可用m 表示2r ，线段BE 的中垂线与x 轴的交点（即圆心N ）横坐标为224m +，可得a ，即可判断.【详解】如图，设F 为抛物线C 的焦点，以线段BE 为直径的圆为M ，则圆心M 为线段BE 的中点．设B ，E 到准线的距离分别为1d ，2d ，M e 的半径为R ，点M 到准线的距离为d ，显然B ，E ，F 三点不共线，则12||||||222d d BF EF BE d R ++==>=．所以①正确．由题意可设直线DE 的方程为2x my =+，代入抛物线C 的方程，有2480y my --=．设点B ，E 的坐标分别为()11,x y ，()22,x y ，则124y y m +=，128y y =-．所以()()()21212121222244x x my my m y y m y y =++=+++=．则直线OB 与直线OE 的斜率乘积为12122y y x x =-．所以②正确．将2x ty =-代入抛物线C 的方程可得，18A y y =，从而，2A y y =-．根据抛物线的对称性可知， A ，E 两点关于x 轴对称，所以过点A ，B ，E 的圆的圆心N 在x 轴上．由上，有124y y m +=，21244x x m +=+，则()()2224212121212||44164832BE x x x x y y y y m m =+-++-=++．所以，线段BE 的中垂线与x 轴的交点（即圆心N ）横坐标为224m +，所以224a m =+．于是，222222421212||||244128222BE x x y y r MN m m m ++⎛⎫⎛⎫⎛⎫=+=+-++++ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭，代入21244x x m +=+，124y y m +=，得24241612r m m =++，所以()()22224224416124a r m m m -=+-++=．所以③正确．故选：D【点睛】本题考查了抛物线的性质综合，考查了学生综合分析，转化划归，数形结合，数学运算的能力，属于较难题.9．已知点1F 是抛物线C ：22x py =的焦点，点2F 为抛物线C 的对称轴与其准线的交点，过2F 作抛物线C 的切线，切点为A ，若点A 恰好在以1F ，2F 为焦点的双曲线上，则双曲线的离心率为（）A ．2B 1C ．2D 1【答案】D【解析】【分析】根据抛物线的性质，设出直线方程，代入抛物线方程，求得k 的值，设出双曲线方程，求得2a ＝丨AF 2丨﹣丨AF 1丨＝（2-1）p ，利用双曲线的离心率公式求得e ．【详解】直线F 2A 的直线方程为：y ＝kx 2p -，F 1（0，2p ），F 2（0，2p -），代入抛物线C ：x 2＝2py 方程，整理得：x 2﹣2pkx+p 2＝0，∴△＝4k 2p 2﹣4p 2＝0，解得：k ＝±1，∴A （p ，2p ），设双曲线方程为：2222y x a b-=1，丨AF 1丨＝p ，丨AF 2丨222p p =+=p ，2a ＝丨AF 2丨﹣丨AF 1丨＝（2-1）p ， 2c ＝p ，∴离心率e 221c a ===+-1，故选：D ．【点睛】本题考查抛物线及双曲线的方程及简单性质，考查转化思想，考查计算能力，属于中档题．10．如图，网格纸上小正方形的边长为1，粗实线画出的是某几何体的三视图，则该几何体的体积为（）A ．32B ．323C ．16D ．163【答案】D【解析】【分析】根据三视图判断出几何体是由一个三棱锥和一个三棱柱构成，利用锥体和柱体的体积公式计算出体积并相加求得几何体的体积.【详解】由三视图可知该几何体的直观图是由一个三棱锥和三棱柱构成，该多面体体积为1122223⨯⨯⨯+11622223⨯⨯⨯⨯=.故选D. 【点睛】本小题主要考查三视图还原为原图，考查柱体和锥体的体积公式，属于基础题.11．已知函数()0,1ln ,1x f x x x <⎧=⎨≥⎩，若不等式()≤-f x x k 对任意的x ∈R 恒成立，则实数k 的取值范围是（）A ．(],1-∞B ．[)1,+∞C ．[)0,1D ．(]1,0- 【答案】A【解析】【分析】先求出函数()f x 在(1,0)处的切线方程，在同一直角坐标系内画出函数()0,1ln ,1x f x x x <⎧=⎨≥⎩和()g x x k =-的图象，利用数形结合进行求解即可.【详解】当1x ≥时，()''1ln ,()(1)1f x x f x f x=⇒=⇒=，所以函数()f x 在(1,0)处的切线方程为：1y x =-，令()g x x k =-，它与横轴的交点坐标为(,0)k .在同一直角坐标系内画出函数()0,1ln ,1x f x x x <⎧=⎨≥⎩和()g x x k =-的图象如下图的所示：利用数形结合思想可知：不等式()≤-f x x k 对任意的x ∈R 恒成立，则实数k 的取值范围是1k ≤. 故选：A【点睛】本题考查了利用数形结合思想解决不等式恒成立问题，考查了导数的应用，属于中档题.12．已知函数()f x 是奇函数，且22()'()ln(1)ln(1)1f x f x x x x -=+----，若对11[,]62x ∀∈，(1)(1)f ax f x +<-恒成立，则a 的取值范围是（）A ．(3,1)--B ．(4,1)--C ．(3,0)-D ．(4,0)- 【答案】A【解析】【分析】先根据函数奇偶性求得()(),f x f x '，利用导数判断函数单调性，利用函数单调性求解不等式即可.【详解】因为函数()f x 是奇函数，所以函数'()f x 是偶函数.22()'()ln(1)ln(1)1f x f x x x x ---=--+--，即22()'()ln(1)ln(1)1f x f x x x x--=--+--，又22()'()ln(1)ln(1)1f x f x x x x-=+----，所以()ln(1)ln(1)f x x x =+--，22'()1f x x =-. 函数()f x 的定义域为(1,1)-，所以22'()01f x x =>-，则函数()f x 在(1,1)-上为单调递增函数.又在(0,1)上，()(0)0f x f >=，所以()f x 为偶函数，且在(0,1)上单调递增. 由(1)(1)f ax f x +<-，可得11111ax x ax ⎧+<-⎨-<+<⎩，对11[,]62x ∈恒成立，则1120ax x a x ⎧+<-⎪⎨-<<⎪⎩，21120a x a x⎧-<<-⎪⎪⎨⎪-<<⎪⎩对11[,]62x ∈恒成立，，得3140a a -<<-⎧⎨-<<⎩，所以a 的取值范围是(3,1)--.故选：A.【点睛】本题考查利用函数单调性求解不等式，根据方程组法求函数解析式，利用导数判断函数单调性，属压轴题.二、填空题：本题共4小题，每小题5分，共20分。

江苏省百校2020届高三下学期5月第五次联考数学试题(附答案及解析)

江苏省百校2020届高三下学期5月第五次联考数学试题一、填空题本大题共14道小题。

1.已知A 为椭圆()222210x y a b a b+=>>上一点，它关于原点的对称点为B ，点F 为椭圆的右焦点，且以AB 为直径的圆过F ，当6ABF π∠=，该椭圆的离心率是_______.答案及解析：1.1【分析】根据题意，由圆的圆周角的性质得出90AFB ∠=，且2AB c =，由于6ABF π∠=，则AF c =，BF =，利用椭圆的定义得2AF BF a +=，即可得出a 和c 的关系，从而可求出椭圆的离心率.【详解】解：由题意知，以AB 为直径的圆过F ，点F 为椭圆的右焦点，则90AFB ∠=，且2AB c =，又6ABF π∠=，则AF c =，BF =，设椭圆的左焦点为E ，由椭圆的对称性可得AE BF =由椭圆的定义得2AF BF AE AF a +=+=，则2c a =，即：1==c a ，所以1e =.答案第2页，总29页……○…………外…………○…………装…………○…………订…………○…………线…………○…………※※请※※不※※要※※在※※装※※订※※线※※内※※答※※题※※……○…………内…………○…………装…………○…………订…………○…………线…………○…………故答案为：31-.【点睛】本题考查椭圆的离心率和简单几何性质，以及椭圆定义的应用和圆的性质的应用. 2.已知集合{}1,2A =，{}1,2,3AB =，则集合中B 必定含有的元素是_______.答案及解析：2.3 【分析】根据题意，结合并集的概念即可得出答案. 【详解】解：∵集合{}1,2A =，{}1,2,3A B =，∴集合中B 必定含有的元素是3. 故答案为：3.【点睛】本题考查对并集概念的理解，属于基础题. 3.已知双曲线2221(0)9x y a a -=>的左、右顶点与点(0，3)构成等腰直角三角形，则该双曲线的渐近线方程是_______.答案及解析：3.y x =±【分析】○…………外…………○…………装…………○…………订…………○…………线…………○…………学校:___________姓名：___________班级：___________考号：___________○…………内…………○…………装…………○…………订…………○…………线…………○…………根据题意，可知双曲线2221(0)9x y a a -=>焦点在x 轴上，且3b =，设左、右顶点为A B 、，点(0，3)为C ，根据双曲线的顶点坐标可知()(),0,,0A a B a -，再结合题目条件得出AC BC ⊥且AC BC =，利用勾股定理222AC BC AB +=，代数求出a 和by x a=±，即可求出双曲线的渐近线方程. 【详解】解：由题意知，双曲线2221(0)9x y a a -=>焦点在x 轴上，且3b =，设左、右顶点为A B 、，点(0，3)为C ，如下图，则()()(),0,,0,0,3A a B a C -，则AO a =，3CO =，29AC a =+，2AB a =，由于左、右顶点与点(0，3)构成等腰直角三角形，所以AC BC ⊥且AC BC =，则222AC BC AB +=，即()()()22222992a a a +++=，解得：3a =，即a b =，所以双曲线的渐近线方程为：by x x a=±=±，故答案为：y x =±.【点睛】本题考查双曲线的渐近线方程和简单几何性质的应用，考查计算能力. 4.斐波那契数列又称黄金分割数列，因数学家列昂纳多·斐波那契以兔子繁殖为例而引入，故又称为“兔子数列”.在数学上，斐波那契数列被以下递推方法定义：数列{a n }满足121a a ==，21n n n a a a +-=+，现从该数列的前12项中随机抽取1项，能被3整除的概率是_______.答案及解析：4.1答案第2页，总29页【分析】根据题意，分别列举出数列的前12项，再列出能被3整除的数，根据古典概型求概率即可得出结果. 【详解】解：根据题意，“兔子数列”满足：121a a ==，21n n n a a a +-=+，则该数列的前12项分别为：1，1，2，3，5，8，13，21，34，55，89，144，其中能被3整除的数有：3，21，144，共3项，故从该数列的前12项中随机抽取1项，能被3整除的概率是31124=. 故答案为：14. 【点睛】本题考查古典概型的概率的计算，通过列举法列出基本事件解决古典概型问题，对所给定义的理解是解题的关键. 5.已知x ，y 均为正数，且11x y +=，则8yy x+的最小值为_______. 答案及解析：5.16 【分析】由题可知，,x y 均为正数，且11x y +=，则10y x y -=>，代入化简得189(1)101y y y x y +=-++-，再利用基本不等式即可求出最小值. 【详解】解：由于,x y 均为正数，且11x y +=，∴10y x y-=>，可得：1y >，∴22(1)2(1)18888(1)8111y y y y y y y y y y x y y y-+-++=+=+=+-+---， 19(1)1010161y y =-++≥=-，即：816y y x+≥，当且仅当43y =时取“＝”，所以8yy x+的最小值为16. 故答案为：16.【点睛】本题考查利用基本不等式求和的最小值，对条件的变形是解题的关键. 6.已知等比数列{a n }的前n 项和为S n ，且2430a a a +=，31S =-，则n a =_______.答案及解析：6.(1)n -【分析】已知{}n a 为等比数列，2430a a a +=，31S =-，利用通项公式和前n 项和公式求出1a 和q ，根据11n n a a q -=即可求出n a .【详解】解：由题可知，{}n a 为等比数列，2430a a a +=，31S =-，2243330,0a a a a a +=∴+=，由于等比数列中0n a ≠，解得：31a =-，31S =-，即：1231a a a ++=-，21111q q--∴+-=-，解得：1q =-， 3121a a q ∴==-，所以()1111(1)(1)n n n n a a q--==-⋅-=-.故答案为：(1)n-.【点睛】本题考查等比数列的通项公式，利用等比数列通项公式和前n 项和公式求出基本量，考查化简运算能力. 7.已知函数tan y x =与sin(3)(0)y x ϕϕπ=-≤<，它们图象有一个交点的横坐标为π，则ϕ的值是答案第2页，总29页_______.答案及解析：7.4π 【分析】根据两函数的图象有一个交点的横坐标为4π，分别代入两个函数解析式，结合ϕ的取值范围，即可求出ϕ的值.【详解】解：由于tan y x =与sin(3)(0)y x ϕϕπ=-≤<的图象有一个交点的横坐标为4π，则tansin 3144ππϕ⎛⎫=⨯-= ⎪⎝⎭， 32,42k k Z ππϕπ∴⨯-=+∈，解得：2,4k k Z πϕπ=-∈，又0ϕπ≤<，∴4πϕ=.故答案为：4π. 【点睛】本题考查三角函数的图象和性质，以及三角函数求值问题，考查计算能力. 8.已知一组数据1，3，5，7，9，则该组数据的方差是_______答案及解析：8.8 【分析】计算均值，再由方差公式得结论．【详解】由题意1357955x ++++==，∴2222221[(15)(35)(55)(75)(95)]85s =-+-+-+-+-=．故答案为：8．【点睛】本题考查方差的计算，掌握方差计算公式是解题基础． 9.若函数()()f x x a =-[1，9]上的最小值为18，则a 的值为_______. 答案及解析：9.78【分析】[]1,3t =∈，则2x t =，将原题转化为函数2()()f t t a t =-⋅在区间[]1,3上的最小值为18，则2()3f t t a '=-，分类讨论a ，通过利用导数研究函数的单调性和最值，即可求出a 的值，【详解】解：由题可知，()()f x x a =-[1，9]上的最小值为18，[]1,3t =∈，则2x t =，则原题转化为：函数2()()f t t a t =-⋅在区间[]1,3上的最小值为18，则2()3f t t a '=-，当0a ≤时，2()30f t t a '=-≥恒成立，则()f t 在区间[]1,3上单调递增，则1(1)8f =，解得：78a （舍去）；当0a >时，令2()30f t t a '=-=，解得：t =t =， 1≤，即03a <≤时，()f t 在区间[]1,3上单调递增，则1(1)8f =，解得：78a ，符合题意； 3≥，即27a ≥时，()f t 在区间[]1,3上单调递减，答案第2页，总29页则1(3)8f =，解得：21524a =（舍去）；若13<<，即327a <<时，()f t 在区间⎡⎢⎣上单调递减，在区间⎤⎥⎦上单调递增，则18f =，无正数解，综上所述：a 的值为78. 故答案为：78. 【点睛】本题考查利用导数研究含参数的函数的单调性和最值，从而求出参数值，同时考查转化和分类讨论思想. 10.已知正方体ABCD ﹣A 1B 1C 1D 1的棱长为2，则三棱锥11B A C D -的体积是_______.答案及解析：10.83【分析】根据题意，得出三棱锥11B A C D -所有棱长都为式即可求出结果.【详解】解：已知正方体1111ABCD A B C D -的棱长为2，则三棱锥11B A C D -所有棱长都为则11AC D ∆的面积为：(1121sin 23A C D S π=⨯⨯=△11AC D ∆的外接圆半径为：23=三棱锥的高为：3h ===，则三棱锥11B A C D -的体积是：11118333A C D V S h =⋅=⨯=△.○…………外…………○…………装…………○…………订…………○…………线…………○…………学校:___________姓名：___________班级：___________考号：___________○…………内…………○…………装…………○…………订…………○…………线…………○…………故答案为：83.【点睛】本题考查三棱锥的体积，涉及正方体的性质和三棱锥的性质，考查计算能力. 11.下图是一个算法的流程图，则输出k 的值是_______.答案及解析：11.6 【分析】根据程序框图可知，利用循环结构计算并输出变量k 的值，模拟程序运行，分析循环中各变量值的变化情况，直到满足条件27100k k -+>，即可得出答案. 【详解】解:根据程序框图，模拟程序运行，输入1k =，继续运行2k =，此时22710272100k k -+=-⨯+=，不满足条件，执行循环体，3k =，此时227103731020k k -+=-⨯+=-<，不满足条件，执行循环体，4k =，此时227104741020k k -+=-⨯+=-<，不满足条件，执行循环体，5k =，此时22710575100k k -+=-⨯+=，不满足条件，执行循环体，6k =，此时227106761040k k -+=-⨯+=>，满足条件，答案第2页，总29页故输出k 的值是6. 故答案为：6.【点睛】本题考查循环程序框图，解题时应模拟程序框图的运行过程，注意循环条件的判断. 12.已知复数()i a i +的模为1（其中i 是虚数单位），则实数a 的值为_______.答案及解析：12.0 【分析】设i(i)1i z a a =+=-+，再根据复数的模运算，即可求出a 的值. 【详解】解：根据题意，设i(i)1i z a a =+=-+，由于复数()i a i +的模为1，即：1z =，则1z ==，0a ∴=.故答案为：0.【点睛】本题考查复数的乘法运算和模的运算，属于基础题. 13.已知角αβ，满足tan 2tan αβ=，若3sin()5αβ+=，则sin()αβ-的值是_______. 答案及解析：13.15【分析】根据题意，由tan 2tan αβ=得出sin cos 2cos sin αβαβ=，由3sin()5αβ+=，根据两角和与差的正弦公式得出3sin cos cos sin 5αβαβ+=，得出2sin cos 5αβ=，1cos sin 5αβ=，从而可求出sin()αβ-的值.【详解】解：由于tan 2tan αβ=，则sin 2sin cos cos αβαβ=， sin cos 2cos sin αβαβ∴=，又3sin()5αβ+=，即：3sin cos cos sin 5αβαβ+=，解得：2sin cos 5αβ=，1cos sin 5αβ=， 211sin()sin cos cos sin 555αβαβαβ∴-=-=-=. 即：sin()αβ-的值为15. 故答案：15. 【点睛】本题考查三角函数的化简求值，涉及同角三角函数商的关系和两角和与差正弦公式的应用，考查化简计算能力. 14.已知当0x >，函数()()ln 0f x a x a =>，且()()f x f x =-，若()2()20g x x m m =->的图像与f (x )的图像在第二象限有公共点，且在该点处的切线相同，当实数m 变化时，实数a 的取值范围是_______.答案及解析：14.()4,4e【分析】根据题意，可知()f x 与()g x 均为偶函数，所以()f x 与()g x 的图像在第二象限有公共点，且在该点处的切线相同，则在第一象限也有公共点，且在该点处的切线也相同，求导得0x >时，()a f x x'=，()4g x x '=，设在第一象限的切点的横坐标为0x ，得出()01,x ∈+∞，则20000ln 24a x x m a x x ⎧=-⎪⎨=⎪⎩，整理得0222000144ln 20x a x m x x x >⎧⎪=⎨⎪=-+>⎩，即可求出0x 的取值范围，从而可求出实数a 的取值范围.答案第2页，总29页【详解】解：由题意知：()()f x f x =-和()2()20g x x m m =->，所以()f x 与()g x 均为偶函数，由于()f x 与()g x 的图像在第二象限有公共点，且在该点处的切线相同，则在第一象限也有公共点，且在该点处的切线也相同，因为0x >时，()()ln 0f x a x a =>，()2()20g x x m m =->所以0x >时，()af x x'=，()4g x x '=，设在第一象限的切点的横坐标为0x ，则00()ln0f x a x =>，可得()01,x ∈+∞，则有20000ln 24a x x m a x x ⎧=-⎪⎨=⎪⎩，即：02022000144ln 20x a x m x x x >⎧⎪=⎨⎪=-+>⎩，由220004ln 20m x x x =-+>，即()200212ln 0x x ->，则012ln 0x ->，解得：0x <综上可得：01x <，则201x e <<，又因为204a x =，所以44a e <<，即：()4,4a e ∈. 故答案为：()4,4e .【点睛】本题考查导数的几何意义的应用，以及函数的奇偶性的应用，考查函数与方程思想、转化与化归思想. 一、解答题本大题共9道小题。

江苏省南通市2020届高三第二学期阶段性模拟考试数学试题(含答案解析)

开始输出n 输入p结束n ←1, S ←0S < pn ←n + 1S ←S + 2n NY（第5题）江苏省南通市2020届高三第二学期阶段性模拟考试数学试题2020.05(总分160分，考试时间120分钟)一、填空题（本大题共14小题，每小题5分，计70分. 不需写出解答过程，请把答案写在答题纸的指定位置上）1．已知集合{}1,2,3,4A =，{}2log (1)2B x x =-<，则A B =I ▲ ． 2．设复数2(2i)z =+（i 为虚数单位），则z 的共轭复数为 ▲ ．3．若以连续掷两次骰子分别得到的点数m ，n 作为点P 的横、纵坐标，则点P 在直线2x ﹣y ﹣1＝0上方的概率为．4．在平面直角坐标系xOy 中，若抛物线22(0)x py p =>上纵坐标为1的一点到焦点的距离为4，则该抛物线的焦点到准线的距离为 ▲ ． 5．执行右边的程序框图，若p ＝14，则输出的n 的值为 ▲ ．6．函数22log (32)y x x =--的值域为 ▲ ．7．等差数列}{n a 中，若100119753=++++a a a a a ，则=-1393a a ▲ ．8．现用一半径为10 cm ，面积为80π cm 2的扇形铁皮制作一个无盖的圆锥形容器（假定衔接部分及铁皮厚度忽略不计，且无损耗），则该容器的容积为 ▲ cm 3．9．已知() 0 αβ∈π，，，且()1tan 2αβ-=，1tan 5β=-，则tan α的值为 ▲ ．10．已知实数,x y 满足40210440x y x y x y +-⎧⎪-+⎨⎪+-⎩≤≥≥，则3z x y =+-的取值范围是 ▲ ．11．若函数()()ππ()sin 63f x a x x =++-是偶函数，则实数a 的值为 ▲ ．12．在△ABC 中，cos 2sin sin A B C =，tan tan 2B C +=-，则tan A 的值为 ▲ ． 13．已知函数2210()0xx mx x e f x e mx x ⎧+<⎪=⎨⎪+>⎩，，，，若函数()f x 有四个不同的零点，则实数m 的取值范围是 ▲ ．14．已知[)0,2θπ∈，若关于k ()33sin cos k θθ-在(],2-∞-上恒成立，则θ的取值范围为 ▲ ．二、解答题（本大题共6小题，计90分. 解答应写出必要的文字说明，证明过程或演算步骤，请把答案写在答题纸的指定区域内） 15．(本小题满分14分)已知sin cos θθ+=，ππ44θ⎛⎫∈- ⎪⎝⎭，．（1）求θ的值；（2）设函数()22()sin sin f x x x θ=-+，x ∈R ，求函数()f x 的单调增区间．16．(本小题满分14分)如图，在四棱锥P ABCD -中，底面ABCD 为梯形，//CD AB ，2AB CD =， AC 交BD 于O ，锐角PAD ∆所在平面PAD ⊥底面ABCD ，PA BD ⊥，点Q 在侧棱PC 上，且2PQ QC =．（1）求证：//PA 平面QBD ；（2）求证：BD AD ⊥．17．(本小题满分14分)在平面直角坐标系xOy 中，圆O ：224x y +=，直线l ：43200x y +-=．43()55A ，为圆O 内一点，弦MN 过点A ，过点O 作MN 的垂线交l 于点P ．（1）若MN ∥l ，求△PMN 的面积．（2）判断直线PM 与圆O 的位置关系，并证明．18．(本小题满分16分)如图，有一正三角形铁皮余料，欲利用余料剪裁出一个矩形(矩形的一个边在三角形的边上)，并以该矩形制作一铁皮圆柱的侧面。

2020届江苏省南通市海安高级中学高三下学期5月第二次检测数学试题解析

2020届江苏省南通市海安高级中学高三下学期5月第二次检测数学试题一、填空题1．设集合{}2,0,M x =，集合{}0,1N =，若N M ⊆，则x = ．答案：1试题分析：由题意1M ∈，所以1x =．【考点】集合间的关系．2．某大学为了解在校本科生对参加某项社会实践活动的意向，拟采用分层抽样的方法，从该校四个年级的本科生中抽取一个容量为300的样本进行调查．已知该校一年级、二年级、三年级、四年级的本科生人数之比为4：5：5：6，则应从一年级本科生中抽取_______名学生．答案：60采用分层抽样的方法，从该校四个年级的本科生中抽取一个容量为300的样本进行调查的. 解：∵该校一年级、二年级、三年级、四年级的本科生人数之比为4:5:5:6， ∴应从一年级本科生中抽取学生人数为：4300604556⨯=+++.故答案为60.3．已知复数z 满足()341(i z i +=为虚数单位)，则z 的模为 .答案：15试题分析：()13451341||3425255i i z z z i -+=⇒==⇒==+【考点】复数及模的概念与复数的运算4．根据如图所示的伪代码，最后输出的S 的值为_________.答案：55解：试题分析：由算法伪代码语言所提供的信息可知(110)1001210552S +⨯=+++⋅⋅⋅+==,应填55.【考点】伪代码语言的理解和运用．5．现有5道试题，其中甲类试题2道，乙类试题3道，现从中随机取2道试题，则至少有1道试题是乙类试题的概率为．答案：910试题分析：从5道试题中随机取2道试题，共有10种基本事件，其中皆不是乙类试题的包含1中基本事件，因此至少有1道试题是乙类试题的概率为1911010-= 【考点】古典概型概率6．在ABC 中，若1AB =，2BC =，5CA =AB BC BC CA CA AB ⋅+⋅+⋅的值是______. 答案：5-利用勾股定理可得知AB BC ⊥，结合平面向量数量积的运算性质可求得AB BC BC CA CA AB ⋅+⋅+⋅的值.解：在ABC 中，1AB =，2BC =，5CA =222AB BC AC +=，AB BC ∴⊥，则0AB BC ⋅=，因此，()25AB BC BC CA CA AB CA AB BC CA AC AC ⋅+⋅+⋅=⋅+=⋅=-=-. 故答案为：5-. 点评：本题考查平面向量数量积的计算，考查平面向量数量积的运算性质，考查计算能力，属于基础题.7．若实数,x y满足约束条件22,{1,1,x yx yx y-≤-≥-+≥则目标函数2z x y=+的最小值为．答案：1解：试题分析：可行域为一个三角形ABC及其内部，其中(3,4),(1,0),(0,1),A B C直线2z x y=+过点(0,1)C时取最小值1【考点】线性规划求最值8．已知()1sin153α︒-=，则()cos302α︒-的值为______.答案：79由题易得3022(15)αα︒︒-=-，然后结合题中条件由余弦的二倍角公式直接计算即可. 解：()()()227cos302cos21512sin15199ααα︒︒︒⎡⎤-=-=--=-=⎣⎦.故答案为：79.点评：本题考查余弦二倍角公式，侧重考查对基础知识的理解和掌握，考查计算能力，属于基础题.9．已知等比数列的前项和为，若，则的值是．答案：-2试题分析：，【考点】等比数列性质及求和公式10．已知双曲线221y x a-=的一条渐近线与直线230x y -+=平行，则离心率e =______.由双曲线方程写出渐近线方程，由平行求得参数a ，然后离心率．解：由已知双曲线的渐近线方程为0x y =和0x y +=，显然直线0x y =与直线230x y -+=2=，14a =，即双曲线方程为22114y x -=，实半轴长为1a '=，虚半轴长为12b '=，半焦距为c ==，所以离心率为c e a =='．点评：本题考查双曲线的离心率，掌握双曲线的渐近线方程与两直线平行的条件是解题关键． 11．一个圆柱和一个圆锥同底等高，若圆锥的侧面积是其底面积的2倍，则圆柱的侧面积是其底面积的_________倍.答案：试题分析：因为一个圆柱和一个圆锥同底等高，所以设底面半径为r ，高为h ，因为圆锥的侧面积是其底面面积的2倍，所以22,2rl r l r ππ==，h =，所以圆柱的侧面积22S rl r π==，其底面积为2r π，所以圆柱的侧面积是底面积的. 【考点】旋转体的侧面积与表面积.【方法点晴】本题主要考查了旋转体的侧面积与表面积的计算，其中解答中涉及到圆柱侧面积、圆锥的侧面积与表面积的计算，圆锥与圆柱的性质等知识点的综合考查，着重考查了学生分析问题和解答问题的能力，以及学生的空间想象能力，解答中利用圆柱和圆锥的侧面积公式，准确计算是解答的关键，试题比较基础，属于基础题.12．已知函数()()(),01,0x e x f x x x ⎧≥⎪=⎨+<⎪⎩，则不等式()()22f x f x <-的解集为______.答案：()2,1-先判断函数单调性，再根据单调性化简不等式，解得结果. 解：,1x y e y x ==+都为单调递增函数，且001e =+()f x ∴在R 上单调递增，()()22f x f x <-， 22x x ∴<-，即()()220210x x x x +-<+-<，∴21x -<< 故答案为：()2,1- 点评：本题考查分段函数单调性、利用函数单调性解不等式，考查基本分析求解能力，属基础题.13．已知函数(0)xy a b b =+>的图像经过点(1,3)P ，如下图所示，则411a b+-的最小值为 .答案：92试题分析：由图可知，a ＞1，点(1，3)在函数(0)xy a b b =+>的图象上，所以 a ＋b ＝3．1＜a ＜3，0＜b ＜2．4114114114192()[(1)]()(5)12121212b a a b a b a b a b a b -+=⨯+=⨯-++=⨯++≥----当且仅当72,33a b ==时取等号【考点】指数函数性质及图象，基本不等式，函数的最值14．已知直线30x y -+=与圆222:O x y r +=()0r >相交于,M N 两点，若3OM ON ⋅=，圆的半径r =______.答案：6求出圆心到弦的距离32=d ，利用余弦二倍角公式与向量的数量积公式化简222(21)d OM ON r r⋅=⋅-可得解：圆心(0,0) 到直线30x y -+=的距离2200+332===221+1d -. ()22222cos cos 2cos 1(21)d OM ON OM ON MON r r MON r MOE r r⋅=∠=⋅⋅∠=∠-=⋅-2222292293662d r r r r r ∴-=⋅-=-=⇒=⇒=.6 点评：本题考查直线与圆相交问题．解题关键是掌握垂径定理及向量的数量积公式二、解答题15．设函数()sin cos 464f x x x πππ⎛⎫=--⎪⎝⎭.（1）求()f x 的单调增区间；（2）若()0,4x ∈，求()y f x =的值域. 答案：（1）单调增区间为：()2108,833k k k Z ⎡⎤-++∈⎢⎥⎣⎦；（2）332⎛- ⎝.（1）由两角差正弦公式化函数为一个角的一个三角函数形式，然后利用正弦函数的单调性得增区间；（2）求出43x ππ-的范围，把它作为一个整体，利用正弦函数性质可得()f x 值域．解：解：（1）()33sin cos sin cos 3sin 46442443f x x x x x x πππππππ⎛⎫⎛⎫=--=-=- ⎪ ⎪⎝⎭⎝⎭∵222432k x k ππππππ-+≤-≤+，∴2108833k x k -+≤≤+，k Z ∈ ∴()f x 的单调增区间为：()2108,833k k k Z ⎡⎤-++∈⎢⎥⎣⎦（2）∵()0,4x ∈，∴23433x ππππ-<-<∴3sin 143x ππ⎛⎫-<-≤ ⎪⎝⎭ ∴()f x 的值域为：3,32⎛⎤- ⎥⎝⎦. 点评：本题考查正弦型三角函数的单调性，值域问题，考查两角和与差的正弦公式，掌握正弦函数的性质是解题关键．16．如图，在多面体ABCDEF 中，四边形ABCD 是菱形，,AC BD 相交于点O ，//EF AB ，2AB EF =，平面BCF ⊥平面ABCD ，BF CF =，点G 为BC 的中点.（1）求证：直线//OG 平面EFCD ；（2）求证：直线AC ⊥平面ODE . 答案：（1）证明见解析；（2）证明见解析. （1）证明OGCD ，再利用线面平行判定定理，即可证明；（2）证明AC ⊥平面ODE 内的两条相交直线EO 、DO ；解：证明：（1）∵四边形ABCD 是菱形，AC BD O =，∴点O 是BD 的中点，∵点G 为BC 的中点，∴OGCD ，又∵OG ⊄平面EFCD ，CD ⊂平面EFCD ，∴直线OG ∥平面EFCD . （2）∵BF CF =，点G 为BC 的中点，∴FG BC ⊥. ∵平面BCF ⊥平面ABCD ，平面BCF ⋂平面ABCD BC =，FG ⊂平面BCF ，FG BC ⊥，∴FG ⊥平面ABCD ，∵AC ⊂平面ABCD ，∴FG AC ，∵OGAB ，12OG AB=，EF AB ∥，12BF AB =， ∴OG EF ∥，OG EF =， ∴四边形EFGO 为平行四边形， ∴FG EO ∥， ∵FGAC ，FG EO ∥，∴AC EO ⊥，∵四边形ABCD 是菱形，∴AC DO ⊥，∵AC EO ⊥，AC DO ⊥，EO DO O ⋂=，EO 、DO 在平面ODE 内， ∴AC ⊥平面ODE . 点评：本题考查线面平行判定定理、线面垂直判定定理的运用，考查转化与化归思想，考查空间想象能力，求解时注意条件书写的完整性.17．如图，已知椭圆()2222:10x y C a b a b+=>>，离心率为12，过原点的直线与椭圆C交于,A B 两点（,A B 不是椭圆C 的顶点）.点D 在椭圆C 上，且AD AB ⊥.（1）若椭圆C 的右准线方程为：4x =，求椭圆C 的方程；（2）设直线BD 、AB 的斜率分别为1k 、2k ，求12k k 的值.答案：（1）22143x y +=；（2）1234k k =. （1）根据右准线以及离心率列方程组解得21a c =⎧⎨=⎩，即得23b =，可得椭圆C 的方程；（2）利用点差法得22110AD BD k k a b +⋅=，结合AD AB ⊥转化为1222111()0k a b k +-⋅=再根据离心率可得12k k 的值. 解：（1）2124c e a a c⎧==⎪⎪⎨⎪=⎪⎩，解得：21a c =⎧⎨=⎩，∴23b =，∴椭圆方程为：22143x y +=.（2）设()11,A x y ，()22,D x y ，则()11,B x y --，∴,A D 在椭圆上∴22112222222211x y a b x y a b ⎧+=⎪⎪⎨⎪+=⎪⎩，∴()()()()1212121222110x x x x y y y y a b +-++-= ∴22110AD BD k k a b +⋅=，∵12c e a ==，∴2234b a =，∴134AD k k =-∵AD AB ⊥，∴21AD k k =-，∴1234314AD ADk k k k -==- 点评：本题考查椭圆标准方程、点差法，考查综合分析求解能力，属中档题.18．如图，某小区有一块矩形地块OABC ，其中2OC =，3OA =，单位：百米.已知OEF 是一个游泳池，计划在地块OABC 内修一条与池边EF 相切于点M 的直路l （宽度不计），交线段OC 于点D ，交线段OA 于点N .现以点O 为坐标原点，以线段OC 所在直线为x 轴，建立平面直角坐标系，若池边EF满足函数(220y x x =-+≤≤的图象，若点M 到y 轴距离记为t .（1）当23t =时，求直路所在的直线方程；（2）当t 为何值时，地块OABC 在直路l 不含泳池那侧的面积取到最大，最大值时多少？答案：（1）42239y x =-+；（2）6t =866. （1）把23t =代入函数22y x =-+，得M 的坐标，再利用导数求切线的斜率，即可得到答案；（2）先求出面积的表达式为31444OND S t t t ⎛⎫=++ ⎪⎝⎭△，再利用导数求函数的最大值，即可得到答案；解：解：（1）把23t =代入函数22y x =-+，得214,39M ⎛⎫ ⎪⎝⎭，∵2y x '=-，∴43k =-， ∴直线方程为42239y x =-+；（2）由（1）知，直线的方程为222y tx t =-++，令0y =，122x t t ⎛⎫=+ ⎪⎝⎭，令0x =，22y t =+， ∴1222t t ⎛⎫+≤ ⎪⎝⎭，223t +≤. ∴221t ≤≤， ∴()231121424224OND S t t t t t t ⎛⎫⎛⎫=++=++ ⎪ ⎪⎝⎭⎝⎭△，令()31444g t t t t ⎛⎫=++ ⎪⎝⎭，∴()()()2222324t t g t t+-'=当t =()0g t '=，当2t ⎛∈- ⎝⎭时，()0g t '<，当3t ⎛⎫∈ ⎪ ⎪⎝⎭时，()0g t '>，()39g t g ⎛≥= ⎝⎭，所以所求面积的最大值为69-. 点评：本题考查函数模型解决面积问题、导数几何意义的运用，考查函数与方程思想、转化与化归思想，考查逻辑推理能力、运算求解能力.19．若函数()y f x =在0x x =处取得极大值或极小值，则称x 为函数()y f x =的极值点.已知函数()()3ln 1f x ax x x a R =+-∈. （1）当0a =时，求()f x 的极值；（2）若()f x 在区间1e e ⎛⎫ ⎪⎝⎭,上有且只有一个极值点，求实数a 的取值范围.答案：（1）极小值31e --；（2）22,0e ⎡⎫-⎪⎢⎣⎭. (1)求出()()3ln 1f x x '=+，令()0f x '=求出方程的解，从而探究()(),f x f x '随x 的变化情况，即可求出极值.(2)求出()()23ln 1f x ax x '=++，令()2ln 1g x ax x =++，分0a >，0a =，0a <三种情况进行讨论，结合零点存在定理求出实数a 的取值范围. 解：解：（1）当0a =时，()3ln 1f x x x =-的定义域为()0,∞+，()()3ln 33ln 1f x x x '=+=+，令()0f x '=，解得1x =，则()(),f x f x '随x 的变化如下表，故()f x 在10,e ⎛⎫ ⎪⎝⎭上是减函数，在1,e ⎛⎫+∞ ⎪⎝⎭上是增函数；故()f x 在1x e=时取得极小值131f e e ⎛⎫=-- ⎪⎝⎭；（2）函数()33ln 1f x ax x x =+-的定义域为()0,∞+，()()23ln 1f x ax x '=++，令()2ln 1g x ax x =++，则()21212ax g x ax x x+'=+=，当0a >时，()0g x '>在()0,∞+恒成立，故()f x '在()0,∞+上是增函数，而2211113ln 130f a a e e e e ⎡⎤⎛⎫⎛⎫⎛⎫'=++=>⎢⎥ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎢⎥⎣⎦，故当1,x e e ⎛⎫∈ ⎪⎝⎭时，()0f x '>恒成立，故()f x 在区间1e e ⎛⎫ ⎪⎝⎭,上单调递增，故()f x 在区间1e e ⎛⎫ ⎪⎝⎭,上没有极值点；当0a =时，由（1）知，()f x 在区间1e e ⎛⎫ ⎪⎝⎭,上没有极值点；当0a <时，令2210ax x+=，解得x =或；故()2ln 1g x ax x =++在⎛ ⎝上是增函数，在⎫+∞⎪⎪⎭上是减函数， ①当()10g e g e ⎛⎫⋅< ⎪⎝⎭，即220a e-<<时， ()g x 在1e e ⎛⎫⎪⎝⎭,上有且只有一个零点，且在该零点两侧异号，②令10g e ⎛⎫= ⎪⎝⎭得20a e=，不符合题意；③令()0g e =得22a e =-1,e e ⎛⎫ ⎪⎝⎭，而1ln 0222e e g g ⎛⎫==+> ⎪⎝⎭，又10g e ⎛⎫< ⎪⎝⎭，所以()g x 在1e e ⎛⎫ ⎪⎝⎭,上有且只有一个零点，且在该零点两侧异号，综上所述，实数a 的取值范围是22,0e ⎡⎫-⎪⎢⎣⎭. 点评：本题考查了极值的求解，考查了已知极值点的范围求解参数.20．已知数列{}n a 的前n 项和为n S ，且对一切正整数n 都有212n n S n a =+. （1）求证：()*142n n a a n n N ++=+∈；（2）求数列{}n a 的通项公式；（3）是否存在实数a，使不等式21211111...1n a a a ⎛⎫⎛⎫⎛⎫---<⎪ ⎪⎪⎝⎭⎝⎭⎝⎭，对一切正整数n 都成立？若存在，求出a 的取值范围；若不存在，请说明理由. 答案：（1）证明见解析；（2）()*2n a n n N=∈；（3）存在；a的取值范围是()3,2⎛⎫-+∞ ⎪ ⎪⎝⎭.（1）由题得()2*12n n S n a n N =+∈①，()()211112n n S n a n N ++=++∈②，②－①即得142n n a a n ++=+；（2）由题得24n n a a +-=.()*n N ∈，再对n 分奇数和偶数两种情况讨论，求出数列{}n a 的通项公式；（3）令()1211111...1n f n a a a ⎛⎫⎛⎫⎛⎫=---⎪ ⎪⎪⎝⎭⎝⎭⎝⎭()*n N ∈，判断函数的单调性，求出其最大值，解不等式322a a<-即得解. 解：（1）证明：∵()2*12n n S n a n N =+∈①， ∴()()211112n n S n a n N ++=++∈② 由②－①得()()22*11111111212222n n n n n n S S n a n a n a a n N +++⎡⎤⎛⎫-=++-+=++-∈ ⎪⎢⎥⎣⎦⎝⎭，∴()*142n n a a n n N++=+∈.（2）∵()*142n n a a n n N++=+∈③∴()2146n n a a n n N +++=+∈，④ ④－③，得24n na a +-=.()*n N ∈从而数列{}n a 的奇数项依次成等差数列，且首项为12a =，公差为4；数列{}n a 的偶数项也依次成等差数列，且首项为2a ，公差为4. 在①中令1n =得211112S a =+，又∵11S a =，∴1111122a a a =+⇒=. 在③中令1n =得2242a +=+，∴24a =. ∴当()*21n k k N =-∈时，12n k +=，()21141422nk a a a k k n -==+-=-=；∴当2n k =()*k N∈时，2nk =，()224142n k a a a k k n ==+-==；综上所述，()*2n a n n N=∈.（3）令()1211111...1n f n a a a ⎛⎫⎛⎫⎛⎫=---⎪ ⎪⎪⎝⎭⎝⎭⎝⎭()*n N ∈，则()0f n > 且()()1121111n f n n f n a +++⎛⎫=-==< ⎪⎝⎭ ∴()()1f n f n +<， ∴()f n 单调递减， ∴()()max []1f n f ==.∴不等式21211111...1n a a a ⎛⎫⎛⎫⎛⎫---<⎪ ⎪⎪⎝⎭⎝⎭⎝⎭对一切正整数n 都成立等价于()32f n a a<-对一切正整数n 都成立，等价于()max f n a <-⎡⎤⎣⎦32a a <-.0<，即(20a a a->，解之得a >02a -<<. 综上所述，存在实数a 的适合题意，a的取值范围是()3,2⎛⎫-+∞ ⎪ ⎪⎝⎭.点评：本题主要考查数列通项的求法，考查数列的单调性的判定和最值的求法，考查数列不等式的恒成立问题的求解，考查不等式的解法，意在考查学生对这些知识的理解掌握水平和分析推理能力.。

江苏省南通市如东县栟茶中学2020届高三数学下学期5月模拟考试试题含解析

,即，
，且，
，即的最小值为．
点睛：基本不等式的考察的一个主要考察方法就是判别式法，可以应用判别式法的题型基本特点：（1）题干条件是二次式；（2）问题是一次式(或可以化简为一次式)．熟悉判别式法的应用，可以提升考试中碰到不等式题型的准确率．
11. 如图，在由5个边长为1，一个顶角为60°的菱形组成的图形中, _____________
（1)求出函数的导数,利用导数的几何意义即可求出函数在处的切线方程
（2)先通过求导，研究函数的单调性,然后利用函数在上有两个零点可得直线与的图像有两个交点，从而得到，求解即可
（3)不妨设，恒成立等价于，化简为 ,然后，令，然后判断的单调性即可求解
【详解】(1）当时， , ，切点坐标为，
又平面 , 平面 ,
∴ 平面，而平面， ∴
∴
点睛：（1)线面垂直的判定可由线线垂直得到,注意线线是相交的，也可由面面垂直得到，注意线在面内且线垂直于两个平面的交线.
（2)线线平行的判定可以由线面平行得到，注意其中一条线是过另一条线的平面与已知平面的交线,也可以由面面平行得到，注意两条线是第三个平面与已知的两个平行平面的交线。
（2）根据设计要求,透光区域与矩形窗面的面积比值越大越好.当该比值最大时，求边的长度.
【答案】（1）关于函数关系式为 ,定义域为；
(2）透光区域与矩形窗面的面积比值最大时，的长度为1 ．
【解析】
试题分析：
（1) 过点作于点，可得关于的函数关系式为，定义域为 ;
(2)由原函数与导函数的关系可得当时，有最大值 ,此时
8。将1个半径为1的小铁球与1个底面周长为 ,高为4的铁制圆柱重新锻造成一个大铁球,则该大铁球的表面积为_____________

江苏省南通市2020届高三5月二模试题数学试题(解析版)

江苏省南通市2020届高三5月二模试题数学一、填空题：本大题共14小题，每小题5分，共70分．请把答案直接填写在答题卡相应位置上.1.记复数z ＝a +bi （i 为虚数单位）的共轭复数为()z a bi a b R =-∈，，已知z ＝2+i ，则2z =_____．【答案】3﹣4i 【解析】【分析】计算得到z 2＝（2+i ）2＝3+4i ，再计算2z 得到答案. 【详解】∵z ＝2+i ，∴z 2＝（2+i ）2＝3+4i ，则234z i =-．故答案为：3﹣4i ．【点睛】本题考查了复数的运算，共轭复数，意在考查学生的计算能力. 2.已知集合U ＝{1,3,5,9}，A ＝{1,3,9}，B ＝{1,9}，则∁U (A∪B)＝________. 【答案】{5} 【解析】易得A∪B ＝A ＝{1,3,9}，则∁U (A∪B)＝{5}．3.某校共有师生1600人，其中教师有1000人，现用分层抽样的方法，从所有师生中抽取一个容量为80的样本，则抽取学生的人数为_____．【答案】30 【解析】【分析】直接根据分层抽样的比例关系得到答案. 【详解】分层抽样的抽取比例为801160020=，∴抽取学生的人数为600120⨯=30．故答案为：30．【点睛】本题考查了分层抽样的计算，属于简单题.4.角α的顶点在坐标原点，始边与x 轴的非负半轴重合，终边经过点P （1，2），则sin （π﹣α）的值是_____．【答案】255【解析】【分析】计算sinα25y r ==，再利用诱导公式计算得到答案. 【详解】由题意可得x ＝1，y ＝2，r 5=sinα25y r ==，∴sin （π﹣α）＝sinα25= 25．【点睛】本题考查了三角函数定义，诱导公式，意在考查学生的计算能力. 5.执行以下语句后，打印纸上打印出的结果应是：_____．【答案】28 【解析】【分析】根据程序框图直接计算得到答案.【详解】程序在运行过程中各变量的取值如下所示：是否继续循环 i x 循环前 1 4 第一圈是 4 4+2 第二圈是 7 4+2+8 第三圈是 10 4+2+8+14退出循环，所以打印纸上打印出的结果应是：28 故答案为：28．【点睛】本题考查了程序框图，意在考查学生的计算能力和理解能力.6.设α、β为互不重合的平面，m ，n 是互不重合的直线，给出下列四个命题： ①若m ∥n ，则m ∥α；②若m ⊂α，n ⊂α，m ∥β，n ∥β，则α∥β； ③若α∥β，m ⊂α，n ⊂β，则m ∥n ；④若α⊥β，α∩β＝m ，n ⊂α，m ⊥n ，则n ⊥β；其中正确命题的序号为_____．【答案】④ 【解析】【分析】根据直线和平面，平面和平面的位置关系依次判断每个选项得到答案.【详解】对于①，当m ∥n 时，由直线与平面平行的定义和判定定理，不能得出m ∥α，①错误；对于②，当m ⊂α，n ⊂α，且m ∥β，n ∥β时，由两平面平行的判定定理，不能得出α∥β，②错误；对于③，当α∥β，且m ⊂α，n ⊂β时，由两平面平行的性质定理，不能得出m ∥n ，③错误；对于④，当α⊥β，且α∩β＝m ，n ⊂α，m ⊥n 时，由两平面垂直的性质定理，能够得出n ⊥β，④正确；综上知，正确命题的序号是④．故答案为：④．【点睛】本题考查了直线和平面，平面和平面的位置关系，意在考查学生的空间想象能力和推断能力.7.已知函数f(x)＝322{102x xx x ≥，，（－），＜＜，若关于x 的方程f(x)＝kx 有两个不同的实根，则实数k 的取值范围是________．【答案】10,2⎛⎫ ⎪⎝⎭【解析】由图可知，当直线y ＝kx 在直线OA 与x 轴(不含它们)之间时，y ＝kx 与y ＝f(x)的图像有两个不同交点，即方程有两个不相同的实根．8.已知关于x 的不等式（ax ﹣a 2﹣4）（x ﹣4）＞0的解集为A ，且A 中共含有n 个整数，则当n 最小时实数a 的值为_____．【答案】-2 【解析】【分析】讨论0,0,0a a a <=>三种情况，a ＜0时,根据均值不等式得到a 4a +=-（﹣a 4a-）≤﹣2=-4，计算等号成立的条件得到答案. 【详解】已知关于x 的不等式（ax ﹣a 2﹣4）（x ﹣4）＞0， ①a ＜0时，[x ﹣（a 4a +）]（x ﹣4）＜0，其中a 4a+＜0，故解集为（a 4a+，4），由于a 4a +=-（﹣a 4a-）≤﹣=-4，当且仅当﹣a 4a=-，即a ＝﹣2时取等号， ∴a 4a +的最大值为﹣4，当且仅当a 4a+=-4时，A 中共含有最少个整数，此时实数a 的值为﹣2；②a ＝0时，﹣4（x ﹣4）＞0，解集为（﹣∞，4），整数解有无穷多，故a ＝0不符合条件；③a ＞0时，[x ﹣（a 4a +）]（x ﹣4）＞0，其中a 4a+≥4， ∴故解集为（﹣∞，4）∪（a 4a+，+∞），整数解有无穷多，故a ＞0不符合条件；综上所述，a ＝﹣2．故答案为：﹣2．【点睛】本题考查了解不等式，均值不等式，意在考查学生的计算能力和综合应用能力.9.已知双曲线22221x y a b -=（a ＞0，b ＞0）的两个焦点为10F ⎛⎫ ⎪ ⎪⎝⎭、20F ⎫⎪⎪⎝⎭，点P 是第一象限内双曲线上的点，且1212tan PF F ∠=，tan ∠PF 2F 1＝﹣2，则双曲线的离心率为_____．【解析】【分析】根据正弦定理得1212122PF sin PF F PF sin PF F ∠==∠，根据余弦定理得2212PF PF +-2PF 1•PF 2cos ∠F 1PF 2212F F ==3，联立方程得到1233PF PF ==，计算得到答案.【详解】∵△PF 1F 2中，sin ∠PF 1F 2═5sin ∠PF 1F 2═5，∴由正弦定理得1212122PF sin PF F PF sin PF F ∠==∠，①又∵1212tan PF F ∠=，tan ∠PF 2F 1＝﹣2， ∴tan ∠F 1PF 2＝﹣tan （∠PF 2F 1+∠PF 1F 2）123214122-=-=+⨯，可得cos ∠F 1PF 245=， △PF 1F 2中用余弦定理，得2212PF PF +-2PF 1•PF 2cos ∠F 1PF 2212F F ==3，②①②联解，得12PF PF ==12PF PF -=∴双曲线的2a =，结合2c =，得离心率22c e a ==.. 【点睛】本题考查了双曲线离心率，意在考查学生的计算能力和转化能力. 10.记S k ＝1k +2k +3k +……+n k ，当k ＝1，2，3，……时，观察下列等式：S 112=n 212+n ，S 213=n 312+n 216+n ，S 314=n 412+n 314+n 2，……S 5＝An 612+n 5512+n 4+Bn 2，…可以推测，A ﹣B ＝_____．【答案】14【解析】【分析】观察知各等式右边各项的系数和为1，最高次项的系数为该项次数的倒数，据此计算得到答案. 【详解】根据所给的已知等式得到：各等式右边各项的系数和为1，最高次项的系数为该项次数的倒数，∴A 16=，A 15212B +++=1，解得B 112=-，所以A ﹣B 1116124=+=．故答案为：14．【点睛】本题考查了归纳推理，意在考查学生的推理能力.11.设函数()f x x x a =-，若对于任意的1x ，2x ∈[2，)+∞，1x ≠2x ，不等式1212()()0f x f x x x ->-恒成立，则实数a 的取值范围是．【答案】2a ≤试题分析：由题意得函数()f x x x a =-在[2，)+∞上单调递增，当2a ≤时()()f x x x a =-在[2，)+∞上单调递增；当2a >时()f x x x a =-在[,)a +∞上单调递增；在[2,)a 上单调递减，因此实数a 的取值范围是2a ≤考点：函数单调性12.已知平面向量a r ，b r ，c r 满足|a r |＝1，|b r |＝2，a r ，b r 的夹角等于3π，且（a c -r r）•（b c -r r ）＝0，则|c r|的取值范围是_____．【答案】⎣⎦【解析】【分析】计算得到|a b +r r |=2c =r |c r |cosα﹣1，解得cosα2=r ，根据三角函数的有界性计算范围得到答案.【详解】由（a c -r r）•（b c -rr ）＝0 可得 2c =r （a b +rr）•c a b -⋅=r r |a b +rr|•|c r|cosα﹣1×2cos3π=|a b +r r |•|c r |cosα﹣1，α为a b +r r 与cr 的夹角．再由 ()222a ba b +=++r r r r 2a r •b =r 1+4+2×1×2cos 3π=7 可得|a b +r r |=∴2c =rc r |cosα﹣1，解得cosα2=r ．∵0≤α≤π，∴﹣1≤cos α≤12≤r 1，即2c r c r |+1≤0，解得≤|c r |≤故答案为22⎣⎦，．【点睛】本题考查了向量模的范围，意在考查学生的计算能力，利用三角函数的有界性是解题的关键.13.在平面直角坐标系xOy 中，直角三角形ABC 的三个顶点都在椭圆()22211x y a a+=＞上，其中A （0，1）为直角顶点．若该三角形的面积的最大值为278，则实数a 的值为_____．【答案】3【分析】设直线AB 的方程为y ＝kx +1，则直线AC 的方程可设为y 1k =-x +1，（k ≠0），联立方程得到B （22221a ka k -+，222211a k a k -+），故S 442221211a k ka a k k +=⎛⎫+++ ⎪⎝⎭，令t 1k k =+，得S 42222(1)a a a t t=-+，利用均值不等式得到答案. 【详解】设直线AB 的方程为y ＝kx +1，则直线AC 的方程可设为y 1k=-x +1，（k ≠0）由22211y kx x y a=+⎧⎪⎨+=⎪⎩消去y ，得（1+a 2k 2）x 2+2a 2kx ＝0，所以x ＝0或x 22221a k a k -=+ ∵A 的坐标（0，1），∴B 的坐标为（22221a k a k -+，k •22221a k a k -++1），即B （22221a k a k -+，222211a k a k-+），因此AB 222222222221(0)(1)111a k a k k a k a k --=-+-=+++22221a k a k+，同理可得：AC 211k =+•22221a kak+.∴Rt △ABC 的面积为S 12=AB •AC 2212k k=++44422422221221111a k a ka a k a a k k k +=⎛⎫⎛⎫++++++ ⎪ ⎪⎝⎭⎝⎭ 令t 1k k =+，得S ()4422422222(1)12a t a a a a t a tt==-++-+. ∵t 1k k =+≥2，∴S △ABC442222(1)(1)2a a a a a t t≤=--⨯.2t t =t 21a a-=时，△ABC 的面积S 有最大值为4227(1)8a a a =-.解之得a ＝3或a 329716+=. ∵a 3297+=时，t 21a a -=＜2不符合题意，∴a ＝3.故答案为：3.【点睛】本题考查了椭圆内三角形面积的最值问题，意在考查学生的计算能力和转化能力.14.设f （x ）＝e tx （t ＞0），过点P （t ，0）且平行于y 轴的直线与曲线C ：y ＝f （x ）的交点为Q ，曲线C 过点Q 的切线交x 轴于点R ，若S （1，f （1）），则△PRS 的面积的最小值是_____．【答案】2e【解析】【分析】计算R （t 1t -，0），PR ＝t ﹣（t 1t -）1t =，△PRS 的面积为S 2te t=，导数S ′()212t e t t-=，由S ′＝0得t ＝1，根据函数的单调性得到最值.【详解】∵PQ ∥y 轴，P （t ，0），∴Q （t ，f （t ））即Q （t ，2t e ），又f （x ）＝e tx （t ＞0）的导数f ′（x ）＝t e tx ，∴过Q 的切线斜率k ＝t 2t e ，设R （r ，0），则k 220t t e te t r-==-，∴r ＝t 1t -，即R （t 1t -，0），PR ＝t ﹣（t 1t -）1t=，又S （1，f （1））即S （1，e t ），∴△PRS 的面积为S 2t et=，导数S ′()212t e t t-=，由S ′＝0得t ＝1，当t ＞1时，S ′＞0，当0＜t ＜1时，S ′＜0，∴t ＝1为极小值点，也为最小值点，∴△PRS 的面积的最小值为2e ．故答案为：2e ．【点睛】本题考查了利用导数求面积的最值问题，意在考查学生的计算能力和应用能力.二、解答题：本大题共6小题，共90分．请在答题卡指定区域内作答，解答时应写出文字说明、证明过程或演算步骤．15.在三角形ABC 中，角A,B,C 的对边分别为a,b,c ，若()31sin ,tan 53A AB =-=，角C 为钝角， 5.b = （1）求sin B 的值；（2）求边c 的长.【答案】（1）sin B =（2）13c = 【解析】【分析】（1）由()sin sin B A A B ⎡⎤=--⎣⎦，分别求得sin cos A A ，，()()sin cos A B A B --，得到答案；（2）利用正弦定理sin sin a A b B=得到 a =13c =．【详解】(1)因为角C 为钝角，3sin 5A = ，所以4cos 5A == ，又()1tan 3A B -= ，所以02A B π<-< ，且()()sinA B A B -=-= ，所以()()()sin sin sin cos cos sin B A A B A A B A A B ⎡⎤=--=---⎣⎦3455=-=(2)因为sin sin a A b B ==，且5b = ，所以a =，又()cos cos cos cos sin sinC A B A B A B =-+=-+= ，则2222cos 952525169c a b ab C ⎛=+-=+-⨯= ⎝ ，所以13c= .16.如图，四棱锥V﹣ABCD中，底面ABCD是菱形，对角线AC与BD交于点O，VO⊥平面ABCD，E是棱VC的中点．（1）求证：VA∥平面BDE；（2）求证：平面VAC⊥平面BDE．【答案】（1）见解析（2）见解析【解析】【分析】（1）连结OE，证明VA∥OE得到答案.（2）证明VO⊥BD，BD⊥AC，得到BD⊥平面VAC，得到证明.【详解】（1）连结OE．因为底面ABCD是菱形，所以O为AC的中点，又因为E是棱VC的中点，所以VA∥OE，又因为OE⊂平面BDE，VA⊄平面BDE，所以VA∥平面BDE；（2）因为VO⊥平面ABCD，又BD⊂平面ABCD，所以VO⊥BD，因为底面ABCD是菱形，所以BD⊥AC，又VO∩AC＝O，VO，AC⊂平面VAC，所以BD⊥平面VAC．又因为BD⊂平面BDE，所以平面VAC⊥平面BDE．【点睛】本题考查了线面平行，面面垂直，意在考查学生的推断能力和空间想象能力.17.已知半径为5的圆的圆心在x轴上，圆心的横坐标是整数，且与直线4x+3y﹣29＝0相切．（1）求圆的方程；（2）设直线ax﹣y+5＝0（a＞0）与圆相交于A，B两点，求实数a的取值范围；（3）在（2）的条件下，是否存在实数a，使得弦AB的垂直平分线l过点P（﹣2，4），若存在，求出实数a的值；若不存在，请说明理由．【答案】（1）（x﹣1）2+y2＝25．（2）（512+∞，）．（3）存在，34a=【解析】分析】（1）设圆心为M（m，0），根据相切得到42955m-=，计算得到答案.（2）把直线ax ﹣y +5＝0，代入圆的方程，计算△＝4（5a ﹣1）2﹣4（a 2+1）＞0得到答案. （3）l 的方程为()124y x a=-++，即x +ay +2﹣4a ＝0，过点M （1，0），计算得到答案. 【详解】（1）设圆心为M （m ，0）（m ∈Z ）．由于圆与直线4x +3y ﹣29＝0相切，且半径为5，所以42955m -=，即|4m ﹣29|＝25．因为m 为整数，故m ＝1．故所求圆的方程为（x ﹣1）2+y 2＝25．（2）把直线ax ﹣y +5＝0，即y ＝ax +5，代入圆的方程，消去y ，整理得（a 2+1）x 2+2（5a ﹣1）x +1＝0，由于直线ax ﹣y +5＝0交圆于A ，B 两点，故△＝4（5a ﹣1）2﹣4（a 2+1）＞0，即12a 2﹣5a ＞0，由于a ＞0，解得a 512＞，所以实数a 的取值范围是（512+∞，）．（3）设符合条件的实数a 存在，则直线l 的斜率为1a-， l 的方程为()124y x a=-++，即x +ay +2﹣4a ＝0，由于l 垂直平分弦AB ，故圆心M （1，0）必在l 上，所以1+0+2﹣4a ＝0，解得34a =．由于35412⎛⎫∈+∞ ⎪⎝⎭，，故存在实数34a = 使得过点P （﹣2，4）的直线l 垂直平分弦AB .【点睛】本题考查了直线和圆的位置关系，意在考查学生的计算能力和转化能力.18.如图，两座建筑物AB ，CD 的底部都在同一个水平面上，且均与水平面垂直，它们的高度分别是10m 和20m ，从建筑物AB 的顶部A 看建筑物CD 的视角∠CAD ＝60°．（1）求BC 的长度；（2）在线段BC 上取一点P （点P 与点B ，C 不重合），从点P 看这两座建筑物的视角分别为∠APB ＝α，∠DPC ＝β，问点P 在何处时，α+β最小？【答案】（1）103m ；（2）当BP 为202103t =时，α+β取得最小值．【解析】【分析】（1）作AE ⊥CD ，垂足为E ，则CE ＝10，DE ＝10，设BC ＝x ，根据()2tan CAD tan CAE ∠=∠得到2200x --=，解得答案.（2）设BP ＝t，则(0CP t t =＜＜，故()10ttan αβ+=，设()f t =，求导得到函数单调性，得到最值.【详解】（1）作AE ⊥CD ，垂足为E ，则CE ＝10，DE ＝10，设BC ＝x ，则()22202210011tan CAEx tan CAD tan CAE tan CAE x ∠∠=∠===-∠-2200x--=，解之得，x =x =（舍），（2）设BP＝t，则(0CP t t =＜＜， ()101t tan t αβ+===-设()f t =，()2'200f t t =-+-令f '（t ）＝0，因为0t ＜＜t =，当(0t ∈，时，f '（t ）＜0，f （t ）是减函数；当(t ∈时，f '（t ）＞0，f （t）是增函数，所以，当t =f （t ）取得最小值，即tan （α+β）取得最小值，因为22000t -+-＜恒成立，所以f （t ）＜0，所以tan （α+β）＜0，2παβπ⎛⎫+∈⎪⎝⎭，，因为y ＝tanx 在2ππ⎛⎫⎪⎝⎭，上是增函数，所以当202103t =α+β取得最小值．【点睛】本题考查了三角恒等变换，利用导数求最值，意在考查学生的计算能力和应用能力. 19.设首项为1的正项数列{a n }的前n 项和为S n ，数列{}2n a 的前n 项和为T n，且()243n nS p T--=，其中p 为常数．（1）求p 的值；（2）求证：数列{a n }为等比数列；（3）证明：“数列a n ，2x a n +1，2y a n +2成等差数列，其中x 、y 均为整数”的充要条件是“x ＝1，且y ＝2”．【答案】（1）p ＝2；（2）见解析（3）见解析【解析】【分析】（1）取n ＝1时，由()24113p --=得p ＝0或2，计算排除p ＝0的情况得到答案.（2）241(2)33n n T S =--，则21141(2)33n n T S ++=--，相减得到3a n +1＝4﹣S n +1﹣S n ，再化简得到2112n n a a ++=，得到证明.（3）分别证明充分性和必要性，假设a n ，2x a n +1，2y a n +2成等差数列，其中x 、y 均为整数，计算化简得2x ﹣2y ﹣2＝1，设k ＝x ﹣（y ﹣2），计算得到k ＝1，得到答案. 【详解】（1）n ＝1时，由()24113p --=得p ＝0或2，若p ＝0时，243n n S T -=，当n ＝2时，()22224113a a-++=，解得a 2＝0或212a =-，而a n ＞0，所以p ＝0不符合题意，故p ＝2；（2）当p ＝2时，241(2)33n n T S =--①，则21141(2)33n n T S ++=--②， ②﹣①并化简得3a n +1＝4﹣S n +1﹣S n ③，则3a n +2＝4﹣S n +2﹣S n +1④，④﹣③得2112n n a a ++=（n ∈N *），又因为2112a a =，所以数列{a n }是等比数列，且112n n a -=；（3）充分性：若x ＝1，y ＝2，由112n n a -=知a n ，2x a n +1，2y a n +2依次为112n -，22n ，142n +，满足112142222n n n -+⨯=+，即a n ，2x a n +1，2y a n +2成等差数列；必要性：假设a n ，2x a n +1，2y a n +2成等差数列，其中x 、y 均为整数，又112n n a -=，所以11111222222x yn n n -+⋅⋅=+⋅，化简得2x ﹣2y ﹣2＝1，显然x ＞y ﹣2，设k ＝x ﹣（y ﹣2），因为x 、y 均为整数，所以当k ≥2时，2x ﹣2y ﹣2＞1或2x ﹣2y ﹣2＜1，故当k ＝1，且当x ＝1，且y ﹣2＝0时上式成立，即证．【点睛】本题考查了根据数列求参数，证明等比数列，充要条件，意在考查学生的综合应用能力. 20.已知函数123()()()()f x x x x x x x =---，123,,x x x R ∈，且123x x x <<．（1）当123012x x x ===，，时，求函数()f x 的减区间；（2）求证：方程()0f x '=有两个不相等的实数根；（3）若方程()0f x '=的两个实数根是()αβαβ<，，试比较122x x +，232x x +与αβ，的大小，并说明理由．【答案】（1）(1,1)33-+（2）详见解析（3）231222x x x x αβ++<<<【解析】【详解】试题分析：（1）当123012x x x ===，，时，322()(1)(2)=32,()362,f x x x x x x x f x x x =---+=-+'，由()0f x <得()f x 减区间(133-+；（2）因为32123122331123()()()f x x x x x x x x x x x x x x x x =-+++++-，所以2123122331()32()()f x x x x x x x x x x x x =-+++'++，因为2221223312[()()()]0x x x x x x ∆=-+-+->所以，方程()0f x '=有两个不相等的实数根；（3）因为21221()()024x x x x f +-=-<'，22323()()024x x x x f +-=-<'，所以231222x x x x αβ++<<<试题解析：（1）当123012x x x ===，，时，322()(1)(2)=32,()362,f x x x x x x x f x x x =---+=-+'，由()0f x <得()f x减区间(1)33-+；（2）法1：32123122331123()()()f x x x x x x x x x x x x x x x x =-+++++-，2123122331()32()()f x x x x x x x x x x x x =-+++'++2221223312[()()()]0x x x x x x ∆=-+-+->，123x x x <<，所以，方程()0f x '=有两个不相等的实数根；法2：122331()()()()()()()f x x x x x x x x x x x x x =--+---'-+，22321()()()0f x x x x x -'=-<，()f x 是开口向上的二次函数，所以，方程()0f x '=有两个不相等的实数根；（3）因为21221()()024x x x x f +-=-<'，22323()()024x x x x f +-=-<'，又()f x 在(,)α-∞和(,)β+∞增，()f x 在(,)αβ减，所以231222x x x x αβ++<<<．考点：利用导数求函数减区间，二次函数与二次方程关系本题包括A ，B 共1小题，每小题10分，共20分．把答案写在答题卡相应的位置上．解答时应写出文字说明、证明过程或演算步骤． [选修4-2：矩阵与变换]21.试求曲线y ＝sinx 在矩阵MN 变换下的函数解析式，其中M 1002⎡⎤=⎢⎥⎣⎦，N 10201⎡⎤⎢⎥=⎢⎥⎣⎦．【答案】y ＝2sin 2x ．【解析】【分析】计算MN 11100022020102⎡⎤⎡⎤⎡⎤⎢⎥⎢⎥==⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦⎣⎦，计算得到函数表达式. 【详解】∵M 1002⎡⎤=⎢⎥⎣⎦，N 10201⎡⎤⎢⎥=⎢⎥⎣⎦，∴MN 11100022020102⎡⎤⎡⎤⎡⎤⎢⎥⎢⎥==⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦⎣⎦， ∴在矩阵MN 变换下，x y ⎡⎤⎢⎥⎣⎦→1'2'2x x y y ⎡⎤⎡⎤⎢⎥=⎢⎥⎢⎥⎣⎦⎣⎦∴曲线y ＝sinx 在矩阵MN 变换下的函数解析式为y ＝2sin 2x ．【点睛】本题考查了矩阵变换，意在考查学生的计算能力.[选修4-4：极坐标与参数方程]22.已知直线l 的极坐标方程为63sin πρθ⎛⎫-= ⎪⎝⎭，圆C 的参数方程为1010x cos y sin θθ=⎧⎨=⎩（θ为参数）．（1）请分别把直线l 和圆C 的方程化为直角坐标方程；（2）求直线l 被圆截得的弦长．【答案】（1120y -+=．x 2+y 2＝100．（2）16 【解析】【分析】（1）直接利用极坐标方程和参数方程公式化简得到答案. （2）圆心()0,0到直线的距离为1262d ==，故弦长为. 【详解】（1）sin 63πρθ⎛⎫-= ⎪⎝⎭，即1sin cos 622ρθθ⎛⎫-= ⎪ ⎪⎝⎭，即162y x =，120y -+=.10cos 10sin x y θθ=⎧⎨=⎩，故22100x y +=. （2）圆心()0,0到直线的距离为1262d ==，故弦长为16=. 【点睛】本题考查了极坐标方程和参数方程，圆的弦长，意在考查学生的计算能力和转化能力.【必做题】本题满分10分．解答时应写出文字说明、证明过程或演算步骤．23.在如图所示的几何体中，四边形ABCD 为矩形，平面ABEF ⊥平面ABCD ，EF ∥AB ，∠BAF ＝90°，AD ＝2，AB ＝AF ＝2EF ＝2，点P 在棱DF 上．（1）若P 是DF 的中点，求异面直线BE 与CP 所成角的余弦值；（2）若二面角D ﹣AP ﹣C 的正弦值为63，求PF 的长度．【答案】（1）3015．（22．【解析】【分析】（1）以A 为原点，AB 为x 轴，AD 为y 轴，AF 为z 轴，建立空间直角坐标系，则BE =u u u r （﹣1，0，2），CP =u u u r（﹣2，﹣1，1），计算夹角得到答案.（2）设FP FD λ=u u u r u u u r，0≤λ≤1，计算P （0，2λ，2﹣2λ），计算平面APC 的法向量n =r（1，﹣1，222λλ-），平面ADF 的法向量m =r（1，0，0），根据夹角公式计算得到答案. 【详解】（1）∵BAF ＝90°，∴AF ⊥AB ，又∵平面ABEF ⊥平面ABCD ，且平面ABEF ∩平面ABCD ＝AB ， ∴AF ⊥平面ABCD ，又四边形ABCD矩形，∴以A 为原点，AB 为x 轴，AD 为y 轴，AF 为z 轴，建立空间直角坐标系， ∵AD ＝2，AB ＝AF ＝2EF ＝2，P 是DF 的中点，∴B （2，0，0），E （1，0，2），C （2，2，0），P （0，1，1），BE =u u u r（﹣1，0，2），CP =u u u r （﹣2，﹣1，1），设异面直线BE 与CP 所成角的平面角为θ，则cosθ2301556BE CP BE CP⋅===⋅⋅u u u r u u u ru u u r u u u r ，∴异面直线BE 与CP 所成角的余弦值为23015．（2）A （0，0，0），C （2，2，0），F （0，0，2），D （0，2，0），设P （a ，b ，c ），FP FD λ=u u u r u u u r，0≤λ≤1，即（a ，b ，c ﹣2）＝λ（0，2，﹣2），解得a ＝0，b ＝2λ，c ＝2﹣2λ，∴P （0，2λ，2﹣2λ），AP =u u u r（0，2λ，2﹣2λ），AC =u u u r （2，2，0），设平面APC 的法向量n =r（x ，y ，z ），则()2220220n AP y z n AC x y λλ⎧⋅=+-=⎨⋅=+=⎩u u uv r u u u v r，取x ＝1，得n =r（1，﹣1，222λλ-），平面ADP 的法向量m =r（1，0，0），∵二面角D ﹣AP ﹣C 的正弦值为6， ∴|cos m n r r ＜，＞|2261()322()22m nm nλλ⋅===-⋅+-r r r r ，解得12λ=，∴P （0，1，1）， ∴PF 的长度|PF |222(00)(10)(12)2=-+-+-=．【点睛】本题考查了异面直线夹角，根据二面角求长度，意在考查学生的空间想象能力和计算能力.【必做题】本题满分10分．解答时应写出文字说明、证明过程或演算步骤．24.甲、乙、丙三名射击运动员射中目标的概率分别为1,,2a a (01)a <<，三人各射击一次，击中目标的次数记为ξ.（1）求ξ的分布列及数学期望；（2）在概率()P i ξ=(i =0，1，2，3)中, 若(1)P ξ=的值最大, 求实数a 的取值范围. 【答案】（1）41a +，ξ的分布列为（2）10,2⎛⎤ ⎥⎝⎦【解析】(1)P(ξ)是“ξ个人命中，3－ξ个人未命中”的概率．其中ξ的可能取值为0、1、2、3.P(ξ＝0)＝01C 112⎛⎫-⎪⎝⎭02C (1－a)2＝12(1－a)2； P(ξ＝1)＝11C ·122C (1－a)2＋01C 112⎛⎫- ⎪⎝⎭12C a(1－a)＝12(1－a 2)； P(ξ＝2)＝11C ·1212C a(1－a)＋01C 112⎛⎫- ⎪⎝⎭22C a 2＝12(2a －a 2)；P(ξ＝3)＝11C ·1222C a 2＝22a . 所以ξ的分布列为ξ的数学期望为E(ξ)＝0×12(1－a)2＋1×12(1－a 2)＋2×12(2a －a 2)＋3×22a＝412a +.(2)P(ξ＝1)－P(ξ＝0)＝12[(1－a 2)－(1－a)2]＝a(1－a)； P(ξ＝1)－P(ξ＝2)＝12[(1－a 2)－(2a －a 2)]＝122a-； P(ξ＝1)－P(ξ＝3)＝12[(1－a 2)－a 2]＝2122a-.由2(1)0,12{0,21202a a a a-≥-≥-≥和0＜a ＜1，得0＜a≤12，即a 的取值范围是10,2⎛⎤ ⎥⎝⎦.。

高考数学母题解密专题06 双曲线(江苏专版)

专题06 双曲线【母题来源一】【2020年高考江苏卷】在平面直角坐标系xOy 中，若双曲线﹣=122x a 25y（a >0）的一条渐近线方程为y x ，则该双曲线的离心率是 ▲ . 【母题来源二】【2019年高考江苏卷】在平面直角坐标系中，若双曲线xOy 经过点（3，4)，则该双曲线的渐近线方程是 ▲ . 2221(0)y x b b -=>【母题来源三】【2018年高考江苏卷】在平面直角坐标系中，若双曲线xOy的右焦点到一条渐近线的距离为，则其离心率的值22221(0,0)x y a b a b -=>>(,0)F c 是________________．【命题意图】通过了解双曲线的定义、几何图形和标准方程，结合数形结合的思想考查它的简单几何性质以及双曲线的简单应用.【命题规律】双曲线的定义、方程与性质是每年高考的热点，难度中档，注重对计算能力以及数形结合思想的考查.从近几年江苏的高考试题来看，主要的命题角度有：（1）对双曲线定义与方程的考查；（2）对双曲线简单几何性质的考查，如求双曲线的渐近线、准线、离心率等；（3）双曲线与其他知识的综合，如平面几何、向量、直线与圆等．【方法总结】（一）对双曲线的定义与标准方程必须掌握以下内容：（1）在求解双曲线上的点到焦点的距离d 时，一定要注意这一隐含条件． d c a ≥-（2）求解双曲线的标准方程时，先确定双曲线的类型，也就是确定双曲线的焦点所在的坐标轴是x 轴还是y 轴，从而设出相应的标准方程的形式，然后利用待定系数法求出方程中的的值，最后写出双曲线的标准方程.22,a b （3）在求双曲线的方程时，若不知道焦点的位置，则进行讨论，或可直接设双曲线的方程为.221(0)Ax By AB +=<（4）常见双曲线方程的设法：①与双曲线(a ＞0，b ＞0)有共同渐近线的双曲线方程可设为22221x y a b-=． 2222(0,0,0)x y a b a b λλ-=>>≠②若双曲线的渐近线方程为，则双曲线方程可设为n y x m=±或． 2222(0,0,0)x y m n m nλλ-=>>≠2222(0,0,0)m n x m y n λλ-=>>≠③与双曲线(a ＞0，b ＞0)共焦点的双曲线方程可设为22221x y a b-=． 22221(0,0,x y a b a k b k-=>>-+22)b k a <-<④过两个已知点的双曲线的标准方程可设为． ()2210mx ny mn +=<⑤与椭圆(a >b >0)有共同焦点的双曲线方程可设为22221x y a b +=． 22221(0,x y a b a b λλ+=>>--22)b a λ<<（二）对于双曲线的渐近线，有下面两种考查方式：（1）已知双曲线的方程求其渐近线方程;（2）给出双曲线的渐近线方程求双曲线方程，由渐近线方程可确定a ，b 的关系，结合已知条件可解.（三）求双曲线的离心率一般有两种方法：（1）由条件寻找满足的等式或不等式，一般利用双曲线中的关系,a c a b c ，，将双曲线的离心率公式变形，即，注意区分222c a b =+c e a ===双曲线中的关系与椭圆中的关系，在椭圆中，而在双a b c ，，a b c ，，222a b c =+曲线中.222c a b =+（2）根据条件列含的齐次方程，利用双曲线的离心率公式转化为含或,a c c e a=e 2e 的方程，求解可得，注意根据双曲线离心率的范围对解进行取舍.1()e ∈+∞,（四）求解双曲线的离心率的范围的方法：一般是根据条件，结合和，得到关于的不等式，求解即得.注意区222c a b =+c e a=e 分双曲线离心率的范围，椭圆离心率的范围.另外，在建立关于1()e ∈+∞,)1(0e ∈，e 的不等式时，注意双曲线上的点到焦点的距离的最值的应用.1．（江苏省苏州市昆山震川高级中学2020届高三下学期三模数学试题）已知双曲线，则该双曲线的渐近线为_______．2221(0)2x y a a -=>2．（江苏省南京市金陵中学、南通市海安高级中学、南京市外国语学校2020届高三下学期第四次模拟数学试题）在平面直角坐标系xOy 中，若双曲线的一()22210y x b b -=>个焦点到一条渐近线的距离为3，则此双曲线的离心率为________．3．（2020届江苏省高三高考全真模拟（六）数学试题）在平面直角坐标系xOy 中，已知双曲线C 的渐近线方程为，且它的一个焦点为，则双曲线C 的一条准y x =±F 线与两条渐近线所成的三角形的面积为______． 4．（2020届江苏省七市（南通、泰州、扬州、徐州、淮安、连云港、宿迁）高三下学期第三次调研考试数学试题）在平面直角坐标系xOy 中，已知抛物线y 2＝4x 的准线是双曲线（a ＞0）的左准线，则实数a 的值是_______． 22212x y a -=5．（江苏省扬州市2020届高三下学期6月最后一卷数学试题）已知抛物线的准22y x =线也是双曲线的一条准线，则该双曲线的两条渐近线方程是________． 2213x y m -=6．（江苏省盐城中学2020届高三下学期第一次模拟数学试题）若双曲线＝12222x y a b －（a >0，b >0）与直线y x 无交点，则离心率e 的取值范围是________．7．（江苏省南通市2020届高三下学期6月模拟考试数学试题）已知离心率的双曲2e =线D ：的左、右焦点分别为，，虚轴的两个端点分别为22221(0,0)x y a b a b-=>>1F 2F 1A，，若四边形的面积为D 的焦距为______．2A 1122A F A F 8．（2020届江苏省南京十校上学期12月高三联合调研数学试题）在平面直角坐标亲xOy 中，若双曲线（，）的离心率为，则该双曲线的渐近线方程22221x y a b-=0a >0b >32为______．9．（江苏省扬州中学2020届高三下学期6月模拟考试数学试题）在平面直角坐标系xOy 中，双曲线的顶点到其渐近线的距离为_________________． 221169x y -=10．（2020届江苏省百校高三下学期第四次联考数学试题）在平面直角坐标系中，双xOy 曲线的焦距为，若过右焦点且与轴垂直的直线与两条渐近22221(0,0)x y a b a b-=>>2c x 线围成的三角形面积为，则双曲线的离心率为____________．2c 11．（2020届江苏省盐城市高三下学期第三次模拟数学试题）若双曲线（a ＞22221x y a b-=0，b ＞0）的离心率为2，则其两条渐近线所成的锐角为_______．12．（2020届江苏省南通市如皋市高三下学期二模数学试题）在平面直角坐标系中，xOy 已知双曲线：的左，右焦点分别为，，设过右焦点C ()222210,0x y a b a b-=>>1F 2F 且与轴垂直的直线与双曲线的两条渐近线分别交于，两点，若2F x l C A B 1F AB 是正三角形，则双曲线的离心率为__________．C 13．（2020届江苏省南京市十校高三下学期5月调研数学试题）双曲线的左，右焦点分别为，过且与轴垂直的直线与双曲22221(0,0)x y a b a b-=>>12F F ，2F x线交于两点，若_____________． A B ，12F F =14．（2020届江苏省南通市高三下学期二模考前综合练习数学试题）已知双曲线（a ＞0，b ＞0）的两个焦点为、，点P 是第一22221x y a b -=10F ⎛⎫ ⎪ ⎪⎝⎭20F ⎫⎪⎪⎭象限内双曲线上的点，且，tan ∠PF 2F 1＝﹣2，则双曲线的离心率为1212tan PF F ∠=_____．15．（2020届江苏省宿迁市沭阳中学高三下学期百日冲刺模拟考试数学试题）已知双曲线的渐近线与准线的一个交点坐标为，则双曲线的焦距为22221(0,0)x y a b a b -=>>(1,______．16．（2020届江苏省南通市基地学校高三下学期第三次大联考数学试题）在平面直角坐标系中，若双曲线的渐近线与圆x 2＋y 2＝5相交于A ，B ，C ，D 四点，则四2214y x -=边形ABCD 的面积为_______．17．（2020届江苏省南通市如皋市高三下学期三模数学试题）已知直线与双曲:2l y x =线的一条渐近线垂直，且右焦点到直线l 的距离为2，则双曲线的标准方22221x y a b-=程为_______．18．（江苏省南京市2020届高三下学期6月第三次模拟考试数学试题）在平面直角坐标系xOy 中，已知双曲线（a ＞0，b ＞0）的右焦点为F ．若以F 为圆心，a 为22221x y a b-=半径的圆交该双曲线的一条渐近线于A ，B 两点，且AB ＝2b ，则该双曲线的离心率为_______．19．（2020届江苏省南通市如皋中学、如东中学高三下学期阶段联合调研数学试题）已知双曲线的两条渐近线与直线22213x y b-=x =__________．20．（2020届江苏省高三高考全真模拟（八）数学试题）在平面直角坐标系中，若双xOy曲线的值是________．如何学()22104x y m m m -=>+m 好数学做选择题时注意各种方法的运用，比较简单的自己会的题正常做就可以了，遇到比较复杂的题时，看看能否用做选择题的技巧进行求解（主要有排除法、特殊值代入法、特例求解法、选项一一带入验证法、数形结合法、逻辑推理验证法等等），一般可以综合运用各种方法，达到快速做出选择的效果。

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

江苏省南通市2020届高三下学期5月阶段性练习数学试题学校:___________姓名：___________班级：___________考号：___________1．已知集合{}2,1,0,1M =--，{}20N x x x =+≤，则M N =_______.2．已知复数2a i i++为纯虚数，其中i 为虚数单位，则实数a 的值是__. 3．某同学5次数学练习的得分依次为114，116，114，114，117，则这5次得分的方差是__.4．根据如图所示的伪代码，当输入的x 为1-时，最后输出的m 的值是__.5．在平面直角坐标系xOy 中，若双曲线22221(0,0)x y a b a b-=>>双曲线的渐近线的方程是__.6．某同学参加“新冠肺炎防疫知识”答题竞赛活动，需从4道题中随机抽取2道作答.若该同学会其中的3道题，则抽到的2道题他都会的概率是__.7．将函数()πsin 23f x x ⎛⎫=+ ⎪⎝⎭的图象向右平移ϕ个单位得到函数()g x 的图象．若()g x 为奇函数，则ϕ的最小正值是______．8．已知非零向量b 与a 的夹角为120︒，且||2a =，24a b +=，则||b =__.9．已知等比数列{}n a 的各项均为正数，且18a ，3a ，26a 成等差数列，则785622a a a a ++的值是__.10．在平面直角坐标系xOy 中，已知过点(10,0)-的圆M 与圆22660x y x y +--=相切于原点，则圆M 的半径是__.11．唐朝的狩猎景象浮雕银杯如图1所示，其浮雕临摹了国画、漆绘和墓室壁画，体现了古人的智慧与工艺.它的盛酒部分可以近似地看作是半球与圆柱的组合体（假设内壁表面光滑，忽略杯壁厚度），如图2所示.已知球的半径为R ，酒杯内壁表面积为2143R π.设酒杯上部分（圆柱）的体积为1V ，下部分（半球）的体积为2V ，则12V V 的值是__.12．已知函数()log (1)a f x x a =>的图象与直线(1)()y k x k R =-∈相交.若其中一个交点的纵坐标为1，则k a +的最小值是__.13．已知函数224,0()1(2),0x x f x x x x +⎧⎪=+⎨⎪+<⎩若关于x 的不等式()10()f x mx m m R ---<∈的解集是1(x ，23)(x x ⋃，)+∞，123x x x <<，则m 的取值范围是__.14．如图，在ABC ∆中，32AC BC =，点M ，N 分别在AC ，BC 上，且13AM AC =，12BN BC =.若BM 与AN 相交于点P ，则CP AB 的取值范围是__.15．在斜三角形ABC 中，角A ，B ，C 的对边分别为a ，b ，c .（1）若2cos a C b =，且2sin sin sin C A B =，求B 的值；（2）若cos(2)3cos 0A B B ++=，求tan tan A C 的值.16．如图，在三棱柱111ABC A B C -中，平面11ACC A ⊥平面11BCC B ，侧面11BCC B 是矩形，点E ，F 分别为BC ，11A B 的中点.求证：（1）1BC AC ⊥；（2）//EF 平面11ACC A .17．如图，某森林公园内有一条宽为100米的笔直的河道（假设河道足够长），现拟在河道内围出一块直角三角形区域养殖观赏鱼.三角形区域记为ABC ∆，A 到河两岸距离AE ，AD 相等，B ，C 分别在两岸上，AB AC ⊥.为方便游客观赏，拟围绕ABC ∆区域在水面搭建景观桥.为了使桥的总长度l （即ABC ∆的周长）最短，工程师设计了以下两种方案：方案1：设ABD α∠=，求出l 关于α的函数解析式()f α，并求出()f α的最小值. 方案2：设EC x =米，求出l 关于x 的函数解析式()g x ，并求出()g x 的最小值.请从以上两种方案中自选一种解答.（注：如果选用了两种解答方案，则按第一种解答计分）18．在平面直角坐标系xOy 中，已知椭圆2222:1(0,0)x y C a b a b+=>>短轴的两个顶点.（1）求椭圆C 的标准方程；（2）直线:(0,0)l y kx m k m =+>≠与椭圆C 交于P ，Q 两点，设直线OP ，OQ 的斜率分别为1k ，2k .已知212·k k k =. ①求k 的值；②当OPQ △的面积最大时，求直线PQ 的方程.19．已知数列{}n a 的前n 项和为n S ，11a =，2121·n n n n a S S S λ++++=，*n N ∈，R λ∈.（1）若3λ=-，21a =-，求3a 的值；（2）若数列{}n a 的前k 项成公差不为0的等差数列，求k 的最大值；（3）若20a >，是否存在R λ∈，使{}n a 为等比数列？若存在，求出所有符合题意的λ的值；若不存在，请说明理由.20．对于定义在D 上的函数()f x ，若存在k ∈R ，使()f x kx <恒成立，则称()f x 为“()m k 型函数”；若存在k ∈R ，使()f x kx 恒成立，则称()f x 为“()M k 型函数”.已知函数()(12)()f x ax lnx a R =-∈.（1）设函数1()()1(1)h x f x x =+.若0a =，且1()h x 为“()m k 型函数”，求k 的取值范围；（2）设函数21()()h x f x x =+.证明：当12a =-，2()h x 为“M （1）型函数”；（3）若a Z ∈，证明存在唯一整数a ，使得()f x 为“1()4m 型函数”.21．已知矩阵A 的逆矩阵13221A -⎡⎤=⎢⎥⎣⎦. （1）求矩阵A ；（2）若向量21α⎡⎤=⎢⎥⎣⎦，计算2A α. 22．在平面直角坐标系xOy中，已知直线1,{(12x t y t ==为参数）.在以坐标原点为极点，x 轴正半轴为极轴的极坐标系中，曲线C 的极坐标方程为4cos()3πρθ=+，设P 为曲线C 上的动点，求点P 到直线l 的距离的最大值.23．若实数x ，y ，z 满足231x y z ++=，求222x y z ++的最小值.24．如图，在平面直角坐标系xOy 中，已知抛物线22(0)y px p =>，过点(4,0)M p 的直线l 交抛物线于1(A x ，1)y ，2(B x ，2)y 两点.当AB 垂直于x 轴时，OAB ∆的面积为（1）求抛物线的方程：（2）设线段AB 的垂直平分线交x 轴于点T .①证明：12y y 为定值：②若//OA TB ，求直线l 的斜率.25．设*n N ∈，k ∈N ，n k .（1）化简：11112··k k n n k k n n C C C C +++++；（2）已知2220122(1)n n n x a a x a x a x -=+++⋯+.记21()(1)nk k k F n n a ==+∑.证明：()F n 能被21n 整除.参考答案1．{}1,0-【解析】【分析】求出集合N ，利用交集的定义可得集合M N ⋂.【详解】{}{}2010N x x x x x =+≤=-≤≤，{}2,1,0,1M =--，因此，{}1,0M N ⋂=-. 故答案为：{}1,0-.【点睛】本题考查交集的求法，考查交集定义等基础知识，考查运算求解能力，是基础题. 2．12-. 【解析】【分析】先把复数2a i i ++化成复数的一般形式，再由纯虚数的定义可求a . 【详解】解：因为复数()(2)2122(2)(2)55a i a i i a a i i i i ++-+-==+++-，由于它为纯虚数，所以2105a +=，且205a -≠，则12a =-，故答案是：12-. 【点睛】本题考查了复数的运算法则、纯虚数的定义，属于基础题.3．85. 【解析】【分析】先求出平均数，再由方差计算公式求出这5次得分的方差.【详解】某同学5次数学练习的得分依次为114，116，114，114，117，平均数为1(114116114114117)1155x =++++=，则这5次得分的方差为：22222218[(114115)(116115)(114115)(114115)(117115)]55S =-+-+-+-+-=. 故答案为：85. 【点睛】本题考查方差的求法，考查平均数、方差的性质等基础知识，考查运算求解能力，是基础题. 4．32. 【解析】【分析】模拟程序的运行，可得程序的功能是计算并输出210230x x m x x ⎧+<=⎨-⎩的值，由题意即可计算得解.【详解】解：模拟程序的运行，可得程序的功能是计算并输出210230x x m x x ⎧+<=⎨-⎩的值，当输入的x 为1-时，可得13212m -=+=. 故答案为：32. 【点睛】本题主要考查了伪代码的应用，属于基础题.5．2y x =±.【解析】【分析】由双曲线的离心率结合隐含条件求得b a的值，则答案可求. 【详解】解：由题意，c e a ==222225c a b a a +==，解得：2b a=， ∴该双曲线的渐近线的方程是2y x =±.故答案为：2y x =±.【点睛】本题考查双曲线的简单性质，注意隐含条件的运用，是基础题.6．12. 【解析】【分析】基本事件总数246n C ==，该同学会其中的3道题，抽到的2道题他都会包含的基本事件个数233m C ==，由此能求出抽到的2道题他都会的概率.【详解】解：某同学参加“新冠肺炎防疫知识”答题竞赛活动，需从4道题中随机抽取2道作答.基本事件总数246n C ==，该同学会其中的3道题，抽到的2道题他都会包含的基本事件个数233m C ==，∴抽到的2道题他都会的概率是3162m p n ===. 故答案为：12. 【点睛】本题考查概率的求法，考查古典概型等基础知识，考查运算求解能力，是基础题. 7．π6【解析】【分析】先由平移求出()g x 的解析式()πsin 223g x x ϕ⎛⎫=-+ ⎪⎝⎭，再由()g x 为奇函数，可得()π2π3k k ϕ-+=∈Z ，从而可求出ϕ的最小正值. 【详解】将函数()πsin 23f x x ⎛⎫=+⎪⎝⎭的图象向右平移ϕ个单位得到，()πsin 223g x x ϕ⎛⎫=-+ ⎪⎝⎭的图象，由于函数()g x 为奇函数，所以()π2π3k k ϕ-+=∈Z ，整理得：()ππ26k k ϕ=-+∈Z ，当0k =时，ϕ的最小正值是π6．故答案为：π6 【点睛】此题考查三角函数的平移变换，正弦函数的性质，属于基础题.8．4.【解析】【分析】先把24a b +=两边平方，再展开，并结合平面向量的数量积运算进行求解即可.【详解】解：由题可知，2(2)16a b +=，∴224||4||||cos12160||a a b b +⋅+=，即214442||()|||162b b ⨯+⨯⨯⋅-+=，解得||4b =.故答案为：4.【点睛】本题考查平面向量的模长、数量积运算，对式子进行平方处理是解决平面向量模长问题的常用手段，考查学生的运算能力，属于基础题.9．16.【解析】【分析】设等比数列的公比为q ，0q >，由等差数列的中项性质和等比数列的通项公式，解方程可得q ，再由等比数列的通项公式，化简可得所求值.【详解】解：等比数列{}n a 的各项均为正数，设公比为q ，0q >，由18a ，3a ，26a 成等差数列，可得312286a a a =+，即有2111286a q a a q =+，即2340q q --=，解得4(1q =-舍去），则22785656562(2)1622a a q a a q a a a a ++===++. 故答案为：16.【点睛】本题考查等差数列的中项性质和等比数列的通项公式的运用，考查方程思想和运算能力，属于基础题.10．【解析】【分析】由已知圆的方程求得圆心坐标与半径，再由所求的圆与圆22660x y x y +--=相切于原点，知两圆圆心的连线在直线y x =上，设所求圆的圆心为(,)a a ，由半径相等列式求得a 值，则答案可求.【详解】解：圆22660x y x y +--=化为22(3)(3)18x y -+-=，圆心坐标为(3,3)，半径为如图，所求的圆与圆22660x y x y +--=相切于原点，∴两圆圆心的连线在直线y x =上，可设所求圆的圆心为(,)a a=解得5a =-，∴所求圆M 的半径为故答案为：【点睛】本题考查圆和圆的位置关系，考查数学转化思想方法与数形结合的，属于中档题. 11．2.【解析】【分析】设圆柱的高为h ，表示出表面积可得43h R =，再分别表示出1V ，2V 即可. 【详解】解：设酒杯上部分高为h ，则酒杯内壁表面积221144223S R Rh R πππ=⨯+=，则43h R =，所以23143V R h R ππ==，321423V R π=⨯，故122V V =，故答案为：2.【点睛】本题考查圆柱、球体积及表面积的公式，需熟记公式，属于基础题.12．3.【解析】【分析】由题知两函数其中一个交点(1,0)，另一个交点的纵坐标为1，得 0k >，利用交点满足两函数解析式可求出(1)1k a -=，由均值不等式求最小值即可.【详解】解：函数()log (1)a f x x a =>与直线(1)()y k x k R =-∈过(1,0)，∴由函数()log (1)a f x x a =>的图象与直线(1)()y k x k R =-∈相交.其中一个交点的纵坐标为1得0k >，设交点(,1)m ，代入()log a f x x =，1log a m =，m a ∴=，再把点(,1)a 代入直线方程：211(1)()2k a k a +-=-，即3k a +，当且仅当1k a =-时，等号成立，k a +取最小值3.故答案为：3.【点睛】本题主要考查对数函数与直线的位置关系，均值不等式的应用，属于中档题.13．(0,2)(2,3)⋃.【解析】【分析】作出函数()y f x =与直线1y mx m =++的图象，找到两个极限情况，结合图象即可得解.【详解】由不等式()10f x mx m ---<得()1f x mx m <++，作出函数()y f x =与直线1y mx m =++的图象如图所示，注意到直线1y mx m =++恒过点(1,1)-，且点(1,1)-也在函数()y f x =上，当直线1y mx m =++与函数2()(2)f x x =+相切时，可得2(4)30x m x m +-+-=，则△2440m m =-+=，解得2m =，当直线1y mx m =++过点(0,4)C 时，则14m +=，解得3m =，由图可知，满足条件的实数m 的取值范围为(0,2)(2,3)⋃.故答案为：(0,2)(2,3)⋃.【点睛】本题主要考查分段函数的应用，二次函数的性质应用，其它不等式的解法，考查数形结合思想，属于中档题.14．1(,2)5.【解析】【分析】设2BC =，3AC =，由三点共线的向量表示可设(1)(1)CP CA CN C C x y y B M x =-+=-+，结合已知条件进一步得到1124CP CA CB =+，由此可得21133()881312cos ,CP AB CA CB =-+⋅-，结合余弦函数的有界性即可得出答案.【详解】解：不妨设2BC =，3AC =，由于A ，P ，N 三点共线，M ，P ，B 三点共线，故由平面向量基本定理可设，(1)(1)CP CA CN C C x y y B M x =-+=-+，11,32AM AC BN BC ==， ∴2(1)(1)23C x y x y CB A P CA C CB =-+=-+， ∴21312x y x y ⎧-=⎪⎪⎨⎪=-⎪⎩，解得1234x y ⎧=⎪⎪⎨⎪=⎪⎩， ∴1124CP CA CB =+， 222()CP CP AB CB CA ⎛⎫∴= ⎪-⎝⎭ 221124()CA CB CB CA ⎛⎫+ ⎪⎝⎭=- 2222111||||cos 41642||||cos CA CB CA CB CA CB CA CB CA CB CA CB ++⋅⋅〈⋅〉=+-⋅⋅〈⋅〉 91132cos 44449232cos CA CB CA CB ++⨯⨯⨯⋅=+-⨯⨯⨯⋅ 106cos 141312cos CA CB CA CB +⋅=⨯-⋅ 12cos 1333181312cos CA CB CA CB ⋅-+=⨯-⋅ 1133881312cos CA CB =-+⨯-⋅, 又1cos ,1CA CB -<<，∴211331()(,4)88251312cos ,CP AB CA CB =-+⋅∈-， ∴1(,2)5CP AB ∈.故答案为：1(,2)5.【点睛】本题考查三角形中的几何计算，涉及了平面向量基本定理的运用，数量积的运算等基础知识点，考查运算求解能力，属于中档题.15．（1）3B π=；（2）tan tan 2A C =.【解析】【分析】（1）由余弦定理化简已知等式可得a c =，利用正弦定理化简已知等式可得2c ab =，从而可得c a b ==，即可得解.（2）利用三角函数恒等变换的应用化简已知等式可得2cos cos sin sin A C A C =，由题意可得cos 0A ≠，cos 0C ≠，利用同角三角函数基本关系式可求tan tan A C 的值.【详解】解：（1）在ABC ∆中，由余弦定理得2222?2a b c a b ab+-=，化简得22a c =，即a c =，因为2sin sin sin C A B =，且2(sin sin sin a b c R R A B C ===为ABC ∆外接圆半径），所以2c ab =，所以c a b ==，所以ABC ∆为正三角形，所以3B π=.（2）因为cos(2)3cos 0A B B ++=，且()B A C π=-+，所以cos[()]3cos[()]0A C A C ππ+-+-+=，所以cos()3cos()A C A C -=-+，即cos cos sin sin 3cos cos 3sin sin A C A C A C A C +=-+，所以2cos cos sin sin A C A C =，因为斜三角形ABC 中，2A π≠，2C π≠，所以cos 0A ≠，cos 0C ≠，所以tan tan 2A C =.【点睛】本题主要考查了余弦定理，正弦定理，三角函数恒等变换的应用，考查了学生的计算能力和转化思想，属于基础题.16．（1）证明见解析；（2）证明见解析.【解析】【分析】（1）推导出1BC CC ⊥，从而BC ⊥平面11ACC A .由此能证明1BC AC ⊥；（2）取11A C 的中点G ，连结FG ，CG .推导出四边形EFGC 为平行四边形，//EF GC .由此能证明//EF 平面11ACC A .【详解】（1）因为侧面11BCC B 是矩形，所以1BC CC ⊥，因为平面11ACC A ⊥平面11BCC B ，平面11ACC A 平面111BCC B C C =，BC 在平面11BCC B 内，所以BC ⊥平面11ACC A ，因为1AC 在平面11ACC A 内，所以1BC AC ⊥；（2）取11A C 的中点G ，连结FG ，CG ，在△111A B C 中，F ，G 分别是11A B ，11A C 的中点，所以11//FG B C ，且1112FG B C =，在矩形11BCC B 中，E 是BC 的中点，所以11//EC B C ，且1112EC B C =，所以//EC FG ，且EC FG =，所以四边形EFGC 为平行四边形，所以//EF GC ，又因为EF 在平面11ACC A 外，GC 在平面11ACC A 内，所以//EF 平面11ACC A .【点睛】本题考查线线平行、线面平行的证明，考查空间中线线、线面、面面间的位置关系等基础知识，考查推理论证能力，是中档题.17．答案不唯一，具体见解析.【解析】【分析】方案1：由AB AC ⊥，得90EAC BAD ∠+∠=︒，可得EAC ABD α∠=∠=，2(0,)απ∈.求解三角形可得50sin AB α=，50cos AC α=，50sin cos BC αα=，即可得到()f α关于α的解析式，其中2(0,)απ∈.设sin cos t αα=+，化为关于t 的函数求解；方案2：由已知证明Rt CAE Rt ABD ∆∆∽，得AC EC AB AD=.由EC x =，得AC ==50AD =，再求得AB ，BC ，可得2500()()g x x x x =++，0x >.然后利用基本不等式求最值. 【详解】解：方案1:AB AC ⊥，90EAC BAD ∴∠+∠=︒，在Rt ABD ∆中，90ABD BAD ∠+∠=︒，EAC ABD α∴∠=∠=，2(0,)απ∈. 50AD AE ==，在Rt ADB ∆和Rt AEC ∆中，50sin AB α=，50cos AC α=，∴50sin cos BC αα===， ∴111sin cos 1()50()50()sin cos sin cos sin cos f ααααααααα++=++=，其中2(0,)απ∈. 设sin cos t αα=+，则sin cos )4t πααα=+=+，2(0,)απ∈，∴t ∈， 212sin cos t αα=+，∴21sin cos 2t αα-=. ∴250(1)100112t y t t +==--，∴当t =时，()100min f α==+.答：景观桥总长的最小值为(100+米；方案2:AB AC ⊥，90EAC BAD ∴∠+∠=︒，在Rt ABD ∆中，90ABD BAD ∠+∠=︒，EAC ABD ∴∠=∠，则Rt CAE Rt ABD ∆∆∽， ∴AC EC AB AD=. EC x =，AC ==50AD =，∴AB =，则2500BC x x===+，∴2500()()g x x x x =++，0x >. 0x，()22500100g x∴=2502100100⨯=.=，且2500xx=，即50x=时取“=”.∴()100ming x=+答：景观桥总长的最小值为(100+米.【点睛】本题考查三角形的解法，训练了利用换元法及基本不等式求最值，考查计算能力，是中档题. 18．（1）2214xy+=；（2）①12k=；②112y x=±.【解析】【分析】（1）设椭圆的焦距为2c，则222c a b=-.利用短轴的两个顶点与右焦点的连线构成等边三角形，求出a，b，然后求解椭圆C的标准方程.（2）①设1(P x，1)y，2(Q x，2)y，联立22,1,4y kx mxy=+⎧⎪⎨+=⎪⎩利用韦达定理，通过直线的斜率求解即可；②由①得12k=，直线PQ的方程为12y x m=+，然后求解弦长，点到直线的距离，求解三角形的面积，然后求解即可.【详解】解：（1）设椭圆的焦距为2c，则222c a b=-.因为短轴的两个顶点与右焦点的连线构成等边三角形，所以=c.，则22ac=所以2a=，1b=，所以椭圆C的标准方程为2214xy+=.（2）①设1(P x，1)y，2(Q x，2)y，联立22,1,4y kx m x y =+⎧⎪⎨+=⎪⎩消去y 得222(41)8440k x kmx m +++-=， 2222644(41)(44)0k m k m ∆=-+->，化简得2241m k <+，所以122841km x x k -+=+，212244·41m x x k -=+，又OP 的斜率111y k x =，OQ 的斜率222y k x =，所以2221212121212121212()()()·y y kx m kx m k x x km x x m k k k x x x x x x +++++====，化简得212()0km x x m ++=，所以228·041km km m k -+=+.又因为0m ≠，即241k =，又0k >，所以12k =.②由①得12k =，直线PQ 的方程为12y x m =+，且122x x m +=-，212·22x x m =-，22m <. 又0m ≠，所以0m <所以12PQ x ==-== 点O 到直线PQ的距离d ==，所以221(2)·122OPQm m SPQ d +-====，当且仅当222m m =-，即1m =±时，OPQ △的面积最大，所以，直线PQ 的方程为112y x =±.【点睛】本题考查椭圆方程的求法，直线与椭圆的位置关系的综合应用，考查转化思想以及计算能力，属于难题.19．（1）33a =-；（2）4；（3）存在；1λ=. 【解析】【分析】（1）记2121·n n n n a S S S λ++++=为(*)式.当3λ=-时，(*)式为21213?n n n n a S S S +++-+=，令1n =得，221323?a S S S -+=，转化求解即可.（2）设公差为d ，若3k =，则22S d =+，333S d =+.在(*)式中，令1n =得，22132·a S S S λ+=，推出21d d λ++=，若4k =，推出2321(12d d d λ++=+，求解可得2d =-，3λ=-.所以4k =符合题意.验证5k =，是否成立，推出结果. （3）假设存在R λ∈，使{}n a 为等比数列，推出(1)0q λ-=，结合112(1)(1)n n n n S S S S +++-=-，推出21111n n n n S S S S +++--=，得到数列11n n S S +⎧⎫-⎨⎬⎩⎭为常数列，转化求解证明即可. 【详解】解：记2121·n n n n a S S S λ++++=为(*)式.（1）当3λ=-时，(*)式为21213?n n n n a S S S +++-+=，令1n =得，221323a S S S ⋅-+=，即221123123()()a a a a a a a -+++=+⋅，由已知11a =，21a =-，解得33a =-.（2）因为前k 项成等差数列，设公差为d ，则21a d =+，312a d =+，若3k =，则22S d =+，333S d =+.在(*)式中，令1n =得，22132·a S S S λ+=，所以2(1)33(2)d d d λ+++=+，化简得21(1)d d d λ++=+，① 若4k =，则446S d =+，在(*)式中，令2n =得，23243·a S S S λ+=，所以2(12)(2)(46)(33)d d d d λ++++=+，化简得2321(12)d d d λ++=+，②②-①得，22d d d λ+=，因为公差不为0，所以0d ≠，所以21d λ+=，代入①得，220d d +=，所以2d =-，3λ=-. 所以4k =符合题意.若5k =，则11a =，21a =-，33a =-，45a =-，57a =-，33S =-，48S =-，515=-S ，在(*)式中，令3n =得，43533(5)(3)(15)60a S S -+=-⨯-+-⨯-=，224(8)64S =-=，所以243543a S S S -+≠，所以k 的最大值为4.（3）假设存在R λ∈，使{}n a 为等比数列，设前3项分别为1，q ，2q ，则21231,1,1S S q S q q ==+=++，(*)式中，令1n =得，22(1)(1)q q q q λ+++=+，化简得(1)0q λ-=，因为20q a =>，所以1λ=，此时(*)式为2121()?n n n n n S S S S S +++-+=，即112(1)(1)(**)n n n n S S S S +++-=-，由11S =，2211S a =+>，得31S >，由2S ，31S >得41S >，⋯，依此类推，10n S ≥>，所以(**)等价于21111n n n nS S S S +++--=，所以数列11n n S S +⎧⎫-⎨⎬⎩⎭为常数列，所以122111n n S S a S S +--==，于是2n 时，12211,1,n n nn S a S S a S +--=⎧⎨-=⎩两式相减得12·n n a a a +=，因为221·a a a =，所以*12·()n n a a a n N +=∈，又1a ，20a ≠，所以12n na a a +=（非零常数），所以存在1λ=，使{}n a 为等比数列. 【点睛】本题考查等差数列以及等比数列的综合应用，考查转化思想以及计算能力，属于难题. 20．（1）(1,)+∞；（2）证明见解析；（3）证明见解析. 【解析】【分析】（1）将0a =代入，依题意，即1lnx k x +>恒成立，设1()(1)lnx g x x x+=，求出函数()g x 的最小值即可得解；（2）分析可知，即证1(1)0x lnx x x ++-，令1()(1)R x x lnx x x =++-，21()x R x lnx x-'=+，方法一：由不等式的性质可知()R x 在(0,1)上单调递减，在(1,)+∞上单调递增，故()(1)0R x R =，即得证；方法二：令211()()F x R x lnx x x='=+-，再对函数()F x 求导，可得当01x <<时，()0R x '<，当1x >时，()0R x '>，进而得到()R x 的单调性，由此得证；（3）问题等价于证明存在唯一整数a ，1()(12)04p x ax lnx x =--<恒成立，易知当0a 及2a 时，不合题意，故只需证明1a =时符合题意即可，方法一：记1()(12)4p x x lnx x =--，分当1x 或102x <以及当112x <<时证明即可；方法二：记1()(12)4p x x lnx x =--，利用导数求其最大值小于0即可得证.【详解】（1）0a =时，1()1h x lnx =+. 因为1()h x 为“()m k 型函数”，所以1()h x kx <恒成立，即1lnx k x+>恒成立. 设1()(1)lnx g x x x +=，则2()0lnxg x x'-=恒成立，所以()g x 在[1，)+∞上单调递减，所以()g x g （1）1=，所以k 的取值范围是(1,)+∞；（2）证明：当12a =-时，要证2()h x 为“M （1）型函数”，即证1(1)x lnx x x ++，即证1(1)0x lnx x x++-. 令1()(1)R x x lnx x x =++-，则22211111()(1)1x R x lnx x lnx lnx x x x x x-=++---+'=+=，方法一：当1x >时，0lnx >，210x x ->，则()0R x '>；当01x <<时，0lnx <，210x x-<，则()0R x '<；所以()R x 在(0,1)上单调递减，在(1,)+∞上单调递增，则()R x R （1），又R （1）0=，所以()0R x ，所以2()h x 为“M （1）型函数”.方法二：令211()F x lnx x x =+-，则22331122()0x x F x x x x x -+=+='->，所以函数()F x 在(0,)+∞上单调递增，又F （1）0=，所以当01x <<时，()0R x '<，当1x >时，()0R x '>，所以()R x 在(0,1)上单调递减，在(1,)+∞上单调递增，以下同方法一.（3）证明：函数()f x 为“1()4m 型函数”等价于1()(12)04p x ax lnx x =--<恒成立，当0a 时，()(12)1044e ep e ae =--->，不合题意；当2a 时，12111()1(4)044a p e e e e e =---->，不合题意；当1a =时，方法一：1()(12)4p x x lnx x =--， ①当1x 或102x <时，1()004p x x -<；②当112x <<时，120x -<，由（2）知1x lnx x->，所以2(12)(1)11()(32)044x x p x x x x x---<-=-，综上，存在唯一整数1a =，使得()f x 为“1()4m 型函数”.方法二：1()(12)4p x x lnx x =--，12119()2244x p x lnx lnx x x -=-+-=-+-'，记19()24x lnx x ϕ=-+-，则221()0x x xϕ'-=-<，所以()()x p x ϕ'=在(0,)+∞上单调递减. 易得1lnx x -，所以991722(21)0444p =-+=='<；又因为199()222120244p ln =+->+->'，所以存在唯一零点01(2x ∈，使得00019()204p x lnx x +-'=-=，且0x 为()p x 的最大值点，所以00000000019(12)()411117()(12)242428x x p x x lnx x x x x --=--=-=+-，注意到117228yx x =+-在1(,22上单调递增，所以017117()()02824p x p <==<，所以()0p x <. 综上，存在唯一整数1a =，使得()f x 为“1()4m 型函数”. 【点睛】本题考查利用导数研究函数的单调性，极值及最值，考查不等式的恒成立问题，考查构造思想，分类讨论思想，函数与方程等数学思想，考查推理论证能力，运算求解能力等，属于较难题目. 21．（1）1223A -⎡⎤=⎢⎥-⎣⎦；（2）23⎡⎤⎢⎥-⎣⎦.【解析】【分析】（1）设出矩阵，利用逆矩阵的运算法则化简求解即可. （2）直接利用矩阵乘法的运算法则化简求解即可. 【详解】解：（1）设矩阵a b A c d ⎡⎤=⎢⎥⎣⎦，则132323210212201a b a c b d A A c d a c b d -++⎡⎤⎡⎤⎡⎤⎡⎤===⎢⎥⎢⎥⎢⎥⎢⎥++⎣⎦⎣⎦⎣⎦⎣⎦，故321,20,{320,21,a c a c b d b d +=+=+=+=解得1,2,{2,3,a b c d =-===-则矩阵1223A -⎡⎤=⎢⎥-⎣⎦.（2）由矩阵1223A -⎡⎤=⎢⎥-⎣⎦，得21212582323813A ---⎡⎤⎡⎤⎡⎤==⎢⎥⎢⎥⎢⎥---⎣⎦⎣⎦⎣⎦，所以2582281313A α-⎡⎤⎡⎤⎡⎤==⎢⎥⎢⎥⎢⎥--⎣⎦⎣⎦⎣⎦.【点睛】本题考查矩阵与逆矩阵的运算法则的应用，是基本知识的考查，中档题. 22．72. 【解析】【分析】首先利用转换关系，把参数方程极坐标方程和直角坐标方程之间进行转换，进一步利用点到直线的距离公式的应用求出结果. 【详解】解：由4cos()3πρθ=+得24cos()2cos sin 3πρρθρθθ=+=-，所以曲线C的直角坐标方程为2220x y x +-+=，即22(1)(4x y -+=，圆心(1,-，半径2r.由直线l的参数方程1,2{12x t y t =+=得1x =+，所以直线l的普通方程为10x -=.所以圆心(1,-到直线l 的距离32d =，所以点P 到直线l 距离的最大值为37222+=. 【点睛】本题主要考查参数方程极坐标方程和直角坐标方程之间的转换，点到直线的距离公式的应用，主要考查学生的运算能力和转换能力及思维能力，属于基础题型. 23．114【解析】【分析】利用条件231x y z ++=,构造柯西不等式()()()222222223123x y z x y z++≤++++，进行解答即可. 【详解】由柯西不等式可知:()()()222222223123x y z x y z++≤++++,即()222141x y z++≥，故222114x y z ++≥,当且仅当123x y z ==,即222x y z ++的最小值为114. 【点睛】本题主要考查了利用柯西不等式求最值,属于中档题.利用柯西不等式求最值时，关键是对原目标函数进行配凑，以保证出现常数结果.同时，要注意等号成立的条件, 配凑过程采取如下方法：一是考虑题设条件；二是对原目标函数进行配凑后利用柯西不等式解答. 24．（1）2y x =；（2）①证明见解析；②±1. 【解析】【分析】（1）当AB 垂直于x 轴时，求出AB 坐标，利用三角形的面积转化求解抛物线方程即可.（2）①由题意可知直线l 与x 轴不垂直.设211(,)A y y ，222(,)B y y ，122212121AB y y k y y y y -==-+.通过A ，M ，B 三点共线，得122y y =-. ②122y y =-，得到21142(,)B y y -.求出线段AB 垂直平分线的方程，结合OA TB k k =，转化求解即可. 【详解】解：（1）当AB 垂直于x轴时，(4,)A p，(4,)B p -所以OAB ∆的面积为211···?422AB OM p ===，因为0p >，所以12p =，所以抛物线的方程为2y x =.（2）①由题意可知直线l 与x 轴不垂直.由（1）知(2,0)M ，设211(,)A y y ，222(,)B y y ，则122212121AB y y k y y y y -==-+. 由A ，M ，B 三点共线，得12221222y y y y =--，因为12y y ≠，化简得122y y =-. ②因为122y y =-，所以21142(,)B y y -. 因为线段AB 垂直平分线的方程为22121212()()22y y y y y y y x ++-=-+-，令0y =，得22212121114(1)22T y y x y y ++==++. 因为//OA TB ，所以OA TB k k =，即1211221121144(1)2y y y y y =++-，整理得2211(1)(4)0y y +-=，解得12y =±，故(4,2)A ±.所以1AM k =±，即直线l 的斜率为±1.【点睛】本题考查直线与抛物线的位置关系的综合应用，抛物线方程的求法，考查转化思想以及计算能力，是中档题. 25．（1）12n n ++；（2）证明见解析. 【解析】【分析】（1）利用组合排列数的计算公式即可得出.（2）由（1）得，11211111111111111111()222k k k n n n k k k k k k k n n n n n n n C C C n n n C n C C n C C n C C ++++++++++++++++++=⋅=⋅=⋅+++⋅⋅+.由122121(1)21(1)(1)[]22k k k k k k k n n n k k n k k a C n C C +++-+--==⋅++，可得22111212121(1)(1)()(1)[]2k k nn k k k k kn n k n k k F n n a C C +==+++--=+=⋅+∑∑，求和即可得出.【详解】（1）解：11112(1)!(1)!(1)!(1)!1!(1)!(1)!()!!(2)!!(2)(1)!2!()!(1)!(1)!k k n n k k n n n n C C n n n n k n k k n k n n C C n n n n k n k k n k +++++++⋅+⋅⋅+++-+-===++⋅+⋅+⋅-++-⋅.（2）证明：由（1）得，11211111111111111111()222k k k n n n k k k k k k k n n n n n n n C C C n n n C n C C n C C n C C ++++++++++++++++++=⋅=⋅=⋅+++⋅⋅+. 因为122121(1)21(1)(1)·[]22k k k k k k k n n n k k n k ka C n C C +++-+--==++，本卷由系统自动生成，请仔细校对后使用，答案仅供参考。