思维导图学数学小升初总复习
初中数学各章节知识图解思维导图(共9张PPT)

应用
特例
定理
勾股定理
证明 内容
文字.符号图形
互逆命题
内容
文字.符号图形
直角三角形
逆定理
全等
证明
应用
知三边定形状
锐角三角函数
有关线段
定义
三角 形
解直角三角形
锐角三角函数
定义
计算
三边关系锐角关 系边角关系
应用
坡度 仰.俯角 方位角
正弦
余弦
符号.几何意义. 特殊角的值
特殊值的运算
正切
作对称轴 作一点到两点距离相等 离相等(外心)
作等腰三角形 作一点到三点距
翻折后与 另一图形重 合
到两点距离相等的 点
点到两点 的距离 相等
性质
判定
应用
垂直平分线
定义
对称点
关于轴对称
基本 图形
对称 轴
特征
要素
利用轴对称制作图案
用
坐
作:关于x轴、
标
y轴的对称点
表
示
轴
对
解决几何中的
称
极值问题
基本图形
一条直线
翻折后与 两部分 重合
对称轴 定义
轴对称图形 静
与y轴交点位置 c>0.
对应角相等, 尺规作角 对应边成比例,
二次函数与 一元二次方程
对称轴垂直平分对称点的连线
作对直称线公轴理
直线
作等腰三角形
磁道问题
利润问题 拱桥问题
在表示原与点画法 c<0.
到寻三找射边线方的法 距离相射等线 在三角形内直线.射线.线段
一次函数与反比例函数
表示与画法
线段
计算与比较
分析运用思维导图提升小学高年级数学复习效率

2019年第15期(总第634期)科学咨询/教学研究教学探讨谭明清(重庆市万州区王牌小学 重庆万州 404000)分析运用思维导图提升小学高年级数学复习效率摘 要:小学高年级数学复习中,应用思维导图的方式,可以帮助学生构建知识网络,能够在后续学习中更加灵活应用数学知识。
文章以运用思维导图提升小学高年级数学复习效率为研究对象,对如何开展教学活动提出几点建议,希望能够提高学生复习效率。
关键词:思维导图;小学数学;高年级;复习效率引言小学数学复习教学十分重要,是巩固基础知识,提高知识应用能力的关键。
在高年级教学中,学生面临着小升初的阶段,良好的数学基础,可以减轻学生学习压力,能够提高学习质量。
思维导图具有直观、形象的特点。
数学教学中应用,可以提高复习效率,能够深化学生对数学知识的理解。
本文就此继续分析。
一、激发学生复习兴趣,提高复习效果兴趣,对于复习教学活动而言,具有非常大的影响。
其是学生学习内在动力,也是保证教学质量的重要因素。
传统复习教学中,教师会将学习内容直接展示学生,让学生在课后消化学习[1]。
这种教学方式,无法保证学生复习质量。
将思维导图应用教学中,可以将复杂的问题简单、直观化,能够深化学生对数学知识的内容。
在教学活动中,教师可以灵活应用这一内容,引导学生复习数学知识,提高教学质量。
例如,复习《长方体和正方体》这一单元内容时,教师可以将思维导图应用复习活动中。
将长方体和正方体作为思维导图中心内容,围绕此,引导学生根据学习过的内容,进行填充,形成一个树形。
当学生填写在以后,教师可以进行系统复习,将关于长方体和正方体的内容全部展示出来,引导学生在课堂活动,对比自己填写思维导图内容,弥补不足。
通过这种方式,可以加深学生对长方体、正方体知识的认识,同时能够提高学生学习质量。
在课后,教师可以根据学生课堂表现,布置课后问题,引导学生将思维导图应用实际问题中,以此提高学生应用能力。
二、复习中应用,提高学生复习能力小学数学高年级复习活动中,将思维导图应用其中,帮助学生梳理数学知识,构建完整知识体系。
初中数学图解思维导图(共9张PPT)

b x1= x2 =
2a
2a
无交
Δ<0
点
关系 二次函数
无实 根
解法
一元二次方程
应用
传播问题 行程问题 效率问题
与y轴交点位置 c>0.在正
开口上方a向<. 0.向a>下0.向对置称轴在左y同轴右的异位半 在轴 负半c=轴0.在原点
c<0.
解析
二次函数 与 一元二
次方程
定义
面积问题
y=ax2+bx+c (a.b.c为常数a≠0)
对表应示与点画法到旋转中心的距离相等
利用腰中点 割补射线成--- 全等三直线角.射线形.线、段 平行四边形 三寻边找射关线方系法 锐角关系边角关系
点表到示与直画线法
的距离
线段
多姿多彩的图形
图形认识初 步 相交线
计算与比较
平行线
性质
立体图形
平面图形
对邻
垂
顶补
直
角角
画法
相交线
判定
条件
同位角相等 内错角相等
y axh2 k yaxx1xx2
(a 0)
a0
ax2+bx+c=0 (a≠0)
角平分线
余角.补角
性质
等角的余角相等 等角的补角相等
和 为1800
相
定义 性质
等
一“放”二“靠” 三“推”四“画”
叠合法
度量法
角的比较
对应点的坐标比为k或-k
角的比较与运算
在原点 c<0.
翻折后与 另一图定义形.表重示 合
y轴的对称点
表
示
轴
对
解决几何中的
称
极值问题
用A4纸制作四年级数学上册思维导图(图文并茂)
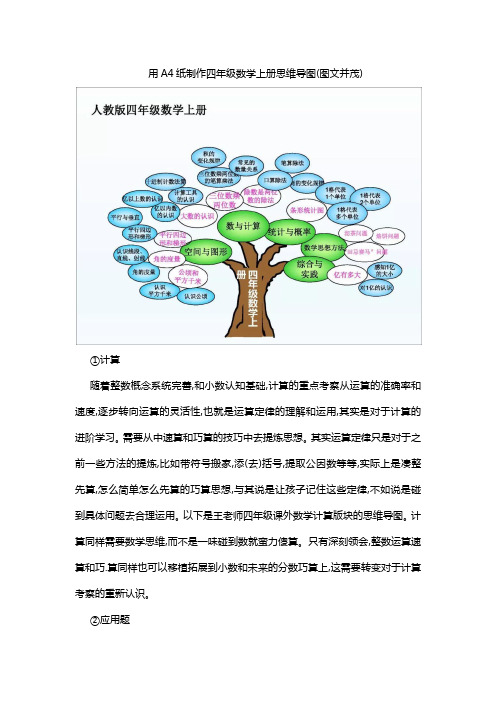
用A4纸制作四年级数学上册思维导图(图文并茂)
①计算
随着整数概念系统完善,和小数认知基础,计算的重点考察从运算的准确率和速度,逐步转向运算的灵活性,也就是运算定律的理解和运用,其实是对于计算的进阶学习。
需要从中速算和巧算的技巧中去提炼思想。
其实运算定律只是对于之前一些方法的提炼,比如带符号搬家,添(去)括号,提取公因数等等,实际上是凑整先算,怎么简单怎么先算的巧算思想,与其说是让孩子记住这些定律,不如说是碰到具体问题去合理运用。
以下是王老师四年级课外数学计算版块的思维导图。
计算同样需要数学思维,而不是一味碰到数就蛮力傻算。
只有深刻领会,整数运算速算和巧.算同样也可以移植拓展到小数和未来的分数巧算上,这需要转变对于计算考察的重新认识。
②应用题
整数应用题是小升初分数、百分数应用题的基础,包括课本上的数学广角都引入了鸡兔同笼等经典算术题型。
所以四年级应用题拓展面会进一步变宽,包括-一些年龄问题,进阶和差倍问题,盈亏问题,归一归总问题,植树问题,方阵问题,页码问题,还原问题基本行程问题等等,目的就是熟悉不同场景下数量关系特征,进一步加强对于所学数学知识的理解。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
思维导图学数学小升初总复习
目录
前言 (1)
数的认识 (1)
数的运算 (5)
方程 (8)
正方形的内切圆和外切圆 (10)
四则运算 (17)
几何知识 (22)
图形的运动 (32)
单位进率换算 (33)
位置与方向 (35)
统计图 (37)
平均数、中位数和众数 (39)
行程问题 (40)
实际问题 (42)
简便运算 (45)
应用 (46)
数学概念汇总 (52)
个性辅导教案 (62)
PPT 讲义 (65)
前言
小学阶段数学课程的学习,是一个系统的课程,由多个不同地知识点组成,总复习就是将这些分散的知识点加以梳理,由点到线,有线到面,帮助学生对于整格时间进行构建。
用最形象的比喻,数学就好比是一个巨大的蜘蛛网,各个知识点都有着紧密的联系,如何让这些知识能够更好的掌握,如何能将知识有效的综合应用是数学学习的关键。
利用思维导图,能够将这些知识加以整理。
思维导图主要让学生自己先对知识进行总结,找出相关的知识点,在结合思维导图将知识综合应用。
比如在学习几何图形的面积时候,结合思维导图能将小学阶段的几何图形知识全面掌握。
第一次学生可能只能掌握一些主要的部分,第二次就能掌握主要的易错地方,多次就能将数学知识应用的炉火纯青。
利用思维导图在完成例题时,将一个例题变成为多个知识点的总结复习,不仅能掌握本题的相关知识,更能掌握于此相关的内容。
进而,做到举一反三的效果。
思维导图有利于学生掌握良好的数学学习方法,没有科学有效的学习方法,就会形成小猴子掰玉米的现象,学了这里忘了那里。
思维导图让学生在学习的过程中,养成良好的学习习惯,养成良好的数学思考习惯。
思维导图的优势还有很多,能将枯燥的知识进而变得有趣,从而提高学生学习数学的兴趣和良好的方法。
内容正方形的内切圆与外切圆
知识点拨
1、正方形中内切圆,正方形与圆的面积比:设内切圆的半径为r,则正方形的边长为2r,则内切圆的面积=πr²、正方形的面积=(2r)²=4r²,所以正方形与内切圆的面积比为:4r²∶πr²=4∶π。
2、正方形与外切圆的面积之比为=2:π。
典型例题
一个正方形的内部有一个四分之一圆(涂色部分)。
已知正方形的面积是10cm2,涂色部分的面积是多少?
特别注意
本题中由于只知道正方形的面积是,要计算出四分之一圆的面积,可以利用比例来计算。
正方形与内切圆的面积比是4:π,则可以列出比例4:π=10:×。
解的×
=7.85.也可以:a2=10cm2,圆的半径就是正方形的边长,
4
1
×3.14×a2=
4
1
×3.14×
10=7.85cm2.
技巧点拨
正方形的内切圆与外切圆之前的关系比较复杂。
1、正方形与内切圆,正方形的边长就是圆的直径,可以
直接将正方形的边长看做2,这样圆的半径也就变成了1;正
方形的面积2×2=4,圆的面积π×12=π。
这样就直接能计算
出正方形与圆的面积比为4:π。
2、正方形与外切圆,由于正方形的边长不在是圆的直
径,而是正方形的对角线才是圆的直径,学生没有学过勾
股定理,我们可以将正方形的两条对角线都做出来,这样
正方形就被分成了四个等腰直角三角形。
三角形的直角边
就是圆的半径。
设直角边为1,则正方形的面积为4×1×1
×
2
1
=2;圆的面积为π×12=π。
故正方形与圆的面积之比
是2:π。
3、在计算正方形内切圆、外切圆的过程中,一方面可以按照半径的方法计算,另一方面也可以使用比例的知识直接进行计算。
需要牢固掌握正方形与内切圆的面积之比为4:π;正方形与外切圆的面积之比为2:π。
4、日常计算中,还有很多的图像也是正方形内切圆、外切圆的变换,如
2
1
、
4
1
图形,计算的时候方法一致,计算出整个的面积,在按照几分之几进行计算。
5、计算过程中,要掌握图形变换或者拼凑的方法,通过转换直接计算。
如下图:
备注
图示解答
解:(4+6)×4÷2÷2﹣3.14×
÷2
=10﹣3.14×4÷2
=10﹣6.28
=3.72(平方厘米)
3.14×32﹣×(3+3)×3,
=28.26﹣9,
=19.26(平方厘米)
阴影部分的面积=梯
形的面积﹣圆的面积,梯形的上底和高都等于圆的半径,上底和下底已知,从而可以求出阴影部分的面积。
解:(4+9)×4÷2﹣3.14
×42×,
=13×4÷2﹣3.14×4,
=26﹣12.56,
=13.44(平方厘米);
答:阴影部分的面积是
13.44平方厘米。
梯形的下
底和高都
等于圆的
半径,且
阴影部分
的面积=
梯形的面
积﹣圆
的面积。
计算组合图形的面积。
相交垂直
直角三角形有一个直角和是
1800.
边的和
大于第
三边。
钝角三角形有一个钝角
按边分任意三角形三条边不相等等腰三角形两条边相等等边三角形三条边相等
三角形具有稳定性。
4、四边形
5、平面图形的周长和面积名
称图示
周长公式面积公式
文字公式字母公式文字公式字母公式推导过程
长方形
长方形的
周长=(长+
宽)×2
C=2
(a+b)
长方形的
面积=长×
宽
S=ab
数方格的
方法推导
出来。
正方
正方形的
周长=边长
C=4a 正方形的
面积=边长
S=a2把正方形
看做是长
面积推导示意图
画旋转图的一般步骤:(1)找准旋转点;(2)确定好顺时针或逆时针的方向;(3)找准与旋转点相连接的2条线段;(4)画准这2条线段旋转90度后的新线段;(5)连接所画新线段,形成新图形。
变换图形位置的方法有平移、旋转等,在变换位置时,每个图形的相应顶点、线段、曲线应同步平移,旋转相同的角度。
不改变图形的形状,只改变它的大小时,通常要使每个图形的要素,如长方形的长与宽,三角形的底与高等同时按相同比例放大或缩小。
对称图形是对称轴两边的图形经对折后能够完全重合,而不是完全相同。
内容位置与方向
知识点拨
1、在地图上,般按上北、下南、左西、右东表示方向。
根据方向和距离可确定物体的位置,方法如下:(1)确定好主方向,用量角器量出被测点和观测点的连线与主方向的夹角的度数;(2)用直尺量出被测点和观测点的图上距离,从而算出实际距离;(3)根据角度和距离可以描述被测点的准确位置。
2、用数对表示位置:在具体的情境中,可以用数对表示物体的具体位置。
数对中第一个数表示物体在第几列,第二个数表示物体在第几行,两个数之间用逗号隔开。
行和列的交点处就是物体的所在位置或所在区域。
3、比例尺:图上距离与实际距离的比,就是比例尺。
比例尺没有单位。
1:100的意思是:图上1厘米代表实际距离100厘米。
三个公式:比例尺=图上距离÷实际距离;实际距离=图上距离÷比例尺图上距离=比例尺×实际距离。
千米化厘米添5个“0”,厘米化千米去掉5个“0”。
解决有关比例尺的问题,一是要统一化成低级单位;二是要熟记比例尺的三个公式。
技巧点拨1、数对:由两个数组成,中间用逗号隔开,用括号括起来。
括号里面的数由左至右为列数和行数,即“先列后行”。
数对的作用:确定一个点的位置。
经度和纬度就是这个原理。
2、确定物体位置的方法:
(1)、先找观测点;(2)、再定方向(看方向夹角的度数);(3)、最后确定距离(看比例尺)。
描绘路线图的关键是选好观测点,建立方向标,确定方向和路程。
位置关系的相对性:两地的位置具有相对性在叙述两地的位置关系时,观测点不同,叙述的方向正好相反,而度数和距离正好相等。
相对位置:东--西;南--北;南偏东--北偏西。
备注小华在小红什么位置?小红在小华什么位置?
在描述相对位置的时候,找到观察点,方向相对,角度不变、距离不变。
本题中小华在小红的西偏北40°方向上,距离是500m;小红则在小华东偏南40°方向上,距离是500m;。
