《金版新学案》高考数学总复习 8.1圆锥曲线方程课件 文 大纲人教版
《走向高考》高三数学 8-1第八章圆锥曲线方程教师讲义手册课件(全国版) 文 新人教A版

的椭圆标准方程为mx2
+ny2=1,将A、B两点坐标代入得
∴所求椭圆标准方程为
(3)由题意,设所求椭圆的方程为 因为椭圆过点 所以 故所求椭圆标准方程为
【例2】 (2009·东北三校)(1)已知椭圆
1(a>b>0),F1、F2分别是其左、右焦点,A为椭圆
的左顶点,过F2作垂直于x轴的一条直线交椭圆于B、C两
的两个焦点分别是F1、F2,P是椭圆在第一象限的点,且
满足
过 点 P 作 倾 斜 角 互 补 的 两 条 直 线 PA 、
PB,分别交椭圆于A、B两点.
(1)求点P的坐标;
(2)求直线AB的斜率.
(2009·安徽,18)已知椭圆
的离心
率为 以原点为圆心、椭圆短半轴长为半径的圆与直线
y=x+2相切.
(b)
[总结评述] 一般地,遇到有关焦点(或准线)问题, 首先应考虑用定义来解题.椭圆上的点到两焦点的距离考 虑第一定义,椭圆上的点到焦点及到准线的距离考虑第二 定义.
(2009·浙江温州十校联考)若以椭圆上一点和两个 焦点为顶点的三角形面积的最大值为1,则椭圆长轴的最 小值为( )
答案:D
解析:易得bc=1.又∵bc≤
5.着力抓好“运算关”.解析几何问题的解题思路 容易分析出来,但往往由于运算不过关而半途而废.因 此,在复习中要注意寻求合理的运算方案,以及简化运算 的基本途径与方法,亲身经历运算困难的发生与克服困难 的完整过程,增强解决复杂问题的信心.
●基础知识 一、椭圆的定义和方程 1.椭圆定义 (1)平面内到两定点F1、F2的距离的和等于常数(大于| F2F2|) 的 点 的 轨 迹 叫 椭 圆 . 这 两 个 定 点 叫 做 椭 圆 的 焦 点 , 两焦点的距离叫做椭圆的焦距. (2)平面内到定点F的距离和到定直线l的距离d之比为 常数e(0<e<1) 的点M的轨迹叫做椭圆,即 定点是椭圆的一个焦点,定直线是椭圆的相应准线.
《金版新学案》高三数学一轮复习 第八章 第1课时 直线的方程课件 文 新人教A版

知识点
知识点
考纲下载
掌握确定圆的几何要素,掌握圆的 圆的方程 标准方程和一般方程.
1.能根据给定直线、圆的方程,判 断直线与圆的位置关系;能根据给 定两个圆的方程,判断两圆的位置 直线、圆 关系. 的位置关 2.能用直线和圆的方程解决一些简 系 单的问题. 3.初步了解用代数方法处理几何问 题的思想.
y2-y1 x 2- x 1 线的斜率公式为 k=________.
【思考探究】
直线的倾斜角 θ 越大,斜率 k
π θθ≠ 知 2
就越大,这种说法正确吗?
提示: 这种说法不正确. 由 k= tan 当 当
π θ∈0, 时, θ 2 π θ∈ , π时,θ 2
知识点
考纲下载 1.了解圆锥曲线的实际背景,感受圆 锥曲线在刻画现实世界和解决实际问 题中的作用. 2.掌握椭圆的定义、标准方程及简单 的几何性质. 了解双曲线的定义、几何图形和标准 方程,知道它的简单几何性质. 掌握抛物线的定义、几何图形和标准 方程,知道它的简单几何性质.
椭圆
双曲线 抛物线
掌握方程的曲线与曲线的方程的对应 曲线与方程 关系.
方程
y-y1 x-x1 不含直线x= = 两点式 ______________ y2-y1 x2-x1 x1(x1≠x2)和直线y =y1(__________ a b
不含垂直于坐标轴 和过原点的直线
______________ Ax+By+C= 平面直角坐标系内 一般式 ______________ 0(A2+B2≠0) 的直线都适用
第1课时 直线的方程
1.直线的倾斜角与斜率 (1)直线的倾斜角 ①定义:当直线l与x轴相交时,我们取x 轴作为基准,x轴______ 正向 与直线l______ 向上 方 向之间所成的角α叫做直线l的倾斜角.当 直线l与x轴平行或重合时,规定它的倾斜 角为____. 0° ②倾斜角的范围为_______________. 0°≤α<180°
《金版新学案》高考总复习(大纲版)数学(课件):第七章 直线和圆的方程7.6-38页文档资料
答案: B
工具
第7章 第6课时
栏目导引
解析: 答案: 0
工具
No.1 知能巧整合 No.2 典例悟内涵 No.3 真题明考向
第7章 第6课时
栏目导引
5.已知圆C1:x2+y2-6x-7=0与圆C2:x2+y2-6y-27=0相交 于A、B两点,则线段AB的中垂线方程为________.
A.相切 B.相离
C.相交 D.不确定
答案: A
No.1 知能巧整合
No.2 典例悟内涵
No.3 真题明考向
工具
第7章 第6课时
栏目导引
解析:
Hale Waihona Puke 答案: D工具No.1 知能巧整合 No.2 典例悟内涵 No.3 真题明考向
第7章 第6课时
栏目导引
3.圆O1:x2+y2-2x=0和圆O2:x2+y2-4y=0的位置关系是( ) A.相离 B.相交 C.外切 D.内切 解析: 圆O1:(x-1)2+y2=1,圆心O1(1,0),半径r=1,圆O2:x2+ (y-2)2=4,圆心O2(0,2),半径R=2,
工具
No.1 知能巧整合 No.2 典例悟内涵 No.3 真题明考向
第7章 第6课时
栏目导引
工具
No.1 知能巧整合 No.2 典例悟内涵 No.3 真题明考向
第7章 第6课时
栏目导引
工具
No.1 知能巧整合 No.2 典例悟内涵 No.3 真题明考向
第7章 第6课时
栏目导引
1.直线4x+3y-35=0与圆x2+y2=49的位置关系为( )
No.1 知能巧整合 No.2 典例悟内涵 No.3 真题明考向
2018届高三数学文一轮复习课件:8-8-1 圆锥曲线的综合问题 精品

故|MN|= 1+k2 x1+x22-4x1x2= 2× 16-4=2 6。
答案:2 6
微考点
中点弦问题
角度一:由中点弦确定直线方程 【典例3】已知(4,2)是直线l被椭圆3x62 +y92=1所截得的线段的中点,则l的方程是________。
解析:设直线l与椭圆相交于A(x1,y1), B(x2,y2), 则3x621 +y921=1,且3x622 +y922=1, 两式相减得yx11--yx22=-4xy11++xy22。 又x1+x2=8,y1+y2=4,所以yx11--yx22=-21,
(4)如果直线x=ty+a与圆锥曲线相交于A(x1,y1),B(x2,y2)两点,则 弦长|AB|= 1+t2|y1-y2|。( √ )
解析:正确。|AB|= x1-x22+y1-y22, 又x1=ty1+a,x2=ty2+a, 所以|AB|= [ty1+a-ty2+a]2+y1-y22 = t2y1-y22+y1-y22= 1+t2|y1-y2|。
第八章 解析几何
第八节 圆锥曲线的综合问题
微知识 小题练 微考点 大课堂 微考场 新提升
微知识 小题练
教材回扣 基础自测
一、知识清单 微知识❶ 直线与圆锥曲线的位置关系 (1)从几何角度看,可分为三类:_无__公__共__点_, __仅__有__一__个__公__共__点_________ 及有两个_相__异__的__公__共__点_____。 (2)从代数角度看,可通过将表示直线的方程代入二次曲线的方程消 元后所得一元二次方程解的情况来判断.设直线l的方程为Ax+By+C= 0,圆锥曲线方程为f(x,y)=0。 由Afxx+,Byy=+0C,=0, 消元。 (如消去y)得ax2+bx+c=0。
《金版新学案》高考总复习(大纲版)数学(课件):第七章 直线和圆的方程7.3精品文档36页

第7章 第3课时
栏目导引
解析:
答案:
工具
No.1 知能巧整合 No.2 典例悟内涵 No.3 真题明考向
第7章 第3课时
栏目导引
解决线性规划实际应用题的一般步骤:
(1)认真审题分析,设出未知数,写出线性约束条件和目标函数.
(2)作出可行域.
(3)作出目标函数值为零时对应的直线l0.
No.1 知能巧整合
No.3 真题明考向
图(1)
图(2)
工具
第7章 第3课时
栏目导引
(2)不等式x-y+5≥0表示直线x-y+5=0上及右下方的点的集合,x +y+1≥0表示直线x+y+1=0上及右上方的点的集合,x≤3表示直线x= 3上及左方的点的集合,所以不等式组表示的平面区域如图(2)所示.
求目标函数的最值的一般步骤是:一画二移三求,其关No键.1是知准能确巧作整出合可 行域,准确理解z的几何意义,对于目标函数z=ax+by而No言.2,典当例b悟>0内时涵,在
(4)由几个不等式组成的不等式组所表示的平面区域,N是o.各1 个知能不巧等整式合所表示
的平面区域的 公共部分 .
No.2 典例悟内涵 No.3 真题明考向
工具
第7章 第3课时
栏目导引
2.线性规划中的基本概念
名称 约束条件
意义
N不o.等1 式知(能组巧)整合
一由次变量x,y组成的No.2 典例悟内涵
在线性约束条件下求线No性.3 目真题标明考函向
数的
第7章 第3课时
或
栏目导引
1.如图所示的平面区域(阴影部分)满足不等式( )
A.x+y-1<0
B.x+y-1>0
C.x-y-1<0
高三数学高考一轮复习系列教案第八章 圆锥曲线 大纲版
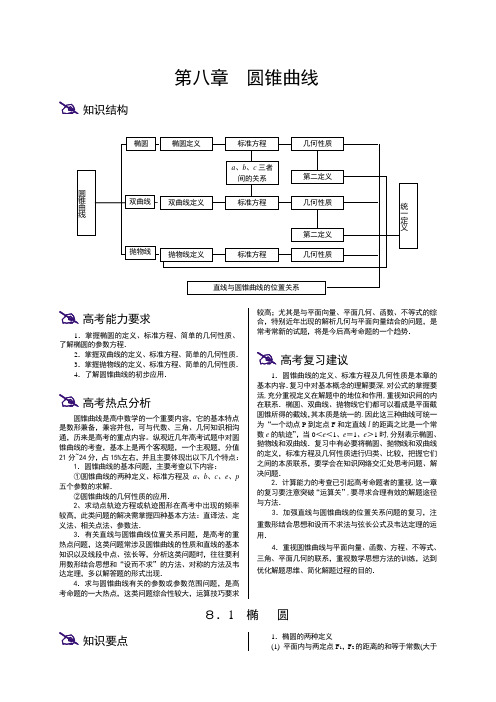
第八章圆锥曲线知识结构高考能力要求1.掌握椭圆的定义、标准方程、简单的几何性质、了解椭圆的参数方程.2.掌握双曲线的定义、标准方程、简单的几何性质.3.掌握抛物线的定义、标准方程、简单的几何性质.4.了解圆锥曲线的初步应用.高考热点分析圆锥曲线是高中数学的一个重要内容,它的基本特点是数形兼备,兼容并包,可与代数、三角、几何知识相沟通,历来是高考的重点内容。
纵观近几年高考试题中对圆锥曲线的考查,基本上是两个客观题,一个主观题,分值21分~24分,占15%左右,并且主要体现出以下几个特点:1.圆锥曲线的基本问题,主要考查以下内容:①圆锥曲线的两种定义、标准方程及a、b、c、e、p 五个参数的求解.②圆锥曲线的几何性质的应用.2、求动点轨迹方程或轨迹图形在高考中出现的频率较高,此类问题的解决需掌握四种基本方法:直译法、定义法、相关点法、参数法.3.有关直线与圆锥曲线位置关系问题,是高考的重热点问题,这类问题常涉及圆锥曲线的性质和直线的基本知识以及线段中点、弦长等,分析这类问题时,往往要利用数形结合思想和“设而不求”的方法、对称的方法及韦达定理,多以解答题的形式出现.4.求与圆锥曲线有关的参数或参数范围问题,是高考命题的一大热点,这类问题综合性较大,运算技巧要求较高;尤其是与平面向量、平面几何、函数、不等式的综合,特别近年出现的解析几何与平面向量结合的问题,是常考常新的试题,将是今后高考命题的一个趋势.高考复习建议1.圆锥曲线的定义、标准方程及几何性质是本章的基本内容.复习中对基本概念的理解要深,对公式的掌握要活,充分重视定义在解题中的地位和作用,重视知识间的内在联系.椭圆、双曲线、抛物线它们都可以看成是平面截圆锥所得的截线,其本质是统一的.因此这三种曲线可统一为“一个动点P到定点F和定直线l的距离之比是一个常数e的轨迹”,当0<e<1、e=1、e>1时,分别表示椭圆、抛物线和双曲线.复习中有必要将椭圆、抛物线和双曲线的定义,标准方程及几何性质进行归类、比较,把握它们之间的本质联系,要学会在知识网络交汇处思考问题、解决问题.2.计算能力的考查已引起高考命题者的重视,这一章的复习要注意突破“运算关”,要寻求合理有效的解题途径与方法.3.加强直线与圆锥曲线的位置关系问题的复习,注重数形结合思想和设而不求法与弦长公式及韦达定理的运用.4.重视圆锥曲线与平面向量、函数、方程、不等式、三角、平面几何的联系,重视数学思想方法的训练,达到优化解题思维、简化解题过程的目的.8.1 椭圆知识要点1.椭圆的两种定义(1) 平面内与两定点F1,F2的距离的和等于常数(大于21F F )的点的轨迹叫椭圆,这两个定点叫做椭圆的 , 之间的距离叫做焦距.注:①当2a =|F 1F 2|时,P 点的轨迹是 .②当2a <|F 1F 2|时,P 点的轨迹不存在.(2) 椭圆的第二定义:到 的距离与到 的距离之比是常数e ,且∈e 的点的轨迹叫椭圆.定点F 是椭圆的 ,定直线l 是 ,常数e 是 .2.椭圆的标准方程(1) 焦点在x 轴上,中心在原点的椭圆标准方程是:12222=+b y a x ,其中( > >0,且=2a ) (2) 焦点在y 轴上,中心在原点的椭圆标准方程是12222=+bx ay ,其中a ,b 满足: .3.椭圆的几何性质(对12222=+by a x ,a > b >0进行讨论)(1) 范围: ≤ x ≤ , ≤ y ≤ (2) 对称性:对称轴方程为 ;对称中心为 .(3) 顶点坐标: ,焦点坐标: ,长半轴长: ,短半轴长: ;准线方程: .(4) 离心率:=e ( 与 的比),∈e ,e 越接近1,椭圆越 ;e 越接近0,椭圆越接近于 .(5) 焦半径公式:设21,F F 分别为椭圆的左、右焦点,),(00y x P 是椭圆上一点,则=1PF ,122PF a PF -== .(6) 椭圆的参数方程为 . 4.焦点三角形应注意以下关系: (1) 定义:r 1+r 2=2a(2) 余弦定理:21r +22r -2r 1r 2cos θ=(2c )2(3) 面积:21F PF S ∆=21r 1r 2 sin θ=21·2c | y 0 |(其中P(00,y x )为椭圆上一点,|PF 1|=r 1,|PF 2|=r 2,∠F 1PF 2=θ)例题讲练【例1】 中心在原点,一个焦点为F 1(0,52)的椭圆被直线y =3x -2截得的弦的中点的横坐标为21,求此椭圆的方程.【例2】 已知点P(3, 4)是椭圆2222b y a x +=1 (a >b >0) 上的一点,F 1、F 2是它的两焦点,若PF 1⊥PF 2,求:(1) 椭圆的方程; (2) △PF 1F 2的面积.【例3】如图,射线OA 、OB 分别与x 轴、 y 轴所成的角均为︒30;已知线段PQ 的长度为2,并且保持线段的端点),(11y x P 在射线OA 上运动,点),(22y x Q 在射线OB 上运动(1) 试求动点),(21x x M 的轨迹C 的方程(2) 求轨迹C 上的动点N 到直线03=--y x 的距离的最大值和最小值.【例4】 (2005年全国卷I )已知椭圆的中心在原点,焦点在x 轴上,斜率为1且过椭圆右焦点F 的直线交椭圆于A 、B 两点,+与=(3, -1)共线.(1) 求椭圆的离心率;(2) 设M 是椭圆上任意一点,且=μλ+(λ、μ∈R),证明22μλ+为定值.小结归纳 1.在解题中要充分利用椭圆的两种定义,灵活处理焦半径,熟悉和掌握a 、b 、c 、e 关系及几何意义,能够减少运算量,提高解题速度,达到事半功倍之效.2.由给定条件求椭圆方程,常用待定系数法.步骤是:定型——确定曲线形状;定位——确定焦点位置;定量——由条件求a 、b 、c ,当焦点位置不明确时,方程可能有两种形式,要防止遗漏.3.解与椭圆的焦半径、焦点弦有关的问题时,一般要从椭圆的定义入手考虑;椭圆的焦半径的取值范围是],[c a c a +-.4.“设而不求”,“点差法”等方法,是简化解题过程的常用技巧,要认真领会.5.解析几何与代数向量的结合,是近年来高考的热点,在2005年的考题中足以说明了这一点,应引起重视.基础训练题 一、选择题1. 动点M 到定点)0,4(1-F 和)0,4(2F 的距离的和为8,则动点M 的轨迹为 ( ) A .椭圆 B .线段 C .无图形 D .两条射线2. (2005年全国高考试题III) 设椭圆的两个焦点分别为F 1、F 2,过F 2作椭圆长轴的垂线交椭圆于点P ,若△F 1PF 2为等腰直角三角形,则椭圆的离心率是 ( )A .22 B .212- C .2-2D .2-13. (2004年高考湖南卷)F 1、F 2是椭圆C :14822=+y x 的焦点,在C 上满足PF 1⊥PF 2的点P 的个数为( ) A .2个 B .4个 C .无数个 D .不确定4. 椭圆171622=+y x 的左、右焦点为F 1、F 2,一直线过F 1交椭圆于A 、B 两点,则△ABF 2的周长为 ( ) A .32 B .16 C .8 D .45. 已知点P 在椭圆(x -2)2+2y 2=1上,则xy的最小值为( )A .36-B .26-C .6-D .66-6. 我们把离心率等于黄金比215-的椭圆称为“优美椭圆”,设)0(12222>>=+b a by a x 是优美椭圆,F 、A 分别是它的左焦点和右顶点,B 是它的短轴的一个端点,则ABF ∠等于 ( ) A .︒60 B .︒75 C .︒90 D .︒120二、填空题 7. 椭圆400162522=+y x 的顶点坐标为 和 ,焦点坐标为 ,焦距为 ,长轴长为 ,短轴长为 ,离心率为 ,准线方程为 .8. 设F 是椭圆16722=+y x 的右焦点,且椭圆上至少有21个不同的点P i (i =1,2, ),使得|FP 1|、|FP 2|、|FP 3|…组成公差为d 的等差数列,则d 的取值范围是 . 9. 设1F ,2F 是椭圆14322=+y x 的两个焦点,P 是椭圆上一点,且121=-PF PF ,则得=∠21PF F . 10.若椭圆2222)1(-+m y m x =1的准线平行于x 轴则m 的取值范围是 .三、解答题11.根据下列条件求椭圆的标准方程(1) 和椭圆1202422=+y x 共准线,且离心率为21.(2) 已知P 点在以坐标轴为对称轴的椭圆上,点P 到两焦点的距离分别为534和532,过P 作长轴的垂线恰好过椭圆的一个焦点.12.椭圆14922=+y x 的焦点为21,F F ,点P 为其上的动点,当∠21PF F 为钝角时,求点P 横坐标的取值范围.13.(2005年高考湖南卷)已知椭圆C :12222=+by a x (a >0,b >0)的左、右焦点分别是F 1、F 2,离心率为e .直线l :y =ex +a 与x 轴,y 轴分别交于点A 、B 、M 是直线l 与椭圆C 的一个公共点,P 是点F 1关于直线l 的对称点,设=λ. (Ⅰ)证明:λ=1-e 2;(Ⅱ)若λ=43,△MF 1F 2的周长为6,写出椭圆C 的方程;(Ⅲ)确定λ的值,使得△PF 1F 2是等腰三角形.提高训练题14.(2006年高考湖南卷)已知C 1:13422=+y x ,抛物线C 2:(y -m )2=2px (p >0),且C 1、C 2的公共弦AB 过椭圆C 1的右焦点.(Ⅰ)当AB ⊥x 轴时,求p 、m 的值,并判断抛物线C 2的焦点是否在直线AB 上;(Ⅱ)若p =34,且抛物线C 2的焦点在直线AB 上,求m 的值及直线AB 的方程.15.(成都市2006届毕业班摸底测试)设向量i =(1, 0),j =(0, 1),=(x +m )i +y j ,=(x -m )i +y j ,且||+||=6,0< m < 3,x >0,y ∈R . ( I )求动点P(x ,y )的轨迹方程;( II ) 已知点A(-1, 0),设直线y =31(x -2)与点P 的轨迹交于B 、C 两点,问是否存在实数m ,使得AC AB ⋅=31?若存在,求出m 的值;若不存在,请说明理由.8.2 双 曲 线知识要点 1.双曲线的两种定义(1) 平面内与两定点F 1,F 2的 常数(小于 )的点的轨迹叫做双曲线.注:①当2a =|F 1F 2|时,p 点的轨迹是 .②2a >|F 1F 2|时,p 点轨迹不存在.(2) 平面内动点P 到一个定点F 和一条定直线l (F 不在 上)的距离的比是常数e ,当∈e 时动点P 的轨迹是双曲线.设P 到1F 的对应准线的距离为d ,到2F 对应的准线的距离为2d ,则e d PF d PF ==22112.双曲线的标准方程 (1) 标准方程:12222=-b y a x ,焦点在 轴上;12222=-bx ay ,焦点在 轴上.其中:a 0,b 0,=2a .(2) 双曲线的标准方程的统一形式:)0(122<=+nm ny mx3.双曲线的几何性质(对0,0,122>>=-b a b y a x 进行讨论)(1) 范围:∈x ,∈y .(2) 对称性:对称轴方程为 ;对称中心为 .(3) 顶点坐标为 ,焦点坐标为 ,实轴长为 ,虚轴长为 ,准线方程为 ,渐近线方程为 .(4) 离心率e = ,且∈e ,e 越大,双曲线开口越 ,e 越小,双曲线开口越 ,焦准距P = .(5) 焦半径公式,设F 1,F 2分别是双曲线的左、右焦点,若),(00y x P 是双曲线右支上任意一点,=1PF ,=2PF ,若),(00y x P 是双曲线左支上任意一点,=1PF ,=2PF . (6) 具有相同渐近线x aby ±=的双曲线系方程为 (7) 的双曲线叫等轴双曲线,等轴双曲线的渐近线为 ,离心率为 .(8) 12222=-b y a x 的共轭双曲线方程为 .例题讲练【例1】 根据下列条件,写出双曲线的标准方程 (1) 中心在原点,一个顶点是(0,6),且离心率是1.5.(2) 与双曲线x 2-2y 2=2有公共渐近线,且过点M(2,-2).【例2】 (04年高考湖北卷)直线l :y =kx +1与双曲线C :2x 2-y 2=1的右支交于不同的两点A 、B .(1)求实数k 的取值范围;(2)是否存在实数k ,使得以线段AB 为直径的圆经过双曲线C 的右焦点F ?若存在,求出k 的值;若不存在,说明理由.【例3】 在双曲线1121322-=-y x 的一支上有不同的三点A(x 1,y 1),B(x 2,6),C(x 3,y 3)与焦点F(0,5)的距离成等差数列.(1)求y 1+y 3;(2)求证:线段AC 的垂直平分线经过某一定点,并求出这个定点的坐标.【例4】 (2004年高考全国卷II )设双曲线C :)0(1222>=-a y a x 与直线l :x +y =1相交于两个不同的点.(1) 求双曲线C 的离心率e 的取值范围;(2) 设直线l 与y 的交点为P ,且=125,求a的值.小结归纳1.复习双曲线要与椭圆进行类比,尤其要注意它们之间的区别,如a 、b 、c 、e 的关系.2.双曲线的渐近线的探求是一个热点.①已知双曲线方程求渐近线方程;②求已知渐近线方程的双曲线方程.3.求双曲线的方程,经常要列方程组,因此,方程思想贯穿解析几何的始终,要注意定型(确定曲线形状)、定位(曲线的位置)、定量(曲条件求参数).4.求双曲线的方程的常用方法: (1) 定义法.(2) 待定系数法.涉及到直线与圆锥曲线的交点问题,经常是“设而不求”.5.例2的第(1)问是数材P 132第13题的引申,因此高考第一轮复习要紧扣教材.6.对于直线与双曲线的位置关系,要注意“数形转化”“数形结合”,既可以转化为方程组的解的个数来确定,又可以把直线与双曲线的渐近线进行比较,从“形”的角度来判断.基础训练题 一、选择题1. A 、B 是平面内两定点,动点P 到A 、B 两点的距离的差是常数,则P 的轨迹是 ( ) A .双曲线 B .椭圆 C .双曲线的一支 D .不能确定2. (04年高考湖南卷)如果双曲线1121322=-y x 上一点p 到右焦点的距离等于13,那么点p 到右焦线的距离是 ( )A .513 B .13 C .5D .1353. 已知双曲线的渐近线方程是2xy ±=,焦点在坐标轴上且焦距是10,则此双曲线的方程为 ( )A .152022=-y x B .152022±=-y x C .120522=-y xD .120522±=-y x4. (2005年高考湖南卷)已知双曲线12222=-by a x (a >0,b >0)的右焦点为F ,右焦线与一条渐近线交于点A ,△OAF 的面积为22a ,(0为原点)则两条渐近线的夹角为( ) A .30° B .45° C .60°D .90°5. 已知双曲线14922=-y x ,则过点A(3,1)且与双曲线仅有唯一的公共点的直线有 ( ) A .1条 B .2条 C .3条 D .4条6. (2005年江苏高考最后冲刺题) 设双曲线16x 2-9y 2=144的右焦点为F 2,M 是双曲线上任意一点,点A 的坐标为(9,2),则|MA|+53|MF 2|的最小值为( )A .9B .536C .542D .554二、填空题7. 中心在原点,坐标轴为对称轴,实轴与虚轴长之差为2,离心率为45的双曲线方程为 .8. (2004年高考·吉林、四川)设中心在原点,坐标轴为对称轴的椭圆与双曲线12222=-y x 有公共焦点,且它们的离心率互为倒数,则椭圆方程为 .9. (2006年高考湖南卷)过双曲线M :1222=-b y x 的左顶点A 作斜率为1的直线l ,若l 与双曲线M 的两条渐近线分别相交于点B 、C ,且|AB|=|BC|,则双曲线M 的离心率是 .10.可以证明函数x bax y +=(b ≠0)的图象是双曲线,试问双曲线C :xx y 33+=的离心率e 等于 .三、解答题11.(1) 已知双曲线的渐近线方程为032=±yx ,且过点(2,-6),求双曲线的方程;(2) 已知双曲线的右准线为x =4,右焦点为F(10,0),离心率为e =2,求双曲线的方程. 12.ABC ∆中,固定底边BC ,让顶点A 移动,已知4=BC ,且A B C sin 21sin sin =-,求顶点A 的轨迹方程.13.双曲线12222=-by a x )0,0(>>b a 的右支上存在与右焦点和左准线等距离的点,求离心率e 的取值范围.提高训练题 14.已知动点p 与双曲线13222=-y x 的两个焦点F 1、F 2的距离之和为定值,且cos ∠F 1PF 2的最小值为-91.(1) 求动点p 的轨迹方程;(2) 若已知点D(0,3),点M 、N 在动点p 的轨迹上且λ=,求实数λ的取值范围.15.(2005年武汉市高三调考)已知等轴双曲线C :)0(222>=-a a y x 上一定点P(00,y x )及曲线C 点上两个动点A 、B ,满足0=⋅PB PA(1) M 、N 分别为PA 、PB 中点,求证:0=⋅ON OM (O 为坐标原点);(2) 求|AB|的最小值及此时A 点坐标.抛 物 线 1.抛物线定义:离 的点的轨迹叫抛物线,焦点, 叫做抛物线的准线2.抛物线的标准方程和焦点坐标及准线方程① px y 22=,焦点为 ,准线为 . ② px y 22-=,焦点为 ,准线为 . ③ py x 22=,焦点为 ,准线为 . ④ py x 22-=,焦点为 ,准线为 . 3.抛物线的几何性质:对)0(22>=p px y 进行讨论. ① 点的范围: 、 . ② 对称性:抛物线关于 轴对称. ③ 离心率=e .④ 焦半径公式:设F 是抛物线的焦点,),(o o y x P 是抛物线上一点,则=PF .⑤ 焦点弦长公式:设AB 是过抛物线焦点的一条弦(焦点弦)i) 若),(11y x A ,),(22y x B ,则AB = ,21y y .ii) 若AB 所在直线的倾斜角为θ()0≠θ则AB = .特别地,当θ2π=时,AB 为抛物线的通径,且AB = .iii) S △AOB = (表示成P 与θ的关系式).iv) ||1||1BF AF +为定值,且等于 . 例题讲练【例1】 已知抛物线顶点在原点,对称轴是x 轴,抛物线上的点),3(n A -到焦点的距离为5,求抛物线的方程和n 的值.【例2】 已知抛物线C :x y 42=的焦点为F ,过点F 的直线l 与C 相交于A 、B .(1) 若316=AB ,求直线l 的方程.(2) 求AB 的最小值.【例3】 若A(3,2),F 为抛物线x y 22=的焦点,P 为抛物线上任意一点,求PA PF +的最小值及取得最小值时的P 的坐标.【例4】 (05全国卷(Ⅲ))设A(x 1,y 1),B(x 2,y 2),两点在抛物线y =2x 2上,l 是AB 的垂直平分线.(1)当且仅当x 1+x 2取何值时,直线l 经过抛物线的焦点F ?证明你的结论?(2)当直线l 的斜率为2时,求在y 轴上的截距的取值范围.小结归纳 1.求抛物线方程要注意顶点位置和开口方向,以便准确设出方程,然后用待定系数法.2.利用好抛物线定义,进行求线段和的最小值问题的转化.3.涉及抛物线的弦的中点和弦长等问题要注意利用韦达定理,能避免求交点坐标的复杂运算.4、解决焦点弦问题时,抛物线的定义有广泛的应用,应注意焦点弦的几何性质.基础训练题 一、选择题1. 过抛物线)0(22>=P px y 的焦点作直线交抛物线于),(11y x A ,),(22y x B 两点,若P x x 321=+,则AB等于( )A .2PB .4PC .6PD .8P2. 已知动点),(y x P 满足22)2()1(5-+-y x =|1243|++y x ,则P 点的轨迹是 ( )A .两条相交直线B .抛物线C .双曲线D .椭圆3. 已知抛物线212:x y C =与抛物线2C 关于直线x y -=对称,则2C 的准线方程是( )A .81-=x B .21=xC .81=x D .21-=x4. (2005年高考上海卷)过抛物线y 2=4x 的焦点作一条直线与抛物线相交于A 、B 两点,它们的横坐标之和等于5,则这样的直线 ( ) A .有且仅有一条 B .有且仅有两条 C .有无数条 D .不存在5. (2003年新课程卷)抛物线2ax y =的准线方程是2=y ,则a 的值为 ( )A .81B .81-C .8D .8-6. (04年高考湖北卷)与直线2x -y +4=0平行的抛物线y =x 2的切线方程是 ( ) A .2x -y +3=0 B .2x -y -3=0 C .2x -y +1=0 D .2x -y -1=0二、填空题7. 点M 与点F(4,0)的距离比它到连线l :x +5=0的距了小1,则点M 的轨迹方程为 . 8. 某桥的桥洞是抛物线,桥下水面宽16米,当水面上涨2米后达警戒水位,水面宽变为12米,此时桥洞顶部距水面高度为 米(精确到0.1米). 9. 过点(3,3)的直线与抛物线y 2=3x 只有一个公共点,则这样的直线的条数为 .10.一个酒杯的轴截面是抛物线的一部分,它的方程是x 2)200(2≤≤=y y ,在杯内放入一个玻璃球,要使球触及酒杯底部,则玻璃球的半径r 的取值范围是三、解答题11.求顶点在原点,对称轴是x 轴,并且顶点与焦点的距离等于6的抛物线方程.12.正方形ABCD 中,一条边AB 在直线y =x +4上,另外两顶点C 、D 在抛物线y 2=x 上,求正方形的面积.13.设A 和B 为抛物线y 2=4px (p >0)上原点以外的两个动点,已知OA ⊥OB ,OM ⊥AB ,求点M 的轨迹方程,并说明它表示什么曲线?提高训练题 14.过抛物线y 2=2px (p >0)的焦点F 作直线交抛物线于A 、B 两点,试问:以AB 为直径的圆与抛物线的准线是相交、相切还是相离?若把抛物线改为椭圆12222=+b y a x 或双曲线12222=-b y a x ,结果又如何呢?15.(2004年高考上海卷)如图,直线x y 21=与抛物线4812-=x y 交于A 、B 两点,线段AB 的垂直平分线与直线5-=y 交于Q 点. (1) 求点Q 的坐标;(2) 当P 为抛物线上位于线段AB(含点A 、B)下方的动点时,求OPQ ∆面积的最大值.8.4 直线与圆锥曲线的位置关系知识要点 1.直线与圆锥曲线的位置关系,常用研究方法是将曲线方程与直线方程联立,由所得方程组的解的个数来决定,一般地,消元后所得一元二次方程的判别式记为△,△>0时,有两个公共点,△=0时,有一个公共点,△<0时,没有公共点.但当直线方程与曲线方程联立的方程组只有一组解(即直线与曲线只有一个交点)时,直线与曲线未必相切,在判定此类情形时,应注意数形结合.(对于双曲线,重点注意与渐近线平行的直线,对于抛物线,重点注意与对称轴平行的直线)2.直线与圆锥曲线的交点间的线段叫做圆锥曲线的弦.设弦AB 端点的坐标为A(x 1,y 1),B(x 2,y 2),直线AB 的斜率为k ,则:|AB |=————————或:—————————.利用这个公式求弦长时,要注意结合韦达定理. 当弦过圆锥曲线的焦点时,可用焦半径进行运算. 3.中点弦问题:设A(x 1,y 1),B(x 2,y 2)是椭圆12222=+b y a x 上不同的两点,且x 1≠x 2,x 1+x 2≠0,M(x 0,y 0)为AB 的中点,则 ⎪⎪⎩⎪⎪⎨⎧=+=+11222222221221b y ax b y a x 两式相减可得2221212121ab x x y y x x y y -=++⋅--即 .对于双曲线、抛物线,可得类似的结论.例题讲练 【例1】 直线y =ax +1与双曲线3x 2-y 2=1相交于A 、B 两点.(1) 当a 为何值时,A 、B 两点在双曲线的同一支上?当a 为何值时,A 、B 两点分别在双曲线的两支上?(2) 当a 为何值时,以AB 为直径的圆过原点?x【例2】 已知双曲线方程2x 2-y 2=2.(1) 求以A(2,1)为中点的双曲线的弦所在直线方程; (2) 过点B(1,1)能否作直线l ,使l 与所给双曲线交于Q 1、Q 2两点,且点B 是弦Q 1Q 2的中点?这样的直线l 如果存在,求出它的方程;如果不存在,说明理由.【例3】 在抛物线y 2=4x 上恒有两点关于直线y =kx +3对称,求k 的取值范围.【例4】 (2006届苏州市高三调研测试)已知椭圆222y ax +=1(a 为常数,且a >1),向量m =(1, t ) (t >0),过点A(-a , 0)且以为方向向量的直线与椭圆交于点B ,直线BO 交椭圆于点C (O 为坐标原点).(1) 求t 表示△ABC 的面积S( t );(2) 若a =2,t ∈[21, 1],求S( t )的最大值.小结归纳1.判断直线与圆锥曲线的位置关系时,注意数形结合;用判别式的方法时,若所得方程二次项的系数有参数,则需考虑二次项系数为零的情况.2.涉及中点弦的问题有两种常用方法:一是“设而不求”的方法,利用端点在曲线上,坐标满足方程,作差构造出中点坐标和斜率的关系,它能简化计算;二是利用韦达定理及中点坐标公式.对于存在性问题,还需用判别式进一步检验.3.对称问题,要注意两点:垂直和中点.基础训练题 一、选择题1. 曲线x 2+4y 2+D x +2E y +F =0与x 轴有两个交点,且这两个交点在原点的两侧的充要条件是 ( ) A .D ≠0,E =0,F >0 B .E =0,F <0 C .D 2-F >0 D .F <0 2. 若椭圆193622=+y x 的弦被点(4,2)平分,则此弦所在直线的斜率为 ( ) A .2 B .-2C .31D .-213. 经过抛物线)0(22>=p px y 的所有焦点弦中,弦长的最小值为 ( ) A .p B .2p C .4p D .不确定4. 过双曲线1222=-y x 的右焦点作直线l ,交双曲线于A 、B 两点,若∣AB ∣=4,则这样的直线l 有( ) A .1条 B .2条 C .3条 D .4条5. (华师大二附中2005年模拟试卷2) 直线l :y =kx +1(k ≠0)椭圆E :1422=+y m x ,若直线l 被椭圆E 所截弦长为d ,则下列直线中被椭圆E 截得的弦长不是d 的是 ( ) A .kx +y +1=0 B .kx -y -1=0 C .kx +y -1=0 D .kx +y =06. 椭圆mx 2+ny 2=1与直线y =1-x 交于M 、N 两点,过两点O 与线段MN 之中点的直线的斜率为22,则xnm的值是 ( )A .22B .332 C .229D .2732二、填空题7. 已知直线x -y =2与抛物线y 2-4x 交于A 、B 两点,那么线段AB 的中点坐标是 .8. 对任意实数k ,直线y =kx +b 与椭圆⎩⎨⎧==θθs i n 4c o s 2y x (0≤θ<2π)恒有公共点,则b 的取值范围是 .9. 已知抛物线y 2=4x 的一条弦AB ,A(x 1,y 1),B(x 2,y 2),AB 所在直线与y 轴交点坐标为(0,2),则2111y y += .10.若直线mx +ny -3=0与圆x 2+y 2=3没有公共点,则m 、n 的关系式为___________;以(m ,n )为点P 的坐标,过点P 的一条直线与椭圆13722=+y x 的公共点有____个.三、解答题 11.已知直线l 交椭圆162022y x +=1于M 、N 两点,B(0,4)是椭圆的一个顶点,若△BMN 的重心恰是椭圆的右焦点,求直线l 的方程.12.已知直线y =(a +1)x -1与曲线y 2=ax 恰有一个公共点,求实数a 的值.13.(05重庆)已知椭圆C 1的方程为1422=+y x ,双曲线C 2的左、右焦点分别为C 1的左、右顶点,而C 2的左、右顶点分别是C 1的左、右焦点. (1)求双曲线C 2的方程;(2)若直线l :y =kx +2与椭圆C 1及双曲线C 2恒有两个不同的交点,且l 与C 2的两个交点A 和B 的满足6<⋅(其中O 为原点),求k 的取值范围. 提高训练题14.已知椭圆的一个顶点为A(0,-1),焦点在x 轴上,若右焦点到直线022=+-y x 的距离为3. ⑴ 求椭圆的方程;⑵ 设椭圆与直线y =kx +m (k ≠0)相交于不同的两点M 、N ,当AN AM =时,求m 的取值范围.15.(04湖南)过抛物线x 2=4y 的对称轴上任一点P(0,m )(m >0),作直线与抛物线交于A 、B 两点,点Q 是点P 关于原点的对称点. (Ⅰ)设点P 分有向线段所成的比为λ,证明:)(λ-⊥;(Ⅱ)设直线AB 的方程是x -2y +12=0,过A 、B 两点的圆C与抛物线在点A处有共同的切线,求圆C的方程.8.5 轨迹方程知识要点1.直接法求轨迹的一般步骤:建系设标,列式表标,化简作答(除杂).2.求曲线轨迹方程,常用的方法有:直接法、定义法、代入法(相关点法、转移法)、参数法、交轨法等.例题讲练【例1】一动圆与圆x2+y2+6x+5=0外切,同时与圆x2+y2-6x-91=0内切,求动圆圆心的轨迹方程,并说明它是什么样的曲线.【例2】已知抛物线过点N(1,-1),且准线为l:x =-3,求抛物线顶点M的轨迹.【例3】已知直线l与椭圆12223=+byax(a>b>0)有且仅有一个交点Q,且与x轴、y轴交于R、S,求以线段SR 为对角线的矩形ORPS的顶点P的轨迹方程.【例4】已知点H(0,-3),点P在x轴上,点Q 在y轴正半轴上,点M在直线PQ上,且满足PMHP⋅=0,MQPM23-=.(1) 当点P在x轴上移动时,求动点M的轨迹曲线C 的方程;(2) 过定点A(a,b)的直线与曲线C相交于两点S、R,求证:抛物线S、R两点处的切线的交点B恒在一条直线上.小结归纳1.直接法求轨迹方程关键在于利用已知条件,找出动点满足的等量关系,这个等量关系有的可直接利用已知条件,有的需要转化后才能用.2.回归定义是解决圆锥曲线轨迹问题的有效途径.3.所求动点依赖于已知曲线上的动点的运动而运动,常用代入法求轨迹.4.参数法求轨迹关键在于如何选择好参数,建立起x ,y 的参数方程,以便消参,选择n 个参数,要建立n +1个方程,消参时,要注意等价性.5.求轨迹比求轨迹方程多一个步骤,求轨迹最后须说明轨迹的形状、大小、位置、方向.基础训练题 一、选择题1. 已知椭圆的焦点是F 1、F 2,P 是椭圆上的一个动点,如果延长F 1P 到Q ,使得| PQ |=| PF 2 |,那么动点Q 的轨迹是 ( ) A .圆 B .椭圆 C .双曲线的一支 D .抛物线2. 动点P 与定点)0,1(,)0,1(B A -的连结的斜率之积为1-,则P 点的轨迹方程是( ) A .x 2+y 2=1 B .x 2+y 2=1)1(±≠x C .x 2+y 2=1)0(≠x D .21x y -=3. 已知动点P(x 、y )满足1022)2()1(-+-y x =|3x +4y+2|,则动点P 的轨迹是( )A .椭圆B .双曲线C .抛物线D .无法确定4. 设P 为椭圆12222=+by a x 上一点,过右焦点F 2作∠F 1PF 2的外角平分线的垂线,垂足为Q ,则点Q 的轨迹是( ) A .直线 B .抛物线 C .圆 D .双曲线 5. 设P 为双曲线12222=-b y a x 上一点, 过右焦点F 2作∠F 1PF 2的内角平分线的垂线,垂足为Q ,则点Q 的轨迹是 ( ) A .圆 B .抛物线 C .直线 D .椭圆 6. 已知点P(x ,y )在以原点为圆心,半径为1的圆上运动,则点(x +y ,xy )的轨迹是 ( ) A .半圆 B .抛物线的一部分 C .椭圆 D .双曲线的一支二、填空题7. 长为2a 的线段AB 的两个端点分别在x 轴、y 轴上滑动,则AB 中点的轨迹方程为 .8. 经过定点M(1,2),以y 轴为准线,离心率为21的椭圆左顶点的轨迹方程 . 9. 已知抛物线)(12R m mx x y ∈-+-=,当m 变化时抛物线焦点的轨迹方程为 . 10.(04北京)在正方体ABCD —A 1B 1C 1D 1中,P 是侧面BB 1C 1C 内一动点,若P 到直线BC 与到直线C 1D 1的距离相等,则动点P 的轨迹是 .三、解答题 11.以动点P 为圆心的圆与圆A :(x +5)2+y 2=49及圆B :(x -5)2+y 2=1都外切,求动点P 的轨迹.12.已知双曲线2222ny m x -=1(m >0,n >0)的顶点为A 1、A 2,与y 轴平行的直线l 交双曲线于点P 、Q. (1) 求直线A 1P 与A 2Q 交点M 的轨迹方程; (2) 当m ≠n 时,求所得圆锥曲线的焦点坐标、准线方程和离心率.13.设直线l :y =kx +1与椭圆C :ax 2+y 2=2(a >1)交于A 、B 两点,以OA 、OB 为邻边作平行四边形OAPB (O 为坐标原点).(1)若k =1,且四边形OAPB 为矩形,求a 的值; (2)若a =2,当k 变化时,(k ∈R),求点P 的轨迹方程.提高训练题14.设椭圆方程为1422=+y x ,过点M(0,1)的直线l 交椭圆于点A 、B ,O 是坐标原点,点P 满足)(21OB OA OP +=,点N 的坐标为)21,21(,当l 绕点M 旋转时,求:(1) 动点P 的轨迹方程; (2) ||NP 的最小值与最大值.A1。
《金新学案》高考数学总复习 第1章第1课时课件 文 大纲人教
3.考查角度: 一是考查集合的概念、集合间的关系及集合的运算. 二是与其他知识相联系,以集合语言和集合思想为载体,考查函数 的定义域、值域,函数、方程与不等式的关系等. 4.命题趋势:对用集合、数形结合、分类讨论等思想解决数学问 题能力的要求逐渐增大.
解析: 答案: -3
答案: C
答案: D
答案: -1
判断集合与集合的关系,基本方法是归纳为判断元素与集合的关系. 对于用描述法表示的集合,要紧紧抓住代表元素及它的属性,可将元素 列举出来直观发现或通过元素特征,求同存异,定性分析.
[注意] 在解题中的应用.
解析: (1)由x2-8x+15=0,得x=3或x=5, ∴A={3,5},
解析:由f(x)=x2+x-1,x=f(x) 得x2-1=0,x=±1,M={-1,1}.
答案: {x|-1<x<2}
1.掌握集合的概念,关键是把握集合中元素的特性,要特别注意 集合中元素的互异性,一方面利用集合元素的互异性能顺利找到解 题的切入点;另一方面,在解答完毕之时,注意检验集合的元素是 否满足互异性以确保答案正确.
2.用描述法表示集合时,首先应清楚集合的类型和元素的性质. 如集合{y|y=2x},{x|y=2x},{(x,y)|y=2x}表示不同的集合.
第一章 集合与简易逻辑
第1课时 集合的概念与运算
1.集合与元素 (1)集合中元素的三个特性: 确定性 、 互异性 、 无序性 . (2)集合中元素与集合的关系 元素与集合的关系:对于元素a与集合A,或者a∈A,或者a A.二 者必居其一.
(3)常见集合的符号表示
数集 自然数集 正整数集
符号
N
N*或N+
集合是高中数学的基础知识,也是高考数学必考内容.通过对近三 年高考试题的统计分析可以看出以下命题规律:
《金版新学案》高考数学总复习 8.4直线与圆锥曲线的位置关系课件 文 大纲人教版
对于中点弦问题,常用的解题方法是点差法.其
解题步骤为:
(1)设点:即设出弦的两端点坐标; (2)代入:即代入圆锥曲线方程; (3)作差:即两式相减,再用平方差公式把上式展 开; (4)整理:即转化为斜率与中点坐标的关系式,然 后求解.
圆锥曲线中求最值与范围问题是高考 题中的常考问题,解决此类问题,一般有
2.定值与最值问题 (1)圆锥曲线中的定值问题 在解析几何问题中,有些几何量和参数无关,这就构成定值问题. 解决这类问题常通过取参数和特殊值来确定“定值”是多少,或者将 该问题涉及的几何式转化为代数式或三角形式,证明该式是恒定的. (2)圆锥曲线中的最值问题 解决圆锥曲线中的最值问题,一般有两种方法:一是几何法,特别 是用圆锥曲线的定义和平面几何的有关结论来解非常巧妙;二是代数 法,将圆锥曲线中的最值问题转化为函数问题(即根据条件列出所求的 目标函数),然后根据函数的特征选用参数法、配方法、判别式法、三 角有界法、函数单调法及均值不等式法等,求解最大或最小值.
练规范、练技能、练速度
第4课时
直线与圆锥曲线程组解的个数,可以研 究直线与圆锥曲线的位置关系,也就是用代数的方法研究几何 问题,这是解析几何的重要思想方法.方程组消元后要注意所 得方程的二次项系数是否含有参数,若含参数,需按二次项系 数是否为零进行分类讨论,只有二次项系数不为零时,方程才 是一元二次方程,后面才可以用判别式Δ 的符号判断方程解的 个数,从而说明直线与圆锥曲线的位置关系.
对近三年高考试题的统计分析,有以下的命题规律: 1.考查热点:定值与最值问题. 2.考查形式:多以解答题形式出现,难度较大. 3.考查角度: 一是对直线与圆锥曲线的位置关系的考查,考查交点个数及直线的条数. 二是对定值与最值问题的考查,对于求曲线方程中参数的取值范围问题. 三是对存在与对称性问题的考查,对于存在性问题,一般是合理转化为等 价的、容易表述的数学问题来解决. 4.命题趋势:向量、函数与圆锥曲线相结合,考查最值问题.
人教版新教材高中数学优质课件 第3课时 圆锥曲线的方程
离心率: = ,且 > 1
返回目录
定义:|| =
圆
标准方程
锥
曲
线
的
方
程
抛物线
焦点在轴上: 2 = ±2( > 0)
焦点在轴上: 2 = ±2( > 0)
焦点: ± ,0 ,准线: = ∓
2
2
焦点在轴上
对称轴:轴
几何性质
焦点: 0, ±
,准线: = ∓
双曲线的离心率为2,则该双曲线的方程为
.
返回目录
= 1,
解析:(1)由题意得
2
故椭圆方程为 4
+
= 2,
1 解得
则 b2=a2-c2=3,
= ,
= 1,
2
2
=1.
3
= 2,
= 1,
(2)由题意得
解得
= 2,
= 2,
则 b2=c2-a2=3,因此双曲线方程为
2
2
16
2
=1(a>0,b>0),其渐近线方程是
2
∵双曲线的一条渐近线方程为
x-√3y=0,∴
又由 a2+b2=c2=48,解得 a2=36,b2=12.
2
∴所求双曲线方程为
36
−
2
=1.
12
=
√3
,
3
y=± x.
返回目录
专题三
圆锥曲线的性质及应用
返回目录
【例3】 (1)如图,椭圆C1,C2与双曲线C3,C4的离心率分别是e1,e2与e3,e4,则
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
用,如求焦半径、焦点三角形的周长和面积、求椭圆的方程等.
二是对椭圆方程的考查,主要是利用待定系数法求解,采用“定 形——定式——定量”的基本解题步骤.
三是对椭圆离心率的考查,这是高考的一个热
点.求解离心率的方法比较多,解题关键是树立
知识点
考纲下载
掌握椭圆的定义、标准方
椭圆 程和椭圆的简单几何性质; 了解椭圆的参数方程. 掌握双曲线的定义、标准 双曲线 方程和双曲线的简单几何
第1课时
椭
圆
1.椭圆的定义
第一定义:平面内与两个定点F1、F2的距离的 和 等于 常数2a(2a > |F1F2|)的点的轨迹叫做椭圆.源自第二定义:平面内一点与一个
定点 的距离和它到一
条 定直线 的距离的比是常数e(e∈ (0,1) )的动点的轨 迹叫做椭圆.
通过对近三年高考试题的统计分析,有以下的命题规律:
1.考查热点:小题中求椭圆的离心率,大题中直线和椭圆的位 置关系问题.
2.考查形式:选择、填空及解答题均可能出现.
目标意识,根据题目的特点灵活选择,最终落脚 点为a与c之间的等量关系.
四是对直线与椭圆的位置关系的考查.也是高
考的热点. 4.命题趋势:椭圆与直线、椭圆与向量的相结
合问题.
练规范、练技能、练速度
