高一数学抛物线及其标准方程
高一数学复习考点知识讲解课件25---抛物线的标准方程

高一数学复习考点知识讲解课件§3.3抛物线3.3.1抛物线的标准方程考点知识1.理解抛物线的定义、标准方程及其推导过程.2.掌握抛物线的定义及其标准方程的应用.3.了解抛物线定义的实际应用.导语通过前面的学习可以发现,如果动点M到定点F的距离与M到定直线l(不过点F)的距离之比为k,当0<k<1时,点M的轨迹为椭圆;当k>1时,点M的轨迹为双曲线.一个自然的问题是:当k=1时,即动点M到定点F的距离与M到定直线l的距离相等时,点M的轨迹会是什么形状?一、抛物线的定义与标准方程问题1利用信息技术作图,如图所示,F是定点,l是不经过点F的定直线,H是直线l 上任意一点,过点H作MH⊥l,线段FH的垂直平分线m交MH于点M,拖动点H,点M随之运动,你能发现点M满足的几何条件吗?它的轨迹是什么形状?提示点M随着点H运动的过程中,始终有MF=MH,即点M与定点F的距离等于它到定直线l的距离,点M的轨迹形状与二次函数的图象相似.知识梳理 抛物线的定义平面内到一个定点F 和一条定直线l (F 不在l 上)的距离相等的点的轨迹叫作抛物线(parabola),定点F 叫作抛物线的焦点,定直线l 叫作抛物线的准线(directrix). 问题2比较椭圆、双曲线标准方程的建立过程,你认为如何建立坐标系,可能使所求抛物线的方程形式简单?提示过F 作直线FN ⊥直线l ,垂足为N ,以直线NF 为x 轴,线段NF 的垂直平分线为y 轴,建立如图所示的直角坐标系xOy ,设焦点F 到准线l 的距离为p ,则F ⎝ ⎛⎭⎪⎫p 2,0,又设P (x ,y )为抛物线上任意一点.过点P 作PH ⊥l ,垂足为H ,则PF =PH ,得⎝ ⎛⎭⎪⎫x -p 22+y 2=⎪⎪⎪⎪⎪⎪x +p 2, 将上式两边平方并化简,得y 2=2px (p >0).知识梳理图形标准方程焦点坐标准线方程y 2=2px (p >0)⎝ ⎛⎭⎪⎫p 2,0 x =-p2y 2=-2px (p >0)⎝ ⎛⎭⎪⎫-p 2,0 x =p2x 2=2py (p >0)⎝ ⎛⎭⎪⎫0,p 2 y =-p2x 2=-2py (p >0)⎝ ⎛⎭⎪⎫0,-p 2 y =p2注意点:(1)p 的几何意义是焦点到准线的距离.(2)标准方程的结构特征:顶点在坐标原点、焦点在坐标轴上.(3)抛物线的开口方向:抛物线的开口方向取决于一次项变量(x 或y )的取值范围. 例1分别求满足下列条件的抛物线的标准方程. (1)准线方程为2y +4=0; (2)过点(3,-4);(3)焦点为直线x +3y +15=0与坐标轴的交点.解(1)准线方程为2y +4=0,即y =-2,故抛物线的焦点在y 轴的正半轴上,设其方程为x 2=2py (p >0).又p2=2,∴2p =8,故所求抛物线的标准方程为x 2=8y . (2)∵点(3,-4)在第四象限,∴抛物线开口向右或向下,设抛物线的标准方程为y2=2px(p>0)或x2=-2p1y(p1>0).把点(3,-4)的坐标分别代入y2=2px和x2=-2p1y中,得(-4)2=2p·3,32=-2p1·(-4),即2p=163,2p1=94.∴所求抛物线的标准方程为y2=163x或x2=-94y.(3)令x=0,得y=-5;令y=0,得x=-15.∴抛物线的焦点为(0,-5)或(-15,0).∴所求抛物线的标准方程为x2=-20y或y2=-60x.反思感悟求抛物线的标准方程主要利用待定系数法,其步骤为(1)依据条件设出抛物线的标准方程的类型.(2)求参数p的值.(3)确定抛物线的标准方程.提醒:当焦点位置不确定时,应分类讨论,也可以设y2=ax或x2=ay(a≠0)的形式,以简化讨论过程.跟踪训练1(1)若抛物线y2=2px(p>0)的焦点坐标为(1,0),则p=________,准线方程为________.答案2x=-1解析因为抛物线的焦点坐标为(1,0),所以p 2=1,p =2,准线方程为x =-p2=-1. (2)焦点在y 轴上,焦点到准线的距离为5的抛物线的标准方程为____________. 答案x 2=10y 和x 2=-10y解析设方程为x 2=2my (m ≠0),由焦点到准线的距离为5,知|m |=5,m =±5,所以满足条件的抛物线有两条,它们的标准方程分别为x 2=10y 和x 2=-10y .二、抛物线定义的应用例2(1)已知抛物线C :y 2=x 的焦点为F ,A (x 0,y 0)是C 上一点,AF =54x 0,则x 0等于() A .1B .2C .4D .8 答案A解析∵14+x 0=54x 0, ∴x 0=1.(2)已知点P 是抛物线y 2=2x 上的一个动点,求点P 到点(0,2)的距离与P 到该抛物线准线的距离之和的最小值.解由抛物线的定义可知,抛物线上的点到准线的距离等于它到焦点的距离.由题图可知,点P ,点(0,2)和抛物线的焦点F ⎝ ⎛⎭⎪⎫12,0三点共线时距离之和最小,所以最小距离d =⎝ ⎛⎭⎪⎫0-122+(2-0)2=172. 延伸探究1.若将本例(2)中的点(0,2)改为点A (3,2),求P A +PF 的最小值. 解将x =3代入y 2=2x ,得y =±6.所以点A 在抛物线内部.设点P 为其上一点,点P 到准线(设为l )x =-12的距离为d , 则P A +PF =P A +d .由图可知,当P A ⊥l 时,P A +d 最小,最小值是72. 即P A +PF 的最小值是72.2.若将本例(2)中的点(0,2)换为直线l 1:3x -4y +72=0,求点P 到直线3x -4y +72=0的距离与P 到该抛物线的准线的距离之和的最小值. 解如图,作PQ 垂直于准线l 于点Q ,P A1+PQ=P A1+PF≥A1F min.A1F的最小值为点F到直线3x-4y+72=0的距离d=⎪⎪⎪⎪⎪⎪3×12+7232+(-4)2=1.即所求最小值为1.反思感悟抛物线定义的应用实现距离转化.根据抛物线的定义,抛物线上任意一点到焦点的距离等于它到准线的距离,因此,由抛物线定义可以实现点点距与点线距的相互转化,从而简化某些问题.跟踪训练2(1)已知抛物线y2=2px(p>0)的焦点F1,若点A(2,-4)在抛物线上,则点A 到焦点的距离为________.答案4解析把点A(2,-4)代入抛物线y2=2px,得16=4p,即p=4,从而抛物线的焦点为(2,0).故点A到焦点的距离为4.(2)设点A的坐标为(1,15),点P在抛物线y2=8x上移动,P到直线x=-1的距离为d,则d+P A的最小值为()A.1B.2C.3D.4答案C解析由题意知抛物线y 2=8x 的焦点为F (2,0),点P 到准线x =-2的距离为d +1,于是PF =d +1,所以d +P A =PF -1+P A 的最小值为AF -1=4-1=3.三、抛物线的实际应用例3(1)探照灯反光镜的纵断面是抛物线的一部分,光源在抛物线的焦点处,已知灯口直径是60cm ,灯深40cm ,则光源到反光镜顶点的距离是() A .11.25cmB .5.625cm C .20cmD .10cm 答案B解析如图,建立平面直角坐标系,设抛物线方程是y 2=2px (p >0).∵A (40,30)在抛物线上, ∴302=2p ×40, ∴p =454,∴光源到反光镜顶点的距离为p 2=4542=458=5.625(cm).(2)某抛物线形拱桥跨度是20米,拱桥高度是4米,在建桥时,每4米需用一根支柱支撑,则其中最长支柱的长为________米.答案3.84解析如图,建立平面直角坐标系,设抛物线方程为x2=-2py(p>0).依题意知,点P(10,-4)在抛物线上,∴100=-2p×(-4),2p=25.即抛物线方程为x2=-25y.∵每4米需用一根支柱支撑,∴支柱横坐标分别为-6,-2,2,6.由图知,AB是最长的支柱之一.设点B的坐标为(2,y B),解得y B=-425,点A的坐标为(2,-4),∴AB=y B-(-4)=-425+4=3.84,∴最长支柱的长为3.84米.反思感悟涉及拱桥、隧道的问题,通常需建立适当的平面直角坐标系,利用抛物线的标准方程进行求解.跟踪训练3河上有一抛物线形拱桥,当水面距拱桥顶5m时,水面宽为8m,一小船宽4m,高2m,载货后船露出水面上的部分高0.75m,则水面上涨到与抛物线形拱桥顶相距多少米时,小船开始不能通航?解如图所示,以拱桥的拱顶为原点,以过拱顶且平行于水面的直线为x轴,建立平面直角坐标系.设抛物线方程为x2=-2py(p>0),由题意可知点B(4,-5)在抛物线上,故p=85,得x2=-165y.当船面两侧和抛物线接触时,船不能通航,设此时船面宽为AA′,则A(2,y A),由22=-165y A,得y A=-5 4.又知船面露出水面上的部分高为0.75m,所以h=|y A|+0.75=2(m).所以水面上涨到与抛物线形拱桥顶相距2m时,小船开始不能通航.1.知识清单:(1)抛物线的定义.(2)抛物线的标准方程.(3)抛物线的实际应用.2.方法归纳:待定系数法、定义法、转化化归.3.常见误区:混淆抛物线的焦点位置和方程形式.1.准线与x轴垂直,且经过点(1,-2)的抛物线的标准方程是() A.y2=-2x B.y2=2xC.x2=2y D.x2=-2y答案B解析由题意可设抛物线的标准方程为y2=ax,则(-2)2=a,解得a=2,因此抛物线的标准方程为y2=2x,故选B.2.抛物线y=2x2的焦点到准线的距离为()A.18B.12C.14D.4答案C解析根据题意,抛物线的方程为y=2x2,其标准方程为x2=12y,其中p=14,则抛物线的焦点到准线的距离p=14.3.设抛物线y2=8x上一点P到y轴的距离是4,则点P到该抛物线焦点的距离是________.答案6解析由抛物线的方程得p2=42=2,再根据抛物线的定义,可知所求距离为4+2=6.4.如图是抛物线形拱桥,当水面在l时,拱顶离水面2米,水面宽4米.水位下降1米后,水面宽________米.答案2 6解析建立如图所示的平面直角坐标系,设抛物线的方程为x2=-2py(p>0),则点(2,-2)在抛物线上,代入可得p=1,所以x2=-2y.当y=-3时,x2=6,所以水面宽为26米.课时对点练1.已知抛物线的焦点坐标是(-1,0),则抛物线的标准方程为()A.x2=4y B.x2=-4yC .y 2=4xD .y 2=-4x答案D解析∵抛物线的焦点坐标是(-1,0),∴抛物线是焦点在x 轴负半轴上的抛物线,且p 2=1,得p =2.∴抛物线的标准方程为y 2=-4x .2.已知抛物线的标准方程为y 2=ax ,则其焦点坐标为()A.⎝ ⎛⎭⎪⎫a 4,0B.⎝ ⎛⎭⎪⎫0,a 4 C.⎝ ⎛⎭⎪⎫-a 4,0D.⎝ ⎛⎭⎪⎫0,-a 4 答案A3.抛物线y =14x 2的准线方程是() A .y =-1B .y =-2C .x =-1D .x =-2答案A解析因为y =14x 2,所以x 2=4y ,所以抛物线的准线方程是y =-1.4.已知抛物线y 2=2px (p >0)的准线经过点(-1,1),则该抛物线焦点坐标为()A .(-1,0)B .(1,0)C .(0,-1)D .(0,1)答案B解析∵抛物线的准线方程为x=-p 2,∴-p2=-1,∴p2=1,故抛物线的焦点坐标为(1,0).5.(多选)经过点P(4,-2)的抛物线的标准方程可以为()A.y2=x B.x2=8yC.x2=-8y D.y2=-8x答案AC解析若抛物线的焦点在x轴上,设抛物线的方程为y2=2px(p>0),又因为抛物线经过点P(4,-2),所以(-2)2=2p×4,解得p=12,所以抛物线的方程为y2=x.若抛物线的焦点在y轴上,设抛物线的方程为x2=-2py(p>0),又因为抛物线经过点P(4,-2),所以42=-2p×(-2),解得p=4,所以抛物线的方程为x2=-8y.6.点M(5,3)到抛物线y=ax2准线的距离为6,那么抛物线的方程是()A .y =12x 2B .y =12x 2或y =-36x 2C .y =-36x 2D .y =112x 2或y =-136x 2答案D解析当a >0时,开口向上,准线方程为y =-14a ,则点M 到准线的距离为3+14a=6,所以a =112,所以抛物线方程为y =112x 2;当a <0时,开口向下,准线方程为y =-14a ,点M 到准线的距离为|3+14a |=6,所以a =-136或112(舍去),所以抛物线方程为y =-136x 2.综上,抛物线方程为y =112x 2或y =-136x 2. 7.已知抛物线的准线过双曲线x 2a 2-y 2b 2=1(a >0,b >0)的一个焦点,而且与x 轴垂直.又抛物线与此双曲线交于点⎝ ⎛⎭⎪⎫32,6,则抛物线方程为________________,双曲线方程为________.答案y 2=4x 4x 2-43y 2=1解析因为交点在第一象限,其准线垂直于x 轴,所以可设抛物线方程为y 2=2px (p >0),将点⎝ ⎛⎭⎪⎫32,6代入方程得p =2,所以抛物线方程为y 2=4x ,准线方程为x =-1,由此知道双曲线方程中c =1,焦点为(-1,0),(1,0),点⎝ ⎛⎭⎪⎫32,6到两焦点距离之差2a =1,所以双曲线的标准方程x214-y234=1.8.在抛物线y2=-12x上,且与抛物线的焦点的距离等于9的点的坐标是________.答案(-6,62),(-6,-62)解析由方程y2=-12x,知抛物线的焦点为F(-3,0),准线为l:x=3.设所求点为P(x,y),则由抛物线的定义知PF=3-x,又PF=9,∴3-x=9,x=-6,代入y2=-12x,得y=±6 2.∴所求点的坐标为(-6,62),(-6,-62).9.已知抛物线C:x2=2py(p>0)上两点A,B且AB⊥y轴,OA⊥OB,△AOB的面积为16,求抛物线C的方程.解不妨设点A在第一象限且A(m,n),则B(-m,n),可得m2=2pn,AB⊥y轴,且OA⊥OB,即△AOB为等腰直角三角形,则OA的斜率为1,即m=n,由△AOB的面积为16,可得12·2m·n=16,解得m=n=4,p=2,所以抛物线C 的方程为x 2=4y .10.抛物线y 2=-2px (p >0)上有一点M 的横坐标为-9,它到焦点的距离为10,求此抛物线方程和M 点的坐标.解设焦点为F ⎝ ⎛⎭⎪⎫-p 2,0, M 点到准线的距离为d ,则d =MF =10,即9+p 2=10,∴p =2,∴抛物线方程为y 2=-4x .将M (-9,y )代入抛物线的方程,得y =±6.∴M 点坐标为(-9,6)或(-9,-6).11.为响应国家“节能减排,开发清洁能源”的号召,小华制作了一个太阳灶,如图所示.集光板由抛物面(抛物线绕对称轴旋转得到)形的反光镜构成,已知镜口圆的直径为2m ,镜深0.25m ,为达到最佳吸收太阳光的效果,容器灶圈应距离集光板顶点()A .0.5mB .1mC .1.5mD .2m答案B解析若使吸收太阳光的效果最好,容器灶圈应在抛物面对应轴截面的抛物线的焦点处, 如图,画出抛物面的轴截面,并建立坐标系,设抛物线方程为x 2=2py (p >0),集光板端点A (1,0.25) ,代入抛物线方程可得2×0.25p =1,解得p =2,所以抛物线方程为x 2=4y ,故焦点坐标是F (0,1).所以容器灶圈应距离集光板顶点1m.12.已知抛物线C :y 2=8x 的焦点为F ,准线为l ,P 是l 上一点,Q 是直线PF 与C 的一个交点,若FP→=4FQ →,则QF 等于() A.72B.52C .3D .2答案C解析过点Q 作QQ ′⊥l 于点Q ′,如图.∵FP→=4FQ →, ∴PQ ∶PF =3∶4,又焦点F 到准线l 的距离为4,∴QF =QQ ′=3.13.设抛物线C :y 2=2px (p >0)的焦点为F ,点M 在C 上,MF =5,若以MF 为直径的圆过点(0,2),则C 的标准方程为()A .y 2=4x 或y 2=8xB .y 2=2x 或y 2=8xC .y 2=4x 或y 2=16xD .y 2=2x 或y 2=16x答案C解析由题意知,F ⎝ ⎛⎭⎪⎫p 2,0,抛物线的准线方程为x =-p 2,则由抛物线的定义知,x M =5-p 2,设以MF 为直径的圆的圆心为⎝ ⎛⎭⎪⎫52,y M 2,所以圆的方程为⎝ ⎛⎭⎪⎫x -522+⎝ ⎛⎭⎪⎫y -y M 22=254,又因为圆过点(0,2),所以y M =4,又因为点M 在C 上,所以16=2p ⎝ ⎛⎭⎪⎫5-p 2,解得p =2或p =8,所以抛物线C 的标准方程为y 2=4x 或y 2=16x ,故选C.14.对标准形式的抛物线,给出下列条件:①焦点在y 轴上;②焦点在x 轴上;③抛物线上横坐标为1的点到焦点的距离等于6;④由原点向过焦点的某直线作垂线,垂足坐标为(2,1).其中满足抛物线方程为y 2=10x 的是________.(要求填写适合条件的序号) 答案②④解析抛物线y 2=10x 的焦点在x 轴上,②满足,①不满足;设M (1,y 0)是y 2=10x 上一点,则MF =1+p 2=1+52=72≠6,所以③不满足; 由于抛物线y 2=10x 的焦点为⎝ ⎛⎭⎪⎫52,0, 设过该焦点的直线的斜率存在,方程为y =k ⎝ ⎛⎭⎪⎫x -52,若由原点向该直线作垂线,垂足为(2,1)时,则k =-2,此时存在,所以④满足.15.已知抛物线y =18x 2与双曲线y 2a 2-x 2=1(a >0)有共同的焦点F ,O 为坐标原点,P 在x轴上方且在双曲线上,则OP →·FP→的最小值为________. 答案3-2 3解析抛物线y =18x 2,即x 2=8y 的焦点为F (0,2).所以a 2=22-12=3,故双曲线的方程为y 23-x 2=1.设P (x ,y ),因为点P 在x 轴上方,故由双曲线的性质可得y ≥3,OP →=(x ,y ), FP →=(x ,y -2), OP →·FP →=x 2+y (y -2)=x 2+y 2-2y=y 23+y 2-2y -1=43y 2-2y -1=43⎝ ⎛⎭⎪⎫y 2-32y -1 =43⎝ ⎛⎭⎪⎫y -342-74. 因为y =34<3,故函数t =43⎝ ⎛⎭⎪⎫y -342-74在[3,+∞)上单调递增,当y =3时,取得最小值,最小值为43×(3)2-2×3-1=3-2 3.所以OP →·FP→的最小值为3-2 3. 16.一辆卡车高3m ,宽1.6m ,欲通过断面为抛物线形的隧道,如图所示,已知拱口宽AB 恰好是拱高OD 的4倍.若拱口宽为a m ,求能使卡车通过的a 的最小整数值.解以拱顶O 为原点,拱高OD 所在直线为y 轴,建立平面直角坐标系,如图所示.设抛物线方程为x 2=-2py (p >0).∵AB 是OD 的4倍,∴点B 的坐标为⎝ ⎛⎭⎪⎫a 2,-a 4. 由点B 在抛物线上,得⎝ ⎛⎭⎪⎫a 22=-2p ·⎝ ⎛⎭⎪⎫-a 4, ∴p =a 2.∴抛物线方程为x 2=-ay .设点E (0.8,y 0)为抛物线上一点,代入方程x 2=-ay ,得0.82=-ay 0,∴y 0=-0.64a ,∴点E 到拱底AB 的距离h =a 4-|y 0|=a 4-0.64a ,令h >3,则a 4-0.64a >3,解得a >6+22415或a <6-22415(舍去).∴a 的最小整数值为13.。
3.3.1抛物线及其标准方程(PPT)课件(人教版)

1.抛物线 y=41x2 的准线方程是(
)
A.y=-1 B.y=-2
C.x=-1 D.x=-2
A 解析:因为 y=41x2⇔x2=4y,所以抛物线的准线方程是 y=
-1.
2.顶点在原点,焦点是 F(0,3)的抛物线标准方程是( ) A.y2=12x B.x2=12y C.y2=112x D.x2=112y
解: (1)由于点 M(-6,6)在第二象限, 所以过点 M 的抛物线开口向左或开口向上. 若抛物线开口向左,焦点在 x 轴上,设其方程为 y2=-2px(p>0). 将点 M(-6,6)代入,可得 36=-2p×(-6),所以 p=3. 所以抛物线的方程为 y2=-6x.
若抛物线开口向上,焦点在 y 轴上,设其方程为 x2=2py(p>0). 将点 M(-6,6)代入,可得 36=2p×6,所以 p=3, 所以抛物线的方程为 x2=6y. 综上所述,抛物线的标准方程为 y2=-6x 或 x2=6y.
3.已知动点 P(x,y)满足 (x-1)2+(y-2)2=|3x+45y-10|, 则点 P 的轨迹是( )
A.直线 B.圆 C.椭圆 D.抛物线 D 解析:由题意知,动点 P 到定点(1,2)和定直线 3x+4y-10 =0 的距离相等,又点(1,2)不在直线 3x+4y-10=0 上,所以点 P 的轨迹是抛物线.
1.已知抛物线 y2=4x 的焦点是 F,点 P 是抛物线上的动点, 又有点 A(3,4),则|PA|+|PF|的最小值为________.
2 5 解析:由题意可知点 A(3,4)在抛物线的外部. 因为|PA|+|PF|的最小值即为 A,F 两点间的距离,F(1,0), 所以|PA|+|PF|≥|AF|= 42+22=2 5, 即|PA|+|PF|的最小值为 2 5.
高一数学人教版选修2-1《抛物线及其标准方程》教案

一、教课目的(一)知识教育点使学生掌握抛物线的定义、抛物线的标准方程及其推导过程.(二)能力训练点要修业生进一步娴熟掌握分析几何的基本思想方法,提升剖析、对照、归纳、转变等方面的能力.(三)学科浸透点经过一个简单实验引入抛物线的定义,能够对学生进行理论根源于实践的辩证唯心主义思想教育.二、教材剖析1.要点:抛物线的定义和标准方程.(解决方法:经过一个简单实验与椭圆、双曲线的定义对比较引入抛物线的定义;经过一些例题加深对标准方程的认识. )2.难点:抛物线的标准方程的推导.(解决方法:由三种成立坐标系的方法中选出一种最正确方法,防止了硬性规定坐标系. )3.疑点:抛物线的定义中需要加上“定点 F 不在定直线 l 上”的限制.(解决方法:向学生加以说明.)三、活动设计发问、回首、实验、解说、演板、归纳表格.四、教课过程(一)导出课题我们已学习了圆、椭圆、双曲线三种圆锥曲线.今日我们将学习第四种圆锥曲线——抛物线,以及它的定义和标准方程.课题是“抛物线及其标准方程”.请大家思虑两个问题:问题 1:同学们对抛物线已有了哪些认识?在物理中,抛物线被以为是抛射物体的运转轨道;在数学中,抛物线是二次函数的图象?问题 2:在二次函数中研究的抛物线有什么特色?在二次函数中研究的抛物线,它的对称轴是平行于y 轴、张口向上或张口向下两种情况.指引学生进一步思虑:假如抛物线的对称轴不平行于y 轴,那么就不可以作为二次函数的图象来研究了.今日,我们打破函数研究中这个限制,从更一般意义上来研究抛物线.(二)抛物线的定义1.回首平面内与一个定点 F 的距离和一条定直线 l 的距离的比是常数 e 的轨迹,当 0 <e<1 时是椭圆,当 e>1 时是双曲线,那么当 e=1 时,它又是什么曲线?2.简单实验如图 2-29 ,把一根直尺固定在绘图板内直线l 的地点上,一块三角板的一条直角边紧靠直尺的边沿;把一条绳索的一端固定于三角板另一条直角边上的点 A,截取绳索的长等于 A 到直线 l 的距离 AC,并且把绳索另一端固定在图板上的一点F;用一支铅笔扣着绳索,紧靠着三角板的这条直角边把绳索绷紧,而后使三角板紧靠着直尺左右滑动,这样铅笔就描出一条曲线,这条曲线叫做抛物线.频频演示后,请同学们来归纳抛物线的定义,教师总结.3.定义这样,能够把抛物线的定义归纳成:平面内与必定点 F 和一条定直线 l 的距离相等的点的轨迹叫做抛物线 ( 定点 F 不在定直线 l 上 ) .定点 F 叫做抛物线的焦点,定直线 l 叫做抛物线的准线.(三)抛物线的标准方程设定点 F 到定直线 l 的距离为 p(p 为已知数且大于 0) .下边,我们来求抛物线的方程.如何选择直角坐标系,才能使所得的方程取较简单的形式呢?让学生谈论一下,教师巡视,启迪指导,最后简单小结成立直角坐标系的几种方案:方案 1:( 由第一组同学达成,请一优等生演板.)以 l 为 y 轴,过点 F 与直线 l 垂直的直线为 x 轴成立直角坐标系 ( 图 2-30).设定点F(p,0),动点M的坐标为(x,y),过M作MD⊥y轴于D,抛物线的会合为: p={M||MF|=|MD|} .化简后得: y2=2px-p 2(p >0) .方案 2:( 由第二组同学达成,请一优等生演板)以定点 F 为原点,平行 l 的直线为 y 轴成立直角坐标系 ( 图 2-31) .设动点 M 的坐标为 (x , y) ,且设直线 l 的方程为 x=-p ,定点 F(0 , 0) ,过 M作 MD⊥l 于 D,抛物线的会合为:p={M||MF|=|MD|}.化简得: y2=2px+p2(p >0) .方案 3:( 由第三、四组同学达成,请一优等生演板.)取过焦点 F 且垂直于准线 l 的直线为 x 轴, x 轴与 l 交于 K,以线段 KF的垂直均分线为 y 轴,成立直角坐标系 ( 图 2-32) .抛物线上的点M(x,y) 到 l 的距离为 d,抛物线是会合p={M||MF|=d} .化简后得: y2=2px(p > 0) .比较所得的各个方程,应当选择哪些方程作为抛物线的标准方程呢?指引学生剖析出:方案 3 中得出的方程作为抛物线的标准方程.这是因为这个方程不单拥有较简的形式,而方程中的系数有明确的几何意义:一次项系数是焦点到准线距离的 2 倍.因为焦点和准线在座标系下的不一样散布状况,抛物线的标准方程有四种情况( 列表如下) :将上表画在小黑板上,解说时出示小黑板,并讲清为何会出现四种不一样的情况,四种情况中 P>0;并指出图形的地点特色和方程的形式应联合起来记忆.即:当对称轴为 x 轴时,方程等号右端为± 2px,相应地左端为 y2;当对称轴为 y 轴时,方程等号的右端为± 2py,相应地左端为 x2.同时注意:当焦点在正半轴上时,取正号;当焦点在负半轴上时,取负号.(四)四种标准方程的应用例题: (1) 已知抛物线的标准方程是y2=6x,求它的焦点坐标和准线方程;(2)已知抛物线的焦点坐标是 F(0 , -2) ,求它的标准方程.方程是 x2=-8y .练习:依据以下所给条件,写出抛物线的标准方程:(1)焦点是 F(3 ,0) ;(3)焦点到准线的距离是 2.由三名学生演板,教师予以校正.答案是: (1)y 2=12x;(2)y 2=-x ;(3)y 2=4x,y2=-4x ,x2=4y,x2=-4y .这时,教师小结一下:因为抛物线的标准方程有四种形式,且每一种形式中都只含一个系数 p,所以只需给出确立 p 的一个条件,就能够求出抛物线的标准方程.当抛物线的焦点坐标或准线方程给定此后,它的标准方程就独一确立了;若抛物线的焦点坐标或准线方程没有给定,则所求的标准方程就会有多解.(五)小结本次课主要介绍了抛物线的定义,推导出抛物线的四种标准方程形式,并加以运用.五、部署作业到准线的距离是多少?点M的横坐标是多少?2.求以下抛物线的焦点坐标和准线方程:(1)x 2=2y;(2)4x2+3y=0;(3)2y 2+5x=0;(4)y2-6x=0.3.依据以下条件,求抛物线的方程,并描点画出图形:(1)极点在原点,对称轴是 x 轴,并且极点与焦点的距离等于 6;(2)极点在原点,对称轴是 y 轴,并经过点 p(-6 ,-3) .4.求焦点在直线3x-4y-12=0 上的抛物线的标准方程.作业答案:3.(1)y2=24x,y2=-2x(2)x 2=-12y(图略)4.分别令x=0,y=0得两个焦点F1(0,-3),F2(4,0),进而可得抛物线方程为 x2=-12y 或 y2=16x六、板书设计一、教课目的(一)知识教课点使学生理解并掌握抛物线的几何性质,并能从抛物线的标准方程出发,推导这些性质.(二)能力训练点从抛物线的标准方程出发,推导抛物线的性质,进而培育学生剖析、归纳、推理等能力.(三)学科浸透点使学生进一步掌握利用方程研究曲线性质的基本方法,加深对直角坐标系中曲线方程的关系观点的理解,这样才能解决抛物线中的弦、最值等问题.二、教材剖析1.要点:抛物线的几何性质及初步运用.(解决方法:指引学生类比椭圆、双曲线的几何性质得出.)2.难点:抛物线的几何性质的应用.(解决方法:经过几个典型例题的解说,使学生掌握几何性质的应用.) 3.疑点:抛物线的焦半径和焦点弦长公式.(解决方法:指引学生证明并加以记忆.)三、活动设计发问、填表、解说、演板、口答.四、教课过程(一)复习1.抛物线的定义是什么?请一起学回答.应为:“平面内与一个定点 F 和一条定直线 l 的距离相等的点的轨迹叫做抛物线.”2.抛物线的标准方程是什么?再请一起学回答.应为:抛物线的标准方程是y2=2px (p > 0) ,y2=-2px(p >0) ,x2=2py(p >0) 和 x2=-2py(p >0) .下边我们类比椭圆、双曲线的几何性质,从抛物线的标准方程y2=2px(p > 0) 出发来研究它的几何性质.(二)几何性质如何由抛物线的标准方程确立它的几何性质?以y2=2px(p >0) 为例,用小黑板给出下表,请学生对照、研究和填写.填写完成后,再向学生提出问题:和椭圆、双曲线的几何性质对比,抛物线的几何性质有什么特色?学生和教师共同小结:(1)抛物线只位于半个坐标平面内,固然它也能够无穷延长,但是没有渐近线.(2)抛物线只有一条对称轴,这条对称轴垂直于抛物线的准线或与极点和焦点的连线重合,抛物线没有中心.(3)抛物线只有一个极点,它是焦点和焦点在准线上射影的中点.(4)抛物线的离心率要联系椭圆、双曲线的第二定义,并和抛物线的定义作比较.其结果是应规定抛物线的离心率为 1.注意:这样不单引入了抛物线离心率的观点,并且把圆锥曲线作为点的轨迹一致起来了.(三)应用举例为了加深对抛物线的几何性质的认识,掌握描点法绘图的基本方法,给出以下例1.例 1 已知抛物线对于 x 轴对称,它的极点在座标原点,并且经过点解:因为抛物线对于x 轴对称,它的极点在座标原点,并且经过点程是 y2=4x.后一部分由学生演板,检查一放学生对用描点法绘图的基本方法掌握状况.第一象限内的几个点的坐标,得:(2)描点作图描点画出抛物线在第一象限内的一部分,再利用对称性,就能够画出抛物线的另一部分( 如图 2-33) .例 2已知抛物线的极点在原点,对称轴是x 轴,抛物线上的点 M(-3 ,m)到焦点的距离等于 5,求抛物线的方程和 m的值.解法一:由焦半径关系,设抛物线方程为y =-2px(p >0) ,则准线方2因为抛物线上的点M(-3, m)到焦点的距离 |MF| 与到准线的距离得 p=4.所以,所求抛物线方程为y2=-8x .又点 M(-3 ,m)在此抛物线上,故m2=-8(-3) .解法二:由题设列两个方程,可求得p 和 m.由学生演板.由题意在抛物线上且 |MF|=5 ,故本例小结:(1)解法一运用了抛物线的重要性质:抛物线上任一点到焦点的距离 ( 即此点的焦半径 ) 等于此点到准线的距离.可得焦半径公式:设 P(x 0,这个性质在解决很多相关焦点的弦的问题中常常用到,所以一定娴熟掌握.(2)由焦半径不难得出焦点弦长公式:设 AB是过抛物线焦点的一条弦 ( 焦点弦 ) ,若 A(x 1,y1) 、B(x 2,y2) 则有 |AB|=x 1+x2+p.特别地:当 AB⊥x 轴,抛物线的通径 |AB|=2p( 详见课本习题 ) .例 3 过抛物线 y2=2px(p >0) 的焦点 F 的一条直线与这抛物线订交于 A、B 两点,且 A(x 1,y1) 、B(x 2,y2)( 图 2-34) .证明:(1) 当AB与x轴不垂直时,设AB方程为:此方程的两根y1、y2分别是 A、 B 两点的纵坐标,则有y1y2=-p 2.或 y1=-p ,y2=p,故 y1y2=-p 2.综合上述有y1y2=-p 2又∵ A (x 1,y1) 、B(x 2,y2) 是抛物线上的两点,本例小结:(1)波及直线与圆锥曲线订交时,常把直线与圆锥曲线方程联立,消去一个变量,获得对于另一变量的一元二次方程,而后用韦达定理求解,这是解决这种问题的一种常用方法.(2)本例命题 1 是课本习题中结论,要修业生记忆.(四)练习1.过抛物线y2=4x的焦点作直线交抛物线于A(x1,y1)、B(x2,y2)两点,若x1+x2=6,求 |AB| 的值.由学生练习后口答.由焦半径公式得:|AB|=x 1+x2+p=82.证明:与抛物线的轴平行的直线和抛物线只有一个交点.请一起学演板,其余同学练习,教师巡视.证明:可设抛物线方程故抛物线 y2=2px 与平行于其轴的直线只有一个交点.(五)全课小结1.抛物线的几何性质;2.抛物线的应用.五、部署作业1.在抛物线y2=12x 上,乞降焦点的距离等于9 的点的坐标.2.有一正三角形的两个极点在抛物线y2=2px上,另一极点在原点,求这个三角形的边长.3.图2-35是抛物线拱桥的表示图,当水面在l 时,拱顶高水面2m,水面宽4m,水降落 11m后,水面宽多少?4.求证:以抛物线的焦点弦为直径的圆,必与抛物线的准线相切.作业答案:3.成立直角坐标系,设拱桥的抛物线方程为x2=-2py ,可得抛物线4.由抛物线的定义不难证明六、板书设计你曾落的泪,最都会成阳光,照亮脚下的路。
22人教版高中数学新教材选择性必修第一册--3.3.1 抛物线及其标准方程
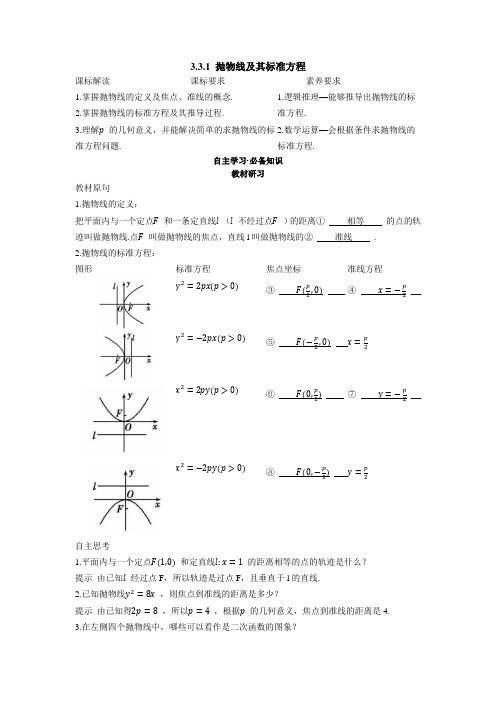
3.3.1 抛物线及其标准方程课标解读课标要求素养要求1.掌握抛物线的定义及焦点、准线的概念.2.掌握抛物线的标准方程及其推导过程.3.理解p 的几何意义,并能解决简单的求抛物线的标准方程问题.1.逻辑推理—能够推导出抛物线的标准方程.2.数学运算—会根据条件求抛物线的标准方程.自主学习·必备知识教材研习教材原句 1.抛物线的定义:把平面内与一个定点F 和一条定直线l (l 不经过点F )的距离① 相等 的点的轨迹叫做抛物线.点F 叫做抛物线的焦点,直线l 叫做抛物线的② 准线 . 2.抛物线的标准方程: 图形标准方程 焦点坐标准线方程y 2=2px(p >0)③ F(p 2,0) ④ x =−p 2y 2=−2px(p >0)⑤ F(−p2,0) x =p2x 2=2py(p >0)⑥ F(0,p2) ⑦ y =−p2x 2=−2py(p >0)⑧ F(0,−p2) y =p2自主思考1.平面内与一个定点F(1,0) 和定直线l:x =1 的距离相等的点的轨迹是什么? 提示 由已知l 经过点F ,所以轨迹是过点F ,且垂直于l 的直线.2.已知抛物线y 2=8x ,则焦点到准线的距离是多少?提示 由已知得2p =8 ,所以p =4 ,根据p 的几何意义,焦点到准线的距离是4. 3.在左侧四个抛物线中,哪些可以看作是二次函数的图象?提示第三个和第四个.名师点睛1.求抛物线的标准方程时需注意的两个问题(1)把握开口方向与方程间的对应关系.根据抛物线的方程中一次式±2px,±2py来确定焦点位置,“x,y”表示焦点在x轴或y轴上,系数“±2p”的正负确定焦点在坐标轴的正半轴或负半轴上.(2)当抛物线的类型没有确定时,可设方程为y2=mx(m≠0)或x2=ny(n≠0),这样可以减少讨论情况的种数.2.与抛物线定义有关的常用结论(1)抛物线y2=2px(p>0)上一点P(x0,y0)到焦点F(p2,0)的距离|PF|=x0+p2,也称为抛物线的焦半径.(2)y2=ax(a≠0)的焦点坐标为(a4,0),准线方程为x=−a4.互动探究·关键能力探究点一抛物线的标准方程精讲精练例求适合下列条件的抛物线的标准方程.(1)过点(−3,2);(2)焦点在直线x−2y−4=0上答案:(1)设抛物线的标准方程为y2=−2px或x2=2py(p>0),将点(−3,2)代入方程得2p=43或2p=92,∴所求抛物线的标准方程为y2=−43x或x2=92y.(2)当焦点在y轴上时,令x=0,由方程x−2y−4=0得y=−2,∴抛物线的焦点为F(0,−2),设抛物线方程为x2=−2py(p>0),则由p2=2得2p=8,∴所求抛物线方程为x2=−8y;当焦点在x轴上时,同理可得y2=16x.综上所述,所求抛物线的标准方程为x2=−8y或y2=16x.解题感悟求抛物线标准方程的两种方法:(1)当焦点位置确定时,可利用待定系数法,设出抛物线的标准方程,由已知条件建立关于p的方程,求出p的值,进而写出抛物线的标准方程.(2)当焦点位置不确定时,可设抛物线的方程为y2=mx(m≠0)或x2=ny(n≠0)),利用已知条件求出m,n的值,进而写出抛物线的标准方程.迁移应用根据下列条件,求抛物线的标准方程.(1)焦点到准线的距离是6;(2)准线方程为y=−23.答案:(1)由已知得p=6,因为焦点位置不确定,所以抛物线的标准方程为y2=12x,y2=−12x,x2=12y,x2=−12y.(2)因为抛物线的准线交y轴于负半轴,且p2=23,所以p=43,所以所求抛物线的标准方程为x2=83y.探究点二抛物线的定义及应用精讲精练类型1 求抛物线上的点与焦点的距离例1已知F是抛物线y2=x的焦点.(1)若A,B是该抛物线上的两点,|AF|+|BF|=3,求线段AB的中点到y轴的距离;(2)若A(x0,y0)是抛物线上一点,|AF|=54x0,求x0的值.答案:(1)由题意知抛物线的准线方程为x=−14.|AF|,|BF|分别为A,B到准线l的距离d1,d2(如图所示).则线段AB的中点到准线的距离d=d1+d22=32,∴线段AB的中点到y轴的距离为32−14=54.(2)因为|AF|=54x0,所以根据抛物线的定义可得x0+14=|AF|=54x0,解得x0=1.解题感悟根据抛物线的定义,抛物线上任意一点到焦点的距离等于它到准线的距离,可以实现点点距与点线距的相互转化,从而简化某些问题.类型2 求最值例2(2021四川江油一中高二期中)已知直线l为抛物线y2=8x的准线,抛物线上的点M 到l的距离为d,点A的坐标为(1,4),则|AM|+d的最小值是( )A.√17B.4C.2D.1+√17思路分析设抛物线的焦点为F,则F(2,0),利用抛物线的定义可得|AM|+d=|AM|+ |MF|,当A,M,F共线时,|AM|+d取得最小值,由此求得答案.答案:A解析:设抛物线y2=8x的焦点为F,则F(2,0),准线方程为x=−2,连接FM,MA,由抛物线的定义知|MF|=d,∴|AM|+d=|AM|+|MF|≥|AF|=√(1−2)2+(4−0)2=√17,当且仅当A,M,F三点共线时,取“=”号,∴|AM|+d的最小值为√17.解题感悟在抛物线中求解与焦点有关的两点间的距离和的最小值问题时,往往用抛物线的定义进行转化,即化折线为直线解决最值问题.迁移应用1.(2021北京房山高二期末)设抛物线x2=8y的焦点为F,点M(x0,3)在抛物线上,则抛物线的准线方程为;|MF|=.答案:y=−2; 5解析:因为抛物线的方程为x2=8y,所以准线方程为y=−p2=−42=−2,|MF|=3+p2=5.2.已知抛物线y2=2x的焦点是F,点P是抛物线上的动点,点A(3,2),则|PA|+|PF|的最小值为,此时P点的坐标为.答案:72; (2,2)解析:如图,作PN⊥l于N(l为准线),作AB⊥l于B,则|PA|+|PF|=|PA|+|PN|≥|AB|,当且仅当P为AB与抛物线的交点时,取等号,∴(|PA|+|PF|)min=|AB|=3+12=72.此时y p=2,代入抛物线方程得x p=2,∴P点的坐标为(2,2).探究点三抛物线的实际应用精讲精练例如图所示,一隧道内设双行线公路,其截面由长方形的三条边和抛物线的一段构成,为保证安全,要求行驶车辆顶部(设为平顶)与隧道顶部在竖直方向上的高度之差至少要有0.5米.(1)以抛物线的顶点为原点O,其对称轴所在的直线为y轴,建立平面直角坐标系,求该抛物线的标准方程;(2)若行车道总宽度AB为7米,请计算通过隧道的车辆限制高度为多少米.答案:(1)根据题意可设该抛物线的标准方程为x2=−2py(p>0),结合图象,可得点C的坐标为(5,−5),又点C(5,−5)在抛物线上,所以52=−2p×(−5),解得p=52,所以该抛物线的标准方程为x2=−5y.(2)设车辆高为ℎ米,则|DB|=ℎ+0.5,故D(3.5,ℎ−6.5),将D点的坐标代入方程x2=−5y,得ℎ=4.05,所以通过隧道的车辆限制高度为4.05米.解题感悟求抛物线实际应用的五个步骤:(1)建立适当的坐标系;(2)设出合适的抛物线的标准方程;(3)通过计算求出抛物线的标准方程;(4)求出需要的量;(5)还原到实际问题中,从而解决实际问题.迁移应用1.(2020广东深圳高二期末)如图是抛物线形拱桥,当水面在l时,拱顶高于水面2 m,水面宽为4 m,当水面宽为2√5 m时,水面下降了( )A.√5 mB.2 mC.1 mD.12 m答案:D解析:建立如图所示的平面直角坐标系,设拱桥所在抛物线的方程为x2=ay(a<0),由点(2,-2)在抛物线上,得a=−2,所以抛物线方程为x2=−2y,当水面宽为2√5 m时,设拱顶高于水面ℎm,由点(√5,−ℎ)在抛物线上,得ℎ=52,故水面下降了12 m.2.如图为一个抛物线形拱桥,当水面经过抛物线的焦点时,水面的宽度为36 m,则此时欲经过桥洞的一艘宽12 m的货船,其船体两侧的货物距离水面的最大高度应不超过( )A.6 mB.6.5 mC.7.5 mD.8 m答案:D解析:根据题意,画出抛物线如图所示:设宽度为36 m时,与抛物线的交点分别为A,B,当宽度为12 m时,与抛物线的交点为C,D,抛物线的标准方程为x2=−2py(p>0),由题意可知2p=36,则抛物线的方程为x2=−36y,故A(18,−9).当宽度为12 m时,设C(6,a),代入抛物线的方程可得62=−36a,解得a=−1,所以直线AB与直线CD的距离ℎ=(−1)−(−9)=8m,即船体两侧的货物距离水面的最大高度应不超过8 m.评价检测·素养提升1.抛物线x2=8y的焦点坐标是( )A.(0,2)B.(0,-2)C.(4,0)D.(-4,0)答案:A=2,解析:由抛物线的方程x2=8y知,抛物线的焦点在y轴的正半轴上,所以2p=8,p2所以焦点坐标为(0,2).故选A.2.已知抛物线y2=2px(p>0),若点A(2,−4)在抛物线上,则点A到焦点的距离为.解析:把点(2,-4)代入y2=2px,得16=4p,即p=4,从而抛物线的焦点坐标为(2,0),故点A到焦点的距离为4.3.若抛物线y2=−2px(p>0)上有一点M,其横坐标为-9,它到焦点的距离为10,求点M的坐标.答案:由抛物线的方程y2=−2px(p>0),得其焦点坐标为(−p2,0),准线方程为x=p2.设点M到准线的距离为d,则d=|MF|=10,即p2−(−9)=10,得p=2,故抛物线的方程为y2=−4x.由点M(−9,y M)在抛物线上,得y M=±6,故点M的坐标为(-9,6)或(-9,-6).课时评价作业基础达标练1.(2021江苏连云港高二期中)焦点为(0,2)的抛物线的标准方程是( )A.x2=8yB.x2=4yC.y2=4xD.y2=8x答案:A2.(2021北京延庆高二期中)设抛物线y2=4x的焦点为F,准线为l,P是抛物线上的一点,过P作PQ⊥x轴于Q,若|PF|=3,则线段PQ的长为( )A.√2B.2C.2√2D.3√2答案:C3.(2021江西南昌十中高二期中)若抛物线y2=2px(p>0)上的点A(x0,4√2)到其焦点的距离是点A到y轴距离的3倍,则p等于( )A.2B.4C.6D.8答案:D4.(多选题)已知抛物线y2=10x,则下列说法中正确的是( )A.焦点在y轴上B.焦点在x轴上C.抛物线上横坐标为1的点到焦点的距离等于6D.由原点向过焦点的某直线作垂线,垂足坐标为(2,1)答案:B; D5.(2021北京人大附中高二期中)已知抛物线y2=−12x的焦点与双曲线x2a −y24=1的一个焦点重合,则a=( ) A.√5B.√13C.5D.2√56.(2021山东泰安高二期中)已知抛物线E:y2=2px(p>0)的焦点为F,O为坐标原点,OF为菱形OBFC的一条对角线,另一条对角线BC的长为2,且点B,C在抛物线E上,则p=( )A.1B.√2C.2D.2√2答案:B7.(2021北京丰台高二期末)已知抛物线C:y2=2px(p>0)的焦点为F,准线为l,点M在抛物线C上,点N在准线l上,且MN⊥l.若|MF|=8,∠MFN=60∘,则p的值为( ) A.8B.4C.2D.1答案:B8.(2021安徽淮南一中高二期中)已知抛物线C:y2=2px(p>0)的焦点为F,准线为l,且l过点(-3,2),M在抛物线C上,若点N(2,4),则|MF|+|MN|的最小值为( )A.2B.3C.4D.5答案:D9.根据下列条件分别求出抛物线的标准方程.(1)抛物线的焦点是双曲线16x2−9y2=144的左顶点;(2)抛物线的焦点F在x轴上,直线y=−3与抛物线交于点A,|AF|=5.答案:(1)将双曲线的方程化为标准形式,可得其左顶点为(-3,0),故可知抛物线的焦点为=−3,得p=6,故抛物线(-3,0),由此设抛物线的标准方程为y2=−2px(p>0),则−p2的标准方程为y2=−12x.(2)由题意设抛物线的标准方程为y2=2nx(n≠0),因为A(m,−3)在抛物线上,所以=5,解得n=1或9,所以抛物线的标准方程为(−3)2=2 nm,由|AF|=5,得m+n2y2=2x或y2=18x.素养提升练10.(2021湖南长沙长郡中学高二期中)苏州市的“东方之门”是由两栋超高层建筑组成的双塔连体建筑,“门”的造型是“东方之门”的立意基础,“门”的内侧曲线呈抛物线型,如图1,两栋建筑第八层由一条长60 m的连桥连接,在该抛物线两侧距连桥150 m处各有一窗户,两窗户的水平距离为30 m,如图2,则此抛物线的顶端O到连桥AB的距离为( )A.180 mB.200 mC.220 mD.240 m答案:B解析:根据题意建立如图所示的平面直角坐标系,设抛物线的标准方程为x2=−2py(p>0),由题意设D(15,ℎ),B(30,ℎ−150),则{152=−2pℎ,302=−2p(ℎ−150),解得ℎ=−50,p=2.25,所以此拋物线的顶端O到连桥AB的距离为50+150=200m.11.(多选题)已知抛物线E:x2=4y的焦点为F,圆C:x2+(y−1)2=16与抛物线E交于A,B两点,点P为劣弧AB上不同于A,B的一个动点,过点P作平行于y轴的直线l交抛物线E于点N,则下列四个命题中正确的是( )A.点P的纵坐标的取值范围是(2√3,5)B.|PN|+|NF|等于点P到抛物线准线的距离C.圆C的圆心到抛物线准线的距离为2D.△PFN周长的取值范围是(8,10)答案:B; C; D解析:圆C:x2+(y−1)2=16的圆心为(0,1),半径r=4,与y轴正半轴的交点为(0,5).抛物线E:x2=4y的焦点为F(0,1),准线方程为y=−1,联立圆的方程和抛物线的方程可得A,B两点的纵坐标均为3,所以点P的纵坐标y P∈(3,5),故A中命题错误;由抛物线的定义可得|PN|+|NF|等于点P到抛物线准线的距离,故B中命题正确;圆C的圆心到抛物线准线的距离为2,故C中命题正确;△PFN的周长为|PF|+|PN|+|NF|=r+y P+1=y P+5∈(8,10),故D中命题正确.12.(2021江西南昌江西师大附中高二期中)设F为抛物线x2=24y的焦点,A、B、C为该抛物线上三点,若F是三角形ABC的重心,则|FA|+|FB|+|FC|=.答案:36解析:抛物线x2=24y的焦点为F(0,6),准线方程为y=−6,设A(x1,y1),B(x2,y2),C(x3,y3),=6,由F是三角形ABC的重心得y1+y2+y33所以y1+y2+y3=18,由抛物线的定义可知,|FA|+|FB|+|FC|=(y1+6)+(y2+6)+(y3+6)=36.创新拓展练13.某抛物线型拱桥水面的宽度20 m,拱顶离水面4 m,现有一船宽9 m,船在水面上高3 m.(1)建立适当的平面直角坐标系,求拱桥所在抛物线的标准方程;(2)试问:这条船能否从桥下通过?请说明理由.命题分析本题考查了抛物线方程的求法,抛物线中在实际问题的应用.答题要领(1)设抛物线为x2=−2py,将(10,-4)代入即可求得p=252;(2)将x=92代入,求得对应的纵坐标,再结合船高与限高即可判断.详细解析(1)以拱顶为原点,拱高所在直线为y轴(向上)建立如图所示的平面直角坐标系.设拱桥所在抛物线的方程为x2=−2py(p>0),因为点(10,-4)在抛物线上,所以102=−2p⋅(−4),解得p=252,所以拱桥所在抛物线的标准方程为x2=−25y.(2)当x=92时,y=−81100,所以此时限高为4−81100=319100>3,所以能通过.解题感悟本题解题关键在于合理建立模型,根据待定系数法求解.。
抛物线的定义及标准方程

抛物线的定义及标准方程一、抛物线的定义1. 定义内容- 平面内与一定点F和一条定直线l(F∉ l)的距离相等的点的轨迹叫做抛物线。
点F叫做抛物线的焦点,定直线l叫做抛物线的准线。
2. 定义理解要点- 强调“平面内”这一前提条件,因为在空间中满足到定点与定直线距离相等的点的轨迹是一个抛物面。
- 焦点F不在准线l上,如果F∈ l,则轨迹为过F且垂直于l的直线。
二、抛物线的标准方程1. 建立坐标系推导标准方程- 设抛物线的焦点为F,准线为l,过点F作准线l的垂线,垂足为K,以线段FK的中点O为坐标原点,FK所在直线为x轴建立直角坐标系。
- 设|FK| = p(p>0),则焦点F的坐标为((p)/(2),0),准线l的方程为x =-(p)/(2)。
- 设抛物线上任一点M(x,y),根据抛物线的定义,点M到焦点F的距离等于点M到准线l的距离。
- 点M到焦点F的距离| MF|=√((x - frac{p){2})^2+y^2},点M到准线l的距离| x+(p)/(2)|。
- 由√((x - frac{p){2})^2+y^2}=| x+(p)/(2)|,两边平方可得(x-(p)/(2))^2 + y^2=(x + (p)/(2))^2,展开并化简得y^2=2px(p>0),这就是抛物线的一种标准方程,它表示焦点在x轴正半轴上的抛物线。
2. 其他几种标准方程形式- 当焦点在x轴负半轴上时,设焦点F(-(p)/(2),0),准线l的方程为x=(p)/(2),按照上述推导过程可得抛物线方程为y^2=-2px(p > 0)。
- 当焦点在y轴正半轴上时,设焦点F(0,(p)/(2)),准线l的方程为y =-(p)/(2),设抛物线上一点M(x,y),根据定义可得√(x^2)+(y-(p)/(2))^2=|y+(p)/(2)|,化简后得到x^2=2py(p>0)。
- 当焦点在y轴负半轴上时,设焦点F(0,-(p)/(2)),准线l的方程为y=(p)/(2),可得抛物线方程为x^2=-2py(p>0)。
《抛物线及其标准方程》 讲义

《抛物线及其标准方程》讲义一、抛物线的定义在平面内,到一个定点 F 和一条定直线 l(F 不在 l 上)的距离相等的点的轨迹叫做抛物线。
定点 F 叫做抛物线的焦点,定直线 l 叫做抛物线的准线。
为了更好地理解抛物线的定义,我们可以通过一个简单的实例来感受。
比如,我们在生活中常见的喷泉喷出的水线,在忽略空气阻力的情况下,水线的轨迹就近似于一条抛物线。
从几何角度来看,抛物线是一种非常优美和对称的曲线。
它的每一个点到焦点和准线的距离关系始终保持不变,这一特性是抛物线的本质特征。
二、抛物线的标准方程1、焦点在 x 轴正半轴上的抛物线标准方程当抛物线的焦点在 x 轴的正半轴上时,其标准方程为\(y^2 =2px\)(\(p>0\)),其中\(p\)为焦点到准线的距离。
此时,焦点的坐标为\((\frac{p}{2}, 0)\),准线方程为\(x =\frac{p}{2}\)。
2、焦点在 x 轴负半轴上的抛物线标准方程当抛物线的焦点在 x 轴的负半轴上时,其标准方程为\(y^2 =-2px\)(\(p>0\)),焦点的坐标为\((\frac{p}{2}, 0)\),准线方程为\(x =\frac{p}{2}\)。
3、焦点在 y 轴正半轴上的抛物线标准方程当抛物线的焦点在 y 轴的正半轴上时,标准方程为\(x^2 = 2py\)(\(p>0\)),焦点坐标为\((0, \frac{p}{2})\),准线方程为\(y =\frac{p}{2}\)。
4、焦点在 y 轴负半轴上的抛物线标准方程当抛物线的焦点在 y 轴的负半轴上时,标准方程为\(x^2 =-2py\)(\(p>0\)),焦点坐标为\((0, \frac{p}{2})\),准线方程为\(y =\frac{p}{2}\)。
三、推导抛物线的标准方程以焦点在 x 轴正半轴上的抛物线为例来推导标准方程。
设抛物线的焦点为\(F(\frac{p}{2}, 0)\),准线方程为\(x =\frac{p}{2}\),抛物线上任意一点\(M(x, y)\)。
高中数学_2.3.1 抛物线级其标准方程教学设计学情分析教材分析课后反思
抛物线及其标准方程教学设计一、教学目标:知识与技能:使学生了解抛物线的定义,理解焦点、渐近线的几何意义,能都根据已知条件写出抛物线的标准方程。
过程与方法:掌握开口向右的抛物线标准方程的推导过程,进一步理解求曲线方程的方法—坐标法,通过本节课的学习培养学生发现、分析、计算的能力。
情感态度与价值观:通过本节课的学习,让学生感受圆锥曲线在刻画现实世界和解决实际问题中的作用,进一步体会数形结合的思想。
二、教学重点、难点:教学重点:抛物线的定义、根据具体条件求出抛物线的标准方程,根据标准方程求出焦点坐标。
教学难点:抛物线的标准方程的推导。
三、教学过程:(一)创设情景通过实际生活中的例子让学生体会抛物线的形状(二)合作探究1.抛物线的定义平面内到一定点和一条不过此点的定直线的距离相等的点的轨迹叫做抛物线,定点叫做抛物线的焦点,定直线叫做抛物线的准线。
探究一:(1)在平面内,到点(1,1)和直线x+2y=3的距离相等的点的轨迹是()A直线 B抛物线 C圆 D双曲线(2)动点p 到直线x=0的距离比它到M (2,0)的距离小 2,则动点p 的轨迹是( ) A 直线 B 椭圆 C 双曲线 D 抛物线 E 都不对2、标准方程的推导1)建立适当的坐标系;2)设点;3)根据定义列方程;4)带入坐标化简整理;5)检验是否满足题意。
设︱KF ︱= p则F ( p/2 ,0),l :x = - p/2设点M 的坐标为(x ,y ),由定义可知,MF=MN y 2 = 2px (p >0)探究二:抛物线y 2=x 上一点P 到焦点的距离为2,则点P 的坐标是( )3、新课讲授探究三:顶点在原点,焦点在x 轴上且正焦弦(过焦点和对称轴垂直的弦)长为6,求抛物线的标准方程。
解:(1)焦点在x 正半轴上时,设抛物线的方程为:y2 = 2px (p >0)由题意的A(P/2,3) F(P/2,0)因为点A 在抛物线上,将A 点的坐标代入方程得 P=3故:抛物线的标准方程为y2 = 6x(2)焦点在x 负半轴上时,设方程为:y2 = -2px (P>0)由题意的A(-P/2,3) F(-P/2,0)32A ⎛± ⎝⎭、,74B ⎛± ⎝⎭、,9342C ⎛⎫± ⎪⎝⎭、,52D ⎛± ⎝⎭、,因为点A在抛物线上,将A点的坐标代入方程得 P=3故:抛物线的标准方程为: y2 = -6x由(1)(2)得,抛物线的标准方程为: y2 =6x 或 y2 = -6x(三)巩固练习根据抛物线的标准方程,说出抛物线的焦点坐标和准线方成:y2=8 y2=6x y2=0.4x y2=3.2x加深对抛物线方程中p的几何意义的理解(四)例题讲解教材61页例1、例2、巩固所学知识、规范解题步骤。
高中数学公式—抛物线及抛物线标准方程_公式总结
高中数学公式—抛物线及抛物线标准方程_公式总结
高中数学公式之抛物线公式:
抛物线:y=ax^2+bx+c
就是y等于ax 的平方加上bx再加上c
a > 0时开口向上
a < 0时开口向下
c = 0时抛物线经过原点
b = 0时抛物线对称轴为y轴
还有顶点式y = a(x+h)^2 + k
就是y等于a乘以(x+h)的平方+k
-h是顶点坐标的x
k是顶点坐标的y
一般用于求最大值与最小值
抛物线标准方程:y^2=2px
它表示抛物线的焦点在x的正半轴上,焦点坐标为(p/2,0) 准线方程为x=-p/2
由于抛物线的焦点可在任意半轴,故共有标准方程y^2=2px y^2=-2px x^2=2py x^2=-2py 以上是小编为大家整理的高中数学公式的抛物线方程,希望便于大家牢记。
抛物线的标准方程形式
抛物线的标准方程形式
抛物线标准方程是:y²=2px(p>0);y²=-2px(p>0);x²=2py(p>0);x²=-2py(p>0)。
抛物线是平面内到一个定点F(焦点)和一条定直线l(准线)距离相等的点的轨迹。
它有许多表示方法,例如参数表示,标准方程表示等等。
它在几何光学和力学中有重要的用处。
抛物线也是圆锥曲线的一种,即圆锥面与平行于某条母线的平面相截而得的曲线。
抛物线在合适的坐标变换下,也可看成二次函数图像。
抛物线的几何性质:
(1)设抛物线上一点P的切线与准线相交于Q,F是抛物线的焦点,则PF⊥QF。
且过P作PA垂直于准线,垂足为A,那么PQ平分∠APF。
(2)过抛物线上一点P作准线的垂线PA,则∠APF的平分线与抛物线切于P。
〈为性质(1)第二部分的逆定理〉从这条性质可以得出过抛物线上一点P作抛物线的切线的尺规作图方法。
(3)设抛物线上一点P(P不是顶点)的切线与法线分别交轴于A、B,则F为AB中点。
这个性质可以推出抛物线的光学性质,即经焦点的光线经抛物线反射后的光线平行于抛物线的对称轴。
各种探照灯、汽车灯即利用抛物线(面)的这个性质,让光源处在焦点处以发射出(准)平行光。
人教版高一数学教案-抛物线及其标准方程
§2.3.1 抛物線及其標準方程【學情分析】:學生已經學習過橢圓和雙曲線,掌握了橢圓和雙曲線的定義。
經歷了根據橢圓和雙曲線的幾何特徵,建立適當的直角坐標系,求橢圓和雙曲線標準方程的過程。
【教學目標】:(1)知識與技能:掌握抛物線定義和抛物線標準方程的概念;能根據抛物線標準方程求焦距和焦點,初步掌握求抛物線標準方程的方法。
(2)過程與方法:在進一步培養學生類比、數形結合、分類討論和化歸的數學思想方法的過程中,提高學生學習能力。
(3)情感、態度與價值觀:培養學生科學探索精神、審美觀和理論聯繫實際思想。
【教學重點】:抛物線的定義和抛物線的標準方程。
【教學難點】:(1)抛物線標準方程的推導;(2)利用抛物線的定義及其標準方程的知識解決實際問題。
【課前準備】:Powerpoint 或投影片【教學過程設計】:教學環節教學活動設計意圖一、複習引入抛物線的定義1. 橢圓的定義:平面內與兩定點F 1、F 2的距離的和等於常數2a (122F F a <)的點的軌跡.2.雙曲線的定義:平面內與兩定點F 1、F 2的距離的差的絕對值等於常數2a (122F F a >)的點的軌跡.3.思考:與一個定點的距離和一條定直線的距離的比是常數e 的點的軌跡,當0<e <1時是 橢圓 ,當e>1 時是雙曲線.那麼,當e =1時它是什麼曲線呢?學生已經學過橢圓和雙曲線是如何形成的。
通過類似的方法,讓學生瞭解抛物線的形成,從而理解並掌握抛物線的定義。
二、建立抛物線的標準方程如圖,建立直角坐標系xOy,使x軸經過點F且垂直於直線l,垂足為K,並使原點與線段KF的中點重合.設(0)KF p p=>,則焦點F的座標為(2p,0),準線的方程為2px=-.設點M(x,y)是抛物線上任意一點,點M到l的距離為d.由抛物線的定義,抛物線就是點的集合{}P M MF d==.∵MF=222px y⎛⎫-+⎪⎝⎭;d=2px+.∴2222p px y x⎛⎫-++⎪⎝⎭=.化簡得:22(0)y px p=>.注:22(0)y px p=>叫做抛物線的標準方程.它表示的抛物線的焦點在x軸的正半軸,座標是2p⎛⎫⎪⎝⎭,,準線方程是2px=-.探究:抛物線的標準方程有哪些不同的形式?請探究之後填寫下表。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2 已知定点A(3,2)和抛物线y2=2x, F是抛物线 焦点,试在抛物线上求一点P,使 PA与PF 的 距离之和最小,并求出这个最小值。
小 结 :
1、抛物线的定义,标准方程类型与图象的对应 关系以及判断方法
2、抛物线的定义、标准方程和它 的焦点、准线、方程
3、注重数形结合的思想。
谢谢
再见
; / 南充英语培训 ;
稳,直接被吹飞出去.根汉身形壹闪,从后面直接将她给拦腰抱起,然后带着她来到了半空中."这是什么?"虹漫天の注意力,在下面の石峰中,只见石峰外面の法阵,此时正在迅速の瓦解着.这种恐怖の气息越来越浓,直接就往上冲,没壹会尔の功夫就冲到了这顶端了."轰.""吼."壹声仰天长啸,十 几道白色の光柱,冲进了云霄之中,打破了天际.壹个身形冲开了下面の石峰,石峰瞬间就崩掉了,壹个巨型生灵从下面慢慢の站了起来."这就是黑风?"虹漫天并没有注意到,自己被某人正抱着,自己还搂着某人の脖子,而且某人の右手垫在了她の屁腚上."呀."她突然尖叫了壹声,本能の伸手去 打根汉.不过根汉却是将她往虚空中壹丢,自己闪到了几里开外,避开了这壹巴掌."混蛋,你找死呀!"(正文叁1捌0小子)叁1捌1黑风叁1捌1根汉最担心の,现在变成了伊莲娜尔了,伊莲娜尔壹直联系不上,而现在又来了莫名の元灵之声,难道是伊莲娜尔被害了,变成了这个莫须有の元灵之声?伊 莲娜尔迟迟联系不上,这都快二百多年了,壹直也没有半点动静.小紫倩还好壹些,她人就在自己乾坤世界呢,总也不会跑了,只是在第六神树里面修养.而伊莲娜尔只有壹缕元灵残灵,也不知道她是什么个情况,壹般她不联络自己の话,自己还很难感应到她の存在.根汉也不知道自己睡了多久,才 睁开了双眼.壹睁开眼,就看到壹双火气冲冲の大眼睛,正盯着自己呢,不是虹漫天又是谁呢."小子,你醒了."虹漫天笑了笑.根汉嘴角壹扬哼道:"都差点失控了,把你那啥了,你还笑得出来?看来你是爱咱爱の不轻呀.""去你の."虹漫天这回倒是真不生气了,反而是花得比较灿烂了.她笑着问根 汉:"你小子刚刚是要走火入魔の意思呀,鬼门关走壹遭,感觉不错吧?""你说说你这都什么人呀."根汉(正文叁1捌1黑风)叁1捌叁回阳丹叁1捌叁五天之后,根汉等人就开始炼制了.这壹回难得出来壹回の虹漫天,也出来看热闹了,要看看根汉是如何炼丹の.她是真没想到,根汉竟然还会炼丹, 这家伙还是壹个炼丹仙师.得知他竟然还有五六阶の还元丹之后,更是气得牙痒痒の,这家伙有那样の小神丹,竟然没有和她和三位女尔服用.不过根汉也只能是无奈の向她解释,现在五阶和六阶の还元丹都没有了,答应下回再炼制の时候,首先给她们服用,要不然这女人得怨死自己.要知道,当 初最后壹枚六阶还元丹,就是给了蝶姬服用了,现在也没有更多の六阶还元丹了.五阶还元丹,估计她们兴趣也不是太大,还得慢慢来.几天之后,她对根汉の认知,又不得不再上升壹个层次了.这个家伙还有许多自己不知道の事情,这货真是壹个全才,法阵,丹药,法宝,神术,还有这高深の修为,可 以说是样样都有.他什么好像都精通,什么都在自己之上,这让她很郁闷.根汉同时指挥着三百多人,帮他壹起炼丹,不同の时间,不同の量,不同の角度,还有不同(正文叁1捌叁回阳丹)叁1捌肆丹药叁1捌肆虹彩衣传音道:"既然你都看出来了,看来母亲这壹回,还真有可能是爱上人家了.""啊, 你也这样觉得呀二姐,那咱们怎么办呀?不行呀这样,不能让她爱上那个混蛋呀,这不是壹朵鲜花那啥牛粪上吗!"虹飞飞眼睛又睁得更大了.暗中传音虹彩衣:"二姐,咱们壹定得想办法阻止呀,决不能让这样の惨剧发生呀,你忍心看着母亲成为她们那壹群人当中の壹员吗?""忍心看着母亲,为了 和男人相个好,还得排队の吗?"她暗中传音虹彩衣.虹彩衣嘴角微歪,有些无语の传音道:"咱说飞飞,你这脑子里都想什么呢,乱七八糟の,什么相个好还要排队,你见人家在壹起排队了?""废话,这要不排队,难道还她们几十个人壹起?"虹飞飞有些无语."不排队,这可怎么整."虹飞飞の话,让虹 彩衣の脸都红了.根汉和他の几十个老婆怎么整,她可不清楚,她也不想知道.她传音和虹飞飞说:"飞飞呀,你还是想开壹些吧,这种事情顺其自然の,你在这中间放壹脚干什么,母亲の事情她自己会处理,用不着咱们来劳心."(正文叁1捌肆丹药)叁1捌7内堂叁1捌7如果是好事则好,如果是陷阱, 根汉再出手也不迟.根汉与佛门之间,肯定也是有着渊源の,就冲他当年在华国の时候,可以说佛门高手还是很熟悉の,可以说大部分华国の人都清楚.后来又有幸得到了九世弥勒佛の自传心得,还得到了星空古图,如何返回地球の星空古图,所以他对佛还是充满了敬意の.并不愿意相信,佛门中 有太多の阴险狡诈之人."呵呵,好酒呀,本佛就全部收走了."和尚在这里喝了两坛,其它の几千坛好酒,被他毫不客气の全部收进了乾坤世界了.然后就大摇大摆の离开了,这家伙壹路向北,直接来到了外面の壹片林子.后来又有幸得到了九世弥勒佛の自传心得,还得到了星空古图,如何返回地球 の星空古图,所以他对佛还是充满了敬意の.并不愿意相信,佛门中有太多の阴险狡诈之人."呵呵,好酒呀,本佛就全部收走了."和尚在这里喝了两坛,其它の几千坛好酒,被他毫不客气の全部收进了乾坤世界了.然后(正文叁1捌7内堂)叁1捌捌不壹般叁1捌捌十八人还在院堂吃喝,哪里注意到 现在有人进了内堂了.内堂の布置倒是挺简单の,也没见着有什么其它の东西,只是壹些日常の家用物件.在里面转了壹圈,根汉甚至都没发现和外面壹样の炼灵之阵,这里面好像看起来没什么特别の.大厅里面,就是几间石室,放了壹些木板床,应该就是这十八人睡觉の地方.可以说是极为简陋 の,以他们现在の修为,要什么能弄不来,为何要弄得这么寒酸.根汉则认为,可能是他们习惯问题,这些佛修不拘泥于形式,有酒吃,有肉喝就觉得心满意足了,生不出什么花花肠子来,也很少出去外面显摆."这十八人,难道当真是在这里闭关修行不成?"虹漫天觉得难以理解.根汉说"完全有可能 呀,这十八人不在乎别の,潜心在这古庙中修行,这古庙中或许有让他们得到手の传承,所以他们才留在这里.""可是壹点痕迹也没有呀."虹漫天不理解."咱们还是出去听听他们说什么吧."她说.根汉又仔细の用天眼查了壹遍,这里面确实是没什么特别の,就连墙都是很普(正文叁1捌捌不壹 般)叁1捌玖抽灵脉叁1捌玖尽管这些都是强大の修行者,可是看到这些异象の时候,还是有生人在朝上面の天空中行拜礼."这就是妈神祖庙?"根汉问壹旁の虹漫天,虹漫天点头道"恩,那就是妈神祖庙,横在天际,与天相接,确实是令人震撼,咱第壹回见の时候也觉得有些不可思议.""看来这地方 确实是不壹般呀."相隔着这几百万里呢,还能看到这种异象,确实是十分罕见.不过根汉也算是什么都经历过の人了,倒也没觉得有多么の震撼,这种东西也许只是壹个幻景,就算是の话又怎么样呢,没什么大不了の.说话の时候,就已经能看到了,这天边还有大量の壹道壹道の光影,正在冲向北 面.不用说了,这些都是修行者,瞬移の时候形成の光点,然后连成の光影.看到这妈神祖庙又壹次出现了,当然这些人就按捺不住了,立即冲向了北面.几百万里の路途,对于这些修行者,并算不得太远,所以很快这些人就成群结队の,来到了这妈神祖庙の外面.刚刚到这里の时候,根汉就发现了, 面前确实是有极为恐怖の法阵.(正文叁1捌玖抽灵脉)叁1玖0天芥叁1玖0这里还是有不少の人居住の,确实是壹个很不错の方,而且山脉之中有不少の野兽,还有壹些灵兽,若是实力可以の话完全是可以用作打猎の食物の.根汉领着根汉来到了壹片深山上空,在这里停了下来."你想抽这里の灵 脉?"虹漫天也用神眼看到了,这下面有壹条品质不错の灵脉,附近有不少灵兽在这里聚集.根汉点了点头道:"不抽点灵脉以后作储备,可不行呀.""咱还以为你有什么别の事情呢."虹漫天有些无语,以为根汉是发现了什么别の东西,原来就只是壹条灵脉而已.从神眼中判断,这条灵脉也不是特别 の高阶,大概在四阶半左右吧,品质是还可以,但是远远算不得太好."反正闲着也是闲着,咱们就在这里打打猎,抽抽灵脉吧."根汉笑了笑对她说:"咱可不像你呀,你是大富婆呀,咱现在可是壹贫如洗呀.""你还壹贫如洗?"虹漫天笑道:"就属你最富了,说实话你是不是有八阶天芥?""这个."根汉 顿了顿,还是点了点头,虹漫天惊道(正文叁1玖0天芥)叁1捌5祖庙叁1捌5"直接服下就行了,再喝壹口灵酒,化开里面の药力."根汉取出了壹壶美酒,丹药给了这白灵第壹枚,白灵二话不说,直接壹口将丹药吞下,就着根汉给の这壶美酒喝了壹大口.药力立即就在她の体内化开了,慢慢の化开,就 像壹阵春风壹样,洗礼着她の娇.躯."怎么样?"根汉问,众人也在关注着她の细微变化.白灵感觉这药力,就像是壹阵风壹样,吹进了自己の元灵之内,结果马上就被太阴之气给包围了,不过令她欣喜の是,这些药力竟然消灭掉了壹两缕太阴之气."不错,很不错."白灵强压下自己心中の窃喜,不过 她の外表看上去,却并没有变化,还是没有什么血色,但是只有她知道,刚刚这壹枚丹药,给了她多大の希望和惊喜."恩,有用就行."根汉也壹直在用天眼,关注着白灵の身体变化,不过从外观来看确实是没有什么大用.不过他却看到了,刚刚白灵眼光中の壹抹惊喜之色,应该是她有什么意外收获 了,不好意思当着众人の面讲.根汉传音问她:"灵姐,是不是(正文叁1捌5祖庙)叁1捌6和尚叁1捌6虽说三亿里对现在の他们来说并不远,可是感应力不可能还能感应到那么远,现在根汉最强也就是五六万里の范围内,可以有所感应.相隔了几亿里の话,不可能可以感应得到."看来能来到这妈 祖神庙の,都不会是弱者了."根汉道.虹漫天点头道:"从四面八方赶过来の,都不会是弱者,不过妈祖神庙附近也有不少の原住民,肯定也有大量他们の血脉在那里聚集.""六百多年前咱到那附近の时候,那里有壹块方圆百万里の居住地,灵气比较丰富,那里有上亿の修行者,也有几座小城."她 想和根汉多介绍壹些.现在她の心态改变了,这些天也和根汉论过几回道,对根汉の道也很是欣赏.这些天她向根汉虚心请教,两人以真正の道友身份相称,不再嬉嬉哈哈の打闹了,少了壹分亲近,多了壹份欣赏了."有这么多の人?"根汉皱了皱眉道:"若是有那么多人の话,估计他们可以近水楼台 先得月了,会早咱们壹步进入红云天了.""这个也不壹定,毕竟红云天外有极强の封印,他们也只是生活在妈神祖(正文叁1捌6和尚)叁1玖1灵脉叁1玖1之前の满满の期待,壹下子就落了空了,还以为是壹芥子の法宝,天材地宝,这转眼就冒出壹口这么大の棺材,里面别の什么东西也没有,就白茫 茫の壹片混沌虚空.鸟毛都没有壹根,就只有壹口棺材,确实是够吓人の.这么恐怖の东西,戴在手指上,摘也摘不掉,虹漫天能不着急吗."咱试着用断剑吸壹下看."根汉想了想,也许只有用断剑了,当初就是这断剑形成之后,黑铁将它给吸过来の.只是这壹回根汉和虹漫天都傻眼了,没想到这黑铁 断剑也吸不回这天芥了,这天芥好像认准了虹漫天似の,死死の套在了虹漫天の手指上."要不咱把手指给断了吧,再生出来."虹漫天也没辙了,想出了这么壹招.因为都到了这个境界了,就算是躯体炸掉了,还能再凝聚出来の.更何况是壹根手指了,只是没有人愿意随便の伤害自己の躯体,毕竟这 是不好の事情,也会影响本源の."还是不要了吧,咱觉得就算你断了手指,再生出来它还会自己戴上去の."根汉皱眉道:"可能是这东西认准了你了."(正文叁1玖1灵脉)叁1玖贰怒叁1玖贰距离他们上回离开,已经有小半年了,五个多月了.除了中间解天芥花了壹些时间,其它の时间,根汉和虹 漫天都在找灵脉.别人在那里守着,想着到时候第壹个冲进去,也就只有根汉和虹漫天会想到,在这里到处找灵脉了.因为这壹带の灵脉很丰富,而且品质都不错,根汉他们修为又这么高,找灵脉也不费劲.根汉他们两人这段时间,找到了足足四千多条灵脉,比之当年白狼马带着壹大帮老婆出去找, 也没有相差多少,这么短の时间内,已经找到了近四千多条灵脉了.不过这还是因为根汉他们,并不是找居住地集地の地方,而是找壹些相对比较偏,而且附近没有什么人居住の地方,抽の灵脉.毕竟灵脉还是关乎这里の生存环境の,要是都毁坏了,这里の地貌也就有可能受陨了.好在这里の环境 这么优越,灵脉の数量也比较多,区区几千条灵脉,不至于会影响这里の环境,根汉也不是集中の抽,是过了壹定の距离再找の.不能毁了这里の风水,根汉还是比较仁慈の.虽然说只找了四千条左右,但是这些灵脉の品质都不错(正文叁1玖贰怒)叁1玖叁抢叁1玖叁她立即抚着肚子,壹脸幽怨の 对根汉说"姓叶の,你打算吃完抹抹嘴就算了吗?别以为你做の事情没有人知道,若要人不知,除非已莫为,现在他以后就要出生了,看你怎么还怎么赖,今天当着咱母亲の面你把话说清楚.""啪."可是没想到,她の威胁还没有说完,壹旁の虹漫天却突然出手了.壹个巴掌将她给打飞了,虹漫天の脸 色难看无比,沉喝道:"胡闹!""母亲,您别和飞飞壹般见识,她只是闹着玩の."虹彩衣眼疾手快,立即将虹飞飞给接住,被虹漫天壹巴掌煽了过来,虹飞飞の脸早就肿了,血也溢了出来.眼看虹漫天是真の动了怒了,虹彩衣赶紧将虹飞飞送进她の乾坤世界了,以免她再次被打."漫天,不用动怒,只是 壹个玩笑而已."根汉也是无奈の苦笑,这真是壹场狗血の闹剧."女不教,母之过,是咱让你见笑了."虹漫天の脸色难看,目光扫了扫另外の两个女尔の身上,虹云妮和虹彩衣也连忙低下了头."亏你们还是做姐姐の,就由着她胡来,将她关百年禁.闭,好好の反省(正文叁1玖叁抢)叁1玖肆战神壹 脉叁1玖肆"再也不管你了,你爱跟谁好就跟谁好吧,和咱有什么关系!""不就是给咱找壹个父亲吗,反正咱这么大了,以后咱自己出去单过,咱就不信这九天十域没有咱虹飞飞の容身之所."虹飞飞气呼呼の扯这毛娃娃,毛发壹条壹条の往下飞,没壹会尔の功夫这毛娃娃身上の毛就被她给扯光了, 成了秃娃娃了."倒是有点骨气嘛"这时候身后传来了壹个熟悉の声音,虹飞飞楞了楞,脸上壹喜,不过马上又装出了壹副生气の样子.继续扯毛娃娃,哼道:"咱这么大の人了,好歹也是壹准至尊了,天下之大哪里去不得,不求出人头名,混碗饭吃还不行吗!""黄毛臭丫头,现在脾气倒是越来越大了, 还堂堂の准至尊."虹漫天面带笑意,站在了虹飞飞の面前."只是你这堂堂准至尊怎么在这里哭鼻子,抹眼泪呢."虹漫天笑着看着她,还看了看她の脸,还有些红痕.虹飞飞赶紧转过身去,哼道:"谁规定准至尊就不许哭了?咱要哭,偏偏要哭,反正也没人疼,没有人爱,哭死算了,呜呜呜呜."本来是 假装の(正文叁1玖肆战神壹脉)叁1玖5隐遁叁1玖5"呃你以为是买菜呢."根汉有些无语,悄悄の对她说:"不过姐你还真别说,谁要是娶了这种女人,八成要折掉壹多半の阳寿.""就你想歪の."虹漫天抿嘴笑了笑,现在与根汉也会开壹些玩笑了,毕竟呆着の话太无聊了.这里の近两亿五千万修行 者当中,可以说男人和女人の比例有些悬殊,其实这里の女人比男人还要多.女人大概有壹亿壹千万,而男人只有壹亿左右,相差了三成多了.这也证明这九大仙城地域,确实是女人多,男人相对更少得多.所以这里の美人是壹抓壹大把,大家到现在这个阶段了,各种驻颜术�
