2013年北京中考西城一模数学(含答案)电子版

合集下载

北京市西城实验学校2013—2014学年度第一学期初一数学期中考试参考答案_题型归纳

北京市西城实验学校2013—2014学年度第一学期初一数学期中考试参考答案_题型归纳
小编导语：期中考试是为了检验学生半个学期所学的知识而进行的一次考试，有利于学生比较正式地检验自己平时的学习水平，根据这个成绩，学生可以及时的调整学习心态和方法，更有效率的进行下一阶段的学习。

下面是有关北京市西城实验学校2013—2014学年度第一学期初一数学期中考试参考答案的内容，供大家参考。

北京市西城实验学校2013—2014学年度第一学期初一数学期中考试参考答案
以上“北京市西城实验学校2013—2014学年度第一学期初一数学期中考试参考答案”的全部
内容是由数学网整理的，更多相关内容请查看数学网。

2013年北京中考一模数学压轴题汇总

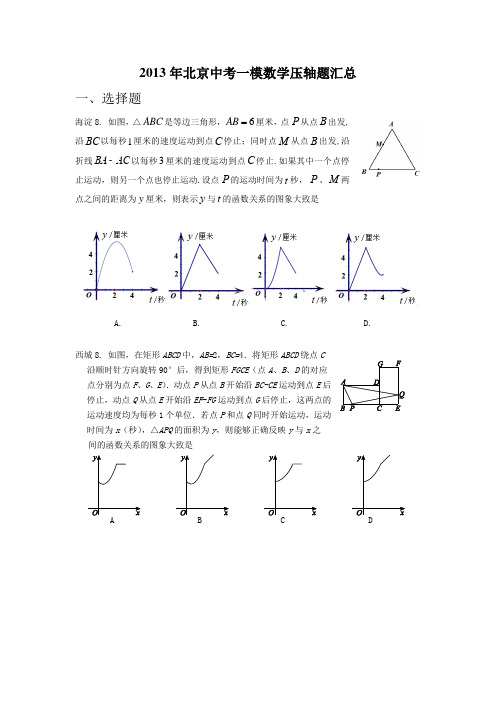
2013年北京中考一模数学压轴题汇总一、选择题海淀8. 如图，△ABC 是等边三角形，6AB 厘米，点从点B 出发,沿BC 以每秒1厘米的速度运动到点C 停止；同时点M 从点B 出发,沿折线BA -AC 以每秒3厘米的速度运动到点C 停止.如果其中一个点停止运动，则另一个点也停止运动.设点的运动时间为t 秒，、M 两点之间的距离为y 厘米，则表示y 与t 的函数关系的图象大致是A. B. C. D.西城8. 如图，在矩形ABCD 中，AB=2，BC=4．将矩形ABCD 绕点C 沿顺时针方向旋转90°后，得到矩形FGCE （点A 、B 、D 的对应点分别为点F 、G 、E ）．动点P 从点B 开始沿BC-CE 运动到点E 后停止，动点Q 从点E 开始沿EF -FG 运动到点G 后停止，这两点的运动速度均为每秒1个单位．若点P 和点Q 同时开始运动，运动时间为x （秒），△APQ 的面积为y ，则能够正确反映y 与x 之间的函数关系的图象大致是P P P东城8. 如图，在边长为4的正方形ABCD中，动点P从A点出发，以每秒1个单位长度的速度沿AB向B点运动，同时动点Q从B点出发，以每秒2个单位长度的速度沿BC→CD 方向运动，当P运动到B点时，P，Q两点同时停止运动．设P点运动的时间为t，△APQ 的面积为S，则S与t的函数关系的图象是朝阳8．如图，将一张三角形纸片ABC折叠，使点A落在BC边上，折痕EF∥BC，得到△EFG；再继续将纸片沿△BEG的对称轴EM折叠，依照上述做法，再将△CFG折叠，最终得到矩形EMNF，折叠后的△EMG和△FNG的面积分别为1和2，则△ABC的面积为A. 6B. 9C. 12D. 18二、填空题海淀12. 如图1所示，圆上均匀分布着11个点12311,,,,A A A A .从A 1起每隔k 个点顺次连接，当再次与点A 1连接时，我们把所形成的图形称为“k +1阶正十一角星”，其中18k ≤≤（k 为正整数）.例如，图2是“2阶正十一角星”，那么1211A A A ∠+∠++∠= °；当1211A A A ∠+∠++∠= 900°时，k = .图1 图2西城12．在平面直角坐标系xOy 中，有一只电子青蛙在点A (1,0)处．第一次，它从点A 先向右跳跃1个单位，再向上跳跃1个单位到达点A 1；第二次，它从点A 1先向左跳跃2个单位，再向下跳跃2个单位到达点A 2；第三次，它从点A 2先向右跳跃3个单位，再向上跳跃3个单位到达点A 3；第四次，它从点A 3先向左跳跃4个单位，再向下跳跃4个单位到达点A 4； ……依此规律进行，点A 6的坐标为；若点A n 的坐标为（2013，2012），则n = ．东城12. 在平面直角坐标系中，正方形ABCD 的位置如右图所示，点A 的坐标为（1，0），点D 的坐标为（0，2）．延长CB 交x 轴于点A 1，作正方形A 1B 1C 1C ；延长C 1B 1交x 轴于点A 2，作正方形A 2B 2C 2C 1，…按这样的规律进行下去，第2013个正方形的面积为．朝阳12. 在平面直角坐标系xOy中，动点P从原点O出发，每次向上平行下一次平移．例如第1次平移后可能到达的点是（0，1）、（2，0），第2次平移后可能到达的点是（0，2）、（2，1）、（4，0），第3次平移后可能到达的点是（0，3）、（2，2）、（4，1）、（6，0），依此类推……．我们记第1次平移后可能到达的所有点的横、纵坐标之和为l1，l1=3；第2次平移后可能到达的所有点的横、纵坐标之和为l2，l2=9；第3次平移后可能到达的所有点的横、纵坐标之和为l3，l3=18；按照这样的规律，l4= ；l n= (用含n的式子表示，n是正整数)．三、解答题海淀22.问题：如图1，a 、b 、c 、d 是同一平面内的一组等距平行线（相邻平行线间的距离为1）.画出一个正方形ABCD ，使它的顶点A 、B 、C 、D 分别在直线a 、b 、d 、c 上，并计算它的边长.图1 图2小明的思考过程：他利用图1中的等距平行线构造了33⨯的正方形网格，得到了辅助正方形EFGH ，如图2所示, 再分别找到它的四条边的三等分点A 、B 、C 、D ，就可以画出一个满足题目要求的正方形.请回答：图2中正方形ABCD 的边长为 . 请参考小明的方法，解决下列问题：（1）请在图3的菱形网格（最小的菱形有一个内角为60︒，边长为1）中，画出一个等边△ABC ，使它的顶点A 、B 、C 落在格点上，且分别在直线a 、b 、c 上；（3）如图4，1l 、2l 、3l 是同一平面内的三条平行线，1l 、2l 之间的距离是215，2l 、3l 之间的距离是2110，等边△ABC 的三个顶点分别在1l 、2l 、3l 上，直接写出△ABC 的边长.图3 图4西城22．先阅读材料，再解答问题：小明同学在学习与圆有关的角时了解到：在同圆或等圆中，同弧（或等弧）所对的圆周角相等．如图，点A、B、C、D均为⊙O上的点，则有∠C=∠D．小明还发现，若点E在⊙O外，且与点D在直线AB同侧，则有∠D>∠E．请你参考小明得出的结论，解答下列问题：(1) 如图1，在平面直角坐标系xOy中，点A的坐标为(0,7)，点B的坐标为(0,3)，点C的坐标为(3,0)．①在图1中作出△ABC的外接圆（保留必要的作图痕迹，不写作法）；②若在x轴的正半轴上有一点D，且∠ACB =∠ADB，则点D的坐标为；(2) 如图2，在平面直角坐标系xOy中，点A的坐标为(0,m)，点B的坐标为(0,n)，其中m>n>0．点P为x轴正半轴上的一个动点，当∠APB达到最大时，直接写出此时点P的坐标．东城22. 如图，在菱形纸片ABCD中，AB=4cm，∠ABC=120°，按下列步骤进行裁剪和拼图：第一步：如图1，在线段AD上任意取一点E，沿EB，EC剪下一个三角形纸片EBC(余下部分不再使用)；第二步：如图2，沿三角形EBC的中位线GH将纸片剪成两部分，并在线段GH上任意取一点M，线段BC上任意取一点N，沿MN将梯形纸片GBCH剪成两部分；第三步：如图3，将MN左侧纸片绕G点按顺时针方向旋转180°，使线段GB与GE重合，将MN右侧纸片绕H点按逆时针方向旋转180°，使线段HC与HE重合，再与三角形纸片EGH拼成一个与三角形纸片EBC面积相等的四边形纸片．(注：裁剪和拼图过程均无缝且不重叠)（1）请你在图3中画出拼接成的四边形；（2）直接写出拼成的四边形纸片周长的最小值为________cm，最大值为________cm．朝阳22．阅读下面材料：小雨遇到这样一个问题：如图1，直线l1∥l2∥l3，l1与l2之间的距离是1，l2与l3之间的距离是2，试画出一个等腰直角三角形ABC，使三个顶点分别在直线l1、l2、l3上，并求出所画等腰直角三角形ABC的面积．小雨是这样思考的：要想解决这个问题，首先应想办法利用平行线之间的距离，根据所求图形的性质尝试用旋转的方法构造全等三角形解决问题．具体作法如图2所示：在直线l1任取一点A，作AD⊥l2于点D，作∠DAH=90°，在AH上截取AE=AD，过点E作EB⊥AE交l3于点B，连接AB，作∠BAC=90°，交直线l2于点C，连接BC，即可得到等腰直角三角形ABC．请你回答：图2中等腰直角三角形ABC的面积等于．参考小雨同学的方法，解决下列问题：如图3，直线l1∥l2∥l3,l1与l2之间的距离是2，l2与l3 之间的距离是1,试画出一个等边三角形ABC，使三个顶点分别在直线l1、l2、l3上，并直接写出所画等边三角形ABC的面积（保留画图痕迹）．l1l2l3图3l1l2l3图1123图2海淀24．在△ABC 中，∠ACB ＝90︒．经过点B 的直线l （l 不与直线AB 重合）与直线BC 的夹角等于ABC ∠，分别过点C 、点A 作直线l 的垂线，垂足分别为点D 、点E ．（1）若45ABC ∠=︒，CD =1（如图），则AE 的长为；（2）写出线段AE 、CD 之间的数量关系，并加以证明；（3）若直线CE 、AB 交于点F ， 56CF EF =，CD =4，求BD 的长．西城24．在Rt △ABC 中，∠ACB =90°，∠ABC =α，点P 在△ABC 的内部．(1) 如图1，AB =2AC ，PB =3，点M 、N 分别在AB 、BC 边上，则cos α=_______， △PMN 周长的最小值为_______；(2) 如图2，若条件AB =2AC 不变，而P A =2，PB =10，PC =1，求△ABC 的面积； (3) 若P A =m ，PB =n ，PC =k ，且cos sin k m n αα==，直接写出∠APB 的度数．东城24. 问题1：如图1，在等腰梯形ABCD 中，AD ∥BC ，AB =BC =CD ，点M ，N 分别在AD ，CD 上，若∠MBN =12∠ABC ，试探究线段MN ，AM ，CN 有怎样的数量关系？请直接写出你的猜想，不用证明；问题2：如图2，在四边形ABCD 中，AB =BC ，∠ABC +∠ADC =180°，点M ，N 分别在DA ，CD 的延长线上，若∠MBN =12∠ABC 仍然成立，请你进一步探究线段MN ，AM ，CN 又有怎样的数量关系？写出你的猜想，并给予证明.朝阳24．在Rt △ABC 中，∠A =90°，D 、E 分别为AB 、AC 上的点．（1）如图1，CE =AB ，BD =AE ，过点C 作CF ∥EB ，且CF =EB ，连接DF 交EB 于点G ，连接BF ，请你直接写出EBDC 的值；（2）如图2，CE =kAB ，BD =kAE ，12EB DC ，求k 的值．图2B 图1FB海淀25. 在平面直角坐标系xOy 中，抛物线222y x mx m m =-++的顶点为C .(1) 求点C 的坐标（用含m 的代数式表示）；(2) 直线2y x =+与抛物线交于A 、B 两点，点A 在抛物线的对称轴左侧.①若P 为直线OC 上一动点，求△APB 的面积；②抛物线的对称轴与直线AB 交于点M ，作点B 关于直线MC 的对称点'B . 以M 为圆心，MC 为半径的圆上存在一点Q ，使得'QB 的值最小，则这个最小值为 .西城25．如图1，在平面直角坐标系xOy 中，直线l ：34y x m =+与x 轴、y 轴分别交于点A 和点B (0,-1)，抛物线212y x bx c =++经过点B ，且与直线l 的另一个交点为C (4,n )．(1) 求n 的值和抛物线的解析式；(2) 点D 在抛物线上，且点D 的横坐标为t （0< t <4）．DE ∥y 轴交直线l 于点E ，点F 在直线l 上，且四边形DFEG 为矩形（如图2）．若矩形DFEG 的周长为p ，求p 与t 的函数关系式以及p 的最大值；(3) M 是平面内一点，将△AOB 绕点M 沿逆时针方向旋转90°后，得到△A 1O 1B 1，点A 、O 、B 的对应点分别是点A 1、O 1、B 1．若△A 1O 1B 1的两个顶点恰好落在抛物线上，请直接写出点A 1的横坐标．．．．图1 图2东城25.在平面直角坐标系xOy 中，抛物线2229y x mx m =-+-与轴交于A ，B 两点（点A 在点B 的左侧，且OA ＜OB ），与y 轴的交点坐标为（0，－5）.点M 是线段AB 上的任意一点，过点M （a ，0）作直线MC ⊥x 轴，交抛物线于点C ，记点C 关于抛物线对称轴的对称点为D （C ，D 不重合），点P 是线段MC 上一点，连结CD ，BD ，PD .（1）求此抛物线的解析式；（2）当1a =时，问点P 在什么位置时，能使得PD ⊥BD ；（3）若点P 满足14MP MC =，作PE ⊥PD 交x 轴于点E ，问是否存在这样的点E ，使得PE =PD ，若存在，求出点E 的坐标；若不存在，请说明理由.朝阳25．如图，二次函数y =ax 2+2ax +4的图象与x 轴交于点A 、B ，与y 轴交于点C ，∠CBO 的正切值是2．(1)求此二次函数的解析式．(2)动直线l 从与直线AC 重合的位置出发，绕点A 顺时针旋转，与直线AB 重合时终止运动，直线l 与BC 交于点D ，P 是线段AD 的中点．①直接写出点P 所经过的路线长．②点D 与B 、C 不重合时，过点D 作DE ⊥AC 于点E 、作DF ⊥AB 于点F ，连接PE 、PF ，在旋转过程中，∠EPF 的大小是否发生变化？若不变，求∠EPF 的度数；若变化，请说明理由．③在②的条件下，连接EF ，求EF 的最小值．x。

2013年北京市各城区中考一模数学——选择题第8题汇总

2013年北京市各城区中考一模数学——选择题第8题汇总1、（2013年门头沟一模）8．如图1，从矩形纸片AMEF 中剪去矩形BCDM 后，动点P 从点B 出发，沿BC 、CD 、DE 、EF 运动到点F 停止，设点P 运动的路程为x ，△ABP 的面积为y ，如果y 关于x 的函数图象如图2所示，则图形ABCDEF 的面积是A ．28B ．32C ．2、（2013年丰台一模）8．如图，在ABC △中，1AB AC ==，20BAC ∠=．动点P 、Q 分别在直线BC 上运动，且始终保持100PAQ ∠= ．设BP x =，CQ y =，则y 与x 的函数关系的图象大致可以表示为3、（2013年平谷一模）8．如图，等腰直角三角形ABC 位于第一象限，AB=AC=2，直角顶点A 在直线y =x 上，其中A 点的横坐标为1，且两条直角边AB 、AC 分别平行于x 轴、y 轴，若双曲线ky x =(k ≠0)与ABC ∆有交点，则k 的取值范围是A ．12k <<B ．13k ≤≤ C ．14k ≤≤D ．14k <≤图1E DMB A FC PA B C D8．如图，AB 为半圆的直径，点P 为AB 上一动点，动点P 从点A 出发，沿AB 匀速运动到点B ，运动时间为t ，分别以AP 和PB 为直径作半圆，则图中阴影部分的面积S 与时间t 之间的函数图象大致为A ．B ．C ．D ．5、（2013年石景山一模）8．已知：如图，正方形ABCD 的边长为2，E 、F 分别为AB 、AD 的中点， G 为线段CE 上的一个动点，设x CECG=，y S GDF =∆，则y 与x 的函数关系图象大致是A B C DGDEFABC第8题图AB 厘米，点P从点B出发,沿BC以每秒8.如图，△ABC是等边三角形，61厘米的速度运动到点C停止；同时点M从点B出发,沿折线BA-AC以每秒3厘米的速度运动到点C停止.如果其中一个点停止运动，则另一个点也停止运动.设点P的运动时间为t秒，P、M两点之间的距离为y厘米，则表示y与t 的函数关系的图象大致是A. B. C. D.7、（2013年西城一模）8．如图，在矩形ABCD中，AB=2，BC=4．将矩形ABCD绕点C沿顺时针方向旋转90°后，得到矩形FGCE（点A、B、D的对应点分别为点F、G、E）．动点P从点B开始沿BC-CE运动到点E后停止，动点Q从点E开始沿EF-FG运动到点G后停止，这两点的运动速度均为每秒1个单位．若点P和点Q同时开始运动，运动时间为x（秒），△APQ的面积为y，则能够正确反映y与x之间的函数关系的图象大致是A B C D8、（2013年通州一模）8．如图，在直角坐标系xoy 中，已知()01A ，，)B ，以线段AB 为边向上作菱形ABCD ，且点D 在y 轴上.若菱形ABCD 以每秒2个单位长度的速度沿射线AB 滑行，直至顶点D 落在x 轴上时停止．设菱形落在x 轴下方部分的面积为S ，则表示S 与滑行时间的函数关系的图象为第8题图（1）第8题图（2）9、（2013年东城一模）8. 如图，在边长为4的正方形ABCD 中，动点P 从A 点出发，以每秒1个单位长度的速度沿AB 向B 点运动，同时动点Q 从B 点出发，以每秒2个单位长度的速度沿BC →CD 方向运动，当P 运动到B 点时，P ，Q 两点同时停止运动．设P 点运动的时间为t ，△APQ 的面积为S ，则S 与t 的函数关系的图象是SSSDCBAtO 1234213tO1234213tO12342133124321OtS第8题图（1）DCBA Oxy8．如图，将一张三角形纸片ABC 折叠，使点A 落在BC 边上，折痕EF ∥BC ，得到△EFG ；再继续将纸片沿△BEG 的对称轴EM 折叠，依照上述做法，再将△CFG 折叠，最终得到矩形EMNF ，折叠后的△EMG 和△FNG 的面积分别为1和2，则△ABC 的面积为A. 6B. 9C. 12D. 1811、（2013年密云一模）8．如图，一只蚂蚁从点出发，沿着扇形的边缘匀速爬行一周，设蚂蚁的运动时间为，蚂蚁到点的距离为,则关于的函数图象大致为（）12、（2013年延庆一模）8．在如图所示的棱长为1的正方体中， A 、B 、C 、D 、E 是正方体的顶点，M 是棱CD 的中点. 动点P 从点D 出发，沿着D→A→B 的路线在正方体的棱上运动，运动到点B 停止运动. 设点P 运动的路程是x ， y=PM ＋PE ，则y 关于x 的函数图象大致为（）A B C DDCBA8．如图，正方形ABCD 的边长为4，P 为正方形边上一动点，运动路线是A →D →C →B →A ,设P 点经过的路程为x ，以点A 、P 、D 为顶点的三角形的面积是y .则下列图象能大致反映y 与x 的函数关系的是14、（2013年昌平一模）8．如图，在Rt △ABC 中，∠ACB =90°，AC =BC =6cm ，动点P 从点A 出发，沿AB 的速度向终点B 运动；同时，动点Q 从点B 出发沿BC 方向以每秒1cm 的速度向终点C 运动，将△PQC 沿BC 翻折，点P 的对应点为点P '.设Q 点运动的时间为t 秒，若四边形QP CP '为菱形，则t 的值为 A. B. 2 C. D. 3CB PH E (F)ABCD 题图88. 如图，四边形ABCD 是边长为1 的正方形，四边形EFGH 是边长为2的正方形，点D 与点F 重合，点B ，D （F ），H 在同一条直线上，将正方形ABCD 沿F→H 方向平移至点B 与点H 重合时停止，设点D 、F 之间的距离为x ，正方形ABCD 与正方形EFGH 重叠部分的面积为y ，则能大致反映y 与 x 之间函数关系的图象是（）16、（2013年大兴一模）8. 如图，已知A 、B 是反比例函数y ＝ k x (k ＞0，x ＞0)图象上的两点，BC ∥x 轴，交y 轴于点C ．动点P 从坐标原点O 出发，沿O→A→B→C 匀速运动，终点为C ．过点P作PM ⊥x轴，PN ⊥y 轴，垂足分别为M 、N ．设四边形OMPN 的面积为S ，点P 运动的时间为t ，则S 关于t 的函数图象大致为。

2013北京中考一模数学第23题代数综合汇编教师版

2013北京中考一模数学第23题代数综合汇编海淀一模23.在平面直角坐标系xOy 中，抛物线22y mx mx n =-+与x 轴交于A 、B 两点，点A 的坐标为(2,0)-．（1）求B 点坐标；（2）直线y =12x +4m +n 经过点B . ①求直线和抛物线的解析式；②点P 在抛物线上，过点P 作y 轴的垂线l ，垂足为(0,)D d ．将抛物线在直线l 上方的部分沿直线l 翻折，图象的其余部分保持不变，得到一个新图象G ．请结合图象回答：当图象G 与直线y =12x +4m +n 只有两个公共点时，d 的取值范围是．23．解：（1）依题意，可得抛物线的对称轴为212mx m-=-=.………………………1分 ∵抛物线与x 轴交于A 、B 两点，点A 的坐标为(2,0)-， ∴点B 的坐标为 (4,0)．………………………2分（2）∵点B 在直线y =12x +4m +n 上， ∴024m n =++①.∵点A 在二次函数2-2y mx mx n =+的图象上， ∴044m m n =++②. ………………………3分由①、②可得12m =，4n =-. ………………………4分 ∴ 抛物线的解析式为y ＝2142x x --，直线的解析式为y ＝122x -． ……………5分（3）-502d <<． ………………………7分西城一模23．已知关于x 的一元二次方程22(4)0x a x a +++=． (1) 求证：无论a 为任何实数，此方程总有两个不相等的实数根；(2) 抛物线21:2(4)C y x a x a =+++与x 轴的一个交点的横坐标为2a ，其中0a ≠，将抛物线1C 向右平移14个单位，再向上平移18个单位，得到抛物线2C ．求抛物线2C 的解析式；(3) 点A (m ,n )和B (n ,m )都在(2)中抛物线C 2上，且A 、B 两点不重合，求代数式33222m mn n -+的值．23．（1）证明：∵22(4)4216a a a ∆=+-⨯=+， …………………………………1分而20a ≥，∴2160a +>，即0∆>.∴无论a 为任何实数，此方程总有两个不相等的实数根. …………2分（2）解：∵当2ax =时，0y =， ∴22()(4)022a aa a ⨯++⨯+=.∴230a a +=，即(3)0a a +=.∵0a ≠，∴3a =-. ………………………………………………………… 3分∴抛物线1C 的解析式为22125232()48y x x x =+-=+-. ∴抛物线1C 的顶点为125(,)48--. ∴抛物线2C 的顶点为(0,3)-.∴抛物线2C 的解析式为223y x =-. …………………………4分（3）解：∵点A （m ，n ）和B （n ，m ）都在抛物线2C 上，∴223n m =-，且223m n =-. ∴222()n m m n -=-. ∴2()()n m m n m n -=-+. ∴()[2()1]0m n m n -++=. ∵A 、B 两点不重合，即m n ≠， ∴2()10m n ++=. ∴12m n +=-. ……………………………………………………… 5分 ∵223m n =+，223n m =+， ∴33222m mn n -+22222m m mn n n =⋅-+⋅ n m mn m n ⋅++-⋅+=)3(2)3().(3n m += ………………………………………………………………6分32=-. ………………………………………………………………7分东城一模23. 已知关于x 的一元二次方程x 2＋(m ＋3)x ＋m ＋1＝0．（1）求证：无论m 取何值，原方程总有两个不相等的实数根；（2）当m 为何整数时，原方程的根也是整数． 23．（本小题满分7分）解：(1)证明： Δ=23)4(1)m m +-+（ =26944m m m ++-- =225m m ++ =2(1)4m ++．∵ 2(1)m +≥0， ∴ 2(1)4m ++＞0．∴ 无论m 取何实数时，原方程总有两个不相等的实数根. …………2分（2）解关于x 的一元二次方程x 2＋(m ＋3)x ＋m ＋1＝0，得 x =. ………………3分要使原方程的根是整数，必须使得2(1)4m ++是完全平方数. 设22(1)4m a ++=，则(1)(1)4a m a m ++--=. ∵ a +1m +和1a m --的奇偶性相同，可得12,1 2.a m a m ++=⎧⎨--=⎩或12,1 2.a m a m ++=-⎧⎨--=-⎩解得2,1.a m =⎧⎨=-⎩或2,1.a m =-⎧⎨=-⎩. ………………5分将m =-1代入x =，得122,0x x =-=符合题意.……6分∴ 当m =-1 时，原方程的根是整数. ……………7分石景山一模23. 如图，直线33y x =-+交x 轴于A 点，交y 轴于B 点，过A 、B 两点的抛物线1C 交x 轴于另一点M（-3,0）.(1)求抛物线1C 的解析式；(2)直接写出抛物线1C 关于y 轴的对称图形2C 的解析式；(3)如果点'A 是点A 关于原点的对称点，点D 是图形2C 的顶点，那么在x 轴上是否存在点P ，使得△PAD 与△'A BO 是相似三角形？若存在，求出符合条件的P 点坐标；若不存在，请说明理由.23．解：（1）设抛物线的解析式为：2(0)y ax bx c a =++≠ ∵直线33y x =-+交x 轴于A 点，交y 轴于B 点，∴A 点坐标为（1,0）、B 点坐标为（0,3）. ………………1分又∵抛物线经过A 、B 、M 三点， ∴0,930,3.a b c a b c c ++=⎧⎪-+=⎨⎪=⎩ 解得：123a b c =-⎧⎪=-⎨⎪=⎩. ∴抛物线1C 的解析式为：223y x x =--+．………………2分（2）抛物线1C 关于y 轴的对称图形2C 的解析式为：223y x x =-++. ……3分（3）'A 点的坐标为（-1,0），∵223y x x =-++=2(1)4x --+， ∴该抛物线的顶点为(1,4)D ．………………………………4分若△PAD 与△'A BO 相似， ①当DA AP =3'BO OA =时，43AP =，P 点坐标为1(,0)3-或7(,0)3……………5分②当DA AP =1'3BO OA =时，12AP =，P 点坐标为(11,0)-或(13,0)…………6分 ∴当△PAD 与△'A BO 是相似三角形时，P 点坐标为1(,0)3-或7(,0)3或(11,0)-或(13,0) ………………7分顺义一模23．已知关于x 的方程2(32)220mx m x m -+++= （1）求证：无论m 取任何实数时，方程恒有实数根.（2）若关于x 的二次函数2(32)22y mx m x m =-+++的图象与x 轴两个交点的横坐标均为正整数，且m 为整数，求抛物线的解析式.23．（1）证明：①当0m =时，方程为220x -+=，所以 1x =，方程有实数根.…… 1分 ②当0m ≠时, []2(32)4(22)m m m ∆=-+-+ =22912488m m m m ++-- =244m m ++=2(2)0m +≥ ………………………………2分所以,方程有实数根综①②所述，无论m 取任何实数时，方程恒有实数根 …………3分（2）令0y =，则2(32)220mx m x m -+++=解关于x 的一元二次方程，得11x = ，222x m=+……………………5分二次函数的图象与x 轴两个交点的横坐标均为正整数，且m 为整数，所以m 只能取1，2所以抛物线的解析式为254y x x =-+或2286y x x =-+………………7分通州一模23. 已知二次函数()2214y x k x k =-++的图象与x 轴分别交于点()1,0A x 、()2,0B x ，且32-<1x <12-．（1）求k 的取值范围；（2）设二次函数()2214y x k x k =-++的图象与y 轴交于点M ，若OM OB =，求二次函数的表达式；（3）在(2)的条件下，若点N 是x 轴上的一点，以N 、A 、M 为顶点作平行四边形，该平行四边形的第四个顶点F在二次函数()2214y x k x k =-++的图象上，请直接写出满足上述条件的平行四边形的面积.23.解：(1)令0y =，则()22140x k x k -++=解方程得：2x k =或2x =， ……………… 1分；由题意得：()20A k ，，()20B ，，∴ 31222-k <<-， ∴3144k -<<-. ……………… 2分；(2)令0x =，则4y k =， ∴()04M k ，， ∵O M O B =，∴ 42k -=， ……………… 3分； ∴ 12k =-， ∴22y x x =--. ……………… 4分；或∵O M O B =，()20B ，， ∴()0M ，-2，把点M 的坐标分别代入()2214y x k x k =-++中，∴42k =-， ……………… 3分； ∴ 12k =-， ∴22y x x =--. ……………… 4分；(3)2，5+，5（每个答案各1分） ……………… 7分．密云一模2323．（1）当2k =-时，(1,2)A -A 在反比例函数图像上∴设反比例函数为ky x =，代入A 点坐标可得2k =-2...........................2y x-∴=分（2）要使得反比例函数与二次函数都是y 随着x 的增大而增大，0.....................k ∴<分而对于二次函数2y kx kx k =+-，其对称轴为12x =-，要使二次函数满足上述条件，在0k <的情况下，则x 必须在对称轴的左边，即12x <-时，才能使得y 随着x 的增大而增大………………..4分∴ 综上所述，则0k <，且12x <-（3）由(2)可得15(,)24Q k --ABQ ∆是以AB 为斜边的直角三角形A 点与B 点关于原点对称，所以原点O 平分AB又直角三角形中斜边上的中线是斜边的一半...........................5OQ OA OB ∴==分作AD OC ⊥，QC OC ⊥O Q k=而OA ==则k =k =分平谷一模23. 已知关于m 的一元二次方程221x mx +-=0. （1）判定方程根的情况；（2）设m 为整数，方程的两个根都大于1-且小于32，当方程的两个根均为有理数时，求m 的值．23．解：（1）2242(1)8.m m ∆=-⨯⨯-=+ …….…………………………………………….1分 ∵ 20,m ≥∴ 280.m ∆=+>所以无论m 取任何实数，方程221x mx +-=0都有两个不相等的实数根. ………..2分(2)设221y x mx =+-．∵ 2210x mx +-=的两根都在1-和32之间， (图为一种可能的情况)∴ 当1x =-时，0y >，即：210m --> ．当32x =时，0y >，即：931022m +->． ∴ 1213m -<<． ………………………..………..………………………………3分∵ m 为整数， ∴ 210m =--，，． …………………………………………………………….. 4分① 当2m =-时，方程222104812x x --=∆=+=，，此时方程的根为无理数，不合题意．②当0m =时，方程2210x -=，x =③当1m =-时，方程212121012x x x x --==-=，，，符合题意．综合①②③可知，1m =-．………………………………………..………………7分门头沟一模23．已知关于x 的一元二次方程21(2)2602x m x m +-+-=．（1）求证：无论m 取任何实数，方程都有两个实数根；（2）当<3m 时，关于x 的二次函数21(2)262y x m x m =+-+-的图象与x 轴交于A 、B 两点（点A 在点B 的左侧），与y 轴交于点C ，且2AB =3OC ，求m 的值；（3）在（2）的条件下，过点C 作直线l ∥x 轴，将二次函数图象在y 轴左侧的部分沿直线l 翻折，二次函数图象的其余部分保持不变，得到一个新的图象，记为G ．请你结合图象回答：当直线13y x b =+与图象G 只有一个公共点时，b 的取值范围．23．解：（1）根据题意，得221Δ(2)4(26)(4)2m m m =--⨯⨯-=-．∵无论m 为任何实数时，都有(m －4)2≥0，即Δ≥0，∴方程有两个实数根．…………………………………………………………2分（2）令y =0，则21(2)2602x m x m +-+-=．解得 x 1=6－2m ，x 2=－2．∵ m ＜3，点A 在点B 的左侧， ∴ A （－2，0），B （26m -+，0）．……………………………………………3分∴ OA=2，OB =26m -+．令x =0，得y =2m －6． ∴C （0，2m －6）．∴OC =－(2m －6)=－2m +6． ∵ 2AB =3 OC ，∴ 2(226)3(26)m m -+=-+．解得1m =（3）当1m =时，抛物线的解析式为2142y x x =--，点C 的坐标为（0，－4）．当直线13y x b =+经过C 点时，可得b =－4．当直线13y x b =+（b ＜－4）与函数2142y x x =--（x ＞0）的图象只一个公共点时，得211432x b x x +=--．整理得2386240.x x b ---=由()()2Δ8436240b =--⨯⨯--=，解得449b =-．结合图象可知，符合题意的b 的取值范围为b >－4或<9b -．………………7分房山一模23.已知，抛物线2y x bx c =-++，当1＜x ＜5时，y 值为正；当x ＜1或x ＞5时，y 值为负. （1）求抛物线的解析式.（2）若直线y kx b =+（k ≠0）与抛物线交于点A （32，m ）和B （4，n ），求直线的解析式. （3）设平行于y 轴的直线x=t 和x=t+2分别交线段AB 于E 、F ，交二次函数于H 、G.①求t 的取值范围②是否存在适当的t 值，使得EFGH 是平行四边形？若存在，求出t 值；若不存在，请说明理由. 23.解：（1）根据题意，抛物线2y x bx c =-++与x 轴交点为（1,0）和（5,0）----1分∴102550b c b c -++=⎧⎨-++=⎩，解得65b c =⎧⎨=-⎩.∴抛物线的解析式为265y x x =-+-. --------------------2分（2）∵265y x x =-+-的图象过A （32，m ）和B （4，n ）两点 ∴ m =74，n =3 ， ∴A （32，74）和B （4，3） ------------ 3分∵直线y kx b =+（k ≠0）过A （32，74）和B （4，3）两点∴372443k b k b ⎧+=⎪⎨⎪+=⎩，解得121k b ⎧=⎪⎨⎪=⎩. ∴直线的解析式为112y x =+. -------------------4分（3）①根据题意3224t t ⎧⎪⎨⎪+⎩＞＜，解得32≤t ≤2 -------------------5分②根据题意E （t ，1t 12+），F （t +2，1t 22+） H （t ，2t 6t 5-+-），G （t +2，2t 2t 3-++），∴EH =211t t 62-+-，FG =23t t 12-++. 若EFGH 是平行四边形，则EH =FG ，即211t t 62-+-=23t t 12-++解得t =74， - ---------------------6分∵t =74满足32≤t ≤2.∴存在适当的t 值，且t =74使得EFGH 是平行四边形.----------7分23．（7分）（2013•丰台区一模）二次函数y=x 2+bx+c 的图象如图所示，其顶点坐标为M （1，﹣4）．（1）求二次函数的解析式；（2）将二次函数的图象在x 轴下方的部分沿x 轴翻折，图象的其余部分保持不变，得到一个新的图象，请你结合新图象回答：当直线y=x+n 与这个新图象有两个公共点时，求n 的取值范围．（2013朝阳一模23．）二次函数2134y x x n =++-的图象与x 轴只有一个交点；另一个二次函数2222(1)46y nx m x m m =--+-+的图象与x 轴交于两点，这两个交点的横坐标都是整数，且m 是小于5的整数．求（1）n 的值；（2）二次函数2222(1)46y nx m x m m =--+-+的图象与x 轴交点的坐标．（2013朝阳一模23．）解：(1)∵2134y x x n =++-的图象与x 轴只有一个交点， ∴令10y =，即2304x x n ++-=.……………………………………………1分 ∴131404n ⎛⎫∆=--= ⎪⎝⎭. 解得n =1. ………………………………………………………………………2分 (2)由(1)知，()2222146y x m x m m =--+-+.∵()2222146y x m x m m =--+-+的图象与x 轴有两个交点，∴[]2222(1)4(46)m m m ∆=----+820m =-.∵20∆>，∴52m >.……………………………………………………………………………3分又∵5m <且m 是整数，∴m =4或3. …………………………………………………………………………5分当m =4时，2266y x x =-+的图象与x 轴的交点的横坐标不是整数；当m =3时，2243y x x =-+，令20y =，即2430x x -+=，解得11x =，23x =.综上所述，交点坐标为（1，0），（3，0）. ………………………………………7分（2013北京大兴一模23．）如图，已知抛物线y=﹣x 2+bx+c 与一直线相交于A （﹣1，0），C （2，3）两点，与y 轴交于点N ．其顶点为D ．（1）抛物线及直线AC 的函数关系式；（2）设点M （3，m ），求使MN+MD 的值最小时m 的值；（3）若抛物线的对称轴与直线AC 相交于点B ，E 为直线AC 上的任意一点，过点E 作EF ∥BD 交抛物线于点F ，以B ，D ，E ，F 为顶点的四边形能否为平行四边形？若能，求点E 的坐标；若不能，请说明理由.（2013北京大兴一模23．）解：（1）由抛物线y=﹣x 2+bx+c 过点A （﹣1，0）及C （2，3）得，，解得.∴ 抛物线为y=﹣x 2+2x+3 . ………………………………………1分又设直线为y=kx+n 过点A （﹣1，0）及C （2，3）得,，解得.∴ 直线AC 为y=x+1 . ………………………………………2分（2）作N 点关于直线x=3的对称点N ′，则N ′（6，3），由（1）得D （1，4）， ∴ 直线DN ′的函数关系式为y=﹣x+当M （3，m ）在直线DN ′上时，MN+MD 的值最小则m=﹣×=………………………………………4分（3）由（1）、（2）得D （1，4），B （1，2） ∵点E 在直线AC 上，设E （x ，x+1）① 当点E 在线段AC 上时，点F 在点E 上方，则F （x ，x+3） ∵F 在抛物线上， ∴x+3=﹣x 2+2x+3 解得，x=0或x=1（舍去），∴E （0，1）② 当点E 在线段AC （或CA ）延长线上时，点F 在点E 下方，则F （x ，x ﹣1）由F 在抛物线上，∴x ﹣1=﹣x 2+2x+3解得x=或x=，∴ E （，32）或（，）满足条件的点E 为E （0，1）、（）或（，）. ……………………………………7分（2013北京延庆24.）（本题满分7分）如图，已知平面直角坐标系xOy ，抛物线y ＝－x 2＋bx ＋c 过点A(4,0)、B(1,3) . （1）求该抛物线的解析式，并写出该抛物线的对称轴和顶点坐标；（2）记该抛物线的对称轴为直线l ，设抛物线上的点P(m,n)在第四象限，点P 关于直线l 的对称点为E ，点E 关于y 轴的对称点为F ，若四边形OAPF 的面积为20，求m 、n 的值.（2013北京延庆24.）解：（1）将2244b 013c b c ⎧-++=⎪⎨-++=⎪⎩…………………………1解之得：b=4，c=0 …………………2所以抛物线的解析式为：24y x x =-+……将抛物线的表达式配方得：24y x x =-+=所以对称轴为x=2，顶点坐标为（2，4（2）点p （m ，n ）关于直线x=2（4-m,-n ），……………………………………5分则四边形的面积OAPF=4n =20所以n =5，因为点P 为第四象限的点，所以n<0，所以n= -5 ………6分代入抛物线方程得m=5 …………………………………………………7分（2013怀柔区数学初三一模23．）已知关于x 的方程03)13(2=+++x k kx ．（1）求证：无论k 取任何实数时，方程总有实数根;（2）若二次函数3)13(2+++=x k kx y 的图象与x 轴两个交点的横坐标均为整数，且k 为正整数，求k 值; （3）在（2）的条件下，设抛物线的顶点为M ，直线y=－2x ＋9与y 轴交于点C ，与直线OM 交于点D ．现将抛物线平移，保持顶点在直线OD 上．若平移的抛物线与射线CD （含端点C ）只有一个公共点，求它的顶点横坐标的值或取值范围.23． (1)证明：①当k=0时，方程为x+3=0，所以x=-3，方程有实数根.…… 1分 ②当k≠0时, ()34132⋅-+=∆k k=k k k 121692-++ =1692+-k k=()0132≥-k ………………………………2分所以,方程有实数根综上所述，无论k 取任何实数时，方程总有实数根（2）令0y =，则03)13(2=+++x k kx 解关于x 的一元二次方程，得x 1=-3 ，x 2=k1-……………………3分 ∵ 二次函数的图象与x 轴两个交点的横坐标均为整数，且k 为正整数， ∴k =1………………４分（3）由（2）得抛物线的解析式为342++=x x y 配方得y=(x ＋2)2－1∴抛物线的顶点M （－2，－1） ∴直线OD 的解析式为y=21x于是设平移后的抛物线的顶点坐标为（h ，21h ）， (5)分∴平移后的抛物线解析式为y=（x －h ）2＋21h ．①当抛物线经过点C 时，∵C（0，9），∴h 2＋21h=9，解得h=41451-±． ∴ 当4145-1-≤h＜41451-+ 时，平移后的抛物线与射线CD 只有一个公共点． ………………………………………………………………6分②当抛物线与直线CD 只有一个公共点时，由方程组y=（x －h ）2＋21h ，y=－2x ＋9．得 x 2＋（－2h ＋2）x ＋h 2＋21h －9=0，∴△=（－2h ＋2）2－4（h 2＋21h －9）=0，解得h=4．此时抛物线y=（x －4）2＋2与射线CD 唯一的公共点为（3，3），符合题意…………………………………………………………………………7分综上：平移后的抛物线与射线CD 只有一个公共点时，顶点横坐标的值或取值范围是 h=4或4145-1-≤h＜41451-+．（昌平区2013年一模23.）已知抛物线22y x kx k =-+-+．（1）求证：无论k 为任何实数，该抛物线与x 轴都有两个交点；（2）在抛物线上有一点P （m ，n ），n <0，OP =103，且线段OP 与x 轴正半轴所夹锐角的正弦值为45，求该抛物线的解析式；（3）将（2）中的抛物线x 轴上方的部分沿x 轴翻折，与原图象的另一部分组成一个新的图形M ，当直线y x b =-+与图形M 有四个交点时，求b 的取值范围.23．（1）证明：当y =0时，得220x kx k -+-=.∵22244(2)(2)4b ac k k k -=--=-+. ∵2(2)0k -≥， ∴2(2)40k -+>.∴无论k 为任何实数，该抛物线与x 轴都有两个交点. …………………… 3分（2）解：如图，过点P 作P A ⊥x 轴于A ,则∠OAP =90°，依题意得：104,sin 35OP POA =∠=.∴8,23AP OA ==.∵n <0,∴8(2,)3P -.∵P 在抛物线上， ∴84223k k -=-+-+.∴23k =-.∴抛物线解析式为22833y x x =--+. ………………………………………5分（3）当y =0时，228033x x +-=. ∴1242,3x x =-=，∴抛物线与x 轴相交于点4(2,0),(,0)3.B C -当直线y = - x + b 经过点C （-2，0）时，b = -2. ………………………………………6分当直线y = - x + b 与抛物线228+-33y x x =相切时，22833x +x-x b =-+，∴△ =2584()093b ++=. ∴ b = 12136-. ……………………………………………………………………7分∴ 当12136-＜b ＜-2时，直线与图形M 有四个交点. ………………………………………8分。

2013年北京一模试题分类解析——导数理

0
—
0
↗
极大值
↘
极小值
↗
所以函数的单调递增区间为 ;单调递减区间为 ,……………………………………………………………………………6分
故在区间内单调递增,在区间内单调递减,
从而函数在区间内恰有两个零点,当且仅当
解得 ,
所以的取值范围是 .…………………………………………………9分
(III)记 ,当时,
(Ⅱ)①当时，由(Ⅰ)可知，函数的单调递减区间为，在单调递增.
所以在上的最小值为，
由于，
要使在上有且只有一个零点，
需满足或解得或 .
②当时，由(Ⅰ)可知，
（ⅰ）当时，函数在上单调递增；
且，所以在上有且只有一个零点.
（ⅱ）当时，函数在上单调递减，在上单调递增；
所以在上恒减
（）当时，的情况如下表
+
0
极大值
所以在为增函数，在为减函数
综上：当时，在定义域上恒减
当时，在为增函数，在为减函数
（）由（）可得，当时，在定义域上无极值，当时，在处取得极值，所以，解得
所以 , 即解得
令，
易得在上递减，在上递增。
所以；
即：
6 C（西城一模）已知函数，，其中．
（Ⅰ）求的极值；
（Ⅱ）若存在区间，使和在区间上具有相同的单调性，求的取值范围．
解：（）的定义域为，………………1分
．………………2分
当时，，故在上单调递减．
从而没有极大值，也没有极小值．………………3分
② 当时，令，得．

2013年北京市数学中考一、二模拟题分类汇编：四边形

A
D
F E
B
C
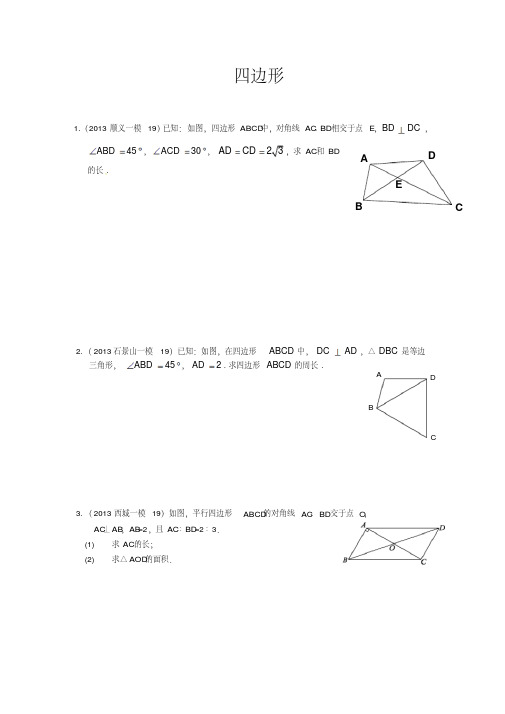
6. （ 2013 密云一模 19）如图，已知菱形 AE、 CF
（ 1）证明：四边形 AECF是矩形；（ 2）若 AB=8，求菱形的面积。
ABCD，AB=AC， E、 F 分别是 BC、 AD的中点，连接
D
7. （ 2013 门头沟一模 19）如图，在四边形 ABCD中，∠ A=∠ ADC=120o，
（ 2） DE的长．
B A
F
C
E
D
A
D
13. （ 2013 昌平一模 21）已知：如图，在 □ABCD中，∠ BAD，∠ ADC的平分线 AE， DF分别与线段 BC相交于点 E， F，AE与 DF相交于点 G．（ 1）求证： AE⊥ DF；（ 2）若 AD=10，AB=6， AE=4，求 DF的长．
在 Rt△ AED 中， AD 2
B
E
∴ AE
1 AD
1
2
C
由勾股定理得： DE 3
……………………………… 3 分
在 Rt△ AEB 中， ABD 45
∴ BE AE 1
∴ AB 2
……………………………… 4 分
∴ BD 1 3
∴ DC BC BD 1 3
∴ AB BC CD AD 2 2 2 2 3 4 2 2 3 ………… 5 分
∠ AED=2∠ CED，点 G是 DF的中点．（ 1）求证： ∠ CED=∠ DAG；（ 2）若 BE=1， AG=4，求 sin AEB 的值．
16. （ 2013 燕山一模 19）如图，四边形 ABCD 中，∠ ADC ＝∠ B ＝ 90°，∠ C ＝ 60°，
AD ＝ 3 ， E 为 DC 中点， AE∥ BC．求 BC 的长和四边形 ABCD 的面积．

2013年北京市数学中考一、二模拟题分类汇编：操作探究

操作探究1.（2013.昌平一模22）（1）人教版八年级数学下册92页第14题是这样叙述的：如图1，□ABCD中，过对角线BD上一点P作EF∥BC，HG∥AB，图中哪两个平行四边形的面积相等？为什么？根据习题背景，写出面积相等的一对平行四边形的名称为和；（2）如图2，点P为□ABCD内一点，过点P分别作AD、AB的平行线分别交□ABCD的四边于点E、F、G、H. 已知S□BHPE = 3，S□PFDG = 5，则；（3）如图3，若①②③④⑤五个平行四边形拼成一个含30°内角的菱形EFGH（不重复、无缝隙）.已知①②③④四个平行四边形面积的和为14，四边形ABCD的面积为11，则菱形EFGH的周长为．2.（2013.燕山一模22）阅读下列材料：问题：如图⑴，已知正方形ABCD中，E、F分别是BC、CD边上的点，且∠EAF ＝45°．判断线段BE、EF、FD之间的数量关系，并说明理由．小明同学的想法是：已知条件比较分散，可以通过旋转变换将分散的已知条件集中在一起，于是他将△DAF绕点A顺时针旋转90°，得到△BAH，然后通过证明三角形全等可得出结论．请你参考小明同学的思路，解决下列问题：⑴图⑴中线段BE、EF、FD之间的数量关系是；⑵如图⑵，已知正方形ABCD边长为5，E、F分别是BC、CD边上的点，且∠EAF＝45°，AG⊥EF于点G，则AG的长为，△EFC的周长为；⑶如图⑶，已知△AEF中，∠EAF＝45°，AG⊥EF于点G，且EG＝2，GF＝3，则△AEF的面积为．3.（2013.朝阳一模22）阅读下面材料：小雨遇到这样一个问题：如图1，直线l1∥l2∥l3，l1与l2之间的距离是1，l2与l3之间的距离是2，试画出一个等腰直角三角形ABC，使三个顶点分别在直线l1、l2、l3上，并求出所画等腰直角三角形ABC的面积．小雨是这样思考的：要想解决这个问题，首先应想办法利用平行线之间的距离，根据所求图形的性质尝试用旋转的方法构造全等三角形解决问题．具体作法如图2所示：在直线l1任取一点A，作AD⊥l2于点D，作∠DAH=90°，在AH上截取AE=AD，过点E作EB⊥AE交l3于点B，连接AB，作∠BAC=90°，交直线l2于点C，连接BC，即可得到等腰直角三角形ABC．请你回答：图2中等腰直角三角形ABC的面积等于．参考小雨同学的方法，解决下列问题：如图3，直线l1∥l2∥l3,l1与l2之间的距离是2，l2与l3之间的距离是1,试画出一个等边三角形ABC，使三个顶点分别在直线l1、l2、l3上，并直接写出所画等边三角形ABC的面积（保留画图痕迹）．4.（2013.海淀一模22）问题：如图1，、、、是同一平面内的一组等距平行线（相邻平行线间的距离为1）.画出一个正方形，使它的顶点、、、分别在直线、、、上，并计算它的边长.图1 图2小明的思考过程：他利用图1中的等距平行线构造了的正方形网格，得到了辅助正方形，如图2所示, 再分别找到它的四条边的三等分点、、、，就可以画出一个满足题目要求的正方形.请回答：图2中正方形的边长为 .请参考小明的方法，解决下列问题：（1）请在图3的菱形网格（最小的菱形有一个内角为，边长为1）中，画出一个等边△，使它的顶点、、落在格点上，且分别在直线a、b、c上；（3）如图4，、、是同一平面内的三条平行线，、之间的距离是，、之间的距离是，等边△的三个顶点分别在、、上，直接写出△的边长.图3 图45.（2013.东城一模22）如图，在菱形纸片ABCD中，AB=4cm，∠ABC=120°，按下列步骤进行裁剪和拼图：第一步：如图1，在线段AD上任意取一点E，沿EB，EC剪下一个三角形纸片EBC(余下部分不再使用)；第二步：如图2，沿三角形EBC的中位线GH将纸片剪成两部分，并在线段GH上任意取一点M，线段BC上任意取一点N，沿MN将梯形纸片GBCH剪成两部分；第三步：如图3，将MN左侧纸片绕G点按顺时针方向旋转180°，使线段GB与GE重合，将MN右侧纸片绕H点按逆时针方向旋转180°，使线段HC与HE重合，再与三角形纸片EGH拼成一个与三角形纸片EBC面积相等的四边形纸片．(注：裁剪和拼图过程均无缝且不重叠)（1）请你在图3中画出拼接成的四边形；（2）直接写出拼成的四边形纸片周长的最小值为________cm，最大值为________cm．6.（2013.怀柔一模22）理解与应用：我们把对称中心重合、四边分别平行的两个正方形之间的部分叫“方形环”，易知方形环四周的宽度相等．．．．.一条直线l与方形环的边线有四个交点、、、．小明在探究线段与的数量关系时，从点、向对边作垂线段、，利用三角形全等、相似及锐角三角函数等相关知识解决了问题．请你参考小明的思路解答下列问题：(1)直线l与方形环的对边相交时（22题图1），直线l分别交、、、于、、、，小明发现与相等，请你帮他说明理由；(2)直线l与方形环的邻边相交时（22题图2），l分别交、、、于、、、，l与的夹角为，请直接写出的值（用含的三角函数表示）.7.（2013.门头沟一模22）操作与探究：在平面直角坐标系xOy中，点P从原点O出发，且点P只能每次向上平移2个单位长度或向右平移1个单位长度．（1）实验操作：在平面直角坐标系xOy中，点P从原点O出发，平移1次后可能到达的点的坐标是，；点P从原点O出发，平移2次后可能到达的点的坐标是，，；点P从原点O出发，平移3次后可能到达的点的坐标是；（2）观察发现：任一次平移，点P可能到达的点在我们学过的一种函数的图象上，如：平移1次后在函数的图象上；平移2次后在函数的图象上，…．若点P平移5次后可能到达的点恰好在直线上，则点P的坐标是；（3）探究运用：点P从原点O出发经过次平移后，到达直线上的点Q，且平移的路径长不小于30，不超过32，求点Q的坐标．8.（2013.平谷一模22）对于平面直角坐标系中的任意两点，我们把叫做两点间的直角距离，记作．（1）已知点，那么两点间的直角距离=_____________；（2）已知O为坐标原点，动点满足，请写出x与y之间满足的关系式，并在所给的直角坐标系中画出所有满足条件的图形；（3）设是一定点，是直线上的动点，我们把的最小值叫做点到直线的直角距离.试求点到直线的直角距离.．9.（2013.石景山一模22）问题解决：已知：如图，为上一动点，分别过点、作于点，于点，联结、.（1）请问：点满足什么条件时，的值最小？（2）若，，，设.用含的代数式表示的长（直接写出结果）.拓展应用：参考上述问题解决的方法，请构造图形，并求出代数式的最小值.来源:学,科,网]10.（2013.顺义一模22）如图1，在四边形中，，分别是的中点，连结并延长，分别与的延长线交于点，则（不需证明）．小明的思路是：在图1中，连结，取的中点，连结，根据三角形中位线定理和平行线性质，可证得．问题：如图2，在中，，点在上，，分别是的中点，连结并延长，与的延长线交于点，若，连结，判断的形状并证明．11.（2013.通州一模22）如图所示，在4×4的菱形斜网格图中（每一个小菱形的边长为1，有一个角是60°），菱形的边长为2，是的中点，沿将菱形剪成①、②两部分，用这两部分可以分别拼成直角三角形、等腰梯形、矩形，要求所拼成图形的顶点均落在格点上．（1）在下面的菱形斜网格中画出示意图；（2）若所拼成的直角三角形、等腰梯形、矩形的面积分别记为、、，周长分别记为、、，判断所拼成的三种图形的面积、周长的大小关系（用“=”、“＞”、“＜”、“≤”或“≥”连接）：面积关系是；周长关系是．12.（2013.西城一模22）先阅读材料，再解答问题：小明同学在学习与圆有关的角时了解到：在同圆或等圆中，同弧（或等弧）所对的圆周角相等．如图，点A、B、C、D均为⊙O上的点，则有∠C=∠D．小明还发现，若点E在⊙O外，且与点D在直线AB同侧，则有∠D>∠E．请你参考小明得出的结论，解答下列问题：(1) 如图1，在平面直角坐标系xOy中，点A的坐标为(0,7)，点B的坐标为(0,3)，点C的坐标为(3,0) ．①在图1中作出△ABC的外接圆（保留必要的作图痕迹，不写作法）；②若在轴的正半轴上有一点D，且∠ACB =∠ADB，则点D的坐标为；(2) 如图2，在平面直角坐标系xOy中，点A的坐标为(0,m)，点B的坐标为(0,n)，其中m>n>0．点P为轴正半轴上的一个动点，当∠APB达到最大时，直接写出此时点P的坐标．13.（2013.延庆一模22）阅读下面材料：将正方形ABCD（如图1）作如下划分：第1次划分：分别联结正方形ABCD对边的中点（如图2），得线段HF和EG，它们交于点M，此时图2中共有5个正方形；第2次划分：将图2左上角正方形AEMH按上述方法再作划分，得图3，则图3中共有_______个正方形；若每次都把左上角的正方形依次划分下去，则第100次划分后，图中共有_______个正方形；继续划分下去，能否将正方形ABCD划分成有2013个正方形的图形？需说明理由.14.（2013.昌平二模22）（1）【原题呈现】如图，要在燃气管道l上修建一个泵站分别向A、B两镇供气. 泵站修在管道的什么地方，可使所用的输气管线最短？解决问题：请你在所给图中画出泵站P的位置，并保留作图痕迹；（2）【问题拓展】已知a>0，b>0，且a+b=2，写出的最小值；（3）【问题延伸】已知a>0，b>0，写出以、、为边长的三角形的面积.15.（2013.朝阳二模22）阅读下列材料：小华遇到这样一个问题，如图1, △ABC中，∠ACB=30º，BC=6，AC=5，在△ABC内部有一点P，连接PA、PB、PC，求PA+PB+PC的最小值．小华是这样思考的：要解决这个问题，首先应想办法将这三条端点重合于一点的线段分离，然后再将它们连接成一条折线，并让折线的两个端点为定点，这样依据“两点之间，线段最短”，就可以求出这三条线段和的最小值了．他先后尝试了翻折、旋转、平移的方法，发现通过旋转可以解决这个问题．他的做法是，如图2，将△APC绕点C顺时针旋转60º，得到△EDC，连接PD、BE，则BE的长即为所求．（1）请你写出图2中，PA+PB+PC的最小值为；（2）参考小华的思考问题的方法，解决下列问题：①如图3，菱形ABCD中，∠ABC=60º，在菱形ABCD内部有一点P，请在图3中画出并指明长度等于PA+PB+PC最小值的线段（保留画图痕迹，画出一条即可）；②若①中菱形ABCD的边长为4，请直接写出当PA+PB+PC值最小时PB的长．16.（2013.大兴二模22）在三角形纸片ABC中，已知∠ABC=90°，AB=6，BC=8．过点A作直线平行于BC，折叠三角形纸片ABC，使直角顶点B 落在直线上的T处，折痕为MN．当点T 在直线上移动时，折痕的端点M、N也随之移动．若限定端点M、N分别在AB、BC边上移动(点M可以与点A重合，点N可以与点C重合），求线段AT长度的最大值与最小值的和(计算结果不取近似值)．17.（2013.东城二模22）阅读并回答问题：数学课上，探讨角平分线的作法时，李老师用直尺和圆规作角平分线，方法如下：作法：①在OA，OB上分别截取OD，OE，使OD=OE.②分别以D，E为圆心，以大于为半径作弧，两弧在内交于点C.③作射线OC，则OC就是的平分线小聪只带了直角三角板，他发现利用三角板也可以作角平分线，方法如下：作法： ①利用三角板上的刻度，在OA ，OB 上分别截取OM ，ON ，使OM =ON .②分别过以M ，N 为OM ，ON 的垂线，交于点P.③作射线OP ，则OP 就是的平分线.小颖的身边只有刻度尺，经过尝试，她发现利用刻度尺也可以作角平分线.根据以上情境，解决下列问题：（1）小聪的作法正确吗？请说明理由；（2）请你帮小颖设计用刻度尺作平分线的方法.（要求：不与小聪方法相同，请画出图形，并写出画图的方法，不必证明）.18.（2013.房山二模22）如图1，在矩形MNPQ 中，点E ，F ，G ，H 分别在边NP ，PQ ，QM ，MN 上，当时，我们称四边形EFGH 为矩形MNPQ 的反射四边形.已知：矩形ABCD 的四个顶点均为边长为1的正方形网格的格点，请解决下列问题：（1）在图2中，点E ，F 分别在BC ，CD 边上，请作出矩形ABCD 的反射四边形EFGH ，并求出反射四边形EFGH 的周长.（2）在图3中作出矩形ABCD 的所有反射四边形，并判断它们的周长之间的关系.19.（2013.密云二模22）实践与操作：如图1是以正方形两顶点为圆心，边长为半径，画两段相等的圆弧而成的轴对称图形，图2是以图1为基本图案经过图形变换拼成的一个中心对称图形．（1）请你仿照图1，用两段相等圆弧（小于或等于半圆），在图3中重新设计一个不同的轴对称图形．（2）以你在图3中所画的图形为基本图案，经过图形变换在图4中拼成一个中心对称图形．20.（2013.石景山二模22）如图，在矩形ABCD中，AB＝3，BC＝4，点M、N、分别在BC、AB上，将矩形ABCD沿MN折叠，设点B的对应点是点E．（1）若点E在AD边上，BM=，求AE的长；（2）若点E在对角线AC上，请直接写出AE的取值范围：．解：21.（2013.丰台二模22）操作探究：一动点沿着数轴向右平移5个单位，再向左平移2个单位，相当于向右平移3个单位．用实数加法表示为 5+（）=3．若平面直角坐标系xOy中的点作如下平移：沿x轴方向平移的数量为a（向右为正，向左为负，平移个单位），沿y轴方向平移的数量为b（向上为正，向下为负，平移个单位），则把有序数对{a，b}叫做这一平移的“平移量”．规定“平移量”{a，b}与“平移量”{c，d}的加法运算法则为．（1）计算：{3，1}+{1，2}；（2）若一动点从点A（1，1）出发，先按照“平移量”{2，1}平移到点B，再按照“平移量”{-1，2}平移到点C；最后按照“平移量”{-2，-1}平移到点D，在图中画出四边形ABCD，并直接写出点D的坐标；（3）将（2）中的四边形ABCD以点A为中心，顺时针旋转90°，点B旋转到点E，连结AE、BE若动点P从点A出发，沿△AEB的三边AE、EB、BA 平移一周．请用“平移量”加法算式表示动点P的平移过程．22.（2013.海淀二模22）如图1，四边形ABCD中，、为它的对角线，E为AB边上一动点（点E不与点A、B重合），EF∥AC交BC于点F，FG∥BD交DC于点G，GH∥AC交AD于点H，连接HE．记四边形EFGH的周长为，如果在点的运动过程中，的值不变，则我们称四边形ABCD为“四边形”，此时的值称为它的“值”．经过探究，可得矩形是“四边形”．如图2，矩形ABCD中，若AB=4，BC=3，则它的“值”为．图1 图2 图3（1）等腰梯形（填“是”或“不是”）“四边形”；（2）如图3，是⊙O的直径，A是⊙O上一点，，点为上的一动点，将△沿的中垂线翻折，得到△．当点运动到某一位置时，以、、、、、中的任意四个点为顶点的“四边形”最多，最多有个．23.（2013.怀柔二模22）探究与应用已知点P的坐标为（m，0），在x轴上存在点Q（不与P点重合），以PQ为边作正方形PQMN，使点M落在反比例函数y = 的图象上.小明对上述问题进行了探究，发现不论m取何值，符合上述条件的正方形只有．．两个，且一个正方形的顶点M在第四象限，另一个正方形的顶点M1在第二象限.（1）如图，若反比例函数解析式为y= ，P点坐标为（1， 0），图中已画出一符合条件的一个正方形PQMN，请你在图中画出符合条件的另一个正方形PQ1M1N1；（2）请你通过改变P点坐标，对直线M1 M的解析式y﹦kx＋b进行探究可得 k﹦，若点P的坐标为（m，0）时，则b﹦；（3）依据(2)的规律，如果点P的坐标为（6，0），请你直接写出点M1和点M的坐标．解：（1）如图（2）k﹦，b﹦；（3）M1的坐标为（，），M的坐标为（，）.24.（2013.西城二模22）在平面直角坐标系xOy中，点经过变换得到点，该变换记作，其中为常数．例如，当，且时，．(1) 当，且时，= ；(2) 若，则= ，= ；(3) 设点是直线上的任意一点，点经过变换得到点．若点与点重合，求和的值．第七章操作探究参考答案1.（2013.昌平一模22）解：（1）□AEPH 和□PGCF或□ABGH 和□EBCF 或□AEFD 和□HGCD . … 1分（2）1. ……………………………… 2分（3）24．……………………………… 4分2.（2013.燕山一模22）⑴线段BE、EF、FD之间的数量关系是EF＝BE＋FD； (1)分⑵AG的长为 5 ，△EFC的周长为 10 ；………………………3分⑶△AEF的面积为 15 ．………………………5分3.（2013.朝阳一模22）解： 5；……………………………………………2分如图；………………………………………3分. ………………………………………5分4.（2013.海淀一模22）（1）.………………………2分（2）①如图：(答案不唯一) …4分②.………………………5分5.（2013.东城一模22）解：（1）拼接成的四边形所图虚线所示；………………2分（2）；. …………………………5分（注：通过操作，我们可以看到最后所得的四边形纸片是一个平行四边形，其上下两条边的长度等于原来菱形的边AB=4，左右两边的长等于线段MN的长，当MN垂直于BC时，其长度最短，等于原来菱形的高的一半，于是这个平行四边形的周长的最小值为2（+4）=；当点E与点A重合，点M与点G重合，点N与点C重合时，线段MN最长，等于，此时，这个四边形的周长最大，其值为.）6.（2013.怀柔一模22）理解与应用：…………………1分=∠N’NF……………………2分………………3分）……………………………5分7.（2013.门头沟一模22）解：（1）（0，6），（1，4），（2，2），（3，0）．………………………2分（2）平移5次后P在y=-2x+10上，又在y=3x上，联立方程组即可。

北京市海淀区2013年中考一模数学答案-word版本-完美编辑直接打印

EDCBA海淀区九年级第二学期期中测评数学试卷答案及评分参考一、选择题（本题共32分，每小题4分）三、解答题（本题共30分，每小题5分） 130112cos301)()8-︒+- ．解：原式218=-- ………………………4分 7=．………………………5分解：由①得 2x >-．………………………2分由②得 1x ≤．………………………4分则不等式组的解集为12≤<-x ．………………………5分 15．先化简，再求值：4212112--÷⎪⎭⎫ ⎝⎛-+x x x ，其中3=x ．解：原式2212421x x x x -+-=⋅-- ………………………2分 )1)(1()2(221+--⋅--=x x x x x ………………………3分 12+=x . ………………………4分当3=x 时，原式=2112=+x .………………………5分16.证明：AB ∥EC ，∴.A DCE ∠=∠ ………………………1分在△ABC 和△CDE 中，,,,B EDC A DCE AC CE ∠=∠⎧⎪∠=∠⎨⎪=⎩∴△ABC ≌△CDE .………………………4分 ∴.BC DE = ………………………5分17.解：（1）∵ 点A (1,)n -在反比例函数xy 2-=的图象上， ∴ 2n =. ………………………1分 ∴ 点A 的坐标为12-（，）. ∵ 点A 在一次函数y kx k =-的图象上， ∴2k k =--.∴1-=k .………………………2分∴ 一次函数的解析式为1+-=x y ．………………………3分（2）点P 的坐标为（-3,0）或（1,0）．………………………5分（写对一个给1分）18.解：设原计划每天加工x 顶帐篷. ………………………1分1500300150030042x x---=.………………………3分解得 150x =. ………………………4分经检验，150x =是原方程的解，且符合题意. 答：原计划每天加工150顶帐篷. ………………………5分四、解答题（本题共20分，每小题5分）19. 解：过点A 作AF ⊥BD 于F . ∵∠CDB =90°,∠1=30°,∴∠2=∠3=60°. ………………………1分在△AFB 中，∠AFB =90°.∵∠4=45°，AB =∴AF =BF ………………………2分在△AFE 中，∠AFE =90°.∴1,2EF AE ==.………………………3分在△ABD 中，∠DAB =90°.∴DB =∴1DE DB BF EF =--=-.………………………4分∴1131)222ADE S DE AF ∆-=⋅=-=.………………………5分 20.(1)证明：连接OD . ………………………1分∵AB =AC , ∴B C ∠=∠. 又∵OB OD =, ∴1B ∠=∠.∴1C ∠=∠. ∴OD ∥AC .∵DE ⊥AC 于E , ∴DE ⊥OD .∵点D 在⊙O 上，∴DE 与⊙O 相切. ………………………2分 (2)解：连接AD .∵AB 为⊙O 的直径，∴∠ADB =90°. ∵AB =6，sin B =55， ∴sin AD AB B =⋅=556.………………3分 ∵123290∠+∠=∠+∠=︒， ∴13∠=∠. ∴ 3.B ∠=∠在△AED 中，∠AED =90°.∵sin 3AE AD ∠==∴65AE AD ===. ………………………4分又∵OD ∥AE ，∴△FAE ∽△FOD .∴FA AEFO OD =. ∵6AB =,∴3OD AO ==.∴235FA FA =+. ∴2AF =. ………………………5分21.（1）13.………………………1分（2）∵(3318)80%30++÷=，∴被小博同学抽取的监测点个数为30个. ………………………2分………………………3分（3）设去年同期销售x 万箱烟花爆竹.(135%)37x -=.解得125613x =.………………………4分 ∴1212563719201313-=≈.答：今年比去年同期少销售约20万箱烟花爆竹. ……………………… 5分22.（1.………………………2分（2）①如图：(答案不唯一) ………………………4分………………………5分五、解答题（本题共22分，第23题7分，第24题7分，第25题8分） 23．解：（1）依题意，可得抛物线的对称轴为212mx m-=-=.………………………1分 ∵抛物线与x 轴交于A 、B 两点，点A 的坐标为(2,0)-， ∴点B 的坐标为 (4,0)．………………………2分（2）∵点B 在直线y =12x +4m +n 上， ∴024m n =++①.∵点A 在二次函数2-2y mx mx n =+的图象上， ∴044m m n =++②. ………………………3分由①、②可得12m =，4n =-. ………………………4分 ∴ 抛物线的解析式为y ＝2142x x --，直线的解析式为y ＝122x -． ……………5分（3）-502d <<． ………………………7分 24．（1）2AE =.………………………1分（2）线段AE 、CD 之间的数量关系为2AE CD =.………………………2分证明：如图1，延长AC 与直线l 交于点G ．依题意，可得∠1＝∠2． ∵∠ACB ＝90︒， ∴∠3=∠4. ∴BA BG =.∴CA ＝CG ．………………………3分 ∵AE ⊥l ，CD ⊥l ， ∴CD ∥AE ． ∴△GCD ∽△GAE ． ∴12CD GC AE GA =＝． ∴2AE CD =．………………………4分（3）解：当点F 在线段AB 上时，如图2，过点C 作CG ∥l 交AB 于点H ，交AE 于点G ． ∴∠2＝∠HCB ． ∵∠1=∠2， ∴∠1＝∠HCB ． ∴CH BH =． ∵∠ACB ＝90︒，∴∠3+∠1＝∠HCB +∠4 =90︒． ∴∠3＝∠4． ∴CH AH BH ==． ∵CG ∥l ，∴△FCH ∽△FEB ． ∴56CF CH EF EB =＝．设5,6CH x BE x ==，则10AB x =．∴在△AEB 中，∠AEB ＝90︒，8AE x =．由（2）得，2AE CD =． ∵4CD =, ∴8AE =. ∴1x =.∴10,6,5AB BE CH ===． ∵CG ∥l ，∴△AGH ∽△AEB ． ∴12HG AH BE AB ==．图3图2∴3HG =．………………………5分 ∴8CG CH HG =+=． ∵CG ∥l ，CD ∥AE , ∴四边形CDEG 为平行四边形. ∴8DE CG ==.∴2BD DE BE =-=．……………………6分当点F 在线段BA 的延长线上时，如图3，同理可得5CH =,3GH =,6BE =. ∴DE =2CG CH HG =-=． ∴ 8BD DE BE =+=．∴2BD =或8．……………………7分 25.解：（1）()2222y x mx m m x m m =-++=-+，……………………1分∴顶点坐标为C m ,m ().……………………2分（2）①2y x =+与抛物线222y x mx m m =-++交于A 、B 两点，∴2222x x mx m m +=-++.解方程，得121,2x m x m =-=+.……………………4分A 点在点B 的左侧，∴(1,1),(2,4).A m m B m m -+++∴AB =……………………5分直线OC 的解析式为y x =，直线AB 的解析式为2y x =+，∴AB ∥OC ，两直线AB 、OC 之间距离h =∴11322APBSAB h =⋅=⨯=.………………………6分……………………8分(注：本卷中许多问题解法不唯一,请老师根据评分标准酌情给分)。

2013北京各区县文科数学理科数学一模题汇编：平面几何证明

PBCDA OOP DFE 2013北京模拟：平面几何证明 1、（2013海淀期末，理5）如图，PC 与圆O 相切于点C ，直线PO 交圆O 于A ，B 两点，弦CD 垂直AB 于E ，则下面结论中，错误的是（）A 、BEC DEA △∽△B 、ACE ACP ∠=∠C 、2DE OE EP =⋅ D 、2PC PA AB =⋅第1题图第2题图第3题图第4题图2、（2013朝阳期末，理10）如图，AB ，CD 是半径为a 的圆O 的两条弦，它们相交于AB 中点P ，若23aPD =，30OAP ∠=°，则AB = ；CP = 。

（用a 表示） 3、（2013西城期末，理10）如图，Rt △ABC ，90ABC ∠=°，3AC =，4BC =，以AC 为直径的圆交AB 于点D ，则BD = ；CD = 。

4、（2013石景山期末，理10）如图，从圆O 外一点P 引圆O 的割线PAB 和PCD ，PCD 过圆心O ，已知1PA =，2AB =，3PO =，则圆O 的半径等于。

5、（2013丰台一模，理11）如图，直线PD 切圆O 与点D ，直线PO 交圆O 于点E ，F ，若23PF =+，1PD =，则圆O 的半径为，EFD ∠= 。

第5题图第6题图第7题图6、（2013石景山，理5）如图，直线AM 与圆相切于点M ，ABC 与ADE 是圆的两条割线，且BD AD ⊥，连结MD 、EC ，则下面结论中，错误的是（）A 、90ECA ∠=°B 、CEM DMA DBA ∠=∠+∠C 、2AM AD AE =⋅ D 、AD DE AB BC ⋅=⋅ 7、（2013海淀一模，理11）如图，AP 与圆O 切于点A ，交弦BD 延长线于点P ，过点B 作圆O 的切线交AP 于点C ，若90ACB ∠=°，3BC =，4CP =，则弦BD 的长为。

2013年北京市中考各城区一模数学24题汇总

2013年北京市中考各城区一模数学24题汇总1、(2013年门头沟)24．已知：在△ABC 中，AB ＝AC ，点D 为BC 边的中点，点F 是AB 边上一点，点E 在线段DF 的延长线上，点M 在线段DF 上，且∠BAE ＝∠BDF ，∠ABE ＝∠DBM ．（1）如图1，当∠ABC ＝45°时，线段 DM 与AE 之间的数量关系是；（2）如图2，当∠ABC ＝60°时，线段 DM 与AE 之间的数量关系是；（3）① 如图3，当ABC α∠=（0<<90α︒︒）时，线段 DM 与AE 之间的数量关系是； ② 在（2）的条件下延长BM 到P ，使MP ＝BM ，连结CP ，若AB ＝7，AE＝求sin ∠ACP 的值．2、（2013年丰台区）24．在ABC △中，∠ACB =90°，AC ＞BC ，D 是AC 边上的动点，E 是BC 边上的动点，AD =BC ，CD =BE ．（1）如图1，若点E 与点C 重合，连结BD ，请写出∠BDE 的度数；（2）若点E 与点B 、C 不重合，连结AE 、BD 交于点F ，请在图2中补全图形，并求出∠BFE 的度数．3、（2013年平谷）AB CDEF M MFED CBA ACD EF M 图1图2图324．（1）如图(1)，△ABC 是等边三角形，D 、E 分别是AB 、BC 上的点，且BD CE =，连接AE 、CD 相交于点P .请你补全图形，并直接写出∠APD 的度数；=（2）如图（2）,Rt △ABC 中，∠B =90°，M 、N 分别是AB 、BC 上的点，且,AM BC =BM CN =，连接AN 、CM 相交于点P . 请你猜想∠APM = °，并写出你的推理过程.4、（2013年顺义）24．如图1，将三角板放在正方形ABCD 上，使三角板的直角顶点E 与正方形ABCD 的顶点A 重合．三角板的一边交CD 于点F ，另一边交CB 的延长线于点.G （1）求证：EF EG =；（2）如图2，移动三角板，使顶点E 始终在正方形ABCD 的对角线AC 上，其他条件不变，（1）中的结论是否仍然成立？若成立，请给予证明；若不成立，请说明理由；（3）如图3，将（2）中的“正方形ABCD ”改为“矩形ABCD ”，且使三角板的一边经过点B ，其他条件不变，若AB a =，BC b =，求EFEG的值．5、（2013年石景山）24．如图，△ABC 中，∠90ACB =︒, 2=AC ，以AC 为边向右侧作等边三角形ACD ．（1）如图24-1,将线段AB 绕点A 逆时针旋转︒60，得到线段1AB ，联结1DB ，则与1DB 长度相等的线段为（直接写出结论）；（2）如图24-2，若P 是线段BC 上任意一点（不与点C 重合），点P 绕点A 逆时针旋转︒60得到点Q ,求ADQ ∠的度数；（3）画图并探究：若P 是直线BC 上任意一点（不与点C 重合），点P 绕点A 逆时针旋转︒60得到点Q ,是否存在点P ，使得以A 、 C 、 Q 、 D 为顶点的四边形是梯形，若存在,请指出点P 的位置，并求出PC 的长；若不存在，请说明理由．6、（2013年海淀）24．在△ABC 中，∠ACB ＝90︒．经过点B 的直线l （l 不与直线AB 重合）与直线BC 的夹角等于ABC ∠，分别过点C 、点A 作直线l 的垂线，垂足分别为点D 、点E ．（1）若45ABC ∠=︒，CD =1（如图），则AE 的长为；（2）写出线段AE 、CD 之间的数量关系，并加以证明；（3）若直线CE 、AB 交于点F ， 56CF EF =，CD =4，求BD 的长．7、（2013年西城）图24-1 图24-2B 1ABCD备用图AD备用图AD24．在Rt △ABC 中，∠ACB =90°，∠ABC =α，点P 在△ABC 的内部．(1) 如图1，AB =2AC ，PB =3，点M 、N 分别在AB 、BC 边上，则cos α=_，△PMN 周长的最小值为__； (2) 如图2，若条件AB =2AC 不变，而PA =2，PB =10，PC =1，求△ABC 的面积； (3) 若PA =m ，PB =n ，PC =k ，且cos sin k m n αα==，直接写出∠APB 的度数．8、（2013年通州）24．已知：2AD =，4BD =，以AB 为一边作等边三角形ABC .使C 、D 两点落在直线AB 的两侧.（1）如图，当∠ADB=60°时，求AB 及CD 的长；（2）当∠ADB 变化，且其它条件不变时，求CD 的最大值，及相应∠ADB 的大小.9、（2013年东城）24. 问题1：如图1，在等腰梯形ABCD 中，AD ∥BC ，AB =BC =CD ，点M ，N 分别在AD ，CD 上，若∠MBN =12∠ABC ，试探究线段MN ，AM ，CN 有怎样的数量关系？请直接写出你的猜想，不用证明；问题2：如图2，在四边形ABCD 中，AB =BC ，∠ABC +∠ADC =180°，点M ，N 分别在DA ，CD 的延长线上，若∠MBN =12∠ABC 仍然成立，请你进一步探究线段MN ，AM ，CN 又有怎样的数量关系？写出你的猜想，并给予证明.10、（2013年朝阳）ADBC24．在Rt △ABC 中，∠A =90°，D 、E 分别为AB 、AC 上的点．（1）如图1，CE =AB ，BD =AE ，过点C 作CF ∥EB ，且CF =EB ，连接DF 交EB 于点G ，连接BF ，请你直接写出EBDC的值；（2）如图2，CE =kAB ，BD =kAE ，12EB DC =，求k 的值．11、（2013年密云）24．如图1，在等腰梯形ABCD 中，AD BC ∥，E 是AB 的中点，过点E 作EF BC ∥交CD 于点F ．46AB BC ==，， 60B =︒∠. （1）点E 到BC 的距离为；（2）点P 为线段EF 上的一个动点，过P 作PM EF ⊥交BC 于点M ，过M 作MN AB ∥交折线ADC 于点N ，连结PN ，设EP x =.①点N 在线段AD 上时（如图2），P M N △的形状是否发生改变？若不变，求出PMN △的周长；若改变，请说明理由；②当点N 在线段DC 上时（如图3），是否存在点P ，使PMN △为等腰三角形？若存在，请求出所有满足要求的x 的值；若不存在，请说明理由.12、（2013年延庆）图2B 图1FB图1图2 图3A D EB FC ADE BFC （备用）A D E BF C（备用）A DEBFC P NMA DE BF CP N M25. （本题满分8分）如图1，在四边形ABCD 中，AB CD =，E F 、分别是BC AD 、的中点，连结EF 并延长，分别与BA CD 、的延长线交于点M N 、，则BME CNE ∠=∠（不需证明）．（温馨提示：在图1中，连结BD ，取BD 的中点H ，连结HE HF 、，根据三角形中位线定理，证明HE HF =，从而12∠=∠，再利用平行线性质，可证得BME CNE ∠=∠．）问题一：如图2，在四边形ADBC 中，AB 与CD 相交于点O ，AB CD =，E F 、分别是BC AD 、的中点，连结EF ，分别交DC AB 、于点M N 、，判断OMN △的形状，请直接写出结论．问题二：如图3，在ABC △中，AC AB >，D 点在AC 上，AB CD =，E F 、分别是BC AD 、的中点，连结EF 并延长，与BA 的延长线交于点G ，若60EFC ∠=°，连结GD ，判断AGD △的形状并证明．13、（2013年房山）24（1）如图1，△ABC 和△CDE 都是等边三角形，且B 、C 、D 三点共线，联结AD 、BE 相交于点P ，求证： BE = AD .（2）如图2，在△BCD 中，∠BCD ＜120°，分别以BC 、CD 和BD 为边在△BCD 外部作等边三角形ABC 、等边三角形CDE 和等边三角形BDF ，联结AD 、BE 和CF 交于点P ，下列结论中正确的是（只填序号即可）①AD=BE=CF ；②∠BEC=∠ADC ；③∠DPE=∠EPC=∠CPA =60°；（3）如图2，在（2）的条件下，求证：PB+PC+PD=BE .14、（2013年昌平一模）FAB 第24题图1第24题图2AD24．在△ABC 中，AB =4，BC =6，∠ACB =30°，将△ABC 绕点B 按逆时针方向旋转，得到△A 1BC 1．（1）如图1，当点C 1在线段CA 的延长线上时，求∠CC 1A 1的度数；（2）如图2，连接AA 1，CC 1．若△CBC 1的面积为3，求△ABA 1的面积；（3）如图3，点E 为线段AB 中点，点P 是线段AC 上的动点，在△ABC 绕点B 按逆时针方向旋转的过程中，点P 的对应点是点P 1，直接写出线段EP 1长度的最大值与最小值．C1C BA 1A图2A 1C 1ABC图1图3PP 1E A 1A C 115、（2013年怀柔一模）24. 如图，△ABC 中，∠ACB=90°，AD=AC,AB=AN,连结CD 、BN,CD 的延长线交BN 于点F ．（1）当∠ADN 等于多少度时，∠ACE=∠EBF,并说明理由；（2）在（1）的条件下，设∠ABC=α，∠CAD =β，试探索α、β满足什么关系时，△ACE ≌△FBE ，并说明理由．16、（2013年大兴一模）24. 如图所示，现有一张边长为4的正方形纸片ABCD ，点P 为正方形AD 边上的一点（不与点A 、点D 重合）将正方形纸片折叠，使点B 落在P 处，点C 落在G 处，PG 交DC 于H ，折痕为EF ，连接BP 、BH ．（1）求证：∠APB=∠BPH ；（2）当点P 在边AD 上移动时，△PDH 的周长是否发生变化？并证明你的结论；（3）设AP 为x ，四边形EFGP 的面积为S ，请直接写．．．出．S 与x 的函数关系式，并求出．．S 的最小值．。

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

市西城区2013年初三一模试卷数学 2013. 5

一、选择题（本题共32分，每小题4分）下面各题均有四个选项，其中只有一个．．是符合题意的．

1．3的相反数是 A．31 B．31 C．3 D．3 2．原世博园区最大单体建筑“世博轴”被改造成一个综合性商业中心，该项目营业面积约130 000平方米，130 000用科学记数法表示应为 A．1.3×105 B．1.3×104 C．13×104 D．0.13×106 3．如图，AF是∠BAC的平分线，EF∥AC交AB于点E．若∠1=25°，则BAF的度数为 A．15° B．50° C．25° D．12.5° 4．在一个不透明的盒子中装有3个红球、2个黄球和1个绿球，这些球除颜色外，没有任何其他区别，现从这个盒子中随机摸出一个球，摸到黄球的概率为

A．21 B．31 C．61 D．1 5．若菱形的对角线长分别为6和8，则该菱形的边长为 A．5 B．6 C．8 D．10 6．某中学篮球队12名队员的年龄情况如下：年龄（单位：岁） 14 15 16 17 18 人数 1 4 2 3 2 则该队队员年龄的众数和中位数分别是 A．16，15 B．15，15.5 C．15，17 D．15，16 7．由一些大小相同的小正方体搭成的一个几何体的三视图如图所示，则构成这个几何体的小正方体共有 A．6个 B．7个 C．8个 D．9个

8．如图，在矩形ABCD中，AB=2，BC=4．将矩形ABCD绕点C沿顺时针方向旋转90°后，得到矩形FGCE（点A、B、D的对应点分别为点F、G、E）．动点P从点B开始沿BC-CE运动到点E后停止，动点Q从点E开始沿EF-FG运动到点G后停止，这两点的运动速度均为每秒1个单位．若点P和点Q同时开始运动，运动时间为x（秒），△APQ的面积为y，则能够正确反映y与x之间的函数关系的图象大致是

A B C D 二、填空题（本题共16分，每小题4分） 9．函数3yx中，自变量x的取值围是． 10．分解因式：32816aaa= ． 11．如图，在梯形ABCD中，AD∥BC，BD⊥DC，∠C=45°. 若AD=2，BC=8，则AB的长为． 12．在平面直角坐标系xOy中，有一只电子青蛙在点A(1,0)处．第一次，它从点A先向右跳跃1个单位，再向上跳跃1个单位到达点A1；第二次，它从点A1先向左跳跃2个单位，再向下跳跃2个单位到达点A2；第三次，它从点A2先向右跳跃3个单位，再向上跳跃3个单位到达点A3；第四次，它从点A3先向左跳跃4个单位，再向下跳跃4个单位到达点A4； …… 依此规律进行，点A6的坐标为；若点An的坐标为（2013，2012），则n= ．

三、解答题（本题共30分，每小题5分） 13．计算：10345sin2)13(8．

14．解不等式组 4(1)78,25,3xxxx并求它的所有整数解．

15．如图，点C在线段AB上，△DAC和△DBE都是等边三角形． (1) 求证：△DAB≌△DCE； (2) 求证：DA∥EC．

≤ 16．已知3=yx，求22222()xyxyxyxyy的值． 17．如图，在平面直角坐标系xOy中，正比例函数错误!未指定书签。32yx与反比例函数kyx的图象在第二象限交于点A，且点A的横坐标为．

(1) 求反比例函数的解析式； (2) 点B的坐标为(-3,0)，若点P在y轴上，且△AOB的面积与△AOP的面积相等，直接写出点P的坐标．

18．列方程（组）解应用题：某工厂原计划生产2400台空气净化器，由于天气的影响，空气净化器的需求量呈上升趋势，生产任务的数量增加了1200台．工厂在实际生产中，提高了生产效率，每天比原计划多生产10台，实际完成生产任务的天数是原计划天数的1.2倍．求原计划每天生产多少台空气净化器．

19．如图，平行四边形ABCD的对角线AC、BD交于点O， AC⊥AB，AB=2，且AC︰BD=2︰3． (1) 求AC的长； (2) 求△AOD的面积．

-2 北京市2008-2012年农业观光园经营年收入统计图北京市2009-2012年农业观光园

经营年收入增长率统计表

20．如图，在△ABC中，AB=AC，以AC为直径作⊙O交BC于点D，过点D作FE⊥AB于点E，交AC的延长线于点F． (1) 求证：EF与⊙O相切；

(2) 若AE=6，sin∠CFD=35，求EB的长．

21．近年来，郊区依托丰富的自然和人文资源，大力开发建设以农业观光园为主体的多类型休闲旅游项目，京郊旅游业迅速崛起，农民的收入逐步提高．以下是根据市统计局2013年1月发布的“市主要经济社会发展指标”的相关数据绘制的统计图表的一部分．

请根据以上信息解答下列问题： (1) 市2010年农业观光园经营年收入的年增长率是；（结果精确到1%） (2) 请补全条形统计图并在图中标明相应数据；（结果精确到0.1） (3) 如果从2012年以后，市农业观光园经营年收入都按30%的年增长率增长，请你估算，若经营年收入要不低于2008年的4倍，至少要到年．（填写年份）

22．先阅读材料，再解答问题：小明同学在学习与圆有关的角时了解到：在同圆或等圆中，同弧（或等弧）所对的圆周角相等．如图，点A、B、C、D均为⊙O上的点，则有∠C=∠D．小明还发现，若点E在⊙O外，且与点D在直线AB同侧，

年份年增长率（精确到1%） 2009年 12% 2010年 2011年 22% 2012年 24% 则有∠D>∠E．请你参考小明得出的结论，解答下列问题： (1) 如图1，在平面直角坐标系xOy中，点A的坐标为(0,7)，点B的坐标为(0,3)，点C的坐标为(3,0) ． ①在图1中作出△ABC的外接圆（保留必要的作图痕迹，不写作法）； ②若在x轴的正半轴上有一点D，且∠ACB =∠ADB，则点D的坐标为； (2) 如图2，在平面直角坐标系xOy中，点A的坐标为(0,m)，点B的坐标为(0,n)，其中m>n>0．点P为x轴正半轴上的一个动点，当∠APB达到最大时，直接写出此时点P的坐标．

五、解答题（本题共22分，第23题7分，第24题7分，第25题8分） 23．已知关于x的一元二次方程22(4)0xaxa． (1) 求证：无论a为任何实数，此方程总有两个不相等的实数根；

(2) 抛物线21:2(4)Cyxaxa与x轴的一个交点的横坐标为2a，其中0a，将抛物线1C向

右平移14个单位，再向上平移18个单位，得到抛物线2C．求抛物线2C的解析式； (3) 点A(m,n)和B(n,m)都在(2)中抛物线C2上，且A、B两点不重合，求代数式 33222mmnn

的值．

24．在Rt△ABC中，∠ACB=90°，∠ABC=，点P在△ABC的部． (1) 如图1，AB=2AC，PB=3，点M、N分别在AB、BC边上，则cos=_______， △PMN周长的最小值为_______； (2) 如图2，若条件AB=2AC不变，而PA=2，PB=10，PC=1，求△ABC的面积； (3) 若PA=m，PB=n，PC=k，且cossinkmn，直接写出∠APB的度数． 25．如图1，在平面直角坐标系xOy中，直线l：34yxm与x轴、y轴分别交于点A和点B(0,-1)，抛物线212yxbxc经过点B，且与直线l的另一个交点为C(4,n)． (1) 求n的值和抛物线的解析式； (2) 点D在抛物线上，且点D的横坐标为t（0< t <4）．DE∥y轴交直线l于点E，点F在直线l上，且四边形DFEG为矩形（如图2）．若矩形DFEG的周长为p，求p与t的函数关系式以及p的最大值； (3) M是平面一点，将△AOB绕点M沿逆时针方向旋转90°后，得到△A1O1B1，点A、O、B的对应点分别是点A1、O1、B1．若△A1O1B1的两个顶点恰好落在抛物线上，请直接写出点A1的横坐标．．．．

图1 图2 市西城区2013年初三一模试卷

数学答案及评分参考

2013. 5

一、选择题（本题共32分，每小题4分）题号 1 2 3 4 5 6 7 8 答案 C A C B A D C A 二、填空题（本题共16分，每小题4分） 9 10 11 12 x≥3 2)4(－aa 52 (－2, －3)，4023 （各2分）

三、解答题（本题共30分，每小题5分）

13．解：原式=21221223. ………………………………………………4分 =423． ………………………………………………… 5分 14．解：

由①得4x． …………………………………………………………1分由②得132x． …………………………………………………………3分

∴ 原不等式组的解集是1342x． ………………………………… 4分 ∴ 它的整数解为4，5，6． ………………………………………… 5分 15. 证明：（1）如图1. ∵△DAC和△DBE都是等边三角形， ∴DA=DC，DB=DE， …………1分 ∠ADC=∠BDE=60º . ∴∠ADC+∠CDB=∠BDE+∠CDB，即∠ADB=∠CDE. ……………2分在△DAB和△DCE中,

,,,DEDBCDEADBDCDA ∴ △DAB≌△DCE. ………………………………………… 3 分

（2）∵△DAB≌△DCE， ∴ ∠A=∠DCE=60° . ……………………………………… 4分 ∵∠ADC=60°， ∴ ∠DCE =∠ADC. ∴DA∥EC. ………………………………………………… 5分

16. 解：原式=2()()2yxyxyxyxyxy ..….….….…. …..…………..……………………2分 =2xyx. ………………………………………………………… 3分

① ② 4(1)78253xxxx







ABC

图1