2017丽水数学试卷(定稿)
2017年9月丽水、衢州、湖州三地市教学质量检测数学试卷

2017年9月丽水、衢州、湖州三地市教学质量检测试卷高三数学注意事项:1.本科目考试分试题卷和答题卷,考生须在答题卷上作答。
2.本试卷分为第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分,共4页,全卷满分150分,考试时间120分钟。
第Ⅰ卷 (选择题,共40分)一、选择题:本大题共10小题,每小题4分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的.1.已知集合{}1, 0, 1P =-,{}11Q x x =-≤<,则P Q =IA .{}0B .{}1, 0-C .[1,0]-D .[1,1)-2.若复数z 满足 i 32i z ⋅=-+ (i 为虚数单位) ,则复数z 的虚部是 A .3- B .3i - C .3 D .3i3.已知角α为第三象限角,且3tan 4α=,则sin cos αα+= A .75- B .15- C .15D .754.若将正方体(如图4-1)截去两个三棱锥,得到如图4-2所示的几何体,则该几何体的侧视图是A .B .C .D .5.若a ∈R ,则“21a -≥”是“0a ≤”的 A .充分不必要条件 B .必要不充分条件C .充要条件D .既不充分也不必要条件6.已知12,F F 分别为双曲线22221(0,0)x y a b a b-=>>的左右焦点,P 为双曲线右支上一点,满足21π2PF F ∠=,连接1PF 交y 轴于点Q,若2QF =,则双曲线的离心率是图4-1图4-2A .2B .3C .12+D .13+7.若关于x 的不等式23x a x -->在(,0)-∞上有解,则实数a 的取值范围是A .13(,3)4-B .13(3,)4- C .13(,)4-∞-D .(3,)+∞ 8.已知,x y ∈R 满足条件10,20,2.x y x y x -+≥⎧⎪+-≥⎨⎪≤⎩若目标函数z ax y =+仅在点(2,3) 处取到最大值,则实数a 的取值范围是A .(, 1)-∞B .(, 1]-∞C .[1, +)-∞D .(1, +)-∞9.已知点O 在二面角AB αβ--的棱上,点P 在半平面α内,且45POB ∠=o.若对于半平面β内异于O的任意一点Q ,都有45POQ ∠≥o,则二面角AB αβ--的取值范围是A .π[0,]4B .ππ[,]42C .π[,π]2D .π[,π]410.已知x ∈R 且0x ≠,θ∈R ,则222(1sin )(1cos )x x xθθ+-+--+的最小值是A .22B .8C .122+D .942-第Ⅱ卷(非选择题部分,共110分)注意事项:用钢笔或签字笔将试题卷中的题目做在答题纸上,做在试题卷上无效.二、填空题:本大题共7小题,多空题每小题6分,单空题每小题4分,共36分.11.已知数列{}n a 的通项公式为31n a n =-*()n ∈N ,则57a a += ▲ ;该数列前n 项和n S =▲ .12.已知随机变量ξ的分布列如右表, 则m = ▲ ;()E ξ= ▲ . 13.若62()a x x-展开式中3x 项的系数为12-,则a = ▲ ;常数项是 ▲ .14.在ABC ∆中,角,,A B C 所对的边分别为,,a b c ,已知π3A ∠=,7,5a b ==,点D 满足2BD DC =u u u r u u u r ,则边c = ▲ ;AD = ▲ .15.已知直线1l :210x y -+=,直线2l :420x y a -+=,圆C :2220x y x +-=.若C 上任意一点P 到两直线1l ,2l 的距离之和为定值5a = ▲ .16.现有7名志愿者,其中只会俄语的有3人,既会俄语又会英语的有4人. 从中选出4人担任“一带一路”峰会开幕式翻译工作,2人担任英语翻译,2人担任俄语翻译,共有 ▲ 种不同的选法. 17.已知向量a,b 满足32-=+=a b a b ,则a 的取值范围是 ▲ .三、解答题:本大题共5小题,共74分,解答应写出文字说明、证明过程或演算步骤. 18.(本小题满分14分)ξ 1 2P13m已知函数()sin3cos cos3sin cos 2f x x x x x x =-+. (Ⅰ) 求π()4f 的值;(Ⅱ) 求()f x 的单调递增区间.19.(本小题满分15分)如图,在几何体111ABC A B C -中,平面11A ACC ⊥底面ABC ,四边形11A ACC 是正方形,11B C BC ∥,Q 是1A B 的中点,且112AC BC B C ==,2π3ACB ∠=. (Ⅰ) 证明:1B Q ∥平面11A ACC ;(Ⅱ) 求直线AB 与平面11A BB 所成角的正弦值.20.(本小题满分15分) 已知函数ln (),xf x x=() (0)=>g x kx k ,函数{}()max (),(),F x f x g x =其中{}max ,a b ,,,.a a b b a b ≥⎧=⎨<⎩(Ⅰ)求()f x 的极值;(Ⅱ)求()F x 在[]1, e 上的最大值(e 为自然对数底数).21.(本小题满分15分)已知1F ,2F 是椭圆C :2212x y +=的左右焦点,,A B 是椭圆C 上的两点,且都在x 轴上方,1AF 2BF ∥,设21,AF BF 的交点为M .(Ⅰ)求证:1211AF BF + 为定值; (Ⅱ)求动点M 的轨迹方程. 22.(本小题满分15分) 已知数列{}n a 满足1n na t =+(,,3,n t t n t *∈≥≤N 证明:(Ⅰ)1e -<n a n a (e 为自然对数底数);(Ⅱ)12111(1)ln(1)nt n a a a +++>++L ; (Ⅲ)123()()()()1ttttn a a a a ++++<L .2017年9月丽水、衢州、湖州三地市教学质量检测试卷高三数学参考答案11. 34,232n n +; 12 . 23, 53;13. 2,60;14. 8,3; 15. 18-; 16. 60;17.[1,2].三、解答题:本大题共5小题,共74分.解答应写出文字说明、证明过程或演算步骤. 18. (本小题满分14分)已知函数()sin3cos cos3sin cos 2f x x x x x x =-+. (Ⅰ) 求π()4f 的值;(Ⅱ) 求()f x 的单调递增区间.解 (Ⅰ) 因为 π3ππ3πππ()sin cos cos sin cos 444442f =-+02222=+⨯+ 1=所以 π()14f = …………………………………………………………5分(Ⅱ) 因为 ()sin(3)cos 2f x x x x =-+π)4x =+ …………………………………………………9分(化简出现在第(Ⅰ)小题中同样给4分)由正弦函数的性质得 πππ2π2+2π242k x k -+≤≤+,Z k ∈ 解得3ππππ88k x k -+≤≤+,Z k ∈ 所以()f x 的单调递增区间是3ππ[π, π]88k k -++,Z k ∈………………………14分 19.(本小题满分15分)如图,在几何体111ABC A B C -中,平面11A ACC ⊥底面ABC ,四边形11A ACC 是正方形,11B C BC ∥,Q 是1A B 的中点,且112AC BC B C ==,2π3ACB ∠=. (Ⅰ) 证明:1B Q ∥平面11A ACC ;(Ⅱ) 求直线AB 与平面11A BB 所成角的正弦值.(Ⅰ) 证明:如图1所示,连接11,AC A C 交于M 点,连接MQ . 因为 四边形11A ACC 是正方形, 所以 M 是1AC 的中点又已知Q 是1A B 的中点 所以 1 2MQ BC ∥又因为 11B C BC ∥且11=2BC B C所以 11 MQ B C ∥,即四边形11B C MQ 是平行四边形所以 11B Q C M ∥,因此 1B Q ∥平面11A ACC .…………………………………………………7分(Ⅱ) 如图2所示,过点B 作面11A B B 与 面ABC 的交线BD ,交直线CA 于D .过A 作线BD 的垂线AH ,垂足为H . 再过A 作线1A H 的垂线AG ,垂足为G . 因为1,AH BD AA BD ⊥⊥, 所以BD ⊥面1A AH ,所以BD ⊥AG ,又因为1A H AG ⊥,所以AG ⊥面11A B B ,所以ABG ∠即AB 与面11A B B 所成的角.………………10分 因为11A B ∥面ABC ,所以11A B ∥BD , 且A 为CD 的中点,如图2所示,CP 为BD 边上的高,ABBD因为011sin12022CB CD BD CP ⋅=⋅所以CP ==2CP AH =因为12AA =,所以1A H ==, 11AH AA AG A H⋅===所以sin 31ABG ∠===………………………………………15分20.(本小题满分15分) 已知函数ln (),xf x x =(),(0)g x kx k =>函数{}()max (),(),F x f x g x =其中{}max ,a b ,,,.a ab b a b ≥⎧=⎨<⎩ (第19题图4)HA(Ⅰ) 求()f x 的极值;(Ⅱ) 求()F x 在[]1,e 上的最大值(e 为自然对数底数). (Ⅰ) 解: 因为21ln ()xf x x-'=由 ()0f x '=,解得:e x =……………………………………………………3分 因为x (0, e)e (e, +)∞()f x '+0 -()f x Z 1e]所以 ()f x 的极大值为1e,无极小值.………………………………………7分 (Ⅱ) 因为()f x 在[1, e]上是增函数, 所以 max 1()(e)ef x f ==……………………………………………………10分 ()g x 在[1, e]上是增函数所以 max ()(e)e g x g k ==……………………………………………………13分所以 2max211, 0<,e e ()1e, .e k F x k k ⎧<⎪⎪=⎨⎪≥⎪⎩……………………………………………15分21.(本小题满分15分)已知1F ,2F 是椭圆C :2212x y +=的左右焦点,,A B 是椭圆C 上的两点,且都在x 轴上方,1AF 2BF ∥,设21,AF BF 的交点为M .(Ⅰ)求证:1211AF BF + 为定值; (Ⅱ)求动点M 的轨迹方程.(I )证1:设直线1AF 所在直线的方程为1x my =- ,与椭圆方程联立2222,1,x y x my ⎧+=⎨=-⎩ 化简可得()22+2-210m y my -= 因为A 点在x 轴上方, 所以22A y m =+所以(1202A m AF m =-=+同理可得:(2202B m BF m -=-=+…………4分所以211AF =,221BF =所以221211+AF BF =2⎛⎫221-m m +⎪⎭=7分 证2:如图2所示,延长1AF 交椭圆于1B ,由椭圆的对称性可知:112B F BF =,所以 只需证明11111+AF B F 为定值, 设直线1AF 所在直线的方程为1x my =- ,与椭圆方程联立2222,1,x y x my ⎧+=⎨=-⎩ 化简可得:()22+2-21m y my -所以11112211111++AF B F y y y⎛⎫=⎪⎪⎭====………………………………………………7分(II)解法1:设直线2AF,1BF所在直线的方程为11x k y=+,21x k y=-121,1,x k yx k y=+⎧⎨=-⎩所以M点的坐标为1221212k kxk kyk k+⎧=⎪-⎪⎨⎪=⎪-⎩……………………………………10分又因为1122A AA A Ax myk my y y--===-,2122B BB B Bx myk my y y++===+所以12222211+=+=222A B B Ak k m m my y y ym⎛⎫-++-⎪⎝⎭⎛⎫=⎝所以()12+226k k m m m=+=,2221-2k k⎛⎫=所以1221212k kxk kyk k+⎧===⎪-⎪⎨⎪===⎪-⎩所以()221 09188x yy+=>……………………………………………………15分解法2:如图3所示,设1122,AF d BF d==,则112MF dMB d=,第21题图312所以1111111212MF d d MF BF BF d d d d =⇒=⋅++又因为122BF BF a +==所以122BF BF d ==所以()121111212d d d MF BF d d d d =⋅=++ ……………………………………10分同理可得()21212d d MF d d =+,所以()()122112121212122d d d d d d MF MF d d d d d d +=+=+++ ……………12分由(I)可知121221111+d d d d d d =+ ……………………………………………14分所以12MF MF +=所以动点M 的轨迹方程为()221 09188x y y +=>………………………………15分 22.(本小题满分15分) 已知数列{}n a 满足1n na t =+(,,3,)n t t n t *∈≥≤N . 证明: (Ⅰ) 1n a n a -<e (e 为自然对数底数);(Ⅱ)12111(1)ln(1)nt n a a a +++>++L ; (Ⅲ) 123()()()()1ttttn a a a a ++++<L . 证明: (Ⅰ) 设1()ex f x x -=- 因为 1()e1x f x -'=-当(0,1)x ∈时,()0f x '<,即()f x 在(0, 1)单调递减因为 0111n n t a t t <=≤<++ 所以 1()e(1)0n a n n f a a f -=->= 即 1n a n a -<e …………………………………………………………………………5分 (Ⅱ) 即证 12111ln(1)(1)(1)(1)nn t a t a t a +++>++++L 即证 1111ln(1)23n n++++>+L 设()ln(1)g x x x =-+1()111x g x x x '=-=++ 因为当0x >时,()0g x '>,即 ()g x 在(0,)+∞上单调递增所以 ()ln(1)(0)0g x x x g =-+>=即 0x >时,有ln(1)x x >+所以 1113411ln 2ln ln ln ln(1)2323n n n n +++++>++++=+L L 所以 12111(1)ln(1)nt n a a a +++>++L ……………………………………10分 (Ⅲ) 因为 123()()()()t t t t n a a a a ++++L3121111(e )(e )(e )(e )n a a a a t t t t ----<++++L2111e (1e )1et tn t t tt -+++-=-22211111e (1e )e 11e 1e t t t t t t t t t t --+++++--≤=-- 设 1e tt q += 因为314e e 2tt q +=≥> 211e 11et t tt -++-=-1111111t t q q q q q ----=<<--- 所以 123()()()()1t t t t n a a a a ++++<L ………………………………15分。
2017年浙江数学高考试题有答案【精编版】

绝密★启用前2017年普通高等学校招生全国统一考试(浙江卷)数 学一、 选择题:本大题共10小题,每小题4分,共40分。
每小题给出的四个选项中,只有一项是符合题目要求的。
1.已知集合{}{}x -1<x Q x =<<<1,=0x 2P ,那么P Q U =A.(-1,2)B.(0,1)C.(-1,0)D.(1,2)2.椭圆x y +=22194的离心率是 A. 133B.5C. 23D. 593.某几何体的三视图如图所示(单位:cm ),则该几何体的体积(单位:3cm )是A.π+12B.π+32 C. π3+12D. π3+32 4.若x,y 满足约束条件x 0x y 30x 2y 0⎧≥⎪≥=+⎨⎪≤⎩+-,则z 2-x y 的取值范围是A.[0,6]B. [0,4]C.[6, +∞)D.[4, +∞) 5.若函数()2f x =++x ax b在区间[0,1]上的最大值是M,最小值是m,则M-mA. 与a 有关,且与b 有关B. 与a 有关,但与b 无关C. 与a 无关,且与b 无关D. 与a 无关,但与b 有关6.已知等差数列{}n a 的公差为d,前n 项和为n S ,则“d>0”是465"+2"S S S >的 A. 充分不必要条件 B. 必要不充分条件 C. 充分必要条件 D.既不充分也不必要条件7.函数y (x)y (x)f f ==,的导函数的图像如图所示,则函数y (x)f =的图像可能是8.已知随机变量i ξ满足P (i ξ=1)=p i ,P (i ξ=0)=1—p i ,i =1,2.若0<p 1<p 2<12,则 A .1E()ξ<2E()ξ,1D()ξ<2D()ξ B .1E()ξ<2E()ξ,1D()ξ>2D()ξ C .1E()ξ>2E()ξ,1D()ξ<2D()ξD .1E()ξ>2E()ξ,1D()ξ>2D()ξ9.如图,已知正四面体D –ABC (所有棱长均相等的三棱锥),P ,Q ,R 分别为AB ,BC ,CA 上的点,AP=PB ,2BQ CRQC RA==,分别记二面角D –PR –Q ,D –PQ –R ,D –QR –P 的平面角为α,β,γ,则A .γ<α<βB .α<γ<βC .α<β<γD .β<γ<α10.如图,已知平面四边形ABCD ,AB ⊥BC ,AB =BC =AD =2,CD =3,AC 与BD 交于点O ,记1·I OA OB u u u r u u u r = ,2·I OB OC u u u r u u u r =,3·I OC OD u u u r u u u r =,则A .I 1<I 2<I 3B .I 1<I 3<I 2C . I 3< I 1<I 2D . I 2<I 1<I 3非选择题部分(共110分)二、填空题:本大题共7小题,多空题每题6分,单空题每题4分,共36分。
2017年浙江数学高考试题有答案【高考】

绝密★启用前2017年普通高等学校招生全国统一考试(浙江卷)数 学一、 选择题:本大题共10小题,每小题4分,共40分。
每小题给出的四个选项中,只有一项是符合题目要求的。
1.已知集合{}{}x -1<x Q x =<<<1,=0x 2P ,那么P Q U =A.(-1,2)B.(0,1)C.(-1,0)D.(1,2)2.椭圆x y +=22194的离心率是 A. 133B.5C. 23D. 593.某几何体的三视图如图所示(单位:cm ),则该几何体的体积(单位:3cm )是A.π+12B.π+32 C. π3+12D. π3+32 4.若x,y 满足约束条件x 0x y 30x 2y 0⎧≥⎪≥=+⎨⎪≤⎩+-,则z 2-x y 的取值范围是A.[0,6]B. [0,4]C.[6, +∞)D.[4, +∞) 5.若函数()2f x =++x ax b在区间[0,1]上的最大值是M,最小值是m,则M-mA. 与a 有关,且与b 有关B. 与a 有关,但与b 无关C. 与a 无关,且与b 无关D. 与a 无关,但与b 有关6.已知等差数列{}n a 的公差为d,前n 项和为n S ,则“d>0”是465"+2"S S S >的 A. 充分不必要条件 B. 必要不充分条件 C. 充分必要条件 D.既不充分也不必要条件7.函数y (x)y (x)f f ==,的导函数的图像如图所示,则函数y (x)f =的图像可能是8.已知随机变量i ξ满足P (i ξ=1)=p i ,P (i ξ=0)=1—p i ,i =1,2.若0<p 1<p 2<12,则 A .1E()ξ<2E()ξ,1D()ξ<2D()ξ B .1E()ξ<2E()ξ,1D()ξ>2D()ξ C .1E()ξ>2E()ξ,1D()ξ<2D()ξD .1E()ξ>2E()ξ,1D()ξ>2D()ξ9.如图,已知正四面体D –ABC (所有棱长均相等的三棱锥),P ,Q ,R 分别为AB ,BC ,CA 上的点,AP=PB ,2BQ CRQC RA==,分别记二面角D –PR –Q ,D –PQ –R ,D –QR –P 的平面角为α,β,γ,则A .γ<α<βB .α<γ<βC .α<β<γD .β<γ<α10.如图,已知平面四边形ABCD ,AB ⊥BC ,AB =BC =AD =2,CD =3,AC 与BD 交于点O ,记1·I OA OB u u u r u u u r = ,2·I OB OC u u u r u u u r =,3·I OC OD u u u r u u u r =,则A .I 1<I 2<I 3B .I 1<I 3<I 2C . I 3< I 1<I 2D . I 2<I 1<I 3非选择题部分(共110分)二、填空题:本大题共7小题,多空题每题6分,单空题每题4分,共36分。
【月考试卷】浙江省湖州、衢州、丽水三市2017届高三9月教学质量检测数学试题Word版含答案
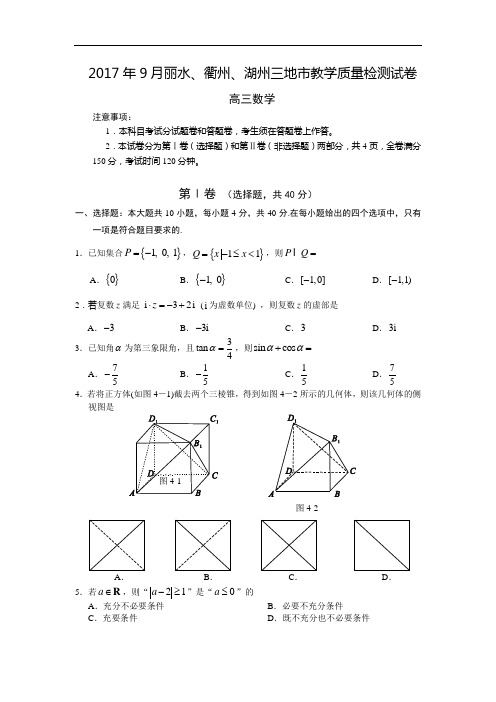
2017年9月丽水、衢州、湖州三地市教学质量检测试卷高三数学注意事项:1.本科目考试分试题卷和答题卷,考生须在答题卷上作答。
2.本试卷分为第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分,共4页,全卷满分150分,考试时间120分钟。
第Ⅰ卷 (选择题,共40分)一、选择题:本大题共10小题,每小题4分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的.1.已知集合{}1, 0, 1P =-,{}11Q x x =-≤<,则P Q =A .{}0B .{}1, 0-C .[1,0]-D .[1,1)-2.若复数z 满足 i 32i z ⋅=-+ (i 为虚数单位) ,则复数z 的虚部是 A .3- B .3i - C .3 D .3i3.已知角α为第三象限角,且3tan 4α=,则sin cos αα+= A .75- B .15- C .15D .754.若将正方体(如图4-1)截去两个三棱锥,得到如图4-2所示的几何体,则该几何体的侧视图是A .B .C .D .5.若a ∈R ,则“21a -≥”是“0a ≤”的 A .充分不必要条件B .必要不充分条件C .充要条件D .既不充分也不必要条件6.已知12,F F 分别为双曲线22221(0,0)x y a b a b-=>>的左右焦点,P 为双曲线右支上一点,图4-2满足21π2PF F ∠=,连接1PF 交y 轴于点Q,若2QF =,则双曲线的离心率是 ABC.1 D.17.若关于x 的不等式23x a x -->在(,0)-∞上有解,则实数a 的取值范围是A .13(,3)4-B .13(3,)4- C .13(,)4-∞- D .(3,)+∞ 8.已知,x y ∈R 满足条件10,20,2.x y x y x -+≥⎧⎪+-≥⎨⎪≤⎩若目标函数z ax y =+仅在点(2,3) 处取到最大值,则实数a 的取值范围是A .(, 1)-∞B .(, 1]-∞C .[1, +)-∞D .(1, +)-∞9.已知点O 在二面角AB αβ--的棱上,点P 在半平面α内,且45POB ∠= .若对于半平面β内异于O 的任意一点Q ,都有45POQ ∠≥ ,则二面角AB αβ--的取值范围是 A .π[0,]4B .ππ[,]42C .π[,π]2D .π[,π]410.已知x ∈R 且0x ≠,θ∈R ,则222(1sin )(1cos )x x xθθ+-+--+的最小值是 A. B .8C.1+ D.9-第Ⅱ卷(非选择题部分,共110分)注意事项:用钢笔或签字笔将试题卷中的题目做在答题纸上,做在试题卷上无效.二、填空题:本大题共7小题,多空题每小题6分,单空题每小题4分,共36分. 11.已知数列{}n a 的通项公式为31n a n =-*()n ∈N ,则57a a += ▲ ;该数列前n 项和n S = ▲ .12.已知随机变量ξ的分布列如右表, 则m = ▲ ;()E ξ= ▲ . 13.若62()a x x-展开式中3x 项的系数为12-,则a = ▲ ;常数项是 ▲ . 14.在ABC ∆中,角,,A B C 所对的边分别为,,a b c ,已知π3A ∠=,7,5a b ==,点D 满足2BD DC =,则边c = ▲ ;AD = ▲ .15.已知直线1l :210x y -+=,直线2l :420x y a -+=,圆C :2220x y x +-=.若C 上任意一点P 到两直线1l ,2l的距离之和为定值a = ▲ . 16.现有7名志愿者,其中只会俄语的有3人,既会俄语又会英语的有4人. 从中选出4人担任“一带一路”峰会开幕式翻译工作,2人担任英语翻译,2人担任俄语翻译,共有▲ 种不同的选法.17.已知向量a,b 满足32-=+=a b a b ,则a 的取值范围是 ▲ .三、解答题:本大题共5小题,共74分,解答应写出文字说明、证明过程或演算步骤. 18.(本小题满分14分)已知函数()sin3cos cos3sin cos 2f x x x x x x =-+. (Ⅰ) 求π()4f 的值;(Ⅱ) 求()f x 的单调递增区间.19.(本小题满分15分)如图,在几何体111ABC A B C -中,平面11A ACC ⊥底面ABC ,四边形11A ACC 是正方形,11B C BC ∥,Q 是1A B 的中点,且112AC BC B C ==,2π3ACB ∠=. (Ⅰ) 证明:1B Q ∥平面11A ACC ;(Ⅱ) 求直线AB 与平面11A BB 所成角的正弦值.20.(本小题满分15分) 已知函数ln (),xf x x=() (0)=>g x kx k ,函数{}()max (),(),F x f x g x =其中{}max ,a b ,,,.a ab b a b ≥⎧=⎨<⎩ (Ⅰ)求()f x 的极值;(Ⅱ)求()F x 在[]1, e 上的最大值(e 为自然对数底数).21.(本小题满分15分)已知1F ,2F 是椭圆C :2212x y +=的左右焦点,,A B 是椭圆C 上的两点,且都在x 轴上方,1AF 2BF ∥,设21,AF BF 的交点为M . (Ⅰ)求证:1211AF BF + 为定值; (Ⅱ)求动点M 的轨迹方程.22.(本小题满分15分) 已知数列{}n a 满足1n na t =+(,,3,)n t t n t *∈≥≤N . 证明:(Ⅰ)1e -<n a n a (e 为自然对数底数); (Ⅱ)12111(1)ln(1)nt n a a a +++>++ ; (Ⅲ)123()()()()1t t t t n a a a a ++++< .2017年9月丽水、衢州、湖州三地市教学质量检测试卷高三数学参考答案一、 选择题:本大题共有10小题,每小题4分,共40分11. 34,232n n +; 12 . 23, 53;13. 2,60;14. 8; 15. 18-; 16. 60; 17.[1,2].三、解答题:本大题共5小题,共74分.解答应写出文字说明、证明过程或演算步骤. 18. (本小题满分14分)已知函数()sin3cos cos3sin cos 2f x x x x x x =-+.(Ⅰ) 求π()4f 的值;(Ⅱ) 求()f x 的单调递增区间.解 (Ⅰ) 因为 π3ππ3πππ()sin cos cos sin cos 444442f =-+02222=++ 1=所以 π()14f = …………………………………………………………5分(Ⅱ) 因为 ()sin(3)cos 2f x x x x =-+π)4x =+ …………………………………………………9分(化简出现在第(Ⅰ)小题中同样给4分) 由正弦函数的性质得 πππ2π2+2π242k x k -+≤≤+,Z k ∈ 解得3ππππ88k x k -+≤≤+,Z k ∈ 所以()f x 的单调递增区间是3ππ[π, π]88k k -++,Z k ∈………………………14分 19.(本小题满分15分)如图,在几何体111ABC A B C -中,平面11A ACC ⊥底面ABC ,四边形11A ACC 是正方形,11B C BC ∥,Q 是1A B 的中点,且112AC BC B C ==,2π3ACB ∠=. (Ⅰ) 证明:1B Q ∥平面11A ACC ;(Ⅱ) 求直线AB 与平面11A BB 所成角的正弦值.(Ⅰ) 证明:如图1所示,连接11,AC AC 交于M因为 四边形11A ACC 是正方形,所以 M 是1AC 的中点 又已知Q 是1A B 的中点 所以 12M Q B C ∥又因为 11B C BC ∥且11=2BC B C所以 11 MQ B C ∥,即四边形11B C MQ 是平行四边形所以 11BQ C M ∥,因此 1B Q ∥平面11A ACC .…………………………………………………7分 (Ⅱ) 如图2所示,过点B 作面11A B B 与 面ABC 的交线BD ,交直线CA 于D .过A 作线BD 的垂线AH ,垂足为H .再过A 作线1A H 的垂线AG ,垂足为G . 因为1,AH BD AA BD ⊥⊥, 所以BD ⊥面1A AH ,所以BD ⊥AG ,又因为1A H AG ⊥,所以AG ⊥面11A B B ,所以ABG ∠即AB 与面11A B B 所成的角.………………10分 因为11A B ∥面ABC ,所以11A B ∥BD , 且A 为CD 的中点,如图2所示,CP 为BD 边上的高,ABBD , 因为011sin12022CB CD BD CP ⋅=⋅所以CP ==2CP AH =因为12AA =,所以1AH ==11AH AA AG A H⋅===所以sin ABG ∠===15分20.(本小题满分15分) 已知函数ln (),xf x x =(),(0)g x kx k =>函数{}()max (),(),F x f x g x =其中{}max ,a b ,,,.a ab b a b ≥⎧=⎨<⎩ (Ⅰ) 求()f x 的极值;(Ⅱ) 求()F x 在[]1,e 上的最大值(e 为自然对数底数). (Ⅰ) 解: 因为21ln ()xf x x -'=由 ()0f x '=,解得:e x =……………………………………………………3分 因为x(0, e)e(e, +)∞()f x '+0 -()f x1e所以 ()f x 的极大值为1e,无极小值.………………………………………7分 (Ⅱ) 因为()f x 在[1, e]上是增函数, 所以 max 1()(e)ef x f ==……………………………………………………10分 ()g x 在[1, e]上是增函数所以 max ()(e)e g x g k ==……………………………………………………13分所以 2max211, 0<,e e ()1e, .e k F x k k ⎧<⎪⎪=⎨⎪≥⎪⎩……………………………………………15分 21.(本小题满分15分)已知1F ,2F 是椭圆C :2212x y +=的左右焦点,,A B 是椭圆C 上的两点,且都在x 轴上方,1AF 2BF ∥,设21,AF BF 的交点为M . (Ⅰ)求证:1211AF BF + 为定值; (Ⅱ)求动点M 的轨迹方程.(I )证1:设直线1AF 所在直线的方程为1x my =-与椭圆方程联立2222,1,x y x my ⎧+=⎨=-⎩ 化简可得()22+2-210m y my -=因为A 点在x 轴上方, 所以22A y m =+所以(1202A m AF y m =-=+同理可得:(2202B m BF y m -=-=+…………4分所以211AF =,221BF =所以221211+AF BF =2⎛⎫221-m m +⎪⎭=7分 证2:如图2所示,延长1AF 交椭圆于1B ,由椭圆的对称性可知:112B F BF =,所以 只需证明11111+AF B F 为定值, 设直线1AF 所在直线的方程为1x my =- ,与椭圆方程联立2222,1,x y x my ⎧+=⎨=-⎩ 化简可得:()22+2-2m y my -所以111121111++AF B F y y ⎛⎫=⎪⎪⎭====7分(II )解法1:设直线2AF ,1BF 所在直线的方程为11x k y =+ ,21x k y =-121,1,x k y x k y =+⎧⎨=-⎩所以M 点的坐标为1221212k k x k k y k k +⎧=⎪-⎪⎨⎪=⎪-⎩……………………………………10分 又因为1122A A A A A x my k m y y y --===- ,2122B B B B Bx my k m y y y ++===+所以12222211+=+=22 2A B B A k k m m m y y y y m ⎛⎫-++- ⎪⎝⎭⎛⎫ =+ ⎝ 所以 ()12+226k k m m m =+=,2221-2k k ⎛⎫=所以1221212k k x k k y k k +⎧===⎪-⎪⎨⎪===⎪-⎩所以 ()221 09188x y y +=>……………………………………………………15分 解法2:如图3所示,设1122,AF d BF d ==,则112MF d MBd =, 所以1111111212MF d d MF BF BF d d d d =⇒=⋅++又因为122BF BF a +==所以122BF BF d ==所以()121111212d d d MF BF d d d d =⋅=++ ……………………………………10分同理可得()21212d d MF d d =+,所以()()122112121212122d d d d d d MF MF d d d d d d +=+=+++ ……………12分由(I)可知121221111+d d d d d d =+ ……………………………………………14分 第21题图312所以12MF MF +=所以动点M 的轨迹方程为()221 09188x y y +=>………………………………15分 22.(本小题满分15分)已知数列{}n a 满足1n n a t =+(,,3,)n t t n t *∈≥≤N . 证明:(Ⅰ) 1n a n a -<e (e 为自然对数底数);(Ⅱ) 12111(1)ln(1)nt n a a a +++>++ ; (Ⅲ) 123()()()()1t t t t n a a a a ++++< .证明:(Ⅰ) 设1()e x f x x -=-因为 1()e 1x f x -'=-当(0,1)x ∈时,()0f x '<,即()f x 在(0, 1)单调递减因为 0111n n t a t t <=≤<++ 所以 1()e (1)0n a n n f a a f -=->=即 1n a n a -<e …………………………………………………………………………5分 (Ⅱ) 即证 12111ln(1)(1)(1)(1)nn t a t a t a +++>++++ 即证 1111l n (1)23n n ++++>+ 设()ln(1)g x x x =-+1()111x g x x x '=-=++ 因为当0x >时,()0g x '>,即 ()g x 在(0,)+∞上单调递增所以 ()ln(1)(0)0g x x x g =-+>=即 0x >时,有ln(1)x x >+所以 1113411ln 2ln ln ln ln(1)2323n n n n +++++>++++=+ 所以 12111(1)ln(1)nt n a a a +++>++ ……………………………………10分 (Ⅲ) 因为 123()()()()t t t t n a a a a ++++ 3121111(e )(e )(e )(e )n a a a a t t t t ----<++++2111e (1e )1et tn t t tt -+++-=-22211111e (1e )e 11e1e t t t t t t t t t t --+++++--≤=-- 设 1e tt q += 因为314e e 2t t q +=≥>211e 11et t tt -++-=-1111111t t q q q q q ----=<<--- 所以 123()()()()1t t t t n a a a a ++++< ………………………………15分。
(精校版)2017年浙江数学高考试题文档版(试题不全%2C无答案)

绝密★启用前2017年普通高等学校招生全国统一考试(浙江卷)数 学本试题卷分选择题和非选择题两部分。
全卷共4页,选择题部分1至2页,非选择题部分3至4页。
满分150分。
考试用时120分钟。
考生注意:1.答题前,请务必将自己的姓名、准考证号用黑色字迹的签字笔或钢笔分别填在试题卷和答题纸规定的位置上。
2.答题时,请按照答题纸上“注意事项”的要求,在答题纸相应的位置上规范作答,在本试题卷上的作答一律无效。
参考公式:球的表面积公式 锥体的体积公式24S R =π13V Sh =球的体积公式 其中S 表示棱锥的底面面积,h 表示棱锥的高 343V R =π台体的体积公式其中R 表示球的半径 1()3a ab b V h S S S S =+⋅+柱体的体积公式 其中S a ,S b 分别表示台体的上、下底面积 V =Shh 表示台体的高其中S 表示棱柱的底面面积,h 表示棱柱的高选择题部分(共40分)一、选择题:本大题共10小题,每小题4分,共40分。
在每小题给出的四个选项中,只有一项是符合题目要求的。
1.2.椭圆22194x y +=的离心率是 A .133B .53C .23D .593.某几何体的三视图如图所示(单位:cm ),则该几何体的体积(单位:cm 3)是A .π2+1B .π2+3 C .3π2+1 D .3π2+3 4.若x ,y 满足约束条件03020x x y x y ≥⎧⎪+-≥⎨⎪-≤⎩,则z =x +2y 的取值范围是A .[0,6]B .[0,4]C .[6,+∞]D .[4,+∞]5.若函数f (x )=x 2+ ax +b 在区间[0,1]上的最大值是M ,最小值是m ,则M – mA .与a 有关,且与b 有关B .与a 有关,但与b 无关C .与a 无关,且与b 无关D .与a 无关,但与b 有关6.已知等差数列[a n ]的公差为d ,前n 项和为S n ,则“d >0”是“S 4 + S 6”>2S 5的A .充分不必要条件B .必要不充分条件C .充分必要条件D .既不充分也不必要条件7.函数y=f (x )的导函数()y f x '=的图像如图所示,则函数y=f (x )的图像可能是8.已知随机变量ξ1满足P (1ξ=1)=p i ,P (1ξ=1)=1—p i ,i =1,2.若0<p 1<p 2<12,则 A .1E()ξ<2E()ξ,1D()ξ<2D()ξ B .1E()ξ<2E()ξ,1D()ξ>2D()ξ C .1E()ξ>2E()ξ,1D()ξ<2D()ξD .1E()ξ>2E()ξ,1D()ξ>2D()ξ9.如图,已知正四面体D –ABC (所有棱长均相等的三棱锥),PQR 分别为AB ,BC ,CA 上的点,AP=PB ,2BQ CRQC RA==,分别学&科网记二面角D –PR –Q ,D –PQ –R ,D –QR –P 的平面较为α,β,γ,则A .γ<α<βB .α<γ<βC .α<β<γD .β<γ<α10.如图,已知平面四边形ABCD ,AB ⊥BC ,AB =BC =AD =2,CD =3,AC 与BD 交于点O ,记1·I OA OB u u u r u u u r = ,2·I OB OC u u u r u u u r =,3·I OC OD u u u r u u u r=,则A .I 1<I 2<I 3B .I 1<I 3<I 2C . I 3< I 1<I 2D . I 2<I 1<I 3非选择题部分(共110分)二、填空题:本大题共7小题,多空题每题6分,单空题每题4分,共36分。
2017年9月丽水衢州湖州三地教学质量检测试卷

图4-12017年9月丽水、衢州、湖州三地市教学质量检测试卷高三数学注意事项:1.本科目考试分试题卷和答题卷,考生须在答题卷上作答。
2.本试卷分为第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分,共4页,全卷满分150分,考试时间120分钟。
第Ⅰ卷 (选择题,共40分)一、选择题:本大题共10小题,每小题4分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的.1.已知集合{}1, 0, 1P =-,{}11Q x x =-≤<,则P Q =A .{}0B .{}1, 0-C .[1,0]-D .[1,1)-2.若复数z 满足 i 32i z ⋅=-+ (i 为虚数单位) ,则复数z 的虚部是 A .3- B .3i - C .3 D .3i3.已知角α为第三象限角,且3tan 4α=,则sin cos αα+= A .75- B .15- C .15D .754.若将正方体(如图4-1)截去两个三棱锥,得到如图4-2所示的几何体,则该几何体的侧视图是A .B .C .D .5.若a ∈R ,则“21a -≥”是“0a ≤”的 A .充分不必要条件 B .必要不充分条件C .充要条件D .既不充分也不必要条件6.已知12,F F 分别为双曲线22221(0,0)x y a b a b-=>>的左右焦点,P 为双曲线右支上一点,满足21π2PF F ∠=,连接1PF 交y 轴于点Q,若2QF =,则双曲线的离心率是ABC.1+ D.1+ 7.若关于x 的不等式23x a x -->在(,0)-∞上有解,则实数a 的取值范围是A .13(,3)4-B .13(3,)4- C .13(,)4-∞-D .(3,)+∞ 8.已知,x y ∈R 满足条件10,20,2.x y x y x -+≥⎧⎪+-≥⎨⎪≤⎩若目标函数z ax y =+仅在点(2,3) 处取到最大值,则实数a 的取值范围是A .(, 1)-∞B .(, 1]-∞C .[1, +)-∞D .(1, +)-∞ 9.已知点O 在二面角AB αβ--的棱上,点P 在半平面α内,且45POB ∠=.若对于半平面β内异于O 的任意一点Q ,都有45POQ ∠≥,则二面角AB αβ--的取值范围是A .π[0,]4B .ππ[,]42C .π[,π]2D .π[,π]410.已知x ∈R 且0x ≠,θ∈R ,则222(1sin )(1cos )x x xθθ+-+--+的最小值是A. B .8 C.1+ D.9-第Ⅱ卷(非选择题部分,共110分)注意事项:用钢笔或签字笔将试题卷中的题目做在答题纸上,做在试题卷上无效.二、填空题:本大题共7小题,多空题每小题6分,单空题每小题4分,共36分.11.已知数列{}n a 的通项公式为31n a n =-*()n ∈N ,则57a a += ▲ ;该数列前n 项和n S = ▲ .12.已知随机变量ξ的分布列如右表,则m = ▲ ;()E ξ= ▲ .13.若62()a x x-展开式中3x 项的系数为12-,则a = ▲ ;常数项是 ▲ . 14.在ABC ∆中,角,,A B C 所对的边分别为,,a b c ,已知π3A ∠=,7,5a b ==,点D 满足2BD DC =,则边c = ▲ ;AD = ▲ .15.已知直线1l :210x y -+=,直线2l :420x y a -+=,圆C :2220x y x +-=.若C 上任意一点P 到两直线1l ,2l 的距离之和为定值a = ▲ . 16.现有7名志愿者,其中只会俄语的有3人,既会俄语又会英语的有4人. 从中选出4人担任“一带一路”峰会开幕式翻译工作,2人担任英语翻译,2人担任俄语翻译,共有 ▲ 种不同的选法. 17.已知向量a,b 满足32-=+=a b a b ,则a 的取值范围是 ▲ .三、解答题:本大题共5小题,共74分,解答应写出文字说明、证明过程或演算步骤. 18.(本小题满分14分)已知函数()sin3cos cos3sin cos 2f x x x x x x =-+. (Ⅰ) 求π()4f 的值;(Ⅱ) 求()f x 的单调递增区间.19.(本小题满分15分)如图,在几何体111ABC A B C -中,平面11A ACC ⊥底面ABC ,四边形11A ACC 是正方形,11B C BC ∥,Q 是1A B 的中点,且112AC BC B C ==,2π3ACB ∠=. (Ⅰ) 证明:1B Q ∥平面11A ACC ;(Ⅱ) 求直线AB 与平面11A BB 所成角的正弦值.20.(本小题满分15分) 已知函数ln (),xf x x=() (0)=>g x kx k ,函数{}()max (),(),F x f x g x =其中{}max ,a b ,,,.a ab b a b ≥⎧=⎨<⎩ (Ⅰ)求()f x 的极值;(Ⅱ)求()F x 在[]1, e 上的最大值(e 为自然对数底数).21.(本小题满分15分)已知1F ,2F 是椭圆C :2212x y +=的左右焦点,,A B 是椭圆C 上的两点,且都在x 轴上方,1AF 2BF ∥,设21,AF BF 的交点为M . (Ⅰ)求证:1211AF BF + 为定值; (Ⅱ)求动点M 的轨迹方程.22.(本小题满分15分) 已知数列{}n a 满足1n na t =+(,,3,)n t t n t *∈≥≤N . 证明: (Ⅰ)1e -<n a n a (e 为自然对数底数);(Ⅱ)12111(1)ln(1)nt n a a a +++>++;(Ⅲ)123()()()()1t t tt n a a a a ++++<.。
2017年9月丽水、衢州、湖州三地市教学质量检测试卷
2017年9月丽水、衢州、湖州三地市教学质量检测试卷高三数学参考答案11. 34,232n n +; 12 . 23, 53;13. 2,60;14. 8,3; 15. 18-; 16. 60; 17.[1,2].三、解答题:本大题共5小题,共74分.解答应写出文字说明、证明过程或演算步骤. 18. (本小题满分14分)已知函数()sin3cos cos3sin cos 2f x x x x x x =-+. (Ⅰ) 求π()4f 的值;(Ⅱ) 求()f x 的单调递增区间.解 (Ⅰ) 因为 π3ππ3πππ()sin cos cos sin cos 444442f =-+0=++ 1=所以 π()14f = …………………………………………………………5分(Ⅱ) 因为 ()sin(3)cos 2f x x x x =-+π)4x =+ …………………………………………………9分(化简出现在第(Ⅰ)小题中同样给4分)由正弦函数的性质得πππ2π2+2π242k x k -+≤≤+,Z k ∈ 解得3ππππ88k x k -+≤≤+,Z k ∈ 所以()f x 的单调递增区间是3ππ[π, π]88k k -++,Z k ∈………………………14分 19.(本小题满分15分)如图,在几何体111ABC A B C -中,平面11A ACC ⊥底面ABC ,四边形11A ACC 是正方形,11B C BC ∥,Q 是1A B 的中点,且112AC BC B C ==,2π3ACB ∠=. (Ⅰ) 证明:1B Q ∥平面11A ACC ;(Ⅱ) 求直线AB 与平面11A BB 所成角的正弦值.(Ⅰ) 证明:如图1所示,连接11,AC AC 交于M 因为 四边形11A ACC 是正方形, 所以 M 是1AC 的中点 又已知Q 是1A B 的中点 所以 12M Q B C ∥又因为 11B C BC ∥且11=2BC B C所以 11 MQ B C ∥,即四边形11B C MQ 是平行四边形所以 11BQ C M ∥,因此 1B Q ∥平面11A ACC .…………………………………………………7分 (Ⅱ) 如图2所示,过点B 作面11A B B 与面ABC 的交线BD,交直线CA 于D .过A 作线BD 的垂线AH ,垂足为H .再过A 作线1AH 的垂线AG ,垂足为G. 因为1,AH BD AA BD ⊥⊥, 所以BD ⊥面1A AH ,所以BD ⊥AG ,又因为1A H AG ⊥,所以AG ⊥面11A B B ,所以ABG∠即AB 与面11A B B 所成的角.………………10分因为11A B ∥面ABC ,所以11A B ∥BD , 且A 为CD的中点,如图2所示,CP 为BD 边上的高,ABBD , 因为011sin12022CB CD BD CP ⋅=⋅ 所以CP ==2CP AH =因为12AA =,所以1AH ==11AH AA AG A H⋅=== (第19题图4)HA所以sin ABG∠===15分20.(本小题满分15分)已知函数ln(),xf xx=(),(0)g x kx k=>函数{}()max(),(),F x f x g x=其中{}max,a b,,,.a a bb a b≥⎧=⎨<⎩(Ⅰ) 求()f x的极值;(Ⅱ) 求()F x在[]1,e上的最大值(e为自然对数底数).(Ⅰ) 解:因为21ln()xf xx-'=由()0f x'=,解得:ex=……………………………………………………3分因为所以()f x的极大值为e,无极小值.………………………………………7分(Ⅱ) 因为()f x在[1, e]上是增函数,所以max1()(e)ef x f==……………………………………………………10分()g x在[1, e]上是增函数所以max()(e)eg x g k==……………………………………………………13分所以2max211, 0<,e e()1e, .ekF xk k⎧<⎪⎪=⎨⎪≥⎪⎩……………………………………………15分21.(本小题满分15分)已知1F ,2F 是椭圆C :2212x y +=的左右焦点,,A B 是椭圆C 上的两点,且都在x 轴上方,1AF 2BF ∥,设21,AF BF 的交点为M . (Ⅰ)求证:1211AF BF +为定值; (Ⅱ)求动点M 的轨迹方程.(I )证1:设直线1AF 所在直线的方程为1x my =-与椭圆方程联立2222,1,x y x my ⎧+=⎨=-⎩化简可得()22+2-210m y my -=因为A 点在x 轴上方, 所以22Ay m =+所以(1202A m AFy m =-=+同理可得:(2202B m BFy m -=-=+…………4分所以211AF =,221BF =所以221211+AF BF =2⎛⎫221-m m +⎪⎭=7分 证2:如图2所示,延长1AF 交椭圆于1B ,由椭圆的对称性可知:112B F BF =,所以 只需证明11111+AF B F 为定值, 设直线1AF 所在直线的方程为1x my =- ,与椭圆方程联立2222,1,x y x my ⎧+=⎨=-⎩ 化简可得:()22+2-2m y my -所以111121111++AF B F y y ⎛⎫=⎪⎪⎭====7分(II )解法1:设直线2AF ,1BF 所在直线的方程为11x k y =+ ,21x k y =-121,1,x k y x k y =+⎧⎨=-⎩所以M 点的坐标为1221212k k x k k y k k +⎧=⎪-⎪⎨⎪=⎪-⎩……………………………………10分 又因为1122A A A A A x my k m y y y --===- ,2122B B B B Bx my k m y y y ++===+所以12222211+=+=22 2A B B A k k m m m y y y y m ⎛⎫-++- ⎪⎝⎭⎛⎫ =+-⎝ 所以 ()12+226k k m m m =+=,2221-2k k ⎛⎫=所以1221212k k x k k y k k +⎧===⎪-⎪⎨⎪===⎪-⎩所以 ()221 09188x y y +=>……………………………………………………15分 解法2:如图3所示,设1122,AF d BF d ==,则112MF d MBd =, 所以1111111212MF d d MF BF BF d d d d =⇒=⋅++又因为122BF BF a +==所以122BF BF d ==所以()121111212d d d MF BF d d d d =⋅=++ ……………………………………10分同理可得()21212d d MF d d =+,所以第21题图312()()122112121212122d d d d d d MF MF d d d d d d +=+=+++ ……………12分由(I)可知121221111+d d d d d d =+ ……………………………………………14分所以12MF MF +=所以动点M 的轨迹方程为()221 09188x y y +=>………………………………15分 22.(本小题满分15分) 已知数列{}n a 满足1n na t =+(,,3,)n t t n t *∈≥≤N . 证明: (Ⅰ) 1n a n a -<e (e 为自然对数底数);(Ⅱ)12111(1)ln(1)nt n a a a +++>++; (Ⅲ) 123()()()()1tttt n a a a a ++++<.证明:(Ⅰ) 设1()e x f x x -=- 因为 1()e 1x f x -'=-当(0,1)x ∈时,()0f x '<,即()f x 在(0, 1)单调递减 因为 0111n n t a t t <=≤<++ 所以 1()e (1)0n a n n f a a f -=->=即 1n a n a -<e…………………………………………………………………………5分(Ⅱ) 即证12111ln(1)(1)(1)(1)nn t a t a t a +++>++++即证 1111l n (1)23n n++++>+ 设()ln(1)g x x x =-+ 1()111x g x x x '=-=++ 因为当0x >时,()0g x '>,即 ()g x 在(0,)+∞上单调递增 所以 ()ln(1)(0)0g x x x g =-+>= 即 0x >时,有ln(1)x x >+ 所以 1113411ln 2ln ln lnln(1)2323n n n n+++++>++++=+ 所以12111(1)ln(1)nt n a a a +++>++……………………………………10分 (Ⅲ) 因为 123()()()()tttt n a a a a ++++ 3121111(e )(e )(e )(e )n a a a a t t t t ----<++++2111e(1e )1et tn t t t t -+++-=-22211111e (1e )e11e1et t t t t t t t t t --+++++--≤=--设 1et t q +=因为314e e 2t t q +=≥>211e11et t t t -++-=-1111111t t q q q q q ----=<<--- 所以 123()()()()1tt t tn a a a a ++++<………………………………15分。
2017年高考真题——数学(浙江卷)word(参考版) Word版含解析
绝密★启用前2017年普通高等学校招生全国统一考试(浙江卷)数学本试题卷分选择题和非选择题两部分。
全卷共4页,选择题部分1至2页,非选择题部分3至4页。
满分150分。
考试用时120分钟。
考生注意:1.答题前,请务必将自己的姓名、准考证号用黑色字迹的签字笔或钢笔分别填在试题卷和答题纸规定的位置上。
2.答题时,请按照答题纸上“注意事项”的要求,在答题纸相应的位置上规范作答,在本试题卷上的作答一律无效。
参考公式:球的表面积公式 锥体的体积公式24S R =π13V Sh =球的体积公式其中S 表示棱锥的底面面积,h 表示棱锥的高 343V R =π 台体的体积公式其中R 表示球的半径 1()3a b V h S S =柱体的体积公式其中S a ,S b 分别表示台体的上、下底面积 V =Shh 表示台体的其中S 表示棱柱的底面面积,h 表示棱柱的高选择题部分(共40分)一、选择题:本大题共10小题,每小题4分,共40分。
在每小题给出的四个选项中,只有一项是符合题目要求的。
1.已知}11|{<<-=x x P ,}02{<<-=x Q ,则=Q PA .)1,2(-B .)0,1(-C .)1,0(D .)1,2(-- 【答案】A【解析】取Q P ,所有元素,得=Q P )1,2(-.2.椭圆22194x y +=的离心率是 ABC .23D .59【答案】B【解析】33e ==,选B. 3.某几何体的三视图如图所示(单位:cm ),则该几何体的体积(单位:cm 3)是A .π2+1 B .π2+3 C .3π2+1 D .3π2+3 【答案】A 【解析】2π1211π3(21)1322V ⨯=⨯⨯+⨯⨯=+,选A. 4.若x ,y 满足约束条件03020x x y x y ≥⎧⎪+-≥⎨⎪-≤⎩,则z =x +2y 的取值范围是A .[0,6]B .[0,4]C .[6,+∞]D .[4,+∞]【答案】D【解析】可行域为一开放区域,所以直线过点(2,1)时取最小值4,无最大值,选D. 5.若函数f (x )=x 2+ ax +b 在区间[0,1]上的最大值是M ,最小值是m ,则M – mA .与a 有关,且与b 有关B .与a 有关,但与b 无关C .与a 无关,且与b 无关D .与a 无关,但与b 有关【答案】B【解析】因为最值在2(0),(1)1,()24a a fb f a b f b ==++-=-中取,所以最值之差一定与b无关,选B.6.已知等差数列[a n ]的公差为d ,前n 项和为S n ,则“d >0”是“S 4 + S 6”>2S 5的A .充分不必要条件B .必要不充分条件C .充分必要条件D .既不充分也不必要条件【答案】C【解析】4652S S S d +-=,所以为充要条件,选C.7.函数y=f (x )的导函数()y f x '=的图像如图所示,则函数y=f (x )的图像可能是【答案】D【解析】原函数先减再增,再减再增,因此选D.8.已知随机变量ξ1满足P (1ξ=1)=p i ,P (1ξ=0)=1—p i ,i =1,2.若0<p 1<p 2<12,则 A .1E()ξ<2E()ξ,1D()ξ<2D()ξ B .1E()ξ<2E()ξ,1D()ξ>2D()ξ C .1E()ξ>2E()ξ,1D()ξ<2D()ξD .1E()ξ>2E()ξ,1D()ξ>2D()ξ8.【答案】A 【解析】112212(),(),()()E p E p E E ξξξξ==∴<111222121212()(1),()(1),()()()(1)0D p p D p p D D p p p p ξξξξ=-=-∴-=---<,选A.9.如图,已知正四面体D –ABC (所有棱长均相等的三棱锥),PQR 分别为AB ,BC ,CA 上的点,AP=PB ,2BQ CRQC RA==,分别记二面角D –PR –Q ,D –PQ –R ,D –QR –P 的平面较为α,β,γ,则A .γ<α<βB .α<γ<βC .α<β<γD .β<γ<α【答案】B【解析】设O 为三角形ABC 中心,则O 到PQ 距离最小,O 到PR 距离最大,O 到RQ 距离居中,而高相等,因此αγβ<<所以选B10.如图,已知平面四边形ABCD ,AB ⊥BC ,AB =BC =AD =2,CD =3,AC 与BD 交于点O ,记1·I OAOB =,2·I OB OC =,3·I OC OD =,则A .I 1<I 2<I 3B .I 1<I 3<I 2C . I 3<I 1<I 2D .I 2<I 1<I 3【答案】C 【解析】因为90AOB COD ∠=∠> ,所以0(,O B O C O A O B O C O D O A⋅>>⋅>⋅<< 选C非选择题部分(共110分)二、填空题:本大题共7小题,多空题每题6分,单空题每题4分,共36分。
2017年高考浙江数学试题及答案(解析版)(2)(最新整理)
3
22
2
【点评】本题考查了空间几何体三视图的应用问题,解题的关键是根据三视图得出原几何体的结构特
征,是基础题目.
x 0 (4)【2017 年浙江,4,4 分】若 x , y 满足约束条件 x y 3 0 ,则 z x 2 y 的取值范围是
x 2 y 0
()
(A) 0,6
(B) 0, 4 (C) 6,
a2
b2
2abi
3
4i
,则
a2 b2
ab
2
3 ,解得
a2
b
2
4 1
,则
a2
b2
5, ab
2
.
【点评】本题考查了复数的运算法则、复数的相等、方程的解法,考查了推理能力与计算能力,属于基础题.
(13)【2017 年浙江,13,6 分】已知多项式 x 11 x 22 x5 a1x4 a2 x3 a3x2 a4 x1 a5 ,则 a4
【答案】A
【解析】 E(1) p1, E(2 ) p2 , E(1) E(2 ) D(1) p1(1 p1), D(2 ) p2 (1 p2 ) , D(1) D(2 ) ( p1 p2 )(1 p1 p2 ) 0 ,故选 A.
【点评】本题考查离散型随机变量的数学期望和方差等基础知识,考查推理论证能力、运算求解能力、空间想象
【点评】本题考查了空间角、空间位置关系、正四面体的性质、法向量的夹角公式,考查了推理能力与计算能力,
属于难题.
(10)【2017 年浙江,10,4 分】如图,已 知平面四 边形 ABCD, AB BC , AB( BC( AD( 2 , CD( 3 , AC 与 BD 交于点 O,记 I1=OA·OB , I2=OB·OC , I3=OC·OD ,则( )
【数学】浙江省金华、丽水、衢州市十二校2017届高三2月联考试题
浙江省金华、丽水、衢州市十二校2017届高三2月联考试题第Ⅰ卷(共60分)一、选择题:本大题共8个小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的.1.已知集合{}{}2|4,|12A x R x B x R x =∈>∈≤≤,则( ) A .A B =∅ B .A B R = C .B A ⊆ D .A B ⊆ 2. ()82x -展开式中含3x 项的系数为( )A .3112xB .31120x -C .112D .11203.已知某几何体的正(主)视图与侧(左)视图都是直角边长为1的等腰直角三角形,且体积为13,则该几何体的俯视图可以是( ) A .B .C .D .4.过点()0,2-的直线交抛物线216y x =于()()1122,,,A x y B x y 两点,且22121y y -=,则OAB ∆(O 为坐标原点)的面积为( )A .12 B .14 C .18 D .1165.设实数,a b ,则“221a b b a -+-≤”是“22113222a b ⎛⎫⎛⎫-+-≤ ⎪ ⎪⎝⎭⎝⎭”的( )A .充分不必要条件B .必要不充分条件C .充要条件D .既不充分也不必要条件 6.回文数是指从左到右读与从右到左读都一样的正整数,如2,11,242,6776,83238等,设n 位回文数个数为n a (n 为正整数),如11是2位回文数,则下列说法正确的是( ) A .4100a = B .()21210n n a a n N ++=∈ C .()22110n n a a n N -+=∈ D .以上说法都不正确7.如图,已知直线y kx m =+与曲线()y f x =相切于两点,则()()F x f x kx =-有( )A .1个极大值点,2个极小值点B .2个极大值点,1个极小值点C .3个极大值点,无极小值点D .3个极小值点,无极大值点8.已知123,,A A A 为平面上三个不共线的定点,平面上点M 满足()11213A M A A A A λ=+(λ是实数),且123MA MA MA ++是单位向量,则这样的点M 有( ) A .0个 B .1个 C .2个 D .无数个第Ⅱ卷二、填空题(每题5分,满分20分,将答案填在答题纸上) 9.在数列{}n a 中,()*111,3n n a a a n N +==∈,则3a=_________,5S =__________.10.设a R ∈,若复数1a ii++(i 为虚数单位)的实部和虚部相等,则a =_________,z =_________.11.若实数,x y 满足303903x y x y y --≤⎧⎪--≥⎨⎪≤⎩,则11y x ++的取值范围是___________.12.若函数()()()22sin23sin 102f x x x πωωω⎛⎫=++-> ⎪⎝⎭的最小正周期为1,则ω=___________,函数()f x 在区间11,64⎡⎤-⎢⎥⎣⎦上的值域为____________. 13.甲、乙两人进行5局乒乓球挑战赛,甲在每局中获胜的概率为23,且各局胜负相互独立.设甲赢的局数为ξ,则()2P ξ==__________,()E ξ=_________,()D ξ=_________.14.如图,已知矩形,2,ABCD AD E =为AB 边上的点,现将ADE ∆沿DE 翻折至ADE ∆,使得点A '在平面EBCD 上的投影在CD 上,且直线A D '与平面EBCD 所成角为30°,则线段AE 的长为_________.15.设{},min ,,y x yx y x x y≥⎧=⎨<⎩,若定义域为R 的函数()(),f x g x 满足()()228xf xg x x +=+,则()(){}min ,f x g x 的最大值为__________. 三、解答题 (本大题共6小题,共70分.解答应写出文字说明、证明过程或演算步骤.) 16.(本小题14分)在ABC ∆中,内角,,A B C 所对的边分别为,,a b c ,()12cos 2cos b A a B -=. (1)证明:2b c =;(2)若1,tan 22a A ==,求ABC ∆的面积. 17.(本小题15分)如图,已知四棱锥P ABCD -的底面为菱形,且060,ABC E ∠=是DP 中点. (1)证明://PB 平面ACE ; (2)若2,2AP PB AB PC ====,求二面角A PC D --的余弦值.18.(本小题15分)已知数列{}n a 的各项都不为零,其前n 项为n S ,且满足:()()*21n n n S a a n N =+∈.(1)若0n a >,求数列{}n a 的通项公式;(2)是否存在满足题意的无穷数列{}n a ,使得20162015a =-?若存在,求出这样的无穷数列的一个通项公式;若不存在,请说明理由. 19.(本小题15分)已知椭圆()22211x y a a+=>的离心率为32,(),P m n 为圆2216x y +=上任意一点,过P作椭圆的切线,PA PB ,设切点分别为()()1122,,,A x y B x y . (1)证明:切线PA 的方程为1114x xy y +=; (2)设O 为坐标原点,求OAB ∆面积的最大值. 20.(本小题15分) 已知函数()()()32ln ,23af x x x a Rg x x x x=-∈=-. (1)若m 为正实数,求函数()1,,y g x x m m ⎡⎤=∈⎢⎥⎣⎦上的最大值和最小值; (2)若对任意的实数1,,22s t ⎡⎤∈⎢⎥⎣⎦,都有()()f s g t ≤,求实数a 的取值范围.参考答案一、选择题 : 12345678ACBDABAC二、填空题: 9. 9,121 10. 0,22 11.14,45⎡⎤⎢⎥⎣⎦12.,2,3π⎡⎤-⎣⎦ 13.401010,,24339 14.433 15.28三、解答题16.解:(1)∵()12cos 2cos b A a B -=,∴由正弦定理得()sin 12cos 2sin cos B A A B -=,解得1cos 3A =,∴22sin 3A =..................................10分由余弦定理有222cos 2b c a A bc +-=,即22214134c c c +-=,解得 2311c =..................13分 ∴2132222sin sin 211311ABC S bc A c A ∆==== .........................15分 17.解:(1)证:连结,BD BD AC F = ,连接EF ,∵四棱锥的底面为菱形,∴F 为BD 中点,又∵E 是DP 中点,∴在BDP 中,EF 是中位线,∴//EF PB ,又∵EF ⊆平面ACE ,而PB ⊄平面ACE ,∴//PB 平面ACE ;.........................6分(2)取AB 的中点Q ,连结PQ 、CQ ,∵菱形ABCD ,且060ABC ∠=,∴正ABC ∆,∴CQ AB ⊥, ∵2AP PB ==,2AB PC ==,∴3CQ =,且等腰直角PAB ∆,即090,APB PQ AB ∠=⊥.∴AB ⊥平面PQC ,且1PQ =,∴222PQ CQ CP +=,∴PQ CQ ⊥.如图,建立空间直角坐标系:以Q 点为原点,BA 所在的直线为x 轴,QC 所在的直线为y 轴,QP 所在的直线为z 轴,则()()()()()0,0,0,1,0,0,0,3,0,0,0,1,2,0,0,Q A C P D ...................9分 平面APC 上,()1,0,1AP =- ,()0,3,1CP =- ;设平面APC 的法向量为()1111,,n x y z =,则有1111111301303x x z y y z z ⎧⎧=-+=⎪⎪⇒=⎨⎨-+=⎪⎪=⎩⎩,即()13,1,3n = ;................................11分设平面DPC 的法向量为()2222,,n x y z =,因为()()2,0,0,0,3,1CD CP ==- ,则有2222030x y z =⎧⎪⎨-+=⎪⎩可取()20,1,3n = ..........................13分∴12121227cos ,7n n n n n n ==⨯,∴ 二面角A PC D --的余弦值为277...................15分 18.(1)∵数列{}n a 的各项都不为零且满足()()*21n n n S a a n N =+∈...........① ∴()1111221S a a a ==+,解得11a =............................2分 ∴()11121n n n S a a +++=+...........................②, ②-①得221112n n n n n a a a a a +++=-+-,整理得到()()1101n n n n a a a a ++=--+,∴11n n a a +-=..................5分 ∴{}n a 是以1为首项,以1为公差的等差数列,∴()111n a n n =+-⨯=...............7分(2)根据(1)()()1111,01n n n n a a a a a ++==--+,可得11n n a a +=+或 1n n a a +=-,............11分 所以从第二项开始每一项都有两个分支,因此通项为()1,201520151,2016n n n n a n -≤⎧⎪=⎨-≥⎪⎩的数列满足题意,使得20162015a =-(其他符合的答案类似给分)...15分19.解:(1)由题,2312c a e a a-===,解得2a =.................2分 ①当10y =时,12x =± ,直线2x =±,∴24x =,代入椭圆方程得到0y =, ∴切线PA 的方程是2x =±.②当10y ≠时,联立2211440440x y x x y y ⎧+-=⎨+-=⎩,消y ,得到2211114404xx x y y ⎛⎫+--= ⎪⎝⎭ ,即2211222111241404x x x x y y y ⎛⎫+-+-= ⎪⎝⎭,.........................5分 所以222221111142242421111111441444144x x x x x y y y y y y y ⎛⎫⎛⎫⎛⎫∆=-+-=--+- ⎪⎪ ⎪⎝⎭⎝⎭⎝⎭()2211222211114444161616160y x y y y y -=-++=-++= ∴切线PA 的方程为1114x xy y +=........................8分 (2)根据(1)可得切线PA 的方程为1114x x y y +=,切线PB 的方程为2114x xy y +=,∴11221414x my n x m y n ⎧+=⎪⎪⎨⎪+=⎪⎩,所以直线AB 方程为14mx ny +=........................9分 ∴2214440mxny x y ⎧+=⎪⎨⎪+-=⎩,消y 得到22222241404m m x x n n n ⎛⎫+-+-= ⎪⎝⎭ ,∴22222221641611414m m n n AB k a n m n-++∆⎛⎫=+=+- ⎪⎝⎭+ ..............11分 又∵原点O 到直线AB 的距离22214d mn =+,∴222222222164161111224144OABm m n n S AB d n m m n n ∆-++⎛⎫==+- ⎪⎝⎭++ 22224444n m n m +-=+............................................13分又∵(),P m n 为圆2216x y +=上任意一点,∴2216m n +=.∴224312316OABn S n ∆+=+,令231223t n =+≥,则24444OAB t S t t t∆==++在)23,⎡+∞⎣上单调递减,所以32OAB S ∆≤...................................15分 20.解:(1)()()26661g x x x x x '=-=-,又10m m <<,∴1m >,∴()g x 在1,1m ⎡⎤⎢⎥⎣⎦上递减,在[]1,m 上递增, ∴()()()()min max 111,max ,g x g g x g g m m ⎧⎫⎛⎫==-=⎨⎬⎪⎝⎭⎩⎭....................5分 令()32321112323g g m m m m m m ⎛⎫-=--+⎪⎝⎭, 32232211111123213m m m m m m m m m m m m ⎛⎫⎛⎫⎛⎫⎛⎫⎛⎫⎛⎫=---=-++-+- ⎪ ⎪ ⎪⎪ ⎪⎪⎝⎭⎝⎭⎝⎭⎝⎭⎝⎭⎝⎭21112321112210m m m m m m m m m m m m ⎡⎤⎛⎫⎛⎫⎛⎫=-+-+-⎢⎥⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎢⎥⎣⎦⎡⎤⎡⎤⎛⎫⎛⎫⎛⎫=-+-++< ⎪ ⎪ ⎪⎢⎥⎢⎥⎝⎭⎝⎭⎝⎭⎣⎦⎣⎦∴()()32max 23g x g m m m ==-.................................8分(2)由题得:问题等价于当1,22x ⎡⎤∈⎢⎥⎣⎦时,()()max min 1f s g x ≤=-..............10分令1s =,则()11f a =≤-................................11分 下面证明:当1a ≤-时,()1f x ≤-成立, ∵()1ln ln a f x x x x x x x =-≤--,故只需证1ln 1x x x --≤-,即1ln 1x x x+≥, 令()11ln ,,22h x x x x x ⎡⎤=+∈⎢⎥⎣⎦,则()()23112ln 1,0h x x h x x x x '''=-+=+> 又()10h '=,所以()h x 在1,12⎡⎤⎢⎥⎣⎦上递减,在[]1,2上递增, 所以()()11h x h ≥=.所以实数a 的取值范围为1a ≤-...............................15分。
