【高教版】中职数学基础模块上册:2.4《含绝对值的不等式》优秀教案
中职数学教案:含绝对值的不等式
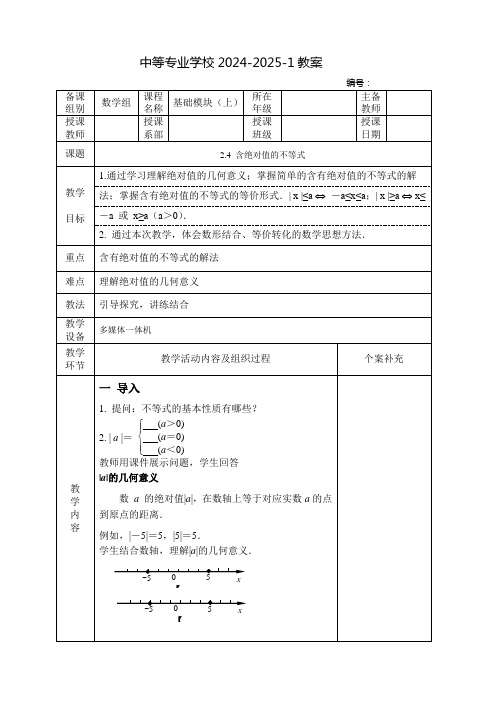
数a的绝对值|a|,在数轴上等于对应实数a的点到原点的距离.
例如,|-5|=5,|5|=5.
学生结合数轴,理解|a|的几何意义.
教
学
内
容
二概念新知
问题1
(1)解方程|x|=5,并说明|x|=5的几何意义是什么?
(2)试叙述|x|>5,|x|<5的几何意义,你能写出其解集吗?
对于每个问题都请学生思考后回答,教师给与恰当的评价并给出正确答案.
中等专业学校2024-2025-1教案
编号:
备课组别
数学组
课程名称
基础模块(上)
所在
年级
主备
教师
授课教师
授课系部
授课班级
授课
日期
课题
2.4含绝对值的不等式
教学
目标
1.通过学习理解绝对值的几何意义;掌握简单的含有绝对值的不等式的解
法;掌握含有绝对值的不等式的等价形式.| x |≤a-a≤x≤a;| x |≥ax≤
-a或x≥a(a>0).
2.通过本次教学,体会数形结合、等价转化的数学思想方法.
重点
含有绝对值的不等式的解法
难点
理解绝对值的几何意义
教法
引导探究,讲练结合
教学设备
多媒体一体机
教学
环节
教学活动内容及组织过程
个案补充
教
学
内
容
一导入
1.提问:不等式的基本性质有哪些?
2. |a|=
教师用课件展示问题,学生回答
(1)|x|=5的几何意义是:在数轴上对应实数5的点到原点的距离等于5,这样的点有二个:对应实数5和5的点;
(2)|x|>5的几何意义是到原点的距离大于5的点,其解集是
高教版(2021)中职数学基础模块上册第2单元《含绝对值的不等式》教学课件

所以不等式 ax b c(c 0) 的解集为 x | c ax b c(c 0)
“大于取两边,小于取中间,” ax b c(c 0),解集为 ax b c(c 0),解集为R
作业:《练习册》2.4
感谢您的聆听
际问题
复习引入
思考:实数的绝对值是如何定义的?几何意义是什么?
绝对值的定义: | a | =
a, a 0 0, a 0
a, a 0
| a |的几何意义:数a点在坐标轴上所对应点到原点的距离。 正数的绝对值是它本身(正数),负数的绝对值是它的相反数。 互为相反数的两个数的绝对值相等即|-a|=|a|
1 2
用区间表示为
1 2
,1 2
典型例题
例3. 解不等式 x 500 5
x 500 5
5 x 500 5
495 x 505
用区间表示为495,505
例4. 解不等式 2x 5 7
2x 5 7
2x 5 7 或 2x 5 7
x 6 或 x 1
x x 6,或x 1
用区间表示为 , 6 1,
课堂练习
课堂练习
课堂小结
1.| X |<a的几何意义:在数轴上x的对应点与原点的距离小于a
课堂小结
求不等式 ax b c(c 0) 的解集:
把 ax b 看作一个整体m时,则可化为
m c(c 0) 然后求解
所以不等式 ax b c(c 0) 的解集为 x | ax b c,或ax b c (c 0)
-2 O
2
x
由数轴图可知 x 2 的解集是
x x 2,或x 2
探究一 带有绝对值的不等式的几何意义
| X |<a的几何意义:在数轴上x的对应点与原点的距离小于a 不等式 x 2 的几何意义:数轴上离开原点的距离小于2的点。
中职生数学基础模块上册课件《含有绝对值的不等式》

不等式的立方性质:如果 a>b,那么a^3>b^3。
新课导入
引出含有绝对值的不等式
01
02
03
04
复习旧知识: 回顾初中所学 的不等式知识
引入新概念: 介绍绝对值的 概念和性质
举例说明:列 举含有绝对值 的不等式的例 子
提出问题:引 导学生思考如 何解决含有绝 对值的不等式 问题
分析绝对值不等式的特点
问题6:如何将含有绝对值不等式的知 识应用到其他学科领域?
课堂总结
回顾本节课内容
绝对值的概念和 性质
含有绝对值的不 等式的解法
绝对值不等式的 应用
课堂练习和问题 解答
强调重点和难点
绝对值的定义和性质 含有绝对值的不等式的解法 绝对值不等式的应用 绝对值不等式的证明方法
对学生进行鼓励和指导
鼓励学生积极思 考,勇于提问
中职生数学基础模块上册课 件《含有绝对值的不等式》
YOUR LOGO
目录
CONTENTS
1 课程导入 2 基础知识复习 3 新课导入 4 新课讲解 5 课堂练习 6 课堂总结
课程导入
课程背景介绍
01
中职生数学基础模块上册是针对中职 生开设的数学课程,旨在提高学生的 数学素养和计算能力。
03
课程导入是课堂教学的重要组成部分, 通过引入有趣的实例或问题,激发学 生的学习兴趣和求知欲。
如矩形、梯形等。
绝对值不等式的解集可以 通过代数方法求解,例如 利用绝对值的性质、不等
式的性质等。
4
5
新课讲解
讲解绝对值不等式的解法
绝对值不等式的定义: 含有绝对值的不等式, 如|x|>a,|x|<a等。
《含绝对值的不等式》中职数学(基础模块)上册2.4【高教版】2

当 c > 0 时, ax + b c 或 ax + b -c |ax + b| c
当 c 0 时, x R
课堂练习一: 试解下列不等式:
(1) | 3 2x |≥ 7
(2) | x2 3 x | 4
解:∵| 3 2x |≥ 7 ∴ 2 x 3 ≥ 7
•
认真听讲的第一个阶段就是上课时间无条件地“往前看”,上课的时候看书往往很容易开小差。摒除杂念,将视线从摊在眼前的书上移开。老师讲课的时候只看前面,集中注意力听老师嘴里说出来的话,那才是认真听讲的态度。
•
低着头,心情就放松了,但那种放松对学习一点好处也没有,之所以会放松,就是因为觉得即便是自己开小差,老师也不知道。如果你往前看,不时地和老师眼神交会一下,注意力必然会集中起来。和老师眼神交汇的那种紧张感会让你注意力集中,并充
即3x643x
1或3x 46
4
1
x
1或x 10 x 3
2 3
5 3
解得 10 x 5 或 1 x 2
Hale Waihona Puke 333故原
不
等式
的
解 集 为
10 3
,
5 3
1,
32 .
学习小结:
解绝对值不等式的基本思路是去绝对值符号 转化为一般不等式来处理。
2019/8/10
教学资料精选
12
谢谢欣赏!
2019/8/10
教学资料精选
13
∴ 2x 3≥ 7或2x 3 ≤ 7 ∴ x ≥ 5或x ≤ 2
高教版中职数学(基础模块)上册2.4《含绝对值的不等式》ppt课件3

小结
1)︱x︱< a与︱x︱> a(a>0)型不等式的解法与解集? 2)︱ax+b︱< c与︱ax+b︱> c(c>0)型不等式的解法与解集?
作业
1、课本P44 习题 1、2 2、分层次练习
编者语
• 要如何做到上课认真听讲?
•
我们都知道一个人的注意力集中时间是有限的,一节课45分钟如何保持时时刻刻都能认真听讲不走神呢?
•
Hale Waihona Puke 认真听讲的第一个阶段就是上课时间无条件地“往前看”,上课的时候看书往往很容易开小差。摒除杂念,将视线从摊在眼前的书上移开。老师讲课的时候只看前面,集中注意力听老师嘴里说出来的话,那才是认真听讲的态度。
•
低着头,心情就放松了,但那种放松对学习一点好处也没有,之所以会放松,就是因为觉得即便是自己开小差,老师也不知道。如果你往前看,不时地和老师眼神交会一下,注意力必然会集中起来。和老师眼神交汇的那种紧张感会让你注意力集中,并充
2019/10/19
教学资料精选
14
谢谢欣赏!
2019/10/19
教学资料精选
15
2.4 含有绝对值的不等式
江宁高职校
复习回顾
问题1:解方程|x|=2? 在数轴上如何表示它的解? |x|=2 的几何意义?
|x|=2的解是x=2或x=-2
. 在数轴上表示如下:
.
-2 -1 0 1 2
|x|=2的几何意义是到原点的距离等于2的点
问题2:解不等式|x|<2 与 |x|>2 ?
1)│x│< 2,它表示到原点的距离小于2.
•
但是,那却是提升成绩最快的方法。学习要带有一定程度的紧张感,坐在前面,自然而然就会紧张起来。没有必要自己费心思集中精神,那种环境就能帮助你做到。虽然看上去好像不太方便,但其实那才是最便于学习的位置。
【高教版】中职数学基础模块上册:2.4《含绝对值的不等式》优秀教案

【教学过程】
教学
过程
教师
行为
学生
行为
教学
意图
*回顾思考复习导入
问题
任意实数的绝对值是如何定义的?其几何意义是什么?
解决
对任意实数 ,有
其几何意义是:数轴上表示实数 的点到原点的距离.
拓展
不等式 和 的解集在数轴上如何表示?
根据绝对值的意义可知,方程 的解是 或 ,不等式 的解集是 (如图(1)所示);不等式 的解集是 (如图(2)所示).
交流
反馈
学习
效果
*实际操作探索新知
问题
如何通过 ( )求解不等式 ?
解决
在不等式 中,设 ,则不等式 化为 ,其解集为
,即 .
利用不等式的性质,可以求出解集.
总结
可以通过“变量替换”的方法求解不等式 或 ( ).
质疑
引导
演示
归纳
思考
观察
体会
理解
通过
实例
使学
生初
步领
会变
量替
换的
思想
*动脑思考感悟新知
不等式 或 ( )可以通过“变量替换”的方法求解.实际运算中,可以省略变量替换的书写过程.
即
说明
强调
理解
记忆
归纳
方法
便于
学生
应用
*巩固知识典型例题
例2解不等式∣∣≤3.
解由原不等式可得-3≤2x-1≤3,
于是-2≤2x≤4,
即-1≤x≤2,
所以原不等式的解集为: .
例3解不等式 .
解由原不等式得 或 ,整理,得
或 ,
所以原不等式的解集为 .
含绝对值的不等式的学习教学设计.docx
含绝对值的不等式教学设计《含绝对值的不等式》教学设计殷姬飞奉化市技工学校【教材分析】《含绝对值的不等式》是高等教育出版社《数学》基础模块第二章第四节的内容,之前学习的不等式的性质和不等式组的解法为本节学习作了铺垫。
通过这节课可渗透数形结合、分类讨论、化归与转化等数学思想方法,并为后续学习(比如求函数的定义域、微积分等)奠定基础。
因此它在本章乃至整个中职数学课程中都占有重要作用。
【学情分析】15(2)班是机电技术应用专业,共有学生30 人, 29 位男生 1 位女生。
学生基础参差不齐,基础好的听课认真,做作业积极;基础差的上课不听,作业抄别人的。
他们初中已经接触过绝对值,知道了如何去绝对值,也知道x 的几何意义,所以本节课先复习这些内容起着承上启下的作用。
【教学目标】1 、知识与技能:掌握x a, x a( a0) 型不等式的解法,掌握ax b c, ax b c(c0) 型不等式的解法;2、过程与方法:培养学生观察、分析、归纳、概况的能力,了解数形结合、分类讨论、转化与化归等数学思想方法;3、情感态度价值观:向学生渗透“具体 -抽象 -具体”辩证唯物主义的认识论观点,使学生形成良好的个性品质。
【教学重点与难点】重点:掌握 x a, x a(a 0) 型不等式的解法,掌握ax b c, ax b c(c0)型不等式的解法;难点:利用绝对值的几何意义分析、解决问题。
【教学过程】教师活动学生活动设计意图一、猜谜:非常合算,绝对值为枯燥的数学课带来打一数学名称。
(约 1,)一些趣味性,同时引出这节课的课题《含绝对值的不等式》二、导入新课(约4,x, x0这是 x 的代数意义,向学)提问:x0, x0生渗透分类讨论的思想1、 x 如何去绝对值?x, x0方法,同时为解x a, x a(a 0) 型不等式作铺垫。
数轴上表示 x 的点到原点这是 x 的几何意义,向学2、 x 的几何意义如的距离。
生渗透数形结合的思想何?方法,为解 x a, x a(a 0)三、新授提问:(约 10,)绝对值方程x 2 的解如何?在数轴上如何表示?x 2 的几何意义如何?在数轴上如何表示?x 4 的解集如何?x a(a0) 呢?x0x2或x 2-0 2数轴上表示 x 的点离原点的距离小于 2,-0 24,4a, a型不等式作铺垫。
中职数学基础模块2.2.4含有绝对值的不等式教学设计教案人教版
课时教学设计首页(试用)第页(总页)课时教学流程☆补充设计☆课时教学流程不等式各边都加3,得—2v 2 x v 8,, 不等式各边都除以2,得—1 v x v 4.所以原不等式解集为{x| V v x v 4}.例2 解不等式|2 x—3|> 5.解由|2 x—3|> 5得2 x —3 w —5 或2 x —3》5,分别解之,得x<—1 或x>4,所以原不等式解集为{x| x<—1 或x>4}.四、含有绝对值的不等式的解法总结|a x + b|v c (c> 0)的解法是先化不等式组-c v a x+ b v c,再由不等式的性质求出原不等式的解集.|a x + b|> c ( c> 0 )的解法是先化不等式组a x + b> c或a x+ b v —c,再由不等式的性质求出原不等式的解集.练习2 解下列不等式(1) |x+ 5|< 7 ; (2) |5 x —3|>2 .教师分析时.可采用整体代换的思想:设z= 2x—3,则由|z|v 5,可得—5v z v 5,所以一5 v 2x—3 v 5, 然后求解.师:在解|ax+ b|> c与|ax+ b|vc (c> 0)型不等式的时候,一定要注意a的正负.当a为负数时,可先把a化成正数再求解.让全体冋学在练习本上做,教师巡视,并请几位冋学在黑板上作.结出解含绝对值不等式的方法步骤.通过启发学生,尽量让学生结合两例题自己归纳出解法,锻炼学生的总结概括能力并加深学生对该知识点的理解.使学生进一步掌握含绝对值不等式的解法.小结:(1) 解含绝对值的不等式关键是转化为不含绝对值符号的不等式;(2) 去绝对值符号时一定要注意不等式的等价性,即去掉绝对值符号后的不等式(组)与原不等式是等价的.学生畅谈本节课的收获,老师引导梳理,总结本节课的知识占八、、♦梳理总结也可针对学生薄弱或易错处进行强调和总结.课时教学设计尾页(试用)☆补充设计☆板书设计一、| a|的几何意义四、含有绝对值的不等式的解法总结二、|x|> a与|x|v a的几何意义三、解含有绝对值的不等式作业设计必做题:P50, A组第2题,选做题:B组第1题.教学后记。
高教版中职数学基础模块上册《含有绝对值的不等式》课件
5.不等式2-|x-1|≥0的解集是(
)A.(-1,3)Fra bibliotekB.(-∞,-1]∪(3,+∞)
C.[-1,3]
√
D.(-∞,-1]∪[3,+∞)
C
[∵不等式2-|x-1|≥0等价于|x-1|≤2,等价于-2≤x-1≤2,
解得-1≤x≤3,故选C.]
6.若不等式|x-1|≤a-2的解集是∅,则实数a的取值范围是(
B.(-1,3)
√
C.(-∞,-1]∪[3,+∞)
D.(-∞,-1)∪(3,+∞)
)
)
4.不等式|x+1|>5的解集是(
)
A.[-6,4]
B.(-6,4)
C.(-∞,-6]∪[4,+∞)
D.(-∞,-6)∪(4,+∞)
√
5.若不等式|x-a|<1的解集是(4,6),则实数a的值是(
A.3
C
B.4
C.5
A.(-∞,2)
√
B.(-∞,2]
C.(2,+∞)
D.[2,+∞)
A
)
[∵不等式|x-1|≤a-2的解集是∅,∴a-2<0,解得a<2,故
选A.]
− 1 >1
7.不等式组
的解集为(
<2
A.{x|-1<x<1}
)
B.{x|-2<x<0}
√
C.{x|-2<x<1或1<x<2}
D.∅
B
[∵不等式|x-1|>1的解集是(-∞,0)∪(2,+∞),不等式|x|<2
3.含有绝对值的不等式的解法
-c<ax+b<c
(1)当c>0时,|ax+b|<c⇔______________;
ax+b<-c或ax+b>c
|ax+b|>c⇔_____________________.
含绝对值不等式教案
含绝对值不等式优秀教案一、教学目标1. 让学生理解绝对值不等式的概念和性质。
2. 培养学生解决含绝对值不等式问题的能力。
3. 提高学生对数学逻辑思维和运算能力的培养。
二、教学内容1. 绝对值不等式的定义和性质2. 含绝对值不等式的解法3. 含绝对值不等式的应用问题三、教学重点与难点1. 绝对值不等式的性质和解法2. 含绝对值不等式的应用问题四、教学方法1. 采用讲解法,引导学生理解绝对值不等式的概念和性质。
2. 采用案例分析法,让学生通过例题掌握含绝对值不等式的解法。
3. 采用练习法,培养学生解决实际问题的能力。
五、教学准备1. 课件和教学素材2. 练习题和答案3. 黑板和粉笔教案内容:第一课时:绝对值不等式的概念和性质一、导入(5分钟)提问:什么是绝对值?绝对值有什么性质?二、新课讲解(20分钟)1. 讲解绝对值不等式的概念举例:解不等式|x| > 2分析:根据绝对值的性质,|x| > 2 等价于x > 2 或x < -22. 讲解绝对值不等式的性质性质1:如果a 是实数,|a| = a 当a ≥0,|a| = -a 当a < 0 性质2:如果a 和b 是实数,|a + b| ≤|a| + |b|性质3:如果a 和b 是实数,|ab| = |a| |b|三、案例分析(10分钟)举例:解不等式|2x 3| ≤12x 3 ≤1 和2x 3 ≥-1解得:x ≤2 和x ≥1原不等式的解集为1 ≤x ≤2四、课堂练习(5分钟)1. 解不等式|3x + 2| > 42. 解不等式|x 5| ≤3第二课时:含绝对值不等式的解法一、导入(5分钟)提问:如何解决含绝对值不等式的问题?二、新课讲解(20分钟)1. 讲解含绝对值不等式的解法步骤1:将含绝对值的不等式转化为两个不等式组步骤2:分别解出每个不等式组的解集步骤3:求出两个解集的交集,即为原不等式的解集2. 举例讲解举例:解不等式组|2x 1| ≤3 和|x + 2| > 1-1 ≤2x 1 ≤3 和x + 2 > 1 或x + 2 < -1根据步骤2和步骤3,解得:x ≤2 和x > -1原不等式组的解集为-1 < x ≤2三、案例分析(10分钟)举例:解不等式|3x 4| + |x + 1| ≤5当x ≤-1 时,3x 4 ≤-x 1当-1 < x ≤4/3 时,3x 4 + x + 1 ≤5当x > 4/3 时,3x 4 + x + 1 > 5四、课堂练习(5分钟)1. 解不等式|x 2| + |x + 3| ≥52. 解不等式|2x + 1x 3| ≤4第三课时:含绝对值不等式的应用问题一六、教学目标1. 让学生能够应用绝对值不等式的解法解决实际问题。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
即
说明
强调
理解
记忆
归纳
方法
便于
学生
应用
*巩固知识典型例题
例2解不等式∣∣≤3.
解 由原不等式可得-3≤2x-1≤3,
于是-2≤2x≤4,
即-1≤x≤2,
所以原不等式的解集为: .
例3解不等式 .
解 由原不等式得 或 ,整理,得
介绍
提问
归纳总结
引导
分析
了解
思考
回答
观察
领会
复习
相关
知识
点为
进一
步学
习做
准备
充分
借助
图像
进行
分析
*动脑思考明确新知
一般地,不等式 ( )的解集是 ;不等式 ( )的解集是 .
试一试:写出不等式 与 ( )的解集.
总结
强化
理解
记忆Байду номын сангаас
强调
特点
*巩固知识典型例题
例1 解下列各不等式:
(1) ;(2)2∣x∣≤6.
解题
交流
反馈
学习
效果
*实际操作探索新知
问题
如何通过 ( )求解不等式 ?
解决
在不等式 中,设 ,则不等式 化为 ,其解集为
,即 .
利用不等式的性质,可以求出解集.
总结
可以通过“变量替换”的方法求解不等式 或 ( ).
质疑
引导
演示
归纳
思考
观察
体会
理解
通过
实例
使学
生初
步领
会变
量替
换的
思想
*动脑思考感悟新知
或 ,
所以原不等式的解集为 .
引领
分析
思路
讲解
观察
思考
领会
主动
求解
巩固
知识
强调
不等
式求
解的
细节
*运用知识强化练习
教材练习2.4.2
解下列各不等式:
(1) ;(2) ;
(3) ;(4) .
巡视
指导
求解
交流
反馈
学习
效果
*归纳小结强化思想
本次课学了哪些内容?重点和难点各是什么?
*自我反思目标检测
本次课采用了怎样的学习方法?
分析:将不等式化成 或 的形式后求解.
解 (1)由不等式 ,得 ,所以原不等式的解集为 ;
(2)由不等式2∣x∣≤6,得∣x∣≤3,所以原不等式的解集为 .
分析
讲解
强调
细节
思考
主动
求解
进一
步巩
固知
识点
*运用知识强化练习
教材练习2.4.1
解下列各不等式:
(1)2∣x∣≥8;(2) ;(3) .
巡视
辅导
【课题】2.4含绝对值的不等式
【教学目标】
1、理解含绝对值不等式 或 的解法;
2、了解 或 的解法;
3、通过数形结合的研究问题,培养观察能力;
4、通过含绝对值的不等式的学习,学会运用变量替换的方法,从而提升计算技能。
【教学重点】
(1)不等式 或 的解法.
(2)利用变量替换解不等式 或 .
【教学难点】
利用变量替换解不等式 或 .
【教学过程】
教学
过程
教师
行为
学生
行为
教学
意图
*回顾思考复习导入
问题
任意实数的绝对值是如何定义的?其几何意义是什么?
解决
对任意实数 ,有
其几何意义是:数轴上表示实数 的点到原点的距离.
拓展
不等式 和 的解集在数轴上如何表示?
根据绝对值的意义可知,方程 的解是 或 ,不等式 的解集是 (如图(1)所示);不等式 的解集是 (如图(2)所示).
你是如何进行学习的?
你的学习效果如何?
引导
总结
反思
交流
培养
学生
总结
学习
过程
能力
*继续探索活动探究
(1)读书部分:教材章节2.4,学习与训练2.4;
(2)书面作业:教材习题2.4,学习与训练2.4训练题.
说明
记录
教学反思
