河北省望都中学2017届高三8月月考数学(文)试题 Word版(含答案)
河北省保定市望都中学2017-2018学年高二上学期第二次月考数学试卷(文科) Word版含解析
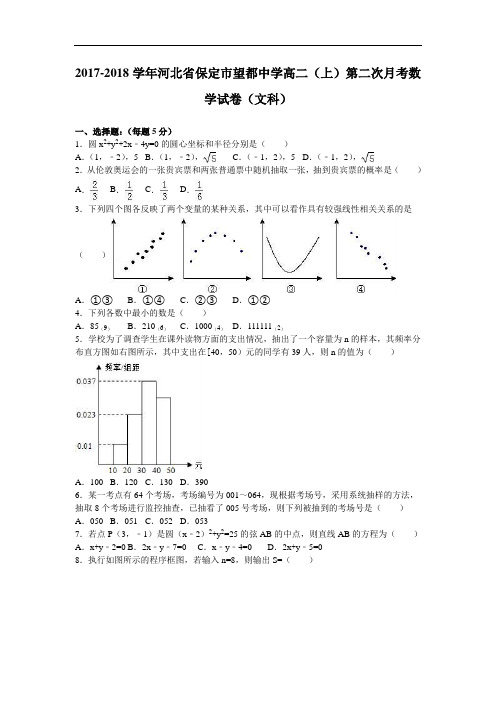
2017-2018学年河北省保定市望都中学高二(上)第二次月考数学试卷(文科)一、选择题:(每题5分)1.圆x2+y2+2x﹣4y=0的圆心坐标和半径分别是()A.(1,﹣2),5 B.(1,﹣2),C.(﹣1,2),5 D.(﹣1,2),2.从伦敦奥运会的一张贵宾票和两张普通票中随机抽取一张,抽到贵宾票的概率是()A.B.C.D.3.下列四个图各反映了两个变量的某种关系,其中可以看作具有较强线性相关关系的是()A.①③B.①④C.②③D.①②4.下列各数中最小的数是()A.85(9)B.210(6)C.1000(4)D.111111(2)5.学校为了调查学生在课外读物方面的支出情况,抽出了一个容量为n的样本,其频率分布直方图如右图所示,其中支出在[40,50)元的同学有39人,则n的值为()A.100 B.120 C.130 D.3906.某一考点有64个考场,考场编号为001~064,现根据考场号,采用系统抽样的方法,抽取8个考场进行监控抽查,已抽看了005号考场,则下列被抽到的考场号是()A.050 B.051 C.052 D.0537.若点P(3,﹣1)是圆(x﹣2)2+y2=25的弦AB的中点,则直线AB的方程为()A.x+y﹣2=0 B.2x﹣y﹣7=0 C.x﹣y﹣4=0 D.2x+y﹣5=08.执行如图所示的程序框图,若输入n=8,则输出S=()A.B.C.D.9.下列程序执行后输出的结果是()A.﹣1 B.0 C.1 D.2=0.95x+a,则a=()11.从集合A={1,2,3,4,5}任意取出两个数,这两个数的和是偶数的概率是()A.B.C.D.12.已知圆C1:(x﹣2)2+(y﹣3)2=1,圆C2:(x﹣3)2+(y﹣4)2=9,M,N分别是圆C1,C2上的动点,P为x轴上的动点,则|PM|+|PN|的最小值为()A.﹣1 B.5﹣4 C.6﹣2D.二、填空题:(每题5分)13.某全日制大学共有学生5400人,其中专科生有1500人,本科生有3000人,研究生有900人.现采用分层抽样的方法调查学生利用因特网查找学习资料的情况,抽取的样本为180人,则应在专科生学生中抽取人.14.若圆O2:(x﹣3)2+(y+3)2=4关于直线l:ax+4y﹣6=0对称,则直线l的斜率是.15.如图所示的程序框图,若输出的S=41,则判断框内应填入的条件是.16.已知圆心在直线2x﹣y﹣3=0上,且过点A(5,2)和点B(3,2),则圆C的方程为.三、解答题:17.已知关于x,y的方程C:x2+y2﹣2x﹣4y+m=0(1)若方程C表示圆,求m的取值范围;(2)若圆C与圆x2+y2﹣8x﹣12y+36=0外切,求m的值.x,y,统计的结果如下面的表格.(II)然后根据表格的内容和公式求出y对x的回归直线方程=x+,并估计当x为10时y的值是多少?=,=﹣.19.《中华人民共和国道路交通安全法》规定:车辆驾驶员血液酒精浓度在20~80mg/100ml (不含80)之间,属于酒后驾车;在80mg/100ml(含80)以上时,属于醉酒驾车.某市公安局交通管理部门在某路段的一次拦查行动中,依法检查了300辆机动车,查处酒后驾车和()绘制出检测数据的频率分布直方图(在图中用实线画出矩形框即可);(2)求检测数据中醉酒驾驶的频率,并估计检测数据中酒精含量的众数、平均数.20.四川一所学校高三年级有10名同学参加2014年北约自主招生,学校对这10名同学进行了辅导,并进行了两次模拟模拟考试,检测成绩的茎叶图如图所示.(1)比较这10名同学预测卷和押题卷的平均分大小;(2)若从押题卷的成绩中随机抽取两名成绩不低于112分的同学,求成绩为118分的同学被抽中的概率.21.已知以点A(﹣1,2)为圆心的圆与直线m:x+2y+7=0相切,过点B(﹣2,0)的动直线l与圆A相交于M、N两点(1)求圆A的方程.(2)当|MN|=2时,求直线l方程.22.2014年“双节”期间,高速公路车辆较多.某调查公司在一服务区从七座以下小型汽车中按进服务区的先后每间隔50辆就抽取一辆的抽样方法抽取40名驾驶员进行询问调查,将他们在某段高速公路的车速(km/h)分成六段:[60,65),[65,70),[70,75),[75,80),[80,85),[85,90)后得到如图的频率分布直方图.(1)求这40辆小型车辆车速的众数、平均数和中位数的估计值;(2)若从车速在[60,70)的车辆中任抽取2辆,求车速在[65,70)的车辆恰有一辆的概率.2015-2016学年河北省保定市望都中学高二(上)第二次月考数学试卷(文科)参考答案与试题解析一、选择题:(每题5分)1.圆x2+y2+2x﹣4y=0的圆心坐标和半径分别是()A.(1,﹣2),5 B.(1,﹣2),C.(﹣1,2),5 D.(﹣1,2),【考点】圆的标准方程.【分析】将圆的方程化为标准方程,找出圆心坐标与半径即可.【解答】解:圆的方程化为标准方程为(x+1)2+(y﹣2)2=5,则圆心是(﹣1,2),半径为.故选D2.从伦敦奥运会的一张贵宾票和两张普通票中随机抽取一张,抽到贵宾票的概率是()A.B.C.D.【考点】计数原理的应用.【分析】从伦敦奥运会的一张贵宾票和两张普通票中随机抽取一张,求出总事件的个数和需要满足条件的个数,根据概率公式计算即可.【解答】解:从伦敦奥运会的一张贵宾票和两张普通票中随机抽取一张,求出总事件的个数为3,需要满足条件的个数为1,则P=.故选:C.3.下列四个图各反映了两个变量的某种关系,其中可以看作具有较强线性相关关系的是()A.①③B.①④C.②③D.①②【考点】变量间的相关关系.【分析】观察两个变量的散点图,若样本点成带状分布,则两个变量具有线性相关关系,若带状越细说明相关关系越强,得到两个变量具有线性相关关系的图是①和④.【解答】解:∵两个变量的散点图,若样本点成带状分布,则两个变量具有线性相关关系,∴两个变量具有线性相关关系的图是①和④.故选B.4.下列各数中最小的数是()A.85(9)B.210(6)C.1000(4)D.111111(2)【考点】进位制.【分析】将四个答案中的数都转化为十进制的数,进而可以比较其大小.【解答】解:85(9)=8×9+5=77,210(6)=2×62+1×6=78,1000(4)=1×43=64,111111(2)=1×26﹣1=63,故最小的数是111111(2)故选:D5.学校为了调查学生在课外读物方面的支出情况,抽出了一个容量为n的样本,其频率分布直方图如右图所示,其中支出在[40,50)元的同学有39人,则n的值为()A.100 B.120 C.130 D.390【考点】频率分布直方图.【分析】根据频率分布直方图,算出[10,40)的比例,得出[40,50)的比例从而得出总人数.【解答】解:由频率分布直方图可知,在[10,20),[20,30),[30,40)的比例为(0.01+0.023+0.037)×10=0.7所以[40,50)所占的比例为0.3.所以n=故选:C6.某一考点有64个考场,考场编号为001~064,现根据考场号,采用系统抽样的方法,抽取8个考场进行监控抽查,已抽看了005号考场,则下列被抽到的考场号是()A.050 B.051 C.052 D.053【考点】系统抽样方法.【分析】求出样本间隔即可得到结论.【解答】解:∵样本容量为8,∴样本间隔为64÷8=8,若随机抽得的一个号码为005,则第二个号码是005+8×6=053,故选:D.7.若点P(3,﹣1)是圆(x﹣2)2+y2=25的弦AB的中点,则直线AB的方程为()A.x+y﹣2=0 B.2x﹣y﹣7=0 C.x﹣y﹣4=0 D.2x+y﹣5=0【考点】直线与圆的位置关系.【分析】由垂径定理可知,圆心C与点P的连线与AB垂直.可求直线AB的斜率,从而由点斜式方程得到直线AB的方程.【解答】解:由(x﹣2)2+y2=25,可得,圆心C(2,0).∴k PC==﹣1.∵PC⊥AB,∴k AB=1.∴直线AB的方程为y+1=x﹣3,即x﹣y﹣4=0.故选:C.8.执行如图所示的程序框图,若输入n=8,则输出S=()A.B.C.D.【考点】程序框图.【分析】由已知中的程序框图及已知中输入8,可得:进入循环的条件为i≤8,即i=2,4,6,8,模拟程序的运行结果,即可得到输出的S值.【解答】解:当i=2时,S=0+=,i=4;当i=4时,S=+=,i=6;当i=6时,S=+=,i=8;当i=8时,S=+=,i=10;不满足循环的条件i≤8,退出循环,输出S=.故选A.9.下列程序执行后输出的结果是()A.﹣1 B.0 C.1 D.2【考点】伪代码.【分析】该程序是一个当型循环结构.第一步:s=0+5=5,n=5﹣1=4;第二步:s=5+4=9,n=4﹣1=3;第三步:s=9+3=12,n=3﹣1=2;第四步:s=12+2=14,n=2﹣1=1;第五步:s=14+1=15,n=1﹣1=0.【解答】解:该程序是一个当型循环结构.第一步:s=0+5=5,n=5﹣1=4;第二步:s=5+4=9,n=4﹣1=3;第三步:s=9+3=12,n=3﹣1=2;第四步:s=12+2=14,n=2﹣1=1;第五步:s=14+1=15,n=1﹣1=0.∵s=15,∴结束循环.∴n=0.故选B;10.已知x,y的取值如表所示,若y与x线性相关,且=0.95x+a,则a=()【考点】线性回归方程.【分析】求出样本中心坐标,代入回归直线方程,求解即可.【解答】解:由题意==2,==4.5.因为回归直线方程经过样本中心,所以4.5=0.95×2+a,所以a=2.6.故选:B.11.从集合A={1,2,3,4,5}任意取出两个数,这两个数的和是偶数的概率是()A.B.C.D.【考点】古典概型及其概率计算公式.【分析】用列举法写出所有基本事件,找出两个数的和是偶数的基本事件,利用个数比求概率.【解答】解:从集合A={1,2,3,4,5}任意取出两个数,基本事件有(1,2),(1,3),(1,4),(1,5),(2,3),(2,4),(2,5),(3,4),(3,5),(4,5)共10个;其中两个数的和是偶数的基本事件有(1,3),(1,5),(2,4),(3,5)共4个,∴两个数的和是偶数的概率为=.故选:C.12.已知圆C1:(x﹣2)2+(y﹣3)2=1,圆C2:(x﹣3)2+(y﹣4)2=9,M,N分别是圆C1,C2上的动点,P为x轴上的动点,则|PM|+|PN|的最小值为()A.﹣1 B.5﹣4 C.6﹣2D.【考点】圆与圆的位置关系及其判定.【分析】求出圆C1关于x轴的对称圆的圆心坐标A,以及半径,然后求解圆A与圆C2的圆心距减去两个圆的半径和,即可求出|PM|+|PN|的最小值.【解答】解:如图圆C1关于x轴的对称圆的圆心坐标A(2,﹣3),半径为1,圆C2的圆心坐标(3,4),半径为3,由图象可知当P,C2,C3,三点共线时,|PM|+|PN|取得最小值,|PM|+|PN|的最小值为圆C3与圆C2的圆心距减去两个圆的半径和,即:|AC2|﹣3﹣1=﹣4=﹣4=5﹣4.故选:B.二、填空题:(每题5分)13.某全日制大学共有学生5400人,其中专科生有1500人,本科生有3000人,研究生有900人.现采用分层抽样的方法调查学生利用因特网查找学习资料的情况,抽取的样本为180人,则应在专科生学生中抽取50人.【考点】分层抽样方法.【分析】先根据总体数和抽取的样本,求出每个个体被抽到的概率,用每一个层次的数量乘以每个个体被抽到的概率就等于每一个层次的值.【解答】解:每个个体被抽到的概率为=,∴专科生被抽的人数是×1500=50,故答案为:50.14.若圆O2:(x﹣3)2+(y+3)2=4关于直线l:ax+4y﹣6=0对称,则直线l的斜率是﹣.【考点】直线与圆的位置关系.【分析】由圆O2:(x﹣3)2+(y+3)2=4关于直线l:ax+4y﹣6=0对称,得到ax+4y﹣6=0过圆心,由此能求出结果.【解答】解:∵圆O2:(x﹣3)2+(y+3)2=4关于直线l:ax+4y﹣6=0对称,∴ax+4y﹣6=0过圆心(3,﹣3),即3a﹣12﹣6=0,解得a=6,∴直线l的斜率是﹣.故答案为:﹣.15.如图所示的程序框图,若输出的S=41,则判断框内应填入的条件是k>4?.【考点】程序框图.【分析】分析程序中各变量、各语句的作用,再根据流程图所示的顺序,可知:该程序的作用是累加并输入S的值,条件框内的语句是决定是否结束循环,模拟执行程序即可得到答案.【解答】解:程序在运行过程中各变量值变化如下表:K S 是否继续循环循环前1 0第一圈2 2 是第二圈3 7 是第三圈4 18 是第四圈5 41 否故退出循环的条件应为k>4?故答案为:k>4?16.已知圆心在直线2x﹣y﹣3=0上,且过点A(5,2)和点B(3,2),则圆C的方程为(x﹣4)2+(y﹣5)2=10.【考点】圆的标准方程.【分析】设圆心C(a,b),由已知,得:,由此能求出圆C的方程.【解答】解:设圆心C(a,b),由已知,得:,解得a=4,b=5,∴圆心C(4,5),半径r==,∴圆C的方程为(x﹣4)2+(y﹣5)2=10.故答案为:(x﹣4)2+(y﹣5)2=10.三、解答题:17.已知关于x,y的方程C:x2+y2﹣2x﹣4y+m=0(1)若方程C表示圆,求m的取值范围;(2)若圆C与圆x2+y2﹣8x﹣12y+36=0外切,求m的值.【考点】直线与圆的位置关系.【分析】(1)把方程C:x2+y2﹣2x﹣4y+m=0,配方得:(x﹣1)2+(y﹣2)2=5﹣m,若方程C表示圆,则5﹣m>0,即可求m的取值范围;(2)两圆的位置关系是外切,所以d=R+r,即可求m的值.【解答】解:(1)把方程C:x2+y2﹣2x﹣4y+m=0,配方得:(x﹣1)2+(y﹣2)2=5﹣m,若方程C表示圆,则5﹣m>0,解得m<5;(2)把圆x2+y2﹣8x﹣12y+36=0化为标准方程得:(x﹣4)2+(y﹣6)2=16,得到圆心坐标(4,6),半径为4,则两圆心间的距离d==5,因为两圆的位置关系是外切,所以d=R+r即4+=5,解得m=4.x,y,统计的结果如下面的表格.(II)然后根据表格的内容和公式求出y对x的回归直线方程=x+,并估计当x为10时y的值是多少?=,=﹣.【考点】线性回归方程.【分析】(I)利用所给数据,可得散点图;(II)利用公式,计算回归系数,即可得到回归方程;x=10代入回归方程,即可得到结论.【解答】解:(I)散点图如图所示;﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣(II)=3,=3.6﹣﹣﹣﹣﹣﹣﹣﹣﹣∴==0.7,=3.6﹣0.7×3=1.5∴=0.7x+1.5﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣当x=10时,=8.5∴预测y的值为8.5﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣19.《中华人民共和国道路交通安全法》规定:车辆驾驶员血液酒精浓度在20~80mg/100ml (不含80)之间,属于酒后驾车;在80mg/100ml(含80)以上时,属于醉酒驾车.某市公安局交通管理部门在某路段的一次拦查行动中,依法检查了300辆机动车,查处酒后驾车和20(2)求检测数据中醉酒驾驶的频率,并估计检测数据中酒精含量的众数、平均数.【考点】极差、方差与标准差.【分析】(1)计算酒精含量(mg/100ml)在各小组中的,绘制出频率分布直方图即可;(2)计算检测数据中酒精含量在80mg/100ml(含80)以上的频率,根据频率分布直方图中小矩形图最高的底边的中点是众数,再计算数据的平均数值.【解答】解:(1)酒精含量(mg/100ml)在[20,30)的为=0.015,在[30,40)的为=0.020,在[40,50)的为=0.005,在[50,60)的为=0.20,在[60,70)的为=0.010,在[70,80)的为=0.015,在[80,90)的为=0.010,在[90,100]的为=0.005;绘制出酒精含量检测数据的频率分布直方图如图所示:…(2)检测数据中醉酒驾驶(酒精含量在80mg/100ml(含80)以上时)的频率是;…根据频率分布直方图,小矩形图最高的是[30,40)和[50,60),估计检测数据中酒精含量的众数是35与55;…估计检测数据中酒精含量的平均数是0.015×10×25+0.020×10×35+0.005×10×45+0.020×10×55+0.010×10×65+0.015×10×75+0.010×10×85+0.005×10×95=55.…20.四川一所学校高三年级有10名同学参加2014年北约自主招生,学校对这10名同学进行了辅导,并进行了两次模拟模拟考试,检测成绩的茎叶图如图所示.(1)比较这10名同学预测卷和押题卷的平均分大小;(2)若从押题卷的成绩中随机抽取两名成绩不低于112分的同学,求成绩为118分的同学被抽中的概率.【考点】古典概型及其概率计算公式;茎叶图.【分析】(1)由已知中的茎叶图,分析出两次模拟模拟考试,进而可得到这10名同学预测卷和押题卷的平均分,比较后可得结论;(2)分别求出从押题卷的成绩中随机抽取两名成绩不低于112分的同学基本事件总数和成绩为118分的同学被抽中的基本事件个数,代入古典概型概率计算公式,可得答案.【解答】解:(1)==110==109.1,故>(2)押题卷成绩不低于112的同学(用分数作为学生的代号)共4个,随机抽取2个共6种不同情况,分别为:,,,,,,其中成绩为118分的同学被抽中的情况有:,,共3种,所以成绩为118分的同学被抽中的概率.21.已知以点A(﹣1,2)为圆心的圆与直线m:x+2y+7=0相切,过点B(﹣2,0)的动直线l与圆A相交于M、N两点(1)求圆A的方程.(2)当|MN|=2时,求直线l方程.【考点】直线与圆相交的性质.【分析】(1)利用圆心到直线的距离公式求圆的半径,从而求解圆的方程;(2)根据相交弦长公式,求出圆心到直线的距离,设出直线方程,再根据点到直线的距离公式确定直线方程.【解答】解:(1)意知A(﹣1,2)到直线x+2y+7=0的距离为圆A半径r,∴,∴圆A方程为(x+1)2+(y﹣2)2=20(2)垂径定理可知∠MQA=90°.且,在Rt△AMQ中由勾股定理易知设动直线l方程为:y=k(x+2)或x=﹣2,显然x=﹣2合题意.由A(﹣1,2)到l距离为1知.∴3x﹣4y+6=0或x=﹣2为所求l方程.22.2014年“双节”期间,高速公路车辆较多.某调查公司在一服务区从七座以下小型汽车中按进服务区的先后每间隔50辆就抽取一辆的抽样方法抽取40名驾驶员进行询问调查,将他们在某段高速公路的车速(km/h)分成六段:[60,65),[65,70),[70,75),[75,80),[80,85),[85,90)后得到如图的频率分布直方图.(1)求这40辆小型车辆车速的众数、平均数和中位数的估计值;(2)若从车速在[60,70)的车辆中任抽取2辆,求车速在[65,70)的车辆恰有一辆的概率.【考点】列举法计算基本事件数及事件发生的概率;散点图.【分析】(1)众数的估计值为最高的矩形的中点,由此能求出众数的估计值;设图中虚线所对应的车速为x,由频率分布直方图能求出中位数的估计值和平均数的估计值.(2)从频率分布直方图求出车速在[60,65)的车辆数、车速在[65,70)的车辆数,设车速在[60,65)的车辆设为a,b,车速在[65,70)的车辆设为c,d,e,f,利用列举法能求出车速在[65,70)的车辆恰有一辆的概率.【解答】解:(1)众数的估计值为最高的矩形的中点,即众数的估计值等于77.5,设图中虚线所对应的车速为x,则中位数的估计值为:0.01×5+0.02×5+0.04×5+0.06×(x﹣75)=0.5,解得x=77.5,即中位数的估计值为77.5,平均数的估计值为:5×(62.5×0.01+67.5×0.02+72.5×0.04+77.5×0.06+82.5×0.05+87.5×0.02)=77.(2)从图中可知,车速在[60,65)的车辆数为:m1=0.01×5×40=2(辆),车速在[65,70)的车辆数为:m2=0.02×5×40=4(辆)设车速在[60,65)的车辆设为a,b,车速在[65,70)的车辆设为c,d,e,f,则所有基本事件有:(a,b),(a,c),(a,d),(a,e),(a,f),(b,c),(b,d),(b,e),(b,f),(c,d),(c,e),(c,f),(d,e),(d,f),(e,f),共15种其中车速在[65,70)的车辆恰有一辆的事件有:(a,c),(a,d),(a,e),(a,f),(b,c),(b,d),(b,e),(b,f)共8种∴车速在[65,70)的车辆恰有一辆的概率为.2016年12月8日。
望都中学2017届高三数学8月月考试题理带答案

望都中学2017届高三数学8月月考试题(理带答案)望都中学2016-2017学年第一学期高三八月月考数学(理)试题一、选择题:本题共13小题,每小题5分,在每小题给出的四个选项中,只有一项是符合题目要求的。
1.已知全集U={1,2,3,4,5,6},集合A={2,3,5},集合B={1,3,4,6},则集合A∩(∁UB)=A.{3}B.{2,5}C.{1,4,6}D.{2,3,5}2.方程的解所在的区间是A.B.C.D.3.设则的大小关系是A.B.C.D.4.已知函数若则实数的值等于A.-3B.-1C.1D.35.若,则A.B.C.1D.6.不等式成立的一个充分不必要条件是A.B.C.D.7.下列有关命题的说法正确的是A.命题“若,则”的否命题为“若,则”B.“”是“”的必要而不充分条件C.命题“,使得”的否定是“,均有”D.命题“若,则”的逆否命题为真命题8.函数的图像大致是9.当时,,则的取值范围是A.B.C.D.10.已知定义在上的函数(为实数)为偶函数,记,,,则的大小关系为A.B.C.D.11.已知函数其中,给出下列四个结论:①函数是最小正周期为的奇函数;②函数图像的一条对称轴是直线;③函数图像的一个对称中心为;④函数的单调递增区间为.其中正确的结论的个数是A.1B.2C.3D.412.将函数图象上的点向左平移()个单位长度得到点,若位于函数的图象上,则A.,的最小值为B.,的最小值为C.,的最小值为D.,的最小值为13.已知函数函数,其中,若函数恰有4个零点,则的取值范围是A.B.C.D.二、填空题:本题共5小题,每小题5分,共25分。
14.函数的值域是.15.已知函数在上单调递增,则实数的取值范围是. 16.若则.17.已知函数是定义在上的奇函数,对任意实数有,当时,,则__________.18.设函数.若无最大值,则实数的取值范围是________.三、解答题:解答应写出文字说明、证明过程或验算步骤。
(全优试卷)河北省望都中学高三8月月考数学(文)试题 Word版(含答案)

望都中学2016-2017学年第一学期高三八月月考数学(文)试题一、选择题:本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一个是符合题目要求的。
1、设集合{}22,A x x x R =-≤∈,{}2|,12B y y x x ==--≤≤,则()R C A B 等于( )A .RB .{},0x x R x ∈≠ C .{}0 D .∅2、已知条件p :x +y ≠-2,条件q :x ≠-1且y ≠-1,则p 是q 的( )A.充要条件B.既不充分也不必要条件C.充分不必要条件D.必要不充分条件3.设()f x 是定义在R 上的奇函数,当x ≤0时,()f x x x 2=2-,则()f 1= (A )-3 (B) -1 (C)1 (D)34、函数)10()2(log )(<<+=a x x f a 的图象必不过A .第一象限B .第二象限C .第三象限D .第四象限5.若偶函数()f x 在(,0]-∞上单调递减,2(log 3a f =),4(log 5)b f =,32(2)c f =,则,,a b c 满足( )A .a b c <<B .b a c <<C .c a b <<D .c b a <<6、不等式2()0f x ax x c =-->的解集为{|21}x x -<<,则函数()y f x =-的图象为( )7、设()f x 是R 上的任意函数,则下列叙述正确的是( )(A)()()f x f x -是奇函数 (B)()()f x f x -是奇函数(C) ()()f x f x --是偶函数 (D) ()()f x f x +-是偶函数8、下列四个函数中,既是奇函数又是定义域上的单调递增的是 A .2xy -= B .tan y x = C .3y x = D .3log y x =9、函数1222--=x x y 的值域为 ( )A .(),1[]2,+∞--∞-B .),1()2,(+∞---∞C .}{Ry y y ∈-≠,1 D .}{R y y y ∈-≠,210、已知)12(+x f 是偶函数,则函数)2(x f 的图象的对称轴是 ( )(A )1-=x(B )x =1 (C )21-=x (D )21=x 11、已知函数()()322,2,03a f x x ax cx g x ax ax c a =++=++≠,则它们的图象可能是( )12、在同一平面直角坐标系中,函数()y f x =和()y g x =的图像关于直线y x =对称.现将()y g x =图像沿x 轴向左平移2个单位,再沿Y 轴向上平移1个单位,所得的图像是由两条线段组成的折线(如图2所示),则函数()f x 的表达式为( )(A)22,10()2,022x x f x x x +-≤≤⎧⎪=⎨+<≤⎪⎩(B)22,10()2,022x x f x x x --≤≤⎧⎪=⎨-<≤⎪⎩(C)22,12()1,242x x f x x x -≤≤⎧⎪=⎨+<≤⎪⎩(D)26,12()3,242x x f x x x -≤≤⎧⎪=⎨-<≤⎪⎩二、填空题:本大题共4小题,每小题4分,共16分.把答案填写在答题卡相应位置上.13、已知集合A ={-1,3,2m -1},集合B ={3,2m }.若B ⊆A ,则实数m = . 14、函数()f x 对于任意实数x 满足条件()()2f x f x +=-,若()15,f =-则()()5f f =__________15、若函数)2(log )(22a x x x f a ++=是奇函数,则a =16、对于函数f (x )定义域中任意的x 1,x 2(x 1≠x 2),有如下结论: ①f (x 1+x 2)=f (x 1)·f (x 2);② f (x 1·x 2)=f (x 1)+f (x 2)③1212()()f x f x x x -->0;④1212()()()22x x f x f x f ++<.当f (x )=l gx 时,上述结论中正确结论的序号是 .三、解答题:本大题共6小题,共74分. 解答应写出文字说明,证明过程或演算步骤. 17.(本小题满分10分)已知P :方程210x mx ++=有两个不等的负实根,Q :方程()244210x m x +-+=无实根。
全国各地2017高3文科数学模拟试卷精彩试题汇编07 Word版含解析

2017届全国各地高三文科数学模拟试卷精彩试题汇编(7)1.( 数学卷·2017届河北省定州中学高三(高补班)上学期周练(一)第3题) 定义在区间),0(+∞上的函数)(x f 使不等式)(3)(')(2x f x xf x f <<恒成立,其中)('x f 为)(x f 的导数,则( )2.( 数学卷·2017届河北省定州中学高三(高补班)上学期周练(一)第5题) 设函数解:由函数解析式的形式可知)(x f 表示平面上的两动点)2,(),ln ,(2a a Q x xP 之间距离d 的平3.( 河北省望都中学2017届高三8月月考数学(文)试题第11题) 已知函数解:B.4.( 湖北省襄阳市第四中学2017届高三七月第三周周考数学(文)试题第11题) 已知F 为抛物线x y =2的焦点,点B A 、在该抛物线上且位于x 轴的两侧,2=⋅OB OA (其中O 为坐标原点),则ABO ∆与AFO ∆面积之和的最小值是( )5.( 黑龙江省牡丹江市第一中学2017届高三上学期开学摸底考试数学(文)试题 第10题) 若221x y +=,则x y +的取值范围是( )A .]2,0[B .]0,2[-C .),2[+∞-D .]2,(--∞解:D.6.( 河北省涞水县波峰中学2017届高三8月月考调研考试数学试题第22题) 对于函数)0(2)1()(2≠-+++=a b x b ax x f ,若存在实数0x ,使00)(x x f =成立,则称0x 为)(x f 的不动点.(1)当a=2,b=-2时,求)(x f 的不动点;(2)若对于任何实数b ,函数)(x f 恒有两相异的不动点,求实数a 的取值范围;(3)在(2)的条件下,若)(x f y =的图象上A 、实数b 的取值范围.解:),0(2)1()(2≠-+++=a b x b ax x f (1)当a=2,b=-2时,.42)(2--=x x x f 设x 为其不动点,即.422x x x =--则.04222=--x x )(.2,121x f x x 即=-=∴的不动点是-1,2.(2)由x x f =)(得:022=-++b bx ax . 由已知,此方程有相异二实根,>∆x 恒成立,即.0)2(42>--b a b 即0842>+-a ab b 对任意R b ∈恒成立. .2003216.02<<∴<-∴<∆∴a a a b7.( 湖北省襄阳市第四中学2017届高三七月第三周周考数学(文)试题第18题) 已知函数()e 1x f x ax =--(a ∈R ).(1)求函数()f x 的单调区间;(2)函数()()ln F x f x x x =-在定义域内存在零点,求a 的取值范围;(3)若()ln(e 1)ln x g x x =--,当(0,)x ∈+∞时,不等式(())()f g x f x <恒成立,求a 的取值范围.由于0x >,e 10x ->,可知当1x >,'()0h x >;当01x <<时,'()0h x <, 故函数()h x 在(0,1)上单调递减,在(1,)+∞上单调递增,故()(1)e 1h x h ≥=-.(随着0x >的增长,e 1x y =-的增长速度越来越快,会超过并远远大于y x =的增长速度,而ln y x =的增长速度则会越来越慢.则当0x >且x 无限接近于0时,()h x 趋向于正无穷大.)∴当e 1a ≥-时,函数()F x 有零点;(3)由(2)知,当0>x 时,x e x>-1,即0)(,0>>∀x g x .先分析法证明:01,0>+->∀x x e xe x ,设)0(1H >+-=x e xe x x x )(,则0)('>=x xe x H ,所以)(x H 在),0(+∞∈x 时函数单调递增,所以0)0(H =>H x )(, 则01,0>+->∀x x e xe x 当1≤a 时,由(1)知,函数)(x f 在),0(+∞∈x 单调递增,则(())()f g x f x <在),0(+∞∈x 恒成立;当1>a 时,由(1)知,函数)(x f 在),(ln +∞a 单调递增,在),(a ln 0单调递减.故当ax ln 0<<时a x x g ln )(0<<<,所以)())((x f x g f >,则不满足题意,舍去.综上,满足题意的实数a 的取值范围为1]-,(∞.。
望都中学2017届高三数学8月月考试题文附答案

望都中学2017届高三数学8月月考试题(文附答案)望都中学2016-2017学年第一学期高三八月月考数学(文)试题一、选择题:本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一个是符合题目要求的。
1、设集合,,则等于()A.B.C.D.2、已知条件p:x+y≠-2,条件q:x≠-1且y≠-1,则p是q的()A.充要条件B.既不充分也不必要条件C.充分不必要条件D.必要不充分条件3.设是定义在上的奇函数,当时,,则(A)(B)(C)1(D)34、函数的图象必不过A.第一象限B.第二象限C.第三象限D.第四象限5.若偶函数在上单调递减,,,,则满足()A.B.C.D.6、不等式的解集为,则函数的图象为()7、设是R上的任意函数,则下列叙述正确的是()(A)是奇函数(B)是奇函数(C)是偶函数(D)是偶函数8、下列四个函数中,既是奇函数又是定义域上的单调递增的是A.B.C.D.9、函数的值域为()A.(B.C.D.10、已知是偶函数,则函数的图象的对称轴是()(A)(B)x=1(C)(D)11、已知函数,则它们的图象可能是()12、在同一平面直角坐标系中,函数和的图像关于直线对称.现将图像沿轴向左平移2个单位,再沿Y轴向上平移1个单位,所得的图像是由两条线段组成的折线(如图2所示),则函数的表达式为()(A)(B)(C)(D)二、填空题:本大题共4小题,每小题4分,共16分.把答案填写在答题卡相应位置上.13、已知集合A=-1,3,2-1,集合B=3,.若BA,则实数=.14、函数对于任意实数满足条件,若则__________15、若函数是奇函数,则a=16、对于函数f(x)定义域中任意的x1,x2(x1≠x2),有如下结论:①f(x1+x2)=f(x1)f(x2);②f(x1x2)=f(x1)+f(x2)③0;④.当f(x)=lgx时,上述结论中正确结论的序号是.三、解答题:本大题共6小题,共74分.解答应写出文字说明,证明过程或演算步骤.17.(本小题满分10分)已知:方程有两个不等的负实根,:方程无实根。
河北省保定市望都中学2017-2018学年高二上学期8月月考数学试题 Word版含解析

2017-2018学年河北省保定市望都中学高二(上)8月月考数学试卷一、选择题:本大题共12小题,每小题5分,共60分.1.在等差数列3,7,11 …中,第5项为()A.15 B.18 C.19 D.232.数列{a n}中,如果a n=3n(n=1,2,3,…),那么这个数列是()A.公差为2的等差数列B.公差为3的等差数列C.首项为3的等比数列D.首项为1的等比数列3.已知m,n是两条不同直线,α,β是两个不同平面,则下列正确的是()A.若α,β垂直于同一平面,则α与β平行B.若m,n平行于同一平面,则m与n平行C.若α,β不平行,则在α内不存在与β平行的直线D.若m,n不平行,则m与n不可能垂直于同一平面4.若x,y满足,则z=x+2y的最大值为()A.0 B.1 C.D.25.不等式|x﹣1|﹣|x﹣5|<2的解集是()A.(﹣∞,4)B.(﹣∞,1)C.(1,4)D.(1,5)6.在△ABC中,AB=5,BC=7,AC=8,则的值为()A.79 B.69 C.5 D.﹣57.一个四棱锥的底面为正方形,其三视图如图所示,则这个四棱锥的体积是()A.1 B.2 C.3 D.48.已知△ABC中,a=4,b=4,A=30°,则B等于()A.30°B.30°或150°C.60°D.60°或120°9.点P是直线3x+y+10=0上的动点,PA,PB与圆x2+y2=4分别相切于A,B两点,则四边形PAOB面积的最小值为()A.B.2 C.2D.410.若{a n}是等差数列,首项a1>0,a4+a5>0,a4•a5<0,则使前n项和S n>0成立的最大自然数n的值为()A.4 B.5 C.7 D.811.直三棱柱ABC﹣A1B1C1中,∠BCA=90°,M,N分别是A1B1,A1C1的中点,BC=CA=CC1,则BM与AN所成角的余弦值为()A.B.C. D.12.正四面体ABCD的棱长为1,G是△ABC的中心,M在线段DG上,且∠AMB=90°,则GM的长为()A.B.C.D.二.填空13.已知△ABC外接圆半径是2cm,∠A=60°,则BC边长为.14.如果一个水平放置的图形的斜二测直观图是一个底面为45°,腰和上底均为1的等腰梯形,那么原平面图形的面积是.15.在△ABC中,角A,B,C所对应的边分别是a,b,c,若a2+c2﹣b2=ac,则角B的值是.16.圆心在直线x﹣y﹣4=0上,并且经过圆x2+y2+6x﹣4=0与圆x2+y2+6y﹣28=0交点的圆的方程为.三.解答.17.(10分)(2015秋•保定校级月考)已知等差数列的首项为31,若此数列从第16项开始小于1,求公差d的取值范围.18.(12分)(2012秋•乐陵市校级期中)如图为了测量河对岸A、B两点的距离,在河的这边测定,∠ADB=∠CDB=30°,∠ACD=60°,∠ACB=45°,求A、B两点的距离.19.(12分)(2015秋•保定校级月考)已知过球面上三点A、B、C的截面到球心的距离等于球半径的一半,且AC=BC=6,AB=4,求球的表面积和体积.20.(12分)(2012秋•喀左县校级期中)设等差数列{a n}的前n项的和为S n,且S4=﹣62,S6=﹣75,求:(1){a n}的通项公式a n及前n项的和S n;(2)|a1|+|a2|+|a3|+…+|a14|.21.(12分)(2010•黄冈校级模拟)已知等比数列{a n}中,a1=a,a2=b,a3=c,a,b,c分别为△ABC的三内角A,B,C的对边,且cosB=.(1)求数列{a n}的公比q;(2)设集合A={x∈N|x2<2|x|},且a1∈A,求数列{a n}的通项公式.22.(12分)(2011•东城区模拟)如图,在四棱锥P﹣ABCD中,底面ABCD是正方形,侧棱PD⊥底面ABCD,PD=DC=2,E是PC的中点,作EF⊥PB交PB于点F.(1)证明:PA∥平面EDB;(2)证明:PB⊥平面EFD.2015-2016学年河北省保定市望都中学高二(上)8月月考数学试卷参考答案与试题解析一、选择题:本大题共12小题,每小题5分,共60分.1.在等差数列3,7,11 …中,第5项为()A.15 B.18 C.19 D.23考点:等差数列的通项公式.专题:计算题.分析:求出等差数列的公差,直接求出数列的第5项.解答:解:因为等差数列3,7,11 …,公差为4,所以数列的第5项:a5=a1+(5﹣1)×4=3+16=19.故选C.点评:本题是基础题,考查等差数列中项的求法,考查计算能力.2.数列{a n}中,如果a n=3n(n=1,2,3,…),那么这个数列是()A.公差为2的等差数列B.公差为3的等差数列C.首项为3的等比数列D.首项为1的等比数列考点:等比数列的通项公式.专题:计算题.分析:令n=1,代入已知的通项公式,求出a1的值,当n大于等于2时,表示出a n﹣1,进而确定出为定值,故此数列为等比数列,可得出首项为a1的值,从而得到正确的选项.解答:解:∵a n=3n,∴当n=1时,a1=3,∴当n≥2时,a n﹣1=3n﹣1,∴=3,∴数列{a n}为首项是3,公比是3的等比数列.故选C点评:此题考查了等比数列的通项公式,其中由当n≥2时,为定值,判断出数列{a n}为首项是3,公比是3的等比数列是解题的关键.3.已知m,n是两条不同直线,α,β是两个不同平面,则下列正确的是()A.若α,β垂直于同一平面,则α与β平行B.若m,n平行于同一平面,则m与n平行C.若α,β不平行,则在α内不存在与β平行的直线D.若m,n不平行,则m与n不可能垂直于同一平面考点:空间中直线与平面之间的位置关系;空间中直线与直线之间的位置关系;平面与平面之间的位置关系.专题:空间位置关系与距离.分析:利用面面垂直、线面平行的性质定理和判定定理对选项分别分析解答.解答:解:对于A,若α,β垂直于同一平面,则α与β不一定平行,例如墙角的三个平面;故A错误;对于B,若m,n平行于同一平面,则m与n平行.相交或者异面;故B错误;对于C,若α,β不平行,则在α内存在无数条与β平行的直线;故C错误;对于D,若m,n不平行,则m与n不可能垂直于同一平面;假设两条直线同时垂直同一个平面,则这两条在平行;故D正确;故选D.点评:本题考查了空间线面关系的判断;用到了面面垂直、线面平行的性质定理和判定定理.4.若x,y满足,则z=x+2y的最大值为()A.0 B.1 C.D.2考点:简单线性规划.专题:不等式的解法及应用.分析:作出题中不等式组表示的平面区域,再将目标函数z=x+2y对应的直线进行平移,即可求出z取得最大值.解答:解:作出不等式组表示的平面区域,当l经过点B时,目标函数z达到最大值∴z最大值=0+2×1=2.故选:D.点评:本题给出二元一次不等式组,求目标函数z=x+2y的最大值,着重考查了二元一次不等式组表示的平面区域和简单的线性规划等知识,属于基础题.5.不等式|x﹣1|﹣|x﹣5|<2的解集是()A.(﹣∞,4)B.(﹣∞,1)C.(1,4)D.(1,5)考点:绝对值不等式的解法.专题:不等式的解法及应用.分析:运用零点分区间,求出零点为1,5,讨论①当x<1,②当1≤x≤5,③当x>5,分别去掉绝对值,解不等式,最后求并集即可.解答:解:①当x<1,不等式即为﹣x+1+x﹣5<2,即﹣4<2成立,故x<1;②当1≤x≤5,不等式即为x﹣1+x﹣5<2,得x<4,故1≤x<4;③当x>5,x﹣1﹣x+5<2,即4<2不成立,故x∈∅.综上知解集为(﹣∞,4).故选A.点评:本题考查绝对值不等式的解法,主要考查运用零点分区间的方法,考查运算能力,属于中档题.6.在△ABC中,AB=5,BC=7,AC=8,则的值为()A.79 B.69 C.5 D.﹣5考点:余弦定理;平面向量数量积的含义与物理意义.专题:计算题.分析:由三角形的三边,利用余弦定理求出cosB的值,然后利用平面向量的数量积的运算法则表示出所求向量的数量积,利用诱导公式化简后,将各自的值代入即可求出值.解答:解:由AB=5,BC=7,AC=8,根据余弦定理得:cosB==,又||=5,||=7,则=||•||cos(π﹣B)=﹣||•||cosB=﹣5×7×=﹣5.故选D点评:此题考查了余弦定理,以及平面向量数量积的运算.注意与的夹角是π﹣B,而不是B,学生做题时容易出错.7.一个四棱锥的底面为正方形,其三视图如图所示,则这个四棱锥的体积是()A.1 B.2 C.3 D.4考点:由三视图求面积、体积.专题:计算题;图表型.分析:由三视图及题设条件知,此几何体为一个四棱锥,其较长的侧棱长已知,底面是一个正方形,对角线长度已知,故先求出底面积,再求出此四棱锥的高,由体积公式求解其体积即可解答:解:由题设及图知,此几何体为一个四棱锥,其底面为一个对角线长为2的正方形,故其底面积为=2由三视图知其中一个侧棱为棱锥的高,其相对的侧棱与高及底面正方形的对角线组成一个直角三角形由于此侧棱长为,对角线长为2,故棱锥的高为=3此棱锥的体积为=2故选B.点评:本题考点是由三视图求几何体的面积、体积,考查对三视图的理解与应用,主要考查三视图与实物图之间的关系,用三视图中的数据还原出实物图的数据,再根据相关的公式求表面积与体积,本题求的是四棱锥的体积,其公式为×底面积×高.三视图的投影规则是:“主视、俯视长对正;主视、左视高平齐,左视、俯视宽相等”,三视图是新课标的新增内容,在以后的高考中有加强的可能.8.已知△ABC中,a=4,b=4,A=30°,则B等于()A.30°B.30°或150°C.60°D.60°或120°考点:正弦定理.专题:解三角形.分析:△ABC中由条件利用正弦定理求得sinB的值,再根据及大边对大角求得B的值.解答:解:△ABC中,a=4,b=4,A=30°,由正弦定理可得,即=,解得sinB=.再由b>a,大边对大角可得B>A,∴B=60°或120°,故选D.点评:本题主要考查正弦定理的应用,以及大边对大角、根据三角函数的值求角,属于中档题.9.点P是直线3x+y+10=0上的动点,PA,PB与圆x2+y2=4分别相切于A,B两点,则四边形PAOB面积的最小值为()A.B.2 C.2D.4考点:直线与圆的位置关系.专题:计算题;直线与圆.分析:由题意可得,PA=PB,PA⊥OA,PB⊥OB则要求S PAOB=2S△PAO=2PA的最小值,转化为求PA最小值,由于PA2=PO2﹣4,当PO最小时,PA最小,结合点到直线的距离公式可知当PO⊥l时,PO有最小值,由点到直线的距离公式可求解答:解:由题意可得,PA=PB,PA⊥OA,PB⊥OB,S PAOB=2S△PAO=2PA又∵在Rt△PAO中,由勾股定理可得,PA2=PO2﹣4,当PO最小时,PA最小,此时所求的面积也最小点P是直线l:3x+y+10=0上的动点,当PO⊥l时,PO有最小值d=,PA=所求四边形PAOB的面积的最小值为2.故选:C.点评:本题主要考查了直线与圆的位置关系中的重要类型:相切问题的处理方法,解题中要注意对性质的灵活应用,体现了转化思想在解题中的应用.10.若{a n}是等差数列,首项a1>0,a4+a5>0,a4•a5<0,则使前n项和S n>0成立的最大自然数n的值为()A.4 B.5 C.7 D.8考点:等差数列的前n项和.专题:等差数列与等比数列.分析:由已知结合等差数列的单调性可得a4+a5>0,a5<0,由求和公式可得S9<0,S8>0,可得结论.解答:解:∵{a n}是等差数列,首项a1>0,a4+a5>0,a4•a5<0,∴a4,a5必定一正一负,结合等差数列的单调性可得a4>0,a5<0,∴S9===9a5<0,S8==>0,∴使前n项和S n>0成立的最大自然数n的值为8故选D点评:本题考查等差数列的前n项的最值,理清数列项的正负变化是解决问题的关键,属基础题.11.直三棱柱ABC﹣A1B1C1中,∠BCA=90°,M,N分别是A1B1,A1C1的中点,BC=CA=CC1,则BM与AN所成角的余弦值为()A.B.C. D.考点:异面直线及其所成的角.专题:空间位置关系与距离.分析:画出图形,找出BM与AN所成角的平面角,利用解三角形求出BM与AN所成角的余弦值.解答:解:直三棱柱ABC﹣A1B1C1中,∠BCA=90°,M,N分别是A1B1,A1C1的中点,如图:BC 的中点为O,连结ON,,则MN0B是平行四边形,BM与AN所成角就是∠ANO,∵BC=CA=CC1,设BC=CA=CC1=2,∴CO=1,AO=,AN=,MB===,在△ANO中,由余弦定理可得:cos∠ANO===.故选:C.点评:本题考查异面直线对称角的求法,作出异面直线所成角的平面角是解题的关键,同时考查余弦定理的应用.12.正四面体ABCD的棱长为1,G是△ABC的中心,M在线段DG上,且∠AMB=90°,则GM的长为()A.B.C.D.考点:棱锥的结构特征.专题:综合题.分析:由题意可知,三角形AMB是等腰直角三角形,求得MA,然后求得MG.解答:解:M在AB垂直平分线上,,;故选D.点评:本题考查棱锥的结构特征,考查空间想象能力,逻辑思维能力,是中档题.二.填空13.已知△ABC外接圆半径是2cm,∠A=60°,则BC边长为2cm.考点:正弦定理.专题:解三角形.分析:利用正弦定理列出关系式,将外接圆半径与sinA的值代入求出a的值,即为BC 的长.解答:解:∵△ABC外接圆半径是2cm,∠A=60°,∴由正弦定理得:=2R,即a=2RsinA=4×=2,则BC=a=2cm,故答案为:2cm点评:此题考查了正弦定理,以及特殊角的三角函数值,熟练掌握正弦定理是解本题的关键.14.如果一个水平放置的图形的斜二测直观图是一个底面为45°,腰和上底均为1的等腰梯形,那么原平面图形的面积是.考点:平面图形的直观图.专题:计算题.分析:水平放置的图形为直角梯形,求出上底,高,下底,利用梯形面积公式求解即可.解答:解:水平放置的图形为一直角梯形,由题意可知上底为1,高为2,下底为1+,S=(1++1)×2=2+.故答案为:2+.点评:本题考查水平放置的平面图形的直观图斜二测画法,也可利用原图和直观图的面积关系求解.属基础知识的考查.15.在△ABC中,角A,B,C所对应的边分别是a,b,c,若a2+c2﹣b2=ac,则角B的值是.考点:余弦定理.专题:计算题.分析:直接利用余弦定理求出B的余弦值,推出B的值即可.解答:解:在△ABC中,角A,B,C所对应的边分别是a,b,c,若a2+c2﹣b2=ac,由余弦定理可知cosB==,因为B是三角形内角,所以B=.故答案为:.点评:本题考查余弦定理的应用,基本知识的考查.16.圆心在直线x﹣y﹣4=0上,并且经过圆x2+y2+6x﹣4=0与圆x2+y2+6y﹣28=0交点的圆的方程为x2+y2﹣x+7y﹣32=0.考点:圆的一般方程.专题:计算题;直线与圆.分析:设要求的圆的方程为(x2+y2+6x﹣4)+λ(x2+y2+6y﹣28)=0,根据它的圆心(﹣,﹣)在直线x﹣y﹣4=0上,求出λ的值,可得所求圆的方程.解答:解:设经过两圆x2+y2+6x﹣4=0和x2+y2+6y﹣28=0的交点的圆的方程为(x2+y2+6x ﹣4)+λ(x2+y2+6y﹣28)=0,即x2+y2+x+y﹣=0,则它的圆心坐标为(﹣,﹣).再根据圆心在直线x﹣y﹣4=0上,可得﹣﹣(﹣)﹣4=0,解得λ=﹣7,故所求的圆的方程为x2+y2﹣x+7y﹣32=0,故答案为:x2+y2﹣x+7y﹣32=0.点评:本题主要考查利用待定系数法求满足条件的圆的方程,属于中档题.三.解答.17.(10分)(2015秋•保定校级月考)已知等差数列的首项为31,若此数列从第16项开始小于1,求公差d的取值范围.考点:等差数列的通项公式.专题:等差数列与等比数列.分析:可得数列的通项公式,由题意可得,解不等式组即可.解答:解:由题意可得等差数列的通项公式为:a n=31+(n﹣1)d,∵数列从第16项开始小于1,∴,∴,解得≤d<﹣2,∴公差d的取值范围为:≤d<﹣2点评:本题考查等差数列的通项公式,涉及不等式组的解法,属基础题.18.(12分)(2012秋•乐陵市校级期中)如图为了测量河对岸A、B两点的距离,在河的这边测定,∠ADB=∠CDB=30°,∠ACD=60°,∠ACB=45°,求A、B两点的距离.考点:余弦定理;正弦定理.专题:计算题;解三角形.分析:在△BCD中,利用正弦定理,可求BC,在△ABC中,由余弦定理,可求AB.解答:解:由题意,AD=DC=AC=,在△BCD中,∠DBC=45°,∴∴在△ABC中,由余弦定理AB2=AC2+BC2﹣2AC•BCcos45°,∴答:A、B两点距离为km.点评:本题考查正弦、余弦定理的运用,考查学生的计算能力,属于基础题.19.(12分)(2015秋•保定校级月考)已知过球面上三点A、B、C的截面到球心的距离等于球半径的一半,且AC=BC=6,AB=4,求球的表面积和体积.考点:球的体积和表面积.专题:空间位置关系与距离.分析:设出球的半径,小圆半径,通过已知条件求出两个半径,再求球的表面积.解答:解:如图,设球的半径为r,O′是△ABC的外心,外接圆半径为R,则OO′⊥面ABC.在Rt△ACD中,cosA=,则sinA=,在△ABC中,由正弦定理得=2R,R=,即O′C=.在Rt△OCO′中,由题意得r2﹣r2=,得r=.球的表面积S=4πr2=4π×=54π.球的体积为.点评:本题考查球面距离弦长问题球的表面积、体积的求法以及正弦定理的应用,考查学生分析问题解决问题能力,空间想象能力.20.(12分)(2012秋•喀左县校级期中)设等差数列{a n}的前n项的和为S n,且S4=﹣62,S6=﹣75,求:(1){a n}的通项公式a n及前n项的和S n;(2)|a1|+|a2|+|a3|+…+|a14|.考点:数列的求和;等差数列的前n项和.专题:计算题;等差数列与等比数列.分析:(1)由S4=﹣62,S6=﹣75,可得到等差数列{a n}的首项a1与公差d的方程组,解之即可求得{a n}的通项公式a n及前n项的和S n;由(1)可知a n,由a n<0得n<8,从而|a1|+|a2|+|a3|+…+|a14|=S14﹣2S7,计算即可.解答:解:(1)设等差数列{a n}的公差为d,依题意得,解得a1=﹣20,d=3.∴a n=﹣20+(n﹣1)×3=3n﹣23;S n==n2﹣n.(2)∵a n=3n﹣23,∴由a n<0得n<8,∴|a1|+|a2|+|a3|+…+|a14|=﹣a1﹣a2﹣…﹣a7+a8+…+a14=S14﹣2S7=×142﹣×14﹣2(×72﹣×7)=7(42﹣43)﹣7(21﹣43)=﹣7﹣7×(﹣22)=147.点评:本题考查数列的求和,着重考查等差数列的通项公式与前n项和公式,考查解方程组的能力,求得a n是关键,属于中档题.21.(12分)(2010•黄冈校级模拟)已知等比数列{a n}中,a1=a,a2=b,a3=c,a,b,c分别为△ABC的三内角A,B,C的对边,且cosB=.(1)求数列{a n}的公比q;(2)设集合A={x∈N|x2<2|x|},且a1∈A,求数列{a n}的通项公式.考点:余弦定理;等比数列的通项公式;等比数列的性质.专题:计算题.分析:(1)由等比数列的性质得出a,b及c的关系式,根据余弦定理表示出cosB,把得出的关系式代入化简后,由已知cosB的值,再根据等比数列的性质得到=q2,可列出关于公比q的方程,求出方程的解得到q的值;(2)把集合A中的不等式左右两边平方,整理后,右边化为0,左边分解因式,转化为一个一元二次不等式,求出不等式的解集,在解集中找出正整数解,确定出集合A,进而确定出a1的值,由(1)求出的公比q的值,写出等比数列的通项公式即可.解答:解:(1)依题意知:b2=ac,由余弦定理得:cosB==×(+)﹣=,(3分)而=q2,代入上式得q2=2或q2=,又在三角形中a,b,c>0,∴q=或q=;(6分)(2)∵x2<2|x|,∴x4﹣4x2<0,即x2(x2﹣4)<0,∴﹣2<x<2且x≠0,(8分)又x∈N,所以A={1},∴a1=1,a n=或a n=(10分)点评:此题考查了等比数列的通项公式,等比数列的性质,余弦定理,以及其他不等式的解法,利用了转化的思想,是高考中常考的题型,数列掌握公式及定理是解本题的关键.22.(12分)(2011•东城区模拟)如图,在四棱锥P﹣ABCD中,底面ABCD是正方形,侧棱PD⊥底面ABCD,PD=DC=2,E是PC的中点,作EF⊥PB交PB于点F.(1)证明:PA∥平面EDB;(2)证明:PB⊥平面EFD.考点:直线与平面平行的判定;棱柱、棱锥、棱台的体积;直线与平面垂直的判定.专题:证明题.分析:(1)由题意连接AC,AC交BD于O,连接EO,则EO是中位线,证出PA∥EO,由线面平行的判定定理知PA∥平面EDB;(2)由PD⊥底面ABCD得PD⊥DC,再由DC⊥BC证出BC⊥平面PDC,即得BC⊥DE,再由ABCD是正方形证出DE⊥平面PBC,则有DE⊥PB,再由条件证出PB⊥平面EFD.解答:解:(1)证明:连接AC,AC交BD于O.连接EO.∵底面ABCD是正方形,∴点O是AC的中点.∴在△PAC中,EO是中位线,∴PA∥EO,∵EO⊂平面EDB,且PA⊄平面EDB,∴PA∥平面EDB.(2)证明:∵PD⊥底面ABCD,且DC⊂底面ABCD,∴PD⊥BC.∵底面ABCD是正方形,∴DC⊥BC,∴BC⊥平面PDC.∵DE⊂平面PDC,∴BC⊥DE.又∵PD=DC,E是PC的中点,∴DE⊥PC.∴DE⊥平面PBC.∵PB⊂平面PBC,∴DE⊥PB.又∵EF⊥PB,且DE∩EF=E,∴PB⊥平面EFD.点评:本题考查了线线、线面平行和垂直的相互转化,通过中位线证明线线平行,再由线面平行的判定得到线面平行;垂直关系的转化是由线面垂直的定义和判定定理实现.。
河北省望都中学2017-2018学年高三年级8月月考历史试卷 Word版含答案
河北望都中学2017-2018学年高三年级8月月考历史试题一、选择题(本大题有50小题,每小题1分,共50分。
在每小题列出的四个选项中,只有一项是符合题目要求的。
)1.拜年是我国的春节习俗,通常在家族的祠堂进行。
拜年时,晚辈要给长辈行跪拜之礼,长辈端坐高堂,接受晚辈的祝福,拜年反映了我国古代的一项制度,这一制度() A.形成了等级森严的官僚政治B.体现了血缘和政治关系C.实现了中央对地方的有效管理D.加剧了统治集团内部的矛盾2.王之法,立天子不使诸侯疑焉,立诸侯不使大夫疑焉,立嫡子不使庶孽疑焉。
疑生争,争生乱,是故诸侯失位则天下乱,大夫无等则朝庭乱。
” 这表明西周实行嫡长子继承制的目的是A.确立嫡长子的最高地位B.防止内部纷争,强化中央集权制度C.解决权位和财产的继承与分配,稳定统治秩序D.保证贵族血统的纯正3.新华网《从“市管县”到“省管县”:地方政府改革展现新图景》一文指出:…我国宪法确定的地方行政区划主要是省县乡三级体制,而目前实行的却是四级体制…“十一五”规划纲要中明确提出,要“理顺省级以下财政管理体制,有条件的地方可实行省级直接对县的管理体制。
”20世纪90年代“省管县”改革在浙江开始试点,迄今已经在全国近20个省进行试点。
回顾历史,阅读下表反映的主要问题是( )西汉实行郡国并行制,郡国下有县邑等A.地方行政分层决策中的矛盾与困局 B.古代王朝执政能力和效率不断提高C.古代中国政治的诡秘多变,反复无常 D.从秦朝到唐末中央集权不断得到强化4.《公羊传》大一统理论主要包括以“尊王”为核心的政治一统,以“内华夏”为宗旨的民族一统,以“崇礼”为中心的文化一统。
这表明大一统源于()A.夏商时期的方国联盟B.西周封建诸侯与分封制度C.秦中央集权国家建立D.董仲舒对儒家学说的改造5.梁启超在《辛亥革命之意义与十年双十节之乐观》中说:“中国历史上有意义的革命,只有三回:第一回是周朝的革命……,第二回是汉朝的革命……,第三回就是我们今天所纪念的辛亥革命了。
望都中学第一学期高三八月月考
望都中学2016-2017学年第一学期高三八月月考化学试题可能用到的相对原子质量:H-1 O-16 Al-27 Cu-64 N-14 C-12 Na-23第Ⅰ卷(共50分)一、选择题(每小题只有一个选项符合题意,每小题2分)1.人们习惯上把金、银、铜、铁、锡五种金属统称为“五金”。
在“五金”顺序中,把一种金属的位置向后移一位,正好符合某化学规律。
这种金属和该化学规律是()A.铁、金属活动性顺序表B.金、质量守恒定律C.银、元素周期律D.铜、金属密度顺序表2.假设与猜想是科学探究的先导和价值所在。
下列假设引导下的探究肯定没有意义的是()A.探究SO2和Na2O2反应可能有Na2SO4生成B.探究浓硫酸与铜在一定条件下反应产生的黑色物质可能是CuOC.探究Na与水的反应可能有O2生成D.探究向滴有酚酞试液的NaOH溶液中通入Cl2,酚酞红色褪去的现象是溶液的酸碱性改变所致,还是HClO的漂白性所致3.分类是化学学习和研究的常用手段,下列分类依据和结论都正确的是()A.冰醋酸、纯碱、芒硝、生石灰分别属于酸、碱、盐、氧化物B.HClO、H2SO4(浓)、HNO3均具有强氧化性,都是氧化性酸C.漂白粉、福尔马林、冰水、王水、氯水均为混合物D.Na2O,NaOH,Na2CO3,NaCl,Na2SO4,Na2O2都属于钠的含氧化合物4.下列有关物质的性质与应用相对应的是()A.二氧化锰具有强氧化性,可用作H2O2分解的氧化剂B.K2FeO4具有还原性,可用于自来水的杀菌消毒C.浓硝酸在常温下能使铝钝化,可用铝槽车运输浓硝酸D.SO2具有漂白性,能使紫色KMnO4溶液褪色5.下列物质的转化在给定条件下能实现的是()①②③④⑤A.①⑤B.②③C.②⑤D.③④6.“秦砖汉瓦”是我国传统建筑文化的一个缩影。
同是由黏土烧制的砖瓦,有的是黑色的,有的却是红色的,你猜测其中的原因可能()A.土壤中含有铁粉、二氧化锰等B.黑砖瓦是煅烧过程中附着了炭黑,红砖则是添加了红色耐高温染料C.土壤中含有的铜元素经过不同工艺煅烧,分别生成了黑色CuO和红色CuD.土壤中含有的铁元素经过不同工艺煅烧,分别生成了黑色Fe3O4或FeO和红色Fe2O37.下列反应所得溶液中一定只含一种溶质的是()A.向稀硝酸中加入铁粉B.向氯化铝溶液中加入过量的氨水C.向NaOH溶液中通入CO2气体D.向MgSO4、H2SO4的混合液中加入过量的Ba(OH)2溶液8.将SO2通入BaCl2溶液至饱和,未见沉淀生成,继续通入另一种气体,仍无沉淀,则通入的气体可能是()A.CO2B.NH3C.NO2D.H2S9.下列叙述正确的是()A.强电解质都是离子化合物,因此NaCl是离子化合物B.醋酸溶液的导电能力可能比稀硫酸强C.SO3的水溶液能导电,SO3是电解质D.硫磺不导电,因此硫磺是非电解质10.中国稀土含量丰富,稀土元素用RE表示。
河北省望都中学2017届高三8月月考英语试题Word版(含答案)
望都中学2016-2017学年高三八月月考英语试题本试卷分第I卷(选择题)和第II卷(非选择题)两部份, 共150分。
考试时刻l20分钟。
第Ⅰ卷选择题第一节听下面5段对话。
每段对话后有一个小题,从题中所给的A、B、C三个选项当选出最正确选项,并标在试卷的相应位置。
每段对话仅读一遍。
1. What time is it now?A. 9:10.B.9:50. C. 10:00.2. What does the woman think of the weather?A. It’s nice.B. It’swarm. C. It’s cold.3. What will the man do?A. Attend a meeting.B. Give a lecture.C. Leave his office.4. What is the woman’s opinion about the course?A. Too hard.B. Worthtaking. C. Very easy.5. What does the woman want the man to do?A. Speak louder.B. Apologize to her.C. Turn off the radio.第二节听下面5段对话或独白。
每段对话或独白读两遍。
听第6段材料,回答第六、7题。
6. How long did Michael stay in China?A. Five days.B. Oneweek. C. Two weeks.7. Where did Michael go last year?A. Russia.B.Norway. C. India.听第7段材料,回答第八、9题。
8. What food does Sally like?A. Chicken. B.Fish. C. Eggs.9. What are the speakers going to do?A. Cook dinner.B. Goshopping. C. Order dishes.听第8段材料,回答第10至12题。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
望都中学2016-2017学年第一学期高三八月月考数学(文)试题一、选择题:本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一个是符合题目要求的。
1、设集合{}22,A x x x R =-≤∈,{}2|,12B y y x x ==--≤≤,则()R C A B 等于( )A .RB .{},0x x R x ∈≠ C .{}0 D .∅ 2、已知条件p :x +y ≠-2,条件q :x ≠-1且y ≠-1,则p 是q 的( )A.充要条件B.既不充分也不必要条件C.充分不必要条件D.必要不充分条件3.设()f x 是定义在R 上的奇函数,当x ≤0时,()f x x x 2=2-,则()f 1= (A )-3 (B) -1 (C)1 (D)3 4、函数)10()2(log )(<<+=a x x f a 的图象必不过A .第一象限B .第二象限C .第三象限D .第四象限 5.若偶函数()f x 在(,0]-∞上单调递减,2(log 3a f =),4(log 5)b f =,32(2)c f =,则,,a b c 满足( ) A .a b c << B .b a c << C .c a b << D .c b a <<6、不等式2()0f x ax x c =-->的解集为{|21}x x -<<,则函数()y f x =-的图象为( )7、设()f x 是R 上的任意函数,则下列叙述正确的是( )(A)()()f x f x -是奇函数 (B)()()f x f x -是奇函数 (C) ()()f x f x --是偶函数 (D) ()()f x f x +-是偶函数 8、下列四个函数中,既是奇函数又是定义域上的单调递增的是 A .2x y -= B .tan y x = C .3y x = D .3log y x =9、函数1222--=x xy 的值域为 ( )A .(),1[]2,+∞--∞-B .),1()2,(+∞---∞C .}{Ry y y ∈-≠,1 D .}{R y y y ∈-≠,210、已知)12(+x f 是偶函数,则函数)2(x f 的图象的对称轴是 ( )(A )1-=x (B )x =1(C )21-=x (D )21=x 11、已知函数()()322,2,03a f x x ax cx g x ax ax c a =++=++≠,则它们的图象可能是( )12、在同一平面直角坐标系中,函数()y f x =和()y g x =的图像关于直线y x =对称.现将()y g x =图像沿x 轴向左平移2个单位,再沿Y 轴向上平移1个单位,所得的图像是由两条线段组成的折线(如图2所示),则函数()f x 的表达式为( )(A)22,10()2,022x x f x x x +-≤≤⎧⎪=⎨+<≤⎪⎩(B)22,10()2,022x x f x x x --≤≤⎧⎪=⎨-<≤⎪⎩(C)22,12()1,242x x f x x x -≤≤⎧⎪=⎨+<≤⎪⎩(D)26,12()3,242x x f x x x -≤≤⎧⎪=⎨-<≤⎪⎩二、填空题:本大题共4小题,每小题4分,共16分.把答案填写在答题卡相应位置上.13、已知集合A ={-1,3,2m -1},集合B ={3,2m }.若B ⊆A ,则实数m = . 14、函数()f x 对于任意实数x 满足条件()()2fx f x +=-,若()15,f =-则()()5f f =__________15、若函数)2(log )(22a x x x f a ++=是奇函数,则a =16、对于函数f (x )定义域中任意的x 1,x 2(x 1≠x 2),有如下结论: ①f (x 1+x 2)=f (x 1)·f (x 2);② f (x 1·x 2)=f (x 1)+f (x 2)③1212()()f x f x x x -->0;④1212()()()22x x f x f x f ++<.当f (x )=l gx 时,上述结论中正确结论的序号是 .三、解答题:本大题共6小题,共74分. 解答应写出文字说明,证明过程或演算步骤. 17.(本小题满分10分)已知P :方程210x mx ++=有两个不等的负实根,Q :方程()244210x m x +-+=无实根。
若P 或Q 为真,P 且Q 为假。
求实数m 的取值范围18、(本小题满分12分)已知函数f (x )和g (x )的图象关于原点对称,且f (x )=x 2+2x . (Ⅰ)求函数g (x )的解析式; (Ⅱ)解不等式g (x )≥f (x )-|x -1|;19、(本小题满分12分)已知a 为实数, 2()(4)()f x x x a =--. (1) 求导数'()f x ;(2) 若'(1)0f -=, 求()f x 在[2,2]-上的最大值和最小值;20、(本小题满分12分) 已知函数12)(+=x xx f 与函数)(x g y =的图象关于直线2=x 对称,(1)求)(x g 的表达式。
(2)若)(1)2(x x Φ=+Φ,当)0,2(-∈x 时,)()(x g x =Φ,求)2005(Φ的值。
21、(本小题满分12分)某地区上年度电价为0.8元/kw h,年用电量为a kw h,本年度计划将电价降到0.55元/kw h 至0.75元/kw h 之间,而用户期望电价为0.4元/kw h 。
经测算,下调电价后新增的用电量与实际电价和用户期望电价的差成反比(比例系数为k ),该地区电力的成本价为0.3元/kw h(1) 写出本年度电价下调后,电力部门的收益y 与实际电价x 的函数关系式;(2) 设k=0.2a ,当电价最低定为多少时仍保证比电力部门的收益比上年至少增长20%(注:收益=实际用电量⨯(实际电价—成本价))22、(本小题满分12分) 已知函数()(1)e 1.x f x x =--. (I )求函数()f x 的最大值;(Ⅱ)设()(),f x g x x= 1,0x x >-≠且 ,证明()g x <1.河北望都中学高三第一次月练 文科数学答案1B 2 B 3A 4A 5B 6C 7 D 8 C 9 B 10 D 11B 12A13 1 14 -1/5 152 /2 16 (2)(3)17 m>=3 或 1<m<=218 解:(I )设函数()y f x =的图象上任一点00(,)Q x y 关于原点的对称点为(,)P x y ,则 000202x xy y +⎧=⎪⎪⎨+⎪=⎪⎩ 即 00x x y y =-⎧⎨=-⎩.∵点00(,)Q x y 在函数()y f x =的图象上.∴22,y x x -=- 即22,y x x =-+ 故g(x)=22x x -+.(II)由()()|1|g x f x x ≥--可得:2|2|1|0x x --≤ 当x ≥1时,221|0x x -+≤ 此时不等式无解。
当1x <时,2210x x -+≤∴112x -≤≤因此,原不等式的解集为.19、解: (1) 22'()2()(4)1324f x x x a x x ax =-+-⨯=--. (2) 2'(1)3(1)2(1)4210f a a -=----=-=, 得12a =. 2'()34(34)(1)f x x x x x ∴=--=-+, 当1x =-或43x =时, '()0f x =. 当(2,1)x ∈--时, '()0f x >, ()f x 递增; 当4(1,)3x ∈-时, '()0f x <, ()f x 递减; 当4(,2)3x ∈时, '()0f x >, ()f x 递增.(2)f -=0, 9(1)2f -=, 450()327f =-, (2)0f =.()f x 在[2,2]-上的最大值为9(1)2f -=, 最小值为450()327f =-. 20、 (1)28()5xg x x -=-;(2)3(2005)5Φ= 21、(1)(0.3)(),[0.55,0.75]0.4ky x a x x =-+∈- (2)0.6元/kwh22、(Ⅰ)f (x )=-x e x.当x ∈(-∞,0)时,f (x )>0,f (x )单调递增; 当x ∈(0,+∞)时,f (x )<0,f (x )单调递减. 所以f (x )的最大值为f (0)=0.…5分(Ⅱ)由(Ⅰ)知,当x >0时,f (x )<0,g (x )<0<1.…7分当-1<x <0时,g (x )<1等价于设f (x )>x . 设h (x )=f (x )-x ,则h (x )=-x e x-1.当x ∈(-1,-0)时,0<-x <1,0<e x <1,则0<-x e x<1, 从而当x ∈(-1,0)时,h (x )<0,h (x )在(-1,0]单调递减. 当-1<x <0时,h (x )>h (0)=0,即g (x )<1. 综上,总有g (x )<1.…12分。
