线性规划及单纯形法PPT课件
合集下载
线性规划与单纯形法PPT课件

Max Z = 50 x1 + 30 x2
第3步 --表示约束条件
4x1+3x2 120(木工工时限制) 2x1+x2 50 (油漆工工时限制)
x1,x2≥0 (变量取非负值限制)
该计划的数学模型
max Z=50x1+30x2 4x1+3x2 120
s.t.
2x1+ x2 50 x1, x2 0
问如何组织生产才能使每月的销售收入最大?
• 第1步 -确定决策变量
是问题中要确定的未知量
xx •设
1 ——桌子的产量 2 ——椅子的产量
,表明规划中的用数量表 示的方案、措施,可由决 策者决定和控制。
z ——利润
x1
x2
第2步 --定义目标函数
Max Z = 50 x1 + 30 x2
第2步 --定义目标函数
线性规模解决的问题
• 给定一定数量的人力、物力、财力等资源, 研究如何充分利用,以发挥其最大效果
• 已给定计划任务,研究如何统筹安排,用最 少的人力、物力、财力去完成
2、线性规划问题的数学模型
线性规划数学模型三要素:
决策变量、目标函数、约束条件
➢ 每一个线性规划问题都有一组决策变量 (x1, x2, ……, xn) , 这组决策变量的值就代表 一个具体方案。
1、问题的提出
例1.1 生产计划问题(资源利用问题) 某家具厂生产桌子和椅子两种家具。 桌子售价50元/个,椅子销售价格30元/个。 需要木工和油漆工两种工种。 生产一个桌子需要木工4小时,油漆工2小时。 生产一个椅子需要木工3小时,油漆工1小时。 该厂每个月可用木工工时为120小时, 油漆工工时为50小时。
第1工厂投污水的水质要求 :(2 x1) 2 500 1000
第3步 --表示约束条件
4x1+3x2 120(木工工时限制) 2x1+x2 50 (油漆工工时限制)
x1,x2≥0 (变量取非负值限制)
该计划的数学模型
max Z=50x1+30x2 4x1+3x2 120
s.t.
2x1+ x2 50 x1, x2 0
问如何组织生产才能使每月的销售收入最大?
• 第1步 -确定决策变量
是问题中要确定的未知量
xx •设
1 ——桌子的产量 2 ——椅子的产量
,表明规划中的用数量表 示的方案、措施,可由决 策者决定和控制。
z ——利润
x1
x2
第2步 --定义目标函数
Max Z = 50 x1 + 30 x2
第2步 --定义目标函数
线性规模解决的问题
• 给定一定数量的人力、物力、财力等资源, 研究如何充分利用,以发挥其最大效果
• 已给定计划任务,研究如何统筹安排,用最 少的人力、物力、财力去完成
2、线性规划问题的数学模型
线性规划数学模型三要素:
决策变量、目标函数、约束条件
➢ 每一个线性规划问题都有一组决策变量 (x1, x2, ……, xn) , 这组决策变量的值就代表 一个具体方案。
1、问题的提出
例1.1 生产计划问题(资源利用问题) 某家具厂生产桌子和椅子两种家具。 桌子售价50元/个,椅子销售价格30元/个。 需要木工和油漆工两种工种。 生产一个桌子需要木工4小时,油漆工2小时。 生产一个椅子需要木工3小时,油漆工1小时。 该厂每个月可用木工工时为120小时, 油漆工工时为50小时。
第1工厂投污水的水质要求 :(2 x1) 2 500 1000
清华大学运筹学课件(完整课件)
2x1 + 3x2 ≤ 4 x1,x2 ≥ 0
化标准型
max z = x1 + 3x2 + 0x3 + 0x4
x1 + 2x2 + x3 = 3
2x1 + 3x2
+ x4 = 4
x1,x2,x3,x4 ≥ 0
系数矩阵
1 A 2
2 3
1 0
0 1
p1
p2
p3 p4 , 则 B p3 p4
取x3、x4为基变量,令非基变量x1= x2=0 ∴ 初始基可行解:X(0) = (0 0 3 4)T
③
3
z = 2x1 + 4x2,此时表示 目标函数的直线与表示
Q2(4,2)
① *
条件①的直线平行,
o
最优点在线段Q3Q2上。
即存在无穷多最优解。
4 Q1
x1
7
(3)无界解
[eg.5]
max z = 2x1 + 3x2 4x1 ≤ 16 x1,x2 ≥ 0
则x2 → ∞,z → ∞。 即存在无界解。
对于
n
m
max z c j x j cni xni
j 1
i 1
n
aij x j xni bi
i 1, , m
j1
x
j
0
j 1, , n m
设 xni 为基变量可行,i 1,, m
x j为非基变量, j 1,, n
n
xni bi aij x j j 1
代入目标函数
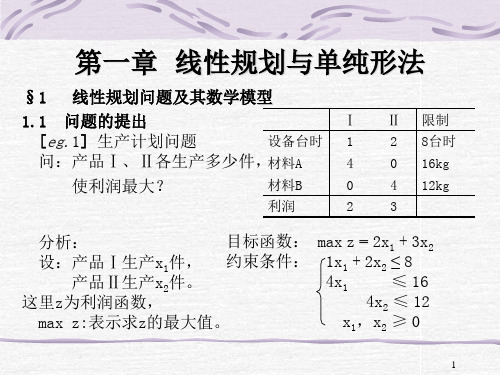
产品Ⅱ生产x2件。
4x1
≤ 16
这里z为利润函数,
4x2 ≤ 12
max z:表示求z的最大值。
化标准型
max z = x1 + 3x2 + 0x3 + 0x4
x1 + 2x2 + x3 = 3
2x1 + 3x2
+ x4 = 4
x1,x2,x3,x4 ≥ 0
系数矩阵
1 A 2
2 3
1 0
0 1
p1
p2
p3 p4 , 则 B p3 p4
取x3、x4为基变量,令非基变量x1= x2=0 ∴ 初始基可行解:X(0) = (0 0 3 4)T
③
3
z = 2x1 + 4x2,此时表示 目标函数的直线与表示
Q2(4,2)
① *
条件①的直线平行,
o
最优点在线段Q3Q2上。
即存在无穷多最优解。
4 Q1
x1
7
(3)无界解
[eg.5]
max z = 2x1 + 3x2 4x1 ≤ 16 x1,x2 ≥ 0
则x2 → ∞,z → ∞。 即存在无界解。
对于
n
m
max z c j x j cni xni
j 1
i 1
n
aij x j xni bi
i 1, , m
j1
x
j
0
j 1, , n m
设 xni 为基变量可行,i 1,, m
x j为非基变量, j 1,, n
n
xni bi aij x j j 1
代入目标函数
产品Ⅱ生产x2件。
4x1
≤ 16
这里z为利润函数,
4x2 ≤ 12
max z:表示求z的最大值。
第一章线性规划与单纯形法ppt课件

x2
解,也不存在最优解。
x11.5x2 8
目 标 函 数 m ax z 2 x1 3x2
4x1=16
x1 2 x2 8
约
束
条
件
:
4 x1
16 4x2 12
3
4x2=12
x1 , x2 0
原可行 域
0
无可行解
增加一个新的约束条件
x1+2x2=8
8
x1
x11.5x28
23
经营者提供商品或者服务有欺诈行为 的,应 当按照 消费者 的要求 增加赔 偿其受 到的损 失,增 加赔偿 的金额 为消费 者购买 商品的 价款或 接受服 务的费 用
Q3
x1 , x2 0
3
Q2
可行域
4x2=12
0
x1+2x2=8
x1
4
8
无穷多最优解(多重最优解)
20
经营者提供商品或者服务有欺诈行为 的,应 当按照 消费者 的要求 增加赔 偿其受 到的损 失,增 加赔偿 的金额 为消费 者购买 商品的 价款或 接受服 务的费 用
x2
可行 域
max z 2 x1 3x2
8—
x1 + x2 5
7—
x2 = -2x1 6 —
5— 4— 3—
x1、 x2 0
6x1 +2x2 24
6x1+ 2x2=24 x1+ x2=5
5
x2
15
最优解
2—
(3.5,1.5)
1—
x1 + x2 5
0
|| | | || | | | 12 3 4 5 6 7 8 9
x1
第一章 线性规划及单纯形法演示文稿ppt

a1n a2n
amn cn
含量
b1 b2
bm
设xj 表示在单位混合饲料中,第j 种配料的含量( j
=1,2,…,n)则有如下的数学模型:
MinZ=c1x1 + c2x2 + … + cnxn
a11x1 + a12x2 + … + a1nxn ≥ b1 a21x1 + a22x2 + … + a2nxn ≥ b2 …… am1x1 + am2x2 + … + amnxn ≥ bm x1 ≥0, x2 ≥0 ,… , xn≥0
目标函数有极大化和极小化; 约束条件有“≤”、“≥”和“=”三种情况; 决策变量一般有非负性要求,有的则没有。
为了求解方便,特规定一种线性规划的标准形式,非标 准型可以转化为标准型计算
(一)标准形式
标准形式为:
目标函数最大化 maxZ=c1x1+c2x2+…+cnxn
约束条件为等式
a11x1+a12x2+…+a1nxn =b1 a21x1+a22x2+…+a2nxn =b2 …………… am1x1+am2x2+…+amnxn=bm
饲料必须含有 m 种不同的营养成份,而且要求每单位混合饲料中
第 i 种营养成份的含量不能低于 bi ( i= 1,2, …, m)。已知第 i 种营 养成份在每单位的第 j 种配料中的含量为 aij , j = 1,2, …, n,每单位 的第 j 种配料的价格为 cj 。现在要求在保证营养条件的前提下,应 采用何种配方,使混合饲料的成本最小.
a11x1+a12x2+…+a1nxn ≤(或=, ≥) b1 a21x1+a22x2+…+a2nxn ≤ (或=, ≥) b2 …………… am1x1+am2x2+…+amnxn≤ (或=, ≥) bm x1,x2,…,xn ≥ (≤)0
线性规划图解法和单纯形法PPT课件

aij x j bi
aij x j xni bi
xni 0 称为剩余变量
常量 bi<0 的变换:约束方程两边乘以(-1)
线性规划问题的数学模型
例1.6 将下列线性规划问题化为标准形式
min Z 2 x1 x2 3 x3
5 x1 x2 x3 7
x1 x2 4 x3 2 3 x1 x2 2 x3 5
36 36 72 27
货运量 (千吨)
25 20 40 20
船只种类 拖轮 A型驳船 B型驳船
船只数 30 34 52
航线号 1 2
合同货运量 200 400
问:应如何编队,才能既完成合同任务,又使总货运成本为最小?
线性规划问题的数学模型
解: 设:xj为第j号类型船队的队数(j = 1,2,3,4),
Chapter1 线性规划
(Linear Programming)
本章主要内容:
LP的数学模型 图解法
单纯形法的进一步讨论-人工变量法 LP模型的应用
线性规划问题的数学模型
1. 规划问题 生产和经营管理中经常提出如何合理安排,使人力、 物力等各种资源得到充分利用,获得最大的效益, 这就是规划问题。
AX ( ) B
X
0
其中: C (c1 c2 cn )
a11 a1n
A
am1 amn
x1
X
xn
b1
B
bm
线性规划问题的数学模型
6. 线性规划问题的标准形式
n
max Z cj xj j 1
s.t
n
aij x j
j 1
bi
i 1, 2, , m
即 max z z c j x j
线性规划与单纯形法2.精选PPT

1 2
x1
1 2
x2
1 2
x3
0
1 4
x1
3 4
x2
1 4
x3
0
s.t .
3 4
x4
1 4
x5
1 4
x6
0
1 2
x4
1 2
x5
1 2
x6
0
x
1
x2
x4 x5
x7 x8
100 100
x3
x6
x9 100
x1 , x2 , x3 , x4 , x5 , x6 , x7 , x8 , x9 0
由表 2中的原材料价格: 6(A 5CB CD C) 原材料 C 3(A 5PB PD P) 原材料 P 3(A 5HB HD H ) 原材料 H
设:
x1=AC x2=AP x3=AH
x4=BC x5=BP x6=BH
x7=DC x8=DP x9=DH
m z a 5 (x 1 x 0 x 2 x 3 ) 3 (x 4 5 x 5 x 6 ) 2 (x 7 5 x 8 x 9 ) 6 (x 1 5 x 4 x 7 ) 2 (x 2 5 x 5 x 8 ) 3 (x 3 5 x 6 x 9 )
1 AP 4 A
BC
1 2
B
1 4AC4 3AP1 4AH0
311 4BC4BP4BH0
111 2BC2BP2BH0
由表 2 中供应量限制: A CB CC CC100 A PB PC PP100 A HB HC HH 100
由表 1中的产品价格: 5(A 0CA PA H ) 产品 A 3(B 5CB PB H ) 产品 B 2(D 5CD PD H ) 产品 D
第1章 线性规划单纯形法aPPT课件

5
线性规划问题解的概念
• 基解:将上述线性规划约束方程AX=b改写如
下形式,即
(B,N)(XB,XN)T=b
从而有 BXB=b-NXN
令
XN=0
得到线性方程组 BXB=b
由此得到XB=(x10,x20个基
本解
X0=(XB, XN)T=(x10,x20,…,xm0,0,0, …,0)T。
21
• 定理1 若线性规划存在可行域,则其可行域 R={X|AX=b,X≥0}是凸集。
证明 有
则 且
即 故
X (1) R , X ( 2 ) R , 及 0 a 1 AX (1) b 且 X (1) 0 AX ( 2 ) b 且 X ( 2 ) 0 X aX (1) (1 a ) X ( 2 ) 0 AX A ( aX (1) (1 a ) X ( 2 ) )
• 基向变变量量量 ; ,: 与记之相 为对X应B应的=(的向x1,变量x2,量P…1,,xx1Pm,x2),2T…,…;, ,Pxmm称称为为基基 • 非基变量:其余的向量为非基向量,记
为非基N=变(P量m+,1,, 记Pm为+2,X…N,=P(xn)m;+1其,xm余+2,的…变,xn量)T 为。
可行域的极点 目标函数等值线: 一组平行线
代数概念
满足一个等式约束的解 满足一个不等式约束的解 满足一组不等式约束的解
基解 基可行解 目标函数值等于一个常 数的解
19
线性规划问题的几何意义
• 凸集 如果集合K中任意两个点的连线上的所有点也属 于这个集合,那么称K为凸集。
• 设K是n维欧氏空间的一个点集,若任意两点X(1)∈K, X(2)∈K均有
第1章 线性规划-单纯形法
线性规划问题解的概念
• 基解:将上述线性规划约束方程AX=b改写如
下形式,即
(B,N)(XB,XN)T=b
从而有 BXB=b-NXN
令
XN=0
得到线性方程组 BXB=b
由此得到XB=(x10,x20个基
本解
X0=(XB, XN)T=(x10,x20,…,xm0,0,0, …,0)T。
21
• 定理1 若线性规划存在可行域,则其可行域 R={X|AX=b,X≥0}是凸集。
证明 有
则 且
即 故
X (1) R , X ( 2 ) R , 及 0 a 1 AX (1) b 且 X (1) 0 AX ( 2 ) b 且 X ( 2 ) 0 X aX (1) (1 a ) X ( 2 ) 0 AX A ( aX (1) (1 a ) X ( 2 ) )
• 基向变变量量量 ; ,: 与记之相 为对X应B应的=(的向x1,变量x2,量P…1,,xx1Pm,x2),2T…,…;, ,Pxmm称称为为基基 • 非基变量:其余的向量为非基向量,记
为非基N=变(P量m+,1,, 记Pm为+2,X…N,=P(xn)m;+1其,xm余+2,的…变,xn量)T 为。
可行域的极点 目标函数等值线: 一组平行线
代数概念
满足一个等式约束的解 满足一个不等式约束的解 满足一组不等式约束的解
基解 基可行解 目标函数值等于一个常 数的解
19
线性规划问题的几何意义
• 凸集 如果集合K中任意两个点的连线上的所有点也属 于这个集合,那么称K为凸集。
• 设K是n维欧氏空间的一个点集,若任意两点X(1)∈K, X(2)∈K均有
第1章 线性规划-单纯形法
最优化方法线性规划单纯形法ppt(共76张PPT)

ii) 如果任何替换都产生不了新的BFS,则问题无界.
◆ 退化基本可行解:某个或某些基变量取零的基本可行解! 问题:基本可行解与基的对应关系?
◎相对费用系数的经济解释!(合成价格、相对价格)
4. 计算过程-单纯形法
单纯形表:BFS对应规范形的表格+
既约费用系数和BFS目标值的相反数
单纯形法的步骤
步2 选取 q 满足
最优值:
原问题的极大值:
退化(degenerate)与循环(cycling)
◎退化问题
⊙ 单纯形法可能出现循环! ⊙ 实际中经常碰到退化问题,但很少出现循环 ⊙ 避免出现循环的措施:摄动法、Bland法则、字典序法
基本可行解是退化的当且仅当单纯形表最后一列有一个或者
多个零!一次转轴是退化的当且仅当目标函数没有发生变化!
B=(a1,a2,a3)
X=(4,3,1,0,0,0)
a4进基
转轴
x=(0,1,3,2,0,0)
3. BFS→目标值减小的相邻BFS
设x是BFS,且规范形如前,则有
◎问题:确定进基变量,转轴后使新BFS的目标值变小? ⊙ 将Ax=b的任一解用非基变量表示; ⊙ 将目标函数
用非基变量表示. ——选取进基变量的依据
一般形式 转化 标准形
称 松弛(slack)/盈余(surplus)变量;自由变量
例5. 化成标准形
等价表示为
基本解与基变量
其中 满秩假定:m×n矩阵A满足m<n,且A的行向量线性无关
• 在满秩假定下,方程组Ax=b总有解,且至少有一个基本 解
定义: 给定含有n个变量,m个方程的线性方程组Ax=b,设B 是由A 的列组成的任一非奇异m×m子阵,则如果置x的所有与B 无关的n-m个分量为零后,所得方程组的解是Ax=b关于基B的 基本解(basic solution) ,称x中与基B对应的分量为基变量(basic
◆ 退化基本可行解:某个或某些基变量取零的基本可行解! 问题:基本可行解与基的对应关系?
◎相对费用系数的经济解释!(合成价格、相对价格)
4. 计算过程-单纯形法
单纯形表:BFS对应规范形的表格+
既约费用系数和BFS目标值的相反数
单纯形法的步骤
步2 选取 q 满足
最优值:
原问题的极大值:
退化(degenerate)与循环(cycling)
◎退化问题
⊙ 单纯形法可能出现循环! ⊙ 实际中经常碰到退化问题,但很少出现循环 ⊙ 避免出现循环的措施:摄动法、Bland法则、字典序法
基本可行解是退化的当且仅当单纯形表最后一列有一个或者
多个零!一次转轴是退化的当且仅当目标函数没有发生变化!
B=(a1,a2,a3)
X=(4,3,1,0,0,0)
a4进基
转轴
x=(0,1,3,2,0,0)
3. BFS→目标值减小的相邻BFS
设x是BFS,且规范形如前,则有
◎问题:确定进基变量,转轴后使新BFS的目标值变小? ⊙ 将Ax=b的任一解用非基变量表示; ⊙ 将目标函数
用非基变量表示. ——选取进基变量的依据
一般形式 转化 标准形
称 松弛(slack)/盈余(surplus)变量;自由变量
例5. 化成标准形
等价表示为
基本解与基变量
其中 满秩假定:m×n矩阵A满足m<n,且A的行向量线性无关
• 在满秩假定下,方程组Ax=b总有解,且至少有一个基本 解
定义: 给定含有n个变量,m个方程的线性方程组Ax=b,设B 是由A 的列组成的任一非奇异m×m子阵,则如果置x的所有与B 无关的n-m个分量为零后,所得方程组的解是Ax=b关于基B的 基本解(basic solution) ,称x中与基B对应的分量为基变量(basic
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
min:minimize , “最小化”
数学 模型
线性规划问题的数学模型由三个 要素组成:
(1)变量,或称决策变量,是问 题中要确定的未知量,它用于表明规 划中的用数量表示的方案、措施,可 由决策者决定和控制;
(2)目标函数,它是决策变量的函 数,按优化目标分别在这个函数前面 加上max或min;
念
题称为线性规划问题。
和 模 型
max(或min) Z c 1 x 1 c 2 x 2 c n x n
a11x1 a12x2 a1nxn (,)b1
s.t.a21x1
a22x2
a2nxn
(,)b2
am1x1 am2x2 amnxn (,)bm
x1, x2,, xn 0 0,自由
表1-2
单位:100m2
月份
1
2
3
4
所需仓库面积
15
10
20
12
表1-3
合同租赁期限 合同期内的租费
1 个月 2800
2 个月 4500
单位:元/100m2
3 个月 6000
4 个月 7300
数 学 模 型
例2中若用变量xij表示捷运公司在第i(i=1,…,4) 个月初签订的租借期为j(j=1,…,4)个月的仓库 面积的合同。因5月份起该公司不需要租借仓
max z c j x j j 1
s.t.
n j 1
aij x j
(, )bi
(i 1,.., m)
x
j
0
(j 1,2,, n)
概 和 模 型
矩阵形式:
max(或min)Z CX
AX(,)b s.t.X 0
x 1
X
x2
x
n
称为决策变量向量
C(c1,c2, ,cn)称为价值系数向量或目标函数系数向量
问 题 的 提 出
例1 美佳公司计划制造Ⅰ、Ⅱ两种家电
产品。已知各制造一件时分别占用的设 备A,B的台时、调试工序时间及每天 可用于这两种家电的能力、各售出一件 时的获利情况,如表1-1所示。问该公 司应制造两种家电各多少件,使获取的 利润为最大。
表1-1
项目
Ⅰ
设备 A(h)
0
设备 B(h)
6
测试工序(h)
(3)约束条件,指决策变量取值时 受到的各种资源条件的限制,通常表 达为含决策变量函数的等式或不等式。
数学 模型
实际问题中线性的含义: (1)严格的比例性 (2)可叠加性 (3)可分性 (4)确定性
定义:
对于求取一组变量xj(j=1,2,…..,n),
概
使之既满足线性约束条件,又使具有线 性的目标函数取得极值的一类最优化问
库,故x24,x33,x34,x42,x43,x44均为零。该
公司希望总的租借费用为最小,故有如下数 学模型:
目标函数
min z = 2 800(x11 + x21 + x31 + x41 )+4 500(x12 + x22 + x32 )
+6 000(x13 + x23 )+7 300x14
约束条件
1
利润(元)
2
Ⅱ
每天可用能力
5
15
2
24
1
5
1
例1中先用变量x1和x2分别表示美佳 公司制造家电Ⅰ和Ⅱ的数量。这时
该 公 司 可 获 取 的 利 润 为 (2x1+x2) 元 ,
令z=2x1+x2,因问题中要求获取的
数
利润为最大,即max z。
学
z是该公司能获取的利润的目标值, 它是变量x1,x2的函数,称为目标
第一章
线性规划及单纯形法
-
1
线性 规划 及单 纯形
法
❖ 线性规划问题及数学模型 ❖ 图解法 ❖ 单纯形法原理 ❖ 单纯形法计算步骤 ❖ 单纯形法进一步讨论 ❖ 数据包络分析 ❖ 其他应用例子
§1线 性 规 划 问 题
问题的提出 线性规划问题的数学模型 线性规划问题的标准形式
问题 的提
出
在生产和经营等管理工作 中,需要经常进行计划或规划。 虽然各行各业计划和规划的内 容千差万别,但其中共同点可 归结为:在现有各项资源条件 的限制下,如何确定方案,使 预期目标达到最优;或者为了 达到预期目标,确定使资源消 耗为最少的方案。
概 念 和 模 型
一般形式:
目标函数
max(或min) Z c 1 x 1 c 2 x 2 c n x n
a11x1 a12x2 a1nxn (,)b1
约束条件s.t.a21x1
a22x2
a2nxn
(,)b2
am1x1 am2x2 amnxn (,)bm
x1, x2,, xn 0 0,自由
(1.1c) (1.1d)
型
max: maximize的缩写, “最大化”,
s.t. subject to的缩写, “受限制于……”
问 题 的 提 出
例2 捷运公司在下一年度的1~4月的4个月内
拟租用仓库堆放物资。已知各月份所需仓 库面积列于表1-2。仓库租借费用随合同期 而定,期限越长,折扣越大,具体数字见 表1-3。租借仓库的合同每月初都可办理, 每份合同具体规定租用面积和期限。因此 该厂可根据需要,在任何一个月初办理租 借合同。每次办理时可签一份合同,也可 签若干份租用面积和租借期限不同的合同, 试确定该公司签订租借合同的最优决策, 目的是使所付租借费用最小。
s.t.
xxx111123
+ x12 + x13 + x14 15 + x13 + x14 + x21 + x22 + x23 + x14 + x22 + x23 + x31 + x32
10 20
x14 + x23 + x32 + x41 12
aij 0(i =1,.., m; j =1,.., n)
a11
A
a21
a12
a22
a1n a2n
am1 am2 amn
称为技术系数或约束系数矩阵
模 型
函数。 x1,x2的取值受到设备A、B和调试工
序能力的限制,用于描述限制条件
的数学表达式称为约束条件。
由此例1的数学模型可表为:
目标函数 max z 2 x1 x 2
数 学
约束条件
5 x 2 15
s
.t
.
6 x
x
1
1
x
2
2
x2
5
24
模
x1 , x 2 0
(1.1a) (1.1b)
xj(j1,2, ,n) 称为决策变量
非负约束
cj(j1,2, ,n) 称为价值系数或目标函数系数
bi(i1,2, ,m) 称为资源常数或约束右端常数
aij0 (i=1 ,..,m ;j=1 ,..,n ) 称为技术系数或约束系数
概 念 和 模 型
紧缩形式:
n
max(或min)Z c j x j j 1 n
