4.7.1整周模糊度的确定一 - 整周模糊度的确定一
整周模糊度的确定

整周模糊度的确定确定整周未知数,是基于载波相位测量进行相对定位,必需解决的另一个关键问题。
精确和快速地求解整周未知数,对于确保相对定位的高精度,提高作业效率,开拓高精度动态定位新方法,都是极其重要的。
确定整周未知数的方法许多,若按解算所需时间的长短区分,可分为经典静态相对定位法和快速解算模糊度(整周未知数)法,而快速解算模糊度法又包括交换天线法,P码双频法、滤波法,搜寻法和模糊函数法等等;若按确定整周未知数时gps接收机的运动状态区分,又可分为静态法和动态法。
上述各种快速解算法皆属于静态法的范畴。
所谓动态法,就是GPS接收机在运动状态中完成求解整周未知数,它是实施高精度实时动态定位的基础。
一、经典静态相对定位法确定整周未知数这种方法是将作为待定的未知参数,在基线平差中与其它未知参数(如δXi、δYi、δZi等)一并求解的方法。
一般是由载波相位观测值组成双差分观测方程式,并进行方程式线性化,得到双差分误差方程式,则该方程式中包含有待定测站三个坐标改正数δXi、δYi、δZi和整周未知数的线性组合这四个未知数[此处]。
只要在已知测站和待定测站上同步观测不少于4颗卫星,则可平差解出整周未知数。
用这种方法一般需观测较长时间(几非常钟至几小时),但解算的精度最高,常用于静态相对定位中,尤其是用于长距离相对定位中。
在平差计算中,依据对的取值方式不同,可分为“整数解”(固定解)和“实数解”(浮动解)两种。
整数解是利用应当是整数的特性[也应为整数],将解得的▽▽N(t0)值进行凑整(凑成最接近的整数),然后将凑整后的作为已知量再代入双差分误差方程,重新平差,解算待定测站坐标改正数。
这种方法,只有当观测误差和外界误差对观测值影响较小,解得的比较接近整数的状况下才有效,此时,它可以提高解算结果的精度。
整数解常用于四、五十公里以下的基线的相对定位。
实数解当联测基线较长时,某些外界误差(如大气折射误差、卫星星历误差等)对基线两端点观测值的影响差别较大(即相关性不强),这时,在两测站间求差分时,就不能较好地消退或减弱其影响,它们在基线平差解算中将被汲取进待定测站坐标改正数和整周未知数中,这样解算出来的整周未知数一般偏离整数值较远,且其精度较低,误差可能大于半周,这时,我们不再考虑的整数特性,而取其实际解算值―实数解。
整周模糊度 伪距增量法

整周模糊度伪距增量法下载温馨提示:该文档是我店铺精心编制而成,希望大家下载以后,能够帮助大家解决实际的问题。
文档下载后可定制随意修改,请根据实际需要进行相应的调整和使用,谢谢!并且,本店铺为大家提供各种各样类型的实用资料,如教育随笔、日记赏析、句子摘抄、古诗大全、经典美文、话题作文、工作总结、词语解析、文案摘录、其他资料等等,如想了解不同资料格式和写法,敬请关注!Download tips: This document is carefully compiled by the editor. I hope that after you download them, they can help yousolve practical problems. The document can be customized and modified after downloading, please adjust and use it according to actual needs, thank you!In addition, our shop provides you with various types of practical materials, such as educational essays, diary appreciation, sentence excerpts, ancient poems, classic articles, topic composition, work summary, word parsing, copy excerpts,other materials and so on, want to know different data formats and writing methods, please pay attention!整周模糊度和伪距增量法是现代卫星导航领域中常用的技术手段,它们可以有效提高定位的准确性和稳定性。
gnss 单历元双差整周模糊度快速确定方法

gnss 单历元双差整周模糊度快速确定方法全球导航卫星系统(GNSS)在现代定位技术中发挥着重要作用。
在GNSS数据处理中,单历元双差整周模糊度的快速确定是提高定位精度和效率的关键。
本文将详细介绍一种gnss单历元双差整周模糊度的快速确定方法。
一、背景介绍GNSS定位技术通过测量卫星信号传播时间来确定接收机的位置。
在静态相对定位中,双差模型被广泛应用以消除接收机钟差、卫星钟差以及大气延迟等误差。
然而,在双差模型中,整周模糊度的确定仍然是一个挑战。
单历元双差整周模糊度快速确定方法可以有效提高定位效率和精度。
二、单历元双差整周模糊度快速确定方法1.数据预处理在进行单历元双差整周模糊度确定之前,需要对原始观测数据进行预处理。
主要包括:(1)数据清洗:去除异常值、周跳等影响定位精度的数据。
(2)卫星选择:选择合适的卫星,确保卫星几何分布良好。
(3)基线向量解算:根据卫星位置和接收机位置,计算基线向量。
2.双差观测模型双差观测模型可以表示为:[ Delta lambda_{AB} = frac{f}{c} left( Deltaho_{AB} + Delta N_{AB}ight) ]其中,$Delta lambda_{AB}$表示双差载波相位观测值;$f$表示载波频率;$c$表示光速;$Deltaho_{AB}$表示双差几何距离;$Delta N_{AB}$表示双差整周模糊度。
3.单历元双差整周模糊度确定单历元双差整周模糊度确定的关键在于快速求解$Delta N_{AB}$。
以下为具体方法:(1)利用预处理后的数据,构建双差观测方程。
(2)采用高斯-牛顿迭代法求解整周模糊度。
(3)在迭代过程中,引入模糊度固定策略,如LAMBDA方法。
(4)当整周模糊度的解算精度满足要求时,停止迭代。
4.精度分析为验证单历元双差整周模糊度快速确定方法的精度,可以采用以下指标:(1)均方根误差(RMSE):评价定位结果的精度。
整周模糊度的解算
GPS精密定位周跳检测与修复(Cycle slip detection and repair)完整的载波相位是由初始整周模糊度N、计数器记录的整周数INT和接收机基频信号与收到到卫星信号的小于一周部分相位差Δφ。
Δφ能以极高的精度测定,但这只有在N和INT都正确无误地确定情况下才有意义。
卫星在观测中失锁后,造成接收机载波整周计数INT误差,这种现象称为周跳。
当重新捕获卫星后,周跳给计数器造成的偏差即为中断期间丢失的整周数,小周跳可以通过检测方法发现后并加以修复,大的周跳或较长时间的失锁,周跳不易修复,需要重新固定整周模糊度。
周跳的探测及修复对于用载波相位精密定位至关重要,成功的修复才能获得高精度的结果。
周跳产生的原因:1.卫星信号暂时阻断;2.仪器线路暂时故障;3.外界环境的突变干扰,如电离层、动态变化。
检测周跳的主要方法:1.屏幕扫描法观测值中出现周跳后。
相位观测值的变化率就不再连续。
凡曲线出现不规则的突然变化时,就意味着在相应的相位观测值中出现了整周跳变。
早期进行GPS相位测量的数据处理时,就是靠作业人员坐在计算机屏幕前依次对每个站、每个时段、每个卫星的相位观测值的变化率的图像进行逐段检查来探测周跳,然后再加以修复。
这种方法比较直观,在早期曾广泛使用。
但由于工作繁琐枯燥乏味,而且需反复进行,所以这种手工编辑方法目前正逐步被淘汰,而很少使用了。
2.高次差或多项式拟合法由于卫星和接收机间的距离在不断变化,因而载波相位测量的观测值INT+Δφ也随时间在不断变化。
但这种变化应是有规律的、平滑的。
周跳将破坏这种规律性。
根据这一特性就能将一些大的周跳寻找出来(尤其是对采样率较高的数据)。
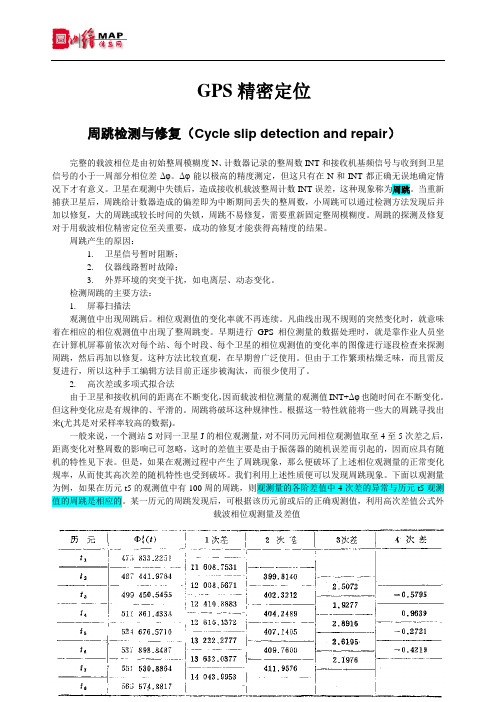
一般来说,一个测站S对同一卫星J的相位观测量,对不同历元间相位观测值取至4至5次差之后,距离变化对整周数的影响已可忽略,这时的差值主要是由于振荡器的随机误差而引起的,因而应具有随机的特性见下表。
但是,如果在观测过程中产生了周跳现象,那么便破坏了上述相位观测量的正常变化规率,从而使其高次差的随机特性也受到破坏。
GNSS测量技术与应用智慧树知到答案2024年陕西铁路工程职业技术学院

GNSS测量技术与应用陕西铁路工程职业技术学院智慧树知到答案2024年第一章测试1.在GPS系统中,启用备用卫星以代替失效的工作卫星的职能,由主控站执行。
()A:对 B:错答案:A2.GPS卫星信号的基准频率是()。
A:102.3 MHzB:1.023MHzC:1023 MHzD:10.23 MHz答案:D3.与经典测量方法相比,GNSS的特点有()。
A:可同时测定点的三维位置B:自动化程度高C:无需通视D:可全天候作业答案:ABCD4.北斗系统空间部分由地球同步轨道、倾斜轨道和中圆轨道卫星组成。
()A:错 B:对答案:B5.GNSS接收机按用途不同划分为,导航型接收机,测地型接收机,授时型接收机。
()A:对 B:错答案:A6.UTC指的是协调世界时。
A:对 B:错答案:A7.2020年北斗卫星导航系统可向全球提供高精度导航、定位、授时的基本服务。
A:错 B:对答案:B8.地球在绕太阳运行时,地球自转轴的方向在天球上缓慢地移动,春分点在黄道上随之缓慢移动,这种现象称为()。
A:黄道 B:岁差 C:黄极 D:黄赤交角答案:C第二章测试1.GPS定位的实质是把卫星视为“动态”的控制点,在已知其瞬时坐标的条件下,以GNSS卫星和用户接收机天线之间的距离为观测量,采用()的方法,确定用户接收机天线所处的位置。
A:空间距离后方交会B:空间距离侧方交会C:空间距离上方交会D:空间距离前方交会答案:A2.根据参考点的不同位置,GNSS定位测量可以分为绝对定位和相对定位。
()A:错 B:对答案:B3.测码伪距测量所使用的测距信号是载波。
()A:对 B:错答案:B4.测码伪距测量的测距精度要高于载波相位测量的测距精度。
()A:错 B:对答案:A5.根据基准站发送的信息方式不同,差分GNSS可分为()。
A:载波相位差分B:单基站差分C:伪距差分D:位置差分答案:ACD6.单点定位也称绝对定位。
A:错 B:对答案:B7.相对定位至少需要2台GNSS接收机。
整周模糊度解算方法

整周模糊度解算方法嘿,朋友们!今天咱来聊聊整周模糊度解算方法。
这玩意儿啊,就像是一把解开神秘大门的钥匙。
你看啊,整周模糊度就像是一团乱麻,我们得想办法把它理清。
这可不是一件容易的事儿,但别怕,咱们有办法对付它!想象一下,我们在一个迷宫里,到处都是弯弯绕绕,而整周模糊度就是那些让我们晕头转向的岔路。
那怎么找到正确的路呢?这就需要用到我们的解算方法啦。
首先呢,我们得有耐心,不能着急。
就像钓鱼一样,得慢慢等鱼儿上钩。
我们得仔细分析那些数据,一点一点地去琢磨。
有时候可能会觉得很枯燥,但是坚持下去,说不定就会有惊喜哦!然后呢,我们要运用各种技巧和工具。
这就好比我们有不同的工具来对付不同的难题。
有时候一个巧妙的算法,就能让那团乱麻瞬间变得清晰起来。
比如说,我们可以通过一些特定的模型来预估整周模糊度的大致范围,这就好像我们先知道了宝藏大概在哪个区域,然后再去仔细寻找。
还有啊,我们可以利用一些统计方法来筛选出最有可能的解,这就像是在一堆沙子里找出金子一样。
而且哦,这个过程中可不能马虎。
就像盖房子,一块砖没放好,可能整栋房子都会不稳。
我们得认真对待每一个数据,每一个步骤。
其实啊,整周模糊度解算方法在很多领域都有大用处呢!比如在导航系统里,要是没有它,我们怎么能准确地找到自己要去的地方呢?在测量领域,它更是不可或缺的。
朋友们,想想看,如果没有这个神奇的方法,我们的生活得失去多少便利呀!所以啊,可别小瞧了它。
总的来说,整周模糊度解算方法就像是一个隐藏在数据世界里的宝藏,等待着我们去挖掘。
只要我们有耐心、有技巧,就一定能把它找出来,让它为我们服务!让我们一起加油,去探索这个充满奥秘的领域吧!。
《GNSS定位基本原理》整周未知数

待 定 参
整 数 解ቤተ መጻሕፍቲ ባይዱ
数
法
~
经
典 方 法
实 数 解
实数解(浮动解)
• 当基线较长(>30km)时,由于测站间各种 误差的相关性差,求差后,误差消除得不完 善,解算的基线向量和整周未知数的精度低, 此时再将整周未知数固定为整数无实际意义, 只是徒劳而已,所以通常将实数解作为最终 解,也称为浮动解
第二部分
• 由于各种误差的影响,平差求得的整周未知数往 往不是整数,而是实数
• 对于短基线(<30km),测站间误差的相关性强, 求差后可使误差大大削弱
• 同时较长时间的静态观测,观测卫星的几何分布 会产生较大的变化,因此能以较高的精度求定整 周未知数
• 确定办法是将其四舍五入,凑整为最接近的整数
整周未知数N0的确定方法
快速定位中常用的方法
快速定位中常用的方法
确定整周未知数的方法
1 号点
• 已知基线法 • 交换天线法
走走停停法 (Stop and Go)
快速静态定位法
• 快速模糊度解算 法(FARA)
基准站 电站
流动站
谢谢观看
待定参数法-经典方法
• 建立双差观测方程,将其作为基线 向量平差中的待定参数,与其他参 数一并求解
整周未知数N0的确定方法
按基线长度不同, 一般采取两种取值方法:
1)整数解: 短基线测量
2)实数解: 长基线测量
整周未知数N0的确定方法
待 定 参
整 数 解
数
法
~
经
典 方 法
实 数 解
整数解 (固定解)
《坐标系统与时间系统》
GNSS定位基本原理-
整周模糊度的确定
智慧树知到《GNSS测量与数据处理》章节测试答案

智慧树知到《GNSS测量与数据处理》章节测试答案第一章1、A-S是指()。
A:精密定位服务B:标准定位服务C:选择可用性D:反电子欺骗正确答案:反电子欺骗2、SA政策是指()。
A:精密定位服务B:标准定位服务C:选择可用性D:反电子欺骗正确答案:选择可用性3、SPS是指()。
A:精密定位服务B:标准定位服务C:选择可用性D:反电子欺骗正确答案:标准定位服务4、PPS是指()。
A:精密定位服务B:标准定位服务C:选择可用性D:反电子欺骗正确答案:精密定位服务5、ε技术干扰( )。
A:星历数据B:C/A 码C:P码D:载波正确答案:星历数据6、δ技术干扰( )。
A:星历数据B:定位信号C:导航电文D:卫星钟频正确答案:卫星钟频7、子午卫星导航系统与GPS相比较,存在的局限性有( )。
A:卫星少,不能实时定位B:定位信号弱,信噪比差C:轨道低,难以精密定轨D:频率低,难以补偿电离层效应的影响正确答案:卫星少,不能实时定位,轨道低,难以精密定轨,频率低,难以补偿电离层效应的影响8、20世纪70年代,美国开始研制GPS系统,三部分构成:空间卫星部分、地面监控站部分和用户部分。
A:对B:错正确答案:对9、地面监控站部分由10个站组成:1个主控站、3个注入站、6个监控站。
A:对B:错正确答案:错10、GPS定位原理是采用空间距离前方交会法。
A:对B:错正确答案:错11、不是GPS用户部分功能的是()。
A:捕获GPS信号B:解译导航电文,测量信号传播时间C:计算测站坐标,速度D:提供全球定位系统时间基准正确答案:提供全球定位系统时间基准12、不是GPS卫星星座功能的是()。
A:向用户发送导航电文B:接收注入信息C:适时调整卫星姿态D:计算导航电文正确答案:计算导航电文13、伽利略系统是由欧盟主持研制开发的,既提供开放服务和商业服务,又提供军用服务的卫星定位系统。
A:对B:错正确答案:对14、目前的几大卫星定位系统(GPS、GALILEO、GLONASS、北斗)中GPS的卫星数最多,轨道最高。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
• 周跳检验量应根据不同的观测数据和设站情况进行适当的选 择。每一种检验量都有其优点和缺点,我们应该灵活使用各 种检验量
相位观测值 464623.1581 475833.2251 487441.9784 499450.5455 511861.4338 524576.5710 537798.8487 551430.8864 565474.8817
14
一次差 11210.0672 11608.7531 12008.5671 12410.8883 12815.1372 13222.2777 13632.0377 14043.9951
二次差 398.6859 399.8140 402.3212 304.2489 507.1405 409.7600 411.9576
16
三次差 1.1281 2.5072 1.9277 2.8916 2.6195 2.1976
三次差 1.1281 2.5072 -98.0723 202.8916 -97.3805 2.1976
接收机根据自身 的 钟 在tR时 刻 所 接 收 到 卫 星 在tS 时刻所tS R
2
3
2.整周跳变(周跳 – Cycle Slips)
计数器中止累积 计数丢失n周
ti 1
Int((t)) 正确
Fr((t)) 正确
ti
Int((t)) 少n周
Fr((t)) 正确
• 通过一些技术手段,确定周跳发生的位置和时刻,并求解出 整周跳变的准确数值,这样就可以对发生周跳后的观测值进 行改正,这一过程被称为整周跳变的探测与修复(Detection and Repair of Cycle-slip)。
6
1.周跳检验量
• 一般是从GPS观测数据流中构建出时间上连续的检测量序列, 通过误差计算设立阈值,来逐一判断检测量,探测周跳进而 改正周跳。把这种检测量序列就称为周跳检验量。
17
四次差 1.3791 -0.5796 0.9639 -0.2721 -0.4219
四次差 1.3791 -100.5796 300.9639 -300.2721 99.5781
18
• 高次差法的问题 • 高次差法探测周跳的功效受接收机稳定度的影响
12
误差(周跳) 一次差 二次差 三次差 四次差
t1
0
t2
0
t3
0
t4
0
t5
t6
t7
t8
0
0
0
0
0
0
3
2
3
0
0
0
0
0
0
组成阶数越高,周跳的放大倍数越明显
13
相位观测值 464623.1581 475833.2251 487441.9784 499450.5455 511861.4338 524676.5710 537898.8487 551530.8864 565574.8817
ti 1
Int((t)) 少n周
Fr((t)) 正确
ti 2
Int((t)) 少n周
Fr((t)) 正确
如果由于某种原因在两个观测历元 [ti1,ti ] 间的某一段时间中止了正常的累 积工作,从而使整周计数较应值减少了n周,那么当计数器恢复正常工作后
,所有的载波观测响位值中的整周计数 Int((t)) 便都会含有同一偏差值—
一次差 11210.0672 11608.7531 12008.5671 12410.8883 12715.1372 13222.2777 13632.0377 14043.9951
15
二次差 398.6859 399.8140 402.3212 404.2489 407.1405 409.7600 411.9576
—较正常值少n周。这种整周计数 Int((t)) 出现系统偏差而不足一周的部
分
仍然保持正确的现F象r(称(t为)) 整周跳变,简称周跳(cycle slip) 。
3
周跳的数值特性
周跳
观测中断
4
粗差
T
T
T
• 只影响整周计数 - 周跳为波长的整数倍
• Fr(依) 然是正确的
• 从周跳发生时刻(历元)之后的所有观测值都含有一个偏 差(周跳)
电离层残 差组合
10
• 高次差法的原理
3,4 4 3
2,3 3 2
2,3 3 2
1,2 2 1
周跳影响
t1 t2 t3 t4
T
11
• 高次差法的原理 • 由于卫星和接收机间的距离在不断变化,因而载波相位测量的观测值也
随时间在不断变化。但这种变化应是有规律的,平滑的。周跳将破坏这 种规律性。 • 将非差载波相位、双差载波相位时间序列或残差组成一阶、二阶甚至高 阶差分,凡在差分中出现剧烈跳变者,表明该处数据含有周跳。 • 组成阶数越高,周跳的放大倍数越明显,但同时噪声也被放大
4
5
产生周跳的原因:
• 信号被遮挡,导致卫星信号无法被跟踪 • 卫星信号信噪比过低,导致整周计数错误 • 接收机在高速动态条件下工作,导致接收机无法正 确跟踪卫星信号 • 卫星瞬时故障,无法产生信号 • ……
5
6
整周跳变的探测与修复
• 对于高精度的载波相位数据处理,需要不含周跳和粗差的相 位数据,也就是“干净”的相位数据。周跳的发生使得相位 中出现了偏差,进而使得数据处理结果可能产生错误。 因此, 有必要进行载波相位数据的周跳的探测与修复。
§5.5 周跳的探测与修复
1
2
1.载波相位测量
(t) N0 Int((t)) Fr((t))
S
整周模糊度
整周计数
• 优点 • 精度高,测距精度可达
0.1mm~3mm量级 • 难点 • 整周未知数问题 • 整周跳变问题
不足1周部分
(tR )
接收机根据自身 的 钟 在tR时 刻 复 制信号的相位
7
8
常用的周跳探测与修复的方法
(1).屏幕扫描法 (2).高次差法 (3).多项式拟合法 (4).MW观测值法 (5).三差法 ……
9
屏幕扫描法
方法:人工在屏幕上观察观 测值曲线的变化是否连续。
特点
费时、只能发现大周跳。
由于原始的载波观测值变化 很快,通常观察的是某种观 测值的组合,如
L1 L1 L2 L2
