实验3 假设测验
假设检验实验报告【范本模板】

实验报告假设检验学院:参赛队员:参赛队员:参赛队员:指导老师:一、实验目的1.了解假设检验的基本内容;2.了解单样本t检验;3.了解独立样本t检验;、4.了解配对样本t检验;5.学会运用spss软件求解问题;6.加深理论与实践相结合的能力。
二、实验环境Spss、office三、实验方法1.单样本t检验;2.独立样本t检验;3.配对样本t检验.四、实验过程1。
1实验过程依题意,设H0:μ= 82,H1:μ>82 (1)定义变量为成绩,将数据输入SPSS;(2)选择:分析→比较均值→单样本T检验;(3)将变量成绩放置Test栏中,并在Test框中输入数据82;(4)观察结果1.2实验结果1。
3结果分析该题是右尾检验,所以右尾P=0。
037/2=0。
0185因为P值明显小于0.05,表明在0.05水平上变量与检验值有显著性差异,故接受原假设,所以该县的英语教学改革成功.问题二:某工艺研究所研究出一种自动装罐机,它可以用来自动装罐头食品,并且可以达到每罐的标准重量为500克。
现在需要检验它的性能。
假定装罐重量服从正态分布。
现随机抽取10罐来检查机器工作情况,这10罐的重量如下:495 502 510 497 506 498503 492 504 5012。
1实验过程依题意,设H0:μ= 500,H1:μ≠500(1)定义变量为成绩,将数据输入SPSS;(2)选择:分析比较均值单样本T检验;(3)将变量成绩放置Test栏中,并在Test框中输入数据500;2。
2实验结果2.3结果分析该题是双检验,所以双尾P=0。
650因为P值明显大于0。
05,表明在0.05水平上变量与检验值无显著性差异,故不能拒绝原假设,接受备择假设,所以自动装罐机性能良好问题三:某对外汉语中心进行了一项汉字教学实验,同一年级的两个平行班参与了该实验。
一个班采用集中识字的方式,然后学习课文;另一班采用分散识字的方式,边学习课文边学习生字。
第5章 假设测验

左尾
0.025 -1.96x 否定区
0.95 0 接受区
0.025 +1.96x 否定区
右尾
双尾测验
(two-sided test)
三、两尾测验与一尾测验
单尾测验
假设:
(one-sided test)
H0 : ≤0 HA : > 0
H0 : ≥0 HA : < 0
0.95
命中率有80%的自由球射手投20球命中的次 数应服从二项分布B(20, 0.8)。
命中的次数小于或等于8的概率约为 0.0001。 即重复实地投射20球10,000次只中8球以下的 情形约只发生一次。
一、假设测验的理论基础
假设宣称的叙述为真(命中率有80%) ,可推 得实验结果发生的可能性很低,则该实验结 果的发生(实地投射20球中8球),即为宣称 的叙述不真的好证据。 “Prove by Contradiction”
2. 计算接受区和否定区 在假设H0为正确的条件下,根据 x 的 抽样分布划出一个区间,如 这一区间外则否定H0 。由于
x
在这一区间内则接受H0,如x 在
P{ 1.96 x x 1.96 x } 0.95
因此,在x 的抽样分布中,落在( 1.96 x, 1.96 x ) 区间内的有95%,落在这一区间外的只有5%。
用来测验假设的概率标准5%或1%等,称为显著水平
( significance level )。 一般以 表示,如 =0.05或 =0.01。
二、假设测验的步骤
综合上述,统计假设测验的步骤可总结如下: (1) 对样本所属的总体提出统计假设,包括无效假设和备 择假设。 (2) 规定测验的显著水平 值。
实验三 假设检验

实验三假设检验一.实验目的和要求在总体分布函数已知但参数未知时,对未知参数提出假设“该参数为真值”,则如何利用样本提供的信息来检验这个假设,即接受此假设还是拒绝此假设,这类问题就是参数的假设检验。
参数估计和假设检验就是利用样本对总体的统计特性提供的信息,建立样本的函数,即估计量或检验统计量,是从不同的角度处理未知参数的两种不同的方法。
二.实验内容1.实验数据为了评价两个学校的教学质量,分别在两个学校抽取样本。
在A学校抽取30名学生,在B学校抽取40名学生,对两个学校的学生同时进行一次英语标准化考试成绩如附表6-1所示。
假设学校A考试成绩的方差为64,学校B考试成绩的方差为100。
检验两个学校的教学质量是否有显著差异。
(α=0.05)学校A70 97 85 87 64 7386 90 82 83 92 7472 94 76 89 73 8891 79 84 76 87 8885 78 83 84 91 74学校B76 91 57 62 89 82 93 6480 78 99 59 79 82 70 8583 87 78 84 84 70 79 7291 93 75 85 65 74 79 6484 66 66 85 78 83 75 742.实验过程z-检验: 双样本均值分析变量 1 变量2平均82.5 78 已知协方差64 100 观测值30 40 假设平均差0z 2.090575P(Z<=z) 单尾0.018283z 单尾临界 1.644854P(Z<=z) 双尾0.036566z 双尾临界 1.959964三.实验结果分析由上述试验过程可知Z>Zα/2,所以拒绝原假设,两所学校之间具有明显差距。
又平均值也可看出A校比B校较为优秀。
第四章假设测验

二、两个样本平均数相比较的假设测验
(二) 成对数据的比较
若试验设计是将性质相同的两个供试单位配成一对,并
设有多个配对,然后对每一配对的两个供试单位分别随机地
给予不同处理,则所得观察值为成对数据。
成对数据,由于同一配对内两个供试单位的试验条件很
是接近,而不同配对间的条件差异又可通过同一配对的差数
予以消除,因而可以控制试验误差,具有较高的精确度。
在分析试验结果时,只要假设两样本的总体差数的
平均数
d
1 2
0,而不必假定两样本的总体方差
2 1
和Hale Waihona Puke 22相同。二、两个样本平均数相比较的假设测验
设两个样本的观察值分别为x1和 x2 ,共配成n对,各个对
的差数为 d =x1-x2,差数的平均数为d x1 x2 ,则差数平 均数的标准误 s 为:
根据以上资料,可以进行两类统计推断:
第一种:
如果要对技术改进后的产品使用寿命进 行统计推断,则可在给定1置信度时对总体 平均值作区间估计,即:
P( X z / 2
n
X z / 2
) 1
n
这表明区间( X z / 2
n
,X
z / 2
)覆盖的概念为1
n
第二种:
如果要问改进后的平均使用寿命是否与 改进前的0有明显的差别,则可在给定显著性 水平时对进行假设检验。
为未知,但可假定
2 1
2 2
2
,而两个样本又为小样本时,用t
测验。
二、两个样本平均数相比较的假设测验
从样本变异算出平均数差数的均方
s
2 e
,
se2
SS1
第3章 假设测验和区间估计
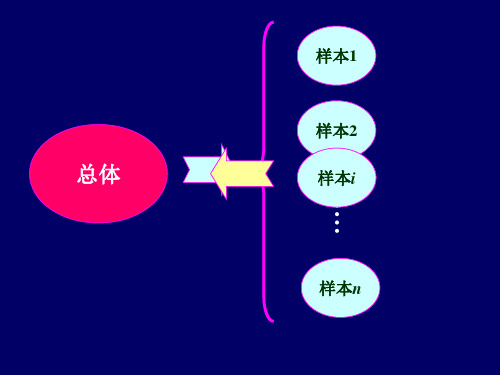
x
x
x
n
x1, x2, , xn n 30
u x 0
Sx
S2 2
Sx
S n
例:某一棉花品种的纤维长度平均为29.8mm,现从一棉花新品 系中n=100进行随机抽样,测得其纤维平均长度为30.1mm,标 准差为1.5mm,问此结果可否认为这一新品种的纤维长度不同 于原棉花品种?
(1)这是一个样本平均数的假设检验,因总体σ2未知, 分 n=100 > 30,可用s2代替σ2进行u测验;
问新育苗方法与常规方法有无显著差异?
(1)这是一个样本平均数的假设检验,总体方差已知,
分 析
故采用u测验。
(2)新育苗方法的育苗效果可能大于也可能低于常规方 法,故两尾测验。
(1) 假设
(2)水平 (3)计算 (4)推断
H0:μ=μ0=7.25(cm), 即新育苗方法与常规方法所育鱼苗一月龄体长相同;
n
10
x
n
8 2.530 10
u x x x 0 502.700 500 1.067
x n
2.530
(4)统计推断
u0.05 1.96
| u | 1.067 u0.05 1.96 P 0.05 不能否定H0
推断该日装罐平均净重与标准净重差异不显著,亦表明 该日装罐机工作属正常状态。
否定区0-1.96x
0
接受区
0+1.9否6定x区
临界值:0 + 1.96x
两尾测验
两尾测验:具有左尾和右尾两个否定区的假设测验。
P(0-2.58x <x< 0 +2.58x) =0.99
左尾 0.005
0.99
0.005 右尾
简述统计假设测验的步骤

简述统计假设测验的步骤统计假设测验是用来检查不能直接用频数描述的统计量(参数),或者用作推断总体参数之间关系的统计方法。
这种统计测验一般由2个测验构成:第一测验先给被试呈现一些刺激或者未知数,第二测验则要求被试对第一测验中呈现的结果做出解释。
1、确定假设的总体,并根据研究目的和问题,确定问题的可能性水平。
最常见的测验工具为二项分布、正态分布和X 2分布等。
有时还要确定问题的类型和抽取样本的数量。
例如,为了回答“你在进行某次聚会时,是否去过卡拉OK”的问题,应该采用正态分布,因为在高于1的概率下你应该去过卡拉OK。
然而,在回答“你在进行某次聚会时,是否饮过酒”的问题时,应该采用二项分布。
这样才有助于回答“你在进行某次聚会时是否去过卡拉OK”的问题。
又例如,为了回答“你是否进行过某项运动”的问题,应该采用正态分布。
2、提出概率度量,即确定样本观察值(X值)的标准差,从而确定“样本估计值”的标准差。
例如,如果希望用Y=10代替X的正态分布的总体,应该提出的标准差为20,而希望用Y=25代替X 2分布的总体,则提出的标准差为5。
有了标准差之后,我们就可以算出总体的期望和方差。
此外,应该提出适当的置信区间,以便进行假设检验。
假设检验的第一步,也就是要先求出总体X的均值和方差。
方差σ的公式为σ=∑x/X3、计算“样本观察值”的平均值,并且用这个平均值除以标准差,得到“样本观察值”的期望值(ΔL),再将样本观察值代入假设检验的第一个公式,得到两个参数之间的相互关系。
样本观察值的标准差用它除以期望值,就可以得到平均变异数,这个平均变异数就是抽样平均误差,它等于样本观察值的标准差乘以总体均值与样本观察值的期望值的比值,或者等于样本观察值的标准差除以方差。
如果只有正态分布和X 2分布的总体,而没有说明总体期望值的大小,则需要用样本容量(N)除以样本标准差(σ/2)得到样本均值,然后把均值代入样本观察值,即得到样本的期望值。
实验三 平均数的假设测验
数据分析
t-检验:双样本 等方差假设
成组数据的平均数比较
3. 两个样本的总体方差 12和 22 为未知,且 12 ≠ 22 时 用近似 t 测验
工具
数据分析
t-检验:双样本 异方差假设
成对数据的平均数比较 用 t 测验
工具
数据分析
t-检验:平均值的 成对二样本分析
在EXCEL中,可以用
(2) 样本百分数的标准误 σ p
pˆ
pq n
(3)求u值
u pˆ p
pˆ
对应的u临界值(u0.05=1.96, u0.01=2.58)
单个样本方差的假设测验求2值 2 =自由度×样本方差 总体方差
求该2值对应的概率(CHIDIST)
求对应的2临界值(CHIINV )
• 成组数据 • 成对数据
单个样本平均数的假设测验
(1)平均数( AVERAGE ) (2) 样本标准差 ( STDEV ) (3)样本平均数的标准误 (4)求t值
求对应的t临界值( TINV ) 求该t值对应的概率( TDIST )
单个样本百分数的假设测验
(1)样本百分数 p
T测验函数(TTSET)
来做成组数据中等方差双样本测验、 异方差双样本测验、 成对数据的假设测验
实验二 统计假设测验
提出假设
计算概率
作出推断
拒绝区H0
拒绝区H0
0.025
-1.96 H0 1.96
y
拒绝区H0
0.05 -1.64 H0
y
拒绝区H0
0.05
H0 1.64
y
• 一个正态总体参数假设测验
• 单个样本平均数 • 单个样本百分数 • 单个方差
田间试验与统计分析教学大纲
田间试验与统计分析教学大纲(农学类专业专科学生)第一部分课程的性质和任务田间试验与统计分析,是运用数理统计理论与方法研究农业科学研究和技术工作中,所需的田间试验设计、实施和试验资料统计分析方法的一门应用学科,是农学类专业的专业基础课。
本课程在高等数学、线性代数、概率论初步等课程的基础上,介绍数理统计的基本概念和基本原理,讲解田间试验的基本要求、设计实施和试验资料统计分析方法。
本课程既涉及一些严谨的数学理论和方法,又紧密结合农业生产和科学研究实践。
通过学习为进一步学习遗传学、作物栽培学、作物育种学等专业基础课和专业课打下坚实的基础,同时学会如何利用这一工具进行农业科学研究和技术工作方法。
第二部分基本要求通过本课程的学习,学生应达到以下要求:1. 有关试验数据分析的基本技能,如整理数据和计算平均数、变异数等,对试验结果有一个数量概念。
2.有关从试验数据进行归纳的统计推断原理和程序。
3. 掌握试验设计的基本原则和各种设计的要点及特点。
4.能根据所给试验条件,能够正确选用试验设计方法,并做出试验设计。
5.掌握EXCEL常见函数主要功能和数据分析工具。
第三部分教学说明及学时分配本课程总共60学时,讲授44学时,实验8个计16学时。
本课程以概率论、数理统计为基础,介绍田间试验与统计分析的基本概念、基本知识和基本方法,着重讲解农学类专业常用田间试验的设计、实施和统计分析方法。
本课程概念较多、理论抽象、系统严密、实践性强、公式复杂、符号繁多、计算量大,除课堂讲授外,要求学生认真完成习题作业,并结合农业生产和科学研究实践,有针对性的安排上机实习和田间实习,注意培养学生运用所学知识和技能分析问题和解决问题的能力。
(一)教学环节1、课堂讲授着重讲解基本概念、基本原理和基本方法,突出重点和难点。
各种统计分析方法的介绍主要结合例题来讲解。
2、实验及习题实验对于帮助学生巩固和加深理解教学的基本内容是很有作用的。
本课程拟安排八个实验,利用EXCEL所提供函数和数据分析工具实现所授统计方法计算。
第三章 统计假设测验
s sx n
返回
【例】已知热带雨林中的某种树木,其 树苗在阳光直射的情况下,每年可生长 1.5m。某生态学家将1998年至1999年 9株该树苗生长情况记载如下。试问这 些数据是否支持已知的说法。 1.9 2.5 1.6 2.0 1.5 2.7 1.9 1.0 2.0
解:
显著水平α =0.05
Location B 650 600 600 575 452 320 660
解:(1) H0:μA=μB
HA: μA≠μB
(2)显著水平α =0.05 (3)计算相关统计数如下: Location A nA=13
x A 618
2 s A 37853.17
Location B nB=7
xB 551
H0:μd=1.5m/year HA: μd≠1.5m/year
计算:
1.9 2.5 2.0 x 1.9 9
2
n 1 2 2 2 1.9 2.5 2.02 9 1.9 2.5 2.0 9 1 0.260
s
x x
三、两个样本平均数相比较的假设测验
(一)成组数据的平均数比较 成组数据:是指当进行只有两个处理的 试验时,将试验单位完全随机地分成 两个组,然后对两组随机施加一个处 理,则所得两组观察值为成组数据。
1、应用条件: (1)两个处理为完全随机设计,各供试单 位彼此独立。 (2)试验单位比较一致,或单位间的差异 不会影响试验指标。
2
2
n
s 0.51
x 1.90 1.50 t 2.35 sx 0.51 9
查附表4,ν=8时,t0.05=2.306,现实得 |t|>t0.05,故p<0.05
实验三 用EXCEL成组和成对数据的t测验
用 EXCEL 对小样本 实验三 资 料 进 行 t 测 验
一、单个样本平均数假设测验 二、成对样本平均数假设测验 三、成组样本平均数假设测验 四、利用 EXCEL 进行区间估计
用EXCEL对小样本资料进行t测验
一、单个样本平均数假设测验
单个样本平均数的假设测验是推断样本所来 自的总体平均数μ(未知)与已知总体的平均数μ0 是否相等,因此其统计假设 H0 : 0 ,而对立的 备择假设有 H A : 0 (两尾)或 H A : 0 (右尾)或
2 1 2 2
2 1 2 2
如果相等则采用t测验,如果不相等则采用近似 t测验。
用EXCEL对小样本资料进行t测验
F
2 s1 2 s2
在EXCEL中,计算F值不必考虑以 大值均方作分子,而以下面的方法来 判断两样本的总体方差是否相等。
F0.025(df1,df2)=1/F0.975(df2,df1)
用EXCEL对小样本资料进行t测验
=stdev(A2:A18)
=count(A2:A18)
=D5/sqrt(D3) =average(A2:A18) =D3-1 =abs((D4-16)/D6)
0
α=0.05,故α×2=0.10
=tinv(0.10,D7)
用EXCEL对小样本资料进行t测验
统计推断 由于 t t0.05 ,故否定 H 0 ,接受 H A, 说明滴灌能显著提高该品种大豆的百粒重。
应用EXCEL的操作方法为:
用EXCEL对小样本资料进行t测验
第一步:开一张工作表,并输入相应的数据, 如A1:A18。
用EXCEL对小样本资料进行t测验
第二步:在其它区域依次输入各统计量的名称, 如C3:C9。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
作业:1作业:2
要求:写出统计假设,做出统计推断
测验两个玉米品种在产量上是否具有显著差异选面积相同的玉米小区10个,各BS24金皇后不去雄,得产量结果如下,试分析
1916去雄
212128
202430
201531
202635
221830
222034
211930
212228
191934
32
假设:H0:即方差无显著性差异假设:H0:ud=0,对HA:ud≠0HA:方差有显著性差异t-检验: 成对双样本均值分析
F-检验 双样本方差分析
平均
金皇后BS24方差
平均2020.5观测值
方差11.55555556 1.1666667泊松相关系数
观测值1010假设平均差
df99df
F9.904761905t Stat
P(F<=f) 单尾0.0010805P(T<=t) 单尾
F 单尾临界 3.178893105t 单尾临界
P(T<=t) 双尾
推断:t 双尾临界
因为P单尾=0.0010805,则P双尾=0.0021610<t0.05
故接受H0 否定HA,即方差有显著性差异 因为
推断:去雄与不去雄对产量有显平均数测验H0:平均数无显著性差异
HA:平均数有显著性差异
t-检验: 双样本异方差假设
BS24金皇后
平均20.520
方差 1.166********.555556
观测值1010
假设平均差0
df11
t Stat0.443290593
P(T<=t) 单尾0.33307383
t 单尾临界 1.795884814
P(T<=t) 双尾0.66614766
t 双尾临界 2.200985159
推断:因为P双尾=0.66614766﹥t0.05,所以接受H0,否定HA.
米小区10个,各分成两半,一半去雄另一半得产量结果如下,试分析去雄对产量是否有显著影响不去雄
25
28
29
29
31
25
28
27
32
27
0:ud=0,对HA:ud≠0
成对双样本均值分析
去雄不去雄
31.5555555628.44444444
5.527777778 4.527777778
99
0.094390564
8
3.09208273
0.007421325
1.859548033
0.014842651
2.306004133
去雄与不去雄对产量有显著影响。
