中考数学压轴题达标测试综合卷检测试卷
2023武汉中考数学压轴题

2023武汉中考数学压轴题一、试卷整体情况哎呀,这2023武汉中考数学压轴题的试卷啊,满分就设为100分啦。
这试卷里的题目那可得安排得妥妥当当的,一道都不能少。
咱就从简单的开始说起。
二、具体题目设置1. 第一题呢,就来个基础的代数运算题,比如化简一个多项式之类的。
这题就占个10分,也就是10%的分数比例。
像化简(2x + 3y)² - (2x - 3y)²这种题,就很考验同学们对平方差公式的掌握程度。
答案就是24xy,解析就是利用平方差公式a² - b²=(a + b)(a - b),这里a = 2x+3y,b = 2x - 3y,代入计算就得出结果啦。
2. 第二题是个简单的几何题,求一个三角形的内角。
这题占8分,8%的分数比例。
例如已知三角形的两个外角分别是120°和130°,求这个三角形的最大内角。
答案是70°,解析就是先求出与这两个外角相邻的内角分别是60°和50°,然后根据三角形内角和为180°,算出最大内角是180 - 60 - 50 = 70°。
3. 接着来个函数题,占12分,12%的比例。
比如给定一个一次函数y = kx +b的图像经过两点(1,3)和( - 1, - 1),求这个函数的表达式。
答案是y = 2x+1,解析呢,把两点坐标代入函数表达式得到方程组,解方程组就能求出k和b的值。
4. 再安排一个概率题,10分,10%的比例。
一个盒子里有3个红球,2个白球,1个黑球,从中随机摸出一个红球的概率是多少?答案是1/2,解析就是用红球的个数除以球的总个数。
5. 然后是个中等难度的几何证明题,15分,15%的比例。
例如证明等腰三角形两腰上的高相等。
这就需要同学们利用三角形的面积公式和等腰三角形的性质来证明啦。
6. 又来一个二次函数的综合题,15分,15%的比例。
已知二次函数y =ax²+bx + c的图像经过三点,求函数的表达式,并且求函数的最值。
二次函数与几何综合压轴题(原卷版)-2024年中考数学

二次函数与几何综合压轴题几乎所有的地方都把二次函数与几何综合压轴题作为中考压轴题。
1.(2023·青海·中考真题)如图,二次函数2y x bx c =−++的图象与x 轴相交于点A 和点()1,0C ,交y 轴于点()0,3B .(1)求此二次函数的解析式;(2)设二次函数图象的顶点为P ,对称轴与x 轴交于点Q ,求四边形AOBP 的面积(请在图1中探索); (3)二次函数图象的对称轴上是否存在点M ,使得△AMB 是以AB 为底边的等腰三角形?若存在,请求出满足条件的点M 的坐标;若不存在,请说明理由(请在图2中探索).2.(2023·内蒙古·中考真题)如图,在平面直角坐标系中,抛物线2y x bx c =−++与x 轴的交点分别为A 和()10B ,(点A 在点B 的左侧),与y 轴交于点()0,3C ,点P 是直线AC 上方抛物线上一动点.(1)求抛物线的解析式;(2)如图1,过点P 作x 轴平行线交AC 于点E ,过点P 作y 轴平行线交x 轴于点D ,求PE PD +的最大值及点P 的坐标;(3)如图2,设点M 为抛物线对称轴上一动点,当点P ,点M 运动时,在坐标轴上确定点N ,使四边形PMCN 为矩形,求出所有符合条件的点N 的坐标.3.(2023·海南·中考真题)如图1,抛物线2y x bx c =++交x 轴于A ,()3,0B 两点,交y 轴于点()0,3C −.点P 是抛物线上一动点.(1)求该抛物线的函数表达式;(2)当点P 的坐标为()1,4−时,求四边形BACP 的面积;(3)当动点P 在直线BC 上方时,在平面直角坐标系是否存在点Q ,使得以B ,C ,P ,Q 为顶点的四边形是矩形?若存在,请求出点Q 的坐标;若不存在,请说明理由;(4)如图2,点D 是抛物线的顶点,过点D 作直线DH y ∥轴,交x 轴于点H ,当点P 在第二象限时,作直线PA ,PB 分别与直线DH 交于点G 和点I ,求证:点D 是线段IG 的中点.4.(2023·西藏·中考真题)在平面直角坐标系中,抛物线2y x bx c =−++与x 轴交于()30A −,,()10B ,两点,与y 轴交于点C .(1)求抛物线的解析式;(2)如图甲,在y 轴上找一点D ,使ACD 为等腰三角形,请直接写出点D 的坐标;(3)如图乙,点P 为抛物线对称轴上一点,是否存在P 、Q 两点使以点A ,C ,P ,Q 为顶点的四边形是菱形?若存在,求出P 、Q 两点的坐标,若不存在,请说明理由.5.(2023·四川甘孜·中考真题)已知抛物线2y x bx c =++与x 轴相交于()10A −,,B 两点,与y 轴相交于点()03C −,.(1)求b ,c 的值;(2)P 为第一象限抛物线上一点,PBC 的面积与ABC 的面积相等,求直线AP 的解析式;(3)在(2)的条件下,设E 是直线BC 上一点,点P 关于AE 的对称点为点P ′,试探究,是否存在满足条件的点E ,使得点P ′恰好落在直线BC 上,如果存在,求出点P ′的坐标;如果不存在,请说明理由.6.(2023·四川达州·中考真题)如图,抛物线2y ax bx c ++过点()()()1,0,3,,00,3A B C −.(1)求抛物线的解析式;(2)设点P 是直线BC 上方抛物线上一点,求出PBC 的最大面积及此时点P 的坐标;(3)若点M 是抛物线对称轴上一动点,点N 为坐标平面内一点,是否存在以BC 为边,点B C M N 、、、为顶点的四边形是菱形,若存在,请直接写出点N 的坐标;若不存在,请说明理由.7.(2023·四川巴中·中考真题)在平面直角坐标系中,抛物线2(0)y ax bx c a ++≠经过点(1,0)A −和(0,3)B ,其顶点的横坐标为1.(1)求抛物线的表达式.(2)若直线x m =与x 轴交于点N ,在第一象限内与抛物线交于点M ,当m 取何值时,使得AN MN +有最大值,并求出最大值.(3)若点P 为抛物线2(0)y ax bx c a ++≠的对称轴上一动点,将抛物线向左平移1个单位长度后,Q 为平移后抛物线上一动点.在(2)的条件下求得的点M ,是否能与A 、P 、Q 构成平行四边形?若能构成,求出Q 点坐标;若不能构成,请说明理由.8.(2023·四川眉山·中考真题)在平面直角坐标系中,已知抛物线2y ax bx c ++与x 轴交于点()()3,0,1,0A B −两点,与y 轴交于点()0,3C ,点P 是抛物线上的一个动点.(1)求抛物线的表达式;(2)当点P 在直线AC 上方的抛物线上时,连接BP 交AC 于点D .如图1.当PD DB的值最大时,求点P 的坐标及PD DB 的最大值; (3)过点P 作x 轴的垂线交直线AC 于点M ,连接PC ,将PCM △沿直线PC 翻折,当点M 的对应点'M 恰好落在y 轴上时,请直接写出此时点M 的坐标.9.(2023·四川内江·中考真题)如图,在平面直角坐标系中,抛物线2y ax bx c ++与x 轴交于()4,0B ,()2,0C −两点.与y 轴交于点()0,2A −.(1)求该抛物线的函数表达式;(2)若点P 是直线AB 下方抛物线上的一动点,过点P 作x 轴的平行线交AB 于点K ,过点P 作y 轴的平行线交x 轴于点D ,求与12PK PD +的最大值及此时点P 的坐标; (3)在抛物线的对称轴上是否存在一点M ,使得MAB △是以AB 为一条直角边的直角三角形:若存在,请求出点M 的坐标,若不存在,请说明理由.10.(2023·湖北黄冈·中考真题)已知抛物线212y x bx c =−++与x 轴交于,(4,0)A B 两点,与y 轴交于点(0,2)C ,点P 为第一象限抛物线上的点,连接,,,CA CB PB PC .(1)直接写出结果;b =_____,c =_____,点A 的坐标为_____,tan ABC ∠=______;(2)如图1,当2PCB OCA ∠=∠时,求点P 的坐标; (3)如图2,点D 在y 轴负半轴上,OD OB =,点Q 为抛物线上一点,90QBD ∠=°,点E ,F 分别为BDQ △的边,DQ DB 上的动点,QE DF =,记BE QF +的最小值为m . ①求m 的值;②设PCB 的面积为S ,若214S m k =−,请直接写出k 的取值范围.11.(2023·湖北武汉·中考真题)抛物线21:28=−−C y x x 交x 轴于,A B 两点(A 在B 的左边),交y 轴于点C .(1)直接写出,,A B C 三点的坐标;(2)如图(1),作直线()04=<<x t t ,分别交x 轴,线段BC ,抛物线1C 于,,D E F 三点,连接CF .若BDE 与CEF △相似,求t 的值;(3)如图(2),将抛物线1C 平移得到抛物线2C ,其顶点为原点.直线2y x =与抛物线2C 交于,O G 两点,过OG 的中点H 作直线MN (异于直线OG )交抛物线2C 于,M N 两点,直线MO 与直线GN 交于点P .问点P 是否在一条定直线上?若是,求该直线的解析式;若不是,请说明理由.12.(2023·湖南郴州·中考真题)已知抛物线24y ax bx ++与x 轴相交于点 1,0A ,()4,0B ,与y 轴相交于点C .(1)求抛物线的表达式;(2)如图1,点P 是抛物线的对称轴l 上的一个动点,当PAC △的周长最小时,求PAPC的值; (3)如图2,取线段OC 的中点D ,在抛物线上是否存在点Q ,使1tan 2QDB ∠=若存在,求出点Q 的坐标;若不存在,请说明理由.且与直线:1l y x =−−交于D E 、两点(点D 在点E 的右侧),点M 为直线l 上的一动点,设点M 的横坐标为t .(1)求抛物线的解析式.(2)过点M 作x 轴的垂线,与拋物线交于点N .若04t <<,求NED 面积的最大值.(3)抛物线与y 轴交于点C ,点R 为平面直角坐标系上一点,若以B C M R 、、、为顶点的四边形是菱形,请求出所有满足条件的点R 的坐标.在此抛物线上,其横坐标分别为,2(0)m m m >,连接AP ,AQ .(1)求此抛物线的解析式.(2)当点Q 与此抛物线的顶点重合时,求m 的值.(3)当PAQ ∠的边与x 轴平行时,求点P 与点Q 的纵坐标的差.(4)设此抛物线在点A 与点P 之间部分(包括点A 和点P )的最高点与最低点的纵坐标的差为1h ,在点A 与点Q 之间部分(包括点A 和点Q )的最高点与最低点的纵坐标的差为2h .当21h h m −=时,直接写出m 的值.15.(2023·青海西宁·中考真题)如图,在平面直角坐标系中,直线l 与x 轴交于点()6,0A ,与y 轴交于点()0,6B −,抛物线经过点A ,B ,且对称轴是直线1x =.(1)求直线l 的解析式; (2)求抛物线的解析式;(3)点P 是直线l 下方抛物线上的一动点,过点P 作PC x ⊥轴,垂足为C ,交直线l 于点D ,过点P 作PM l ⊥,垂足为M .求PM 的最大值及此时P 点的坐标.16.(2023·湖南·中考真题)如图,二次函数2y x bx c =++的图象与x 轴交于A ,B 两点,与y 轴交于C 点,其中()10B ,,()0,3C .(1)求这个二次函数的表达式;(2)在二次函数图象上是否存在点P ,使得PAC ABC S S =△△?若存在,请求出P 点坐标;若不存在,请说明理由;(3)点Q 是对称轴l 上一点,且点Q 的纵坐标为a ,当QAC △是锐角三角形时,求a 的取值范围.17.(2023·辽宁营口·中考真题)如图,抛物线()210y ax bx a +−≠与x 轴交于点 1,0A 和点B ,与y 轴交于点C ,抛物线的对称轴交x 轴于点()3,0D ,过点B 作直线l x ⊥轴,过点D 作DE CD ⊥,交直线l 于点E .(1)求抛物线的解析式;(2)如图,点P 为第三象限内抛物线上的点,连接CE 和BP 交于点Q ,当57BQ PQ =时.求点P 的坐标; (3)在(2)的条件下,连接AC ,在直线BP 上是否存在点F ,使得DEF ACD BED ∠=∠+∠?若存在,请直接写出点F 的坐标;若不存在,请说明理由.18.(2023·湖南湘西·中考真题)如图(1),二次函数25y ax x c =−+的图像与x 轴交于()4,0A −,(),0B b 两点,与y 轴交于点()0,4C −.(1)求二次函数的解析式和b 的值.(2)在二次函数位于x 轴上方的图像上是否存在点M ,使13BOM ABC S S =△△?若存在,请求出点M 的坐标;若不存在,请说明理由.(3)如图(2),作点A 关于原点O 的对称点E ,连接CE ,作以CE 为直径的圆.点E ′是圆在x 轴上方圆弧上的动点(点E ′不与圆弧的端点E 重合,但与圆弧的另一个端点可以重合),平移线段AE ,使点E 移动到点E ′,线段AE 的对应线段为A E ′′,连接E C ′,A A ′,A A ′的延长线交直线E C ′于点N ,求AA CN′的值.19.(2023·辽宁盘锦·中考真题)如图,抛物线23y ax bx ++与x 轴交于点()10A −,,()30B ,,与y 轴交于点C .(1)求抛物线的解析式.(2)如图1,点Q 是x 轴上方抛物线上一点,射线QM x ⊥轴于点N ,若QM BM =,且4tan 3MBN ∠=,请直接写出点Q 的坐标.(3)如图2,点E 是第一象限内一点,连接AE 交y 轴于点D ,AE 的延长线交抛物线于点P ,点F 在线段CD 上,且CF OD =,连接FA FE BE BP ,,,,若AFE ABE S S =△△,求PAB 面积.20.(2023·重庆·中考真题)如图,在平面直角坐标系中,抛物线22y ax bx ++过点()1,3,且交x 轴于点()1,0A −,B 两点,交y 轴于点C .(1)求抛物线的表达式;(2)点P 是直线BC 上方抛物线上的一动点,过点P 作PD BC ⊥于点D ,过点P 作y 轴的平行线交直线BC 于点E ,求PDE △周长的最大值及此时点P 的坐标;(3)在(2)中PDE △周长取得最大值的条件下,将该抛物线沿射线CB M 为平移后的抛物线的对称轴上一点.在平面内确定一点N ,使得以点A ,P ,M ,N 为顶点的四边形是菱形,写出所有符合条件的点N 的坐标,并写出求解点N 的坐标的其中一种情况的过程.21.(2023·四川广安·中考真题)如图,二次函数2y x bx c =++的图象交x 轴于点A B ,,交y 轴于点C ,点B 的坐标为()1,0,对称轴是直线=1x −,点P 是x 轴上一动点,PM x ⊥轴,交直线AC 于点M ,交抛物线于点N .(1)求这个二次函数的解析式.(2)若点P 在线段AO 上运动(点P 与点A 、点O 不重合),求四边形ABCN 面积的最大值,并求出此时点P 的坐标.(3)若点P 在x 轴上运动,则在y 轴上是否存在点Q ,使以M 、N C Q 、、为顶点的四边形是菱形?若存在,请直接写出所有满足条件的点Q 的坐标;若不存在,请说明理由.22.(2023·湖北十堰·中考真题)已知抛物线28y ax bx ++过点()4,8B 和点()8,4C ,与y 轴交于点A .(1)求抛物线的解析式;(2)如图1,连接,AB BC ,点D 在线段AB 上(与点,A B 不重合),点F 是OA 的中点,连接FD ,过点D 作DE FD ⊥交BC 于点E ,连接EF ,当DEF 面积是ADF △面积的3倍时,求点D 的坐标;(3)如图2,点P 是抛物线上对称轴右侧的点,(),0H m 是x 轴正半轴上的动点,若线段OB 上存在点G (与点,O B 不重合),使得GBP HGP BOH ∠=∠=∠,求m 的取值范围.23.(2023·四川·中考真题)如图1,在平面直角坐标系中,已知二次函数24y ax bx ++的图象与x 轴交于点()2,0A −,()4,0B ,与y 轴交于点C .(1)求抛物线的解析式;(2)已知E 为抛物线上一点,F 为抛物线对称轴l 上一点,以B ,E ,F 为顶点的三角形是等腰直角三角形,且90BFE ∠=°,求出点F 的坐标; (3)如图2,P 为第一象限内抛物线上一点,连接AP 交y 轴于点M ,连接BP 并延长交y 轴于点N ,在点P 运动过程中,12OM ON +是否为定值?若是,求出这个定值;若不是,请说明理由.24.(2023·黑龙江绥化·中考真题)如图,抛物线21y ax bx c =++的图象经过(6,0)A −,(2,0)B −,(0,6)C 三点,且一次函数6y kx =+的图象经过点B .(1)求抛物线和一次函数的解析式.(2)点E ,F 为平面内两点,若以E 、F 、B 、C 为顶点的四边形是正方形,且点E 在点F 的左侧.这样的E ,F 两点是否存在?如果存在,请直接写出所有满足条件的点E 的坐标:如果不存在,请说明理由.(3)将抛物线21y ax bx c =++的图象向右平移8个单位长度得到抛物线2y ,此抛物线的图象与x 轴交于M ,N 两点(M 点在N 点左侧).点P 是抛物线2y 上的一个动点且在直线NC 下方.已知点P 的横坐标为m .过点P 作PD NC ⊥于点D .求m 为何值时,12CD PD +有最大值,最大值是多少?25.(2023·四川德阳·中考真题)已知:在平面直角坐标系中,抛物线与x 轴交于点(4,0)A −,(2,0)B ,与y 轴交于点(0,4)C −.(1)求抛物线的解析式;(2)如图1,如果把抛物线x 轴下方的部分沿x 轴翻折180°,抛物线的其余部分保持不变,得到一个新图象.当平面内的直线6y kx =+与新图象有三个公共点时,求k 的值; (3)如图2,如果把直线AB 沿y 轴向上平移至经过点D ,与抛物线的交点分别是E ,F ,直线BC 交EF 于点H ,过点F 作FG CH ⊥于点G ,若DF HG=F 的坐标.26.(2023·辽宁锦州·中考真题)如图,抛物线2y bx c ++交x 轴于点()1,0A −和B ,交y 轴于点(C ,顶点为D .(1)求抛物线的表达式;(2)若点E 在第一象限内对称右侧的抛物线上,四边形ODEB 的面积为E 的坐标;(3)在(2)的条件下,若点F 是对称轴上一点,点H 是坐标平面内一点,在对称轴右侧的抛物线上是否存在点G ,使以E ,F ,G ,H 为顶点的四边形是菱形,且60EFG ∠=°,如果存在,请直接写出点G 的坐标;如果不存在,请说明理由.27.(2023·辽宁鞍山·中考真题)如图1,抛物线253y ax x c =++经过点()3,1,与y 轴交于点()0,5B ,点E 为第一象限内抛物线上一动点.(1)求抛物线的解析式.(2)直线243y x =−与x 轴交于点A ,与y 轴交于点D ,过点E 作直线EF x ⊥轴,交AD 于点F ,连接BE .当BE DF =时,求点E 的横坐标.(3)如图2,点N 为x 轴正半轴上一点,OE 与BN 交于点M .若OE BN =,3tan 4BME ∠=,求点E 的坐标.28.(2023·辽宁丹东·中考真题)抛物线24y ax bx +−与x 轴交于点()4,0A −,()2,0B ,与y 轴交于点C .(1)求抛物线的表达式;(2)如图,点D 是抛物线上的一个动点,设点D 的横坐标是()42m m −<<,过点D 作直线DE x ⊥轴,垂足为点E ,交直线AC 于点F .当D ,E ,F 三点中一个点平分另外两点组成的线段时,求线段DF 的长;(3)若点P 是抛物线上的一个动点(点P 不与顶点重合),点M 是抛物线对称轴上的一个点,点N 在坐标平面内,当四边形CMPN 是矩形邻边之比为1:2时,请直接写出点P 的横坐标.。
最新初三九年级数学上册 压轴解答题综合测试卷(word含答案)
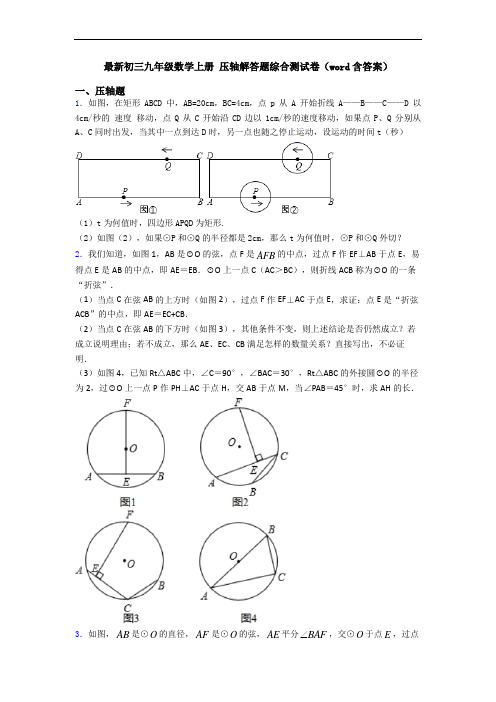
最新初三九年级数学上册压轴解答题综合测试卷(word含答案)一、压轴题1.如图,在矩形ABCD中,AB=20cm,BC=4cm,点p从A开始折线A——B——C——D以4cm/秒的速度移动,点Q从C开始沿CD边以1cm/秒的速度移动,如果点P、Q分别从A、C同时出发,当其中一点到达D时,另一点也随之停止运动,设运动的时间t(秒)(1)t为何值时,四边形APQD为矩形.(2)如图(2),如果⊙P和⊙Q的半径都是2cm,那么t为何值时,⊙P和⊙Q外切?2.我们知道,如图1,AB是⊙O的弦,点F是AFB的中点,过点F作EF⊥AB于点E,易得点E是AB的中点,即AE=EB.⊙O上一点C(AC>BC),则折线ACB称为⊙O的一条“折弦”.(1)当点C在弦AB的上方时(如图2),过点F作EF⊥AC于点E,求证:点E是“折弦ACB”的中点,即AE=EC+CB.(2)当点C在弦AB的下方时(如图3),其他条件不变,则上述结论是否仍然成立?若成立说明理由;若不成立,那么AE、EC、CB满足怎样的数量关系?直接写出,不必证明.(3)如图4,已知Rt△ABC中,∠C=90°,∠BAC=30°,Rt△ABC的外接圆⊙O的半径为2,过⊙O上一点P作PH⊥AC于点H,交AB于点M,当∠PAB=45°时,求AH的长.,交⊙O于点E,过点3.如图,AB是⊙O的直径,AF是⊙O的弦,AE平分BAFE 作直线ED AF ⊥,交AF 的延长线于点D ,交AB 的延长线于点C .(1)求证:CD 是⊙O 的切线; (2)若10,6AB AF ==,求AE 的长.4.如图,已知AB 是⊙O 的直径,AB =8,点C 在半径OA 上(点C 与点O 、A 不重合),过点C 作AB 的垂线交⊙O 于点D ,连结OD ,过点B 作OD 的平行线交⊙O 于点E 、交射线CD 于点F .(1)若ED =BE ,求∠F 的度数:(2)设线段OC =a ,求线段BE 和EF 的长(用含a 的代数式表示); (3)设点C 关于直线OD 的对称点为P ,若△PBE 为等腰三角形,求OC 的长.5.某校网球队教练对球员进行接球训练,教练每次发球的高度、位置都一致.教练站在球场正中间端点A 的水平距离为x 米,与地面的距离为y 米,运行时间为t 秒,经过多次测试,得到如下部分数据: t 秒 0 1.5 2.5 4 6.5 7.5 9 … x 米 0 4 8 10 12 16 20 … y 米24.565.8465.844.562…(2)网球落在地面时,与端点A 的水平距离是多少? (3)网球落在地面上弹起后,y 与x 满足(256y a x k =-+①用含a 的代数式表示k ;②球网高度为1.2米,球场长24米,弹起后是否存在唯一击球点,可以将球沿直线扣杀到A 点,若有请求出a 的值,若没有请说明理由.6.已知抛物线y=﹣14x2+bx+c经过点A(4,3),顶点为B,对称轴是直线x=2.(1)求抛物线的函数表达式和顶点B的坐标;(2)如图1,抛物线与y轴交于点C,连接AC,过A作AD⊥x轴于点D,E是线段AC上的动点(点E不与A,C两点重合);(i)若直线BE将四边形ACOD分成面积比为1:3的两部分,求点E的坐标;(ii)如图2,连接DE,作矩形DEFG,在点E的运动过程中,是否存在点G落在y轴上的同时点F恰好落在抛物线上?若存在,求出此时AE的长;若不存在,请说明理由.7.如图,抛物线y=x2+bx+c交x轴于A、B两点,其中点A坐标为(1,0),与y轴交于点C(0,﹣3).(1)求抛物线的函数表达式;(2)如图1,连接AC,点Q为x轴下方抛物线上任意一点,点D是抛物线对称轴与x轴的交点,直线AQ、BQ分别交抛物线的对称轴于点M、N.请问DM+DN是否为定值?如果是,请求出这个定值;如果不是,请说明理由.(3)如图2,点P为抛物线上一动点,且满足∠PAB=2∠ACO.求点P的坐标.8.如图,抛物线2)12(0y ax x c a =-+≠交x 轴于,A B 两点,交y 轴于点C .直线122y x =-经过点,B C .(1)求抛物线的解析式;(2)点P 是抛物线上一动点,过P 作x 轴的垂线,交直线BC 于M .设点P 的横坐标是t .①当PCM ∆是直角三角形时,求点P 的坐标;②当点P 在点B 右侧时,存在直线l ,使点,,A C M 到该直线的距离相等,求直线解析式y kx b =+(,k b 可用含t 的式子表示).9.如图,抛物线2y x bx c =-++与x 轴的两个交点分别为(1,0)A ,(30)B ,.抛物线的对称轴和x 轴交于点M .(1)求这条抛物线对应函数的表达式;(2)若P 点在该抛物线上,求当PAB △的面积为8时,求点P 的坐标.(3)点G 是抛物线上一个动点,点E 从点B 出发,沿x 轴的负半轴运动,速度为每秒1个单位,同时点F 由点M 出发,沿对称轴向下运动,速度为每秒2个单位,设运动的时间为t .①若点G 到AE 和MF 距离相等,直接写出点G 的坐标.②点C 是抛物线的对称轴上的一个动点,以FG 和FC 为边做矩形FGDC ,直接写出点E 恰好为矩形FGDC 的对角线交点时t 的值.10.对于线段外一点和这条线段两个端点连线所构成的角叫做这个点关于这条线段的视角.如图1,对于线段AB 及线段AB 外一点C ,我们称∠ACB 为点C 关于线段AB 的视角.如图2,点Q在直线l上运动,当点Q关于线段AB的视角最大时,则称这个最大的“视角”为直线l关于线段AB的“视角”.(1)如图3,在平面直角坐标系中,A(0,4),B(2,2),点C坐标为(﹣2,2),点C关于线段AB的视角为度,x轴关于线段AB的视角为度;(2)如图4,点M是在x轴上,坐标为(2,0),过点M作线段EF⊥x轴,且EM=MF =1,当直线y=kx(k≠0)关于线段EF的视角为90°,求k的值;(3)如图5,在平面直角坐标系中,P(3,2),Q(3+1,1),直线y=ax+b(a>0)与x轴的夹角为60°,且关于线段PQ的视角为45°,求这条直线的解析式.11.在平面直角坐标系xOy中,对于任意三点A,B,C,给出如下定义:如果矩形的任何一条边均与某条坐标轴平行,且A,B,C三点都在矩形的内部或边界上,则称该矩形为点A,B,C的覆盖矩形.点A,B,C的所有覆盖矩形中,面积最小的矩形称为点A,B,C的最优覆盖矩形.例如,下图中的矩形A1B1C1D1,A2B2C2D2,AB3C3D3都是点A,B,C的覆盖矩形,其中矩形AB3C3D3是点A,B,C的最优覆盖矩形.(1)已知A(﹣2,3),B(5,0),C(t,﹣2).①当t=2时,点A,B,C的最优覆盖矩形的面积为;②若点A,B,C的最优覆盖矩形的面积为40,求直线AC的表达式;(2)已知点D(1,1).E(m,n)是函数y=4x(x>0)的图象上一点,⊙P是点O,D,E的一个面积最小的最优覆盖矩形的外接圆,求出⊙P的半径r的取值范围.12.如图,在边长为5的菱形OABC中,sin∠AOC=45,O为坐标原点,A点在x轴的正半轴上,B,C两点都在第一象限.点P以每秒1个单位的速度沿O→A→B→C→O运动一周,设运动时间为t(秒).请解答下列问题:(1)当CP⊥OA时,求t的值;(2)当t<10时,求点P的坐标(结果用含t的代数式表示);(3)以点P为圆心,以OP为半径画圆,当⊙P与菱形OABC的一边所在直线相切时,请直接写出t的值.【参考答案】***试卷处理标记,请不要删除一、压轴题1.(1)4;(2)t为4s,203s,283s时,⊙P与⊙Q外切.【解析】试题分析:(1)四边形APQD为矩形,也就是AP=DQ,分别用含t的代数式表示,解即可;(2)主要考虑有四种情况,一种是P在AB上,一种是P在BC上时.一种是P在CD上时,又分为两种情况,一种是P在Q右侧,一种是P在Q左侧.并根据每一种情况,找出相等关系,解即可.试题解析:(1)根据题意,当AP=DQ时,四边形APQD为矩形.此时,4t=20-t,解得t=4(s).答:t为4时,四边形APQD为矩形(2)当PQ=4时,⊙P与⊙Q外切.①如果点P在AB上运动.只有当四边形APQD为矩形时,PQ=4.由(1),得t=4(s);②如果点P在BC上运动.此时t≥5,则CQ≥5,PQ≥CQ≥5>4,∴⊙P与⊙Q外离;③如果点P在CD上运动,且点P在点Q的右侧.可得CQ=t,CP=4t-24.当CQ-CP=4时,⊙P与⊙Q外切.此时,t-(4t-24)=4,解得t=203(s);④如果点P在CD上运动,且点P在点Q的左侧.当CP-CQ=4时,⊙P与⊙Q外切.此时,4t-24-t=4,解得t=283(s),∵点P从A开始沿折线A-B-C-D移动到D需要11s,点Q从C开始沿CD边移动到D需要20s,而283<11,∴当t为4s,203s,283s时,⊙P与⊙Q外切.考点:1.矩形的性质;2.圆与圆的位置关系.2.(1)见解析;(2)结论AE =EC+CB 不成立,新结论为:CE =BC+AE ,见解析;(3)AH 的长为3﹣1或3+1. 【解析】 【分析】(1)在AC 上截取AG =BC ,连接FA ,FG ,FB ,FC ,证明△FAG ≌△FBC ,根据全等三角形的性质得到FG =FC ,根据等腰三角形的性质得到EG =EC ,即可证明.(2)在CA 上截取CG =CB ,连接FA ,FB ,FC ,证明△FCG ≌△FCB ,根据全等三角形的性质得到FG =FB ,得到FA =FG ,根据等腰三角形的性质得到AE =GE ,即可证明. (3)分点P 在弦AB 上方和点P 在弦AB 下方两种情况进行讨论. 【详解】解:(1)如图2,在AC 上截取AG =BC ,连接FA ,FG ,FB ,FC , ∵点F 是AFB 的中点,FA =FB , 在△FAG 和△FBC 中,,FA FB FAG FBC AG BC =⎧⎪∠=∠⎨⎪=⎩∴△FAG ≌△FBC (SAS ), ∴FG =FC , ∵FE ⊥AC , ∴EG =EC ,∴AE =AG+EG =BC+CE ;(2)结论AE =EC+CB 不成立,新结论为:CE =BC+AE , 理由:如图3,在CA上截取CG=CB,连接FA,FB,FC,∵点F是AFB的中点,∴FA=FB,FA FB=,∴∠FCG=∠FCB,在△FCG和△FCB中,,CG CBFCG FCBFC FC=⎧⎪∠=∠⎨⎪=⎩∴△FCG≌△FCB(SAS),∴FG=FB,∴FA=FG,∵FE⊥AC,∴AE=GE,∴CE=CG+GE=BC+AE;(3)在Rt△ABC中,AB=2OA=4,∠BAC=30°,∴12232BC AB AC===,,当点P在弦AB上方时,如图4,在CA上截取CG=CB,连接PA,PB,PG,∵∠ACB=90°,∴AB为⊙O的直径,∴∠APB=90°,∵∠PAB=45°,∴∠PBA=45°=∠PAB,∴PA =PB ,∠PCG =∠PCB ,在△PCG 和△PCB 中, ,CG CB PCG PCB PC PC =⎧⎪∠=∠⎨⎪=⎩∴△PCG ≌△PCB (SAS ), ∴PG =PB , ∴PA =PG , ∵PH ⊥AC , ∴AH =GH ,∴AC =AH+GH+CG =2AH+BC ,∴22AH =+,∴1AH =, 当点P 在弦AB 下方时,如图5, 在AC 上截取AG =BC ,连接PA ,PB ,PC ,PG ∵∠ACB =90°, ∴AB 为⊙O 的直径, ∴∠APB =90°, ∵∠PAB =45°, ∴∠PBA =45°=∠PAB , ∴PA =PB , 在△PAG 和△PBC 中,,AG BCPAG PBC PA PB =⎧⎪∠=∠⎨⎪=⎩∴△PAG ≌△PBC (SAS ), ∴PG =PC , ∵PH ⊥AC , ∴CH =GH ,∴AC =AG+GH+CH =BC+2CH ,∴22CH ,=+∴1CH =,∴)11AH AC CH =-==,即:当∠PAB =45°时,AH11.【点睛】考查弧,弦的关系,全等三角形的判定与性质,等腰三角形的判定与性质等,综合性比较强,注意分类讨论思想方法在解题中的应用.3.(1)详见解析;(2)45【解析】【分析】(1)通过证明OE∥AD得出结论OE⊥CD,从而证明CD是⊙0的切线;(2)在Rt△ADE中,求出AD,DE,利用勾股定理即可解决问题.【详解】(1)证明:∵AE平分∠DAC,∴∠CAE=∠DAE.∵OA=OE,∴∠OEA=∠OAE.∴∠DAE=∠AEO,.∴AD∥OE.∵AD⊥CD,∴OE⊥CD.∴CD是⊙O的切线.(2)解:连接BF交OE于K.∵AB是直径,∴∠AFB=90°,∵AB=10,AF=6,∴BF228,106∵OE∥AD,∴∠OKB=∠AFB=90°,∴OE ⊥BF ,∴FK =BK =4,∵OA =OB ,KF =KB ,∴OK =12AF =3, ∴EK =OE ﹣OK =2,∵∠D =∠DFK =∠FKE =90°,∴四边形DFKE 是矩形,∴DE =KF =4,DF =EK =2,∴AD =AF+DF =8,在Rt △ADE 中,AE =22AD DE +=2284+=45 .【点睛】本题考查切线的判定和性质,勾股定理,矩形的判定和性质等知识,解题的关键是学会添加常用辅助线,属于中考常考题型.4.(1)30°;(2)EF=;(3)CO 的长为或时,△PEB 为等腰三角形.【解析】试题分析:(1)利用圆周角定理以及三角形内角和定理得出即可;(2)首先证明△HBO ≌△COD (AAS ),进而利用△COD ∽△CBF ,得出比例式求出EF 的长;(3)分别利用①当PB=PE ,不合题意舍去;②当BE=EP ,③当BE=BP ,求出即可. 试题解析:(1)如图1,连接EO ,∵∴∠BOE=∠EOD ,∵DO ∥BF ,∴∠DOE=∠BEO ,∵BO=EO ,∴∠OBE=∠OEB ,∴∠OBE=∠OEB=∠BOE=60°,∵CF ⊥AB ,∴∠FCB=90°,∴∠F=30°;(2)如图1,作HO⊥BE,垂足为H,∵在△HBO和△COD中,∴△HBO≌△COD(AAS),∴CO=BH=a,∴BE=2a,∵DO∥BF,∴△COD∽△CBF,∴∴,∴EF=;(3)∵∠COD=∠OBE,∠OBE=∠OEB,∠DOE=∠OEB,∴∠COD=∠DOE,∴C关于直线OD的对称点为P在线段OE上,若△PEB为等腰三角形,设CO=x,∴OP=OC=x,则PE=EO-OP=4-x,由(2)得:BE=2x,①当PB=PE,不合题意舍去;②当BE=EP,2x=4-x,解得:x=,③当BE=BP,作BM⊥EO,垂足为M,∴EM=PE=,∴∠OEB=∠COD,∠BME=∠DCO=90°,∴△BEM∽△DOC,∴,∴,整理得:x2+x-4=0,解得:x=(负数舍去),综上所述:当CO 的长为或时,△PEB 为等腰三角形. 考点:圆的综合题.5.(1)10;(2)1056+米;(3)①100k a =-;②不存在,理由见解析【解析】【分析】(1)利用表格中数据直接得出网球达到最大高度时的时间及最大值;(2)首先求出函数解析式,进而求出网球落在地面时,与端点A 的水平距离;(3)①由(2)得网球落在地面上时,得出对应点坐标,代入计算即可;②由球网高度及球桌的长度可知其扣杀路线解析式为110y x =,若要击杀则有(215610010a x a x --=,根据有唯一的击球点即该方程有唯一实数根即可求得a 的值,继而根据对应x 的值取舍可得.【详解】(1)由表格中数据可得4t =,(秒),网球达到最大高度,最大高度为6;(2)以A 为原点,以球场中线所在直线为x 轴,网球发出的方向为x 轴的正方向,竖直运动方向为y 方向,建立平面直角坐标系.由表格中数据,可得y 是x 的二次函数,且顶点坐标为(10,6),可设2(10)6y m x =-+,将(0,2)代入,可得:125m =-, ∴21(10)625y x =--+, 当0y =,得5610x =±(负值舍去),∴网球落在地面上时,网球与端点A 的距离为1056+米;(3)①由(2)得网球落在地面上时,对应的点为(1056+,0)代入(256y a x k =-+,得100k a =-;②不存在. ∵网高1.2米,球网到A 的距离为24122=米, ∴扣杀路线在直线经过(0,0)和(12,1.2)点,∴扣杀路线在直线110y x =上,令(2110010a x a x --=,整理得:2150010ax x a ⎛⎫-+= ⎪⎝⎭, 当0=时符合条件, 221106200010a a ⎛⎫=+-= ⎪⎝⎭, 解得1a =,2a =. 开口向下,0a <, ∴1a ,2a 都可以,将1a ,2a 分别代入(2110010a x a x --=,得到得解都是负数,不符合实际. 【点睛】本题主要考查了二次函数的实际应用,由实际问题建立起二次函数的模型并将二次函数的问题转化为一元二次方程求解是解题的关键.6.(1)y =﹣14x 2+x +3,顶点B 的坐标为(2,4);(2)(i )点E 的坐标为(85,3)或(125,3);(ii )存在;当点G 落在y 轴上的同时点F 恰好落在抛物线上,此时AE 的长为43. 【解析】【分析】(1)由题意得出21441,43,124b c b ⎧-⨯++=⎪⎪⎨-=⎪⎛⎫⨯-⎪ ⎪⎝⎭⎩,解得1,3,b c =⎧⎨=⎩,得出抛物线的函数表达式为:y =﹣14x 2+x +3=﹣14(x ﹣2)2+4,即可得出顶点B 的坐标为(2,4); (2)(i )求出C (0,3),设点E 的坐标为(m ,3),求出直线BE 的函数表达式为:y =12m --x +462m m --,则点M 的坐标为(4m ﹣6,0),由题意得出OC =3,AC =4,OM =4m ﹣6,CE =m ,则S 矩形ACOD =12,S 梯形ECOM =15182m -,分两种情况求出m 的值即可; (ii )过点F 作FN ⊥AC 于N ,则NF ∥CG ,设点F 的坐标为:(a ,﹣14a 2+a +3),则NF =3﹣(﹣14a2+a+3)=14a2﹣a,NC=﹣a,证△EFN≌△DGO(ASA),得出NE=OD=AC=4,则AE=NC=﹣a,证△ENF∽△DAE,得出NF NEAE AD=,求出a=﹣43或0,当a=0时,点E与点A重合,舍去,得出AE=NC=﹣a=43,即可得出结论.【详解】(1)∵抛物线y=﹣14x2+bx+c经过点A(4,3),对称轴是直线x=2,∴21441, 43,124b cb⎧-⨯++=⎪⎪⎨-=⎪⎛⎫⨯-⎪ ⎪⎝⎭⎩解得1,3, bc=⎧⎨=⎩∴抛物线的函数表达式为:y=﹣14x2+x+3,∵y=﹣14x2+x+3=﹣14(x﹣2)2+4,∴顶点B的坐标为(2,4);(2)(i)∵y=﹣14x2+x+3,∴x=0时,y=3,则C点的坐标为(0,3),∵A(4,3),∴AC∥OD,∵AD⊥x,∴四边形ACOD是矩形,设点E的坐标为(m,3),直线BE的函数表达式为:y=kx+n,直线BE交x轴于点M,如图1所示:则24,3, k nmk n+=⎧⎨+=⎩解得:1,246,2kmmnm-⎧=⎪⎪-⎨-⎪=⎪-⎩,∴直线BE的函数表达式为:y=12m--x+462mm--,令:y=12m--x+462mm--=0,则x=4m﹣6,∴点M的坐标为(4m﹣6,0),∵直线BE将四边形ACOD分成面积比为1:3的两部分,∴点M在线段OD上,点M不与点O重合,∵C(0,3),A(4,3),M(4m﹣6,0),E(m,3),∴OC=3,AC=4,OM=4m﹣6,CE=m,∴S矩形ACOD=OC•AC=3×4=12,S梯形ECOM=12(OM+EC)•OC=12(4m﹣6+m)×3=15182m-,分两种情况:①S ECOMS ACOD梯形矩形=14,即1518212m-=14,解得:m=85,∴点E的坐标为:(85,3);②S ECOMS ACOD梯形矩形=34,即1518212m-=34,解得:m=125,∴点E的坐标为:(125,3);综上所述,点E的坐标为:(85,3)或(125,3);(ii)存在点G落在y轴上的同时点F恰好落在抛物线上;理由如下:由题意得:满足条件的矩形DEFG在直线AC的下方,过点F作FN⊥AC于N,则NF∥CG,如图2所示:设点F的坐标为:(a,﹣14a2+a+3),则NF=3﹣(﹣14a2+a+3)=14a2﹣a,NC=﹣a,∵四边形DEFG与四边形ACOD都是矩形,∴∠DAE=∠DEF=∠N=90°,EF=DG,EF∥DG,AC∥OD,∴∠NEF=∠ODG,∠EMC=∠DGO,∵NF∥CG,∴∠EMC=∠EFN,∴∠EFN=∠DGO,在△EFN和△DGO中,∠NEF=∠ODG,EF=DG,∠EFN=∠DGO,∴△EFN≌△DGO(ASA),∴NE=OD=AC=4,∴AC﹣CE=NE﹣CE,即AE=NC=﹣a,∵∠DAE=∠DEF=∠N=90°,∴∠NEF+∠EFN=90°,∠NEF+∠DEA=90°,∴∠EFN=∠DEA,∴△ENF∽△DAE,∴NE NFAD AE=,即43=214a aa--,整理得:34a2+a=0,解得:a=﹣43或0,当a=0时,点E与点A重合,∴a=0舍去,∴AE=NC=﹣a=43,∴当点G落在y轴上的同时点F恰好落在抛物线上,此时AE的长为43.【点睛】本题是二次函数综合题目,考查了二次函数解析式的求法、二次函数的性质、一次函数解析式的求法、坐标与图形性质、矩形的判定与性质、全等三角形的判定与性质、相似三角形的判定与性质、梯形面积公式等知识;本题综合性强,属于中考压轴题型.7.(1)223y x x=+-;(2)是,定值为8;(3)1557,416⎛⎫-⎪⎝⎭或939,416⎛⎫--⎪⎝⎭【解析】【分析】(1)把点A 、C 坐标代入抛物线解析式即可求得b 、c 的值.(2)设点Q 横坐标为t ,用t 表示直线AQ 、BN 的解析式,把x =1-分别代入即求得点M 、N 的纵坐标,再求DM 、DN 的长,即得到DM +DN 为定值.(3)点P 可以在x 轴上方或下方,需分类讨论.①若点P 在x 轴下方,延长AP 到H ,使AH =AB 构造等腰△ABH ,作BH 中点G ,即有∠PAB =2∠BAG =2∠ACO ,利用∠ACO 的三角函数值,求BG 、BH 的长,进而求得H 的坐标,求得直线AH 的解析式后与抛物线解析式联立,即求出点P 坐标.②若点P 在x 轴上方,根据对称性,AP 一定经过点H 关于x 轴的对称点H ',求得直线AH '的解析式后与抛物线解析式联立,即求出点P 坐标.【详解】解:(1)∵抛物线y =x 2+bx +c 经过点A (1,0),C (0,-3),∴10003b c c ++=⎧⎨++=-⎩解得:23b c =⎧⎨=-⎩, ∴抛物线的函数表达式为y =x 2+2x -3.(2)结论:DM +DN 为定值.理由:∵抛物线y =x 2+2x -3的对称轴为:直线x =-1,∴D (﹣1,0),x M =x N =﹣1,设Q (t ,t 2+2t ﹣3)(﹣3<t <1),设直线AQ 解析式为y =dx +e∴2023d e dt e t t +=⎧⎨+=+-⎩解得:33d t e t =+⎧⎨=--⎩, ∴直线AQ :y =(t +3)x ﹣t ﹣3,当x =﹣1时,y M =﹣t ﹣3﹣t ﹣3=﹣2t ﹣6,∴DM =0﹣(﹣2t ﹣6)=2t +6,设直线BQ 解析式为y =mx +n ,∴23023m n mt n t t -+=⎧⎨+=+-⎩解得:133m t n t =-⎧⎨=-⎩, ∴直线BQ :y =(t ﹣1)x +3t ﹣3,当x =﹣1时,y N =﹣t +1+3t ﹣3=2t ﹣2,∴DN =0﹣(2t ﹣2)=﹣2t +2,∴DM +DN =2t +6+(﹣2t +2)=8,为定值.(3)①若点P 在x 轴下方,如图1,延长AP 到H ,使AH =AB ,过点B 作BI ⊥x 轴,连接BH ,作BH 中点G ,连接并延长AG 交BI 于点F ,过点H 作HI ⊥BI 于点I .∵当x2+2x﹣3=0,解得:x1=﹣3,x2=1,∴B(﹣3,0),∵A(1,0),C(0,﹣3),∴OA=1,OC=3,AC221310+=AB=4,∴Rt△AOC中,sin∠ACO=01010AAC=,cos∠ACO=31010OCAC=,∵AB=AH,G为BH中点,∴AG⊥BH,BG=GH,∴∠BAG=∠HAG,即∠PAB=2∠BAG,∵∠PAB=2∠ACO,∴∠BAG=∠ACO,∴Rt△ABG中,∠AGB=90°,sin∠BAG=10 BGAB=,∴BG=1010 105AB=,∴BH=2BG=105,∵∠HBI+∠ABG=∠ABG+∠BAG=90°,∴∠HBI=∠BAG=∠ACO,∴Rt△BHI中,∠BIH=90°,sin∠HBI=HIBH10,cos∠HBI=310BIBH=,∴HI 10BH=43,BI310BH=125,∴x H=411355-+=-,y H=125-,即1112,55H⎛⎫--⎪⎝⎭,设直线AH解析式为y=kx+a,∴0 1112 55 k ak a+=⎧⎪⎨-+=-⎪⎩,解得:3434ka⎧=⎪⎪⎨⎪=-⎪⎩,∴直线AH:3344y x=-,∵2334423y xy x x⎧=-⎪⎨⎪=+-⎩解得:1xy=⎧⎨=⎩(即点A)或943916xy⎧=-⎪⎪⎨⎪=-⎪⎩,∴939,416P⎛⎫--⎪⎝⎭.②若点P在x轴上方,如图2,在AP上截取AH'=AH,则H'与H关于x轴对称.∴1112,55H⎛'⎫-⎪⎝⎭,设直线AH'解析式为y k x a='+',∴111255k ak a+='''⎧-'⎪⎨+=⎪⎩,解得:3434ka⎧=-⎪⎪⎨''⎪=⎪⎩,∴直线AH':3344y x=-+,∵2334423y xy x x⎧=-+⎪⎨⎪=+-⎩解得:1xy=⎧⎨=⎩(即点A)或1545716xy⎧=-⎪⎪⎨⎪=⎪⎩,∴1557,416P⎛⎫-⎪⎝⎭.综上所述,点P的坐标为939,416⎛⎫--⎪⎝⎭或1557,416⎛⎫-⎪⎝⎭.【点睛】本题属于二次函数综合题,考查了求二次函数解析式、求一次函数解析式,解一元二次方程、二元一次方程组,等腰三角形的性质,三角函数的应用.运用到分类讨论的数学思想,理清线段之间的关系为解题关键.8.(1)211242y x x =--;(2)①P (2,−2)或(-6,10),②1122y x =-或324y x t =-+-或4412424t t y x t t --=+-++ 【解析】【分析】(1)利用一次函数与坐标轴交点的特征可求出点B ,C 的坐标,根据点B ,C 的坐标,利用待定系数法可求出二次函数解析式;(2)①由PM ⊥x 轴可得出∠PMC≠90°,分∠MPC=90°及∠PCM=90°两种情况考虑: (i )当∠MPC=90°时,PC //x 轴,利用二次函数可求出点P 的坐标;(ii )当∠PCM=90°时,设PC 与x 轴交于点D ,易证△BOC ∽△COD ,利用相似三角形的性质可求出点D 的坐标,根据点C ,D 的坐标,利用待定系数法可求出直线PC 的解析式,联立直线PC 和抛物线的解析式,通过解方程组可求出点P 的坐标; ②在ACM 中,如果存在直线使A 、C 、M 到该直线距离相等,则该直线应为ACM 的中位线,分开求解三条中位线方程即可求解.【详解】解:(1)因为直线交抛物线于B 、C 两点,∴当x =0时,y =12x −2=−2, ∴点C 的坐标为(0,−2);当y =0时,12x −2=0, 解得:x =4,∴点B 的坐标为(4,0).将B 、C 的坐标分别代入抛物线,得:2144022a c c ⎧⨯-⨯+=⎪⎨⎪=-⎩,解得:142a c ⎧=⎪⎨⎪=-⎩, ∴抛物线的解析式为211242y x x =--. (2)①∵PM ⊥x 轴,M 在直线BC 上,∴∠PMC 为固定角且不等于90,∴可分两种情况考虑,如图1所示:(i )当∠MPC=90时,PC //x 轴,∴点P 的纵坐标为﹣2,将y p =-2,代入抛物线方程可得:2112242x x --=-解得: x 1=2,x 2=0(为C 点坐标,故舍去),∴点P 的坐标为(2,−2);(ii )当∠PCM=90°时,设PC 与x 轴交于点D ,∵∠OBC+∠OCB=90°,∠OCB+∠OCD=90°,∴∠OBC=∠OCD ,又∵∠BOC=∠COD=90°,∴BOC ∽COD (AAA ), ∴OD OC OC OB =,即OD=2OC OB, 由(1)知,OC=2,OB=4,∴OD=1,又∵D 点在X 的负半轴∴点D 的坐标为(-1,0),设直线PC 的解析式为:y =kx +b (k ≠0,k 、b 是常数),将C(0,−2),D(-1,0)代入直线PC 的解析式,得:20b k b =-⎧⎨-+=⎩,解得:22k b =-⎧⎨=-⎩, ∴直线PC 的解析式为y =-2x −2,联立直线PC 和抛物线方程,得:22122142x x x -=---, 解得:x 1=0,y 1=−2,x 2=-6,y 2=10,点P 的坐标为(-6,10),综上所述:当PCM 是直角三角形时,点P 的坐标为(2,−2)或(-6,10);②如图2所示,在ACM 中,如果存在直线使A 、C 、M 到该直线距离相等,则该直线应为ACM 的中位线;(a )当以CM 为底时,过A 点做CM 的平行线AN ,直线AN 平行于CM 且过点A ,则斜率为12,AN 的方程为:1(+2)2y x =,则中位线方程式为:1122y x =-; (b )当以AM 为底时,因为M 为P 点做x 轴垂线与CB 的交点,则M 的横坐标为t ,且在直线BC 上,则M 的坐标为:1,22M t t -(),其中4t >,则AM 的方程为:44+242t t y x t t --=++,过C 点做AM 的平行线CQ ,则CQ 的方程为:4224t y x t -=-+ ,则中位线方程式为:4412424t t y x t t --=+-++; (c )当以AC 为底时,AC 的方程式为:2y x =--,由b 可知M 的坐标为:1,22M t t -(),过M 做AC 的平行线MR ,则MR 的方程为:322y x t =-+-,则中位线方程式为:324y x t =-+-; 综上所述:当点P 在点B 右侧时,存在直线l ,使点,,A C M 到该直线的距离相等,直线解析式为:1122y x =-或324y x t =-+-或4412424t t y x t t --=+-++. 【点睛】本题考查了一次函数坐标轴的交点坐标、待定系数法求二次函数解析式、相似三角形的判定与性质以及平行线的性质等,解题的关键是掌握三角形的顶点到中位线的距离相等.9.(1)243y x x =-+-;(2)点P 坐标为(-1,-8),(5,-8);(3)①G 的坐标.3551+-,3551(---5515(+--,5515--+;②5134t +=或5134t -= 【解析】【分析】(1)将A 、B 两点坐标代入抛物线解析式,可确定抛物线解析式;(2)根据A 、B 两点坐标得AB=3-1=2,由三角形面积公式求P 点纵坐标的绝对值,得出P 点纵坐标的两个值,代入抛物线解析式求P 点横坐标;(3)①根据题意,可分为两种情况进行分析:当点G 在对称轴右侧;当点G 在对称轴左侧;结合图像,分别求出点G 的坐标即可;②根据题意,可分为两种情况进行分析:当点G 在对称轴左侧;当点G 在对称轴右侧;结合图像,分别列出方程,求出t 的值即可.【详解】解:(1)把点(1,0)A ,(3,0)B 代入抛物线2y x bx c =-++上,求得:4b =,3c =-,∴243y x x =-+-;(2)依题意,得312AB =-=,设P 点坐标为(,)a n ,当0n >时,则8n =,故2–438x x +-=,即24110x x ++=,∴441111644280∆=-⨯⨯=-=-<2(-), 方程24110x x -++=无实数根;当0n <时,则8n =-故2438x x -+-=-,即2450x x -+-=,解得:11x =-,25x =所求点P 坐标为(-1,-8),(5,-8).(3)①分两种情况当点G 在对称轴右侧,设点G D 的横坐标为m ,则点D 到对称轴的距离为2m -,∵点D 到x 轴和到对称轴的距离相等所以点D 的纵坐标为2m -或2m -﹐当点D 的坐标为(,2)m m -,有2243m m m -=-+-,解得:1352m =,2352m =(不符题意舍去),此时点D 的坐标为:3551(,)22+-. 当点D 的坐标为(,2)m m -时,有 2243m m m -=-+-,解得:1552m +=,2552m -=(不符题意舍去), 此时点D 的坐标为:5515(,)22+--. 当点G 在对称轴左侧,设点D 的横坐标为m ,则点D 到对称轴的距离为2m -﹐因为点D 到x 轴和到对称轴的距离相等所以点D 的纵坐标为2m -或2m -,分别代入解析式可求出点D 的坐标分别为:3551(,)---,5515(,)--+. 综上所述点D 的坐标为:3551(,)+-﹐5515(,)+--,3551(,)---,5515(,)--+. ②分两种情况当点G 在对称轴左侧,此时有1EN t =-,2NF t =﹐因为//EN GF ,点E 为CG 的中点,所以222GF EN t ==-,所以点G 的坐标为(42,2)t t --,将(42,2)t t --代入243y x x =-+-中,得2(42)4(42)3t t t -=--+-2-,解得:1513t +=,2513t -=(不合题意舍去). 当点G 在对称轴右侧,此时有1EN t =-,2NF t =,因为//EN GF ,点E 为CG 的中点,所以222GF EN t ==-,所以点G 的坐标为(42,2)t t --,将(42,2)t t --代入243y x x =-+-中,得 2(42)4(42)3t t t -=--+-2-,解得:15134t +=(不合题意舍去),25134t -=. 综上所述:5134t +=或5134t -=. 【点睛】本题考查了待定系数法求抛物线解析式,三角形面积公式的运用.关键是熟练掌握求二次函数解析式的方法,掌握三角形的高与P 点纵坐标的关系,注意运用数形结合和分类讨论的思想进行解题.10.(1)45,45;(2)k =33±3)y 33﹣2 【解析】【分析】(1)如图3,连接AC ,则∠ABC=45°;设M 是x 轴的动点,当点M 运动到点O 时,∠AOB=45°,该视角最大,即可求解;(2)如图4,以点M 为圆心,长度1为半径作圆M ,当圆与直线y=kx 相切时,直线y=kx (k≠0)关于线段EF 的视角为90°,即∠EQF=90°,则MQ ⊥直线OE ,OQ=1,OM=2,故直线的倾斜角为30°,即可求解;(3)直线PQ 的倾斜角为45°,分别作点Q 、P 作x 轴、y 轴的平行线交于点R ,RQ=RP=1,以点R 为圆心以长度1为半径作圆R ,由(1)知,设直线与圆交于点Q′,由(1)知,当PQ′Q 为等腰三角形时,视角为45°,则QQ=2RQ=2,故点Q′3,1),【详解】(1)如图3,连接AC,则∠ABC=45°;设M是x轴的动点,当点M运动到点O时,∠AOB=45°,该视角最大,由此可见:当△ABC为等腰三角形时,视角最大;故答案为:45,45;(2)如图4,以点M为圆心,长度1为半径作圆M,当圆与直线y=kx相切时,直线y=kx(k≠0)关于线段EF的视角为90°,即∠EQF=90°,则MQ⊥直线OE,MQ=1,OM=2,故直线的倾斜角为30°,故k=3±;(3)直线PQ的倾斜角为45°,分别作点Q、P作x轴、y轴的平行线交于点R,RQ=RP=1,以点R为圆心以长度1为半径作圆R,由(1)知,设直线与圆交于点Q′,由(1)知,当PQ′Q为等腰三角形时,视角为45°,则QQ=2RQ=2,故点Q′31,1),直线y=ax+b(a>0)与x轴的夹角为60°,则直线的表达式为:y3,将点Q′的坐标代入上式并解得:直线的表达式为:y332【点睛】本题考查的是一次函数综合运用,涉及到解直角三角形、圆的基本知识等,此类新定义题目,通常按照题设的顺序求解,一般比较容易.11.(1)35,5784y x=+;(21722r≤.【分析】(1)①由矩形的任何一条边均与某条坐标轴平行,且A,B,C三点都在矩形的内部或边界上,则称该矩形为点A,B,C的覆盖矩形.点A,B,C的所有覆盖矩形中,面积最小的矩形称为点A,B,C的最优覆盖矩形,得出最优覆盖矩形的长为:2+5=7,宽为3+2=5,即可得出结果;②由定义可知,t=-3或6,即点C坐标为(-3,-2)或(6,-2),设AC表达式为y=kx+b,代入即可求出结果;(2)OD所在的直线交双曲线于点E,矩形OFEG是点O,D,E的一个面积最小的最优覆盖矩形,OD所在的直线表达式为y=x,得出点E的坐标为(2,2),⊙P的半径最小r=2,当点E的纵坐标为1时,⊙P的半径最大r=172,即可得出结果.【详解】(1)①∵A(﹣2,3),B(5,0),C(2,﹣2),矩形的任何一条边均与某条坐标轴平行,且A,B,C三点都在矩形的内部或边界上,则称该矩形为点A,B,C的覆盖矩形.点A,B,C的所有覆盖矩形中,面积最小的矩形称为点A,B,C的最优覆盖矩形,∴最优覆盖矩形的长为:2+5=7,宽为3+2=5,∴最优覆盖矩形的面积为:7×5=35;②∵点A,B,C的最优覆盖矩形的面积为40,∴由定义可知,t=﹣3或6,即点C坐标为(﹣3,﹣2)或(6,﹣2),设AC表达式为y=kx+b,∴3223k bk b=-+⎧⎨-=-+⎩或3226k bk b=-+⎧⎨-=+⎩∴513kb=⎧⎨=⎩或5874kb⎧=-⎪⎪⎨⎪=⎪⎩∴y=5x+13或5784y x=-+;(2)①OD所在的直线交双曲线于点E,矩形OFEG是点O,D,E的一个面积最小的最优覆盖矩形,如图1所示:∵点D(1,1),∴OD 所在的直线表达式为y =x ,∴点E 的坐标为(2,2),∴OE =222+2=22,∴⊙P 的半径最小r =2,②当DE ∥x 轴时,即:点E 的纵坐标为1,如图2所示:∵点D (1,1).E (m ,n )是函数y =4x (x >0)的图象上一点 ∴1=4x ,解得x =4, ∴OE ═224+117, ∴⊙P 的半径最大r =172, 172r ≤. 【点睛】 本题是圆的综合题目,考查了矩形的性质、勾股定理、待定系数法求直线的解析式、坐标与图形性质、反比例函数等知识;本题综合性强,有一定难度.12.(1)t =3;(2)P (35t +2,45t ﹣4);(3)t 的值为209秒或4秒或16秒或1609秒 【解析】【分析】(1)如图1,过点C 作CP ⊥OA ,交x 轴于点P .就可以求出OP 的值,由勾股定理就可以求出的OP 值,进而求出结论;(2)t <10时,P 在OA 或AB 上运动,所以分两种情况:①当0≤t≤5时,如图1,点P 在OA 上,OP=t ,可得P 的坐标;②当5<t <10时,如图2,点P 在AB 上,构建直角三角形,根据三角函数定义可得P 的坐标;(3)设切点为G ,连接PG ,分⊙P 与四边相切,其中P 在AB 和BC 时,与各边都不相切,所以分两种情况:①当P 在OA 上时,根据三角函数列式可得t 的值;②当P 在OC 上时,同理可得结论.【详解】(1)如图1,当CP ⊥OA 时,sin ∠AO 45CP C OC==, 4455CP CP 即=,=, 在Rt △OPC 中,OC =5,PC =4,则OP =3, ∴331t ==(2)当0≤t ≤5时,如图1,点P 在OA 上, ∴P (t ,0);当5<t <10时,如图2,点P 在AB 上, 过P 作PH ⊥x 轴,垂足为H ,则∠AOC =∠PAH ,∴sin ∠PAH =sin ∠AO 45C =, 44 4555PH PH t t ∴=-即=﹣, ∴333255HA t OH OA AH t ++=﹣,==,∴34P t+2t 455(,﹣);(3)设切点为G ,连接PG ,分两种情况:①当P 在OA 上时,如图3,⊙P与直线AB相切,∵OC∥AB,∴∠AOC=∠OAG,∴sin∠AOC=sin∠OA45PGGAP==,t45-t5 =,∴209t=;⊙P与BC相切时,如图4,则PG=t=OP=4;②当点P在OC上时,⊙P与AB相切时,如图5,∴OP=PG=4,∴4×5﹣t=4,t=16,⊙P与直线BC相切时,如图6,∴PG⊥BC,∵BC∥AO,∴∠AOC=∠GCP,∴sin∠AOC=sin∠GC45PGPPC==,∵OP=PG=20﹣t,∴42051tt-=-,∴1609t=,综上所述,t的值2016041699为秒或秒或秒或秒【点睛】本题考查了菱形的性质、直角三角形的性质、勾股定理、锐角三角函数等知识,解答时运用等角的三角函数列方程是关键,并注意运用分类讨论的思想,做到不重不漏.。
初三九年级数学上册数学压轴题综合测试卷(word含答案)

初三九年级数学上册数学压轴题综合测试卷(word含答案)一、压轴题1.已知P是⊙O上一点,过点P作不过圆心的弦PQ,在劣弧PQ和优弧PQ上分别有动点A、B(不与P,Q重合),连接AP、BP. 若∠APQ=∠BPQ.(1)如图1,当∠APQ=45°,AP=1,BP=22时,求⊙O的半径;(2)如图2,选接AB,交PQ于点M,点N在线段PM上(不与P、M重合),连接ON、OP,若∠NOP+2∠OPN=90°,探究直线AB与ON的位置关系,并证明.2.如图1,△ABC中,AB=AC=4,∠BAC=100,D是BC的中点.小明对图1进行了如下探究:在线段AD上任取一点E,连接EB.将线段EB绕点E逆时针旋转80°,点B的对应点是点F,连接BF,小明发现:随着点E在线段AD上位置的变化,点F的位置也在变化,点F可能在直线AD的左侧,也可能在直线AD上,还可能在直线AD的右侧.请你帮助小明继续探究,并解答下列问题:(1)如图2,当点F在直线AD上时,连接CF,猜想直线CF与直线AB的位置关系,并说明理由.(2)若点F落在直线AD的右侧,请在备用图中画出相应的图形,此时(1)中的结论是否仍然成立,为什么?(3)当点E在线段AD上运动时,直接写出AF的最小值.3.如图,矩形OABC的顶点A、C分别在x轴、y轴的正半轴上,点B的坐标为(3,4),一次函数23y x b=-+的图像与边OC、AB分别交于点D、E,并且满足OD BE=,M是线段DE上的一个动点(1)求b的值;(2)连接OM,若ODM△的面积与四边形OAEM的面积之比为1:3,求点M的坐标;(3)设N是x轴上方平面内的一点,以O、D、M、N为顶点的四边形是菱形,求点N的坐标.4.在平面直角坐标系xOy中,对于任意三点A,B,C,给出如下定义:若矩形的任何一条边均与某条坐标轴平行,且A,B,C三点都在矩形的内部或边界上,则称该矩形为点A,B,C的外延矩形.点A,B,C的所有外延矩形中,面积最小的矩形称为点A,B,C的最佳外延矩形.例如,图中的矩形,,都是点A,B,C的外延矩形,矩形是点A,B,C的最佳外延矩形.(1)如图1,已知A(-2,0),B(4,3),C(0,).①若,则点A,B,C的最佳外延矩形的面积为;②若点A,B,C的最佳外延矩形的面积为24,则的值为;(2)如图2,已知点M(6,0),N(0,8).P(,)是抛物线上一点,求点M,N,P的最佳外延矩形面积的最小值,以及此时点P的横坐标的取值范围;(3)如图3,已知点D(1,1).E(,)是函数的图象上一点,矩形OFEG是点O,D,E的一个面积最小的最佳外延矩形,⊙H是矩形OFEG的外接圆,请直接写出⊙H的半径r的取值范围.5.如图1,有一块直角三角板,其中AB 16=,ACB 90∠=,CAB 30∠=,A 、B 在x 轴上,点A 的坐标为()20,0,圆M 的半径为33,圆心M 的坐标为()5,33-,圆M 以每秒1个单位长度的速度沿x 轴向右做平移运动,运动时间为t 秒;()1求点C 的坐标;()2当点M 在ABC ∠的内部且M 与直线BC 相切时,求t 的值;()3如图2,点E 、F 分别是BC 、AC 的中点,连接EM 、FM ,在运动过程中,是否存在某一时刻,使EMF 90∠=?若存在,直接写出t 的值,若不存在,请说明理由.6.翻转类的计算问题在全国各地的中考试卷中出现的频率很大,因此初三(5)班聪慧的小菲同学结合2011年苏州市数学中考卷的倒数第二题对这类问题进行了专门的研究。
初三九年级上册数学压轴题达标检测卷(Word版 含解析)

初三九年级上册数学压轴题达标检测卷(Word 版 含解析)一、压轴题1.如图,在平面直角坐标系中,直线1l :162y x =-+分别与x 轴、y 轴交于点B 、C ,且与直线2l :12y x =交于点A .(1)分别求出点A 、B 、C 的坐标;(2)若D 是线段OA 上的点,且COD △的面积为12,求直线CD 的函数表达式; (3)在(2)的条件下,设P 是射线CD 上的点,在平面内里否存在点Q ,使以O 、C 、P 、Q 为顶点的四边形是菱形?若存在,直接写出点Q 的坐标;若不存在,请说明理由.2.如图,在四边形ABCD 中,9054ABC BCD AB BC cm CD cm ∠=∠=︒===,,点P 从点C 出发以1/cm s 的速度沿CB 向点B 匀速移动,点M 从点A 出发以15/cm s 的速度沿AB 向点B 匀速移动,点N 从点D 出发以/acm s 的速度沿DC 向点C 匀速移动.点P M N 、、同时出发,当其中一个点到达终点时,其他两个点也随之停止运动,设移动时间为ts . (1)如图①,①当a 为何值时,点P B M 、、为顶点的三角形与PCN △全等?并求出相应的t 的值; ②连接AP BD 、交于点E ,当AP BD ⊥时,求出t 的值; (2)如图②,连接AN MD 、交于点F .当3883a t ==,时,证明:ADF CDF S S ∆∆=.3.如图, AB 是⊙O 的直径,点D 、E 在⊙O 上,连接AE 、ED 、DA ,连接BD 并延长至点C ,使得DAC AED ∠=∠.(1)求证: AC是⊙O的切线;(2)若点E是BC的中点, AE与BC交于点F,=;①求证: CA CF②若⊙O的半径为3,BF=2,求AC的长.4.如图,在▱ABCD中,AB=4,BC=8,∠ABC=60°.点P是边BC上一动点,作△PAB的外接圆⊙O交BD于E.(1)如图1,当PB=3时,求PA的长以及⊙O的半径;(2)如图2,当∠APB=2∠PBE时,求证:AE平分∠PAD;(3)当AE与△ABD的某一条边垂直时,求所有满足条件的⊙O的半径.5.如图,B是O的半径OA上的一点(不与端点重合),过点B作OA的垂线交O于点C,D,连接OD,E是O上一点,CE CA=,过点C作O的切线l,连接OE并延长交直线l于点F.(1)①依题意补全图形.②求证:∠OFC=∠ODC.(2)连接FB,若B是OA的中点,O的半径是4,求FB的长.6.平面直角坐标系xOy 中,矩形OABC 的顶点A ,C 的坐标分别为(2,0),(0,3),点D 是经过点B ,C 的抛物线2y x bx c =-++的顶点. (1)求抛物线的解析式;(2)点E 是(1)中抛物线对称轴上一动点,求当△EAB 的周长最小时点E 的坐标; (3)平移抛物线,使抛物线的顶点始终在直线CD 上移动,若平移后的抛物线与射线..BD 只有一个公共点,直接写出平移后抛物线顶点的横坐标m 的值或取值范围.7.如图 1,抛物线21:4C y ax ax c =-+交x 轴正半轴于点()1,0,A B ,交y 轴正半轴于C ,且OB OC =.(1)求抛物线1C 的解析式;(2)在图2中,将抛物线1C 向右平移n 个单位后得到抛物线2C ,抛物线2C 与抛物线1C 在第一象限内交于一点P ,若CAP ∆的内心在CAB △内部,求n 的取值范围(3)在图3中,M 为抛物线1C 在第一象限内的一点,若MCB ∠为锐角,且3tan MCB ∠>,直接写出点M 横坐标M x 的取值范围___________8.如图,抛物线2()20y ax x c a =++<与x 轴交于点A 和点B (点A 在原点的左侧,点B在原点的右侧),与y 轴交于点C ,3OB OC ==. (1)求该抛物线的函数解析式.(2)如图1,连接BC ,点D 是直线BC 上方抛物线上的点,连接OD ,CD .OD 交BC 于点F ,当32COFCDFSS=::时,求点D 的坐标.(3)如图2,点E 的坐标为(03)2-,,点P 是抛物线上的点,连接EB PB PE ,,形成的PBE △中,是否存在点P ,使PBE ∠或PEB ∠等于2OBE ∠?若存在,请直接写出符合条件的点P 的坐标;若不存在,请说明理由.9.已知点(4,0)、(2,3)-为二次函数图像抛物线上两点,且抛物线的对称轴为直线2x =.(1)求抛物线的解析式;(2)将抛物线平移,使顶点与原点重合,已知点(,1)M m -,点A 、B 为抛物线上不重合的两点(B 在A 的左侧),且直线MA 与抛物线仅有一个公共点.①如图1,当点M 在y 轴上时,过点A 、B 分别作AP y ⊥轴于点P ,BQ x ⊥轴于点Q .若APM △与BQO △ 相似, 求直线AB 的解析式;②如图2,当直线MB 与抛物线也只有一个公共点时,记A 、B 两点的横坐标分别为a 、b .当点M 在y 轴上时,直接写出m am b--的值为 ;当点M 不在y 轴上时,求证:m am b--为一个定值,并求出这个值.10.如图,在平面直角坐标系中,直线l分别交x轴、y轴于点A,B,∠BAO = 30°.抛物线y = ax2 + bx + 1(a < 0)经过点A,B,过抛物线上一点C(点C在直线l上方)作CD∥BO交直线l于点D,四边形OBCD是菱形.动点M在x轴上从点E( -3,0)向终点A匀速运动,同时,动点N在直线l上从某一点G向终点D匀速运动,它们同时到达终点.(1)求点D的坐标和抛物线的函数表达式.(2)当点M运动到点O时,点N恰好与点B重合.①过点E作x轴的垂线交直线l于点F,当点N在线段FD上时,设EM = m,FN = n,求n 关于m的函数表达式.②求△NEM面积S关于m的函数表达式以及S的最大值.11.如图,抛物线y=﹣(x+1)(x﹣3)与x轴分别交于点A、B(点A在B的右侧),与y轴交于点C,⊙P是△ABC的外接圆.(1)直接写出点A、B、C的坐标及抛物线的对称轴;(2)求⊙P的半径;(3)点D在抛物线的对称轴上,且∠BDC>90°,求点D纵坐标的取值范围;(4)E是线段CO上的一个动点,将线段AE绕点A逆时针旋转45°得线段AF,求线段OF的最小值.12.如图,在⊙O中,弦AB、CD相交于点E,AC=BD,点D在AB上,连接CO,并延长CO交线段AB于点F,连接OA、OB,且OA5tan∠OBA=12.(1)求证:∠OBA=∠OCD;(2)当△AOF是直角三角形时,求EF的长;(3)是否存在点F,使得S△CEF=4S△BOF,若存在,请求EF的长,若不存在,请说明理由.【参考答案】***试卷处理标记,请不要删除一、压轴题1.(1)A(6,3),B(12,0),C(0,6);(2)y=-x+6;(3)满足条件的Q点坐标为:(-3,3)或22)或(6,6).【解析】【分析】(1)根据坐标轴上点的坐标特点,可求出B,C两点坐标.两个函数解析式联立形成二元一次方程组,可以确定A点坐标.(2)根据坐标特点和已知条件,采用待定系数法,即可作答.(3)在(2)的条件下,设P是射线CD上的点,在平面内存在点Q,使以O、C、P、2为顶点的四边形是菱形,如图所示,分三种情况考虑:①当四边形OP1Q1C为菱形时,由∠COP1=90°,得到四边形OP1Q1C为正方形;②当四边形OP2CQ2为菱形时;③当四边形OQ3P3C为菱形时;分别求出Q坐标即可.【详解】解:(1)由题意得16212y xy x⎧=-+⎪⎪⎨⎪=⎪⎩解得63xy=⎧⎨=⎩∴A(6,3)在y=-162x+中,当y=0时,x=12,∴B(12,0)当x=0时,y=6,∴C(0,6).(2)∵点D在线段OA上,∴设D(x,12x) (0≤x≤6)∵S△COD=12∴12×6x=12x=4∴D(4,2),设直线CD的表达式为y=kx+b,把(10,6)与D(4,2)代入得624bk b=⎧⎨=+⎩解得16 kb=-⎧⎨=⎩直线CD的表达式为y=-x+6(3) 存在点2,使以O、C、P、Q为顶点的四边形是菱形,如图所示,分三种情况考虑:①当四边形OP1Q1C为菱形时OC==OP1,由∠COP1=90°,得到四边形OP1Q1C为正方形,此时Q1P1=OP1=OC=6,即Q:(6,6);②当四边形OP2CQ2为菱形时,OP2=CP2,由C坐标为(0,6),得到Q2纵坐标为3,把y=3代入直线OQ2解析式y=-x中,得:x=-3,此时Q2(-3,3);③当四边形0Q3P3C为菱形时,OC=CP3,则有OQ3=OC=CP3=P3Q3=6,设坐标为(x,-x+6),∵OC=CP3∴x2+x2= CP32= OC2=62解得,2P的坐标为2,2)此时Q322).综上,点Q的坐标是(-3,3)或2,2)或(6,6).【点睛】本题是一次函数、勾股定理、特殊的平行四边形的综合应用,是一道压轴题,在考试中第一问必须作答,二三问可以根据自己的情况进行取舍.2.(1)① 2.5t =, 1.1a =或2t =,0.5a =;②1t =;(2)见解析 【解析】 【分析】(1)①当PBM PCN ≅△△时或当MBP PCN ≅△△时,分别列出方程即可解决问题; ②当AP BD ⊥时,由ABP BCD ≅△△,推出BP CD =,列出方程即可解决问题; (2)如图②中,连接AC 交MD 于O 只要证明AOM COD ≅△△,推出OA OC =,可得ADO CDO S S ∆∆=,AFO CFO S S ∆∆=,推出ADO AFO CDO CFO S S S S ∆∆∆∆-=-,即ADF CDF S S ∆∆=;【详解】解:(1)①90ABC BCD ∠=∠=︒,∴当PBM PCN ≅△△时,有BM NC =,即5t t -=①5 1.54t at -=-②由①②可得 1.1a =, 2.5t =.当MBP PCN ≅△△时,有BM PC =,BP NC =,即5 1.5t t -=③ 54t at -=-④,由③④可得0.5a =,2t =.综上所述,当 1.1a =, 2.5t =或0.5a =,2t =时,以P 、B 、M 为顶点的三角形与PCN △全等; ②AP BD ⊥, 90BEP ∴∠=︒,90APB CBD ∴∠+∠=︒,90ABC ∠=︒,90APB BAP ∴∠+∠=︒, BAP CBD ∴∠=∠,在ABP △和BCD 中,BAP CBD AB BCABC BCD ∠=∠⎧⎪=⎨⎪∠=∠⎩, ()ABP BCD ASA ∴≅△△,BP CD ∴=, 即54t -=, 1t ∴=;(2)当38a =,83t =时,1DN at ==,而4CD =,DN CD ∴<,∴点N 在点C 、D 之间, 1.54AM t ==,4CD =, AM CD ∴=,如图②中,连接AC 交MD 于O ,90ABC BCD∠=∠=︒,180ABC BCD∴∠+∠=︒,//AB BC∴,AMD CDM∴∠=∠,BAC DCA∠=∠,在AOM和COD△中,AMD CDMAM CDBAC DCA∠=∠⎧⎪=⎨⎪∠=∠⎩,()AOM COD ASA∴≅△△,OA OC∴=,ADO CDOS S∆∆∴=,AFO CFOS S∆∆=,ADO AFO CDO CFOS S S S∆∆∆∆∴-=-,ADF CDFS S∆∆∴=.【点睛】本题考查三角形综合题、全等三角形的判定和性质、等高模型等知识,解题的关键是灵活运用所学知识解决问题,学会用分类讨论的思想思考问题,属于中考压轴题.3.(1)详见解析;(2)①详见解析;②8【解析】【分析】(1)先得到90ADB∠=︒,利用圆周角定理得到DBA DAC∠=∠,即可证明AC是切线;(2)①利用等弧所对的圆周角相等,得到BAE DAE∠=∠,然后得到CFA CAF∠=∠,即可得到结论成立;②设AC CF x==,利用勾股定理,即可求出AC的长度.【详解】(1)证明:∵AB是⊙O的直径,∴90ADB∠=︒,∴90DBA DAB∠+∠=︒,∵DEA DBA∠=∠,DAC DEA∠=∠,∴DBA DAC∠=∠,∴90DAC DAB ∠+∠=︒, ∴90CAB ∠=︒, ∴AC 是⊙O 的切线; (2)① ∵点E 是弧BD 的中点, ∴BAE DAE ∠=∠,∵CFA DBA BAE ∠=∠+∠,CAF CAD DAE ∠=∠+∠, ∴CFA CAF ∠=∠ ∴CA CF =; ② 设CA CF x ==, 在Rt ABC ∆中,2BC x =+,CA x =,6AB =, 由勾股定理可得222(2)6x x +=+,解得:8x =, ∴8AC =. 【点睛】本题考查了切线的判定,等角对等边,以及勾股定理,要证直线是圆的切线,已知此线过圆上某点,连接圆心与这点(即为半径),再证垂直即可.4.(1)PA O 的半径为3;(2)见解析;(3)⊙O 的半径为2或【解析】 【分析】(1)过点A 作BP 的垂线,作直径AM ,先在Rt △ABH 中求出BH ,AH 的长,再在Rt △AHP 中用勾股定理求出AP 的长,在Rt △AMP 中通过锐角三角函数求出直径AM 的长,即求出半径的值;(2)证∠APB =∠PAD =2∠PAE ,即可推出结论;(3)分三种情况:当AE ⊥BD 时,AB 是⊙O 的直径,可直接求出半径;当AE ⊥AD 时,连接OB ,OE ,延长AE 交BC 于F ,通过证△BFE ∽△DAE ,求出BE 的长,再证△OBE 是等边三角形,即得到半径的值;当AE ⊥AB 时,过点D 作BC 的垂线,通过证△BPE ∽△BND ,求出PE ,AE 的长,再利用勾股定理求出直径BE 的长,即可得到半径的值. 【详解】(1)如图1,过点A 作BP 的垂线,垂足为H ,作直径AM ,连接MP , 在Rt △ABH 中,∠ABH =60°, ∴∠BAH =30°, ∴BH =12AB =2,AH =AB •sin60°=∴HP =BP ﹣BH =1,∴在Rt △AHP 中,AP∵AB 是直径,∴∠APM =90°,在Rt △AMP 中,∠M =∠ABP =60°,∴AM =AP sin 60︒=3,∴⊙O ,即PA ⊙O (2)当∠APB =2∠PBE 时,∵∠PBE =∠PAE ,∴∠APB =2∠PAE ,在平行四边形ABCD 中,AD ∥BC ,∴∠APB =∠PAD ,∴∠PAD =2∠PAE ,∴∠PAE =∠DAE ,∴AE 平分∠PAD ;(3)①如图3﹣1,当AE ⊥BD 时,∠AEB =90°,∴AB 是⊙O 的直径,∴r =12AB =2; ②如图3﹣2,当AE ⊥AD 时,连接OB ,OE ,延长AE 交BC 于F ,∵AD ∥BC ,∴AF ⊥BC ,△BFE ∽△DAE , ∴BF AD =EF AE, 在Rt △ABF 中,∠ABF =60°, ∴AF =AB •sin60°=BF =12AB =2, ∴28,∴EF , 在Rt △BFE 中,BE5,∵∠BOE=2∠BAE=60°,OB=OE,∴△OBE是等边三角形,∴r;③当AE⊥AB时,∠BAE=90°,∴AE为⊙O的直径,∴∠BPE=90°,如图3﹣3,过点D作BC的垂线,交BC的延长线于点N,延开PE交AD于点Q,在Rt△DCN中,∠DCN=60°,DC=4,∴DN=DC•sin60°=CN=12CD=2,∴PQ=DN=设QE=x,则PE=x,在Rt△AEQ中,∠QAE=∠BAD﹣BAE=30°,∴AE=2QE=2x,∵PE∥DN,∴△BPE∽△BND,∴PEDN =BPBN,∴BP 10,∴BP=10x,在Rt△ABE与Rt△BPE中,AB2+AE2=BP2+PE2,∴16+4x2=(10x)2+(x)2,解得,x1=(舍),x2,∴AE=∴BE=∴r,∴⊙O的半径为2.【点睛】此题主要考查圆与几何综合,解题的关键是熟知圆的基本性质、勾股定理及相似三角形的判定与性质.5.(1)①补图见解析;②证明见解析;(2)FB=21【解析】【分析】(1)①根据题意,补全图形即可;②由CD⊥OA可得∠ODC+∠AOD=90°,根据垂径定理可得AD AC=,利用等量代换可得AD CE=,根据圆周角定理可得∠EOC=∠AOD,由切线性质可得OC⊥FC,可得∠OFC+∠FOC=90°,即可证明∠OFC=∠ODC;(2)连接BF,作BG⊥l于G,根据OB=12OA,可得∠OCB=30°,利用勾股定理可求出BC的长,根据垂径定理可得CD的长,由(1)可知∠OFC=∠ODC,可得FC=CD,由BG⊥l,OC⊥l可得OC//BG,根据平行线的性质可得∠CBG=30°,根据含30°角的直角三角形的性质可求出CG的长,利用勾股定理可求出BG的长,即可求出FG的长,利用勾股定理求出FB 的长即可.【详解】(1)①延长OE,交直线l于F,如图即为所求,②∵OA⊥CD,OA为⊙O半径,∴AD AC=,∵CE CA=,∴AD CE=,∴∠EOC=∠AOD,∵FC是⊙O的切线,∴OC⊥FC,∴∠OFC+∠FOC=90°,∴∠OFC=∠ODC.(2)连接BF,作BG⊥l于G,∵B是OA的中点,⊙O半径为4,∴OB=12OA=12OC=2,∵OA⊥CD,∴∠OCD=30°,22OC OB-2242-3∴CD=2BC=43由(1)可知∠OFC=∠ODC,∴FC=CD=3∵BG⊥l,OC⊥l,∴OC//BG,∴∠CBG=∠OCD=30°,∴CG=12BC=3,BG=22BC CG -=3, ∴FG=FC+CG=53,∴BF=22FG BG +=221.【点睛】本题考查切线的性质、垂径定理、含30°角的直角三角形的性质及勾股定理,圆的切线垂直于过切点的半径;垂直于弦的直径平分弦,并且平分弦所对的两条弧;30°角所对的直角边,等于斜边的一半;熟练掌握相关性质及定理是解题关键.6.(1)2y x 2x 3=-++;(2)3(1,)2;(3)14m <≤或78m =【解析】【分析】(1)根据题意可得出点B 的坐标,将点B 、C 的坐标分别代入二次函数解析式,求出b 、c 的值即可.(2)在对称轴上取一点E ,连接EC 、EB 、EA ,要使得EAB 的周长最小,即要使EB+EA 的值最小,即要使EA+EC 的值最小,当点C 、E 、A 三点共线时,EA+EC 最小,求出直线AC 的解析式,最后求出直线AC 与对称轴的交点坐标即可.(3)求出直线CD 以及射线BD 的解析式,即可得出平移后顶点的坐标,写出二次函数顶点式解析式,分类讨论,如图:①当抛物线经过点B 时,将点B 的坐标代入二次函数解析式,求出m 的值,写出m 的范围即可;②当抛物线与射线恰好只有一个公共点H 时,将抛物线解析式与射线解析式联立可得关于x 的一元二次方程,要使平移后的抛物线与射线BD 只有一个公共点,即要使一元二次方程有两个相等的实数根,即0∆=,列式求出m 的值即可.【详解】(1)矩形OABC , ∴OC=AB ,A(2,0),C(0,3),∴OA=2,OC=3,∴B(2,3),将点B ,C 的坐标分别代入二次函数解析式,4233b c c -++=⎧⎨=⎩, ∴23b c =⎧⎨=⎩, ∴抛物线解析式为:2y x 2x 3=-++.(2)如图,在对称轴上取一点E ,连接EC 、EB 、EA ,当点C 、E 、A 三点共线时,EA+EC 最小,即EAB 的周长最小,设直线解析式为:y =kx +b ,将点A 、C 的坐标代入可得:203k b b +=⎧⎨=⎩, 解得:323k b ⎧=-⎪⎨⎪=⎩,∴一次函数解析式为:3=32y x -+. 2y x 2x 3=-++=2(1)4x -+-,∴D(1,4),令x =1,y =332-+=32. ∴E(1,32).(3)设直线CD 解析式为:y =kx +b ,C(0,3),D(1,4),∴43k b b +=⎧⎨=⎩, 解得13k b =⎧⎨=⎩, ∴直线CD 解析式为:y =x +3,同理求出射线BD 的解析式为:y =-x +5(x ≤2),设平移后的顶点坐标为(m ,m +3),则抛物线解析式为:y =-(x -m )2+m +3,①如图,当抛物线经过点B 时,-(2-m )2+m +3=3,解得m =1或4,∴当1<m ≤4时, 平移后的抛物线与射线只有一个公共点;②如图,当抛物线与射线恰好只有一个公共点H 时,将抛物线解析式与射线解析式联立可得:-(x -m )2+m +3=-x +5,即x 2-(2m +1)x +m 2-m +2=0,要使平移后的抛物线与射线BD 只有一个公共点,即要使一元二次方程有两个相等的实数根,∴22[(21)]4(2)0m m m ∆=-+⨯-+=-,解得78m =. 综上所述,14m <≤或78m =时,平移后的抛物线与射线BD 只有一个公共点.【点睛】本题为二次函数、一次函数与几何、一元二次方程方程综合题,一般作为压轴题,主要考查了图形的轴对称、二次函数的平移、函数解析式的求解以及二次函数与一元二次方程的关系,本题关键在于:①将三角形的周长最小问题转化为两线段之和最小问题,利用轴对称的性质解题;②将二次函数与一次函数的交点个数问题转化为一元二次方程实数根的个数问题.7.(1)()221y x =--;(2)1023n <<;(3)552M x << 【解析】【分析】(1)由题意可得对称轴方程,有二次函数对称性,由A 点坐标可求B 点坐标,代入解析式可得;(2)根据函数图像平移可得新抛物线解析式,画出图像可得交点P ,由题意可得ACB BCP ∠>∠,过点C 作//l x 轴.作PD l ⊥,可得ACO PCD ∠=∠,设()2,43P t t t -+,由13tan ACD tan PCD ∠=∠=可得关于t 的方程,解得t, 再将P 代入2C 解析式中得n 的值,根据Q,P 在第一象限内得n 的取值范围;(3) 当MCB ∠为直角时,可求直线CB 的解析式为:y=-x+3,直线CM 的解析式为:y=x+3,运用直线与曲线联立,可求CM 与抛物线的交点M 横坐标为:x=5;当MCB ∠为锐角且3tan MCB ∠=时,过点M 作MN CB ⊥于N,则3MN CN=,设M 点坐标为()2,43t t t -+,直线CB 解析式为y=-x+3,可求直线MN 解析式为:253y x t t =+-+,将直线MN 与直线CB 解析式联立可得:N 221515,32222t t t t ⎛⎫-+-+ ⎪⎝⎭, 由两点间距离公式可得2MN = 2213222t t ⎛⎫- ⎪⎝⎭;2CN =2215222t t ⎛⎫- ⎪⎝⎭;由3MN CN =可得:52t =,进而可得满足已知条件的点M 横坐标M x 的取值范围. 【详解】解:()1对称轴为422a x a-=-= ()3,0B ∴()0,1C ∴代入()224321y x x x ∴=-+=-- ()()222:21C x n ---()2423x n x =-++CAP ∆的内心I 在CAB △内部,ACB BCP ∴∠>∠∴当ACB BCP ∠=∠时过C 作//l x 轴.作PD l ⊥,ACB BCP ∠=∠90,OCD ∠=45,DCB ∠=,ACO PCD ∴∠=∠13tan ACD tan PCD ∠=∠= 设()2,43P t t t -+ 13PD CD ∴= 3p y DP OC +==214333t t t ∴-++= 113t = 将P 代入2C 解析式中 103n ∴=又P 在第一象限内h AB ∴>2n ∴>1023n ∴<<(3) 552M x <<; 当MCB ∠为直角时,如下图所示:由(1)(2)可得:直线CB 的解析式为:y=-x+3,MCB ∠为直角,C(0,3),∴直线CM 的解析式为:y=x+3,则CM 与抛物线的交点坐标M 横坐标为:2343x x x +=-+,解得:x=5或0(舍去),所以,当MCB ∠为直角时,5M x =;当MCB ∠为锐角且3tan MCB ∠=时,如下图所示: 过点M 作MN CB ⊥于N,则3MN CN=,设M 点坐标为()2,43t t t -+, MN CB ⊥,直线CB 解析式为y=-x+3,∴MN 解析式可设:y=x+b,将P ()2,43t t t -+代入解析式可得:b=253t t -+,则直线MN 解析式为:253y x t t =+-+,将直线MN 与直线CB 解析式联立可得: N 点坐标为221515,32222t t t t ⎛⎫-+-+ ⎪⎝⎭, ∴2MN =2222215154332222t t t t t t t ⎛⎫⎛⎫+-+-+-+- ⎪ ⎪⎝⎭⎝⎭ = 2213222t t ⎛⎫- ⎪⎝⎭; 2CN = 222215152222t t t t ⎛⎫⎛⎫-+-+ ⎪ ⎪⎝⎭⎝⎭ =2215222t t ⎛⎫- ⎪⎝⎭; 由3MN CN=可得:2213221522t t t t --=3; 解得:52t =或0(舍去) ; ∴MCB ∠为锐角,且3tan MCB ∠>时,点M 的横坐标M x 的取值范围为:552M x <<. 【点睛】本题综合考查了二次函数的图像和性质,题目较难,熟练掌握二次函数的图像和性质,运用数形结合解决二次函数综合问题是解题的关键. 8.(1)2y x 2x 3=-++;(2)点D 的坐标为(14),或(2)3,;(3)点P 的坐标为:(14),或17()24-,或13209()24--,或(54178+-,. 【解析】【分析】(1)由3OB OC ==及图像可得B 、C 两点坐标,然后利用待定系数法直接进行求解即可;(2)由题意易得35COF COD S S =,进而得到点D 、F 横坐标之间的关系为53D F x x =,设F 点横坐标为3t ,则D 点横坐标为5t ,则有直线BC 的解析式为3y x =-+,然后可直接求解;(3)分∠PBE 或∠PEB 等于2∠OBE 两种情况分别进行求解即可.【详解】解:(1)3OB OC ==,则:()()3003B C ,,,, 把B C 、坐标代入抛物线方程,解得抛物线方程为:2y x 2x 3=-++①;(2)∵32COF CDF S S =△△::, ∴35COF COD S S =,即:53D F x x =, 设F 点横坐标为3t ,则D 点横坐标为5t , 点F 在直线BC 上,而BC 所在的直线表达式为:3y x =-+,则33(3)F t t -,, 则直线OF 所在的直线表达式为:3313t t y x x t t--==, 则点55(5)D t t -,, 把D 点坐标代入抛物线解析式,解得:15t =或2 5,则点D 的坐标为(14),或(2)3,; (3)①当2PBE OBE ∠=∠时,当BP 在x 轴上方时,如图2,设1BP 交y 轴于点E ', ∴12PBE OBE ∠=∠ , ∴E BO EBO ∠'=∠ ,又60E OB EBO BO BO ∠'=∠=︒=, ,∴()E BO EBO AAS '≌ ,∴32EO EO ==, ∴点3(20)E ',,直线1BP 过点BE '、,则其直线方程为:1322y x =-+②, 联立①②并解得:12x =- , 故点P 1的坐标为17()24-,;当BP 在x 轴下方时, 如图2,过点E 作//EF BE '交2BP 于点F ,则FEB EBE ∠=∠',∴222E BE OBE EBP OBE ∠'=∠∠=∠, ,∴FEB EBF ∠=∠ ,∴FE BF = ,直线EF 可以看成直线BE '平移而得,其k 值为12-,则其直线表达式为:1322y x =-- , 设点13()22F m m --,,过点F 作FH y ⊥轴交于点H ,作BK HF ⊥于点K , 则点13()202H m --,,13()232K m --,, ∵EF BF =,则22FE BF =, 即:()2222331313()()22222m m m m +-++=-++, 解得:52m =, 则点511()24F -,, 则直线BF 表达式为:113322y x =-…③, 联立①③并解得:132x =-或3(舍去3), 则点213209()24P --,; ②当2PEB OBE ∠=∠时,当EP 在BE 上方时,如图3,点E '为图2所求,设BE '交3EP 于点F ,∵2EBE OBE ∠'=∠,∴3EBE P EB ∠'=∠ ,∴FE BF = ,由①知,直线BE '的表达式为:1322y x =-+, 设点13()22F n n -+,,13()232K n -+,, 由FE BF =,同理可得:12n =,故点15()24F ,,则直线EF 的表达式为:11322y x =-④, 联立①④并解得:1n =或92- (舍去负值), ∴34(1)P , ; 当EP 在BE 下方时,同理可得:54x ±=(舍去负值),故点4P . 故点P 的坐标为:(14),或17()24-,或13209()24--,或. 【点睛】 本题主要考查二次函数的综合,关键是熟练掌握二次函数的性质与一次函数的性质,利用数形结合及分类讨论思想进行求解.9.(1)214y x x =-;(2)①122y x =-+,②1,见解析,定值为1 【解析】【分析】(1)利用待定系数法把点(4,0)、(2,3)-代入解析式,再结合抛物线对称轴方程得到三元一次方程组,解方程组即可.(2)①先求出平移后的抛物线解析式,设出直线MA 的解析式1y kx =-,再联立抛物线解析式2114y kx y x =-⎧⎪⎨=⎪⎩,得到21104x kx -+=,令210k ∆=-=,求出k 的值,得出APM ∆为等腰直角三角形,运用APM ∆与BQO ∆相似得出90BQO APM ∠=∠=,故AB :y mx n =+,则2144m n m n +=⎧⎨-+=⎩即可求出AB 函数关系式. ②当M 在y 轴上时,m=0,再根据图像对称性可得A 、B 两点关于y 轴对称,得出a ,b 的关系,即可求出答案;当M 不在与轴上时,设MA :111y k x k m =--,联立抛物线解析式112114y k x k m y x =--⎧⎪⎨=⎪⎩,得出2114440x k x k m -++=,令212=16(1)0k k m ∆--=,同理设出MB ,令22216(1)0k k m ∆=--=,故1k ,2k 为方程210x mx --=不相等两个实数根,得出12k k m +=,即可求出答案.【详解】解:(1)设2y=ax +bx+c a (≠0),把点(4,0)、(2,3)-代入 ∵对称轴为x=2 ∴164042322a b c a b c b a ⎧⎪++=⎪-+=⎨⎪⎪-=⎩解得1410a b c ⎧=⎪⎪=-⎨⎪=⎪⎩∴抛物线解析式214y x x =-. (2)①(0,1)M -,平移后抛物线214y x =设MA :1y kx =- 则联立2114y kx y x =-⎧⎪⎨=⎪⎩,21104x kx -+= 210k ∆=-=1k ∴=±又由图,A 在y 轴右侧故1k =,(2,1)A2AP PM ∴==,APM ∆为等腰直角三角形又APM ∆与BQO ∆相似∴△BQO 为等腰直角三角形,设B (﹣x ,x ),带入抛物线解析式得:214x x = 解得x=4或x=0(舍去)∴B (﹣4,4)设AB :y mx n =+,把(2,1)A ,B (﹣4,4)带入得: 则2144m n m n +=⎧⎨-+=⎩,122m n ⎧=-⎪⎨⎪=⎩ ∴AB 解析式为:122y x =-+.②(i )∵214y x =关于y 轴对称,M 在y 轴上,且MA ,MB 与抛物线只有一个交点 ∴A 、B 两点关于y 轴对称,∴a=﹣b ∴m a m b --=0+b 0b-=1, 故答案是:1;(ii )设MA :111y k x k m =--, 则联立112114y k x k m y x =--⎧⎪⎨=⎪⎩, 2114440x k x k m -++=,此方程仅一个根, 故11422k a k ==, 且212=16(1)0k k m ∆--=,同理设MB :221y k x k m =--,亦有22b k =,22216(1)0k k m ∆=--=,故1k ,2k 为方程210x mx --=不相等两个实数根,12k k m +=, ()111122122m k m k m a m b m m k k m---∴===----, 即m a m b--为一定值1, ∴当点M 不在y 轴上时,m a m b --为一个定值1. 【点睛】本题考查的是二次函数综合题型,二次函数待定系数法求函数解析式,二次函数与一元二次方程的综合应用,二次函数与相似三角形的综合应用,解题关键在于理解题意,正确分析题目,运用数形结合思想进行解题.10.(1)点D 的坐标为(2,12),抛物线的解析式为24 ?1?3y x =-+;(2)①13n m =+;②23124S m m =-+,S的最大值为16 【解析】【分析】 (1)由抛物线的解析式为y = ax 2 + bx + 1,得到OB=1,根据菱形的性质结合含30度的直角三角形的性质点A 、D 、C 的坐标,再利用待定系数法即可求解;(2)①在Rt △FEA 中,FB=12FA=2,FD=FB+BD=3,根据题意设此一次函数解析式为:n km b =+,求得3m =时,2n FB ==,23m =时,3n FD ==,代入n km b =+,即可求解;②求得NA 33m =-,过N 作NQ ⊥EA ,得到NQ=12NA=332m -,利用面积公式得到S 关于m 的函数表达式,再利用二次函数的性质即可求解.【详解】(1)∵抛物线的解析式为y = ax 2 + bx + 1,∴OB=1,∵∠BAO=30︒,∠BOA=90︒,∴AB=2OB=2,OA=2222AB OB 213-=-=,∠ABO=60︒,∴点A 的坐标为(3,0),又∵四边形OBCD 是菱形,且∠ABO=60︒,∴OD=CD=OB=1,∴△DOB 为等边三角形,∴∠BOD=60︒,∠DOA=30︒,BD=BO=OD=DA=1,延长CD 交OA 于H ,则CH ⊥OA ,∴DH=12OD=12,3CH=CD+DH=32, ∴点D 的坐标为312),点C 的坐标为332), 将A 30) , C 的坐标为332)代入抛物线的解析式y = ax 2 + bx + 1,得:31033142a a ⎧+=⎪⎨+=⎪⎩,解得:43a b ⎧=-⎪⎨⎪=⎩,∴抛物线的解析式为24 ?1?3y x =-+; (2)①在Rt △FEA 中,∠FAE=30︒,FA=2AB=4,∴FB=12FA=2,FD=FB+BD=3, ∵动点M 、N 同时作匀速直线运动,∴n 关于m 成一次函数,故设此一次函数解析式为:n km b =+,当点M 运动到点O 时,点N 恰好与点B 重合,∴m =2n FB ==,当点M 运动到点A 时,点N 恰好与点D 重合,∴m =3n FD ==,代入n km b =+,得:23b b⎧=+⎪⎨=+⎪⎩,解得:1k b ⎧=⎪⎨⎪=⎩∴此一次函数解析式为:13n m =+; ②NA=FA-FN=4- 3n =, 过N 作NQ ⊥EA ,则NQ=12NA=326m -,∴2133224S m m ⎛⎫==+ ⎪ ⎪⎝⎭,∵0<,当32m==⎝⎭时,在0m≤≤范围内,∴132226216S⎛⎫=⨯-⨯=⎪⎪⎝⎭最大.【点睛】本题主要考查了二次函数的综合应用,涉及待定系数法、菱形的性质、等边三角形的判定和性质、二次函数的性质、函数图象的交点等.本题涉及知识点较多,综合性较强,难度较大.11.(1)点B的坐标为(﹣1,0),点A的坐标为(3,0),点C的坐标为(0,3);抛物线的对称轴为直线x=1;(2)⊙P;(3)1<y<2;(4)3.【解析】【分析】(1)分别代入y=0、x=0求出与之对应的x、y的值,进而可得出点A、B、C的坐标,再由二次函数的对称性可找出抛物线的对称轴;(2)连接CP、BP,在Rt△BOC中利用勾股定理可求出BC的长,由等腰直角三角形的性质及圆周角定理可得出∠BPC=90°,再利用等腰直角三角形的性质可求出BP的值即可;(3)设点D的坐标为(1,y),当∠BDC=90°时,利用勾股定理可求出y值,进而可得出:当1<y<2时,∠BDC>90°;(4)将△ACO绕点A逆时针方向旋转45°,点C落在点C′处,点O落在点O′处,根据旋转的性质可找出点C′的坐标及∠AC′O′=45°,进而可找出线段C′O′所在直线的解析式,由点E在CO上可得出点F在C′O′上,过点O作OF⊥C′O′于点F,则△OC′F 为等腰直角三角形,此时线段OF取最小值,利用等腰直角三角形的性质即可求出此时OF 的长即可.【详解】(1)当y=0时,﹣(x+1)(x﹣3)=0,解得:x1=﹣1,x2=3,∴点B的坐标为(﹣1,0),点A的坐标为(3,0);当x=0时,y=﹣(0+1)×(0﹣3)=3,∴点C的坐标为(0,3);∵抛物线与x轴交于点(﹣1,0)、(3,0),∴抛物线的对称轴为直线x=1;(2)连接CP、BP,如图1所示,在Rt△BOC中,BC=∵∠AOC=90°,OA=OC=3,∴∠OAC=∠OCA=45°,∴∠BPC=2∠OAC=90°,∴CP=BP=2BC=5,∴⊙P的半径为5;(3)设点D的坐标为(1,y),当∠BDC=90°时,BD2+CD2=BC2,∴[(﹣1﹣1)2+(0﹣y)2]+[(0﹣1)2+(3﹣y)2]=10,整理,得:y2﹣3y+2=0,解得:y1=1,y2=2,∴当1<y<2时,∠BDC>90°;(4)将△ACO绕点A逆时针方向旋转45°,点C落在点C′处,点O落在点O′处,如图2所示.∵AC=2232OA OC+=,∠ACO=45°,∴点C′的坐标为(3﹣32,0),∠AC′O′=45°,∴线段C′O′所在直线的解析式为y=﹣x+3﹣32,∵点E在线段CO上,∴点F在线段C′O′上.过点O作OF⊥C′O′于点F,则△OC′F为等腰直角三角形,此时线段OF取最小值,∵△OC′F为等腰直角三角形,∴OF=22OC′=22(32﹣3)=3﹣322.【点睛】本题考查了二次函数图象上点的坐标特征、二次函数的性质、圆周角定理、勾股定理、旋转以及等腰直角三角形,解题的关键是:(1)利用二次函数图象上点的坐标特征求出点A、B、C的坐标;(2)利用圆周角定理找出∠BPC=90°;(3)利用极限值法求出点D纵坐标;(4)利用点到直线之间垂直线段最短确定点F的位置.12.(1)见解析;(2)EF=32或512;(3)存在【解析】【分析】(1)先判断出∠ECB=∠EBC,再判断出∠OCB=∠OBC,即可得出结论;(2)先求出EF,再分两种情况,利用锐角三角函数和相似三角形的性质即可得出结论;(3)先利用面积关系得出53CO FO =,进而利用△OAF ∽△EFC 得出比例式,即可得出结论.【详解】 解:(1)如图1,连接BC ,∵AC BD = ,∴∠ECB =∠EBC ,∵OB =OC ,∴∠OCB =∠OBC ,∴∠OCD =∠ECF =∠ECB ﹣∠OCB =∠EBC ﹣∠OBC =∠OBA ;(2)∵OA =OB ,∴∠OAF =∠OBA ,∴∠OAF =∠ECF ,①当∠AFO =90°时,∵OA tan ∠OBA =12,∴OC =OA OF =1,AB =4,∴EF =CF •tan ∠ECF =CF•tan ∠OBA ②当∠AOF =90°时,∵OA =OB ,∴∠OAF =∠OBA ,∴tan ∠OAF =tan ∠OBA =12,∵OA∴OF =OA •tan ∠OAF , ∴AF =52, ∵∠OAF =∠OBA =∠ECF ,∠OFA =∠EFC ,∴△OFA ∽△EFC ,∴5EF CF OC OF OF AF AF +===,∴EF OF =32,即:EF =32; (3)存在,如图2,连接OE ,∵∠ECB=∠EBC,∴CE=EB,∵OE=OE,OB=OC,∴△OEC≌△OEB,∴S△OEC=S△OEB,∵S△CEF=4S△BOF,∴S△CEO+S△EOF=4(S△BOE﹣S△EOF),∴53CEOEFOSS∆∆=,∴53COFO=,∴FO=35CO=35,∵△OFA∽△EFC,∴53CE AD COEF FO FO===,∴BF=BE﹣EF=CE﹣EF=23EF,∴AF=AB﹣BF=4﹣23EF,∵△OAF∽△EFC,∴CF EFFA FO=,∴85523543EF=-,∴EF=3﹣35.【点睛】圆的综合题,主要考查了圆的性质,锐角三角函数,全等三角形的判定和性质,相似三角形的判定和性质,分类讨论的思想,判断出53CE AD CO EF FO FO ===是解本题的关键.。
最新初三九年级数学上册 压轴解答题综合测试卷(word含答案)

最新初三九年级数学上册 压轴解答题综合测试卷(word 含答案)一、压轴题1.如图,在平面直角坐标系中,直线1l :162y x =-+分别与x 轴、y 轴交于点B 、C ,且与直线2l :12y x =交于点A .(1)分别求出点A 、B 、C 的坐标;(2)若D 是线段OA 上的点,且COD △的面积为12,求直线CD 的函数表达式; (3)在(2)的条件下,设P 是射线CD 上的点,在平面内里否存在点Q ,使以O 、C 、P 、Q 为顶点的四边形是菱形?若存在,直接写出点Q 的坐标;若不存在,请说明理由.2.问题提出(1)如图①,在ABC 中,42,6,135AB AC BAC ==∠=,求ABC 的面积.问题探究(2)如图②,半圆O 的直径10AB =,C 是半圆AB 的中点,点D 在BC 上,且2CD BD =,点P 是AB 上的动点,试求PC PD +的最小值.问题解决(3)如图③,扇形AOB 的半径为20,45AOB ∠=在AB 选点P ,在边OA 上选点E ,在边OB 上选点F ,求PE EF FP ++的长度的最小值.3.如图,等边ABC 内接于O ,P 是AB 上任一点(点P 不与点A 、B 重合),连接AP 、BP ,过点C 作CM BP 交PA 的延长线于点M .(1)求APC ∠和BPC ∠的度数;(2)求证:ACM BCP △≌△;(3)若1PA =,2PB =,求四边形PBCM 的面积;(4)在(3)的条件下,求AB 的长度.4.数学概念若点P 在ABC ∆的内部,且APB ∠、BPC ∠和CPA ∠中有两个角相等,则称P 是ABC ∆的“等角点”,特别地,若这三个角都相等,则称P 是ABC ∆的“强等角点”. 理解概念(1)若点P 是ABC ∆的等角点,且100APB ∠=,则BPC ∠的度数是 .(2)已知点D 在ABC ∆的外部,且与点A 在BC 的异侧,并满足180BDC BAC ∠+∠<,作BCD ∆的外接圆O ,连接AD ,交圆O 于点P .当BCD ∆的边满足下面的条件时,求证:P 是ABC ∆的等角点.(要求:只选择其中一道题进行证明!)①如图①,DB DC =②如图②,BC BD =深入思考(3)如图③,在ABC ∆中,A ∠、B 、C ∠均小于120,用直尺和圆规作它的强等角点Q .(不写作法,保留作图痕迹)(4)下列关于“等角点”、“强等角点”的说法:①直角三角形的内心是它的等角点;②等腰三角形的内心和外心都是它的等角点;③正三角形的中心是它的强等角点;④若一个三角形存在强等角点,则该点到三角形三个顶点的距离相等;⑤若一个三角形存在强等角点,则该点是三角形内部到三个顶点距离之和最小的点,其中正确的有 .(填序号)5.如图,在矩形ABCD中,E、F分别是AB、AD的中点,连接AC、EC、EF、⊥.FC,且EC EF∽;(1)求证:AEF BCEAC=,求AB的长;(2)若23△的外接圆圆心之间的距离?(3)在(2)的条件下,求出ABC的外接圆圆心与CEF6.在长方形ABCD中,AB=5cm,BC=6cm,点P从点A开始沿边AB向终点B以cm s的速度移动,与此同时,点Q从点B开始沿边BC向终点C以2/cm s的速度移1/动.如果P、Q分别从A、B同时出发,当点Q运动到点C时,两点停止运动.设运动时间为t秒.(1)填空:______=______,______=______(用含t的代数式表示);(2)当t为何值时,PQ的长度等于5cm?26cm?若存在,请求出此时t的(3)是否存在t的值,使得五边形APQCD的面积等于2值;若不存在,请说明理由.7.如图,已知矩形ABCD中,BC=2cm,AB3cm,点E在边AB上,点F在边AD上,点E由A向B运动,连结EC、EF,在运动的过程中,始终保持EC⊥EF,△EFG为等边三角形.(1)求证△AEF∽△BCE;(2)设BE的长为xcm,AF的长为ycm,求y与x的函数关系式,并写出线段AF长的范围;(3)若点H是EG的中点,试说明A、E、H、F四点在同一个圆上,并求在点E由A到B 运动过程中,点H移动的距离.8.翻转类的计算问题在全国各地的中考试卷中出现的频率很大,因此初三(5)班聪慧的小菲同学结合2011年苏州市数学中考卷的倒数第二题对这类问题进行了专门的研究。
中考数学综合压轴题100题(含答案)
中考数学综合压轴题100题(含答案)一、中考压轴题1.如图1,在直角坐标系中,点A的坐标为(1,0),以OA为边在第四象限内作等边△AOB,点C为x轴的正半轴上一动点(OC>1),连接BC,以BC为边在第四象限内作等边△CBD,直线DA交y轴于点E.(1)试问△OBC与△ABD全等吗?并证明你的结论;(2)随着点C位置的变化,点E的位置是否会发生变化?若没有变化,求出点E的坐标;若有变化,请说明理由;(3)如图2,以OC为直径作圆,与直线DE分别交于点F、G,设AC=m,AF=n,用含n的代数式表示m.【分析】(1)由等边三角形的性质知,OBA=∠CBD=60°,易得∠OBC=∠ABD,又有OB=AB,BC=BD故有△OBC≌△ABD;(2)由1知,△OBC≌△ABD⇒∠BAD=∠BOC=60°,可得∠OAE=60°,在Rt△EOA 中,有EO=OA•tan60°=,即可求得点E的坐标;(3)由相交弦定理知1•m=n•AG,即AG=,由切割线定理知,OE2=EG•EF,在Rt△EOA中,由勾股定理知,AE==2,故建立方程:()2=(2﹣)(2+n),就可求得m与n关系.【解答】解:(1)两个三角形全等.∵△AOB、△CBD都是等边三角形,∴OBA=∠CBD=60°,∴∠OBA+∠ABC=∠CBD+∠ABC,即∠OBC=∠ABD;∵OB=AB,BC=BD,△OBC≌△ABD;(2)点E位置不变.∵△OBC≌△ABD,∴∠BAD=∠BOC=60°,∠OAE=180°﹣60°﹣60°=60°;在Rt△EOA中,EO=OA•tan60°=,或∠AEO=30°,得AE=2,∴OE=∴点E的坐标为(0,);(3)∵AC=m,AF=n,由相交弦定理知1•m=n•AG,即AG=;又∵OC是直径,∴OE是圆的切线,OE2=EG•EF,在Rt△EOA中,AE==2,()2=(2﹣)(2+n)即2n2+n﹣2m﹣mn=0解得m=.【点评】命题立意:考查圆的相交弦定理、切线定理、三角形全等等知识,并且将这些知识与坐标系联系在一起,考查综合分析、解决问题的能力.2.广安市某楼盘准备以每平方米6000元的均价对外销售,由于国务院有关房地产的新政策出台后,购房者持币观望,房地产开发商为了加快资金周转,对价格经过两次下调后,决定以每平方米4860元的均价开盘销售.(1)求平均每次下调的百分率.(2)某人准备以开盘价均价购买一套100平方米的住房,开发商给予以下两种优惠方案以供选择:①打9.8折销售;②不打折,一次性送装修费每平方米80元,试问哪种方案更优惠?【分析】(1)根据题意设平均每次下调的百分率为x,列出一元二次方程,解方程即可得出答案;(2)分别计算两种方案的优惠价格,比较后发现方案①更优惠.【解答】解:(1)设平均每次下调的百分率为x,则6000(1﹣x)2=4860,解得:x1=0.1=10%,x2=1.9(舍去),故平均每次下调的百分率为10%;(2)方案①购房优惠:4860×100×(1﹣0.98)=9720(元);方案②可优惠:80×100=8000(元).故选择方案①更优惠.【点评】本题主要考查一元二次方程的实际应用,解题关键是要读懂题目的意思,根据题目给出的条件,找出合适的等量关系,列出方程,再求解,属于中档题.3.如图,一次函数y=﹣x﹣2的图象分别交x轴、y轴于A、B两点,P为AB的中点,PC⊥x轴于点C,延长PC交反比例函数y=(x<0)的图象于点Q,且tan∠AOQ=.(1)求k的值;(2)连接OP、AQ,求证:四边形APOQ是菱形.【分析】(1)由一次函数解析式确定A点坐标,进而确定C,Q的坐标,将Q的坐标代入反比例函数关系式可求出k的值.(2)由(1)可分别确定QC=CP,AC=OC,且QP垂直平分AO,故可证明四边形APOQ是菱形.【解答】(1)解:∵y=﹣x﹣2令y=0,得x=﹣4,即A(﹣4,0)由P为AB的中点,PC⊥x轴可知C点坐标为(﹣2,0)又∵tan∠AOQ=可知QC=1∴Q点坐标为(﹣2,1)将Q点坐标代入反比例函数得:1=,∴可得k=﹣2;(2)证明:由(1)可知QC=PC=1,AC=CO=2,且A0⊥PQ∴四边形APOQ是菱形.【点评】本题考查了待定系数法求函数解析式,又结合了几何图形进行考查,属于综合性比较强的题目,有一定难度.4.如图,反比例函数的图象经过点A(4,b),过点A作AB⊥x轴于点B,△AOB的面积为2.(1)求k和b的值;(2)若一次函数y=ax﹣3的图象经过点A,求这个一次函数的解析式.【分析】(1)由△AOB的面积为2,根据反比例函数的比例系数k的几何意义,可知k的值,得出反比例函数的解析式,然后把x=4代入,即可求出b的值;(2)把点A的坐标代入y=ax﹣3,即可求出这个一次函数的解析式.【解答】解:(1)∵反比例函数的图象经过点A,AB⊥x轴于点B,△AOB的面积为2,A(4,b),∴OB×AB=2,×4×b=2,∴AB=b=1,∴A(4,1),∴k=xy=4,∴反比例函数的解析式为y=,即k=4,b=1.(2)∵A(4,1)在一次函数y=ax﹣3的图象上,∴1=4a﹣3,∴a=1.∴这个一次函数的解析式为y=x﹣3.【点评】本题主要考查了待定系数法求一次函数的解析式和反比例函数中k的几何意义.这里体现了数形结合的思想,做此类题一定要正确理解k的几何意义.5.如果将点P绕定点M旋转180°后与点Q重合,那么称点P与点Q关于点M对称,定点M叫做对称中心.此时,M是线段PQ的中点.如图,在直角坐标系中,△ABO的顶点A,B,O的坐标分别为(1,0),(0,1),(0,0).点列P1,P2,P3,…中的相邻两点都关于△ABO的一个顶点对称:点P1与点P2关于点A对称,点P2与点P3关于点B对称,点P3与点P4关于点O对称,点P4与点P5关于点A对称,点P5与点P6关于点B对称,点P6与点P7关于点O对称…对称中心分别是A,B,O,A,B,O,…,且这些对称中心依次循环.已知点P1的坐标是(1,1),试求出点P2,P7,P100的坐标.【分析】通过作图可知6个点一个循环,那么P7的坐标和P1的坐标相同,P100的坐标与P4的坐标一样,通过图中的点可很快求出.【解答】解:P2的坐标是(1,﹣1),P7的坐标是(1,1),P100的坐标是(1,﹣3).理由:作P1关于A点的对称点,即可得到P2(1,﹣1),分析题意,知6个点一个循环,故P7的坐标与P1的坐标一样,P100的坐标与P4的坐标一样,所以P7的坐标等同于P1的坐标为(1,1),P100的坐标等同于P4的坐标为(1,﹣3).【点评】解决本题的关键是读懂题意,画出图形,仔细观察,分析,得到相应的规律.6.如图,已知△BEC是等边三角形,∠AEB=∠DEC=90°,AE=DE,AC,BD的交点为O.(1)求证:△AEC≌△DEB;(2)若∠ABC=∠DCB=90°,AB=2 cm,求图中阴影部分的面积.【分析】(1)在△AEC和△DEB中,已知AE=DE,BE=CE,且夹角相等,根据边角边可证全等.(2)由图可知,在连接EO并延长EO交BC于点F,连接AD之后,整个图形是一个以EF所在直线对称的图形.即△AEO和△DEO面积相等,只要求出其中一个即可,而三角形AEO面积=•OE•FB,所以解题中心即为求出OE和FB,有(1)中结论和已知条件即可求解.【解答】(1)证明:∵∠AEB=∠DEC=90°,∴∠AEB+∠BEC=∠DEC+∠BEC,即∠AEC=∠DEB,∵△BEC是等边三角形,∴CE=BE,又AE=DE,∴△AEC≌△DEB.(2)解:连接EO并延长EO交BC于点F,连接AD.由(1)知AC=BD.∵∠ABC=∠DCB=90°,∴∠ABC+∠DCB=180°,∴AB∥DC,AB==CD,∴四边形ABCD为平行四边形且是矩形,∴OA=OB=OC=OD,又∵BE=CE,∴OE所在直线垂直平分线段BC,∴BF=FC,∠EFB=90°.∴OF=AB=×2=1,∵△BEC是等边三角形,∴∠EBC=60°.在Rt△AEB中,∠AEB=90°,∠ABE=∠ABC﹣∠EBC=90°﹣60°=30°,∴BE=AB•cos30°=,在Rt△BFE中,∠BFE=90°,∠EBF=60°,∴BF=BE•cos60°=,EF=BE•sin60°=,∴OE=EF﹣OF==,∵AE=ED,OE=OE,AO=DO,∴△AOE≌△DOE.∴S△AOE=S△DOE∴S阴影=2S△AOE=2וEO•BF=2×××=(cm2).【点评】考查综合应用等边三角形、等腰三角形、解直角三角形、直角三角形性质,进行逻辑推理能力和运算能力.7.如图,△ABC内接于⊙O,AB=6,AC=4,D是AB边上一点,P是优弧BAC的中点,连接P A、PB、PC、PD.(1)当BD的长度为多少时,△P AD是以AD为底边的等腰三角形?并证明;(2)在(1)的条件下,若cos∠PCB=,求P A的长.【分析】(1)根据等弧对等弦以及全等三角形的判定和性质进行求解;(2)过点P作PE⊥AD于E.根据锐角三角函数的知识和垂径定理进行求解.【解答】解:(1)当BD=AC=4时,△P AD是以AD为底边的等腰三角形.∵P是优弧BAC的中点,∴=.∴PB=PC.又∵∠PBD=∠PCA(圆周角定理),∴当BD=AC=4,△PBD≌△PCA.∴P A=PD,即△P AD是以AD为底边的等腰三角形.(2)过点P作PE⊥AD于E,由(1)可知,当BD=4时,PD=P A,AD=AB﹣BD=6﹣4=2,则AE=AD=1.∵∠PCB=∠P AD(在同圆或等圆中,同弧所对的圆周角相等),∴cos∠P AD=cos∠PCB=,∴P A=.【点评】综合运用了等弧对等弦的性质、全等三角形的判定和性质、锐角三角函数的知识以及垂径定理.8.经统计分析,某市跨河大桥上的车流速度v(千米/小时)是车流密度x(辆/千米)的函数,当桥上的车流密度达到220辆/千米时,造成堵塞,此时车流速度为0千米/小时;当车流密度不超过20辆/千米时,车流速度为80千米/小时,研究表明:当20≤x≤220时,车流速度v是车流密度x的一次函数.(1)求大桥上车流密度为100辆/千米时的车流速度;(2)在交通高峰时段,为使大桥上的车流速度大于40千米/小时且小于60千米/小时,应控制大桥上的车流密度在什么范围内?(3)车流量(辆/小时)是单位时间内通过桥上某观测点的车辆数,即:车流量=车流速度×车流密度.求大桥上车流量y的最大值.【分析】(1)当20≤x≤220时,设车流速度v与车流密度x的函数关系式为v=kx+b,根据题意的数量关系建立方程组求出其解即可;(2)由(1)的解析式建立不等式组求出其解即可;(3)设车流量y与x之间的关系式为y=vx,当x<20和20≤x≤220时分别表示出函数关系由函数的性质就可以求出结论.【解答】解:(1)设车流速度v与车流密度x的函数关系式为v=kx+b,由题意,得,解得:,∴当20≤x≤220时,v=﹣x+88,当x=100时,v=﹣×100+88=48(千米/小时);(2)由题意,得,解得:70<x<120.∴应控制大桥上的车流密度在70<x<120范围内;(3)设车流量y与x之间的关系式为y=vx,当0≤x≤20时y=80x,∴k=80>0,∴y随x的增大而增大,∴x=20时,y最大=1600;当20≤x≤220时y=(﹣x+88)x=﹣(x﹣110)2+4840,∴当x=110时,y最大=4840.∵4840>1600,∴当车流密度是110辆/千米,车流量y取得最大值是每小时4840辆.【点评】本题考查了车流量=车流速度×车流密度的运用,一次函数的解析式的运用,一元一次不等式组的运用,二次函数的性质的运用,解答时求出函数的解析式是关键.9.在△ABC中,AB=BC,将△ABC绕点A沿顺时针方向旋转得△A1B1C1,使点C1落在直线BC上(点C1与点C不重合),(1)如图,当∠C>60°时,写出边AB1与边CB的位置关系,并加以证明;(2)当∠C=60°时,写出边AB1与边CB的位置关系(不要求证明);(3)当∠C<60°时,请你在如图中用尺规作图法作出△AB1C1(保留作图痕迹,不写作法),再猜想你在(1)、(2)中得出的结论是否还成立并说明理由.【分析】(1)AB1∥BC.因为等腰三角形,两底角相等,再根据平行线的判定,内错角相等两直线平行,可证明两直线平行.(2)当∠C=60°时,写出边AB1与边CB的位置关系也是平行,证明方法同(1)题.(3)成立,根据旋转变换的性质画出图形.利用三角形全等即可证明.【解答】解:(1)AB1∥BC.证明:由已知得△ABC≌△AB1C1,∴∠BAC=∠B1AC1,∠B1AB=∠C1AC,∵AC1=AC,∴∠AC1C=∠ACC1,∵∠C1AC+∠AC1C+∠ACC1=180°,∴∠C1AC=180°﹣2∠ACC1,同理,在△ABC中,∵BA=BC,∴∠ABC=180°﹣2∠ACC1,∴∠ABC=∠C1AC=∠B1AB,∴AB1∥BC.(5分)(2)如图1,∠C=60°时,AB1∥BC.(7分)(3)如图,当∠C<60°时,(1)、(2)中的结论还成立.证明:显然△ABC≌△AB1C1,∴∠BAC=∠B1AC1,∴∠B1AB=∠C1AC,∵AC1=AC,∴∠AC1C=∠ACC1,∵∠C1AC+∠AC1C+∠ACC1=180°,∴∠C1AC=180°﹣2∠ACC1,同理,在△ABC中,∵BA=BC,∴∠ABC=180°﹣2∠ACC1,∴∠ABC=∠C1AC=∠B1AB,∴AB1∥BC.(13分)【点评】考查图形的旋转,等腰三角形的性质,平行线的判定.本题实质是考查对图形旋转特征的理解,旋转前后的图形是全等的.10.九年级(1)班课外活动小组利用标杆测量学校旗杆的高度,已知标杆高度CD=3m,标杆与旗杆的水平距离BD=15m,人的眼睛与地面的高度EF=1.6m,人与标杆CD的水平距离DF=2m,求旗杆AB的高度.【分析】利用三角形相似中的比例关系,首先由题目和图形可看出,求AB的长度分成了2个部分,AH和HB部分,其中HB=EF=1.6m,剩下的问题就是求AH的长度,利用△CGE∽△AHE,得出,把相关条件代入即可求得AH=11.9,所以AB=AH+HB=AH+EF=13.5m.【解答】解:∵CD⊥FB,AB⊥FB,∴CD∥AB∴△CGE∽△AHE∴即:∴∴AH=11.9∴AB=AH+HB=AH+EF=11.9+1.6=13.5(m).【点评】主要用到的解题思想是把梯形问题转化成三角形问题,利用三角形相似比列方程来求未知线段的长度.11.如图,⊙O是等边△ABC的外接圆,AB=2,M、N分别是边AB、AC的中点,直线MN交⊙O于E、F两点,BD∥AC交直线MN于点D.求出图中线段DM上已有的一条线段的长.【分析】连接OA交MN于点G,则OA⊥BC,由三角形的中位线的性质可得MN的长,易证得△BMD≌△AMN,有DM=MN,由相交弦定理得ME•MF=MA•MB,就可求得EM,DE的值.【解答】解:∵M,N分别是边AB,AC的中点∴MN∥BC,MN=BC=1又∵BD∥AC∴∠DBA=∠A=60°∵BM=AM,∠BMD=∠AMN∴△BMD≌△AMN∴DM=MN=1连接OA交MN于点G,则OA⊥BC∴OA⊥EF∴EG=FG,MG=FN由相交弦定理得:ME•MF=MA•MB∴EM(EM+1)=1解得EM=(EM=不合题意,舍去)∴DE=DM﹣EM=∴DE(3﹣DE)=1解得DE=(DE=不合题意,舍去).【点评】本题利用了三角形的中位线的性质,等边三角形的性质,全等三角形的判定和性质,一元二次方程的解法求解.12.如图,有一直径MN=4的半圆形纸片,其圆心为点P,从初始位置Ⅰ开始,在无滑动的情况下沿数轴向右翻滚至位置Ⅴ,其中,位置Ⅰ中的MN平行于数轴,且半⊙P与数轴相切于原点O;位置Ⅱ和位置Ⅳ中的MN垂直于数轴;位置Ⅲ中的MN在数轴上;位置Ⅴ中的点N到数轴的距离为3,且半⊙P与数轴相切于点A.解答下列问题:(1)位置Ⅰ中的MN与数轴之间的距离为2;位置Ⅱ中的半⊙P与数轴的位置关系是相切;(2)求位置Ⅲ中的圆心P在数轴上表示的数;(3)纸片半⊙P从位置Ⅲ翻滚到位置Ⅳ时,求点N所经过路径长及该纸片所扫过图形的面积;(4)求OA的长.[(2),(3),(4)中的结果保留π].【分析】(1)先求出圆的半径,再根据切线的性质进行解答;(2)根据位置Ⅰ中的长与数轴上线段ON相等求出的长,再根据弧长公式求出的长,进而可得出结论;(3)作NC垂直数轴于点C,作PH⊥NC于点H,连接P A,则四边形PHCA为矩形,在Rt△NPH中,根据sin∠NPH==即可∠NPH、∠MP A的度数,进而可得出的长,【解答】解:(1)∵⊙P的直径=4,∴⊙P的半径=2,∵⊙P与直线有一个交点,∴位置Ⅰ中的MN与数轴之间的距离为2;位置Ⅱ中的半⊙P与数轴的位置关系是相切;故答案为:2,相切;(2)位置Ⅰ中的长与数轴上线段ON相等,∵的长为=π,NP=2,∴位置Ⅲ中的圆心P在数轴上表示的数为π+2.(3)点N所经过路径长为=2π,S半圆==2π,S扇形==4π,半⊙P所扫过图形的面积为2π+4π=6π.(4)如图,作NC垂直数轴于点C,作PH⊥NC于点H,连接P A,则四边形PHCA为矩形.在Rt△NPH中,PN=2,NH=NC﹣HC=NC﹣P A=1,于是sin∠NPH==,∴∠NPH=30°.∴∠MP A=60°.从而的长为=,于是OA的长为π+4+π=π+4.【点评】本题考查的是直线与圆的关系、弧长的计算、扇形的面积公式,在解答此题时要注意Ⅰ中的长与数轴上线段ON相等的数量关系.13.(1)已知一元二次方程x2+px+q=0(p2﹣4q≥0)的两根为x1、x2;求证:x1+x2=﹣p,x1•x2=q.(2)已知抛物线y=x2+px+q与x轴交于A、B两点,且过点(﹣1,﹣1),设线段AB的长为d,当p为何值时,d2取得最小值,并求出最小值.【分析】(1)先根据求根公式得出x1、x2的值,再求出两根的和与积即可;(2)把点(﹣1,﹣1)代入抛物线的解析式,再由d=|x1﹣x2|可知d2=(x1﹣x2)2=(x1+x2)2﹣4 x1•x2=p2,再由(1)中x1+x2=﹣p,x1•x2=q即可得出结论.【解答】证明:(1)∵a=1,b=p,c=q∴△=p2﹣4q∴x=即x1=,x2=∴x1+x2=+=﹣p,x1•x2=•=q;(2)把(﹣1,﹣1)代入y=x2+px+q得1﹣p+q=﹣1,所以,q=p﹣2,设抛物线y=x2+px+q与x轴交于A、B的坐标分别为(x1,0)、(x2,0)∵d=|x1﹣x2|,∴d2=(x1﹣x2)2=(x1+x2)2﹣4x1•x2=p2﹣4q=p2﹣4p+8=(p﹣2)2+4当p=2时,d2的最小值是4.【点评】本题考查的是抛物线与x轴的交点及根与系数的关系,熟知x1,x2是方程x2+px+q =0的两根时,x1+x2=﹣p,x1x2=q是解答此题的关键.14.如图,在△ABC中,∠BAC=30°,以AB为直径的⊙O经过点C.过点C作⊙O的切线交AB的延长线于点P.点D为圆上一点,且=,弦AD的延长线交切线PC于点E,连接BC.(1)判断OB和BP的数量关系,并说明理由;(2)若⊙O的半径为2,求AE的长.【分析】(1)首先连接OC,由PC切⊙O于点C,可得∠OCP=90°,又由∠BAC=30°,即可求得∠COP=60°,∠P=30°,然后根据直角三角形中30°角所对的直角边等于斜边的一半,证得OB=BP;(2)由(1)可得OB=OP,即可求得AP的长,又由=,即可得∠CAD=∠BAC=30°,继而求得∠E=90°,继而在Rt△AEP中求得答案.【解答】解:(1)OB=BP.理由:连接OC,∵PC切⊙O于点C,∴∠OCP=90°,∵OA=OC,∠OAC=30°,∴∠OAC=∠OCA=30°,∴∠COP=60°,∴∠P=30°,在Rt△OCP中,OC=OP=OB=BP;(2)由(1)得OB=OP,∵⊙O的半径是2,∴AP=3OB=3×2=6,∵=,∴∠CAD=∠BAC=30°,∴∠BAD=60°,∵∠P=30°,∴∠E=90°,在Rt△AEP中,AE=AP=×6=3.【点评】此题考查了切线的性质、直角三角形的性质以及圆周角定理.此题难度适中,注意掌握数形结合思想的应用,注意掌握辅助线的作法.15.⊙O1与⊙O2相交于A、B两点,如图(1),连接O2O1并延长交⊙O1于P点,连接P A、PB并分别延长交⊙O2于C、D两点,连接CO2并延长交⊙O2于E点.已知⊙O2的半径为R,设∠CAD=α.(1)求CD的长(用含R、α的式子表示);(2)试判断CD与PO1的位置关系,并说明理由;(3)设点P’为⊙O1上(⊙O2外)的动点,连接P’A、P’B并分别延长交⊙O2于C’、D’,请你探究∠C’AD’是否等于α?C’D’与P’O1的位置关系如何?并说明理由.(注:图(2)与图(3)中⊙O1和⊙O2的大小及位置关系与图(1)完全相同,若你感到继续在图(1)中探究问题(3),图形太复杂,不便于观察,可以选择图(2)或图(3)中的一图说明理由).【分析】(1)作⊙O2的直径CE,连接DE.根据圆周角定理的推论,得∠E=∠CAD=α,再利用解直角三角形的知识求解;(2)连接AB,延长PO1与⊙O1相交于点E,连接AE.根据圆内接四边形的性质,得∠ABP′=∠C′,根据圆周角定理的推论,得∠ABP′=∠E,∠EAP′=90°,从而证明∠AP′E+∠C′=90°,则CD与PO1的位置关系是互相垂直;(3)根据同弧所对的圆周角相等,则说明∠C’AD’等于α;根据(2)中的证明过程,则可以证明C’D’与P’O1的位置关系是互相垂直.【解答】解:(1)连接DE.根据圆周角定理的推论,得∠E=∠CAD=α.∵CE是直径,∴∠CDE=90°.∴CD=CE•sin E=2R sinα;(2)CD与PO1的位置关系是互相垂直.理由如下:连接AB,延长PO1与⊙O1相交于点E,连接AE.∵四边形BAC′D′是圆内接四边形,∴∠ABP′=∠C′.∵P′E是直径,∴∠EAP′=90°,∴∠AP′E+∠E=90°.又∠ABP′=∠E,∴∠AP′E+∠C′=90°,即CD与PO1的位置关系是互相垂直;(3)根据同弧所对的圆周角相等,则说明∠C’AD’等于α;根据(2)中的证明过程,则可以证明C’D’与P’O1的位置关系是互相垂直.【点评】此题综合运用了圆周角定理及其推论、直角三角形的性质、圆内接四边形的性质.注意:连接两圆的公共弦、构造直径所对的圆周角都是圆中常见的辅助线.16.一个不透明的口袋里有红、黄、绿三种颜色的球(除颜色外其余都相同),其中红球有2个,黄球有1个,任意摸出一个黄球的概率为.(1)试求口袋里绿球的个数;(2)若第一次从口袋中任意摸出一球(不放回),第二次任意摸出一球,请你用树状图或列表法,求出两次都摸到红球的概率.【分析】(1)根据概率的求解方法,利用方程求得绿球个数;(2)此题需要两步完成,所以采用树状图法或者列表法都比较简单,解题时要注意是放回实验还是不放回实验,此题为不放回实验.【解答】解:(1)设口袋里绿球有x个,则,解得x=1.故口袋里绿球有1个.(2)红一红二黄绿红一红二,红一黄,红一绿,红一红二红一,红二黄,红一绿,红二黄红一,黄红二,黄绿,黄绿红一,绿红二,绿黄,绿故,P(两次都摸到红球)=.【点评】(1)解题时要注意应用方程思想;(2)列表法可以不重复不遗漏的列出所有可能的结果,适合于两步完成的事件.用到的知识点为:概率=所求情况数与总情况数之比.17.如图①,有四张编号为1、2、3、4的卡片,卡片的背面完全相同.现将它们搅匀并正面朝下放置在桌面上.(1)从中随机抽取一张,抽到的卡片是眼睛的概率是多少?(2)从四张卡片中随机抽取一张贴在如图②所示的大头娃娃的左眼处,然后再随机抽取一张贴在大头娃娃的右眼处,用树状图或列表法求贴法正确的概率.【分析】根据概率的求法,找准两点:①全部情况的总数;②符合条件的情况数目;二者的比值就是其发生的概率.【解答】解:(1)所求概率为;(2)方法①(树状图法)共有12种可能的结果:(1,2),(1,3),(1,4),(2,1),(2,3),(2,4),(3,1),(3,2),(3,4),(4,1),(4,2),(4,3)∵其中有两种结果(1,2),(2,1)是符合条件的,∴贴法正确的概率为,方法②(列表法)1 2 3 4第一次抽取第二次抽取1(2,1)(3,1)(4,1)2(1,2)(3,2)(4,2)3(1,3)(2,3)(4,3)4(1,4)(2,4)(3,4)共有12种可能的结果:(1,2),(1,3),(1,4),(2,1),(2,3),(2,4),(3,1),(3,2),(3,4),(4,1),(4,2),(4,3),∵其中有两种结果(1,2),(2,1)是符合条件的,∴贴法正确的概率为.【点评】此题考查概率的求法:如果一个事件有n种可能,而且这些事件的可能性相同,其中事件A出现m种结果,那么事件A的概率P(A)=.18.已知:y关于x的函数y=(k﹣1)x2﹣2kx+k+2的图象与x轴有交点.(1)求k的取值范围;(2)若x1,x2是函数图象与x轴两个交点的横坐标,且满足(k﹣1)x12+2kx2+k+2=4x1x2.①求k的值;②当k≤x≤k+2时,请结合函数图象确定y的最大值和最小值.【分析】(1)分两种情况讨论,当k=1时,可求出函数为一次函数,必与x轴有一交点;当k≠1时,函数为二次函数,若与x轴有交点,则△≥0.(2)①根据(k﹣1)x12+2kx2+k+2=4x1x2及根与系数的关系,建立关于k的方程,求出k 的值;②充分利用图象,直接得出y的最大值和最小值.【解答】解:(1)当k=1时,函数为一次函数y=﹣2x+3,其图象与x轴有一个交点.当k≠1时,函数为二次函数,其图象与x轴有一个或两个交点,令y=0得(k﹣1)x2﹣2kx+k+2=0.△=(﹣2k)2﹣4(k﹣1)(k+2)≥0,解得k≤2.即k≤2且k≠1.综上所述,k的取值范围是k≤2.(2)①∵x1≠x2,由(1)知k<2且k≠1,函数图象与x轴两个交点,∴k<2,且k≠1.由题意得(k﹣1)x12+(k+2)=2kx1①,将①代入(k﹣1)x12+2kx2+k+2=4x1x2中得:2k(x1+x2)=4x1x2.又∵x1+x2=,x1x2=,∴2k•=4•.解得:k1=﹣1,k2=2(不合题意,舍去).∴所求k值为﹣1.②如图,∵k1=﹣1,y=﹣2x2+2x+1=﹣2(x﹣)2+.且﹣1≤x≤1.由图象知:当x=﹣1时,y最小=﹣3;当x=时,y最大=.∴y的最大值为,最小值为﹣3.【点评】本题考查了抛物线与x轴的交点、一次函数的定义、二次函数的最值,充分利用图象是解题的关键.19.如图,菱形、矩形与正方形的形状有差异,我们将菱形、矩形与正方形的接近程度称为“接近度”.在研究“接近度”时,应保证相似图形的“接近度”相等.(1)设菱形相邻两个内角的度数分别为m°和n°,将菱形的“接近度”定义为|m﹣n|,于是|m﹣n|越小,菱形越接近于正方形.①若菱形的一个内角为70°,则该菱形的“接近度”等于40;②当菱形的“接近度”等于0时,菱形是正方形.(2)设矩形相邻两条边长分别是a和b(a≤b),将矩形的“接近度”定义为|a﹣b|,于是|a﹣b|越小,矩形越接近于正方形.你认为这种说法是否合理?若不合理,给出矩形的“接近度”一个合理定义.【分析】(1)根据相似图形的定义知,相似图形的形状相同,但大小不一定相同,相似图形的“接近度”相等.所以若菱形的一个内角为70°,则该菱形的“接近度”等于|m﹣n|;当菱形的“接近度”等于0时,菱形是正方形;(2)不合理,举例进行说明.【解答】解:(1)①∵内角为70°,∴与它相邻内角的度数为110°.∴菱形的“接近度”=|m﹣n|=|110﹣70|=40.②当菱形的“接近度”等于0时,菱形是正方形.(2)不合理.例如,对两个相似而不全等的矩形来说,它们接近正方形的程度是相同的,但|a﹣b|却不相等.合理定义方法不唯一.如定义为,越接近1,矩形越接近于正方形;越大,矩形与正方形的形状差异越大;当时,矩形就变成了正方形,即只有矩形的越接近1,矩形才越接近正方形.【点评】正确理解“接近度”的意思,矩形的“接近度”|a﹣b|越小,矩形越接近于正方形.这是解决问题的关键.20.如图,方格纸中的每个小方格都是边长为1个单位的正方形,在建立平面直角坐标系后,△ABC的顶点均在格点上,点B的坐标为(1,0)①画出△ABC关于x轴对称的△A1B1C1;②画出将△ABC绕原点O按逆时针旋转90°所得的△A2B2C2;③△A1B1C1与△A2B2C2成轴对称图形吗?若成轴对称图形,画出所有的对称轴;④△A1B1C1与△A2B2C2成中心对称图形吗?若成中心对称图形,写出所有的对称中心的坐标.【分析】(1)将三角形的各顶点,向x轴作垂线并延长相同长度得到三点的对应点,顺次连接;(2)将三角形的各顶点,绕原点O按逆时针旋转90°得到三点的对应点.顺次连接各对应点得△A2B2C2;(3)从图中可发现成轴对称图形,根据轴对称图形的性质画出对称轴即连接两对应点的线段,做它的垂直平分线;(4)成中心对称图形,画出两条对应点的连线,交点就是对称中心.【解答】解:如下图所示:(3)成轴对称图形,根据轴对称图形的性质画出对称轴即连接两对应点的线段,作它的垂直平分线,或连接A1C1,A2C2的中点的连线为对称轴.(4)成中心对称,对称中心为线段BB2的中点P,坐标是(,).【点评】本题综合考查了图形的变换,在图形的变换中,关键是找到图形的对应点.21.如图,矩形ABCD的边AD、AB分别与⊙O相切于点E、F,(1)求的长;(2)若,直线MN分别交射线DA、DC于点M、N,∠DMN=60°,将直线MN沿射线DA方向平移,设点D到直线的距离为d,当时1≤d≤4,请判断直线MN与⊙O的位置关系,并说明理由.【分析】(1)连接OE、OF,利用相切证明四边形AFOE是正方形,再根据弧长公式求弧长;(2)先求出直线M1N1与圆相切时d的值,结合1≤d≤4,划分d的范围,分类讨论.【解答】解:(1)连接OE、OF,∵矩形ABCD的边AD、AB分别与⊙O相切于点E、F,∴∠A=90°,∠OEA=∠OF A=90°∴四边形AFOE是正方形∴∠EOF=90°,OE=AE=∴的长==π.(2)如图,将直线MN沿射线DA方向平移,当其与⊙O相切时,记为M1N1,切点为R,交AD于M1,交BC于N1,连接OM1、OR,∵M1N1∥MN∴∠DM1N1=∠DMN=60°∴∠EM1N1=120°∵MA、M1N1切⊙O于点E、R∴∠EM1O=∠EM1N1=60°在Rt△EM1O中,EM1===1∴DM1=AD﹣AE﹣EM1=+5﹣﹣1=4.过点D作DK⊥M1N1于K在Rt△DM1K中DK=DM1×sin∠DM1K=4×sin∠60°=2即d=2,∴当d=2时,直线MN与⊙O相切,当1≤d<2时,直线MN与⊙O相离,当直线MN平移到过圆心O时,记为M2N2,点D到M2N2的距离d=DK+OR=2+=3>4,∴当2<d≤4时,MN直线与⊙O相交.【点评】本题考查的是直线与圆的位置关系,解决此类问题可通过比较圆心到直线距离d 与圆半径大小关系完成判定.22.如图,AD是⊙O的直径.(1)如图①,垂直于AD的两条弦B1C1,B2C2把圆周4等分,则∠B1的度数是22.5°,∠B2的度数是67.5°;(2)如图②,垂直于AD的三条弦B1C1,B2C2,B3C3把圆周6等分,分别求∠B1,∠B2,∠B3的度数;(3)如图③,垂直于AD的n条弦B1C1,B2C2,B3C3,…,B n∁n把圆周2n等分,请你用含n的代数式表示∠B n的度数(只需直接写出答案).【分析】根据条件可以先求出圆的各段弧的度数,根据圆周角等于所对弧的度数的一半,就可以求出圆周角的度数.【解答】解:(1)垂直于AD的两条弦B1C1,B2C2把圆周4等分,则是圆的,因而度数是45°,因而∠B1的度数是22.5°,同理的度数是135度,因而,∠B2的度数是67.5°;(2)∵圆周被6等分∴===360°÷6=60°∵直径AD⊥B1C1∴==30°,∴∠B1==15°∠B2==×(30°+60°)=45°∠B3==×(30°+60°+60°)=75°;(3)B n∁n把圆周2n等分,则弧BnD的度数是:,则∠B n AD=,在直角△AB n D中,.【点评】本题是把求圆周角的度数的问题转化为求弧的度数的问题,依据是圆周角等于所对弧的度数的一半.23.下框中是小明对一道题目的解答以及老师的批改.题目:某村计划建造如图所示的矩形蔬菜温室,要求长与宽的比为2:1,在温室内,沿前侧内墙保留3m的空地,其他三侧内墙各保留1m的通道,当温室的长与宽各为多少时,矩形蔬菜种植区域的面积是288m2?解:设矩形蔬菜种植区域的宽为xm,则长为2xm,根据题意,得x•2x=288.解这个方程,得x1=﹣12(不合题意,舍去),x2=12所以温室的长为2×12+3+1=28(m),宽为12+1+1=14(m)答:当温室的长为28m,宽为14m时,矩形蔬菜种植区域的面积是288m2.我的结果也正确!小明发现他解答的结果是正确的,但是老师却在他的解答中画了一条横线,并打了一个?.结果为何正确呢?(1)请指出小明解答中存在的问题,并补充缺少的过程:变化一下会怎样…(2)如图,矩形A′B′C′D′在矩形ABCD的内部,AB∥A′B′,AD∥A′D′,且AD:AB=2:1,设AB与A′B′、BC与B′C′、CD与C′D′、DA与D′A′之间的距离分别为a、b、c、d,要使矩形A′B′C′D′∽矩形ABCD,a、b、c、d应满足什么条件?请说明理由.【分析】(1)根据题意可得小明没有说明矩形蔬菜种植区域的长与宽之比为2:1的理由,所以应设矩形蔬菜种植区域的宽为xm,则长为2xm,然后由题意得,矩形蔬菜种植区域的长与宽之比为2:1,再利用小明的解法求解即可;(2)由使矩形A′B′C′D′∽矩形ABCD,利用相似多边形的性质,可得,即,然后利用比例的性质,即可求得答案.。
初三九年级数学上册 压轴解答题综合测试卷(word含答案)
初三九年级数学上册 压轴解答题综合测试卷(word 含答案)一、压轴题 1.问题提出(1)如图①,在ABC 中,42,6,135AB AC BAC ==∠=,求ABC 的面积.问题探究(2)如图②,半圆O 的直径10AB =,C 是半圆AB 的中点,点D 在BC 上,且2CD BD =,点P 是AB 上的动点,试求PC PD +的最小值.问题解决(3)如图③,扇形AOB 的半径为20,45AOB ∠=在AB 选点P ,在边OA 上选点E ,在边OB 上选点F ,求PE EF FP ++的长度的最小值.2.如图,在矩形ABCD 中,AB=20cm ,BC=4cm ,点p 从A 开始折线A ——B ——C ——D 以4cm/秒的 速度 移动,点Q 从C 开始沿CD 边以1cm/秒的速度移动,如果点P 、Q 分别从A 、C 同时出发,当其中一点到达D 时,另一点也随之停止运动,设运动的时间t (秒)(1)t 为何值时,四边形APQD 为矩形.(2)如图(2),如果⊙P 和⊙Q 的半径都是2cm ,那么t 为何值时,⊙P 和⊙Q 外切? 3.在长方形ABCD 中,AB =5cm ,BC =6cm ,点P 从点A 开始沿边AB 向终点B 以1/cm s 的速度移动,与此同时,点Q 从点B 开始沿边BC 向终点C 以2/cm s 的速度移动.如果P 、Q 分别从A 、B 同时出发,当点Q 运动到点C 时,两点停止运动.设运动时间为t 秒.(1)填空:______=______,______=______(用含t 的代数式表示);(2)当t 为何值时,PQ 的长度等于5cm ?(3)是否存在t 的值,使得五边形APQCD 的面积等于226cm ?若存在,请求出此时t 的值;若不存在,请说明理由.4.如图,Rt ABC ∆中,90C ∠=︒,4AC =,3BC =.点P 从点A 出发,沿着A CB →→运动,速度为1个单位/s ,在点P 运动的过程中,以P 为圆心的圆始终与斜边AB 相切,设⊙P 的面积为S ,点P 的运动时间为t (s )(07t <<). (1)当47t <<时,BP = ;(用含t 的式子表示) (2)求S 与t 的函数表达式;(3)在⊙P 运动过程中,当⊙P 与三角形ABC 的另一边也相切时,直接写出t 的值.5.如图,Rt △ABC ,CA ⊥BC ,AC =4,在AB 边上取一点D ,使AD =BC ,作AD 的垂直平分线,交AC 边于点F ,交以AB 为直径的⊙O 于G ,H ,设BC =x . (1)求证:四边形AGDH 为菱形; (2)若EF =y ,求y 关于x 的函数关系式; (3)连结OF ,CG .①若△AOF 为等腰三角形,求⊙O 的面积;②若BC =3,则30CG+9=______.(直接写出答案).6.如图,在Rt △ABC 中,∠A=90°,0是BC 边上一点,以O 为圆心的半圆与AB 边相切于点D ,与BC 边交于点E 、F ,连接OD ,已知BD=3,tan ∠BOD=34,CF=83.(1)求⊙O 的半径OD ; (2)求证:AC 是⊙O 的切线; (3)求图中两阴影部分面积的和.7.如图,⊙M 与菱形ABCD 在平面直角坐标系中,点M 的坐标为(﹣3,1),点A 的坐标为(2,0),点B 的坐标为(1,﹣3),点D 在x 轴上,且点D 在点A 的右侧. (1)求菱形ABCD 的周长;(2)若⊙M 沿x 轴向右以每秒2个单位长度的速度平移,菱形ABCD 沿x 轴向左以每秒3个单位长度的速度平移,设菱形移动的时间为t (秒),当⊙M 与AD 相切,且切点为AD 的中点时,连接AC ,求t 的值及∠MAC 的度数;(3)在(2)的条件下,当点M 与AC 所在的直线的距离为1时,求t 的值.8.如图 1,抛物线21:4C y ax ax c =-+交x 轴正半轴于点()1,0,A B ,交y 轴正半轴于C ,且OB OC =.(1)求抛物线1C 的解析式;(2)在图2中,将抛物线1C 向右平移n 个单位后得到抛物线2C ,抛物线2C 与抛物线1C 在第一象限内交于一点P ,若CAP ∆的内心在CAB △内部,求n 的取值范围(3)在图3中,M 为抛物线1C 在第一象限内的一点,若MCB ∠为锐角,且3tan MCB ∠>,直接写出点M 横坐标M x 的取值范围___________9.抛物线()20y ax bx c a =++≠的顶点为(),P h k ,作x 轴的平行线4y k =+与抛物线交于点A 、B ,无论h 、k 为何值,AB 的长度都为4. (1)请直接写出a 的值____________; (2)若抛物线当0x =和4x =时的函数值相等, ①求b 的值;②过点()0,2Q 作直线2y =平行x 轴,交抛物线于M 、N 两点,且4QM QN +=,求c 的取值范围;(3)若1c b =--,2727b -<<AB 与抛物线所夹的封闭区域为S ,将抛物线绕原点逆时针旋转α,且1tan 2α=,此时区域S 的边界与y 轴的交点为C 、D 两点,若点D 在点C 上方,请判断点D 在抛物线上还是在线段AB 上,并求CD 的最大值.10.如图,抛物线2()20y ax x c a =++<与x 轴交于点A 和点B (点A 在原点的左侧,点B 在原点的右侧),与y 轴交于点C ,3OB OC ==.(1)求该抛物线的函数解析式.(2)如图1,连接BC ,点D 是直线BC 上方抛物线上的点,连接OD ,CD .OD 交BC 于点F ,当32COFCDFSS=::时,求点D 的坐标.(3)如图2,点E 的坐标为(03)2-,,点P 是抛物线上的点,连接EB PB PE ,,形成的PBE △中,是否存在点P ,使PBE ∠或PEB ∠等于2OBE ∠?若存在,请直接写出符合条件的点P 的坐标;若不存在,请说明理由.11.对于线段外一点和这条线段两个端点连线所构成的角叫做这个点关于这条线段的视角.如图1,对于线段AB 及线段AB 外一点C ,我们称∠ACB 为点C 关于线段AB 的视角. 如图2,点Q 在直线l 上运动,当点Q 关于线段AB 的视角最大时,则称这个最大的“视角”为直线l 关于线段AB 的“视角”.(1)如图3,在平面直角坐标系中,A (0,4),B (2,2),点C 坐标为(﹣2,2),点C 关于线段AB 的视角为 度,x 轴关于线段AB 的视角为 度;(2)如图4,点M 是在x 轴上,坐标为(2,0),过点M 作线段EF ⊥x 轴,且EM =MF =1,当直线y =kx (k ≠0)关于线段EF 的视角为90°,求k 的值;(3)如图5,在平面直角坐标系中,P (3,2),Q (3+1,1),直线y =ax +b (a >0)与x 轴的夹角为60°,且关于线段PQ 的视角为45°,求这条直线的解析式. 12.如图,扇形OMN 的半径为1,圆心角为90°,点B 是上一动点,BA ⊥OM 于点A ,BC ⊥ON 于点C ,点D 、E 、F 、G 分别是线段OA 、AB 、BC 、CO 的中点,GF 与CE 相交于点P ,DE 与AG 相交于点Q . (1)当点B 移动到使AB :OA=:3时,求的长;(2)当点B 移动到使四边形EPGQ 为矩形时,求AM 的长. (3)连接PQ ,试说明3PQ 2+OA 2是定值.【参考答案】***试卷处理标记,请不要删除一、压轴题1.(1)12;(2)53;(3)202. 【解析】 【分析】(1)如图1中,过点B 作BD CA ⊥,交CA 延长线于点D ,通过构造直角三角形,求出BD 利用三角形面积公式求解即可.(2)如图示,作点D 关于AB 的对称点Q ,交AB 于点H ,连接CQ ,交AB 于点P ,连接PD 、OD 、OC ,过点Q 作QM CO ⊥,交CO 延长线于点M ,确定点P 的位置,利用勾股定理与矩形的性质求出CQ 的长度即为答案.(3)解图3所示,在AB 上这一点作点P 关于OA 的对称点S ,作点P 关于OB 的对称点N ,连接SN ,交OA 于点E ,交OB 于点F ,连接OS ON OP EP FP 、、、、,通过轴对称性质的转化,最终确定最小值转化为SN 的长. 【详解】(1)如解图1所示,过点B 作BD CA ⊥,交CA 延长线于点D ,135BAC ∠=,180********BAD BAC ∴∠=-∠=-=,BD CA ⊥,交CA 延长线于点D ,BAD ∴为等腰直角三角形,且90BDA ∠=,BD AD ∴=,在BAD 中,,90BD AD BDA =∠=,222BD AD AB ∴+=,即222BD AB =,42AB =2222(42)32BD AB ∴===,解得:4BD =,6AC =,11641222ABCSAC BD ∴=⋅=⨯⨯=.(2)如解图2所示,作点D 关于AB 的对称点Q ,交AB 于点H ,连接CQ ,交AB 于点P ,连接PD 、OD 、OC ,过点Q 作QM CO ⊥,交CO 延长线于点M ,D 关于AB 的对称点Q ,CQ 交AB 于点P ,PD PQ ∴=,PC PD PC PQ CQ ∴+=+=,点P 为AB 上的动点,PC PD CQ ∴+≥,∴当点P 处于解图2中的位置,PC PD +取最小值,且最小值为CQ 的长度,点C 为半圆AB 的中点,90COB ∴∠=,90BOD COD COB ∠+∠=∠=,11903033BOD COB ∴∠=∠=⨯=,10AB =,1110522OD AB ∴==⨯=,在Rt ODH △中,由作图知,90OHD ∠=,且30HOD BOD ∠=∠=,155,222DH OD QH DH ∴==∴==,2222553522OH OD DH ⎛⎫∴=-=-=⎪⎝⎭, 由作图知,四边形OMQH 为矩形,553,22OM QH MQ OH ∴====, 515522CM OM OC ∴=+=+=,222215535322CQ CM MQ ⎛⎫⎛⎫∴=+=+= ⎪ ⎪ ⎪⎝⎭⎝⎭, PC PD ∴+的最小值为53.(3)如解图3所示,在AB 上这一点作点P 关于OA 的对称点S ,作点P 关于OB 的对称点N ,连接SN ,交OA 于点E ,交OB 于点F ,连接OS ON OP EP FP 、、、、, 点P 关于OA 的对称点S ,点P 关于OB 的对称点N ,连接SN ,交OA 于点E ,交OB 于点F ,PE SE ∴=,FP FN =,SOA POA ∠=∠,,NOB POB OS OP ON ∠=∠==,.PE EF FP SE EF FN SN ∴++=++=,SOA NOB POA POB ∠+∠=∠+∠, E 为OA 上的点,F 为OB 上的点 PE EF FP SN ∴++≥,∴当点E F 、处于解图3的位置时,PE EF FP ++的长度取最小值,最小值为SN 的长度,45POA POB AOB ∠+∠=∠=, 45SOA NOB ∴∠+∠=,454590SON SOA AOB NOB ∴∠=∠+∠+∠=+=.扇形AOB 的半径为20,20OS ON OP ∴===,在Rt SON 中,90SON ∠=,20,90OS ON SON ==∠=PE EF FP ∴++的长度的最小值为202【点睛】本题主要考察了轴对称、勾股定理、圆、四边形等相关内容,理解题意,作出辅助线是做题的关键.2.(1)4;(2)t为4s,203s,283s时,⊙P与⊙Q外切.【解析】试题分析:(1)四边形APQD为矩形,也就是AP=DQ,分别用含t的代数式表示,解即可;(2)主要考虑有四种情况,一种是P在AB上,一种是P在BC上时.一种是P在CD上时,又分为两种情况,一种是P在Q右侧,一种是P在Q左侧.并根据每一种情况,找出相等关系,解即可.试题解析:(1)根据题意,当AP=DQ时,四边形APQD为矩形.此时,4t=20-t,解得t=4(s).答:t为4时,四边形APQD为矩形(2)当PQ=4时,⊙P与⊙Q外切.①如果点P在AB上运动.只有当四边形APQD为矩形时,PQ=4.由(1),得t=4(s);②如果点P在BC上运动.此时t≥5,则CQ≥5,PQ≥CQ≥5>4,∴⊙P与⊙Q外离;③如果点P在CD上运动,且点P在点Q的右侧.可得CQ=t,CP=4t-24.当CQ-CP=4时,⊙P与⊙Q外切.此时,t-(4t-24)=4,解得t=203(s);④如果点P在CD上运动,且点P在点Q的左侧.当CP-CQ=4时,⊙P与⊙Q外切.此时,4t-24-t=4,解得t=283(s ), ∵点P 从A 开始沿折线A-B-C-D 移动到D 需要11s ,点Q 从C 开始沿CD 边移动到D 需要20s ,而283<11, ∴当t 为4s ,203s ,283s 时,⊙P 与⊙Q 外切. 考点:1.矩形的性质;2.圆与圆的位置关系.3.(1)BQ ,2tcm ,PB ,()5t cm -;(2)当t =0秒或2秒时,PQ 的长度等于5cm ;(3)存在t =1秒,能够使得五边形APQCD 的面积等于226cm .理由见解析. 【解析】 【分析】(1)根据点P 从点A 开始沿边AB 向终点B 以1/cm s 的速度移动,与此同时,点Q 从点B 开始沿边BC 向终点C 以2/cm s 的速度移动,可以求得BQ ,PB .(2)用含t 的代数式分别表示PB 和BQ 的值,运用勾股定理求得PQ 为22(5)(2)t t -+=25据此求出t 值.(3)根据题干信息使得五边形APQCD 的面积等于226cm 的t 值存在,利用长方形ABCD 的面积减去PBQ △的面积即可,有PBQ △的面积为4,由此求得t 值.【详解】解:(1)点Q 从点B 开始沿边BC 向终点C 以2/cm s 的速度移动,故BQ 为2tcm ,点P 从点A 开始沿边AB 向终点B 以1/cm s 的速度移动,AB =5cm ,故PB 为()5t cm -.(2)由题意得:22(5)(2)t t -+=25,解得:1t =0,2t =2;当t =0秒或2秒时,PQ 的长度等于5cm ;(3)存在t =1秒,能够使得五边形APQCD 的面积等于226cm .理由如下: 长方形ABCD 的面积是:56⨯=()230cm,使得五边形APQCD 的面积等于226cm ,则PBQ △的面积为3026-=()24cm,()15242t t -⨯⨯=, 解得:1t =4(不合题意舍去),2t =1.即当t =1秒时,使得五边形APQCD 的面积等于226cm . 【点睛】本题结合长方形考查动点问题,其本质运用代数式求值,利用含t 的代数式表示各自线段的直接,根据题干数量关系即可确立等量关系式,从而求出t 值.4.(1)7-t (2)()()()22904;25{1674725t t S t t ππ<≤=-<<(3)516,23t t == 【解析】【分析】(1)先判断出点P 在BC 上,即可得出结论;(2)分点P 在边AC 和BC 上两种情况:利用相似三角形的性质得出比例式建立方程求解即可得出结论;(3)分点P 在边AC 和BC 上两种情况:借助(2)求出的圆P 的半径等于PC ,建立方程求解即可得出结论.【详解】(1)∵AC =4,BC =3,∴AC +BC =7.∵4<t <7,∴点P 在边BC 上,∴BP =7﹣t .故答案为:7﹣t ;(2)在Rt △ABC 中,AC =4,BC =3,根据勾股定理得:AB =5,由运动知,AP =t ,分两种情况讨论:①当点P 在边AC 上时,即:0<t ≤4,如图1,记⊙P 与边AB 的切点为H ,连接PH ,∴∠AHP =90°=∠ACB .∵∠A =∠A ,∴△APH ∽△ACB ,∴PH AP BC AB =,∴35PH t =,∴PH 35=t ,∴S 925=πt 2; ②当点P 在边BC 上时,即:4<t <7,如图,记⊙P 与边AB 的切点为G ,连接PG ,∴∠BGP =90°=∠C .∵∠B =∠B ,∴△BGP ∽△BCA ,∴PG BP AC AB =,∴745PG t -=,∴PG 45=(7﹣t ),∴S 1625=π(7﹣t )2. 综上所述:S 22904251674725t t t t ππ⎧≤⎪⎪=⎨⎪-⎪⎩(<)()(<<); (3)分两种情况讨论:①当点P 在边AC 上时,即:0<t ≤4,由(2)知,⊙P 的半径PH 35=t . ∵⊙P 与△ABC 的另一边相切,即:⊙P 和边BC 相切,∴PC =PH .∵PC =4﹣t ,∴4﹣t 35=t ,∴t 52=秒; ②当点P 在边BC 上时,即:4<t <7,由(2)知,⊙P 的半径PG 45=(7﹣t ). ∵⊙P 与△ABC 的另一边相切,即:⊙P 和边AC 相切,∴PC =PG .∵PC=t﹣4,∴t﹣445=(7﹣t),∴t163=秒.综上所述:在⊙P运动过程中,当⊙P与三角形ABC的另一边也相切时,t的值为52秒或163秒.【点睛】本题是圆的综合题,主要考查了切线的性质,勾股定理,相似三角形的判定和性质,用分类讨论的思想解决问题是解答本题的关键.5.(1)证明见解析;(2)y=18x2(x>0);(3)①163π或8π或(17)π;②21【解析】【分析】(1)根据线段的垂直平分线的性质以及垂径定理证明AG=DG=DH=AH即可;(2)只要证明△AEF∽△ACB,可得AE EFAC BC=解决问题;(3)①分三种情形分别求解即可解决问题;②只要证明△CFG∽△HFA,可得GFAF=CGAH,求出相应的线段即可解决问题;【详解】(1)证明:∵GH垂直平分线段AD,∴HA=HD,GA=GD,∵AB是直径,AB⊥GH,∴EG=EH,∴DG=DH,∴AG=DG=DH=AH,∴四边形AGDH是菱形.(2)解:∵AB是直径,∴∠ACB=90°,∵AE⊥EF,∴∠AEF=∠ACB=90°,∵∠EAF=∠CAB,∴△AEF∽△ACB,∴AE EF AC BC=,∴124x yx=,∴y=18x2(x>0).(3)①解:如图1中,连接DF.∵GH垂直平分线段AD,∴FA=FD,∴当点D与O重合时,△AOF是等腰三角形,此时AB=2BC,∠CAB=30°,∴AB=83,∴⊙O的面积为163π.如图2中,当AF=AO时,∵AB22AC BC+216x+∴OA=2 162x +,∵AF=22EF AE+=2221182x⎛⎫⎛⎫+⎪ ⎪⎝⎭⎝⎭,∴2162x+=2221182x⎛⎫⎛⎫+⎪ ⎪⎝⎭⎝⎭,解得x=4(负根已经舍弃),∴AB=42,∴⊙O的面积为8π.如图2﹣1中,当点C与点F重合时,设AE=x,则BC=AD=2x,AB=2164x+,∵△ACE∽△ABC,∴AC2=AE•AB,∴16=x•2164x+,解得x2=217﹣2(负根已经舍弃),∴AB2=16+4x2=817+8,∴⊙O的面积=π•14•AB2=(217+2)π综上所述,满足条件的⊙O的面积为163π或8π或(217+2)π;②如图3中,连接CG.∵AC=4,BC=3,∠ACB=90°,∴AB=5,∴OH=OA=52,∴AE=32,∴OE=OA﹣AE=1,∴EG=EH,∵EF=18x2=98,∴FG=2﹣98,AF158,AH,∵∠CFG=∠AFH,∠FCG=∠AHF,∴△CFG∽△HFA,∴GF CG AF AH=,∴9 28158-=∴CG,=.故答案为【点睛】本题考查圆综合题、相似三角形的判定和性质、垂径定理、线段的垂直平分线的性质、菱形的判定和性质、勾股定理、解直角三角形等知识,解题的关键是学会添加常用辅助线,构造相似三角形解决问题,学会用分类讨论的思想思考问题.6.(1)OD=4,(2)证明过程见详解(3)504 3π-【解析】【分析】(1)根据AB与圆O相切,在Rt△OBD中运用tan∠BOD=34,即可求出OD的长,(2)作辅助线证明四边形ADOG是矩形,得DO∥AC,sin∠OCG=35,在Rt△OCG中,求出OG的长等于半径即可解题,(3)利用S阴影=S Rt△BAC-S正方形ADOG-14S圆O,求出AC长度即可解题.【详解】解:(1)∵AB与圆O相切,∴OD⊥AB,在R t△OBD中,BD=3,tan∠BOD=BDOD=34,∴OD=4,(2)过点O作OG垂直AC于点G,∵∠A=90°,AB与圆O相切,∴四边形ADOG是矩形,∴DO∥AC,∴∠BOD=∠OCG,∵tan∠BOD=BDOD=34,∴sin∠OCG=3 5 ,∵CF=83,OF=4,∴OG=OGsin∠OCG=4=r,∴AC是⊙O的切线(3)由前两问可知,四边形ADOG是边长为4的正方形,扇形DOE和扇形GOF的面积之和是四分之一圆的面积,在R t△ABC中,tan∠C=34,AB=4+3=7,∴AC=ABtan C∠=734=283,∴S阴影=S Rt△BAC-S正方形ADOG-14S圆O=212817444234π⨯⨯-⨯-=5043π-【点睛】本题考查了三角函数的应用和直线与圆的位置关系,中等难度,熟悉三角函数并熟练应用是解题关键.7.(1)菱形的周长为8;(2)t=65,∠MAC=105°;(3)当t=1﹣35或t=1+315时,圆M 与AC 相切.【解析】 试题分析:(1)过点B 作BE ⊥AD ,垂足为E .由点A 和点B 的坐标可知:BE=3,AE=1,依据勾股定理可求得AB 的长,从而可求得菱形的周长;(2)记 M 与x 轴的切线为F ,AD 的中点为E .先求得EF 的长,然后根据路程=时间×速度列出方程即可;平移的图形如图3所示:过点B 作BE ⊥AD ,垂足为E ,连接MF ,F 为 M 与AD 的切点.由特殊锐角三角函数值可求得∠EAB=60°,依据菱形的性质可得到∠FAC=60°,然后证明△AFM 是等腰直角三角形,从而可得到∠MAF 的度数,故此可求得∠MAC 的度数;(3)如图4所示:连接AM ,过点作MN ⊥AC ,垂足为N ,作ME ⊥AD ,垂足为E .先求得∠MAE=30°,依据特殊锐角三角函数值可得到AE 的长,然后依据3t+2t=5-AE 可求得t 的值;如图5所示:连接AM ,过点作MN ⊥AC ,垂足为N ,作ME ⊥AD ,垂足为E .依据菱形的性质和切线长定理可求得∠MAE=60°,然后依据特殊锐角三角函数值可得到EA=33,最后依据3t+2t=5+AE .列方程求解即可. 试题解析:(1)如图1所示:过点B 作BE AD ⊥,垂足为E ,∵()B 1,3-,()A 2,0,∴BE 3=,AE 1=,∴22AB AE BE 2=+=,∵四边形ABCD 为菱形,∴AB BC CD AD ===,∴菱形的周长248=⨯=.(2)如图2所示,⊙M 与x 轴的切线为F ,AD 中点为E ,∵()M 3,1-,∴()F 3,0-,∵AD 2=,且E 为AD 中点,∴()E 30,,EF 6=, ∴2t 3t 6+=,解得6t 5=. 平移的图形如图3所示:过点B 作BE AD ⊥,垂足为E ,连接MF ,F 为⊙M 与AD 切点,∵由(1)可知,AE 1=,BE 3=∴tan EAB 3∠=∴EAB 60∠=︒,∴FAB 120∠=︒,∵四边形ABCD 是菱形,∴11FAC FAB 1206022∠∠==⨯︒=︒, ∵AD 为M 切线,∴MF AD ⊥,∵F 为AD 的中点,∴AF MF 1==,∴AFM 是等腰直角三角形,∴MAF 45∠=︒,∴MAC MAF FAC 4560105∠∠∠=+=︒+︒=︒.(3)如图4所示:连接AM ,过点作MN AC ⊥,垂足为N ,作ME AD ⊥,垂足为E ,∵四边形ABCD 为菱形,DAB 120∠=︒,∴DAC 60∠=︒.∵AC 、AD 是圆M 的切线∴MAE 30∠=︒,∵ME MN 1==.∴EA 3=, ∴3t 2t 53+=-, ∴3t 1=-. 如图5所示:连接AM ,过点作MN AC ⊥,垂足为N ,作ME AD ⊥,垂足为E ,∵四边形ABCD 为菱形,DAB 120∠=︒,∴DAC 60∠=︒,∴NAE 120∠=︒,∵AC 、AD 是圆M 的切线,∴MAE 60∠=︒,∵ME MN 1==,∴3EA 3=, ∴33t 2t 5+=+, ∴3t 1=+.综上所述,当t 15=-或t 115=+时,圆M 与AC 相切. 点睛:此题是一道圆的综合题.圆中的方法规律总结:1、分类讨论思想:研究点、直线和圆的位置关系时,就要从不同的位置关系去考虑,即要全面揭示点、直线和元的各种可能的位置关系.这种位置关系的考虑与分析要用到分类讨论思想.1、转化思想:(1)化“曲面”为“平面”(2)化不规则图形面积为规则图形的面积求解.3、方程思想:再与圆有关的计算题中,除了直接运用公式进行计算外,有时根据图形的特点,列方程解答,思路清楚,过程简捷.8.(1)()221y x =--;(2)1023n <<;(3)552M x << 【解析】【分析】(1)由题意可得对称轴方程,有二次函数对称性,由A 点坐标可求B 点坐标,代入解析式可得;(2)根据函数图像平移可得新抛物线解析式,画出图像可得交点P ,由题意可得ACB BCP ∠>∠,过点C 作//l x 轴.作PD l ⊥,可得ACO PCD ∠=∠,设()2,43P t t t -+,由13tan ACD tan PCD ∠=∠=可得关于t 的方程,解得t, 再将P 代入2C 解析式中得n 的值,根据Q,P 在第一象限内得n 的取值范围;(3) 当MCB ∠为直角时,可求直线CB 的解析式为:y=-x+3,直线CM 的解析式为:y=x+3,运用直线与曲线联立,可求CM 与抛物线的交点M 横坐标为:x=5;当MCB ∠为锐角且3tan MCB ∠=时,过点M 作MN CB ⊥于N,则3MN CN=,设M 点坐标为()2,43t t t -+,直线CB 解析式为y=-x+3,可求直线MN 解析式为:253y x t t =+-+,将直线MN 与直线CB 解析式联立可得:N 221515,32222t t t t ⎛⎫-+-+ ⎪⎝⎭, 由两点间距离公式可得2MN = 2213222t t ⎛⎫- ⎪⎝⎭;2CN =2215222t t ⎛⎫- ⎪⎝⎭;由3MN CN =可得:52t =,进而可得满足已知条件的点M 横坐标M x 的取值范围.【详解】解:()1对称轴为422a x a-=-= ()3,0B ∴()0,1C ∴代入()224321y x x x ∴=-+=--()()222:21C x n ---()2423x n x =-++CAP ∆的内心I 在CAB △内部,ACB BCP ∴∠>∠∴当ACB BCP ∠=∠时过C 作//l x 轴.作PD l ⊥,ACB BCP ∠=∠90,OCD ∠=45,DCB ∠=,ACO PCD ∴∠=∠13tan ACD tan PCD ∠=∠= 设()2,43P t t t -+ 13PD CD ∴= 3p y DP OC +==214333t t t ∴-++= 113t = 将P 代入2C 解析式中103n ∴=又P 在第一象限内h AB ∴>2n ∴>1023n ∴<<(3) 552M x <<; 当MCB ∠为直角时,如下图所示:由(1)(2)可得:直线CB 的解析式为:y=-x+3,MCB ∠为直角,C(0,3),∴直线CM 的解析式为:y=x+3,则CM 与抛物线的交点坐标M 横坐标为:2343x x x +=-+,解得:x=5或0(舍去),所以,当MCB ∠为直角时,5M x =;当MCB ∠为锐角且3tan MCB ∠=时,如下图所示:过点M 作MN CB ⊥于N,则3MN CN=,设M 点坐标为()2,43t t t -+, MN CB ⊥,直线CB 解析式为y=-x+3,∴MN 解析式可设:y=x+b,将P ()2,43t t t -+代入解析式可得:b=253t t -+,则直线MN 解析式为:253y x t t =+-+,将直线MN 与直线CB 解析式联立可得: N 点坐标为221515,32222t t t t ⎛⎫-+-+ ⎪⎝⎭, ∴2MN =2222215154332222t t t t t t t ⎛⎫⎛⎫+-+-+-+- ⎪ ⎪⎝⎭⎝⎭ = 2213222t t ⎛⎫- ⎪⎝⎭; 2CN = 222215152222t t t t ⎛⎫⎛⎫-+-+ ⎪ ⎪⎝⎭⎝⎭ =2215222t t ⎛⎫- ⎪⎝⎭; 由3MN CN=可得:2213221522t t t t --=3; 解得:52t =或0(舍去) ; ∴MCB ∠为锐角,且3tan MCB ∠>时,点M 的横坐标M x 的取值范围为:552M x <<. 【点睛】本题综合考查了二次函数的图像和性质,题目较难,熟练掌握二次函数的图像和性质,运用数形结合解决二次函数综合问题是解题的关键.9.(1)1;(2)①4b =-;②26c ≤<;(3)D 一定在线段AB上,=CD 【解析】【分析】(1)根据题意顶点P (k ,h )可将二次函数化为顶点式:()2y a x k h =-+,又4y k =+与抛物线交于点A 、B ,无论h 、k 为何值,AB 的长度都为4,即可得出a 的值; (2)①根据抛物线x=0和x=4时函数值相等,可得到顶点P 的横坐标,根据韦达定理结合(1)即可得到b 的值,②根据(1)和(2)①即可得二次函数对称轴为x=2,利用点Q (0,2)关于对称轴的对称点R (4,2)可得QR=4,又QR 在直线y=2上,故令M 坐标(t ,2)(0≤t <2),代入二次函数即求得c 的取值范围;(3)由c=-b-1代入抛物线方程即可化简,将抛物线绕原点逆时针旋转αα,且tanα=2,转化为将y 轴绕原点顺时针旋转α得到直线l ,且tanα=2,可得到直线l 的解析式,最后联立直线方程与抛物线方程运算求解.【详解】解:(1)根据题意可知1二次函数2y ax bx c =++(a≠0)的顶点为P (k ,h ),故二次函数顶点式为()2y a x k h =-+,又4y k =+与抛物线交于点A 、B ,且无论h 、k 为何值,AB 的长度都为4,∴a=1;故答案为:a=1.(2)①∵二次函数当0x =和4x =时的函数值相等 ∴222b b x a =-=-= ∴4b =-故答案为:4b =-.②将点Q 向右平移4个单位得点()4,2R当2c =时,242y x x =-+令2y =,则2242x x =-+解得14x =,20x =此时()0,2M ,()4,2N ,4MN QR ==∵4QM QN +=∵QM NR =∴4QN NR QR +==∴N 在线段QR 上,同理M 在线段QR 上设(),2M m ,则02m ≤<,224m m c =-+ 2242(2)6c m m m =-++=--+∵10-<,对称轴为2m =,02m ≤<∴c 随着m 的增大而增大∴26c ≤<故答案为:26c ≤<.(3)∵1c b =--∴21y x bx b =+--将抛物线绕原点逆时针旋转α,且tan 2α=,转化为将y 轴绕原点顺时针旋转α得到直线l ,且tan 2α=,∴l 的解析式为2y x =221y x y x bx b =⎧⎨=+--⎩∴2(2)10x b x b +---= ∴2224(2)448b ac b b b ∆=-=-++=+∴x =∴12D b -++⎝⎭ 22244124442444AB ac b b b b y k b a ---+-+=+=+==-++122442244AB D b b y y b b ⎛⎫-+-+-=-++-++= ⎪⎝⎭∵20b ≥∴12404410444D AB b y y -+-+-=≥==> ∴点1D 始终在直线AB 上方∵222b C b ⎛-+--+- ⎝⎭∴22442244B C A b b y y b b ⎛⎫-+---=-+--++= ⎪⎝⎭∴AB C y y -==)22164-+=∵b -<<2028b ≤<,∴4≤<设n,4n ≤< ∴2(2)164AB C n y y --+-= ∵104-<,对称轴为2n =∴当4n ≤<时,AB C y y -随着n 的增大而减小∴当4n =时,0AB C y y -=∴当4n ≤<时,AB C y y >∴区域S 的边界与l 的交点必有两个∵1D AB y y >∴区域S 的边界与l 的交点D 一定在线段AB 上∴D AB y y = ∴2(2)164D C C AB n y y y y --+-=-=∴当n =D C y y -有最大值1+此时12D C x x +-= 由勾股定理得:2CD ==,故答案为:5102=CD . 【点睛】 本题考查二次函数一般式与顶点式、韦达定理的运用,以及根与系数的关系判断二次函数交点情况,正确理解相关知识点是解决本题的关键.10.(1)2y x 2x 3=-++;(2)点D 的坐标为(14),或(2)3,;(3)点P 的坐标为:(14),或17()24-,或13209()24--,或(579491778+-,. 【解析】【分析】(1)由3OB OC ==及图像可得B 、C 两点坐标,然后利用待定系数法直接进行求解即可;(2)由题意易得35COF COD S S =,进而得到点D 、F 横坐标之间的关系为53D F x x =,设F 点横坐标为3t ,则D 点横坐标为5t ,则有直线BC 的解析式为3y x =-+,然后可直接求解;(3)分∠PBE 或∠PEB 等于2∠OBE 两种情况分别进行求解即可.【详解】解:(1)3OB OC ==,则:()()3003B C ,,,, 把B C 、坐标代入抛物线方程,解得抛物线方程为:2y x 2x 3=-++①;(2)∵32COF CDF S S =△△::, ∴35COF COD S S =,即:53D F x x =, 设F 点横坐标为3t ,则D 点横坐标为5t , 点F 在直线BC 上,而BC 所在的直线表达式为:3y x =-+,则33(3)F t t -,, 则直线OF 所在的直线表达式为:3313t t y x x t t--==, 则点55(5)D t t -,,把D 点坐标代入抛物线解析式,解得:15t =或2 5, 则点D 的坐标为(14),或(2)3,; (3)①当2PBE OBE ∠=∠时,当BP 在x 轴上方时,如图2,设1BP 交y 轴于点E ', ∴12PBE OBE ∠=∠ , ∴E BO EBO ∠'=∠ ,又60E OB EBO BO BO ∠'=∠=︒=, ,∴()E BO EBO AAS '≌ ,∴32EO EO ==, ∴点3(20)E ',,直线1BP 过点BE '、,则其直线方程为:1322y x =-+②, 联立①②并解得:12x =- , 故点P 1的坐标为17()24-,;当BP 在x 轴下方时, 如图2,过点E 作//EF BE '交2BP 于点F ,则FEB EBE ∠=∠',∴222E BE OBE EBP OBE ∠'=∠∠=∠, ,∴FEB EBF ∠=∠ ,∴FE BF = ,直线EF 可以看成直线BE '平移而得,其k 值为12-, 则其直线表达式为:1322y x =-- , 设点13()22F m m --,,过点F 作FH y ⊥轴交于点H ,作BK HF ⊥于点K , 则点13()202H m --,,13()232K m --,, ∵EF BF =,则22FE BF =, 即:()2222331313()()22222m m m m +-++=-++, 解得:52m =, 则点511()24F -,, 则直线BF 表达式为:113322y x =-…③, 联立①③并解得:132x =-或3(舍去3), 则点213209()24P --,; ②当2PEB OBE ∠=∠时,当EP 在BE 上方时,如图3,点E '为图2所求,设BE '交3EP 于点F ,∵2EBE OBE ∠'=∠,∴3EBE P EB ∠'=∠ ,∴FE BF = ,由①知,直线BE '的表达式为:1322y x =-+, 设点13()22F n n -+,,13()232K n -+,,由FE BF =,同理可得:12n =, 故点15()24F ,,则直线EF 的表达式为:11322y x =-④, 联立①④并解得:1n =或92- (舍去负值), ∴34(1)P , ; 当EP 在BE 下方时,同理可得:x =舍去负值),故点458(417P +-+,.故点P 的坐标为:(14),或17()24-,或13209()24--,或. 【点睛】 本题主要考查二次函数的综合,关键是熟练掌握二次函数的性质与一次函数的性质,利用数形结合及分类讨论思想进行求解.11.(1)45,45;(2)k =3)y ﹣2 【解析】【分析】(1)如图3,连接AC ,则∠ABC=45°;设M 是x 轴的动点,当点M 运动到点O 时,∠AOB=45°,该视角最大,即可求解;(2)如图4,以点M 为圆心,长度1为半径作圆M ,当圆与直线y=kx 相切时,直线y=kx (k≠0)关于线段EF 的视角为90°,即∠EQF=90°,则MQ ⊥直线OE ,OQ=1,OM=2,故直线的倾斜角为30°,即可求解;(3)直线PQ 的倾斜角为45°,分别作点Q 、P 作x 轴、y 轴的平行线交于点R ,RQ=RP=1,以点R 为圆心以长度1为半径作圆R ,由(1)知,设直线与圆交于点Q′,由(1)知,当PQ′Q 为等腰三角形时,视角为45°,则QQ=2RQ=2,故点Q′,1),即可求解.【详解】(1)如图3,连接AC ,则∠ABC =45°;设M是x轴的动点,当点M运动到点O时,∠AOB=45°,该视角最大,由此可见:当△ABC为等腰三角形时,视角最大;故答案为:45,45;(2)如图4,以点M为圆心,长度1为半径作圆M,当圆与直线y=kx相切时,直线y=kx(k≠0)关于线段EF的视角为90°,即∠EQF=90°,则MQ⊥直线OE,MQ=1,OM=2,故直线的倾斜角为30°,故k=33 ;(3)直线PQ的倾斜角为45°,分别作点Q、P作x轴、y轴的平行线交于点R,RQ=RP=1,以点R为圆心以长度1为半径作圆R,由(1)知,设直线与圆交于点Q′,由(1)知,当PQ′Q为等腰三角形时,视角为45°,则QQ=2RQ=2,故点Q′(3﹣1,1),直线y=ax+b(a>0)与x轴的夹角为60°,则直线的表达式为:y=3x+b,将点Q′的坐标代入上式并解得:直线的表达式为:y=3x+3﹣2【点睛】本题考查的是一次函数综合运用,涉及到解直角三角形、圆的基本知识等,此类新定义题目,通常按照题设的顺序求解,一般比较容易.12.(1)证明见解析(2)当AM的长为(1﹣)时,四边形EPGQ是矩形(3)定值【解析】【分析】(1)先利用三角函数求出∠AOB=30°,再用弧长公式即可得出结论;(2)易得△AED∽△BCE,根据相似三角形的对应边成比例与勾股定理,即可求得OA的长,即可得出结论;(3)连接GE交PQ于O′,易得O′P=O′Q,O′G=O'E,然后过点P作OC的平行线分别交BC、GE于点B′、A′,由△PCF∽△PEG,根据相似三角形的对应边成比例与勾股定理,即可求得3PQ2+OA2的值.【详解】解:(1)证明:连接OB,如图①,∵四边形OABC是矩形,∴∠AOC=∠OAB=90°,在Rt△AOB中,tan∠AOB==,∴∠AOB=30°,∴==;(2)如图②,∵▱EPGQ是矩形.∴∠CED=90°∴∠AED+∠CEB=90°.又∵∠DAE=∠EBC=90°,∴∠AED=∠BCE.∴△AED∽△BCE,∴.设OA=x,AB=y,则=,得y2=2x2,又 OA2+AB2=OB2,即x2+y2=12.∴x2+2x2=1,解得:x=.∴AM=OM﹣OA=1﹣当AM的长为(1﹣)时,四边形EPGQ是矩形;(3)如图③,连接GE交PQ于O′,∵四边形EPGQ是平行四边形,∴O′P=O′Q,O′G=O′E.过点P作OC的平行线分别交BC、GE于点B′、A′.由△PCF∽△PEG得, =2,∴PA′=A′B′=AB,GA′=GE=OA,∴A′O′=GE﹣GA′=OA.在Rt△PA′O′中,PO′2=PA′2+A′O′2,即=+,又 AB2+OA2=1,∴3PQ2=AB2+,∴OA2+3PQ2=OA2+(AB2+)=是定值.【点睛】此题是圆的综合题,主要考查了相似三角形的判定与性质、平行四边形的判定与性质、矩形的判定与性质以及勾股定理,锐角三角函数,弧长公式等知识,解题的关键是注意准确作出辅助线,注意数形结合思想与方程思想的应用.。
最新初三九年级上册数学 压轴解答题综合测试卷(word含答案)
最新初三九年级上册数学压轴解答题综合测试卷(word含答案)一、压轴题1.如图,⊙O的直径AB=26,P是AB上(不与点A,B重合)的任一点,点C,D为⊙O 上的两点.若∠APD=∠BPC,则称∠DPC为直径AB的“回旋角”.(1)若∠BPC=∠DPC=60°,则∠DPC是直径AB的“回旋角”吗?并说明理由;(2)猜想回旋角”∠DPC的度数与弧CD的度数的关系,给出证明(提示:延长CP交⊙O 于点E);(3)若直径AB的“回旋角”为120°,且△PCD的周长为24+133,直接写出AP的长.2.如图, AB是⊙O的直径,点D、E在⊙O上,连接AE、ED、DA,连接BD并延长至∠=∠.点C,使得DAC AED(1)求证: AC是⊙O的切线;(2)若点E是BC的中点, AE与BC交于点F,=;①求证: CA CF②若⊙O的半径为3,BF=2,求AC的长.3.在长方形ABCD中,AB=5cm,BC=6cm,点P从点A开始沿边AB向终点B以cm s的速度移动,与此同时,点Q从点B开始沿边BC向终点C以2/cm s的速度移1/动.如果P、Q分别从A、B同时出发,当点Q运动到点C时,两点停止运动.设运动时间为t秒.(1)填空:______=______,______=______(用含t的代数式表示);(2)当t为何值时,PQ的长度等于5cm?26cm?若存在,请求出此时t的(3)是否存在t的值,使得五边形APQCD的面积等于2值;若不存在,请说明理由.4.如图,已知矩形ABCD中,BC=2cm,AB=23cm,点E在边AB上,点F在边AD上,点E由A向B运动,连结EC、EF,在运动的过程中,始终保持EC⊥EF,△EFG为等边三角形.(1)求证△AEF∽△BCE;(2)设BE的长为xcm,AF的长为ycm,求y与x的函数关系式,并写出线段AF长的范围;(3)若点H是EG的中点,试说明A、E、H、F四点在同一个圆上,并求在点E由A到B 运动过程中,点H移动的距离.5.如图,Rt△ABC,CA⊥BC,AC=4,在AB边上取一点D,使AD=BC,作AD的垂直平分线,交AC边于点F,交以AB为直径的⊙O于G,H,设BC=x.(1)求证:四边形AGDH为菱形;(2)若EF=y,求y关于x的函数关系式;(3)连结OF,CG.①若△AOF为等腰三角形,求⊙O的面积;②若BC=3,则30CG+9=______.(直接写出答案).6.如图,抛物线y=x2+bx+c交x轴于A、B两点,其中点A坐标为(1,0),与y轴交于点C(0,﹣3).(1)求抛物线的函数表达式;(2)如图1,连接AC ,点Q 为x 轴下方抛物线上任意一点,点D 是抛物线对称轴与x 轴的交点,直线AQ 、BQ 分别交抛物线的对称轴于点M 、N .请问DM +DN 是否为定值?如果是,请求出这个定值;如果不是,请说明理由.(3)如图2,点P 为抛物线上一动点,且满足∠PAB =2∠ACO .求点P 的坐标.7.抛物线()20y ax bx c a =++≠的顶点为(),P h k ,作x 轴的平行线4y k =+与抛物线交于点A 、B ,无论h 、k 为何值,AB 的长度都为4. (1)请直接写出a 的值____________; (2)若抛物线当0x =和4x =时的函数值相等, ①求b 的值;②过点()0,2Q 作直线2y =平行x 轴,交抛物线于M 、N 两点,且4QM QN +=,求c 的取值范围;(3)若1c b =--,2727b -<<,设线段AB 与抛物线所夹的封闭区域为S ,将抛物线绕原点逆时针旋转α,且1tan 2α=,此时区域S 的边界与y 轴的交点为C 、D 两点,若点D 在点C 上方,请判断点D 在抛物线上还是在线段AB 上,并求CD 的最大值.8.如图1(注:与图2完全相同)所示,抛物线212y x bx c =-++经过B 、D 两点,与x 轴的另一个交点为A ,与y 轴相交于点C . (1)求抛物线的解析式.(2)设抛物线的顶点为M ,求四边形ABMC 的面积(请在图1中探索)(3)设点Q 在y 轴上,点P 在抛物线上.要使以点A 、B 、P 、Q 为顶点的四边形是平行四边形,求所有满足条件的点P 的坐标(请在图2中探索)9.()1尺规作图1:已知:如图,线段AB 和直线且点B 在直线上求作:点C ,使点C 在直线上并且使ABC 为等腰三角形.作图要求:保留作图痕迹,不写作法,做出所有符合条件的点C .()2特例思考:如图一,当190∠=时,符合()1中条件的点C 有______个;如图二,当160∠=时,符合()1中条件的点C 有______个.()3拓展应用:如图,AOB 45∠=,点M ,N 在射线OA 上,OM x =,ON x 2=+,点P 是射线OB 上的点.若使点P ,M ,N 构成等腰三角形的点P 有且只有三个,求x 的值. 10.在平面直角坐标系xOy 中,对于任意三点A ,B ,C ,给出如下定义:如果矩形的任何一条边均与某条坐标轴平行,且A ,B ,C 三点都在矩形的内部或边界上,则称该矩形为点A ,B ,C 的覆盖矩形.点A ,B ,C 的所有覆盖矩形中,面积最小的矩形称为点A ,B ,C 的最优覆盖矩形.例如,下图中的矩形A 1B 1C 1D 1,A 2B 2C 2D 2,AB 3C 3D 3都是点A ,B ,C 的覆盖矩形,其中矩形AB 3C 3D 3是点A ,B ,C 的最优覆盖矩形. (1)已知A (﹣2,3),B (5,0),C (t ,﹣2). ①当t =2时,点A ,B ,C 的最优覆盖矩形的面积为 ;②若点A ,B ,C 的最优覆盖矩形的面积为40,求直线AC 的表达式;(2)已知点D (1,1).E (m ,n )是函数y =4x(x >0)的图象上一点,⊙P 是点O ,D ,E 的一个面积最小的最优覆盖矩形的外接圆,求出⊙P 的半径r 的取值范围.11.如图,在边长为5的菱形OABC 中,sin∠AOC=45,O 为坐标原点,A 点在x 轴的正半轴上,B ,C 两点都在第一象限.点P 以每秒1个单位的速度沿O→A→B→C→O 运动一周,设运动时间为t (秒).请解答下列问题: (1)当CP⊥OA 时,求t 的值;(2)当t <10时,求点P 的坐标(结果用含t 的代数式表示);(3)以点P 为圆心,以OP 为半径画圆,当⊙P 与菱形OABC 的一边所在直线相切时,请直接写出t 的值.12.如图,正方形ABCD 中,点O 是线段AD 的中点,连接OC ,点P 是线段OC 上的动点,连接AP 并延长交CD 于点E ,连接DP 并延长交AB 或BC 于点F , (1)如图①,当点F 与点B 重合时,DEDC等于多少; (2)如图②,当点F 是线段AB 的中点时,求DEDC的值; (3)如图③,若DE CF ,求DEDC的值.【参考答案】***试卷处理标记,请不要删除一、压轴题1.(1)∠DPC 是直径AB 的回旋角,理由见解析;(2)“回旋角”∠CPD 的度数=CD 的度数,证明见解析;(3)3或23. 【解析】 【分析】(1)由∠BPC =∠DPC =60°结合平角=180°,即可求出∠APD =60°=∠BPC ,进而可说明∠DPC 是直径AB 的回旋角;(2)延长CP 交圆O 于点E ,连接OD ,OC ,OE ,由“回旋角”的定义结合对顶角相等,可得出∠APE =∠APD ,由圆的对称性可得出∠E =∠D ,由等腰三角形的性质可得出∠E =∠C ,进而可得出∠D =∠C ,利用三角形内角和定理可得出∠COD =∠CPD ,即“回旋角”∠CPD 的度数=CD 的度数;(3)①当点P 在半径OA 上时,在图3中,过点F 作CF ⊥AB ,交圆O 于点F ,连接PF ,则PF =PC ,利用(2)的方法可得出点P ,D ,F 在同一条直线上,由直径AB 的“回旋角”为120°,可得出∠APD=∠BPC=30°,进而可得出∠CPF=60°,即△PFC是等边三角形,根据等边三角形的性质可得出∠CFD=60°.连接OC,OD,过点O作OG⊥CD于点G,则∠COD=120°,根据等腰三角形的性质可得出CD=2DG,∠DOG=12∠COD=60°,结合圆的直径为26可得出CD=133,由△PCD的周长为24+133,可得出DF=24,过点O作OH⊥DF于点H,在Rt△OHD和在Rt△OHD中,通过解直角三角形可得出OH,OP的值,再根据AP=OA﹣OP可求出AP的值;②当点P在半径OB上时,用①的方法,可得:BP=3,再根据AP=AB﹣BP可求出AP的值.综上即可得出结论.【详解】(1)∵∠BPC=∠DPC=60°,∴∠APD=180°﹣∠BPC﹣∠DPC=180°﹣60°﹣60°=60°,∴∠APD=∠BPC,∴∠DPC是直径AB的回旋角.(2)“回旋角”∠CPD的度数=CD的度数,理由如下:如图2,延长CP交圆O于点E,连接OD,OC,OE.∵∠CPB=∠APE,∠APD=∠CPB,∴∠APE=∠APD.∵圆是轴对称图形,∴∠E=∠D.∵OE=OC,∴∠E=∠C,∴∠D=∠C.由三角形内角和定理,可知:∠COD=∠CPD,∴“回旋角”∠CPD的度数=CD的度数.(3)①当点P在半径OA上时,在图3中,过点F作CF⊥AB,交圆O于点F,连接PF,则PF=PC.同(2)的方法可得:点P,D,F在同一条直线上.∵直径AB的“回旋角”为120°,∴∠APD=∠BPC=30°,∴∠CPF=60°,∴△PFC是等边三角形,∴∠CFD=60°.连接OC ,OD ,过点O 作OG ⊥CD 于点G ,则∠COD =120°, ∴CD =2DG ,∠DOG =12∠COD =60°, ∵AB=26, ∴OC=13, ∴1332CG =∴CD =2×133=133. ∵△PCD 的周长为24+133, ∴PD +PC +CD =24+133, ∴PD +PC =DF =24.过点O 作OH ⊥DF 于点H ,则DH =FH =12DF =12. 在Rt △OHD 中,OH =222213125OD DH -=-=, 在Rt △OHP 中,∠OPH =30°, ∴OP =2OH =10,∴AP =OA ﹣OP =13﹣10=3; ②当点P 在半径OB 上时, 同①的方法,可得:BP =3, ∴AP =AB ﹣BP =26﹣3=23. 综上所述,AP 的长为:3或23.【点睛】此题是圆的综合题,考查圆的对称性质,直角三角形、等腰三角形与圆的结合,(3)是此题的难点,线段AP 的长度由点P 所在的位置决定,因此必须分情况讨论. 2.(1)详见解析;(2)①详见解析;②8 【解析】 【分析】(1)先得到90ADB ∠=︒,利用圆周角定理得到DBA DAC ∠=∠,即可证明AC 是切线;(2)①利用等弧所对的圆周角相等,得到BAE DAE ∠=∠,然后得到CFA CAF ∠=∠,即可得到结论成立;②设AC CF x ==,利用勾股定理,即可求出AC 的长度. 【详解】(1)证明: ∵AB 是⊙O 的直径, ∴90ADB ∠=︒, ∴90DBA DAB ∠+∠=︒,∵DEA DBA ∠=∠,DAC DEA ∠=∠, ∴DBA DAC ∠=∠, ∴90DAC DAB ∠+∠=︒, ∴90CAB ∠=︒, ∴AC 是⊙O 的切线; (2)① ∵点E 是弧BD 的中点, ∴BAE DAE ∠=∠,∵CFA DBA BAE ∠=∠+∠,CAF CAD DAE ∠=∠+∠, ∴CFA CAF ∠=∠ ∴CA CF =; ② 设CA CF x ==, 在Rt ABC ∆中,2BC x =+,CA x =,6AB =, 由勾股定理可得222(2)6x x +=+,解得:8x =, ∴8AC =. 【点睛】本题考查了切线的判定,等角对等边,以及勾股定理,要证直线是圆的切线,已知此线过圆上某点,连接圆心与这点(即为半径),再证垂直即可.3.(1)BQ ,2tcm ,PB ,()5t cm -;(2)当t =0秒或2秒时,PQ 的长度等于5cm ;(3)存在t =1秒,能够使得五边形APQCD 的面积等于226cm .理由见解析. 【解析】 【分析】(1)根据点P 从点A 开始沿边AB 向终点B 以1/cm s 的速度移动,与此同时,点Q 从点B 开始沿边BC 向终点C 以2/cm s 的速度移动,可以求得BQ ,PB .(2)用含t 的代数式分别表示PB 和BQ 的值,运用勾股定理求得PQ 为22(5)(2)t t -+=25据此求出t 值.(3)根据题干信息使得五边形APQCD 的面积等于226cm 的t 值存在,利用长方形ABCD 的面积减去PBQ △的面积即可,有PBQ △的面积为4,由此求得t 值. 【详解】解:(1)点Q 从点B 开始沿边BC 向终点C 以2/cm s 的速度移动,故BQ 为2tcm ,点P从点A 开始沿边AB 向终点B 以1/cm s 的速度移动,AB =5cm ,故PB 为()5t cm -.(2)由题意得:22(5)(2)t t -+=25,解得:1t =0,2t =2;当t =0秒或2秒时,PQ 的长度等于5cm ;(3)存在t =1秒,能够使得五边形APQCD 的面积等于226cm .理由如下: 长方形ABCD 的面积是:56⨯=()230cm,使得五边形APQCD 的面积等于226cm ,则PBQ △的面积为3026-=()24cm,()15242t t -⨯⨯=, 解得:1t =4(不合题意舍去),2t =1.即当t =1秒时,使得五边形APQCD 的面积等于226cm . 【点睛】本题结合长方形考查动点问题,其本质运用代数式求值,利用含t 的代数式表示各自线段的直接,根据题干数量关系即可确立等量关系式,从而求出t 值.4.(1)详见解析;(2)21y 2x =-,302AF ≤≤;(3)3. 【解析】 【分析】(1)由∠A =∠B =90°,∠AFE =∠BEC ,得△AEF ∽△BCE ;(2)由(1)△AEF ∽BCE 得AF AEBE BC =,y x =,即212y x =-+,然后求函数最值;(3)连接FH ,取EF 的中点M ,证MA =ME =MF =MH ,则A 、E 、H 、F 在同一圆上;连接AH ,证∠EFH =30°由A 、E 、H 、F 在同一圆上,得∠EAH =∠EFH =30°,线段AH 即为H 移动的路径,在直角三角形ABH 中,60AH sin AB =︒=,可进一步求AH. 【详解】解:(1)在矩形ABCD 中,∠A =∠B =90°, ∴∠AEF +∠AFE =90°, ∵EF ⊥CE , ∴∠AEF +∠BEC =90°, ∴∠AFE =∠BEC , ∴△AEF ∽△BCE ; (2)由(1)△AEF ∽BEC 得AF AE BE BC =,y x =,∴2132y x x =-+, ∵2132y x x =-+=213(3)22x --+, 当3x =时,y 有最大值为32, ∴302AF ≤≤; (3)如图1,连接FH ,取EF 的中点M , 在等边三角形EFG 中,∵点H 是EG 的中点, ∴∠EHF =90°, ∴ME =MF =MH ,在直角三角形AEF 中,MA =ME =MF , ∴MA =ME =MF =MH , 则A 、E 、H 、F 在同一圆上; 如图2,连接AH ,∵△EFG 为等边三角形,H 为EG 中点,∴∠EFH =30° ∵A 、E 、H 、F 在同一圆上∴∠EAH =∠EFH =30°, 如图2所示的线段AH 即为H 移动的路径,在直角三角形ABH 中,360AH sin AB =︒=, ∵AB =23 ∴AH =3,所以点H 移动的距离为3. 【点睛】此题主要考查圆的综合问题,会证明三角形相似,会分析四点共圆,会运用二次函数分析最值,会分析最短轨迹并解直角三角形是得分的关键. 5.(1)证明见解析;(2)y =18x 2(x >0);(3)①163π或8π或(17)π;②21 【解析】 【分析】(1)根据线段的垂直平分线的性质以及垂径定理证明AG=DG=DH=AH即可;(2)只要证明△AEF∽△ACB,可得AE EFAC BC=解决问题;(3)①分三种情形分别求解即可解决问题;②只要证明△CFG∽△HFA,可得GFAF=CGAH,求出相应的线段即可解决问题;【详解】(1)证明:∵GH垂直平分线段AD,∴HA=HD,GA=GD,∵AB是直径,AB⊥GH,∴EG=EH,∴DG=DH,∴AG=DG=DH=AH,∴四边形AGDH是菱形.(2)解:∵AB是直径,∴∠ACB=90°,∵AE⊥EF,∴∠AEF=∠ACB=90°,∵∠EAF=∠CAB,∴△AEF∽△ACB,∴AE EF AC BC=,∴124x yx=,∴y=18x2(x>0).(3)①解:如图1中,连接DF.∵GH垂直平分线段AD,∴FA=FD,∴当点D与O重合时,△AOF是等腰三角形,此时AB=2BC,∠CAB=30°,∴AB=833,∴⊙O的面积为163π.如图2中,当AF=AO时,∵AB=22AC BC+=216x+,∴OA=2 16x +,∵AF=22EF AE+=2221182x⎛⎫⎛⎫+⎪ ⎪⎝⎭⎝⎭,∴216x+=2221182x⎛⎫⎛⎫+⎪ ⎪⎝⎭⎝⎭,解得x=4(负根已经舍弃),∴AB=42,∴⊙O的面积为8π.如图2﹣1中,当点C与点F重合时,设AE=x,则BC=AD=2x,AB=2164x+,∵△ACE∽△ABC,∴AC2=AE•AB,∴16=2164x+解得x2=217﹣2(负根已经舍弃),∴AB2=16+4x2=817+8,∴⊙O的面积=π•14•AB2=(217+2)π综上所述,满足条件的⊙O的面积为163π或8π或(217+2)π;②如图3中,连接CG.∵AC=4,BC=3,∠ACB=90°,∴AB=5,∴OH=OA=52,∴AE=32,∴OE=OA﹣AE=1,∴EG=EH2512⎛⎫-⎪⎝⎭212,∵EF=18x2=98,∴FG 21﹣98,AF22AE EF+158,AH22AE EH+30,∵∠CFG=∠AFH,∠FCG=∠AHF,∴△CFG∽△HFA,∴GF CG AF AH=,∴219281530 8-=∴CG =5﹣10,=.故答案为【点睛】本题考查圆综合题、相似三角形的判定和性质、垂径定理、线段的垂直平分线的性质、菱形的判定和性质、勾股定理、解直角三角形等知识,解题的关键是学会添加常用辅助线,构造相似三角形解决问题,学会用分类讨论的思想思考问题.6.(1)223y x x =+-;(2)是,定值为8;(3)1557,416⎛⎫-⎪⎝⎭或939,416⎛⎫-- ⎪⎝⎭【解析】【分析】(1)把点A 、C 坐标代入抛物线解析式即可求得b 、c 的值.(2)设点Q 横坐标为t ,用t 表示直线AQ 、BN 的解析式,把x =1-分别代入即求得点M 、N 的纵坐标,再求DM 、DN 的长,即得到DM +DN 为定值.(3)点P 可以在x 轴上方或下方,需分类讨论.①若点P 在x 轴下方,延长AP 到H ,使AH =AB 构造等腰△ABH ,作BH 中点G ,即有∠PAB =2∠BAG =2∠ACO ,利用∠ACO 的三角函数值,求BG 、BH 的长,进而求得H 的坐标,求得直线AH 的解析式后与抛物线解析式联立,即求出点P 坐标.②若点P 在x 轴上方,根据对称性,AP 一定经过点H 关于x 轴的对称点H ',求得直线AH '的解析式后与抛物线解析式联立,即求出点P 坐标.【详解】解:(1)∵抛物线y =x 2+bx +c 经过点A (1,0),C (0,-3), ∴10003b c c ++=⎧⎨++=-⎩解得:23b c =⎧⎨=-⎩, ∴抛物线的函数表达式为y =x 2+2x -3.(2)结论:DM +DN 为定值.理由:∵抛物线y =x 2+2x -3的对称轴为:直线x =-1,∴D (﹣1,0),x M =x N =﹣1,设Q (t ,t 2+2t ﹣3)(﹣3<t <1),设直线AQ 解析式为y =dx +e∴2023d e dt e t t +=⎧⎨+=+-⎩解得:33d t e t =+⎧⎨=--⎩, ∴直线AQ :y =(t +3)x ﹣t ﹣3,当x =﹣1时,y M =﹣t ﹣3﹣t ﹣3=﹣2t ﹣6,∴DM =0﹣(﹣2t ﹣6)=2t +6,设直线BQ 解析式为y =mx +n ,∴23023m n mt n t t -+=⎧⎨+=+-⎩解得:133m t n t =-⎧⎨=-⎩,∴直线BQ:y=(t﹣1)x+3t﹣3,当x=﹣1时,y N=﹣t+1+3t﹣3=2t﹣2,∴DN=0﹣(2t﹣2)=﹣2t+2,∴DM+DN=2t+6+(﹣2t+2)=8,为定值.(3)①若点P在x轴下方,如图1,延长AP到H,使AH=AB,过点B作BI⊥x轴,连接BH,作BH中点G,连接并延长AG交BI于点F,过点H作HI⊥BI于点I.∵当x2+2x﹣3=0,解得:x1=﹣3,x2=1,∴B(﹣3,0),∵A(1,0),C(0,﹣3),∴OA=1,OC=3,AC221310+=AB=4,∴Rt△AOC中,sin∠ACO=01010AAC=,cos∠ACO=31010OCAC=,∵AB=AH,G为BH中点,∴AG⊥BH,BG=GH,∴∠BAG=∠HAG,即∠PAB=2∠BAG,∵∠PAB=2∠ACO,∴∠BAG=∠ACO,∴Rt△ABG中,∠AGB=90°,sin∠BAG=10 BGAB=,∴BG 10210AB=,∴BH=2BG 410,∵∠HBI+∠ABG=∠ABG+∠BAG=90°,∴∠HBI=∠BAG=∠ACO,∴Rt△BHI中,∠BIH=90°,sin∠HBI=HIBH=1010,cos∠HBI=31010BIBH=,∴HI 10BH=43,BI310BH=125,∴x H=411 355 -+=-,y H=125-,即1112,55H⎛⎫--⎪⎝⎭,设直线AH解析式为y=kx+a,∴111255k ak a+=⎧⎪⎨-+=-⎪⎩,解得:3434ka⎧=⎪⎪⎨⎪=-⎪⎩,∴直线AH:3344y x=-,∵2334423y xy x x⎧=-⎪⎨⎪=+-⎩解得:1xy=⎧⎨=⎩(即点A)或943916xy⎧=-⎪⎪⎨⎪=-⎪⎩,∴939,416P⎛⎫--⎪⎝⎭.②若点P在x轴上方,如图2,在AP上截取AH'=AH,则H'与H关于x轴对称.∴1112,55H⎛'⎫-⎪⎝⎭,设直线AH'解析式为y k x a='+',∴111255k ak a+='''⎧-'⎪⎨+=⎪⎩,解得:3434ka⎧=-⎪⎪⎨''⎪=⎪⎩,∴直线AH':3344y x=-+,∵2334423y xy x x⎧=-+⎪⎨⎪=+-⎩解得:1xy=⎧⎨=⎩(即点A)或1545716xy⎧=-⎪⎪⎨⎪=⎪⎩,∴1557,416P ⎛⎫- ⎪⎝⎭. 综上所述,点P 的坐标为939,416⎛⎫-- ⎪⎝⎭或1557,416⎛⎫- ⎪⎝⎭. 【点睛】本题属于二次函数综合题,考查了求二次函数解析式、求一次函数解析式,解一元二次方程、二元一次方程组,等腰三角形的性质,三角函数的应用.运用到分类讨论的数学思想,理清线段之间的关系为解题关键.7.(1)1;(2)①4b =-;②26c ≤<;(3)D 一定在线段AB 上,=CD 【解析】【分析】(1)根据题意顶点P (k ,h )可将二次函数化为顶点式:()2y a x k h =-+,又4y k =+与抛物线交于点A 、B ,无论h 、k 为何值,AB 的长度都为4,即可得出a 的值; (2)①根据抛物线x=0和x=4时函数值相等,可得到顶点P 的横坐标,根据韦达定理结合(1)即可得到b 的值,②根据(1)和(2)①即可得二次函数对称轴为x=2,利用点Q (0,2)关于对称轴的对称点R (4,2)可得QR=4,又QR 在直线y=2上,故令M 坐标(t ,2)(0≤t <2),代入二次函数即求得c 的取值范围;(3)由c=-b-1代入抛物线方程即可化简,将抛物线绕原点逆时针旋转αα,且tanα=2,转化为将y 轴绕原点顺时针旋转α得到直线l ,且tanα=2,可得到直线l 的解析式,最后联立直线方程与抛物线方程运算求解.【详解】解:(1)根据题意可知1二次函数2y ax bx c =++(a≠0)的顶点为P (k ,h ),故二次函数顶点式为()2y a x k h =-+,又4y k =+与抛物线交于点A 、B ,且无论h 、k 为何值,AB 的长度都为4,∴a=1;故答案为:a=1.(2)①∵二次函数当0x =和4x =时的函数值相等 ∴222b b x a =-=-= ∴4b =-故答案为:4b =-. ②将点Q 向右平移4个单位得点()4,2R当2c =时,242y x x =-+令2y =,则2242x x =-+解得14x =,20x =此时()0,2M ,()4,2N ,4MN QR ==∵4QM QN +=∵QM NR =∴4QN NR QR +==∴N 在线段QR 上,同理M 在线段QR 上设(),2M m ,则02m ≤<,224m m c =-+2242(2)6c m m m =-++=--+∵10-<,对称轴为2m =,02m ≤<∴c 随着m 的增大而增大∴26c ≤<故答案为:26c ≤<.(3)∵1c b =--∴21y x bx b =+--将抛物线绕原点逆时针旋转α,且tan 2α=,转化为将y 轴绕原点顺时针旋转α得到直线l ,且tan 2α=,∴l 的解析式为2y x =221y x y x bx b =⎧⎨=+--⎩∴2(2)10x b x b +---= ∴2224(2)448b ac b b b ∆=-=-++=+∴x =∴12,22b D b ⎛-+-++ ⎝⎭ 2224412444244AB ac b b b b y k b a ---+-+=+=+==-++124224AB D b y y b b ⎛⎫-+-=-++-++= ⎪⎝⎭∵20b ≥∴12404410444D AB b y y -+-+-=≥==> ∴点1D 始终在直线AB 上方∵222b C b ⎛-+--+- ⎝⎭∴222 24448 28244BC Ab b by y b b b⎛⎫-+--+ -=-+-+--++=⎪⎝⎭∴2222448848416 AB Cb b b by y-+++--++-+ -==()2282164b-+-+=∵2727b-<<,即2028b≤<,∴22284b≤+<设28n b=+,224n≤<∴2(2)164AB Cny y--+-=∵14-<,对称轴为2n=∴当224n≤<时,AB Cy y-随着n的增大而减小∴当4n=时,0AB Cy y-=∴当224n≤<时,AB Cy y>∴区域S的边界与l的交点必有两个∵1D ABy y>∴区域S的边界与l的交点D一定在线段AB上∴D ABy y=∴2(2)164D C CABny y y y--+-=-=∴当22n=时,D Cy y-有最大值122+此时1222D Cx x+-=由勾股定理得:()()2252102C CD DCD x x y y+=-+-=,故答案为:5210+=CD . 【点睛】 本题考查二次函数一般式与顶点式、韦达定理的运用,以及根与系数的关系判断二次函数交点情况,正确理解相关知识点是解决本题的关键.8.(1)21322y x x =-++;(2)92;(3)点P 的坐标为:3(2,)2或(4,52-)或(4-,212-). 【解析】【分析】(1)由图可知点B 、点D 的坐标,利用待定系数法,即可求出抛物线的解析式;(2)过点M 作ME ⊥AB 于点E ,由二次函数的性质,分别求出点A 、C 、M 的坐标,然后得到OE 、BE 的长度,再利用切割法求出四边形的面积即可;(3)由点Q 在y 轴上,设Q (0,y ),由平行四边形的性质,根据题意可分为:①当AB 为对角线时;②当BQ 2为对角线时;③当AQ 3为对角线时;分别求出三种情况的点P 的坐标,即可得到答案.【详解】解:(1)根据题意,抛物线212y x bx c =-++经过B 、D 两点, 点D 为(2-,52-),点B 为(3,0),则2215(2)22213302b c b c ⎧-⨯--+=-⎪⎪⎨⎪-⨯++=⎪⎩, 解得:132b c =⎧⎪⎨=⎪⎩,∴抛物线的解析式为21322y x x =-++; (2)∵22131(1)2222y x x x =-++=--+, ∴点M 的坐标为(1,2) 令213022x x -++=, 解得:11x =-,23x =,∴点A 为(1-,0);令0x =,则32y =, ∴点C 为(0,32); ∴OA=1,OC=32, 过点M 作ME ⊥AB 于点E ,如图:∴2ME =,1OE =,2BE =,∴111()222ABMC S OA OC OC ME OE BE ME =•++•+•四边形, ∴131313791(2)122222222442ABMC S =⨯⨯+⨯+⨯+⨯⨯=++=四边形; (3)根据题意,点Q 在y 轴上,则设点Q 为(0,y ),∵点P 在抛物线上,且以点A 、B 、P 、Q 为顶点的四边形是平行四边形,如图所示,可分为三种情况进行分析:①AB 为对角线时,则11PQ 为对角线;由平行四边形的性质,∴点E 为AB 和11PQ 的中点,∵E 为(1,0),∵点Q 1为(0,y ),∴点P 1的横坐标为2;当2x =时,代入21322y x x =-++, ∴32y =,∴点13(2,)2P ;②当BQ 2是对角线时,AP 也是对角线,∵点B (3,0),点Q 2(0,y ),∴BQ 2中点的横坐标为32,∵点A 为(1-,0),∴点P 2的横坐标为4,当4x =时,代入21322y x x =-++, ∴52y =-, ∴点P 2的坐标为(4,52-); ③当AQ 3为对角线时,BP 3也是对角线;∵点A 为(1-,0),点Q 3(0,y ),∴AQ 3的中点的横坐标为12-, ∵点B (3,0),∴点P 3的横坐标为4-,当4x =-时,代入21322y x x =-++, ∴212y =-, ∴点P 3的坐标为(4-,212-); 综合上述,点P 的坐标为:3(2,)2或(4,52-)或(4-,212-). 【点睛】本题考查了二次函数的性质,平行四边形的性质,解一元二次方程,以及坐标与图形等知识,解题的关键是熟练掌握二次函数的性质进行解题,注意利用分类讨论和数形结合的思想进行分析.9.(1) 见解析;(2) 2,2 ;(3)0或2或2x <<【解析】【分析】()1根据等腰三角形的定义,用分类讨论的思想解决问题即可;()2通过画图分析可得,当190∠=时,符合()1中条件的点C 有2个,当160∠=时,符合()1中条件的点C 有2个;()3分三种情形讨论求解即可.【详解】解:()1如图1中,点1C ,2C ,3C ,4C 即为所求.()2如图一,当190∠=时,符合()1中条件的点C 有2个;如图二,当160∠=时,符合()1中条件的点C 有2个,当∠1=90°或∠1=60°时,符合条件的点C 都是在点B 左右各一个,当∠1=60°时,符合条件的点C 如图所示:故答案为2,2.()3①如图31-中,当x 0=时,当PM PN =时,有点1P ,当ON OP =时,有点2P ,当NO NP =时,有点3P ,此时有3个P 点.②如图32-中,当N 与OB 相切于点1P 时,1OP N 是等腰直角三角形,1ON 2NP 22∴==,OM ON MN 222∴=-=-,此时有3个P 点.③如图33-中,当M 经过点O 时,此时只有2个P 点,如图34-中,M 与OB 相交时,此时有3个P 点,如图35-中,当M 与OB 相切时,只有2个P 点.此时OM 22=, 综上所述,当2x 22<<3个P 点.∴满足条件的x 的值为0或222或2x 22<<【点睛】本题考查等腰三角形的判定和性质,尺规作图,直线与圆的位置关系等知识,解题的关键是灵活运用所学知识解决问题,属于中考常考题型.10.(1)35,5784y x =+ ;(21722r ≤. 【解析】【分析】(1)①由矩形的任何一条边均与某条坐标轴平行,且A ,B ,C 三点都在矩形的内部或边界上,则称该矩形为点A ,B ,C 的覆盖矩形.点A ,B ,C 的所有覆盖矩形中,面积最小的矩形称为点A ,B ,C 的最优覆盖矩形,得出最优覆盖矩形的长为:2+5=7,宽为3+2=5,即可得出结果;②由定义可知,t=-3或6,即点C 坐标为(-3,-2)或(6,-2),设AC 表达式为y=kx+b ,代入即可求出结果;(2)OD所在的直线交双曲线于点E,矩形OFEG是点O,D,E的一个面积最小的最优覆盖矩形,OD所在的直线表达式为y=x,得出点E的坐标为(2,2),⊙P的半径最小r=2,当点E的纵坐标为1时,⊙P的半径最大r=17,即可得出结果.【详解】(1)①∵A(﹣2,3),B(5,0),C(2,﹣2),矩形的任何一条边均与某条坐标轴平行,且A,B,C三点都在矩形的内部或边界上,则称该矩形为点A,B,C的覆盖矩形.点A,B,C的所有覆盖矩形中,面积最小的矩形称为点A,B,C的最优覆盖矩形,∴最优覆盖矩形的长为:2+5=7,宽为3+2=5,∴最优覆盖矩形的面积为:7×5=35;②∵点A,B,C的最优覆盖矩形的面积为40,∴由定义可知,t=﹣3或6,即点C坐标为(﹣3,﹣2)或(6,﹣2),设AC表达式为y=kx+b,∴3223k bk b=-+⎧⎨-=-+⎩或3226k bk b=-+⎧⎨-=+⎩∴513kb=⎧⎨=⎩或5874kb⎧=-⎪⎪⎨⎪=⎪⎩∴y=5x+13或5784y x=-+;(2)①OD所在的直线交双曲线于点E,矩形OFEG是点O,D,E的一个面积最小的最优覆盖矩形,如图1所示:∵点D(1,1),∴OD所在的直线表达式为y=x,∴点E的坐标为(2,2),∴OE222+2=22∴⊙P的半径最小r2②当DE∥x轴时,即:点E的纵坐标为1,如图2所示:∵点D (1,1).E (m ,n )是函数y =4x (x >0)的图象上一点 ∴1=4x ,解得x =4, ∴OE ═224+117, ∴⊙P 的半径最大r 17, 172r ≤. 【点睛】 本题是圆的综合题目,考查了矩形的性质、勾股定理、待定系数法求直线的解析式、坐标与图形性质、反比例函数等知识;本题综合性强,有一定难度.11.(1)t =3;(2)P (35t +2,45t ﹣4);(3)t 的值为209秒或4秒或16秒或1609秒 【解析】【分析】(1)如图1,过点C 作CP ⊥OA ,交x 轴于点P .就可以求出OP 的值,由勾股定理就可以求出的OP 值,进而求出结论;(2)t <10时,P 在OA 或AB 上运动,所以分两种情况:①当0≤t≤5时,如图1,点P 在OA 上,OP=t ,可得P 的坐标;②当5<t <10时,如图2,点P 在AB 上,构建直角三角形,根据三角函数定义可得P 的坐标;(3)设切点为G ,连接PG ,分⊙P 与四边相切,其中P 在AB 和BC 时,与各边都不相切,所以分两种情况:①当P 在OA 上时,根据三角函数列式可得t 的值;②当P 在OC 上时,同理可得结论.【详解】(1)如图1,当CP ⊥OA 时,sin ∠AO 45CP C OC==, 4455CP CP 即=,=, 在Rt △OPC 中,OC =5,PC =4,则OP =3,∴331t ==(2)当0≤t ≤5时,如图1,点P 在OA 上,∴P (t ,0);当5<t <10时,如图2,点P 在AB 上,过P 作PH ⊥x 轴,垂足为H ,则∠AOC =∠PAH ,∴sin ∠PAH =sin ∠AO 45C =, 44 4555PH PH t t ∴=-即=﹣, ∴333255HA t OH OA AH t ++=﹣,==,∴34P t+2t 455(,﹣);(3)设切点为G ,连接PG ,分两种情况:①当P 在OA 上时,如图3,⊙P与直线AB相切,∵OC∥AB,∴∠AOC=∠OAG,∴sin∠AOC=sin∠OA45PGGAP==,t45-t5 =,∴209t=;⊙P与BC相切时,如图4,则PG=t=OP=4;②当点P在OC上时,⊙P与AB相切时,如图5,∴OP=PG=4,∴4×5﹣t=4,t=16,⊙P与直线BC相切时,如图6,∴PG ⊥BC ,∵BC ∥AO ,∴∠AOC =∠GCP ,∴sin ∠AOC =sin ∠GC 45PG P PC ==, ∵OP =PG =20﹣t , ∴42051t t -=-, ∴1609t =, 综上所述,t 的值2016041699为秒或秒或秒或秒 【点睛】本题考查了菱形的性质、直角三角形的性质、勾股定理、锐角三角函数等知识,解答时运用等角的三角函数列方程是关键,并注意运用分类讨论的思想,做到不重不漏.12.(1)12;(2)tan EAD ∠=13;(3)51DE CD -= 【解析】【分析】(1)先证明△ADP ≌△CDP ,得到∠DAP=∠DCP ,再证明△ADE ≌△CDO ,得到DE=DO ,根据O 是AD 的中点,AD=CD ,即可得到答案;(2)先证明△AFD ≌△DOC ,得到∠AFD=∠DOC ,进而得到∠OPD=90°,即可得到△OPD ∽△FAD ,根据对应边成比例得到DP OD AD DF =,设AF=OD=x ,则AD=2x ,5x ,得到25x ,求出35x ,再证明△DEP ∽△FAP ,得到23DE AF =,根据AF=12CD ,即可得到答案;(3)先证明△FCD ≌△EDA ,得到∠EAD=∠FDC ,进而得到∠EPD=∠APD=90°,根据直角三角形的性质可得OP=OD=12AD ,设OD=OP=x ,则CD=2x ,5x ,可得PC=OC-5x x -,根据△DPO ∽△FPC ,得到51OD FC +=,进而得到51251CF CD ==+,即可得到结论.【详解】(1)如图①中,∵四边形ABCD 是正方形,PDA PDC ∴∠=∠,DP DP =,DA DC =,PDA ∴≌()PDC SAS ,DAE DCO ∴∠=∠,90ADE CDO ∠=∠=︒,AD CD =,ADE ∴≌()CDO ASA ,OD DE ∴=,AO OD ∴=,CE DE ∴=,12DE DC ∴=. (2)如图②中,连接OF .设OA OD a ==.AF FB =,OA OD =,AB AD =,AF OD ∴=,AD DC =,90FAD ODC ∠=∠=︒,FAD ∴≌()ODC SAS ,FDA OCD ∴∠=∠,90FDA CDP ∠=∠=︒,∴ 90OCD CDP ∠=∠=︒,90CPD ∴∠=︒,90FAO FPO ∠=∠=︒,∴A ,F ,P ,O 四点共圆,PAO PFO ∴∠=∠,1tan 2OP OPD PD∠==, 5OP a ∴=,25PD a =, 5DF a =,35PF a ∴=, 1tan tan 3OP PFO PAO PF ∴∠=∠==, tan EAD ∴∠= 13DE DE AD CD ==. (3)如图③中,连接EF .设CF DE y ==,EC x =.CF DE =,90FCD EDA ∠=∠=︒,CD DA =,∴ FCD ≌EDA ()SAS ,CDF EAD ∴∠=∠,90CDF ADP ∠=∠=︒,∴ 90DAE ADP ∠+∠=︒,∴ 90APD ∠=︒,OA OD =,∴ OP OA OD ==,∴ OAP OPA CPE ∠=∠=∠,90ECF EPF ∠=∠=︒,∴E ,C ,F ,P 四点共圆,∴ CFE EPC ∠=∠,∴ CFE DCF ∠=∠,ECF DCF ∠=∠,∴ FCE ∽DCF ,∴ 2·CF CE CD =,∴ ()2y x x y =+,∴ 220y xy x --=,∴ y x =x (舍弃),∴ 12y x +=,∴ DE y CD x y ===+. 【点睛】本题考查了正方形的性质,全等三角形的判定和性质,相似三角形的判定与性质,求根公式法解一元二次方程,锐角三角函数及四点共圆等知识,用到的知识点较多,难度较大,解题的关键是学会利用参数解决问题,属于中考压轴题.。
2023年九年级数学中考专题:二次函数综合压轴题附答案附答案
2023年九年级数学中考专题:二次函数综合压轴题附答案1.如图,已知抛物线2y x bx c =++(b ,c 是常数)与x 轴交于()1,0A ,()3,0B -两点,顶点为C ,点P 为线段AB 上的动点(不与A 、B 重合),过P 作PQ BC ∥交抛物线于点Q ,交AC 于点D .(1)求该抛物线的表达式;(2)求CPD △面积的最大值;(3)连接CQ ,当CQ PQ ⊥时,求点Q 的坐标;(4)点P 在运动过程中,是否存在以A 、O 、D 为顶点的三角形是等腰三角形?若存在,求出所有点P 的坐标;若不存在,请说明理由2.在平面直角坐标系中,抛物线24y x x c =--+与x 轴交于点A ,B (点A 在点B 的左侧),与y 轴交于点C ,且点A 的坐标为()5,0-.(1)求点C 的坐标;(2)如图1,若点P 是第二象限内抛物线上一动点,求点P 到直线AC 距离的最大值,并求出此时点P 的坐标;(3)如图2,若点M 是抛物线上一点,点N 是抛物线对称轴上一点,是否存在点M 使以A ,C ,M ,N 为顶点的四边形是平行四边形?若存在,请直接写出点M 的坐标;若不存在,请说明理由.3.已知:如图,抛物线()2430y mx mx m =++>交x 轴于E 、F 两点,交y 轴于A 点,直线AE :y x b =+交x 轴于E 点,交y 轴于A 点.(1)求抛物线的解析式;(2)若Q 为抛物线上一点,连接,QE QA ,设点Q 的横坐标为()3t t <-,QAE 的面积为S ,求S 与t 函数关系式;(不要求写出自变量t 的取值范围)(3)在(2)的条件下,点M 在线段QA 上,点N 是位于Q 、E 两点之间的抛物线上一点,15S =,QMN AEM ∠=∠,且MN EM =,求点N 的坐标.4.如图,抛物线22y ax ax c =++经过()()1003B C ,,,两点,与x 轴交于另一点A ,点D 是抛物线的顶点.(1)求抛物线的解析式及点D 的坐标;(2)如图1,连接AC ,点E 在直线AC 上方的抛物线上,连接EA EC ,,当EAC 面积最大时,求点E 坐标;(3)如图2,连接AC BC 、,在抛物线上是否存在点M ,使ACM BCO ∠=∠,若存在,求出M 点的坐标;若不存在,请说明理由.5.抛物线21164y ax x =+-与x 轴交于(,0),(8,0)A t B 两点,与y 轴交于点C ,直线6y kx =-经过点B .点P 在抛物线上,设点P 的横坐标为m .(1)求二次函数与一次函数的解析式;(2)如图1,连接AC ,AP ,PC ,若APC △是以CP 为斜边的直角三角形,求点P 的坐标;(3)如图2,若点P 在直线BC 上方的抛物线上,过点P 作PQ BC ⊥,垂足为Q ,求12CQ PQ +的最大值.6.在平面直角坐标系中,抛物线223y x x =-++与x 轴交于点A 、B (A 在B 左侧),与y 轴交于点C ,顶点为D ,对称轴为直线l ,点P 是抛物线上位于点B 、C 之间的动点.(1)求ABC ∠的度数;(2)若PBC ACO ∠=∠,求点P 的坐标;(3)已知点(),P p n ,若点(),Q q n 在抛物线上,且p q >;①仅用无刻度的直尺在图2中画出点Q ;②若2PQ t =,求232022p tq t +-+的值.7.如图,在平面直角坐标系中,抛物线2y x bx c =-++经过()0,1A ,()4,1B -.直线AB 交x 轴于点C ,P 是直线AB 上方且在对称轴右侧的一个动点,过P 作PD AB ⊥,垂足为D ,E 为点P 关于抛物线的对称轴的对应点.(1)求抛物线的函数表达式;(2)PE +的最大值时,求此时点P PE +的最大值;(3)将抛物线y 关于直线3x =作对称后得新抛物线y ',新抛物线与原抛物线相交于点F ,M 是新抛物线对称轴上一点,N 是平面中任意一点,是否存在点N ,使得以C ,F ,M ,N 为顶点的四边形是菱形,写出所有符合条件的点N 的坐标,并写出求解点N 的坐标的其中一种情况的过程.8.如图所示,在平面直角坐标系中,直线3y x =-+交坐标轴于B 、C 两点,抛物线23y ax bx =++经过B 、C 两点,且交x 轴于另一点()1,0A -.点D 为抛物线在第一象限内的一点,过点D 作DQ CO ∥,DQ 交BC 于点P ,交x 轴于点Q .(1)求抛物线的解析式;(2)设点P 的横坐标为m ,在点D 的移动过程中,存在DCP DPC ∠=∠,求出m 值;(3)在抛物线上取点E ,在平面直角坐标系内取点F ,问是否存在以C 、B 、E 、F 为顶点且以CB 为边的矩形?如果存在,请求出点F 的坐标;如果不存在,请说明理由.9.在平面直角坐标系中,抛物线2y ax bx c =++与x 轴交于点()1,0A -和点B ,与y 轴交于点C ,顶点D 的坐标为()1,4-.(1)求出抛物线的解析式;(2)如图1,若点P 在抛物线上且满足PCB CBD ∠=∠,求点P 的坐标;(3)如图2,M 是线段CB 上一个动点,过点M 作MN x ⊥轴交抛物线于点N ,Q 是直线AC 上一个动点,当QMN 为等腰直角三角形时,直接写出此时点M 的坐标.10.二次函数2y ax bx c =++交x 轴于点()10A -,和点()30B -,,交y 轴于点()03C -,.(1)求二次函数的解析式;(2)如图1,点E 为抛物线的顶点,点()0T t ,为y 轴负半轴上的一点,将抛物线绕点T 旋转180︒,得到新的抛物线,其中B ,E 旋转后的对应点分别记为B E '',,当四边形BEB E ''的面积为12时,求t 的值;(3)如图2,过点C 作CD x ∥轴,交抛物线于另一点D .点M 是直线CD 上的一个动点,过点M 作x 轴的垂线,交抛物线于点P .是否存在点M 使PBC 为直角三角形,若存在,请直接写出点M 的坐标,若不存在,请说明理由.11.如图,已知抛物线2y ax 2x c =++交x 轴于点()10A -,和点()30B ,,交y 轴于点C ,点D 与点C 关于抛物线的对称轴对称.(1)求该抛物线的表达式,并求出点D 的坐标;(2)若点E 为该抛物线上的点,点F 为直线AD 上的点,若EF x ∥轴,且1EF =(点E 在点F 左侧),求点E 的坐标;(3)若点P 是该抛物线对称轴上的一个动点,是否存在点P ,使得APD △为直角三角形?若不存在,请说明理由;若存在,直接写出点P 坐标.12.在平面直角坐标系中,O 为坐标原点,直线3y x =-+与x 轴、y 轴分别交于B 、C 两点,抛物线2y x bx c =-++经过B 、C 两点,与x 轴的另一个交点为A .(1)如图1,求b 、c 的值;(2)如图2,点P 是第一象限抛物线2y x bx c =-++上一点,直线AP 交y 轴于点D ,设点P 的横坐标为t ,ADC △的面积为S ,求S 与t 的函数关系式;(3)如图3,在(2)的条件下,E 是直线BC 上一点,45EPD ∠=︒,ADC △的面积S 为54,求E 点坐标.13.抛物线24y ax =-经过A 、B 两点,且OA OB =,直线EC 过点()41E -,,()03C -,,点D 是线段OA (不含端点)上的动点,过D 作PD x ⊥轴交抛物线于点P ,连接PC 、PE .(1)求抛物线与直线CE 的解析式;(2)求证:PC PD +为定值;(3)在第四象限内是否存在一点Q ,使得以C 、P 、E 、Q 为顶点的平行四边形面积最大,若存在,求出Q 点坐标;若不存在,请说明理由.14.如图,已知抛物线()230y ax bx a =++≠与x 轴交于()1,0A 、()4,0B 两点,与y 轴交于点C ,点D 为抛物线的顶点.(1)求抛物线的函数表达式及点D 的坐标;(2)若四边形BCEF 为矩形,3CE =.点M 以每秒1个单位的速度从点C 沿CE 向点E 运动,同时点N 以每秒2个单位的速度从点E 沿EF 向点F 运动,一点到达终点,另一点随之停止.当以M 、E 、N 为顶点的三角形与BOC 相似时,求运动时间t 的值;(3)抛物线的对称轴与x 轴交于点P ,点G 是点P 关于点D 的对称点,点Q 是x 轴下方抛物线上的动点.若过点Q 的直线l :94y kx m k ⎛⎫=+< ⎪⎝⎭与抛物线只有一个公共点,且分别与线段GA 、GB 相交于点H 、K ,求证:GH GK +为定值.15.在平面直角坐标系中,已知抛物线2y ax bx =+经过(40)(13)A B ,,,两点.P 是抛物线上一点,且在直线AB的上方.(1)求抛物线的表达式;(2)若OAB 面积是PAB 面积的2倍,求点P 的坐标;(3)如图,OP 交AB 于点C ,PD BO ∥交AB 于点D .记CPB △,BCO 的面积分别为12S S ,,判断12S S 是否存在最大值.若存在,求出最大值;若不存在,请说明理由.16.已知抛物线212y x bx c =-++(b 、c 是常数)的顶点B 坐标为()1,2-,抛物线的对称轴为直线l ,点A 为抛物线与x 轴的右交点,作直线AB .点P 是抛物线上的任意一点,其横坐标为m ,过点P 作x 轴的垂线交直线AB 于点Q ,过点P 作PN l ⊥于点N ,以PQ PN 、为边作矩形PQMN .(1)b =___________,c =___________.(2)当点Q 在线段AB 上(点Q 不与A 、B 重合)时,求PQ 的长度d 与m 的函数关系式,并直接写出d 的最大值.(3)当抛物线被矩形PQMN 截得的部分图象的最高点纵坐标与最低点纵坐标的距离为2时,求点P 的坐标.(4)矩形PQMN 的任意两个顶点到直线AB 的距离相等时,直接写出m 的值.17.如图1.在平面直角坐标系中,抛物线2(0)y ax bx c a =++≠与x 轴交于点()2,0A -,点()4,0B ,与y 轴交于点()0,2C .(2)点P 是第一象限内的抛物线上一点.过点P 作PH x ⊥轴于点H ,交直线BC 于点Q ,求PQ 的最大值,并求出此时点P 的坐标;(3)如图2.将地物线沿射线BC()2111110y a x b x c a =++≠,新抛物线与原抛物线交于点G ,点M 是x 轴上一点,点N 是新抛物线上一点,若以点C 、G 、M 、N 为顶点的四边形是平行四边形时,请直接写出点N 的坐标.18.如图,抛物线()20y ax bx c a =++≠与x 轴交于A 、B 两点,与y 轴交于点()0,6C ,顶点为D ,且()1,8D .(1)求抛物线的解析式;(2)若在线段BC 上存在一点M ,过点O 作OH OM ⊥交BC 的延长线于H ,且MO HO =,求点M 的坐标;(3)点P 是y 轴上一动点,点Q 是在对称轴上一动点,是否存在点P ,Q ,使得以点P ,Q ,C ,D 为顶点的四边形是菱形?若存在,求出点Q 的坐标;若不存在,请说明理由.参考答案:1.(1)223y x x =+-(2)2(3)11524Q ⎛⎫-- ⎪⎝⎭(4)1,05⎛⎫- ⎪ ⎪⎝⎭或()0,0或1,05⎛⎫ ⎪⎝⎭2.(1)()0,5(2)点P 到直线AC 距离为8,此时535,24P ⎛⎫- ⎪⎝⎭(3)点M 的坐标为()3,8-或()7,16--或()3,16-3.(1)243y x x =++(2)23922S t t =+(3)()2N -4.(1)223y x x =--+,()14D -,(2)E 的坐标为31524⎛⎫- ⎪⎝⎭,(3)存在,()45M --,或5724⎛⎫- ⎪⎝⎭,5.(1)2111644y x x =-+-;364y x =-(2)710,2P ⎛⎫- ⎪⎝⎭(3)169166.(1)45︒(2)(1,4)P(3)①见解析;②20237.(1)2712y x x =-++PE +的最大值为1,此时点P 的坐标为961,416⎛⎫ ⎪⎝⎭(3)存在点N ,使以C ,F ,M ,N 为顶点的四边形是菱形,此时点N 的坐标为215,424N ⎛+ ⎝⎭或215,424⎛- ⎝⎭或13,544N ⎛⎫+ ⎪ ⎪⎝⎭或13,544N ⎛- ⎝⎭或299,204N ⎛⎫ ⎪⎝⎭8.(1)223y x x =-++(2)2m =(3)存在,此时点F 的坐标为()4,1或()5,2--9.(1)2=23y x x --(2)满足PCB CBD ∠=∠,点P 的坐标为(4,5)或(2,2)-(3)M 点的坐标为(1,2)-或(2,5)--或924,55⎛⎫-- ⎪⎝⎭10.(1)243y x x =---(2)3t =-(3)存在,532⎛⎫-- ⎪ ⎪⎝⎭或532⎛⎫-- ⎪ ⎪⎝⎭或(23)--,或(53)--,11.(1)223y x x =-++,()23D ,(2)11024E ++⎝⎭,或1124E --+⎝⎭,(3)存在点P ,使得APD △为直角三角形,此时点P 的坐标为312⎛⎫+ ⎪⎝⎭,或312⎛ ⎝⎭,或()12-,或()14,12.(1)2b =,3c =(2)12S t =(3)3513,1616⎛⎫ ⎪⎝⎭13.(1)2144y x =-;132y x =-(2)见解析(3)存在,754Q ⎛⎫- ⎪⎝⎭,14.(1)2315344y x x =-+,527,216D ⎛⎫- ⎪⎝⎭(2)当911t =或65t =时(3)见解析15.(1)24y x x=-+(2)(24)P ,或(3,3)(3)见解析16.(1)1-,32(2)21122d m =-+()11m -<<,d 最大值为12(3)()3,0-或1--(4)3-或0或317.(1)211242y x x =-++;(2)5PQ +最大值为94,此时点5(3,4P ;(3)(1-,14-或(1-,1)4-或(1-+1)4或(1--1)4.18.(1)2246y x x =-++(2)129,55⎛⎫ ⎪⎝⎭(3)(1,8或(1,8或271,4⎛⎫ ⎪⎝⎭。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
矿产资源开发利用方案编写内容要求及审查大纲
矿产资源开发利用方案编写内容要求及《矿产资源开发利用方案》审查大纲一、概述
㈠矿区位置、隶属关系和企业性质。
如为改扩建矿山, 应说明矿山现状、
特点及存在的主要问题。
㈡编制依据
(1简述项目前期工作进展情况及与有关方面对项目的意向性协议情况。
(2 列出开发利用方案编制所依据的主要基础性资料的名称。
如经储量管理部门认定的矿区地质勘探报告、选矿试验报告、加工利用试验报告、工程地质初评资料、矿区水文资料和供水资料等。
对改、扩建矿山应有生产实际资料, 如矿山总平面现状图、矿床开拓系统图、采场现状图和主要采选设备清单等。
二、矿产品需求现状和预测
㈠该矿产在国内需求情况和市场供应情况
1、矿产品现状及加工利用趋向。
2、国内近、远期的需求量及主要销向预测。
㈡产品价格分析
1、国内矿产品价格现状。
2、矿产品价格稳定性及变化趋势。
三、矿产资源概况
㈠矿区总体概况
1、矿区总体规划情况。
2、矿区矿产资源概况。
3、该设计与矿区总体开发的关系。
㈡该设计项目的资源概况
1、矿床地质及构造特征。
2、矿床开采技术条件及水文地质条件。
