小学奥数题目-一年级-几何-数图形知识点习题
小学奥数--几何模型分类总结汇总版(鸟头、燕尾、风筝、一般模型等)

目录目录 (1)模型一——《等积变换》 (2)一、知识点梳理 (2)二、例题精讲 (3)三、自我提升 (5)四、答案与解析 (7)模型二——《一半模型》 (11)一、知识点梳理 (11)二、例题精讲 (13)三、自我提升 (15)四、答案与解析 (16)模型三——《鸟头(共角)模型》 (19)一、知识点梳理 (19)二、例题精讲 (20)三、自我提升 (22)四、答案与解析 (24)模型四——《蝴蝶模型》 (25)一、知识点梳理 (25)二、例题精讲 (26)模型五——《沙漏模型》 (32)一、知识点梳理 (32)二、例题精讲 (32)三、自我提升 (35)四、答案与解析 (36)模型六——《燕尾模型》 (38)一、知识点梳理 (38)二、例题精讲 (39)三、自我提升 (41)四、答案与解析 (43)模块七——《长、正方体、圆柱、圆锥》 (45)一、知识点梳理 (45)二、例题精讲 (46)三、自我提升 (48)四、自我提升答案 (50)模型八——《圆、扇形》 (52)一、知识点梳理 (52)二、例题精讲 (53)三、自我提升 (55)四、答案与解析 (57)模型一——《等积变换》一、知识点梳理二、例题精讲三、自我提升四、答案与解析模型二——《一半模型》一、知识点梳理一半模型其实是等积变换模型的延伸,只是将三角形和平行四边形进行了整合与综合考查,但是学生往往遇到此类题目之后很难想到用等积变换,所以我们专门提炼出一半模型,帮助学生加深此部分知识点的理解,提高应用能力。
21b a ba ⨯⨯====⨯=∆∆∆∆BCP S BCD S BCF S BCE S ABCD S 口 平行四边形同理不规则图形ba 21b2b1a 21b2a 21b1a 21b2a 21b1a 21ba ⨯=+⨯=⨯⨯+⨯=+=⨯⨯=⨯=⨯=∆∆∆∆)(阴影;口BCE S ADE S BCE S ADE S ABCD S 拓展图形(比例应用)ba 41b2b1a 41b2221b1221b2221b1221b41b 221⨯=+⨯=⨯⨯+⨯⨯=+=⨯⨯=⨯⨯=⨯=⨯⨯==∆∆∆∆∆)(阴影;右图:左图:阴影a a BEG S AFG S aBEG S a AFG S a a BFE S常见图形的认识二、例题精讲例1如图所示,四边形ABCD与AEGF都是平行四边形,请你证明它们的面积相等.例2如图所示,正方形ABCD的边长为8厘米,长方形EBGF的长BG为10厘米,那么长方形的宽为几厘米?例3如图,正方形ABCD的边长为6,AE=1.5,CF=2.长方形EFGH的面积为.例4图中两个正方形的边长分别是6厘米和4厘米,则图中阴影部分三角形的面积是多少平方厘米.A BG CEFDHGFEDCBAGFED CBA例5正方形ABCD 和正方形CEFG ,且正方形ABCD 边长为10厘米,则图中阴影面积为多少平方厘米?例6如图,长方形ABCD 的面积是56平方厘米,点E 、F 、G 分别是长方形ABCD 边上的中点,H 为AD 边上的任意一点,求阴影部分的面积例7 如图,有三个正方形的顶点D 、G 、K 恰好在同一条直线上,其中正方形GFEB 的边长为10厘米,求阴影部分的面积.E BA KEBA三、自我提升1、右图是由大、小两个正方形组成的,小正方形的边长是4厘米,求三角形ABC 的面积.2、如图,ABCD 与AEFG 均为正方形,三角形ABH 的面积为6平方厘米,图中阴影部分的面积为 .3、长方形ABCD 的面积是2011平方厘米.梯形AFGE 的顶点F 在BC 上,D 是腰EG 的中点.试求梯形AFGE 的面积.G4AB CDEF A B C D E FG H4、已知正方形ABCD 边长为10,正方形BEFG 边长为6,求阴影部分的面积.5、右图中,ABCD 和CGEF 是两个正方形,AG 和CF 相交于H ,已知CH 等于CF 的三分之一,三角形CHG 的面积等于6平方厘米,求五边形ABGEF 的面积.6、如图,正方形ABCG 和正方形FCDE 并排放置,BE 与FC 相交于点H ,已知AB=6厘米,则阴影部分的面积是_________________平方厘米? 四、答案与解析1、【分析】如图所示,连接AD ,则BC 平行AD ,三角形ABC 和三角形BCD 等底等高,因此三角形ABCJIHGA BCD EF HG F E D C B A的面积就等于小正方形的面积的一半,据此即可得解.解:据分析可知:4×4÷2=8(平方厘米);答:三角形ABC的面积是8平方厘米.2、【分析】方法一:如图所示,连接AF和BD,则AF平行BD,三角形FAD与三角形FAB等底等高,即面积相同。
小学奥数-数数图形

例题:下面图形中有多少正方形?
难度: 适用范围:小学三年级及以上
题目解析:
采用分类数的方法,仔细数,不要遗漏。
题目
类数的方法,
首先确定正方形的类型,一共上面3种,分别数这3种 正方形的个数,按照一定的顺序数,仔细数☺。
3 × 6 = 18 (个) 5 × 2 = 10 (个)
4 × 1 = 4 (个) 合计:18 + 10 + 4 = 32(个)
题目解析:
难度: 适用范围:小学三年级及以上
A
E
F
G
B
J
M
I
D
C
题目
像 AFG一样的三角形有5个。 像 ABF一样的三角形有10个。 像 ABG一样的三角形有5个。 像 ABE一样的三角形有5个。 像 ACD一样的三角形有5个。
图中共有: 5+10+5+5+5+5=35(个) 三角形。
像 A MD一样的三角形有5个。
数数图形(五)
例题:数一数图中共有多少个三角形?
题目解析: 最小的小三角形有16个。
难度: 适用范围:小学三年级及以上
两个小三角形拼接成的三角形有10个。 图中共有
16 +10 + 8+ 2 =36(个)
题目
四个小三角形拼接成的三角形有8个。 三角形。
八个小三角形拼接成的三角形有2个。
数数图形(四)
数数图形(二)
例题:下面图形中有多少个三角形?
题目解析:
继续采用分类数的方法
小三角形共5个。
难度: 适用范围:小学三年级及以上
两个小三角形组成的三角形共6个。
题目
(完整版)小学一年级奥数题及答案 - 100道综合练习题及答案

an d A l l t h i n g s i n t h e i r b e i n g a r e g o o d f o r s o 7. 在一个箱子里面,乱七八糟的放着4只红色袜子和4只白色袜子。
现在小红把手伸进去摸,请问至少摸几只就能保证拿到相同颜色的袜子?答案:2+1=3(只),至少摸3只就能保证拿到相同颜色的袜子8. 数一数共有多少个角?答案:共有3个角9. 小青两次画了17个 ,第一次画了9个,第二次画了多少个?答案:17-9=8(个),所以第二次画了8个10. 0、3、6、9、12、( )、( )答案:后一项总比前一项多3,所以 0、3、6、9、12、(15 )、( 18 )11. 花园里有兰花40盆,菊花60盆,兰花再种多少盆就和菊花同样多?答案:2012. 天色已晚,妈妈叫小明打开房间电灯,可淘气的小明一连拉了9下开关。
请你说说这时灯是亮还是不亮?拉20下呢?拉100下呢? 【小结】初步认识奇偶数的概念。
答案:开、关、关。
13. 小动物们举行动物运动会,在长跑比赛中有4只动物跑在小松鼠的前面,有3只动物跑在小松鼠的后面,一共有几只动物参加长跑比赛?答案:这道题要明确问题的关键,我们可以把跑步的所有小动物看成一个队列,小松鼠前面有4只小动物,后面有3只小动物,在这个队列中,就是没有数松鼠自己,所以求这队的总数还要把小松鼠加上。
4+3+1=8(只),一共有8只动物参加长跑比赛。
14. 小强和大强的苹果数相同,小强把自己的苹果给了大强2个,那么现在大强的苹果比小强多了多少个?答案:2+2=4(个)15. 1、2、3、4、5这5个数的和是单数还是双数?答案:单数16.爷爷家有15个萝卜,爷爷要给家里的每个小兔子都吃一个萝卜,喂到最后还剩下3个萝卜。
小朋友,你知道爷爷家一共有多少只小兔子吗?答案:15-3=12(只),爷爷家一共有12只兔子17.三个人吃3个馒头,用3分钟才吃完;照这样计算,九个人吃9个馒,需要分钟才吃完?答案:318.煮熟2个生鸡蛋用6分钟,煮熟10个生鸡蛋用几分钟?答案:煮熟2个生鸡蛋用6分钟,煮10个生鸡蛋当然会放在一个锅里煮,煮熟的时候还是需要6分钟了19. 1、2、3、4、5、7、9这7个数的和是单数还是双数?答案:单数(有5个单数)20.你知道2,5,8,11,14,17,20,23,26,29相加和是单数还是双数?答案:单数21.小明拍皮球,第一次拍35下,第二次比第一次少拍7下,第二次拍多少下?答案:2822. 24+21+5+6的结果是单数还是双数?答案:双数23.一条马路两旁各种上48棵树,一共种树多少棵?答案:48+48=96(棵),所以一共种树96棵24.在10米长的一段马路的一侧种树,每隔1米种一棵,两头都种,共种11棵,如果把三块“爱护树木”的小牌任意挂在三棵树上,然后再把每两棵挂牌的树之间的距离是多少米?答案:825. 45个小朋友排成一队去春游。
小学奥数题目-一年级-数字敏感度类-数阵图之初步知识点习题

数阵图1.概念简析数阵图:就是把一些数按照一定的规则,排列成各种各样的图形,这种图形就称作数阵图。
幻方就是一种特殊的数阵图,而数独可以说是幻方的延伸。
2.解题步骤(1)分拆法:将总和进行拆分。
(2)求关键数:其中的关键数也叫公共数。
例1如右图所示,把适当的数填到三角形的空圈里,使每条直线上3个圈中的数相加都是10.1.在圆圈中填数,使每条线上的三个数之和都等于15.问空白处的三个数的和为_______.2.在下面的○里填上适当的数,使每条线上的三个数之和都是12.问空白处的三个数之和为_________.例2如右图,把3、4、6、7四个数填在四个空格里,使横行、竖行三个数相加都等于14,问怎么填?1.把3、4、5、6、7这五个数字分别填入下图的五个方格中,使横行、竖列三个数的和都是14。
问最中间的数字为_____.2.把数字1,2,3,5,6,7,9填在下面的○里,使每边上的和为15.问最上行左右两个数字之和为_______.例3如右图所示,把1、2、3、4、5五个数填入五个圆圈内,要求分别满足以下条件:(1)使横行、竖行圆圈里的数加起来都等于8;(2)使横行、竖行圆圈里的数加起来都等于9;(3)使横行、竖行圆圈里的数加起来都等于10.1.见图。
把2、3、4、5、6填入下图的五个方格里,使横行、竖行三个数之和相等,那么当它们的和取11、12、13时。
问最中间数分别是___、___、___.(按前后顺序回答,答案用一个空格隔开,例如:2 3 4)2.将1,2,3,4,5,6这6个数分别填入下图中,使两个大圆上4个数的和都等于14.问已知数字4上面的数字为_______.例4如右图所示,圆圈里填上不同的数,使每条直线上的三个数相加之和都等于10.1.把2,3,4,5,6这五个数分别填入圆圈中,使每条线上三个数相加的和都等于12.问最中间的数为______.2.把3,4,5,6,7这五个数分别填入下面的空格里,使横行、竖行的三个数相加都得15.问最中间的数为_______.例5如图所示,在圆圈里填上不同的数,使每条直线上三个数相加之和都是15.(圆圈内数字不考虑数字0)1.在下列两图的空格中填上数,使每条对角线上的三个数相加都等于16(圆圈中的数字不能相同,也不考虑数字0)。
小学奥数-几何五大模型(鸟头模型)

模型二 鸟头模型如图在ABC △中,,D E 分别是,AB AC 上的点如图 ⑴(或D 在BA 的延长线上,E 在AC 上如图 2), 则:():()ABC ADE S S AB AC AD AE =⨯⨯△△EDCBAEDCB A图⑴ 图⑵【例 1】 如图在ABC △中,,D E 分别是,AB AC 上的点,且:2:5AD AB =,:4:7AE AC =,16ADE S =△平方厘米,求ABC △的面积.EDCBAEDCBA【解析】 连接BE ,::2:5(24):(54)ADE ABE S S AD AB ===⨯⨯△△,::4:7(45):(75)ABE ABC S S AE AC ===⨯⨯△△,所以:(24):(75)ADE ABC S S =⨯⨯△△,设8ADE S =△份,则35ABC S =△份,16ADE S =△平方厘米,所以1份是2平方厘米,35份就是70平方厘米,ABC △的面积是70平方厘米.由此我们得到一个重要的定理,共角定理:共角三角形的面积比等于对应角(相等角或互补角)两夹边的乘积之比 .【巩固】如图,三角形ABC 中,AB 是AD 的5倍,AC 是AE 的3倍,如果三角形ADE 的面积等于1,那三角形等高模型与鸟头模型么三角形ABC 的面积是多少?EDC B AA B C DE【解析】 连接BE .∵3EC AE = ∴3ABC ABE S S = 又∵5AB AD =∴515ADE ABE ABC S S S =÷=÷,∴1515ABC ADE S S ==.【巩固】如图,三角形ABC 被分成了甲(阴影部分)、乙两部分,4BD DC ==,3BE =,6AE =,乙部分面积是甲部分面积的几倍?乙甲E DCBAA BCDE甲乙【解析】 连接AD .∵3BE =,6AE =∴3AB BE =,3ABD BDE S S = 又∵4BD DC ==,∴2ABC ABD S S =,∴6ABC BDES S=,5S S =乙甲.【例 2】 如图在ABC △中,D 在BA 的延长线上,E 在AC 上,且:5:2AB AD =,:3:2AE EC =,12ADE S =△平方厘米,求ABC △的面积.EDCBA EDCBA【解析】 连接BE ,::2:5(23):(53)ADE ABE S S AD AB ===⨯⨯△△[]::3:(32)(35):(32)5ABE ABC S S AE AC ==+=⨯+⨯△△,所以[]:(32):5(32)6:25ADE ABC S S =⨯⨯+=△△,设6ADE S =△份,则25ABC S =△份,12ADE S =△平方厘米,所以1份是2平方厘米,25份就是50平方厘米,ABC △的面积是50平方厘米.由此我们得到一个重要的定理,共角定理:共角三角形的面积比等于对应角(相等角或互补角)两夹边的乘积之比【例 3】 如图所示,在平行四边形ABCD 中,E 为AB 的中点,2AF CF =,三角形AFE (图中阴影部分)的面积为8平方厘米.平行四边形的面积是多少平方厘米?【解析】 连接FB .三角形AFB 面积是三角形CFB 面积的2倍,而三角形AFB 面积是三角形AEF 面积的2倍,所以三角形ABC 面积是三角形AEF 面积的3倍;又因为平行四边形的面积是三角形ABC 面积的2倍,所以平行四边形的面积是三角形AFE 面积的326⨯=()倍.因此,平行四边形的面积为8648⨯=(平方厘米).【例 4】 已知DEF △的面积为7平方厘米,,2,3BE CE AD BD CF AF ===,求ABC △的面积.FED CBA【解析】 :():()(11):(23)1:6BDE ABCS S BD BE BA BC =⨯⨯=⨯⨯=△△,:():()(13):(24)3:8CEF ABC S S CE CF CB CA =⨯⨯=⨯⨯=△△:():()(21):(34)1:6ADF ABC S S AD AF AB AC =⨯⨯=⨯⨯=△△设24ABC S =△份,则4BDE S =△份,4ADF S =△份,9CEF S =△份,244497DEF S =---=△份,恰好是7平方厘米,所以24ABC S =△平方厘米【例 5】 如图,三角形ABC 的面积为3平方厘米,其中:2:5AB BE =,:3:2BC CD =,三角形BDE 的面积是多少?AB EC DDC EB A【解析】 由于180ABC DBE ︒∠+∠=,所以可以用共角定理,设2AB =份,3BC =份,则5BE =份,325BD =+=份,由共角定理:():()(23):(55)6:25ABC BDE S S AB BC BE BD =⨯⨯=⨯⨯=△△,设6ABC S =△份,恰好是3平方厘米,所以1份是0.5平方厘米,25份就是250.512.5⨯=平方厘米,三角形BDE 的面积是12.5平方厘米【例 6】 (2007年”走美”五年级初赛试题)如图所示,正方形ABCD 边长为6厘米,13AE AC =,13CF BC =.三角形DEF 的面积为_______平方厘米.A【解析】 由题意知13AE AC =、13CF BC =,可得23CE AC =.根据”共角定理”可得,():():()12:(33)2:9CEF ABC S S CF CE CB AC =⨯⨯=⨯⨯=△△;而66218ABC S =⨯÷=△;所以4CEF S =△;同理得,:2:3CDE ACD S S =△△;,183212CDE S =÷⨯=△,6CDF S =△ 故412610DEF CEF DEC DFC S S S S =+-=+-=△△△△(平方厘米).【例 7】 如图,已知三角形ABC 面积为1,延长AB 至D ,使BD AB =;延长BC 至E ,使2CE BC =;延长CA 至F ,使3AF AC =,求三角形DEF 的面积.F EDCB AABCDEF【解析】 (法1)本题是性质的反复使用.连接AE 、CD . ∵11ABC DBC S S =,1ABC S =, ∴S 1DBC =.同理可得其它,最后三角形DEF 的面积18=.(法2)用共角定理∵在ABC 和CFE 中,ACB ∠与FCE ∠互补, ∴111428ABC FCE S AC BC S FC CE ⋅⨯===⋅⨯. 又1ABCS=,所以8FCES=.同理可得6ADFS =,3BDES=.所以186318DEFABCFCEADFBDESS SS S=+++=+++=.【例 8】 如图,平行四边形ABCD ,BE AB =,2CF CB =,3GD DC =,4HA AD =,平行四边形ABCD 的面积是2, 求平行四边形ABCD 与四边形EFGH 的面积比.HGAB CD EFHGA B CD EF【解析】 连接AC 、BD .根据共角定理∵在ABC △和BFE △中,ABC ∠与FBE ∠互补,∴111133ABC FBE S AB BC S BE BF ⋅⨯===⋅⨯△△. 又1ABC S =△,所以3FBE S =△.同理可得8GCF S =△,15DHG S =△,8AEH S =△.所以8815+3+236EFGH AEH CFG DHG BEF ABCD S S S S S S =++++=++=△△△△.所以213618ABCD EFGH S S ==.【例 9】 如图,四边形EFGH 的面积是66平方米,EA AB =,CB BF =,DC CG =,HD DA =,求四边形ABCD 的面积.H GFED CBAA BCDEFGH【解析】 连接BD .由共角定理得:():()1:2BCD CGF S S CD CB CG CF =⨯⨯=△△,即2CGF CDB S S =△△同理:1:2ABD AHE S S =△△,即2AHE ABD S S =△△ 所以2()2AHE CGF CBD ADB ABCD S S S S S +=+=△△△△四边形 连接AC ,同理可以得到2DHG BEF ABCD S S S +=△△四边形5AHE CGF HDG BEF EFGH ABCD ABCD S S S S S S S =++++=△△△△四边形四边形四边形所以66513.2ABCD S =÷=四边形平方米【例 10】 如图,将四边形ABCD 的四条边AB 、CB 、CD 、AD 分别延长两倍至点E 、F 、G 、H ,若四边形ABCD 的面积为5,则四边形EFGH 的面积是 .A B CD E F GHA B CD EF GH【解析】 连接AC 、BD .由于2BE AB =,2BF BC =,于是4BEF ABC S S ∆∆=,同理4HDG ADC S S ∆∆=.于是444BEF HDG ABC ADC ABCD S S S S S ∆∆∆∆+=+=.再由于3AE AB =,3AH AD =,于是9AEH ABD S S ∆∆=,同理9CFG CBD S S ∆∆=. 于是999AEH CFG ABD CBD ABCD S S S S S ∆∆∆∆+=+=.那么491260EFGH BEF HDG AEH CFG ABCD ABCD ABCD ABCD ABCD S S S S S S S S S S ∆∆∆∆=+++-=+-==.【例 11】 如图,在ABC △中,延长AB 至D ,使BD AB =,延长BC 至E ,使12CE BC =,F 是AC 的中点,若ABC △的面积是2,则DEF △的面积是多少?A BCDEF【解析】 ∵在ABC △和CFE △中,ACB ∠与FCE ∠互补,∴224111ABC FCE S AC BC S FC CE ⋅⨯===⋅⨯△△. 又2ABCS=,所以0.5FCES=.同理可得2ADF S =△,3BDE S =△.所以20.532 3.5DEF ABC CEF DEB ADF S S S S S =++-=++-=△△△△△【例 12】 如图,1ABC S =△,5BC BD =,4AC EC =,DG GS SE ==,AF FG =.求FGSS.SGF E DCBA【解析】 本题题目本身很简单,但它把本讲的两个重要知识点融合到一起,既可以看作是”当两个三角形有一个角相等或互补时,这两个三角形的面积比等于夹这个角的两边长度的乘积比”的反复运用,也可以看作是找点,最妙的是其中包含了找点的3种情况.最后求得FGS S △的面积为4321115432210FGS S =⨯⨯⨯⨯=△.【例 13】 如图所示,正方形ABCD 边长为8厘米,E 是AD 的中点,F 是CE 的中点,G 是BF 的中点,三角形ABG 的面积是多少平方厘米?ABCD EF GABCDEF G【解析】 连接AF 、EG .因为218164BCF CDE S S ==⨯=△△,根据”当两个三角形有一个角相等或互补时,这两个三角形的面积比等于夹这个角的两边长度的乘积比”8AEF S =,8EFG S =,再根据”当两个三角形有一个角相等或互补时,这两个三角形的面积比等于夹这个角的两边长度的乘积比”,得到16BFCS =,32ABFE S =,24ABFS=,所以12ABGS=平方厘米.【例 14】 四个面积为1的正六边形如图摆放,求阴影三角形的面积.【解析】 如图,将原图扩展成一个大正三角形DEF ,则AGF ∆与CEH ∆都是正三角形.假设正六边形的边长为为a ,则AGF ∆与CEH ∆的边长都是4a ,所以大正三角形DEF 的边长为4217⨯-=,那么它的面积为单位小正三角形面积的49倍.而一个正六边形是由6个单位小正三角形组成的,所以一个单位小正三角形的面积为16,三角形DEF 的面积为496.由于4FA a =,3FB a =,所以AFB ∆与三角形DEF 的面积之比为43127749⨯=.同理可知BDC ∆、AEC ∆与三角形DEF 的面积之比都为1249,所以ABC ∆的面积占三角形DEF 面积的1213134949-⨯=,所以ABC ∆的面积的面积为4913136496⨯=.【巩固】已知图中每个正六边形的面积都是1,则图中虚线围成的五边形ABCDE 的面积是 .B DCEA【解析】 从图中可以看出,虚线AB 和虚线CD 外的图形都等于两个正六边形的一半,也就是都等于一个正六边形的面积;虚线BC 和虚线DE 外的图形都等于一个正六边形的一半,那么它们合起来等于一个正六边形的面积;虚线AE外的图形是两个三角形,从右图中可以看出,每个三角形都是一个正六边形面积的16,所以虚线外图形的面积等于11132363⨯+⨯=,所以五边形的面积是12103633-=.8、这个世界并不是掌握在那些嘲笑者的手中,而恰恰掌握在能够经受得住嘲笑与批忍不断往前走的人手中。
小学奥数思维训练-几何(三)立体图形(拓展训练)(通用,含答案)
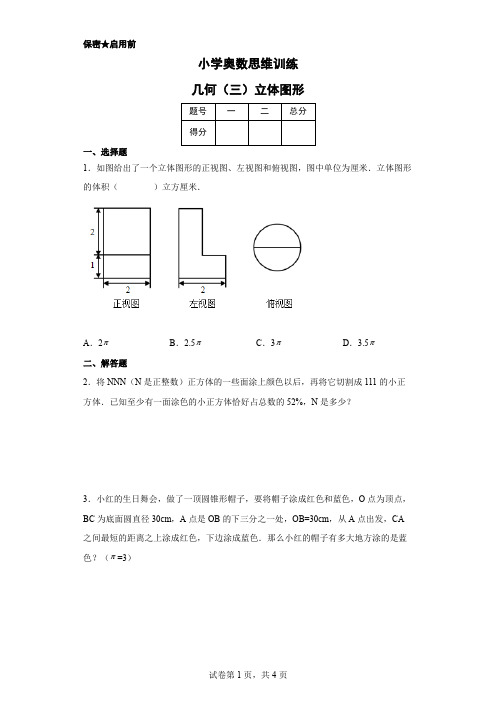
保密★启用前小学奥数思维训练几何(三)立体图形一、选择题1.如图给出了一个立体图形的正视图、左视图和俯视图,图中单位为厘米.立体图形的体积()立方厘米.A.2πB.2.5πC.3πD.3.5π二、解答题2.将NNN(N是正整数)正方体的一些面涂上颜色以后,再将它切割成111的小正方体.已知至少有一面涂色的小正方体恰好占总数的52%,N是多少?3.小红的生日舞会,做了一顶圆锥形帽子,要将帽子涂成红色和蓝色,O点为顶点,BC为底面圆直径30cm,A点是OB的下三分之一处,OB=30cm,从A点出发,CA 之间最短的距离之上涂成红色,下边涂成蓝色.那么小红的帽子有多大地方涂的是蓝色?(π=3)4.一个正方体纸盒中恰好能放入一个体积为628立方厘米的圆柱,纸盒的容积有多大?(π=3.14)5.图中的立体图形是由14个棱长为5cm的立方体组成的,求这个立体图形的表面积?6.圆柱形的售报亭的高和底面直径相等(如图),开一个边长等于底面半径的正方形售报窗口.问窗口处挖去的圆柱部分的面积占圆柱形侧面积的几分之几?7.一个正方体木块,棱长是15.从它的八个顶点处各截去棱长分别是1、2、3、4、5、6、7、8的小正方体.这个木块剩下部分的表面积最少是多少?8.如图,一个正方体形状的木块,棱长1米,沿水平方向将它锯成3片,每片又锯成4长条,每条又锯成5小块,共得到大大小小的长方体60块.那么这60块长方体表面积的和是多少平方米?9.如图是一个棱长为2厘米的正方体,在正方体上表面的正中,向下挖一个棱长为1厘米的正方体小洞,接着在小洞的底面正中向下挖一个棱长为1/2厘米的正方形小洞,第三个正方形小洞的挖法和前两个相同,棱长为1/4厘米,那么最后得到的立体图形的表面积是多少平方厘米?10.把一个棱长为2cm正方体在同一平面的边的中点用线段连接起来,如图.然后把正方体顶点上的三角锥锯掉,请问最后所得的立体图形的表面积的多少平方厘米?(1.732×1.732=3)参考答案:1.A【解析】【详解】首先确定此图形为“不完整的圆柱”,先求出圆柱体积,再求出缺失的半个小圆柱,最后作差.如图,从给定的正视图、左视图和俯视图可以看出,该立体图形由一个半径为1厘米、高为1厘米的圆柱和一个半径为1厘米、高为2厘米的半圆柱组成..π×1×1×(1+2)-12π×1×1×2=2π,选A【点睛】这里的要点在于还原,还原的技巧在于先补全,再细雕刻2.5【解析】【详解】一个正整数×52%=另一个正整数,那么这个正整数必须能被25整除1352%25⎛⎫=⎪⎝⎭因为.那么N必须能被5整除.当N取最小N=5 正方体有5×5×5=125个小正方体涂色的小正方体5×5×5×52%=65(个)不可能被涂色的小正方体3×3×3=27(个)27+65小于125成立当N=2×5=10时,正方体有10×10×10=1000个小正方体涂色的小正方体10×10×10×52%=520(个)不可能被涂色的小正方体 8×8×8=512(个) 512+520大于1000 不成立同理N 大于10都不成立所以 N=53.750平方厘米【解析】【详解】底面周长为圆锥展开后 扇形的弧长蓝色面积=圆锥侧面积-红色面积底面周长=30×π=30×3=90侧面展开后扇形所在圆的周长=2×π×30=1809011802= 所以侧面展开图为半圆 蓝色面积=π×30×30×12-12×(20+20) ×30 =1350-600=750(平方厘米)4.800cm 3【解析】【详解】设纸盒棱长为x圆柱体积=22x x x π⨯⨯⨯=628 整理上边式子得x 3=800(cm 3) 即为纸盒容积.5.1050平方厘米【解析】【详解】用透视法观察 上、下两个面的面积相等4个侧面的每个侧面面积为6个小正方形面积底面棱长5×3=15 上、下两个面的面积=15×15×2=4504个侧面面积=4×6×5×5=600总面积=450+600=1050(平方厘米)6.1 12【解析】【详解】窗口上下的弧长为底面圆周长的六分之一窗口的高为圆柱的高的二分之一挖去的圆柱部分的面积占圆柱形侧面积的16×12=1127.1252【解析】【详解】截去一个小正方体,表面积不变.只有在截去的小正方体的面相重合时,表面积才会减少.所以要使木块剩下部分的表面积尽可能小,应该在同一条棱的两端各截去棱长7与8的小正方体(如图所示),这时剩下部分的表面积比原正方体的表面积减少最多.剩下部分的表面积最小是:15×15×6-7×7×2=1252.想想为什么不是15×15×6-7×7-8×8.8.24平方米【解析】【详解】我们知道每切一刀,多出的表面积恰好是原正方体的2个面的面积.现在一共切了(3-1)+(4-1)+(5-1)=9刀,而原正方体一个面的面积1×1=1(平方米),所以表面积增加了9×2×1=18(平方米).原来正方体的表面积为6×1=6(平方米).所以现在的这些小长方体的表积之和为6+18=24(平方米).9.29.25平方厘米【解析】【详解】俯视图发现上表面积就是大正方体的一个面的面积表面积为大正方体表面积加上3个小正方体的侧面积2×2×6+1×1×4+12×12×4+14×14×4=24+4+1+1 4=29.25(平方厘米)10.18.928cm2【解析】【详解】所得立体图形表面为6个正方形和8个等边三角形勾股定理等边三角形的高的平方=底边的平方-半个底边的平方=34底边的平方6个正方形面积=6×(1×1+1×1)=6×2=12等边三角形的高的平方=34×2=32等边三角形的高的平方×底边的平方=32×2=3所以等边三角形的高×底边=1.732,等边三角形的面积=1/2×1.732=0.866立体图形的表面积=12+8×0.866=18.928(cm2)。
小学一年级上学期数学几何图形专项知识点综合题青岛版
小学一年级上学期数学几何图形专项知识点综合题青岛版班级:姓名:1. 左边的图形是由右边的哪两个图形拼成的?请圈出来。
2. 每种图形里有哪些数,看一看,填一填。
(1)□里有()和()。
(2)△里有( )和( )。
(3)○里有( )和( )。
(4)里有( )( )( )( )( )。
3. 我会数也会涂。
涂一涂红色蓝色黄色绿色______个 ______个 ______个 ______个4. 想一想,数一数下图中有______个三角形。
5. 观察图形,填一填。
大正方形被分割后(包含复合图形)一共有______个长方形,一共有______个正方形。
6. 用哪些立体图形可以画出右面的图形?圈一圈7. 把有关系的两个图形连起来。
8. 下面的一块是从上面哪个图形中剪下来的?连一连。
9. 能用七巧板拼出来的图形画“√”,不能的画“×”。
10. 想一想,填一填。
(1)三角形比长方形少______条边,六边形比三角形多______条边。
(2)要拼一个大正方形最少需要______个小正方形,或______个小三角形。
(3)七巧板是由______种图形组成,其中有______个□,有______个△(4)黑板的面是______形,地板砖的面是______形,红领巾的面是______形,硬币的面是______形。
(5)正方形有______条边,长方形有______条边,三角形有______条边。
11. 圈出合适的图形。
12. 下面的图案分别是由哪些图形组成的?填一填。
______________ ______________ ______________13. 动动脑,想一想,填一填。
(1)剪成______个______形。
(2)看图填数,剪成______个______形。
14. 下图右面的4小块布料中,哪一块是从这块布上剪下来的?把序号填在框里______。
15. 下面的物体分别从正面、侧面、上面看到的形状分别是什么?请你在纸上画出来。
小学奥数 图形的分割 精选练习例题 含答案解析(附知识点拨及考点)
几何面积问题除了利用常规的五大模型、各种公式求得之外,还可以用图形分割的思想来做。
我们发现,在迎春杯几何问题中,这类题目很多。
掌握好这种思想方法,可以帮助我们解决很多几何难题。
解题关键:分割其实就是运用特殊的三角形(等角直角三角形、等边三角形等)、正方形、等边图形的特殊性质进行分割而得,所以分割的关键是利用了特殊图形的关系解题。
解题思想:这其实就是一种化整为零的思想,各位同学不仅要学会几何题中的这种方法,更要细细体味这种思想在解决各种问题中的妙用。
模块一、简单分割【例 1】 3个相同的正方形纸片按相同的方向叠放在一起(如图),顶点A 和B 分别与正方形中心点重合,如果所构成图形的周长是48厘米,那么这个图形覆盖的面积是__________平方厘米.【考点】图形的分割 【难度】2星 【题型】填空 【关键词】迎春杯,中年级组,复试,4题【解析】 将这3个正方形分割,可知这个图形的周长即为两个正方形纸片的周长之和,故正方形边长为48÷8=6(厘米),则图中每个分割得到的小正方形边长为6÷2=3(厘米),所以这个图形覆盖的面积为6×6×2+3×3×2=90(平方厘米)。
【答案】90平方厘米【例 2】 正方形ABCD 的面积是1平方米,将四条边分别向两端各延长一倍,连结八个端点得到一个正方形(如图),求大正方形的面积.DCB A【考点】图形的分割 【难度】2星 【题型】解答【解析】 四条边分别向两端各延长一倍,很容易可以观察出,大正方形有9个小正方形组成,所以,大正方形的面积是:199⨯=(平方米).【答案】9平方米【例 3】 将边长为a 的正方形各边的中点连结成第二个正方形,再将第二个正方形各边的中点连结成第三个正方形,依此规律,继续下去,得到下图那么,边长为a 的正方形面积是图中阴影部分面积的例题精讲知识点拨4-2-4.图形的分割________ 倍.【考点】图形的分割 【难度】3星 【题型】填空 【关键词】希望杯,四年级,复赛,第6题,4分 【解析】 阴影部分是大正方形的0.5×0.5×0.5×0.5=116,所以正方形是阴影的16倍 【答案】16倍【例 4】 正三角形ABC 的面积是1平方米,将三条边分别向两端各延长一倍,连结六个端点得到一个六边形(如右图),求六边形的面积.CBA【考点】图形的分割 【难度】3星 【题型】解答【解析】 采用分割法,过A 、B 、C 分别作平行线,得到右上图,其中所有小三角形的面积都相同,所以六边形面积等于13平方米.【答案】13平方米【例 5】 正六边形ABCDEF 的面积是1平方米,将六条边分别向两端各延长一倍,交于六个点,组成如下图的图形,求这个图形的面积.FED CB A FAB CDE【考点】图形的分割 【难度】3星 【题型】解答【解析】 采用分割法,连接正六边形的对角线,会发现,所有的三角形面积都相同,一共有12个小三角形,原来正六边形的面积是1平方米,由6个小三角形组成,所以现在的大图形的面积是:122⨯= (平方米)【答案】2平方米【例 6】 长方形ABCD 的面积是40平方厘米,E 、F 、G 、H 分别为AC 、AH 、DH 、BC 的中点。
小学奥数--几何模型分类总结汇总版(鸟头、燕尾、风筝、一般模型等)
小学奥数--几何模型分类总结汇总版(鸟头、燕尾、风筝、一般模型等)目录模型一——《等积变换》一、知识点梳理二、例题精讲三、自我提升模型一——《等积变换》一、知识点梳理等积变换是指平面图形在平移、旋转、翻折、错位四种变换中,不改变其面积大小的变换。
在等积变换中,图形的各个部分相对位置关系保持不变,因此,等积变换也称为等面积变换或保角变换。
在等积变换中,我们需要掌握以下几个概念:1.平移:指图形沿着某一方向移动一段距离,保持图形大小和形状不变。
2.旋转:指图形绕某一点旋转一定角度,保持图形大小和形状不变。
3.翻折:指图形沿着某一直线对称,保持图形大小和形状不变。
4.错位:指图形中的各个部分按照一定规律移动,保持图形大小和形状不变。
二、例题精讲例1:如图,正方形ABCD经过变换后得到图形A'B'C'D',则该变换是什么变换?解析:首先,我们可以看出图形A'B'C'D'与正方形ABCD的形状相同,因此,该变换是等积变换。
其次,我们可以发现,图形A'B'C'D'是将正方形ABCD逆时针旋转了90度得到的,因此,该变换是旋转变换。
例2:如图,图形ABCD经过变换得到图形A'B'C'D',则该变换是什么变换?解析:首先,我们可以看出图形A'B'C'D'与图形ABCD的形状相同,因此,该变换是等积变换。
其次,我们可以发现,图形A'B'C'D'是将图形ABCD沿着直线EF翻折得到的,因此,该变换是翻折变换。
三、自我提升1.如果一个图形经过等积变换后,其面积大小发生了改变,那么这个变换是什么变换?2.如果一个图形经过等积变换后,其形状发生了改变,那么这个变换是什么变换?3.如果一个图形经过等积变换后,其面积大小和形状都没有发生改变,那么这个变换是什么变换?四、答案与解析本部分为题目的答案和解析,帮助读者检验自己的答题情况和巩固知识点。
小学奥数题库《几何》-直线型-鸟头模型-3星题(含解析)
几何-直线型几何-鸟头模型-3星题课程目标知识提要鸟头模型•概念两个三角形中有一个角相等或者互补,这两个三角形叫做共角三角形。
•特征共角三角形的面积比等于共角〔相等角或者互补角〕两夹边的乘积之比。
$S_{\triangle ABC}\mathbin{:}S_{\triangle ADE}=(AB\times AC)\mathbin{:}(AD\times AE)$精选例题鸟头模型1. 如下列图所示,点Qʹ和Rʹ三等分XʹX,Rʹ和Pʹ三等分YʹY,Qʹ和Pʹ三等分ZʹZ.△PQR 面积是△PʹQʹRʹ面积的倍.【答案】25【分析】连接ZYʹ,XʹY,XZʹ,根据鸟头模型,可以得到△PʹYʹZ,△XʹYRʹ,△XQʹZʹ都是△PʹQʹRʹ的4倍,那么可以得到平行四边形PZPʹYʹ、XʹRʹYR、XQʹZʹQ均为△PʹQʹRʹ的8倍,图中的三个小三角形的面积都与△PʹQʹRʹ的面积相等,那么△PQR面积是△PʹQʹRʹ面积的8×3+1= 25(倍).2. 如下图,正方形ABCD边长为6厘米,AE=13AC,CF=13BC.三角形DEF的面积为平方厘米.【答案】10【分析】由题意知AE=13AC、CF=13BC,可得CE=23 AC.根据〞共角定理〞可得,S△CEF:S△ABC=(CF×CE):(CB×AC)=(1×2):(3×3)=2:9;而S△ABC=6×6÷2=18;所以S△CEF=4;同理得,S△CDE:S△ACD=2:3,S△CDE=18÷3×2=12,S△CDF=6故S△DEF=S△CEF+S△DEC−S△DFC=4+12−6=10(平方厘米).3. 如下列图所示,三角形ABC的面积为1,且AD=13AB,BE=14BC,CF=15CA,那么三角形DEF的面积是.【答案】512【分析】先分别求出△ADF、△BDE、△CEF的面积,再用△ABC的面积减去这三个三角形的面积即为△DEF的面积.因为,AD=13AB,CF=15CA,所以,AF=45AC,根据“鸟头定理〞,S△ADF=45×13S△ABC=415,同理可得,S△BDE=23×14×1=16,S△CEF=34×15×1=320,所以S△DEF=1−415−16−320=512.4. 如图,三角形ABC中,延长BA到D,使DA=AB,延长CA到E,使EA=2AC,延长CB 到F,使FB=3BC.如果三角形ABC的面积是1,那么三角形DEF的面积是.【答案】7【分析】S△CAB:S△CEF=(1×1):(3×4)=1:12,所以S△CEF=12,S△ABC:S△ADE=(1×1):(1×2)=1:2,所以S△ADE=2,S△BAC:S△BDF=(1×1):(2×3)=1:6,所以S△BDF=6,所以S△DEF=S△CEF−S△ABC+S△ADE−S△BDF=12−1+2−6=7.5. 如图.将三角形ABC的AB边延长1倍到D,BC边延长2倍到E,CA边延长3倍到F.如果三角形ABC的面积等于1,那么三角形DEF的面积是.【答案】18【分析】〔法1〕连接AE、CD.因为S△ABCS△DBC =11,S△ABC=1,所以S△DBC=1.同理可得其它,最后三角形DEF的面积=18.〔法2〕用共角定理因为在△ABC和△CFE中,∠ACB与∠FCE互补,所以S△ABC S△FCE =AC⋅BCFC⋅CE=1×14×2=18.又S△ABC=1,所以S△FCE=8.同理可得S△ADF=6,S△BDE=3.所以S△DEF=S△ABC+S△FCE+S△ADF+S△BDE=1+8+6+3=18.6. 如图,将四边形ABCD的四条边AB、CB、CD、AD分别延长两倍至点E、F、G、H,假设四边形ABCD的面积为5,那么四边形EFGH的面积是.【答案】60【分析】连接AC、BD.由于BE=2AB,BF=2BC,于是S△BEF=4S△ABC,同理S△HDG=4S△ADC,于是S△BEF+S△HDG=4S△ABC+4S△ADC=4S ABCD,再由于AE=3AB,AH=3AD,于是S△AEH=9S△ABD,同理S△CFG=9S△CBD,于是S△AEH+S△CFG=9S△ABD+9S△CBD=9S ABCD,那么S EFGH=S△BEF+S△HDG+S△AEH+S△CFG−S ABCD=4S ABCD+9S ABCD−S ABCD=12S ABCD=60.7. 正方形ABCD边长为6厘米,AE=13AC,CF=13BC.三角形DEF的面积为平方厘米.【答案】10【分析】正方形的面积为6×6=36(平方厘米),那么根据鸟头模型可以得出S△ADE=13×S△ACD=13×12×36=6(平方厘米),S△CDF=13×S△BCD=13×12×36=6(平方厘米),S ABFE=S△ABC−S△CEF=18−18×13×23=14(平方厘米),阴影局部面积为36−6−6−14=10(平方厘米).8. 如图,在△ABC中,点D是边AC的中点,点E、F是边BC的三等分点,假设△ABC的面积为1,那么四边形CDMF的面积是.【答案】730【分析】由于点D是边AC的中点,点E、F是边BC的三等分点,如果能求出BN、NM、MD三段的比,那么说分成的六小块的面积可以求出来,其中当然也包括四边形CDMF的面积.连接CM、CN.根据燕尾模型,S△ABM:S△ACM=BF:CF=2:1,S△ACM=2S△ADM,S△ABM=2S△ACM=4S△ADM,那么BM=4DM,即BM=45 BD.那么S△BMF=BMBD×BFBC×S△BCD=45×23×12=415,S 四边形CDMF =12 − 415=730.另解:得出 S △ABM =2S △ACM =4S △ADM 后,可得S △ADM =15S △ABD =15×12=110,那么S 四边形CDMF =S △ACF −S △ADM =13−110=730.9. 如图,P 为四边形 ABCD 内部的点,AB:BC:DA =3:1:2,∠DAB =∠CBA =60°.图中所有三角形的面积都是整数.如果三角形 PAD 和 三角形 PBC 的面积分别为 20 和 17,那么四边形 ABCD 的面积最大是 .【答案】 147【分析】 延长 AD ,BC 交于点 Q ,连接 PQ .∠DAB =∠CBA =60°,所以三角形 ABQ 为正三角形. 由于AB:BC:DA =3:1:2,所以 PCQD 的面积为20÷2+17×2=44;而三角形QCD面积占QAB面积的1 3×23=29,ABCD面积是QCD面积的(1−29)÷29=72.注意到ABCD中各三角形面积均为整数,所以QAB面积为9的倍数.QCD面积是2的倍数,所以QCD面积最大为42,ABCD面积最大为42×72=147.10. 如图,AD=DB,AE=EF=FC,阴影局部面积为5平方厘米,△ABC的面积是平方厘米.【答案】30平方厘米【分析】S△ADE=S△DEF,S△ADE:S△ABC=(AD×AE):(AB×AC)=(1×1):(2×3)=1:6,所以S△ABC=5×6=30(平方厘米).11. 如图,在平行四边形ABCD中,E为AB的中点,AF=2CF,三角形AFE〔图中阴影局部〕的面积为8平方厘米.平行四边形ABCD的面积是多少平方厘米?【答案】48平方厘米【分析】S△AEF:S△ABC=(AE×AF):(AB×AC)=(1×2):(2×3)=1:3,S△ABC=3S△AEF=3×8=24,S四边形ABCD=2×24=48(平方厘米).12. △CEF的面积为9平方厘米,BE=CE,AD=2BD,CF=3AF,求△DEF的面积.【答案】7平方厘米.【分析】S△CEF:S△ABC=(CE×CF):(CB×CA)=(1×3):(2×4)=3:8=9:24,所以三角形ABC的面积为24平方厘米S△BDE:S△ABC=(BD×BE):(BA×BC)=(1×1):(2×3)=1:6=4:24,S△ADF:S△ABC=(AD×AF):(AB×AC)=(2×1):(3×4)=1:6=4:24,所以S△DEF=24−4−4−9=7(平方厘米).13. 如图,把三角形DEF的各边向外延长1倍后得到三角形ABC,三角形ABC的面积为1.三角形DEF的面积是多少?【答案】17【分析】令三角形DEF为1份,那么根据共角模型,有:S△DEF S△AFC =EF×DFCF×FA=12.所以三角形AFC的面积为2份,同理,三角形ABD的面积为2份,三角形BEF的面积为2份.那么三角形ABC的面积为7份,对应面积为1,所以S三角形DEF =17.14. 如图,三角形ABC的面积为3,其中AB:BE=2:5,BC:CD=3:2,三角形BDE的面积是多少?【答案】12.5【分析】BC:BD=3:(3+2)=3:5,S△ABC :S△BDE=(2×3):(5×5)=6:25,S△ABC=25 6S△BDE=256×3=12.5.15. ,AC:AE=5:1,BC:CD=4:1,BA:BF=6:1,那么,△DEF的面积是△ABC的几分之几?【答案】61120【分析】S△AEFS△ABC =AE×AFAC×AB=1×55×6=16,S△BDF S△ABC =BD×BFBC×BA=3×14×6=18,S△CDE S△ABC =CD×CECB×CA=1×44×5=15,S△DEFS△ABC=S△ABC−S△AEF−S△BDF−S△CDES△ABC=1−16−18−15=61120.16. 如下列图所示,在三角形ABC中,BC=6BD、AC=5EC、DG=GH=HE、AF= FG.请问三角形FGH与三角形ABC的面积比为何?【答案】19【分析】根据鸟头模型,S△ADC=56S△ABC,S△AED=45S△ADC,S△AGE=23S△AED,S△GHF=12×12×S△AGE,最后可以得出S△GHF=56×45×23×12×12×S△ABC=19S△ABC.17. 如图, AE =13AC ,CD =14BC ,BF =15AB ,试求 $\dfrac{\text{三角形$ DEF $的面积}}{\text{三角形$ ABC $的面积}}$ 的值?【答案】 512【分析】 S △AEF S △ABC=AE×AF AC×AB =1×43×5=415,S △BDF S △ABC=BD×BF BC×BA=1×35×4=320,S △CDES △ABC=CD×CE CB×CA=1×24×3=16,所以S △DEF S △ABC=S △ABC −S △AEF −S △BDF −S △CDES △ABC=1−415−320−16=512.18. 如图,把三角形 DEF 的各边向外延长 2 倍后得到三角形 ABC ,三角形 ABC 的面积为 1. 三角形 DEF 的面积是多少?【答案】 119【分析】 令三角形 DEF 为 1 份,那么根据共角模型,有:S△DEF S△AFC =EF×DFCF×FA=16.所以三角形AFC的面积为6份,同理,三角形ABD的面积为6份,三角形BEF的面积为6份.那么三角形ABC的面积为1+6+6+6=19份,对应面积为1,所以S三角形DEF =119.19. 如图,四边形EFGH的面积是75平方米,EA=AB,CB=BF,DC=CG,HD=DA,求四边形ABCD的面积.【答案】15平方米.【分析】连接BD,由鸟头知:S△BCD S△FCG =BC⋅DCFC⋅CG=1×12×1=12S△ABD S△AEH =AD⋅ABAH⋅AE=1×12×1=12,所以S△FCG+S△AEH=2S四边形ABCD 连接AC,同理可得:S△BEF+S△DHG=2S四边形ABCD,S四边形EFGH =5S四边形ABCD又因为四边形EFGH的面积是75平方米所以四边形ABCD的面积是75÷5=15(平方米).20. 如图,△ABC的面积是36,并且AE=13AC,CD=14BC,BF=15AB,试求△DEF的面积.【答案】15【分析】详解:由鸟头模型可得,S△AEF=36×45×13=485,S△BED=36×15×34=275,S△CDE=36×14×23=6,S△DEF=36−485−275−6=15.21. 分别延长四边形ABCD的四个边,使得AB=BAʹ,BC=CBʹ,CD=DCʹ,DA=ADʹ〔如下列图所示〕.如果四边形ABCD的面积是1平方厘米,请问四边形AʹBʹCʹDʹ的面积为多少平方厘米?【答案】5【分析】连接BD,根据鸟头模型,可得S△AAʹDʹ=1×2×S△ABD=2S△ABD,S△CCʹBʹ=1×2×S△BCD=2S△BCD,那么可得S△AAʹDʹ+S△CCʹBʹ=2S四边形ABCD连接AC,同理可得:S△DDʹCʹ+S△BBʹAʹ=2S四边形ABCD所以整个图形的面积是2+2+1=5(平方厘米).22. 如图,平行四边形ABCD,BE=AB,CF=2CB,GD=3DC,HA=4AD,平行四边形ABCD的面积是2,求平行四边形ABCD与四边形EFGH的面积比.【答案】1:18【分析】连接AC,根据共角定理:S△ABC S△FBE =BA×BCBE×BF=1×11×3=13,又因为S△ABC=1,所以,S△FBE=3,同理可得:S△GCF=8,连接BD,S△DHG=15,S△AEH=8.所以S EFGH=S△AEH+S△CFG+S△DHG+S△BEF=8+8+15+3+2=36,S ABCD:S EFGH=2:36=1:18.23. 如图,三角形ABC面积为1,延长BA至D,使得DA=AB;延长CA至E,使得EA=2AC;延长CB至F,使得FB=3BC,求三角形DEF的面积?【答案】7【分析】S△ADE S△ABC =AD×AEAB×AC=2,S△CEF S△ABC =CE×CFCA×CB=3×4=12,S△DBF S△ABC =DB×BFBA×CB=2×3=6,S△DEF=S△ADE+S△CEF−S△DBF−S△ABC =2+12−6−1=7.24. 三角形ABC中,BD的长度是的AB的14,AE的长度是AC的13.三角形AED的面积是8,那么三角形ABC的面积是多少?【答案】32【分析】简答:8÷(34×13)=32.25. 如图在△ABC中,D在BA的延长线上,E在AC上,且AB:AD=5:2,AE:EC=3:2,S△ADE=12平方厘米,求△ABC的面积.【答案】50平方厘米【分析】S△ADE:S△ABC=(AD×AE):(AB×AC)=(3×2):(5×5)=6:25,因为S△ADE=12(平方厘米),所以S△ABC=12÷6×25=50(平方厘米).26. 如图,在三角形ABC中,AD的长度是BD的3倍,AC的长度是EC的3倍.三角形AED 的面积是10,那么三角形ABC的面积是多少?【答案】20【分析】 详解:AD 是 AB 的 34,AE 是 AC 的 23,根据鸟头模型,有 △ADE 的面积是 △ABC 面积的 34×23=12.那么 △ABC 的面积是 20.27. 如图, AE =15AC ,CD =14BC ,BF =16AB ,那么 S△DEF S △ABC 等于多少?【答案】 61120【分析】 设 S △ABC =1,那么根据 悬空=整体−空白,S △DEF =S △ABC −S △AEF −S △BDF −S △DEC现在分别去求 S △AEF 、S △BDF 、S △DEC ,由鸟头定理知道:S △AEF =(AF AB ×AE AC )S △ABC =(56×15)S △ABC =16S △ABC同理:S △BDF =(BF AB ×BD BC )S △ABC =16×34S △ABC =18S △ABC S △DEC =(EC AC ×DC BC )S △ABC =45×14S △ABC =15S △ABC所以: S △DEF =(1−16−18−15)S △ABC =61120S △ABC,S △DEF S △ABC =61120.28. 如图,在三角形 ABC 中,D 为 BC 的中点,E 为 AB 上的一点,且 BE =13AB ,四边形 ACDE 的面积是 35,求三角形 ABC 的面积.【答案】42【分析】S△BDE:S△ABC=(BD×BE):(BC×BA)=(1×1):(2×3)=1:6,那么S△BDE=16S△ABC,S四边形ACDE=S△ABC−16S△ABC=56S△ABC,所以:S△ABC=35÷56=42.29. 边长为8厘米和12厘米的两个正方形并放在一起,那么图中阴影三角形的面积是多少平方厘米?【答案】16.2【分析】给图形标注字母,按顺时针方向标注,大正方形为ABCD,小正方形为MNDE,EB分别交AC,AD于O,H两点,AO:OC=AB:EC=12:20=3:5,AH:BC=AO:OC=3:5,所以AO:AC=3:8,AH:AD=3:5,S△AHO:S△ADC=9:40.因为S△ADC=12×122=72,所以S△AHO=940S△ADC=940×72=16.2.30. 如图,三角形ABC中,AB是AD的5倍,AC是AE的3倍,如果三角形ADE的面积等于1,那么三角形ABC的面积是多少?【答案】15【分析】S△ADE :S△ABC=(1×1):(5×3)=1:15,S△ABC=15S△ADE=15×1=15.31. 如下图,正方形ABCD边长为8厘米,E是AD的中点,F是CE的中点,G是BF的中点,三角形ABG的面积是多少平方厘米?【答案】12【分析】连接AF、EG.因为S△CDE=14×82=16,根据“当两个三角形有一个角相等或互补时,这两个三角形的面积比等于夹这个角的两边长度的乘积比〞,S△AEF=8,S△EFG=8,再根据“当两个三角形有一个角相等或互补时,这两个三角形的面积比等于夹这个角的两边长度的乘积比〞,得到S△BFC=16,S ABFE=32,S△ABF=24,所以S△ABG=12(平方厘米).32. 如图,AD:DB=1:4,AE:EC=1:5,如果△ABC的面积是120,那么△ADE的面积是多少?【答案】4【分析】简答:由条件得AD:AB=1:5,AE:AC=1:6,利用“共角三角形〞性质得三角形AED的面积是120×15×16=4.33. 如图,三角形ABC被分成了甲、乙两局部BD=DC=4,BE=3,AE=6,乙局部面积是甲局部面积的几倍?【答案】5【分析】BD:BC=4:(4+4)=1:2,BE:BA=3:(3+6)=1:3,S△BDE :S△ABC=(1×1):(3×2)=1:6,S△BDE =16S△ABC,S四边形ACDE=S△ABC−16S△ABC=56S△ABC,S△BDE:S四边形ACDE =16:56=1:5.34. 如图,三角形ABC面积为1,延长AB至D,使BD=AB;延长BC至E,使CE=2BC;延长CA至F,使AF=3AC,求三角形DEF的面积.【答案】18【分析】S△ADFS△ABC =AD×AFAB×AC=2×31×1=6,S△BDE S△ABC =BD×BEAB×BC=1×31×1=3,S△CEF S△ABC =CE×CFBC×AC=2×41×1=8.所以S△DEF S△ABC =S△ADFS△ABC+S△BDES△ABC+S△CEFS△ABC+S△ABCS△ABC =6+3+8+1=18,S△DEF=18S△ABC=18.35. 如图,三角形ABC的面积为3平方厘米,其中AB:BE=2:5,BC:CD=3:2,三角形BDE的面积是多少?【答案】12.5平方厘米.【分析】由于∠ABC+∠DBE=180∘,所以可以用共角定理,设AB=2份,BC=3份,那么BE=5份,BD=3+2=5份,由共角定理S△ABC:S△BDE=(AB×BC):(BE×BD)=(2×3):(5×5)=6:25,设S△ABC=6份,恰好是3平方厘米,所以1份是0.5平方厘米,25份就是25×0.5=12.5(平方厘米),三角形BDE的面积是12.5平方厘米.36. 如图,长方形的面积是16,BE=3BD,CE=CF.请问:三角形BEC的面积是多少?【答案】3【分析】详解:连结DF,根据鸟头模型,可知△BCE面积是△DEF面积的3 4×12=38.那么△BCE的面积是16×12×38=3.37. 如图,长方形ABCD的面积是1,M是AD边的中点,N在AB边上,且2AN=BN.那么,阴影局部的面积是多少?【答案】512【分析】S△ABD=12,S△AMN:S△ABD=(AM×AN):(AB×AD)=1:6,S△AMN=112,所以阴影局部的面积为S阴=12−112=512.38. 如图,在△ABC中,延长AB至D,使BD=AB,延长BC至E,使CE=12BC,F是AC 的中点,假设△ABC的面积是2,那么△DEF的面积是多少?【答案】 3.5【分析】因为在△ABC和△CFE中,∠ACB与∠FCE互补,所以S△ABC S△FCE =AC⋅BCFC⋅CE=2×21×1=41.又因为S△ABC=2,所以S△FCE=0.5.同理可得S△ADF=2,S△BDE=3.所以S△DEF=S△ABC+S△CEF+S△DEB−S△ADF=2+0.5+3−2=3.5.39. 如图在△ABC中,D在BA的延长线上,E在AC上,且AB:BD=5:7,AE:EC=3:2,S△ADE=36平方厘米,求△ABC的面积.【答案】150平方厘米【分析】S△ADE:S△ABC=(AD×AE):(AB×AC)=[3×(7−5)]:[5×(3+2)]=6:25,因为S△ADE=36(平方厘米),所以S△ABC=36÷6×25=150(平方厘米).40. △DEF的面积为7平方厘米,BE=CE,AD=2BD,CF=3AF,求△ABC的面积.【答案】24平方厘米【分析】S△BDES△ABC =BD×BEBA×BC=1×13×2=16,S△CEF S△ABC =CE×CFCB×CA=1×32×4=38,S△ADF S△ABC =AD×AFAB×AC=2×13×4=16,S△DEFS△ABC=S△ABC−S△BDE−S△CEF−S△ADFS△ABC=1−16−38−16=724,又△DEF的面积为7平方厘米,所以S△ABC=7÷724=24(平方厘米).41. 鸟和大虾在武林大会上相遇,争夺武林盟主的地位.三百回合大战后,两人不分胜负.突然,菜鸟向对手发出一枚飞镖.说时迟,那时快,飞镖已经接近大虾的胸口,只见大虾迅速抽身向左闪开,同时用手中的宝剑向飞镖劈去,只听见“嘡〞的一声,飞镖被劈成了两半.如下列图所示,菜鸟的飞镖是正六角星的形状,边长为5.被大虾劈开的刀口如虚线所示,那么较小的那局部残片占到整体面积的几分之几?【答案】107300【分析】对图形进行分割,分割过程如下:即所给我我们的图形共有12个小正三角形组成,令每一个小正三角形的面积为1,那么根据共角模型有:S三角形BDE S三角形BAC =BD×BEAB×AC=11×1315×15=143225.所以四边形ACDE的面积为:(1−143225)×9=8225.所以较小的残片的面积为:82 25+1=10725.所以较小残片占整个面积的:10725 12= 107 300.42. 如图,在梯形ABCD中,三角形ABE的面积为4.6平方厘米,BE=EF=FD,求三角形ABF、CDF、ABD、ACD的面积.【答案】9.2平方厘米;9.2平方厘米;13.8平方厘米;13.8平方厘米.【分析】S△ABF:S△ABE=(AB×FB):(AB×EB)=2,所以S△ABF=2×S△ABE=9.2(平方厘米);因为△ABD和△ACD同底等高,所以S△ABD=S△ACD,因而S△CDF=S△ACD−S△AFD=S△ABD−S△AFD=S△ABF=9.2(平方厘米);S△ABD:S△ABE=(AB×DB):(AB×EB)=3,所以S△ABD=3×S△ABE=13.8;所以S△ACD=S△ABD=13.8(平方厘米).43. 如图,三角形ABC中,AB是AD的6倍,EC是AE的3倍,如果三角形ADE的面积等于1,那么三角形ABC的面积是多少?【答案】24【分析】S△ADE:S△ABC=(1×1):(6×4)=1:24,S△ABC=24S△ADE=24×1=24.44. 把四边形ABCD的各边都延长2倍,得到一个新的四边形EFGH.如果ABCD的面积是5平方厘米,那么EFGH的面积是多少?【答案】65平方厘米【分析】连接BD,由共角定理知:S△ABD S△AEH =AB×ADAE×AH=1×12×3=16,S△BCD S△CFG =BC×CDCF×CG=1×13×2=16,S△AEH+S△CFG=6S ABCD,同理连接AC,可得:S△BEF+S△DGH=6S ABCD,所以S EFGH=(6+6+1)S ABCD=13×5=65cm2.45. 如图,把四边形ABCD的各边都延长1倍,得到一个新四边形EFGH.如果ABCD的面积是5平方厘米,那么EFGH的面积是多少平方厘米?【答案】25平方厘米【分析】连接BD,有△ABD中∠EAD+∠BAD=180∘,又夹成两角的边EA、AH、AB、AD的乘积比,EA×AHAB×AD=2,所以S△EAH=2S△EAD.类似的,还可得S△FCG=2S△BCD,有S△EAH+S△FCG=2(S△ABD+S△BCD)=10,同理可证:S△EBF+S△DHG=2(S△ABD+S△BCD)=10,所以四边形EFGH的面积是10+10+5=25(立方厘米).46. 下列图中的三角形ABC被分成了甲〔阴影局部〕、乙两局部,BD=DC=4,BE=3,AE= 6.求甲局部面积占乙局部面积的几分之几.【答案】15【分析】BEBA =33+6=13,BDBC=44+4=12,根据鸟头模型,甲局部占整个图形面积的13×12=16,那么甲局部占乙局部的15.47. 如图,在△ABC中,D、E分别是AB、AC上的点,且AD:AB=2:5,AE:AC=4:7,S△ADE=16平方厘米,求△ABC的面积.【答案】70平方厘米【分析】S△ADE:S△ABC=(AD×AE):(AB×AC)=(2×4):(7×5)=8:35,因为S△ADE=16(平方厘米),所以S△ABC=16÷8×35=70(平方厘米).48. 长方形ABCD的面积为36平方厘米,E、F、G为各边中点,H为AD边上任意一点,问阴影局部面积是多少?【答案】13.5平方厘米【分析】解法一:寻找可利用的条件,连接BH、HC,如下列图:可得:S△EHB=12S△AHB、S△FHB=12S△CHB、S△DHG=12S△DHC,而S ABCD=S△AHB+S△CHB+S△CHD=36(平方厘米).即S△EHB+S△BHF+S△DHG=12(S△AHB+S△CHB+S△CHD)=12×36=18.而S△EHB+S△BHF+S△DHG=S阴影+S△EBFS△EBF=12×BE×BF=12×(12×AB)×(12×BC)=18×36=4.5.所以阴影局部的面积是:S阴影=18−S△EBF=18−4.5=13.5(平方厘米).解法二:特殊点法.找H的特殊点,把H点与D点重合,那么图形就可变成下列图:这样阴影局部的面积就是△DEF的面积,根据鸟头定理,那么有:S阴影7=S ABCD−S△AED−S△BEF−S△CFD=36−12×12×36−12×12×12×36−12×12×36=13.549. 如下图,平行四边形ABCD的面积是1,E、F是AB、AD的中点,BF交EC于M,求△BMG的面积.【答案】130【分析】解法一:由题意可得,E、F是AB、AD的中点,得EF∥BD,而FD:BC=FH:HC=1:2,EB:CD=BG:GD=1:2.所以CH:CF=GH:EF=2:3,并得G、H是BD的三等分点,可得BG=GH,所以BG:EF=BM:MF=2:3,所以BM=25 BF,S△BFD=12S△ABD=12×12S平行四边形ABCD=14;又因为BG=13 BD,所以S△BMG=13×25×S△BFD=13×25×14=130.解法二:延长CE交DA于I,如下列图,可得,AI:BC=AE:EB=1:1,从而可以确定M的点的位置,BM:MF=BC:IF=2:3,BM=25 BF,BG=13 BD可得S△BMG=25×13S△BDF=25×13×14S平行四边形ABCD=130.50. 如下图,在长方形ABCD中,DE=CE,CF=2BF,如果长方形ABCD的面积为18,那么阴影局部的面积是多少?【答案】6【分析】简答:由于长方形ABCD的面积为18,可知三角形BCD的面积为9,三角形CEF 的面积为三角形BCD的面积的1 2×23=13,那么阴影局部的面积是9×(1−13)=6.51. 如图,△ABC中,AD:AB=2:3,AE:AC=4:5,求:△AED的面积是△ABC面积的几分之几?【答案】815【分析】S△ADE:S△ABC=(AD×AE):(AB×AC)=(2×4):(3×5)=8:15,所以△AED的面积是△ABC面积的815.52. 如图,长方形ABCD的面积是48,BE:CE=3:5,DF:CF=1:2.三角形CFE面积是多少?【答案】10【分析】简答:48×12×58×23=10.53. 如下图,∠A=∠B=60∘,且AB=24,BD=16,AC=8,而且三角形CDE的面积等于四边形ABEC的面积.请问:DE的长度是多少?【答案】14【分析】如下列图所示,延长AC和BD交于点F.由于∠A=∠B=60∘,因此△ABF为等边三角形,那么AF=BF=AB=24.而BD=16,AC=8,由此可得CF=16,DF=8,所以△CDF是△ABF的16×8 24×24= 2 9.又知△CDE的面积等于四边形ABEC的面积,△CDE的面积是△ABF的(1−29)×12=718,那么DF:DE=29:718=4:7,因此DE=14.54. 如下图,在直角三角形ABC中,AC的长3厘米,CB的长4厘米,AB的长5厘米,有一只小虫从C点出发,沿CB以1厘米/秒的速度向B爬行;另一只小虫从B点出发,沿BA以1厘米/秒的速度向A爬行.请问经过多少秒后,两只小虫所在的位置D、E与B组成的三角形DBE是等腰三角形?〔请写出所有答案〕【答案】2秒、2013秒或3213秒.【分析】设经过了x秒,那么BE=x厘米,CD=x厘米,两只小虫所在的位置D、E与B 组成的三角形DBE是等腰三角形的情况有三种:〔1〕以B为等腰三角形顶角所在的顶点,即BD=BE〔如图1〕.这个最好算,BD=4−x,BE=x,故x=4−x,解得x=2;〔2〕以E为等腰三角形顶角所在的顶点,即ED=EB,如图2,从E向BD作垂线,垂足为F,在金字塔BEFAC种,BEBA =BFBC,即x5=BF4,所以BF=45x.利用CD+DF+FB=4列出方程x+45x+45x=4,解得x=2013;〔或者利用△BEF和△BAC相似,得BEBF=54,即xBF=54,所以BF=45x〕〔3〕以D为等腰三角形顶角所在的顶点,即ED=DB,如图3,从D向AB作垂线,垂足为F,利用△BFD和△BCA相似得BFBD =45,即BF4−x=45,所以BF=45(4−x).利用BE=2BF列出方程x=45(4−x)×2,解得x=3213.综上,经过2秒或2013秒或3213秒后,两只小虫所在的位置D、E与B组成的三角形DBE是等腰三角形.55. 长方形ABCD的面积为36cm2,E、F、G为各边中点,H为AD边上任意一点,问阴影局部面积是多少?【答案】 13.5【分析】 解法一:寻找可利用的条件,连接 BH 、HC ,如下列图:可得:S △EHB =12S △AHB 、S △FHB =12S △CHB 、S △DHG =12S △DHC ,而 S ABCD =S △AHB +S △CHB +S △CHD =36. 即S △EHB +S △BHF +S △DHG=12(S △AHB +S △CHB +S △CHD )=12×36=18;而 S △EHB +S △BHF +S △DHG =S 阴影+S △EBF ,S △EBF =12×BE ×BF=12×(12×AB)×(12×BC)=18×36=4.5. 所以阴影局部的面积是:S 阴影=18−S △EBF =18−4.5=13.5. 解法二:特殊点法.找 H 的特殊点,把 H 点与 D 点重合, 那么图形就可变成下列图:。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
(一)基本概念
数出某种图形的个数是一类有趣的图形问题。由于图形千变万化,错综
复杂,所以要想准确地数出其中包含的某种图形的个数,还真需要动点
脑筋。要想有条理、不重复、不遗漏地数出所要图形的个数,最常用的
方法就是分类数。
(二)基本方法
简单的分类计数
如:计算左图由4个小长方形构成的网格中一共有多少个长方形。
例1数一数图中_________个三角形
1.
数一数下面有________个三角形。
2.
数一数下面有________个三角形。
例2数一数,图中有_________个三角形
1.
数一数下面有________个三角形。
2.
数一数下面有________个三角形。
例3数一数,图中有多少个长方形?
1.
数一数图中有________个正方形?
2.
数一数图中有________个正方形?
例4数一数,图中一共有________个正方形
1.
数一数图中有________个正方形。
2.
数一数图中有________个正方形。
例5数一数图中_________个圆
1.
数一数图中有________个圆?
2.
数一数图中有________个圆?
例6数一数,图中有________个三角形
1.
数一数,下面有________个三角形。
2.
数一数,下面有________个三角形。
