空间曲面的法向量方位余弦推导
法向量求二面角余弦值公式

法向量求二面角余弦值公式二面角余弦值公式是一种计算二面角的方法,也是数学中最重要的理论之一。
它是基于三角函数的概念而演变而来。
今天,我们将介绍法向量求二面角余弦值公式,它是求解二面角余弦值的简便方法。
法向量求二面角余弦值公式可以用来求解任意给定的二面角的余弦值。
首先,我们需要求出每个角的法向量,比如,角A的法向量是(1, 0, -1),角B的法向量是(2, 1, -1)。
然后,我们可以使用下面的公式计算它们之间的余弦值:cos = (A B)/ (|A| |B|)其中A、B表示两个角的法向量,AB表示A、B的点积,而|A|和|B|表示A、B的模。
由此,我们可以使用以上公式来求解任意二面角之间的余弦值。
举例来说,若要计算角A(1,0,-1)和角B(2,1,-1)的余弦值,我们只需要将之前的公式中的A、B分别换成这两个角的法向量即可:cos = (12 + 01 + (-1)*(-1))/ (|1|× |2,1,-1|)cos = 3 / (√63)cos = 0.948因此,角A(1,0,-1)和角B(2,1,-1)之间的余弦值为0.948。
通过以上的计算,我们可以得出结论:法向量求二面角余弦值公式是一种用来求解任意二面角之间的余弦值的简便方法。
它也是利用三角函数基础概念而演变而来的基本计算公式之一。
由于它的方法简单易行,所以,它在很多领域,如几何学、地理学、机械工程、电子工程等,都有着广泛的应用。
综上所述,法向量求二面角余弦值公式是一个简单而实用的求解方法,它不仅可以求出二面角之间的余弦值,而且还可以用于几何学、地理学、机械工程、电子工程等多个领域。
它对于改善人们的生活、发展科学技术具有重要意义,为我们现在的生活带来了无穷的便利。
怎么求曲面的法向量

怎么求曲面的法向量
求曲面的法向量可以通过曲面的方程和偏导数来计算。
以下是一种常用的求法向量的方法:
1. 假设曲面的方程为F(x, y, z) = 0,其中F是关于x、y、z的函数。
2. 分别对x、y、z求偏导数,得到F对x的偏导数(∂F/∂x)、F对y的偏导数(∂F/∂y)和F对z的偏导数(∂F/∂z)。
3. 法向量的方向与曲面在某点的切平面垂直,因此法向量的方向即为(∂F/∂x, ∂F/∂y, ∂F/∂z)。
4. 对法向量进行归一化,使其长度为1,即可得到单位法向量。
需要注意的是,以上方法适用于一般的曲面方程。
对于一些特殊的曲面,如球面、平面等,求法向量的方法可能会有所不同。
在特殊情况下,可以使用特定的方法来求解。
空间曲线与曲面的切向量与法向量

空间曲线与曲面的切向量与法向量空间曲线和曲面的切向量与法向量在微积分学中,我们经常会遇到空间曲线和曲面的问题。
为了研究它们的性质和行为,我们需要引入切向量和法向量的概念。
本文将介绍空间曲线和曲面的切向量与法向量的定义、性质以及应用。
一、空间曲线的切向量与法向量空间曲线是三维空间中的一条曲线,可以使用参数方程或者隐式方程进行表示。
在曲线上的每一点,都存在一个切向量和一个法向量。
切向量是曲线在该点处的切线方向,而法向量则垂直于切线,垂直于曲线所在的平面。
对于参数方程表示的曲线,切向量可以通过对参数求导来求得。
假设曲线的参数方程为:x = x(t),y = y(t),z = z(t),其中,t是参数。
那么在曲线上的某一点处,曲线的切向量可以表示为:T = (dx/dt, dy/dt, dz/dt)。
注意,切向量的方向是沿着曲线的正方向,因此需要保持t的增加方向与曲线前进的方向一致。
对于隐式方程表示的曲线,我们可以使用参数方程的方式来求得切向量。
首先,我们可以将隐式方程表示为参数方程:x = x(t),y = y(t),z = z(t)。
然后,我们再计算参数方程表示的曲线的切向量。
同样地,空间曲线上的某一点还有一个法向量,可以通过切向量的求导来得到。
法向量的方向垂直于曲线所在的平面,可以表示为:N = (dy/dt * dz/dt, -dx/dt * dz/dt, dx/dt * dy/dt)。
二、曲面的切向量与法向量曲面是三维空间中的一个二维曲面,可以用参数方程或者隐式方程进行表示。
在曲面上的每一点处,都存在一个切平面和一个法向量。
切平面是曲面在该点处的切平面,而法向量则垂直于切平面。
对于参数方程表示的曲面,切向量可以通过对参数求偏导数来求得。
假设曲面的参数方程为:x = x(u, v),y = y(u, v),z = z(u, v),其中,u和v是参数。
那么在曲面上的某一点处,曲面的切向量可以表示为:T = (∂x/∂u, ∂y/∂u, ∂z/∂u) * (∂u/∂t) + (∂x/∂v, ∂y/∂v, ∂z/∂v) * (∂v/∂t)。
曲面积分的计算定理

Dxy R(x, y, z(x,y)) d x d y
机动 目录 上页 下页 返回 结束
说明: 如果积分曲面 取下侧, 则
R(x, y, z) d x d y Dxy R(x, y, z(x, y))d x d y
•若
则有
P(x,
y,
z)d
ydz
Dyz
P(x( y,
f (x, y, z(x, y) )
Dxy
1
z
2 x
z
2 y
dxd y
(曲面的其他两种情况类似)
• 注意利用球面坐标、柱面坐标、对称性、重心公式 简化计算的技巧.
机动 目录 上页 下页 返回 结束
9.2.2 第二型曲面积分
一、有向曲面及曲面元素的投影
双侧曲面 • 曲面分类
单侧曲面
曲面分内侧和 外侧
2
d
x d y
x)d x
d
y
3a d x d y Dx y
机动 目录 上页 下页 返回 结束
内容小结
1. 两类曲面积分及其联系
定义:
n
•
f
(x,
y,
z)d S
lim
0
i 1
f
(i
, i
,i
) Si
•
P
d
y
d
z
Q
d
n
z
d
x
R
d
x
d
y
lim
z)
,
y, z) d y d z
(前正后负)
•若
空间曲面法向量的计算公式

空间曲面法向量的计算公式空间曲面法向量是指在三维坐标系中的曲面上的每一个点上的一个向量,它垂直于曲面并指向曲面的外部。
计算空间曲面法向量的公式可以根据曲面的类型和参数方程的不同而有所变化。
下面将分别介绍常见曲面的计算方法。
一、平面的法向量计算公式对于平面而言,它是一个没有弯曲的曲面,所以在平面上的每一个点上的法向量是相同的。
平面的法向量可以通过平面的法线方程来计算。
设平面的法线方程为ax+by+cz+d=0,其中(a, b, c)是法线的方向向量。
则平面上的每一个点的法向量都是(a, b, c)。
二、曲面的参数化方程的法向量计算公式对于通过参数化方程给出的曲面,法向量可以通过参数方程对参数求偏导数得到。
设曲面的参数方程为:x = f(u, v)y = g(u, v)z = h(u, v)则曲面上任意一点(x, y, z)的法向量可以通过以下公式计算:N = (∂y/∂u * ∂z/∂v - ∂z/∂u * ∂y/∂v, ∂z/∂u * ∂x/∂v -∂x/∂u * ∂z/∂v, ∂x/∂u * ∂y/∂v - ∂y/∂u * ∂x/∂v)其中,N为法向量,∂y/∂u表示y对u求偏导数,其他类似。
三、球面的法向量计算公式对于球面而言,它是一个具有球对称性的曲面。
球面的法向量在球面上的每一个点上均指向球心。
设球的球心为O,球面上的任意一点为P,则球面的法向量可以通过OP向量的方向来确定。
四、圆柱面的法向量计算公式对于圆柱面而言,它是一个具有柱对称性的曲面。
圆柱面的法向量在圆柱面上的每一个点上均垂直于圆柱轴线。
设圆柱轴线的方向向量为n,圆柱面上的任意一点为P,则圆柱面的法向量可以通过OP向量减去OP在n上的投影得到。
通过以上公式,我们可以计算出曲面上任意一点的法向量。
这些法向量在计算机图形学、物理学、工程学等领域都有广泛的应用。
在计算曲面的法向量时,我们需要注意点的选择,对于参数化方程要正确地求偏导数,以及向量运算的顺序等。
空间余弦定理
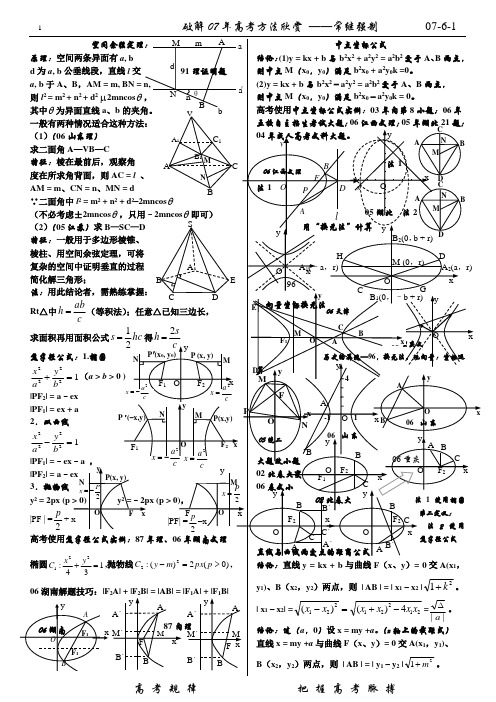
(2)y = kx + b与b2x2-a2y2= a2b2交于A、B两点,
则中点M(x0,y0)满足b2x0-a2y0k = 0。
高考使用中点坐标公式实例:03年内第8小题;06年
五校自主招生考试大题;06江西文理;05年湖北21题;04年成人高考文科大题。
法1
用“换元法”计算
向量坐标换元法
06重庆文
结论:过(a,0)设x = my +a。(x轴上的截距式)
直线x = my +a与曲线F(x、y)= 0交A(x1,y1)、
B(x2,y2)两点,则| AB | = | y1– y2| 。
千古绝唱3—“法向量任你选,向量法使你如虎添翼”
结论:(1)点到平面的距离公式:
或
或真懂后直接用
(2)直线和平面所成的角
度在所求角背面,则AC =l、
AM = m、CN = n、MN = d
∵二面角中l² = m² + n² + d²–2mncos
(不必考虑±2mncos ,只用–2mncos 即可)
(2)(05江苏)求B—SC—D
特征:一般用于多边形棱锥、
棱柱、用空间余弦定理,可将
复杂的空间中证明垂直的过程
简化解三角形;
空间余弦定理:
原理:空间两条异面有a, b
d为a, b公垂线段,直线l交91理证明题
a, b于A、B,AM = m, BN = n,
则l2= m2+ n2+ d2 2mncos ,
其中 为异面直线a、b的夹角。
一般有两种情况适合这种方法:
(1前后,观察角
方向余弦法
方向余弦法姿态更新的方向余弦法实质上就是直接求解姿态矩阵解微分方程. 设r 为某一空间向量,b 为机体坐标系,导航坐标系n 取地理坐标系g,则根据哥氏定理,||n b nb dr dr r dt dtω=+⨯ (9.5.2) 上式两边诸向量向b 坐标系投影,||()b b b n b nb dr dr r dt dtω=+⨯ (9.5.3) 由于|()b b b b b bnb nb dr r dt r r ωω=⨯=⨯所以式(9.5.3)可写成|b b b b n nb dr r r dtω=-⨯ (9.5.4) 另外,根据向量在不同坐标系的变换关系,有b b n n r C r =上式两边对时间求导|b b n b n b n b n n n n n n dr r C r C r C r C dt=+=+ 上式中, |n n dr dt 是ndr dt 在n 坐标系中的投影,经b n C 左乘后即为在b 坐标系中的投影,所以|b b n b b n n n dr r C r C dt=+ (9.5.5) 比较式(9.5.4) 和式(9.5.5),得b n b b b b n bk b n n nb nb n nb nC r r C r C r ωωω=-⨯=-⨯=- 所以b bk b n nb nC C ω=- (9.5.6)式中, bk nb ω是由b nb ω构造的反对称矩阵,即若b nb ω=[b nbx ω b nby ω b nbz ω ] T则 000b b nbz nby bk b b nbnbz nbx b b nby nbx ωωωωωωω⎡⎤-⎢⎥=-⎢⎥⎢⎥-⎣⎦(9.5.7) 式(9.5.6)式姿态矩阵微分方程的一种形式,根据计算方便,姿态矩阵微分方程还可以改写成其他形式.若式(9.5.2)两边诸向量向导航坐标系n 投影,则有 |n n n n b nb dr r r dtω=+⨯ (9.5.8) 根据向量的坐标系变换公式:C n n b b r r =对上式两边求时间导数,得:||n n b n b n b n b n b n b b b b b b b dr dr r C r C r C r C C r dt dt=+=+=+ (9.5.9) 比较(9.5.8)和(9.5.9),得C C n b n n nk n b b nb nb br r r ωω=⨯= 所以 C C n nk n b nb bω= (9.5.10) 式中000n n nbz nby nk n n nb nbznbx n n nby nbx ωωωωωωω⎡⎤-⎢⎥=-⎢⎥⎢⎥-⎣⎦(9.5.11) n nb ω=[ n nbxω n nby ω n nbz ω]T 若分别对式(9.5.6)和(9.5.10)两边求转置,则得姿态矩阵微分方程的另外两种形式:C C n n bk b b nb ω= (9.5.12) C C b b nk n n nbω=- (9.5.13)。
空间曲面参数方程的法向量
空间曲面参数方程的法向量
1. 隐函数法向量,对于一个隐函数表示的曲面,我们可以使用
梯度向量来计算法向量。
梯度向量是函数在某一点的偏导数构成的
向量。
对于曲面方程F(x, y, z) = 0,梯度向量的分量就是对应坐
标的偏导数,即(∂F/∂x, ∂F/∂y, ∂F/∂z)。
这个向量就是曲面
在该点处的法向量。
2. 参数方程法向量,对于一个参数方程表示的曲面,我们可以
通过求导来计算法向量。
设曲面的参数方程为P(u, v) = (x(u, v), y(u, v), z(u, v)),其中u和v分别是参数。
我们可以分别对u和
v求偏导数,得到两个切向量,然后通过叉乘得到法向量。
法向量
的计算公式为N = ∂P/∂u × ∂P/∂v。
3. 法向量的几何解释,从几何角度来看,曲面的法向量指向曲
面上某一点的垂直方向。
可以通过计算曲面上两个切向量的叉乘来
得到法向量。
这个法向量的方向可以用来判断曲面的凸凹性,以及
曲面上某一点的切平面的方向。
需要注意的是,以上方法适用于大多数常见的曲面类型。
对于
特殊的曲面,可能需要采用其他的方法来计算法向量。
总结起来,空间曲面参数方程的法向量可以通过梯度向量、参数方程的导数,或者几何方法来计算,它在几何上表示了曲面在给定点处的方向。
2-25 空间曲面的切平面与法线
空间曲面的切平面与法线设曲面方程为),,(=z y x F 一、曲面的切平面与法线n τM M.θ),cos(lim 00=∑∈→n MM M M MnM .C),(),(),(:t z z t y y t x x C ===的参数方程设曲线))(),(),((000t z t y t x '''=→τ0)](),(),([≡t z t y t x F 0)(),,()(),,()(),,(000000000000='+'+'t z z y x F t y z y x F t x z y x F z y x )},,(),,,(),,,({000000000z y x F z y x F z y x F n z y x =记0=⋅τ n 则板书上,在曲面曲线∑C ,对应的参数上任一点曲线0t M C 点处的切向量0M τ)},,(),,,(),,,({000000000z y x F z y x F z y x F n z y x =令则,T n⊥ 由于曲线是曲面上通过0M 的任意一条曲线,它们在0M 的切线都与同一向量n垂直,故曲面上通过0M 的一切曲线在点0M 的切线都在同一平面上,这个平面称为曲面在点0M 的切平面.切平面方程为))(,,())(,,())(,,(000000000000=-+-+-z z z y x F y y z y x F x x z y x F z y x通过点),,(0000z y x M 而垂直于切平面的直线 称为曲面在该点的法线.法线方程为),,(),,(),,(000000000000z y x F z z z y x F y y z y x F x x z y x -=-=-)},,(),,,(),,,({000000000z y x F z y x F z y x F n z y x =曲面在M 0处的法向量即垂直于曲面上切平面的向量称为曲面的法向量.特殊地:空间曲面方程形为),(y x f z =曲面在M 0处的切平面方程为,))(,())(,(0000000z z y y y x f x x y x f y x -=-+-曲面在M 0处的法线方程为.1),(),(0000000--=-=-z z y x f y y y x f x x y x ,),(),,(z y x f z y x F -=令}),,(),,({0000-1y x f y x f n y x =特殊地:空间曲面方程形为),(x z f y =曲面在M 0处的切平面方程为,))(,())(,(0000000y y z z x z f x x x z f z x -=-+-曲面在M 0处的法线方程为.),(1),(0000000x z f z z y y x z f x x z x -=--=-,),(),,(y x z f z y x F -=令)},(,1),,({0000x z f x z f n z x -=特殊地:空间曲面方程形为),(z y f x =曲面在M 0处的切平面方程为,))(,())(,(0000000x x z z z y f y y z y f z y -=-+-曲面在M 0处的法线方程为.),(),(10000000z y f z z z y f y y x x z y -=-=--,),(),,(x z y f z y x F -=令)},(),,(,1{0000z y f z y f n z y -=))(,())(,(0000000y y y x f x x y x f z z y x -+-=-切平面上点的竖坐标的增量的全微分在点函数),(),(00y x y x f z =因为曲面在M 0处的切平面方程为),(y x f z =在),(00y x 的全微分,表示曲面),(y x f z =在点),,(000z y x 处的切平面上的点的竖坐标的增量.二、全微分的几何意义若α、β、γ表示曲面的法向量的方向角,并假定法向量的方向是向上的,即使得它与z 轴的正向所成的角γ是锐角,则法向量的方向余弦为,1cos 22yx xf f f ++-=α,1cos 22yxyf f f ++-=β.11cos 22yx f f ++=γ),(00y x f f x x =),(00y x f f y y =其中例 求曲面2132222=++z y x 平行于平面064=++z y x 的各切平面方程. 解设为曲面上的切点,),,(000z y x 切平面方程为0)(6)(4)(2000000=-+-+-z z z y y y x x x 依题意,切平面方程平行于已知平面,得,664412000z y x ==.2000z y x ==⇒因为是曲面上的切点,),,(000z y x ,10±=∴x 所求切点为满足方程),2,2,1(),2,2,1(---0)2(12)2(8)1(2=-+-+-z y x 2164=++⇒z y x 0)2(12)2(8)1(2=+-+-+-z y x 2164-=++⇒z y x 切平面方程(1)切平面方程(2)三、小结曲面的切平面与法线(求法向量的方向余弦时注意符号)。
空间向量夹角余弦值计算公式
空间向量夹角余弦值计算公式在数学中,空间向量夹角余弦值是一种用于描述空间向量之间夹角大小的计算公式。
它表示两个空间向量a、b夹角的余弦值,符号为a·b。
其求值公式为:a·b=|a|·|b|·cosθ其中|a|、|b|表示两个空间向量的模长,θ表示两个向量之间的夹角(单位:弧度或角度)。
由余弦定理可得,只要知道这两个向量的模长和夹角,就可以使用空间向量夹角余弦值来求出夹角余弦值。
例子1:计算空间向量 a = (1,1,1) 与 b = (1,2,3) 夹角的余弦值由定义可知,此时|a|=√3,|b|=√14。
从四边形几何图可知,a点到b点的距离是13,该距离即为两点连线的模长,故|a-b| = 13;根据余弦定理求得,cosθ=|a-b|/|a|·|b|,即θ≈0.824。
最终求得,a·b的余弦值为a·b =13/√3·√14≈0.824。
例子2:计算空间向量 a = (-2,2,2) 与 b = (2,-2,2) 夹角的余弦值由定义可知,此时|a|=2√3,|b|=2√3。
从四边形几何图可知,a点到b点的距离是8,该距离即为两点连线的模长,故|a-b| = 8;根据余弦定理求得,cosθ=|a-b|/|a|·|b|,即θ≈π/2。
最终求得,a·b的余弦值为a·b = 8/2√3·2√3 ≈ 0.000。
以上就是空间向量夹角余弦值计算的求值公式和应用实例,空间向量夹角余弦值的求取过程比较繁琐,但是可以从中体会到数学的精妙之处,以及空间向量在研究自然界现象中的重要性。
虽然空间向量夹角余弦值是一种抽象概念,但它可以用于更加直观地理解复杂的自然现象。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
空间曲面的法向量方位余弦推导
空间曲面的法向量方位余弦可以通过曲线切线方向的余弦来推导。
假设有空间曲面上的一点P(x, y, z),该点所在的曲线为C。
定义曲线切线方向的单位向量为T,曲面法向量的单位向量为N。
曲线切线方向的余弦可以表示为:
cosθ = T·i + T·j + T·k
其中,i、j、k分别表示坐标轴的单位向量。
曲面法向量方位余弦可以表示为:
cosφ = N·i + N·j + N·k
现在我们要推导曲面法向量方位余弦与曲线切线方向余弦之间的关系。
考虑空间曲面上的一小段曲线,其两个端点分别为P1(x1, y1, z1)和P2(x2, y2, z2)。
假设曲线切
线方向的单位向量在P1和P2两点的余弦分别为cosθ1和cosθ2,曲面法向量的单位向量在P1
和P2两点的方位余弦分别为cosφ1和cosφ2。
由于曲线切线方向的单位向量T是切线方向的极限情况,我们可以得到以下关系式:
cosθ = lim(Δs→0) (ΔP · T) / Δs
其中,ΔP表示曲线上两点之间的位移向量,Δs表示曲线上两点之间的弧长。
类似地,曲面法向量的单位向量N是法向量的极限情况,我们可以得到以下关系式:
cosφ = lim(ΔA→0) (ΔP · N) / ΔA
其中,ΔA表示曲面上一个小区域的面积。
根据定义,曲线弧长的差分和曲面面积的差分可以表示为:
Δs = |ΔP| = sqrt[(Δx)² + (Δy)² + (Δz)²]
ΔA = |ΔP × ΔPφ|
其中,ΔP×表示曲面上两个位置向量的叉乘,Ά表示与曲面在点P处垂直的单位向量。
由于曲线切线方向的余弦与曲面法向量方位余弦都是单位向量,我们可以得到以下关系式:T·T = 1
N·N = 1
接下来,我们将曲线切线方向的余弦和曲面法向量方位余弦在P1和P2两点处展开为泰勒级数,然后利用上述关系式进行化简。
最终可以得到以下结果:
cosφ2 = cosθ2
这个结果说明,曲线切线方向的余弦和曲面法向量方位余弦在点P1和P2处是相等的。
也就是说,曲线切线方向的单位向量与曲面法向量的单位向量在点P处是同向的。
通过上述的推导,我们可以得到空间曲面的法向量方位余弦的推导过程。
