几何五大模型之四(相似定理)
几何五大模型

、等面积变换模型⑴等底等高的两个三角形面积相等;反之,如果S A ACD BCD,则可知直线AB平行于CD等底等高长方形-平行四边形-梯形的面积相等;三角形面积等于与它等底等高的平行四边形面积的一半;正方形的面积等于对角线长度平方的一半;⑵两个三角形高相等,面积比等于它们的底之比;两个三角形底相等,面积比等于它们的高之比。
如上图S =a :b、共角定理(鸟头定理)模型两个三角形中有一个角相等或互补,这两个三角形叫做共角三角形。
共角三角形的面积比等于对应角(相等角或互补角)两夹边的乘积之比。
如图,在△ ABC中,D,E分别是AB,AC上的点(如图1)或D在BA的延长线上,E在AC上(如图2),则SA ABC :SA ADE 二(AB AC):(AD AE)三、蝴蝶定理模型(不规则四边形的面积问题)①或者s S3P S4 ② AO:OC =I S S2 : S4 S3梯形中:①S I:S B二a2:b2图2②S!: S3 : S2: S4 =a2 :b2: ab: ab ;不论大小怎样改变它③梯形S 的对应份数为a b 2四、相似模型B G金字塔模型① AD _ AE _ DE _ AF AB AC BC AG所谓的相似三角形, 就是形状相同,大小不同的三角形(只要其形状不改变, 们都相似),与相似三角形相关的常用的性质及定理如下:⑴相似三角形的一切对应线段的长度成比例,并且这个比例等于它们的相似比;⑵相似三角形的面积比等于它们相似比的平方。
五、燕尾定理模型B E CS A ABG : S A AGC =S A BGE : S A EGC = BE :ECS A BGA : S A BGC =S A AGF : S^FGC =AF : FCS A AGC : S ABCG =S A ADG :&DGB =AD : DB ② S ^ADE :S ^ABC 二 AF 2: AG 2。
沙漏模型0.15倍,黄色三角形的面积是 如图,三角形田地中有两条小路 AE 和CF ,交叉处为D ,张大伯常走这两条小路, 且AD = 2DE 。
小学奥数平面几何五种面积模型(等积-鸟头-蝶形-相似-共边)汇总

小学奥数平面几何五种模型(等积,鸟头,蝶形,相似,共边)目标:熟练掌握五大面积模型等积,鸟头,蝶形,相似(含金字塔模型和沙漏模型),共边(含燕尾模型和风筝模型), 掌握五大面积模型的各种变形 知识点拨一、等积模型①等底等高的两个三角形面积相等; ②两个三角形高相等,面积比等于它们的底之比; 两个三角形底相等,面积比等于它们的高之比;如右图12::S S a b =③夹在一组平行线之间的等积变形,如右图ACD BCD S S =△△; 反之,如果ACD BCD S S =△△,则可知直线AB 平行于CD .④等底等高的两个平行四边形面积相等(长方形和正方形可以看作特殊的平行四边形);⑤三角形面积等于与它等底等高的平行四边形面积的一半;⑥两个平行四边形高相等,面积比等于它们的底之比;两个平行四边形底相等,面积比等于它们的高之比. 二、鸟头定理两个三角形中有一个角相等或互补,这两个三角形叫做共角三角形. 共角三角形的面积比等于对应角(相等角或互补角)两夹边的乘积之比. 如图在ABC △中,,D E 分别是,AB AC 上的点如图 ⑴(或D 在BA 的延长线上,E 在AC 上),则:():()ABC ADE S S AB AC AD AE =⨯⨯△△EDCBAEDCBA图⑴ 图⑵ 三、蝶形定理任意四边形中的比例关系(“蝶形定理"):①1243::S S S S =或者1324S S S S ⨯=⨯②()()1243::AO OC S S S S =++蝶形定理为我们提供了解决不规则四边形的面积问题的一个途径.通过构造b a S 2S 1DC BA S 4S 3S 2S 1O DCBA模型,一方面可以使不规则四边形的面积关系与四边形内的三角形相联系;另一方面,也可以得到与面积对应的对角线的比例关系.梯形中比例关系(“梯形蝶形定理”):①2213::S S a b = ②221324::::::S S S S a b ab ab =; ③S 的对应份数为()2a b +.四、相似模型(一)金字塔模型 (二) 沙漏模型GF E ABCDAB CDEF G①AD AE DE AF ABACBCAG===;②22:ADE ABC S S AF AG =△△:.所谓的相似三角形,就是形状相同,大小不同的三角形(只要其形状不改变,不论大小怎样改变它们都相似),与相似三角形相关的常用的性质及定理如下:⑴相似三角形的一切对应线段的长度成比例,并且这个比例等于它们的相似比;⑵相似三角形的面积比等于它们相似比的平方;⑶连接三角形两边中点的线段叫做三角形的中位线.三角形中位线定理:三角形的中位线长等于它所对应的底边长的一半. 相似三角形模型,给我们提供了三角形之间的边与面积关系相互转化的工具.在小学奥数里,出现最多的情况是因为两条平行线而出现的相似三角形. 五、共边定理(燕尾模型和风筝模型)在三角形ABC 中,AD ,BE ,CF 相交于同一点O ,那么::ABO ACO S S BD DC ∆∆=.上述定理给出了一个新的转化面积比与线段比的手段,因为ABO ∆和ACO ∆的形状很象燕子的尾巴,所以这个定理被称为燕尾定理.该定理在许多几何题目中都有着广泛的运用,它的特殊性在于,它可以存在于任何一个三角形之中,为三A BC D O ba S 3S 2S 1S 4O FED C BA角形中的三角形面积对应底边之间提供互相联系的途径。
几何五大模型精讲-第3讲-相似模型

x x 1 ,解得 x 48 , 120 80
即正方形的边长为 48 毫米. 【例 5】
E M B N
O
F
相似三角形的对应边成比例有: 则 NF , EM ,
5 9 5 3
EM 1 NF 3 ; , 1 2 2 3 2 3 1 2
1 9 5 1 S阴 2 2 2 5 3 30
A B
G F
D
E
C
【例 8】 如图, 长方形 ABCD 中,E 为 AD 的中点,AF 与 BE 、BD 分别交于 G 、H ,
OE 垂直 AD 于 E ,交 AF 于 O ,已知 AH 5 cm , HF 3 cm ,求 AG .
A G
E
D
O
H
F C
B
作业题
1、 测量小玻璃管口径的量具 ABC , AB 的长为 15 厘米, AC 被分为 60 等份.如 果小玻璃管口 DE 正好对着量具上 20 等份处( DE 平行 AB ), 那么小玻璃管口径
10 40 cm . 13 13 1 2 1 2
3 2
作业题
1、 有一个金字塔模型,所以 DE : AB DC : AC , DE :15 40: 60 ,所以 DE 10 厘 米.
2、 设 S△ ADE 1 份, S△ ADE : S△ AFG AD2 : AF 2 1: 4 ,因此 S△ AFG 4 份,进而有
4 4 32 . S△ ABE (4 4 2) 47 11 11
法二:连接 AE, EF ,
S△ ABF 4 2 2 4 ,
S△ AEF 4 4 4 1 2 3 2 2 4 7 ,
几何五大模型
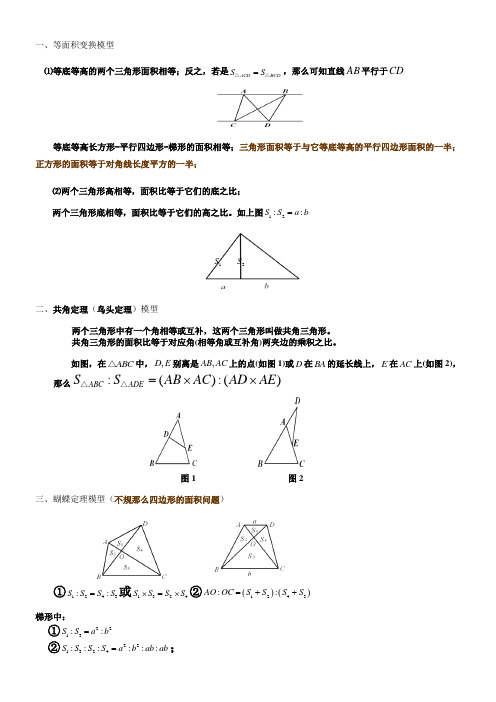
一、等面积变换模型⑴等底等高的两个三角形面积相等;反之,若是ACD BCD S S =△△,那么可知直线AB 平行于CD等底等高长方形-平行四边形-梯形的面积相等;三角形面积等于与它等底等高的平行四边形面积的一半;正方形的面积等于对角线长度平方的一半;⑵两个三角形高相等,面积比等于它们的底之比;两个三角形底相等,面积比等于它们的高之比。
如上图12::S S a b =二、共角定理(鸟头定理)模型两个三角形中有一个角相等或互补,这两个三角形叫做共角三角形。
共角三角形的面积比等于对应角(相等角或互补角)两夹边的乘积之比。
如图,在ABC △中,,D E 别离是,AB AC 上的点(如图1)或D 在BA 的延长线上,E 在AC 上(如图2),那么:():()ABCADE S S AB AC AD AE =⨯⨯△△图1 图2三、蝴蝶定理模型(不规那么四边形的面积问题)①1243::S S S S =或1324S S S S ⨯=⨯②()()1243::AO OC S S S S =++梯形中:①2213::S S a b =②221324::::::S S S S a b ab ab =;1S 2S③梯形S的对应份数为()2a b+。
四、相似模型金字塔模型沙漏模型①AD AE DE AF AB AC BC AG===;②22::ADE ABCS S AF AG=△△。
所谓的相似三角形,确实是形状相同,大小不同的三角形(只要其形状不改变,不论大小如何改变它们都相似),与相似三角形相关的经常使用的性质及定理如下:⑴相似三角形的一切对应线段的长度成比例,而且那个比例等于它们的相似比;⑵相似三角形的面积比等于它们相似比的平方。
五、燕尾定理模型S△ABG:S△AGC=S△BGE:S△EGC=BE:ECS△BGA:S△BGC=S△AGF:S△FGC=AF:FCS△AGC:S△BCG=S△ADG:S△DGB=AD:DB典型例题精讲例1一个长方形分成4个不同的三角形,绿色三角形面积是长方形面积的0.15倍,黄色三角形的面积是21平方厘米。
小学数学几何必考五大模型

它们的高之比.
精选2021版课件
4
二、鸟头定理
两个三角形中有一个角相等或互补,这两个三角形叫做共角三角形.
共角三角形的面积比等于பைடு நூலகம்应角(相等角或互补角)两夹边的乘积之比.
A
D
D E
A E
B
C
图⑴
B
C
图 (2)
如图在 E在AC上),则
中,D、E分别是AB、AC上的点如图 ⑴(或D在BA的延长线上,
精选2021版课件
S1 S2
如右图
a
b
C
D
③夹在一组平行线之间的等积变形,如右图
;
反之,如果
,则可知直线 平行于 。
④等底等高的两个平行四边形面积相等(长方形和正方形可以看作特殊的平行四边形);
⑤三角形面积等于与它等底等高的平行四边形面积的一半;
⑥两个平行四边形高相等,面积比等于它们的底之比;两个平行四边形底相等,面积比等于
精选2021版课件
7 五、燕尾定理(共边定理、燕尾模型和风筝模型)
在三角形ABC中,AD,BE,CF相交于同一点O,那么
.
上述定理给出了一个新的转化面积比与线段比的手段,因为和的形状很象燕子的尾巴, 所以这个定理被称为燕尾定理.该定理在许多几何题目中都有着广泛的运用,它的特殊性在于 ,它可以存在于任何一个三角形之中,为三角形中的三角形面积对应底边之间提供互相联系的 途径.
⑴相似三角形的一切对应线段的长度成比例,并且这个比例等于它们的相似比; ⑵相似三角形的面积比等于它们相似比的平方; ⑶连接三角形两边中点的线段叫做三角形的中位线. 三角形中位线定理:三角形的中位线长等于它所对应的底边长的一半. 相似三角形模型,给我们提供了三角形之间的边与面积关系相互转化的工具. 在小学小学数学里,出现最多的情况是因为两条平行线而出现的相似三角形.
小学数学几何五大模型教师版新

几何五大模型一、五大模型简介(1)等积变换模型? ? 1、等底等高的两个三角形面积相等;? ? 2、两个三角形高相等,面积之比等于底之比,如图①所示,S1:S2=a:b;? ? 3、两个三角形底相等,面积在之比等于高之比,如图②所示,S1:S2=a:b;? ? 4、在一组平行线之间的等积变形,如图③所示,S△ACD=S△BCD;反之,如果S△ACD=S△BCD,则可知直线AB平行于CD。
例、如图,三角形ABC的面积是24,D、E、F分别是BC、AC、AD的中点,求三角形DEF的面积。
(2)鸟头(共角)定理模型? ? 1、两个三角形中有一个角相等或互补,这两个三角形叫共角三角形;? ? 2、共角三角形的面积之比等于对应角(相等角或互补角)两夹边的乘积之比。
? ?如图下图三角形ABC中,D、E分别是AB、AC上或AB、AC延长线上的点? ? 则有:S△ABC:S△ADE=(AB×AC):(AD×AE)? ? 我们现在以互补为例来简单证明一下共角定理!如图连接BE,根据等积变化模型知,S△ADE:S△ABE=AD:AB、S△ABE:S△CBE=AE:CE,所以S△ABE:S△ABC=S△ABE:(S△ABE+S△CBE)=AE:AC,因此S△ADE:S△ABC=(S△ADE:S△ABE)×(S△ABE:S△ABC)=(AD:AB)×(AE:AC)。
例、如图在ΔABC中,D在BA的延长线上,E在AC上,且AB:AD=5:2,AE:EC=3:2,△ADE的面积为12平方厘米,求ΔABC的面积。
(3)蝴蝶模型? ? 1、梯形中比例关系(“梯形蝴蝶定理”)例、如图,梯形ABCD,AB与CD平行,对角线AC、BD交于点O,已知△AOB、△BOC 的面积分别为25平方厘米、35平方厘米,求梯形ABCD的面积。
? ? 2、任意四边形中的比例关系(“蝴蝶定理”):例、如图,四边形ABCD的对角线AC、BD交于点O,如果三角形ABD的面积等于三角形BCD面积的1/3,且AO=2、DO=3,求CO的长度是DO长度的几倍。
小学数学几何五大模型教师版
小学数学几何五大模型教师版五大几何模型简介等积变换模型:等积变换模型有四个基本特点,分别是:等底等高的两个三角形面积相等;两个三角形高相等,面积之比等于底之比;两个三角形底相等,面积在之比等于高之比;在一组平行线之间的等积变形。
例如,对于一个三角形ABC,如果D、E、F 分别是BC、AC、AD的中点,那么三角形DEF的面积可以通过等积变换模型求得。
鸟头(共角)定理模型:鸟头(共角)定理模型有两个基本特点,分别是:两个三角形中有一个角相等或互补,这两个三角形叫共角三角形;共角三角形的面积之比等于对应角两夹边的乘积之比。
例如,在一个三角形ABC中,如果D、E分别是AB、AC上或AB、AC延长线上的点,那么可以通过共角定理求得S△ADE:S△ABC=(AD:AB)×(AE:AC)。
蝴蝶模型:蝴蝶模型有两个基本特点,分别是:梯形中比例关系(“梯形蝴蝶定理”);任意四边形中的比例关系(“蝴蝶定理”)。
例如,在一个梯形ABCD中,如果对角线AC、BD交于点O,已知△AOB、△BOC的面积分别为25平方厘米、35平方厘米,那么可以通过梯形蝴蝶定理求得梯形ABCD的面积。
另外,在一个四边形ABCD中,如果对角线AC、BD交于点O,且三角形ABD的面积等于三角形BCD面积的1/3,且AO=2、DO=3,那么可以通过蝴蝶定理求得CO的长度是DO长度的几倍。
相似模型:相似模型有两个基本特点,分别是:两个相似三角形的面积之比等于它们的边长之比的平方;两个相似四边形的面积之比等于它们的边长之比的平方。
例如,在一个相似三角形ABC和DEF中,如果AB:DE=2:3,BC:EF=3:4,那么可以通过相似模型求得S△ABC:S△DEF=4:9.相似三角形是指形状相同但大小不相等的两个三角形,要找到相似模型的前提是平行线。
平行于三角形一边的直线和其他两边或两边延长线相交,所构成的三角形与原三角形相似。
相似三角形的一切对应线段(对应高、对应边)的比等于相似比,周长的比等于相似比,面积的比等于相似比的平方。
平面几何五大定理
定义推广:
四、等积变换定理:
五、沙漏定理:
平面几何五大定理几何五大模型平面几何欧拉定理蝶形定理数学三角形五大定理初中几何解题模型初中数学解题模型鸟头定理四边形中幂等定理燕尾定理
一、燕尾定理:
在三角形ABC中,AD,BE,CF相交于同一点O,有
S△AOB∶S△AOC=BD∶CD
S△AOB∶S△COB=AE∶CE
S△BOC∶S△AOC=BF∶AF
定理推广:
四边形ABCD(不一定是凸四边形),设AC,BD相交于E则有BE:DE=S△ABC∶S△ADC
二、鸟头定理:
三、梯形蝴蝶定理:
如图,在梯形中,存在以下关系:
1.相似图形,面积比等于对应边长比的平方S1:S2=a2/b2
2.S1:S2:S3:S4= a2:b2:ab:ab
3.S3=S4
4.S1×S2=S3×S4(由S1/S3=S4/S2推导出)
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
任意四边形、梯形与相似模型
模型四 相似三角形模型
(一)金字塔模型 (二) 沙漏模型
G
F
E
A
B
C
D
ABCDEFG
①ADAEDEAFABACBCAG;
②22:ADEABCSSAFAG△△:。
所谓的相似三角形,就是形状相同,大小不同的三角形(只要其形状不改变,不论大小怎样
改变它们都相似),与相似三角形相关的常用的性质及定理如下:
⑴相似三角形的一切对应线段的长度成比例,并且这个比例等于它们的相似比;
⑵相似三角形的面积比等于它们相似比的平方;
⑶连接三角形两边中点的线段叫做三角形的中位线。
三角形中位线定理:三角形的中位线长等于它所对应的底边长的一半。
相似三角形模型,给我们提供了三角形之间的边与面积关系相互转化的工具。
在小学奥数里,出现最多的情况是因为两条平行线而出现的相似三角形。
【例 1】 如图,已知在平行四边形ABCD中,16AB,10AD,4BE,那么FC的长
度是多少?
F
EDCB
A
【例 2】 如图,测量小玻璃管口径的量具ABC,AB的长为15厘米,AC被分为60等份。
如果小玻璃管口DE正好对着量具上20等份处(DE平行AB),那么小玻璃管口径
DE
是多大?
605040302010
0
E
A
D
C
B
【例 3】 如图,DE平行BC,若:2:3ADDB,那么:ADEECBSS△△________。
A
E
D
C
B
【例 4】 如图, ABC△中,DE,FG,BC互相平行,ADDFFB,
则::ADEDEGFFGCBSSS△四边形四边形 。
E
G
F
A
D
C
B
【巩固】如图,DE平行BC,且2AD,5AB,4AE,求AC的长。
A
E
D
C
B
【巩固】如图, ABC△中,DE,FG,MN,PQ,BC互相平行,ADDFFMMPPB,
则::::ADEDEGFFGNMMNQPPQCBSSSSS△四边形四边形四边形四边形 。
Q
E
G
N
M
F
P
A
D
C
B
【例 5】
已知ABC△中,DE平行BC,若:2:3ADDB,且DBCES梯形比ADES△大28.5cm,
求ABCS△。
A
E
D
C
B
【例 6】 如图:MN平行BC, :4:9MPNBCPSS△△,4cmAM,求BM的长度
N
M
P
A
C
B
【巩固】如图,已知DE平行BC,:3:2BOEO,那么:ADAB________。
O
E
D
C
B
A
【例 7】 如图,ABC中,14AEAB,14ADAC,ED与BC平行,EOD的面积是1
平方厘米。那么AED的面积是 平方厘米。
A
B
C
D
E
O
【例 8】 在图中的正方形中,A,B,C分别是所在边的中点,CDOV的面积是ABOV面
积的几倍?
A
B
C
D
O
E
F
A
B
C
D
O
【例 9】 如图,线段AB与BC垂直,已知4ADEC,6BDBE,那么图中阴影部分
面积是多少?
EABCD E
A
B
C
D
O
【例 10】 (2008年第二届两岸四地”华罗庚金杯”少年数学精英邀请赛)如图,四边形
ABCD和EFGH都是平行四边形,四边形ABCD的面积是16,:3:1BGGC
,则
四边形EFGH的面积________.
H
G
F
EDCBA
【例 11】 已知三角形ABC的面积为a,:2:1AFFC,E是BD的中点,且EF∥BC,
交CD于G,求阴影部分的面积.
ABCDEGF
【例 12】 已知正方形ABCD,过C的直线分别交AB、AD的延长线于点E、F,且
10cmAE,15cmAF
,求正方形ABCD的边长.
F
A
E
D
C
B
【例 13】 如图,三角形ABC是一块锐角三角形余料,边120BC毫米,高80AD毫
米,要把它加工成正方形零件,使正方形的一边在BC上,其余两个顶点分别在
AB
、AC上,这个正方形零件的边长是多少?
HGNPADCB
【巩固】如图,在ABC△中,有长方形DEFG,G、F在BC上,D、E分别在AB、
AC
上,AH是ABC△ 边BC的高,交DE于M,:1:2DGDE,12BC厘米,
8AH
厘米,求长方形的长和宽.
EHGMFAD
C
B
【例 14】 图中ABCD是边长为12cm的正方形,从G到正方形顶点C、D连成一个三角
形,已知这个三角形在AB上截得的EF长度为4cm,那么三角形GDC的面积是
多少?
AB
C
D
EF
G
N
M
AB
C
D
EF
G
【例 15】 如图,将一个边长为2的正方形两边长分别延长1和3,割出图中的阴影部分,
求阴影部分的面积是多少?
B
M
N
F
O
E
【例 16】 (2008年101中学考题)图中的大小正方形的边长均为整数(厘米),它们的面
积之和等于52平方厘米,则阴影部分的面积是 .
H
G
FE
D
C
B
A
【例 17】 如图,三角形PDM的面积是8平方厘米,长方形ABCD的长是6厘米,宽是
4
厘米,M是BC的中点,则三角形APD的面积是 平方厘米.
A
BC
D
P
M
【例 18】 边长为8厘米和12厘米的两个正方形并放在一起,那么图中阴影三角形的面
积是多少平方厘米?
H
O
E
D
C
B
M
N
A
【例 19】 如右图,长方形ABCD中,16EF,9FG,求AG的长.
D
A
B
C
E
F
G
课后作业
1、已知ABC△中,DE平行BC,若:2:3ADDB,且DBCES梯形比ADES△大28.5cm,
求ABCS△.
A
E
D
C
B
2、如图,O是矩形一条对角线的中点,图中已经标出两个三角形的面积为3和4,
那么阴影部分的一块直角三角形的面积是多少?
34O
F
E
DCBA
3、如图,已知在平行四边形ABCD中,16AB,10AD,4BE,那么FC的长
度是多少?
F
EDCB
A
4、如图, ABC△中,DE,FG,BC互相平行,ADDFFB,
则::ADEDEGFFGCBSSS△四边形四边形 .
Q
E
G
N
M
F
P
A
D
C
B
5、已知正方形ABCD,过C的直线分别交AB、AD的延长线于点E、F,且
10cmAE,15cmAF
,求正方形ABCD的边长.
F
A
E
D
C
B
6、如图,三角形ABC是一块锐角三角形余料,边120BC毫米,高80AD毫米,
要把它加工成正方形零件,使正方形的一边在BC上,其余两个顶点分别在AB、
AC
上,这个正方形零件的边长是多少?
H
G
N
P
A
D
C
B
