2018年 北师大版八年级数学(上册)知识点归纳总结(最新)
2017-2018学年北师大版八年级数学上册教师用书(pdf版):4.1函数

围是㊀ ㊀ ㊀ ㊀ . ㊀ (4) (2016 安顺) 在函数 y = 范围是㊀ ㊀ ㊀ ㊀ . ㊀ (5) (2016 朝阳 ) 函数 y = 的取值范围是㊀ ㊀ ㊀ ㊀ .
2. 函数概念的理解:
们就说 x 是自变量ꎬy 是 x 的 ㊀ 函数 ㊀ . 如果当 x = a 时ꎬ y = bꎬ则 b 叫作当自变量的值为 a 时的㊀ 函数值㊀ .
C. x <1 x+1 x D. xɤ1 (㊀ x-1 x-2
㊀ 八年级( 上) 册
������������
������������������������������������������������������������������
巅峰对决������数学
x - 1 中ꎬ自变量 x 的取值范 ㊀ )
3. 函数的三种常用表示法: 列表法 ( 即表格 ) ㊁ 图像法㊁ 解 析法( 即函数解析式) .
函数的认识 ʌ 例 1ɔ 下列变量之间的关系是不是函数关系? 为什么? ㊀ (1) 三角形的面积 S 与它的一边长 x 的关系ꎻ ㊀ (2) 圆的周长与面积ꎻ ㊀ (3) 长方形的面积与周长.
㊀ 分析: 根据函数定义中的三个要素进行分析: ① 变化 过程中只有两个变化的量ꎬ② 一个变量随另一个变量的 值变化而变化ꎬ ③ 自变量每取定一个值ꎬ 对应的函数值 是否存在唯一的值与它对应.
㊀ (1) (2016 重庆) 函数 y = ㊀ A. xʂ0 围是 B. x > - 2
㊀ (2) B. xȡ1
㊀ (3) (2016 天水) 函数 y = 1. 在一个变化过程中的两个变量 xꎬyꎬ并且对于 x 的 ㊀ 每
一个㊀ 确定的值 ꎬy 都有 ㊀ 唯一㊀ 的值与其对应 ꎬ 那么我
2017-2018学年北师大版八年级数学上册教师用书(pdf版):3.3轴对称与坐标变化
位置如图所示ꎬ线段 M1N1 与 MN 关 于 y 轴 对 称ꎬ 则 点 M
(2) (2n ꎬ3) 、(2n+1 ꎬ0) .
归纳: 先观察给出的点的特点ꎬ再分析各数据之间的关系ꎬ 如和、倍、分等数量关系ꎻ再将对比得出的结论用文字或 数学式子表示出来.
1.如图ꎬ在方格纸中ꎬ有一平行四边形 ABCDꎬ则它关于 x 轴对称的图形的顶点坐标是( 2ꎬ- 1) 、( 4ꎬ- 1) 、( 6ꎬ- 3)
图形变换的运用
【 例 3】 如图所示ꎬ在直角坐标 系中ꎬ第一次将△OAB 变换成 △OA1B1ꎬ 第 二 次 将 △OA1B1 变 换 成 △OA2B2ꎬ 第 三 次 将 △OA2B2 变换成△OA3B3ꎬ已 知 A ( 1ꎬ3)、A1 ( 2ꎬ3)、A2 ( 4ꎬ 3) 、A3( 8ꎬ3) ꎬB( 2ꎬ0) 、B1( 4ꎬ0) 、B2( 8ꎬ0) 、B3( 16ꎬ0) . (1)观察每次变换前后的三角形有何变化ꎬ找出规律ꎬ 按此变换规律再次将△OA3 B3 变换成△OA4 B4 ꎬ则 A4 的 坐标是 ꎬB4 的坐标是 . (2) 若按(1) 找到的规律ꎬ将△OAB 进行了 n 次变换ꎬ 得到△OAn Bn ꎬ推测 An 的坐标是 ꎬBn 的坐标是 . 分析:观察图形分析、对比各点的横坐标和纵坐标ꎬ可 知 An 的横坐标是按 2n 变化的ꎬ 而 Bn 的横坐标是按 2n+1 变化的. 解:(1)(16ꎬ3)、(32ꎬ0)ꎻ
������������
第 3 章 位置与坐标
第 4 课 轴对称与坐标变化
知识目标 重、难点 思维目标
掌握点关于两轴对称的点的坐标特点ꎬ学 习图形的变化与点的坐标变化. 图形坐标变化与图形轴对称之间关系的 探索. 数形结合思想ꎬ发展形象思维能力.
北师大版八年级上册数学第一章勾股定理全章知识点及习题(经典)
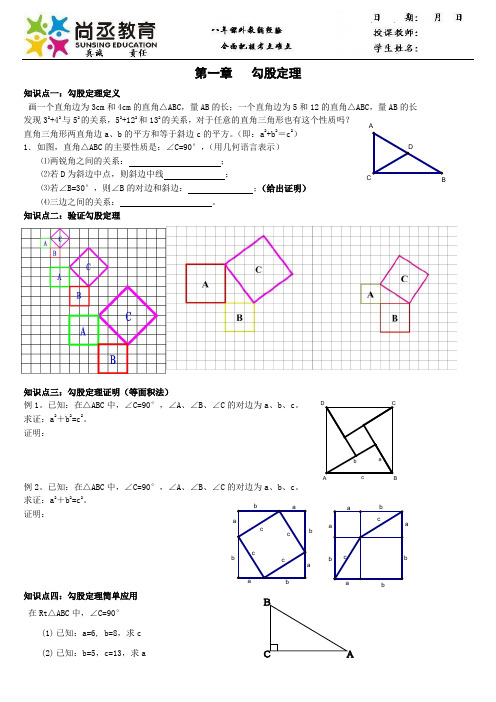
cbaD CAB第一章 勾股定理知识点一:勾股定理定义画一个直角边为3cm 和4cm 的直角△ABC ,量AB 的长;一个直角边为5和12的直角△ABC ,量AB 的长 发现32+42与52的关系,52+122和132的关系,对于任意的直角三角形也有这个性质吗? 直角三角形两直角边a 、b 的平方和等于斜边c 的平方。
(即:a 2+b 2=c 2) 1.如图,直角△ABC 的主要性质是:∠C=90°,(用几何语言表示)⑴两锐角之间的关系: ; ⑵若D 为斜边中点,则斜边中线 ;⑶若∠B=30°,则∠B 的对边和斜边: ;(给出证明) ⑷三边之间的关系: 。
知识点二:验证勾股定理知识点三:勾股定理证明(等面积法)例1。
已知:在△ABC 中,∠C=90°,∠A 、∠B 、∠C 的对边为a 、b 、c 。
求证:a 2+b 2=c 2。
证明:例2。
已知:在△ABC 中,∠C=90°,∠A 、∠B 、∠C 的对边为a 、b 、c 。
求证:a 2+b 2=c 2。
证明:知识点四:勾股定理简单应用 在Rt △ABC 中,∠C=90°(1) 已知:a=6, b=8,求c bbbbccccaaaabbb ba accaaACBDAB如果三角形的三边长为c b a ,,,满足222c b a =+,那么,这个三角形是直角三角形. 利用勾股定理的逆定理判别直角三角形的一般步骤: ①先找出最大边(如c )②计算2c 与22a b +,并验证是否相等。
若2c =22a b +,则△ABC 是直角三角形。
若2c ≠22a b +,则△ABC 不是直角三角形。
1.下列各组数中,以a ,b ,c 为边的三角形不是Rt △的是( ) A.a=7,b=24,c=25 B.a=7,b=24,c=24C.a=6,b=8,c=10D.a=3,b=4,c=52.三角形的三边长为ab c b a 2)(22+=+,则这个三角形是( )A. 等边三角形B. 钝角三角形C. 直角三角形D. 锐角三角形3.已知0)10(862=-+-+-z y x ,则由此z y x ,,为三边的三角形是 三角形. 知识点六:勾股数(1)满足222c b a =+的三个正整数,称为勾股数.(2)勾股数中各数的相同的整数倍,仍是勾股数,如3、4、5是勾股数,6、8、10也是勾股数. (3)常见的勾股数有:①3、4、5②5、12、13;③8、15、17;④7、24、25; ⑤11、60、61;⑥9、40、41.1.设a 、b 、c 是直角三角形的三边,则a 、b 、c 不可能的是( ).A.3,5,4B. 5,12,13C.2,3,4D.8,17,15 1. 若线段a ,b ,c 组成Rt △,则它们的比可以是( )A.2∶3∶4B.3∶4∶6C.5∶12∶13D.4∶6∶7知识点七:确定最短路线1.一只长方体木箱如图所示,长、宽、高分别为5cm 、4cm 、3cm, 有一只甲虫从A 出发,沿表面爬到C ',最近距离是多少?2.如图,一圆柱高8cm,底面半径2cm,一只蚂蚁从点A 爬到点B 处吃食,要爬行的最短路程(π 取3)是 .知识点八:逆定理判断垂直1.在△ABC 中,已知AB 2-BC 2=CA 2,则△ABC 的形状是( )A .锐角三角形;B .直角三角形;C .钝角三角形;D .无法确定. 2.如图,正方形网格中的△ABC ,若小方格边长为1,则△ABC 是( )ABCD A 'B 'C 'D 'BC5米3米1.在我国古代数学著作《九章算术》中记载了一道有趣的问题,这个问题的意思是:有一个水池,水面是一个边长为10尺的正方形,在水池正中央有一根新生的芦苇,它高出水面1尺,如果把这根芦苇垂直拉向岸边,它的顶端恰好到达岸边的水面,请问这个水池的深度和这根芦苇的长度各是多少?2.如图为某楼梯,测得楼梯的长为5米,高3米,计划在楼梯表面铺地毯,地毯的长度至少需要________米.3.一根直立的桅杆原长25m,折断后,桅杆的顶部落在离底部的5m处,则桅杆断后两部分各是多长?4.某中学八年级学生想知道学校操场上旗杆的高度,他们发现旗杆上的绳子垂到地面还多1米,当他们把绳子的下端拉开5米后,发现下端刚好触地面,你能帮他们把旗杆的高度和绳子的长度计算出来吗?综合练习一一、选择题1、下面几组数:①7,8,9;②12,9,15;③m 2+ n 2, m 2– n 2, 2mn(m,n 均为正整数,m >n);④2a ,12+a ,22+a .其中能组成直角三角形的三边长的是( )A.①②;B.①③;C.②③;D.③④2已知一个Rt △的两边长分别为3和4,则第三边长的平方是( )A.25B.14C.7D.7或253.三角形的三边长为ab c b a 2)(22+=+,则这个三角形是( )A. 等边三角形;B. 钝角三角形;C. 直角三角形;D. 锐角三角形. 4.△ABC 的三边为a 、b 、c 且(a+b)(a-b)=c 2,则( )A.a 边的对角是直角B.b 边的对角是直角C.c 边的对角是直角D.是斜三角形5.以下列各组中的三个数为边长的三角形是直角三角形的个数有( )①6、7、8,②8、15、17,③7、24、25,④12、35、37,⑤9、40、41 A 、1个 B 、2个 C 、3个 D 、4个6.将直角三角形的三边扩大相同的倍数后,得到的三角形是 ( ) A.直角三角形 B.锐角三角形 C.钝角三角形 D.不是直角三角形7.若△ABC 的三边a 、b 、c 满足(a-b)(a 2+b 2-c 2)=0,则△ABC 是 ( ) A.等腰三角形 B.直角三角形C.等腰直角三角形D.等腰三角形或直角三角形8.如图,∠C =∠B =90°,AB =5,BC =8,CD =11,则AD 的长为 ( )A 、10B 、11C 、12D 、139.如图、山坡AB 的高BC =5m ,水平距离AC =12m ,若在山坡上每隔0.65m 栽一棵茶树,则从上到下共 ( )A 、19棵B 、20棵C 、21棵D 、22棵10.Rt △ABC 中,∠C =90°,∠A 、∠B 、∠C 所对的边分别是a 、b 、c ,若c =2,则2a +2b +2c 的值是 ( )A 、6B 、8C 、10D 、4 11.下列各组数据中,不能构成直角三角形的一组数是( )A、9,12,15 B 、45,1,43C 、0.2,0.3,0.4D 、40,41,9 12.已知,一轮船以16海里/时的速度从港口A 出发向东北方向航行,另一轮船以12海里/时的速度同时从港口A 出发向东南方向航行,离开港口2小时后,则两船相距( )A.25海里B.30海里C.35海里D.40海里二、填空题1.在Rt △ABC 中,∠C=90°,①若a=5,b=12,则c=___________;②若a=15,c=25,则b=___________;③若c=61,b=60,则a=__________;④若a ∶b=3∶4,c=10则S Rt △ABC =________2.现有长度分别为2cm 、3cm 、4cm 、5cm 的木棒,从中任取三根,能组成直角三角形,则其周长为 cm .3.勾股定理的作用是在直角三角形中,已知两边求 ;勾股定理的逆定理的作用是用来证明 .4.如图中字母所代表的正方形的面积:A = B = . A815.在△ABC 中,∠C =90°,若 a =5,b =12,则 c = .6.△ABC 中,AB=AC=17cm ,BC=16cm ,则高AD= ,S △ABC = 。
2017-2018学年北师大版八年级数学上册教师用书(pdf版):1.1探索勾股定理

点ꎬ则 CD 的长为
25 8
.
������������������������������������������������������������������
������������������������������������������������������������������
解:(1) 在 Rt△ABC 中ꎬc2 = a2 +b2 = 36+64 = 100ꎬ
∴ c = 10ꎻ
∵ S△ABC =
1 2
AC������BC =
1 2
AB������CDꎬ
∴ AC������BC = AB������CDꎬ
∴
CD
=
AC×BC AB
=
6×8 10
=
4.8ꎻ
(2) 在 Rt△ABC 中ꎬc2 = a2 +b2 ꎬ
C.8
D.10
2.等腰三角形底边上的高为 8ꎬ周长为 32ꎬ则三角形的面
积为
( B )A.56B. Nhomakorabea8C.40
D.32
3.已知直角三角形的两直角边长分别是 3 和 4ꎬ则第三
边长为 5 .
4. ( 2015 西 宁 ) 如 图ꎬ Rt △ABC 中ꎬ ∠B = 90°ꎬ AB = 4ꎬ
BC = 3ꎬAC 的垂直平分线 DE 分别交 ABꎬAC 于 DꎬE 两
2017-2018学年北师大版八年级数学上册教师用书(pdf版):1.2+1.3

������������
= m 4 +2m 2 n2 +n4 ꎬ ʑ a 2 +b 2 = c 2 ꎬ
归纳:
ʑ әABC 是直角三角形.
㊀ (1) 已知三角形的三边边长判定三角形的形状时ꎬ 一 般做法是:验证较小两边的平方和与最长边的平方之间 的关系ꎬ满足 a 2 + b 2 = c 2 ( c 为最长边 ) 形式ꎬ 就是直角 三角形ꎬ否则不是. 勾股定理逆定理进行几何证明 ʌ 例 2 ɔ 如图所示ꎬ 正方形 ABCD 中ꎬ E 为 AB 中 点ꎬ 点 F 在 BC 上ꎬ 且 BF = ㊀ 分析:要证明两条线段互相垂直ꎬ可 联想到证明这两线段所在三角形是直 角三角形ꎬ于是连接 DFꎬ设 BF = aꎬ利用勾股定理表示出 DEꎬEFꎬDF 的长度ꎬ从而用勾股定理逆定理证明即可.
2 2
B.3 组
C.4 组
D.5 组
( ㊀ A㊀ ) ( ㊀ D㊀ )
3.已知әABC 的三边长分别为 aꎬbꎬcꎬ 且 aꎬbꎬc 满足 a2 - 6a + 9+( b - 4) 2 +∣ c - 5 ∣ = 0ꎬ则әABC 的形状是㊀ 直角㊀ 4. 如图ꎬD 为 әABC 边 BC 上一点ꎬ AB = 20ꎬAC = 13ꎬAD = 12ꎬDC = 5ꎬ则 S әABC = ㊀ 126㊀ .
3a. 根据勾股定理ꎬ
1 BC. 求证:DEʅEF. 4
㊀ 证明:连接 DFꎬ设正方形的边长为 4aꎬ则 AE = EB = 2aꎬBF = aꎬCF =
在 RtәADE 中ꎬDE2 = AD2 +AE2 = 16a 2 +4a 2 = 20a 2 ꎬ 在 RtәBEF 中ꎬEF2 = EB2 +BF2 = 4a 2 +a 2 = 5a 2 ꎬ ʑ DE2 + EF2 = DF2 ꎬ ʑ øDEF = 90ʎ ꎬ即 DEʅEF. 在 RtәDCF 中ꎬDF2 = DC2 +CF2 = 16a 2 +9a 2 = 25a 2 ꎬ
北师大版八年级数学上册 第二章实数知识点及经典例题讲解 (学案)

初二数学上册实数知识点及经典例题讲解一、平方根如果一个数x 的平方等于a ,那么,这个数x 就叫做a 的平方根;也即,当)0(2≥=a a x 时,我们称x 是a 的平方根,记做:)0(≥±=a a x 。
因此:1.当a=0时,它的平方根只有一个,也就是0本身;2.当a >0时,也就是a 为正数时,它有两个平方根,且它们是互为相反数,通常记做:a x ±=。
3.当a <0时,也即a 为负数时,它不存在平方根。
例1.(1) 的平方是64,所以64的平方根是 ; (2) 的平方根是它本身。
(3)若x 的平方根是±2,则x= ;的平方根是 (4)当x 时,x 23-有意义。
(5)一个正数的平方根分别是m 和m-4,则m 的值是多少?这个正数是多少? 二、算术平方根(1)如果一个正数x 的平方等于a ,即a x =2,那么,这个正数x 就叫做a 的算术平方根,记为:“a ”,读作,“根号a”,其中,a 称为被开方数。
特别规定:0的算术平方根仍然为0。
(2)算术平方根的性质:具有双重非负性,即:)0(0≥≥a a 。
(3)算术平方根与平方根的关系:算术平方根是平方根中正的一个值,它与它的相反数共同构成了平方根。
例2.(1)下列说法正确的是 ( )A .1的平方根是1±;B .24±=; (C )、81的平方根是3±; (D )、0没有平方根;(2)下列各式正确的是( )A 、981±=B 、14.314.3-=-ππC 、3927-=-D 、235=-(32(3)0y +=,则x -y 的值为( ) A 、1 B 、-1 C 、7 D 、-7(4)若a 、b 为实数,且满足20a -=,则b -a 的值为( )A 、2 B 、0 C 、-2 D 、以上都不对(5)2)3(-的算术平方根是 。
(6)若x x -+有意义,则=+1x ___________。
2017-2018学年北师大版八年级数学上册教师用书(pdf版):6.4数据的离散程度
㊀ ( 其中 x 1 ᶄꎬ x 2 ᶄꎬ x 3 ᶄꎬ������ꎬ x n ᶄ 分别等于 x 1 - aꎬ x 2 - aꎬ x 3 - aꎬ 2. 标准差:方差的算术平方根. ������ꎬx n - aꎬxᶄ是数据组 x 1 ᶄꎬx 2 ᶄꎬx 3 ᶄꎬ������ꎬx n ᶄ的平均数)
3. 方差( 标准差 ) 的意义: 方差 ( 标准差 ) 越大ꎬ 数据的波 齐. 差) 越小ꎬ数据的波动就 ㊀ 越小 ㊀ ꎬ 数据就越稳定ꎬ 越整 才利用方差来判断它们的波动情况. 动就㊀ 越大㊀ ꎬ数据就越不稳定ꎬ 越不整齐ꎻ 方差 ( 标准
归纳:
kx 1 ꎬkx 2 ꎬ������ꎬkx n kx 1 + aꎬkx 2 + aꎬ������ꎬkx n + a
样本 x 1 ꎬx 2 ꎬ������ꎬx n x 1 + aꎬx 2 + aꎬ������ꎬx n + a
平均数 x x +aFra bibliotek方差 s
2
ȵ
s2 k s
2 2
kx k x +a
6+6.5 25 = ꎻ (3) 第四次调价后ꎬ对于 A 产品ꎬ这四次单价的中位数为 2 4 对于 B 产品ꎬȵ m >0ꎬʑ 第四次单价大于 3ꎬ ȵ 3. 5+4 13 25 ˑ2-1 = > ꎬʑ 第四次单价小于 4ꎬ 2 2 4 3( 1+m% ) +3. 5 25 ˑ2-1 = ꎬʑ m = 25. ʑ 2 4
1 43 < ꎬʑ B 产品的方差小ꎬʑ B 产品的单价波动小ꎻ 6 150
1 1 [( 3. 5-3. 5) 2 +( 4-3. 5) 2 +( 3-3. 5) 2 ] = ꎬ 3 6
k2 s2
方差在实际问题中的评价作用 ʌ 例 2ɔ (2015 河北 ) 某厂生产 AꎬB 两种产品ꎬ 其单价随 市场变化而做相应调整. 营销人员根据前三次单价变化 的情况ꎬ绘制了如下统计表及不完整的折线图. AꎬB 产品单价变化统计表 第一次 3.5 6 第二次 5.2 4
2017-2018学年北师大版八年级数学上册教师用书(pdf版):5.1认识二元一次方程组
第5章㊀二元一次方程组㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀第1课㊀认识二元一次方程组知识目标认识二元一次方程和二元一次方程组ꎻ了解二元一次方程和二元一次方程组的解ꎻ会判断一组数是不是二元一次方程组的解.重㊁难点认识二元一次方程和二元一次方程组.思维目标方程思想.1.含有㊀两㊀个未知数ꎬ并且所含未知数项的次数都是㊀1㊀的方程叫作二元一次方程.注意:㊀①二元一次方程两个未知项的次数是1ꎬ且系数不为0ꎻ㊀②二元一次方程的左边和右边都应是整式.2.共含有㊀两个㊀未知数的两个一次方程所组成的一组方程叫二元一次方程组.3.适合一个二元一次方程的一组未知数的值叫作二元一次方程的一个解(二元一次方程的解有无数个).4.二元一次方程组中各个方程的㊀公共解㊀ꎬ叫作二元一次方程组的解.二元一次方程定义与特征ʌ例1ɔ填选题:㊀(1)下列方程:①y=3x2+xꎻ②3x+y=1ꎻ③2x+4z=5zꎻ④xy=2ꎻ⑤x+y3+y=0ꎻ⑥x+y+z=1ꎻ⑦1y+x=4ꎬ是二元一次方程的有(㊀B㊀)㊀A.2个B.3个C.4个D.5个㊀(2)下列方程组中是二元一次方程组的是(㊀A㊀)㊀A.x+y=42x+3y=7{B.2a-3b=115b-4c=6{㊀C.x2=9y=2x{D.x+y=8x2-y=4{㊀(3)方程x∣a∣-1+(a-2)y=2是关于xꎬy的二元一次方程ꎬ则a的值为㊀-2㊀.㊀分析:(1)(2)按二元一次方程(组)的定义即可得解ꎻ(3)要注意未知项的次数为1ꎬ且系数不为0ꎬ则有∣a∣-1=1且a-2ʂ0ꎬ解之即得.二元一次方程(组)解的含义及运用ʌ例2ɔ填选题:㊀(1)已知一个二元一次方程组的解是x=-1y=-2{ꎬ则这个方程组是(㊀C㊀)㊀A.x+y=-3xy=2{B.x+y=-3x-2y=1{㊀C.2x=yx+y=-3{D.x+y=03x-y=5{㊀(2)已知x=2y=-1{是方程组mx+y=3x-ny=6{的解ꎬ则m=㊀2㊀ꎬn=㊀4㊀.㊀分析:(1)用验证法即可排除ꎬ要注意A选项不是二元一次方程组ꎻ(2)若知道方程(组)的解ꎬ则直接代入相关方程ꎬ则可求出相应字母的值.㊀解:(1)Cꎻ(2)2ꎬ4.特定条件下的二元一次方程组的解ʌ例3ɔ求二元一次方程3x+2y=19的正整数解.㊀分析:观察方程特点ꎬ发现2y是偶数ꎬ则3x应是奇数ꎬ故x应是奇数ꎬ故让x=1ꎬ3ꎬ5即可得到相应的y值.㊀解:由已知得y=19-3x2ꎬʑ当x=1时ꎬy=8ꎻ当x=3时ꎬy=5ꎻ当x=5时ꎬy=2ꎻʑ方程的正整数解为x=1y=8{ꎬx=3y=5{ꎬx=5y=2{.1.下列方程组中是二元一次方程组的是(㊀D㊀)A.xy=1x+y=2{B.5x-2y=31x+y=3{C.2x+z=13x-y=15{D.x=5x2+y3=7{2.(2016临沂)为了绿化校园ꎬ30名学生共种78棵树苗.其中男生每人种3棵ꎬ女生每人种2棵ꎬ该班男生有x人ꎬ女生有y人.根据题意ꎬ所列方程组正确的是(㊀D㊀)A.x+y=783x+2y=30{B.x+y=782x+3y=30{C.x+y=302x+3y=78{D.x+y=303x+2y=78{3.已知方程2x+3y-4=0ꎬ用含x的式子表示y为:y=㊀4-2x3㊀ꎻ用含y的式子表示x为:x=㊀4-3y2㊀.4.已知x=-2y=3{ꎬ是方程x-ky=1的解ꎬ那么k=㊀-1㊀.1.记清二元一次方程(组)的定义与其指数特征ꎻ2.了解二元一次方程的解有无数组ꎬ但在某些特定条件下其解可能是有限的ꎻ但二元一次方程组的解常常是唯一的ꎻ3.要学会设两个未知数来表达应用题中的未知量.A组㊀夯实基础一.选择题1.(2014泰安)方程5x+2y=-9与下列方程构成的方程组的解为x=-2y=12{的是(㊀D㊀)A.x+2y=1B.3x+2y=-8C.5x+4y=-3D.3x-4y=-82.二元一次方程x-2y=1有无数多个解ꎬ下列四组值中不是∙∙该方程的解的是(㊀B㊀)A.x=0y=-12{B.x=1y=1{C.x=1y=0{D.x=-1y=-1{3.(2016毕节)已知关于xꎬy的方程x2m-n-2+4ym+n+1=6是二元一次方程ꎬ则mꎬn的值为(㊀A㊀)A.m=1ꎬn=-1B.m=-1ꎬn=1C.m=13ꎬn=-43D.m=-13ꎬn=434.(2016龙东)为了丰富学生课外小组活动ꎬ培养学生动手操作能力ꎬ王老师让学生把5m长的彩绳截成2m或1m的彩绳ꎬ用来做手工编织ꎬ在不造成浪费的前提下ꎬ你有几种不同的截法(㊀C㊀)A.1B.2C.3D.4二.填空题5.已知x=3y=-2{是方程组2x-y=mx+ny=-3{的解ꎬ则m=㊀8㊀ꎬn=㊀3㊀.6.已知│x-1│+(2y+1)2=0ꎬ且2x-ky=4ꎬ则k=㊀4㊀.7.(2016吉林)某学校要购买电脑ꎬA型电脑每台5000元ꎬB型电脑每台3000元ꎬ购买10台电脑共花费34000元.设购买A型电脑x台ꎬ购买B型电脑y台ꎬ则根据题意可列方程组为㊀x+y=105000x+3000y=34000{㊀.三.解答题8.若方程x2m-1+5y3n-2=7是关于x㊁y的二元一次方程ꎬ求m㊁n的值.㊀解:由已知得2m-1=13n-2=1{ꎬ解得m=1n=1{.9.根据题意ꎬ列出方程组(不解):㊀(1)某班共有学生45人ꎬ其中男生比女生的2倍少9人ꎬ该班男生㊁女生各有多少人?设该班男生有x人ꎬ女生有y人.㊀(2)将一摞笔记本分给若干同学ꎬ每个同学5本ꎬ则剩下8本ꎻ每个同学8本ꎬ又差了7本ꎬ共有多少本笔记本㊁多少个同学?设共有笔记本x本ꎬy个同学.㊀(3)将若干只鸡放入若干笼中ꎬ若每个笼中放4只ꎬ则有一鸡无笼可放ꎻ若每个笼里放5只ꎬ则有一笼无鸡可放ꎬ问有多少只鸡ꎬ多少个笼?设x只鸡ꎬy个笼.㊀解:(1)x+y=45x=2y-9{ꎻ(2)5y+8=x8y-7=x{ꎻ(3)4y=x-15(y-1)=x{.10.甲种物品每个4kgꎬ乙种物品每个7kgꎬ现有甲种物品x个ꎬ乙种物品y个ꎬ共76kg.(1)列出关于xꎬy的二元一次方程㊀㊀㊀㊀ꎻ(2)若x=12ꎬ则y=㊀㊀㊀㊀ꎻ(3)若有乙种物品8个ꎬ则甲种物品有㊀㊀㊀㊀个ꎻ(4)请你用含x的式子表示出yꎬ然后再探究出满足条件的xꎬy的全部数值.解:(1)4x+7y=76ꎻ(2)4ꎻ(3)5ꎻ(4)y=76-4x7ꎬ经探究可知:满足条件的xꎬy有两组:x=12y=4{ꎬx=5y=8{.B组㊀提高巩固11.(2016齐齐哈尔)足球比赛规定:胜一场得3分ꎬ平一场得1分ꎬ负一场得0分.某足球队共进行了6场比赛ꎬ得了12分ꎬ该队获胜的场数可能是(㊀C㊀)A.1或2B.2或3C.3或4D.4或5(提示:设该队胜x场ꎬ平y场ꎬ则负(6-x-y)场ꎬ根据题意ꎬ得:3x+y=12ꎬ即:x=12-y3ꎬȵx㊁y均为非负整数ꎬ且x+yɤ6ꎬʑ当y=0时ꎬx=4ꎻ当y=3时ꎬx=3ꎻ即该队获胜的场数可能是3场或4场ꎬ故选C.)12.二元一次方程2x+y=7的正整数解为㊀x=1y=5{ꎬx=2y=3{ꎬx=3y=1{㊀.(提示:将原方程变形为y=7-2x.ȵxꎬy均为正整数ꎬʑx只能取小于4的正整数ꎬ共有1ꎬ2ꎬ3三个.当x=1时ꎬy=5ꎻ当x=2时ꎬy=3ꎻ当x=3时ꎬy=1.)13.某电视台有黄金时段的2min广告时间内ꎬ计划插播长度为15s和30s的两种广告.15s广告每播1次收费0.6万元ꎬ30s广告每播1次收费1万元.若要求每种广告播放不少于2次ꎬ问:(1)两种广告的播放次数有几种安排方式?(2)电视台选择哪种方式播放收益较大?解:设播15s的广告x次ꎬ播30s的广告y次ꎬ则有15x+30y=120.即x+2y=8ꎬ又xȡ2ꎬyȡ2ꎬ且x㊁y为整数ꎬʑx=2y=3{或x=4y=2{ꎻ当x=2y=3{时ꎬ收费为2ˑ0.6+3ˑ1=4.2(万元)ꎬ当x=4y=2{时ꎬ收费为4ˑ0.6+2ˑ1=4.4(万元).应选择15s广告播4次ꎬ30s广告播2次.㊀。
平面直角坐标系(知识讲解)八年级数学上册基础知识讲与练(北师大版)
专题3.3 平面直角坐标系(知识讲解)【学习目标】1.理解平面直角坐标系概念,能正确画出平面直角坐标系;2.能在平面直角坐标系中,根据坐标确定点,以及由点的位置求出坐标;3.掌握点位置与其坐标的符号特征;3.由数轴到平面直角坐标系,渗透类比的数学思想.【要点梳理】要点一、有序数对定义:把有顺序的两个数a与b组成的数对,叫做有序数对,记作(a,b).特别说明::有序,即两个数的位置不能随意交换,(a,b)与(b,a)顺序不同,含义就不同,如电影院的座位是8排9号,可以写成(8,9)的形式,而(9,8)则表示9排8号.要点二、平面直角坐标系与点的坐标的概念1. 平面直角坐标系在平面内画两条互相垂直、原点重合的数轴就组成平面直角坐标系.水平的数轴称为x 轴或横轴,习惯上取向右为正方向;竖直的数轴称为y轴或纵轴,取向上方向为正方向,两坐标轴的交点为平面直角坐标系的原点(如图1).特别说明::平面直角坐标系是由两条互相垂直且有公共原点的数轴组成的.2. 点的坐标平面内任意一点P,过点P分别向x轴、y轴作垂线,垂足在x轴、y轴上对应的数a,b分别叫做点P的横坐标、纵坐标,有序数对(a,b)叫做点P的坐标,记作:P(a,b),如图2.特别说明::(1)表示点的坐标时,约定横坐标写在前,纵坐标写在后,中间用“,”隔开.(2)点P(a,b)中,|a|表示点到y轴的距离;|b|表示点到x轴的距离.(3) 对于坐标平面内任意一点都有唯一的一对有序数对(x,y)和它对应,反过来对于任意一对有序数对,在坐标平面内都有唯一的一点与它对应,也就是说,坐标平面内的点与有序数对是一一对应的.要点三、坐标平面1. 象限建立了平面直角坐标系以后,坐标平面就被两条坐标轴分成如图所示的Ⅰ、Ⅱ、Ⅲ、Ⅳ四个部分,分别叫做第一象限、第二象限、第三象限和第四象限,如下图.特别说明::(1)坐标轴x 轴与y 轴上的点(包括原点)不属于任何象限.(2)按方位来说:第一象限在坐标平面的右上方,第二象限在左上方,第三象限在左下方,第四象限在右下方.2. 坐标平面的结构坐标平面内的点可以划分为六个区域:x 轴,y 轴、第一象限、第二象限、第三象限、第四象限. 这六个区域中,除了x 轴与y 轴有一个公共点(原点)外,其他区域之间均没有公共点.要点四、点坐标的特征1.各个象限内和坐标轴上点的坐标符号规律特别说明::(1)对于坐标平面内任意一个点,不在这四个象限内,就在坐标轴上.(2)坐标轴上点的坐标特征:x 轴上的点的纵坐标为0;y 轴上的点的横坐标为0.(3)根据点的坐标的符号情况可以判断点在坐标平面上的大概位置;反之,根据点在坐标平面上的位置也可以判断点的坐标的符号情况.2.象限的角平分线上点坐标的特征第一、三象限角平分线上点的横、纵坐标相等,可表示为(a ,a);第二、四象限角平分线上点的横、纵坐标互为相反数,可表示为(a ,-a).3.平行于坐标轴的直线上的点平行于x 轴的直线上的点的纵坐标相同;平行于y 轴的直线上的点的横坐标相同.要点五、两点之间距离公式及中点坐标公式1. 两点之间距离公式1122(,),A B x y AB =点(x ,y )则2.中点坐标公式12121122(,),;22x x y y A B x y AB C y ++=点(x ,y )线段中点为(x,y ),则x= 【典型例题】类型一、建立平面直角坐标系并求点的坐标(建系)1.如图,正三角形ABC 的边长为 4 , 建立适当的直角坐标系 ,并写出各个顶点的坐标 .【答案】A (0,,B (-2,0 ),C (2,0)解:如图,以边BC 所在的直线为x 轴,以边BC 的中垂线为y 轴建立直角坐标系. 由正三角形的性质可知AO =ABC 各个顶点A ,B ,C 的坐标分别为A(0,,B (-2,0 ),C (2,0).举一反三:【变式1】如图,点A 、B 、C 都在方格纸的格点上,若点A 的坐标为()0,2,点B 的坐标为()2,0,试建立恰当的直角坐标系,写出点C 的坐标.【答案】图见分析,()2,1C【分析】根据点的坐标建立坐标系,再确定坐标.解:如图所示建立直角坐标系:∴点C 的坐标为(2,1).【点拨】本题考查了坐标系及其点的坐标,正确建立平面直角坐标系是解题的关键.【变式2】如图,建立平面直角坐标系,正方形ABFG和正方形CDEF中,使点B、C -和(0,0)的坐标分别为(4,0)(1)请直接写出A,D,E,F的坐标;(2)求正方形CDEF的面积.【答案】(1)A(﹣6,3),D(2,1),E(1,3),F(﹣1,2)(2)5【分析】(1)先利用点B和点C的坐标画出平面直角坐标系,然后根据点的坐标的意义即可得到点A、D、E、F的坐标;(2)利用正方形的面积公式和勾股定理解答即可.(1)解:如图所示:∴A(﹣6,3),D(2,1),E(1,3),F(﹣1,2).(2)解:∴ CD∴正方形CDEF的面积=5.【点拨】本题考查了坐标与图形性质:利用点的坐标求线段长和判断线段与坐标轴的位置关系;记住坐标系中坐标特征是解题的关键.类型二、点到坐标轴的距离2.已知点(23,4)A a a -+在第一象限,且点A 到x 轴和y 轴的距离相等,求点A 的坐标.【答案】(11,11)【分析】直接利用第一象限内点的坐标特点,横纵坐标的符号关系,结合点A 到x 轴和y 轴的距离相等,得出横纵坐标相等,进而得出答案. 解:点(23,4)A a a -+在第一象限,点A 到x 轴和y 轴的距离相等,234a a ∴-=+,解得:7a =,故2327311a -=⨯-=,411a +=,则点A 的坐标为:(11,11).【点拨】本题主要考查了第一象限内点的坐标特点,解题的关键是结合点A 到x 轴和y 轴的距离相等,得出横纵坐标相等,进而得出答案.举一反三:【变式1】已知平面直角坐标系中有一点(21,3)M m m --.(1)当点M 到y 轴的距离为1时,求点M 的坐标;(2)当点M 到x 轴的距离为2时,求点M 的坐标.【答案】(1)点M 的坐标是(1,2)-或(1,3)--;(2)点M 的坐标是(9,2)或(1,2)-【分析】根据点到坐标轴的距离为其横坐标或纵坐标的绝对值求解即可.解:(1)|21|1m -=,211m ∴-=或211m -=-,解得1m =或0m =,∴点M 的坐标是(1,2)-或(1,3)--.(2)|3|2m -=,32m ∴-=或32m -=-,解得5m =或1m =,∴点M 的坐标是(9,2)或(1,2)-.【点拨】本题考查的知识点是根据点到坐标轴的距离求点的坐标,需注意多解问题,不要漏解.【变式2】已知平面直角坐标系中有一点M(m -1,2m +3).(1) 当m 为何值时,点M 到x 轴的距离为1?(2) 当m 为何值时,点M 到y 轴的距离为2?【答案】(1)m =-1或m =-2.(2)m =3或m =-1.试题分析:(1)让纵坐标的绝对值为1列式求值即可;(2)让横坐标的绝对值为2列式求值即可.解:(1)∴|2m+3|=12m+3=1或2m+3=-1∴m=-1或m=-2;(2)∴|m -1|=2m -1=2或m -1=-2∴m=3或m=-1.考点:点的坐标.类型三、判断点所在的象限3.已知点(3,22)-+A a b ,以点A 为坐标原点建立直角坐标系.(1) 求a ,b 的值;(2) 判断点(24,31)--B a b 、点(3,)-+C a b 所在的位置.【答案】(1)a =3,b =−1(2)B (2,−4)在第四象限;C (0,−1)在y 轴的负半轴上且到x 轴的距离为1.【分析】(1)根据点A 为原点,则点A 的横纵坐标都为0,解答即可;(2)把a =3,b =−1分别代入B ,C 即可求解.(1)解:∴点A 为原点,∴a −3=0,2b +2=0,解得:a =3,b =−1;(2)解:把a =3,b =−1代入点B 得:2a −4=2×3−4=2,3b −1=3×(−1)−1=−4,∴B (2,−4)在第四象限;把a =3,b =−1代入点C 得:−a +3=−3+3=0,b =−1,∴C (0,−1)在y 轴的负半轴上且到x 轴的距离为1.【点拨】本题考查了点的坐标,解题的关键是掌握x 轴,y 轴上点的坐标特征. 举一反三:【变式1】已知a ,b 都是实数,设点P (a ,b ),若满足3a =2b +5,则称点P 为“新奇点”.(1) 判断点A (3,2 )是否为“新奇点”,并说明理由;(2) 若点M (m -1,3m +2)是“新奇点”,请判断点M 在第几象限,并说明理由.【答案】(1)点A (3,2)是“新奇点”,理由见分析,(2)点M 在第三象限,理由见分析.【分析】(1)根据题目中“新奇点”的判断方法,将3a =,2b =,代入判断325a b =+,即可证明;(2)根据点()132M m m -+,是“新奇点”,可得()()312325m m -=++,求解代入得出4m =-,即可确定点的坐标,然后判断在哪个象限即可.(1)解:点()32A ,是“新奇点”,理由如下: 当A (3,2)时,3a =,2b =,∴39a =,259b +=,∴325a b =+.∴点()32A ,是“新奇点”; (3) 点M 在第三象限,理由如下:∴点()132M m m -+,是“新奇点”, ∴1a m =-,32b m =+,∴()()312325m m -=++,解得:4m =-,∴15m -=-,3210m +=-,∴点()5,10M --在第三象限.【点拨】题目主要考查求代数式的值及解一元一次方程,判定点所在象限,理解题中新的定义是解题关键.【变式2】在图中建立适当的平面直角坐标系,使A 、B 两点的坐标分别为(-4,1)和(-1,4),写出点C 、D 的坐标,并指出它们所在的象限.【分析】首先根据点A 、B 的坐标确定坐标原点和x 、y 轴的正方向,进而建立平面直角坐标系,再结合图形得出C 、D 两点的坐标,进而判断这两个点所在的象限.解:建立平面直角坐标系如图:得C (-1,-2)、D (2,1).由图可知,点C 在第三象限,点D 在第一象限.【点拨】本题考查了已知两点确定直角坐标系的知识,根据两点的坐标建立平面直角坐标系是解题的关键.类型四、已知点的象限求参数4.在平面直角坐标系中,有一点M (a -2,2a +6),试求满足下列条件的a 值或取值范围.(1) 点M 在y 轴上;(2) 点M 在第二象限;(3) M 到x 轴的距离为2.【答案】(1)a =2(2)-3<a <2(3)a =–2或–4【分析】(1)点在y 轴上,该点的横坐标为0即可求解;(2)根据第二象限的点的横坐标小于0,纵坐标大于0即可求解;(3)根据点到x 轴的距离为2,则该点的纵坐标的绝对值为2,据此计算即可.(1)解:由题意得,a ﹣2=0,解得a =2;(2)解:由20260a a -⎧⎨+⎩<>, 解得,﹣3<a <2;(3)解:由|2a +6|=2,解得a =–2或–4.【点拨】本题考查了各象限内点的坐标的符号特征,记住各象限内点的坐标的符号是解决的关键,四个象限内点的坐标的符号特点分别是:第一象限(+,+);第二象限(﹣,+);第三象限(﹣,﹣);第四象限(+,﹣).举一反三:【变式1】已知点()39,210A m m --,分别根据下列条件解决问题:(1) 点A 在x 轴上,求m 的值;(2) 点A 在第四象限,且m 为整数,求点A 的坐标.【答案】(1)5m = (2)()3,2A -【分析】(1)根据x 轴上的点的纵坐标等于零,可得方程,解方程可得答案;(2)根据第四象限点的符号特征(),+-,列出不等式组求出m 的值,求出点A 坐标;(1)解:由2100m -=,得5m =;(2)∴点()39,210A m m --在第四象限,∴3902100m m ->⎧⎨-<⎩①②, 解不等式∴得3m >,解不等式∴得5m <,所以,m 的取值范围是35m <<,∴m 为整数,∴4m =,∴()3,2A -.【点拨】本题考查平面直角坐标中点的坐标,x 轴上的点的纵坐标等于零,各象限点的特征,解题关键是熟记点的特征.【变式2】已知平面直角坐标系中一点()25,3A a a -+,分别求出满足下列条件的点A 的坐标.(1) 点A 在过点()3,3-且平行于x 轴的直线上;(2) 点A 在第一、三象限的角平分线上;(3) 点A 在第二象限,且到两坐标轴的距离之和为10.【答案】(1)()17,3--(2)()11,11(3)()9,1-【分析】(1)根据平行于x 轴的直线上点的纵坐标相同,即可求解;(2)根据在第一、三象限的角平分线上的点横纵坐标相同,即可求解;(3)根据点A 在第二象限,可得25030a a -<⎧⎨+>⎩,再由点A 到两坐标轴的距离之和为10,可得52310a a -++=,即可求解.(1)解:∴点A 在过点()3,3-且平行于x 轴的直线上,∴33a +=-,解得:6a =-,∴2517,33a a -=-+=-,∴点A 的坐标为()17,3--;(2)解:∴点A 在第一、三象限的角平分线上,∴253a a -=+,解得:8a =,∴25311a a -=+=,∴点A 的坐标为()11,11;(3)解:∴点A 在第二象限,∴25030a a -<⎧⎨+>⎩,解得:532a -<<, ∴点A 到两坐标轴的距离之和为10,25310a a -++=,∴52310a a -++=,解得:2a =-,∴259,31a a -=-+=,∴点A 的坐标为()9,1-.【点拨】本题主要考查了平面直角坐标系中各象限内点的坐标的特征及点到坐标轴的距离的应用,点在第一、三象限的角平分线上的坐标特征,熟练掌握相关知识点是解题的关键.类型五、坐标系中描点5.在平面直角坐标系中,把以下各组点描出来,并顺次连接各点.(0,-4),(3,-5),(6,0),(0,-1),(-6,0),(-3,-5),(0,-4).解:如图:举一反三:【变式1】如图,点A 、B 在单位长度为1的正方形网格的格点上,建立平面直角坐标系,使点A 、B 的坐标分别为(3,0)(2,0)-、(1)请在图中建立平面直角坐标系.(2)若C 、D 两点的坐标分别为(1,2)、(2,2)-,请描出C 、D 两点.C 、D 两点的坐标有什么异同?直线CD 与x 轴有什么关系?(3)若点(24,1)E m m +-为直线CD 上的一点,则m =___________,点E 的坐标为___________.【答案】(1)答案见分析 (2)答案见分析 (3)3;()10,2E【分析】(1)根据A 、B 两点的坐标即可建立坐标系;(2)直接描出C 、D 两点坐标即可,根据横、纵坐标即可找到规律;(3)根据直线CD 上点的坐标规律即可求出m .(1)解:如图所示,(2)解:C 、D 两点如图所示,由图可知C 、D 两点横坐标不同,纵坐标相同;直线CD 与x 轴平行;(3)解:由(2)可知//CD x 轴,点(24,1)E m m +-为直线CD 上的一点,12m ∴-=,3m ∴=,2410m ∴+=,()10,2E ∴ .【点拨】本题主要考查坐标与图形,平面直角坐标系等知识,解题的关键是正确作出平面直角坐标系.【变式2】已知平面直角坐标系内有4个点:A (0,2),B (-2,0),C (1,-1),D (3,1).(1)在平面直角坐标系中描出这4个点;(2)顺次连接A 、B 、C 、D 组成四边形ABCD ,请用两种方法求出四边形ABCD 的面积.【答案】(1)见分析(2)8【分析】(1)根据平面直角坐标系描出点的坐标;(2)根据ΔΔΔΔAEB BFC CGD DHA EFGH ABCD S S S S S S =----长方形四边形,ΔΔΔΔABP BCQ CDM ADN PQMN ABCD S S S S S S =++++正方形四边形求面积即可求解.(1)解:如图所示:点A 、B 、C 、D 为所描的点.(2)方法一:如图所示,作长方形EFGH :则有ΔΔΔΔAEB BFC CGD DHA EFGH ABCD S S S S S S =----长方形四边形111153221322132222=⨯-⨯⨯-⨯⨯-⨯⨯-⨯⨯ 8=方法二:如图所示,将四边形ABCD 分割为△ABP 、△BCQ 、△CMD 、△AND 和正方形PQMN ,则有ΔΔΔΔABP BCQ CDM ADN PQMN ABCD S S S S S S =++++正方形四边形11111221322132222=+⨯⨯+⨯⨯+⨯⨯+⨯⨯ 8=.【点拨】本题考查了坐标与图形,数形结合是解题的关键.类型六、坐标与图形6.如图,在长方形OABC 中,O 为平面直角坐标系的原点,点A 的坐标为(a , 0),点C 的坐标为(0,b ),且a 、b 满足8a -+|b - 12|=0,点B 在第一象限内,点P 从原点出发,以每秒2个单位长度的速度沿着O →A →B →C →O 的路线移动.(1) 点B 的坐标为________;当点 P 移动5秒时,点P 的坐标为(2) 在移动过程中,当点P 移动11秒时,求△OPB 的面积.(3) 在(2)的条件下,坐标轴上是否存在点Q ,使△OPQ 与△OPB 的面积相等.若存在,直接写出点Q 的坐标;若不存在,请说明理由.【答案】(1)(8,12),(8,2);(2)当点P 移动11秒时,△OPB 的面积为12;(3)(0,4)、(0,-4)、(2,0)、(-2,0).【分析】(1)利用非负数的性质求出a ,b ,可得B 点坐标,再求出点P 移动5秒的路程,可得P 点坐标;(2)求出点P 的坐标,可得PB =2,然后根据三角形面积公式计算即可;(3)分情况讨论:∴当点Q 在y 轴上时,∴当点Q 在x 轴上时,分别根据S △OPQ =S △OPB列式求出OQ ,即可得到对应的点Q 的坐标.(1)解:120b -=,∴80a -=,120b -=,∴8a =,12b =,∴A (8,0),B (0,12),∴OA =BC =8,OC =AB =12,∴B (8,12),∴点P 移动5秒时,移动的路程为5×2=10,∴P (8,2),故答案为:(8,12),(8,2);(2)当点P 移动11秒时,移动的路程为:11×2=22,∴P (6,12),∴PB =8-6=2,∴S △OPB =1212122⨯⨯=; (3)分情况讨论:∴当点Q 在y 轴上时,∴点P 移动11秒时,P 点坐标为(6,12),S △OPB =12,∴由S △OPQ =S △OPB 得:16122OQ ⨯=,∴4OQ =,∴点Q 的坐标为:(0,4)或(0,-4);∴当点Q 在x 轴上时,∴点P 移动11秒时,P 点坐标为(6,12),S △OPB =12,∴由S △OPQ =S △OPB 得:112122OQ ⨯=,∴2OQ ,∴点Q 的坐标为:(2,0)或(-2,0),综上,点Q 坐标为:(0,4)或(0,-4)或(2,0)或(-2,0).【点拨】本题考查了算术平方根和绝对值的非负性,坐标与图形,三角形面积计算等知识,熟练掌握数形结合思想与分类讨论思想的应用是解题的关键.举一反三:【变式1】如图,长方形OABC 的顶点O 为平面直角坐标系的原点,点A 和点C 分别在x 轴和y 轴的正半轴上,点B 的坐标为(),a b ,且20a b -+=.(1) 求点B 的坐标;(2) 点D 是线段AB 的中点,求OAD △的面积;【答案】(1 ) ()3,5B (2)154OAD S =△【分析】(1)由绝对值和算术平方根的非负性质得2032190a b a b -+=⎧⎨+-=⎩,即可得出结论; (2)由矩形的性质得到90OAB ∠=︒,3OA = 5AB =, 再求出AD 的长,即可解决问题.(1)解:∴20a b -+,∴2032190a b a b -+=⎧⎨+-=⎩ 解得35a b =⎧⎨=⎩, ∴()3,5B ;(2)解:()3,5B ,四边形OABC 是矩形,90OAB ︒∴∠=,3OA =,5AB =,∴点D 是线段AB 的中点, ∴1522AD AB == , ∴15153224OAD S =⨯⨯=△. 【点拨】本题主要考查矩形的性质,绝对值和算术平方根的非负性,二元一次方程组的解法,熟练掌握矩形的性质是解题的关键.【变式2】有一张图纸被损坏,但上面有如图的两个标志点A (-3,1),B (-3,-3)可认,而主要建筑C (3,2)破损.(1) 建立直角坐标系;(2) 标出图中C 点的位置;(3) 求出线段AC 的长.【答案】(1)作图见分析;(2)作图见分析;.【分析】(1)以点A向右3个单位,向下1个单位为坐标原点建立平面直角坐标系;(2)根据C(3,2)确定出点C的位置即可;(3)利用勾股定理即可求得线段AC的长.(1)解:建立直角坐标系如下图所示,(2)解:图中C点的位置如下图所示,(3)解:如下图,∴在Rt ∴ACF 中,∴AFC =90°,CF =1,F A =6,∴AC =【点拨】考查了确定坐标系中点的位置及勾股定理,根据已知点的坐标准确确定出坐标原点的位置是解题的关键.类型七、点坐标的规律7.如图,每个小方格边长为1,已知点1(1,0)A ,2(1,1)A ,3(1,1)A -,4(1,1)A --,5(2,1)A -,6(2,2)A ,7(2,2)A -,8(2,2)--A ,…(1)将图中的平面直角坐标系补画完整;(2)按此规律,请直接写出点的坐标:9A ,10A ;(3)按此规律,则点2022A 的坐标为 .【答案】(1)见分析(2)(3,2)-,(3,3)(3)(506,506)【分析】(1)根据点的坐标确定坐标轴即可;(2)根据图示及坐标系各象限横纵坐标符号特点即可得出结果;(3)观察图象及各点的坐标特点得出A 4n +2(n +1,n +1),再由2022=4×505+2,即可确定点的坐标.(1)解:根据题意补画得平面直角坐标系如图所示:(2)根据图示坐标系各象限横纵坐标符号特点可得:A 9(3,-2),A 10(3,3); (3)观察图形发现,下标为4n +2的点落在第一象限的对角线上,∴A 2(1,1), A 6(2,2),∴A 4n +2(n +1,n +1),∴2022=4×505+2,∴A 2022(506,506),故答案为:(506,506).【点拨】题目主要考查坐标系中点的特点,确定坐标系等,理解题意,确定坐标系中点的坐标变化规律是解题关键.举一反三:【变式1】在平面直角坐标系中,一蚂蚁从原点O 出发,按向上、向右、向下、向右的方向依次不断移动,每次移动1个单位.其行走路线如下图所示.(1)填写下列各点的坐标:4A (______,______),8A (______,______);(2)写出点4n A 的坐标(n 是正整数)4n A (______,______);(3)求出2022A 的坐标.【答案】(1) 2,0,4,0(2) 2,0n (3) ()1011,1【分析】(1)观察图形,即可求解;(2)观察图形,由(1)发现规律,即可求解;(3)由(1)发现规律:44142(2,0),(2,1),(21,1)n n n A n A n A n +++,即可求解.解:(1)观察图形得∴12834567(0,1),(1,1),(1,0),(2,0),(2,1),(3,1),(3,0),(4,0)A A A A A A A A ,故答案为:2,0,4,0;(2)由(1)发现规律:4(2,0)n A n ,故答案为:2,0n ;(3)解:由(1)发现规律:44142(2,0),(2,1),(21,1)n n n A n A n A n +++,∴202245052=⨯+,∴2022A 的坐标为()20221011,1A .【点拨】本题主要考查规律型:点的坐标,读懂题意,准确找出点的坐标规律是解答此题的关键.【变式2】如图,某小区绿化区的护栏是由两种大小不等的正方形间隔排列组成,将护栏的图案放在平面直角坐标系中.已知小正方形的边长为1,1A 的坐标为()2,2,2A 的坐标为()5,2.(1)3A 的坐标为______,n A 的坐标为______(用含n 的代数式表示);(2)若护栏长为2020,则需要小正方形______个,大正方形______个.【答案】(1)(8,2);(3n ﹣1,2)(2)674;673【分析】(1)根据已知条件与图形可知,大正方形的对角线长为2,由此可得规律:A 1,A 2,A 3,…,An 各点的纵坐标均为2,横坐标依次比前一个增加3,继而即可求解;(2)先求出一个小正方形与一个大正方形所构成的护栏长度,再计算2020包含多少这样的长度,进而便可求出结果.解:(1)∴A 1的坐标为(2,2)、A 2的坐标为(5,2),∴A 1,A 2,A 3,…,An 各点的纵坐标均为2,∴小正方形的边长为1,∴A 1,A 2,A 3,…,An 各点的横坐标依次比前一个增加3,∴A 3(5+3,2),An (233...3++++,2),即A 3(8,2),An (3n ﹣1,2),故答案为(8,2);(3n ﹣1,2);(2)由已知可得,所有小正方形和大正方形之间的直角三角形是全等的等腰直角三角形 ∴直角三角形的直角边长等于小正方形边长,长度是1,∴一个小正方形与一个大正方形所构成的护栏长度:1+1+1=3,∴2020÷3=673…1,∴需要小正方形673+1=674(个),大正方形673个.故答案为:674;673.【点拨】本题是点的坐标的规律题,首先应找出图形哪些部分发生了变化,是按照什么规律变化的,通过分析找到各部分的变化规律后直接利用规律求解.探寻规律要认真观察、仔细思考,善用联想来解决这类问题.。
2017-2018学年北师大版八年级数学上册教师用书(pdf版):2.7二次根式
㊀ 分析:利用 ab =
a ������ b ( a ȡ0ꎬ b ȡ0 ) 和
( aȡ0ꎬb > 0 ) 可以把二次根式化简ꎬ 被开方数较大的时 带分数化简时先要化为假分数. ㊀ 解:( 1) 原式 = 6 2 ꎻ( 2) 原式 = 20ꎻ( 3) 原式 = 归纳:
8 4b 2 ꎻ( 4) 原式 = . 7 3a
4. (1) 已知 y = (2) 已知
x-2 +
18n 是整数ꎬ则最小正整数 n = ㊀ 2㊀ .
9. 化简下列各式: (1)
8.x 是怎样的数时ꎬ下列各式有意义? (1) x 2 + 1 ꎻ (3) (5) -x ꎻ ( x - 1) (2 - x) ꎻ (2) (4) (6)
三. 解答题
棱长为㊀
2 ㊀ dm.
2. 下列各式中属于最简二次根式的是 3. 化简: (1) (3) A. x 2 + 1 B. x 2 y 5 12
3 且 xʂ -1ꎻ( 3) x = 3ꎻ( 4) xɤ2 且 xʂ1. 2
数ꎻ②分母不能为 0ꎻ③0 次方或负指数的底数不能为 0ꎻ
二次根式的化简 ʌ 例 3ɔ 化简下列各式: ㊀ (1) ㊀ (3) 72 ꎻ 1 15 ꎻ 49 (2) (4) ( - 16) ˑ ( - 25) ꎻ 16b 4 9a 2 . a a = b b
2
号内为非 负 数 的 根 式 即 可ꎬ 从 而㊀ 判定一个代数式是否是二次根式ꎬ 只需比对定义ꎬ 抓 住两个要点:一是二次根号ꎻ二是被开方数非负. 确定字母取值范围 ʌ 例 2ɔ 填空: ㊀ (1) 当 ㊀ ㊀ ㊀ ㊀ ꎻ
3 - x 在实数范围内有意义时ꎬ x 的取值范围为
知识目标 思维目标 重㊁难点
b
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
初二数学(上册)知识点总结第一章 勾股定理1、勾股定理直角三角形两直角边a ,b 的平方和等于斜边c 的平方,即222c b a =+2、勾股定理的逆定理(直角三角形的判定条件)如果三角形的三边长a ,b ,c 有关系222c b a =+,那么这个三角形是直角三角形,且最长边所对的角是直角。
3、勾股数:满足222c b a =+的三个正整数,称为勾股数。
第二章 实 数一、实数的概念及分类1、实数的分类正有理数有理数 零 有限小数和无限循环小数实数 负有理数正无理数无理数 无限不循环小数负无理数2、无理数:无限不循环小数叫做无理数。
在理解无理数时,要抓住“无限不循环”这一时之,归纳起来有四类:(1)开方开不尽的数,如32,7等;(2)有特定意义的数,如圆周率π,或化简后含有π的数,如3π+8等;(3)有特定结构的数,如0.1010010001…等;(4)某些三角函数值,如sin60o 等二、实数的倒数、相反数和绝对值1、相反数实数与它的相反数时一对数(只有符号不同的两个数叫做互为相反数,零的相反数是零),从数轴上看,互为相反数的两个数所对应的点关于原点对称,如果a 与b 互为相反数,则有a+b=0,a=—b ,反之亦成立。
2、绝对值在数轴上,一个数所对应的点与原点的距离,叫做该数的绝对值。
(|a|≥0)。
零的绝对值是它本身,也可看成它的相反数,若|a|=a ,则a ≥0;若|a|=-a ,则a ≤0。
3、倒数如果a 与b 互为倒数,则有ab=1,反之亦成立。
倒数等于本身的数是1和-1。
零没有倒数。
4、数轴规定了原点、正方向和单位长度的直线叫做数轴(画数轴时,要注意上述规定的三要素缺一不可)。
解题时要真正掌握数形结合的思想,理解实数与数轴的点是一一对应的,并能灵活运用。
5、估算三、平方根、算术平方根和立方根1、算术平方根:一般地,如果一个正数x 的平方等于a ,即x 2=a ,那么这个正数x 就叫做a 的算术平方根。
特别地,0的算术平方根是0。
表示方法:记作“a ”,读作根号a 。
性质:正数和零的算术平方根都只有一个,零的算术平方根是零。
2、平方根:一般地,如果一个数x 的平方等于a ,即x 2=a ,那么这个数x 就叫做a 的平方根(或二次方根)。
表示方法:正数a 的平方根记做“a ±”,读作“正、负根号a ”。
性质:一个正数有两个平方根,它们互为相反数;零的平方根是零;负数没有平方根。
开平方:求一个数a 的平方根的运算,叫做开平方。
0≥a注意a 的双重非负性:a ≥03、立方根一般地,如果一个数x 的立方等于a ,即x 3=a 那么这个数x 就叫做a 的立方根(或三次方根)。
表示方法:记作3a性质:一个正数有一个正的立方根;一个负数有一个负的立方根;零的立方根是零。
注意:33a a -=-,这说明三次根号内的负号可以移到根号外面。
四、实数大小的比较1、实数比较大小:正数大于零,负数小于零,正数大于一切负数;数轴上的两个点所表示的数,右边的总比左边的大;两个负数,绝对值大的反而小。
2、实数大小比较的几种常用方法(1)数轴比较:在数轴上表示的两个数,右边的数总比左边的数大。
(2)求差比较:设a 、b 是实数, ,0b a b a >⇔>-,0b a b a =⇔=-b a b a <⇔<-0(3)求商比较法:设a 、b 是两正实数,;1;1;1b a ba b a b a b a b a <⇔<=⇔=>⇔> (4)绝对值比较法:设a 、b 是两负实数,则b a b a <⇔>。
(5)平方法:设a 、b 是两负实数,则b a b a <⇔>22。
五、算术平方根有关计算(二次根式)1、含有二次根号“”;被开方数a 必须是非负数。
2、性质:(1))0()(2≥=a a a )0(≥a a(2)==a a 2 )0(<-a a(3))0,0(≥≥∙=b a b a ab ()0,0(≥≥=∙b a ab b a )(4))0,0(>≥=b a b a b a ()0,0(>≥=b a b a ba ) 3、运算结果若含有“a ”形式,必须满足:(1)被开方数的因数是整数,因式是整式;(2)被开方数中不含能开得尽方的因数或因式;(3)分母中不能含有根号。
六、实数的运算(1)六种运算:加、减、乘、除、乘方 、开方(2)实数的运算顺序先算乘方和开方,再算乘除,最后算加减,如果有括号,就先算括号里面的。
(3)运算律加法交换律 a b b a +=+加法结合律 )()(c b a c b a ++=++乘法交换律 ba ab =乘法结合律 )()(bc a c ab =乘法对加法的分配律 ac ab c b a +=+)(第三章 位置与坐标一、在平面内,确定物体的位置一般需要两个数据。
二、平面直角坐标系及有关概念1、平面直角坐标系在平面内,两条互相垂直且有公共原点的数轴,组成平面直角坐标系。
其中,水平的数轴叫做x 轴或横轴,取向右为正方向;铅直的数轴叫做y 轴或纵轴,取向上为正方向;x 轴和y 轴统称坐标轴。
它们的公共原点O 称为直角坐标系的原点;建立了直角坐标系的平面,叫做坐标平面。
2、为了便于描述坐标平面内点的位置,把坐标平面被x 轴和y 轴分割而成的四个部分,分别叫做第一象限、第二象限、第三象限、第四象限。
[注意]:x 轴和y 轴上的点(坐标轴上的点),不属于任何一个象限。
3、点的坐标的概念●对于平面内任意一点P,过点P 分别x 轴、y 轴向作垂线,垂足在上x 轴、y 轴对应的数a ,b 分别叫做点P 的横坐标、纵坐标,有序数对(a ,b )叫做点P 的坐标。
●点的坐标用(a ,b )表示,其顺序是横坐标在前,纵坐标在后,中间有“,”分开,横、纵坐标的位置不能颠倒。
平面内点的坐标是有序实数对,当b a ≠时,(a ,b )和(b ,a )是两个不同点的坐标。
●平面内点的与有序实数对是一一对应的。
4、不同位置的点的坐标的特征(1)、各象限内点的坐标的特征点P(x,y)在第一象限0,0>>⇔y x 点P(x,y)在第二象限0,0><⇔y x点P(x,y)在第三象限0,0<<⇔y x 点P(x,y)在第四象限0,0<>⇔y x(2)、坐标轴上的点的特征点P(x,y)在x 轴上0=⇔y ,x 为任意实数点P(x,y)在y 轴上0=⇔x ,y 为任意实数点P(x,y)既在x 轴上,又在y 轴上⇔x ,y 同时为零,即点P 坐标为(0,0)即原点(3)、两条坐标轴夹角平分线上点的坐标的特征点P(x,y)在第一、三象限夹角平分线(直线y=x )上⇔x 与y 相等点P(x,y)在第二、四象限夹角平分线上⇔x 与y 互为相反数(4)、和坐标轴平行的直线上点的坐标的特征位于平行于x 轴的直线上的各点的纵坐标相同。
位于平行于y 轴的直线上的各点的横坐标相同。
(5)、关于x 轴、y 轴或原点对称的点的坐标的特征点P 与点p ’关于x 轴对称⇔横坐标相等,纵坐标互为相反数,即点P (x ,y )关于x 轴的对称点为P ’(x ,-y )点P 与点p ’关于y 轴对称⇔纵坐标相等,横坐标互为相反数,即点P (x ,y )关于y 轴的对称点为P ’(-x ,y )点P 与点p ’关于原点对称⇔横、纵坐标均互为相反数,即点P (x ,y )关于原点的对称点为P ’(-x ,-y )(6)、点到坐标轴及原点的距离点P(x,y)到坐标轴及原点的距离:(1)点P(x,y)到x 轴的距离等于y (2)点P(x,y)到y 轴的距离等于x(3)点P(x,y)到原点的距离等于22y x +三、坐标变化与图形变化的规律:第四章 一次函数一、函数:一般地,在某一变化过程中有两个变量x 与y ,如果给定一个x 值,相应地就确定了一个y 值,那么我们称y 是x 的函数,其中x 是自变量,y 是因变量。
二、自变量取值范围使函数有意义的自变量的取值的全体,叫做自变量的取值范围。
一般从整式(取全体实数),分式(分母不为0)、二次根式(被开方数为非负数)、实际意义几方面考虑。
三、函数的三种表示法及其优缺点(1)关系式(解析)法两个变量间的函数关系,有时可以用一个含有这两个变量及数字运算符号的等式表示,这种表示法叫做关系式(解析)法。
(2)列表法把自变量x 的一系列值和函数y 的对应值列成一个表来表示函数关系,这种表示法叫做列表法。
(3)图象法用图象表示函数关系的方法叫做图象法。
四、由函数关系式画其图像的一般步骤(1)列表:列表给出自变量与函数的一些对应值 (2)描点:以表中每对对应值为坐标,在坐标平面内描出相应的点 (3)连线:按照自变量由小到大的顺序,把所描各点用平滑的曲线连接起来。
五、正比例函数和一次函数1、正比例函数和一次函数的概念●一般地,若两个变量x ,y 间的关系可以表示成b kx y +=(k ,b 为常数,k ≠0)的形式,则称y 是x 的一次函数(x 为自变量,y 为因变量)。
●特别地,当一次函数b kx y +=中的b=0时(即kx y =)(k 为常数,k ≠0),称y 是x 的正比例函数。
2、一次函数的图像: 所有一次函数的图像都是一条直线3、一次函数、正比例函数图像的主要特征:一次函数b kx y +=的图像是经过点(0,b )的直线;正比例函数kx y =的图像是经过原点(0,0)一般地,正比例函数kx y =有下列性质:(1)当k>0时,图像经过第一、三象限,y 随x 的增大而增大;(2)(2)当k<0时,图像经过第二、四象限,y 随x 的增大而减小。
5、一次函数的性质一般地,一次函数b kx y +=有下列性质:(1)当k>0时,y 随x 的增大而增大 (2)当k<0时,y 随x 的增大而减小6、正比例函数和一次函数解析式的确定确定一个正比例函数,就是要确定正比例函数定义式kx y =(k ≠0)中的常数k 。
确定一个一次函数,需要确定一次函数定义式b kx y +=(k ≠0)中的常数k 和b 。
解这类问题的一般方法是待定系数法。
7、一次函数与一元一次方程的关系:任何一个一元一次方程都可转化为:kx+b=0(k 、b 为常数,k ≠0)的形式. 而一次函数解析式形式正是y=kx+b (k 、b 为常数,k ≠0).当函数值为0时,•即kx+b=0就与一元一次方程完全相同. 结论:由于任何一元一次方程都可转化为kx+b=0(k 、b 为常数,k ≠0)的形式.所以解一元一次方程可以转化为:当一次函数值为0时,求相应的自变量的值.从图象上看,这相当于已知直线y=kx+b 确定它与x 轴交点的横坐标值.第五章 二元一次方程组1、二元一次方程含有两个未知数,并且所含未知数的项的次数都是1的整式方程叫做二元一次方程。
