2015-2016年最新审定北师大版八年级数学上册《2.7二次根式(第2课时)》ppt(优秀课件)
合集下载
北师大版八年级数学上册 2.7.1 二次根式 课件(共23张PPT)

3
3
(3)
1 2
2 ( 4) 9
2
50
3 10
2
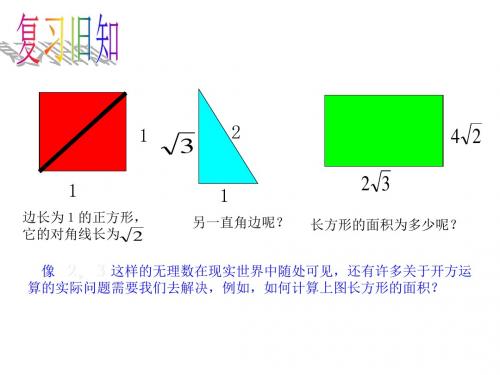
3、一个直角三角形的斜边长为15cm,一条直角边长为10cm,
求另一条直角边长。5 5cm
选做题(2分钟)
设 a0,b0,化简下列二次根式。
1 72
2 8a2b3
解:1 72 98 3222232 2 6 2
或 72 362 62 2 6 2
2 8a2b3 2•22•a2•b2•b2ab 2b
在实数范围内,负数没有平方根
二次根式
根指数为2 被开方数是非负数
例2 x取何值时,下列二次根式有意义?
(1) x1 x 1 (2) 3x x0
( 3 ) x2 2x 1
(4) 1
2x 5
解: x2 2x 1 (x 1)2 解:当2x 50时
当x为任意数时(x 1)2 0 即x 5,原式有意义
6 7
=
6 7
.
4 9 = 49 16 25= 1625
4 =
4
9
9
16 = 16
25
25
观察上面的结果你可得出什么规律 ?
二次根式的性质
a ba•b(a0,b0)
积的算术平方根等于它们算术平方根的积。
a a(a0,b0) 注意公式中的条件 bb
商的算术平方根等于它们算术平方根的 商。
例3 化简:
(1) 8164 (2) 256
(3) 5
9
最简二次根式的定义
带根号的数的化简要求: (1)被开方数中不含分母 (2)被开方数中不含能开得尽方的因 数或因式;
如例3化简结果中的 5 6 5
3
例4 化简:
【教学课件】2.7二次根式 北师大版 八年级数学上册

(a 0,b 0)
问题2:请验证下列等式是否成立?
(1) 4 4 ; (2) 81 81 ; (3) 9 9
25 25
100 100
4 4
请学生总结:
a b
a b
a a bb
(a 0,b 0) 这是二次根式的除法 法则。
(a 0,b 0)
例2 计算:
(1) 3 ; (2) 4 4 ; (3) 64 (4) 2 1 1
北师大版数学八年级上册
第二章 实数 7.二次根是
二次根式概念
形如 a(a≥0)的式子叫做二次根式.
【说明】 二次根式必须具备以下特点; (1)有二次根号; (2)被开方数不能小于0。
指出下列各式中哪些是二次根式,哪些不是, 为什么?
5, a (a 0), 3 8, a (a 0)
探索交流,研究发现
算一算: (1) 4 25 ______; 4 25 _____;
(2) 9 49 ______; 9 49 _____;
(3) 36 1 ______; 36 1 _____;
4
9
答案:(1)10、10 (2)21、21 (3)3、2
ห้องสมุดไป่ตู้
根据填空你能发现什么?
一般情况下,当 a 0,b 0时,ab与 a b
100
9
9
2 10
答案 : (1) 3 10
(3) 8 2 2 33
(2) 2 10 3
(4)5
回顾联系,形成结构
进行二次根式的乘除法运算,要注意必备的条件, 正确使用公式,并要能灵活地与其他有关知识联系 起来,使运算便捷。
有什么关系?
想一想 (4) (9) 4 9
北师大版八年级数学上册教学课件 2.7二次根式
5 a 2a 2√ 6 a bab ×
73 5m2 ×
8 x2 1 √
一、计算下列各式,你能得到什么猜想?
(1) 4 9 36 6
(3)
4 2 93
(2) 4 9 23 6
(4)
4 9
2 3
1、积的算术平方根等于算术平方根的积;
本节课你学习了什么知识?
1、什么叫做二次根式。 2,最简二次根式
二次根式
被开方数a≥0; 根指数为2.
最简二次根式特点:
1、被开方数不含分母, 2、被开方数不含能开得尽方的因数或因式, 3、分母不含根号。
化简:
(1) 32; (2) 72; (3) 12; 7
(4)1.5; (5)1 。 5
7
3
解: (1) 50 25 2 25 2 5 2
(2) 2 2 2 7 14 7 7 7 7 7
(3) 1 1 3 3 3 3 3 3
(1)你是怎么发现 50含有开得尽方的因数?
你是怎么判断 14 是最简二次根式的? 7
(2)将二次根式化成最简二次根式,你有哪 些经验与体会?与同伴进行交流。
观察例一的化简结果 (关键看被开方数), 想一想有什么共同特 征?
最简二次根式概念:
一般地,被开方数不含分母,也不含能开得尽方的 因数或因式,这样的二次根式,叫做最简二次根式。
最简二次根式特点: 1、被开方数不含分母, 2、被开方数不含能开得尽方的因数或因式, 3、分母不含根号。
例2:(1) 50;(2) 2;(3)1
由于 22 4, 22 4 ,而其他数的平方不会等于
4,因此4的平方根有且只有两个:2 与-2 (2)2的平方根有哪些?算术平方根呢?
八级数学上册2.7二次根式课件(新版)北师大版

四种运算
加 、减、乘、除
初中数学
初中数学
1. x取何值时,下列二次根式有意义?
(1) x 1 x≥0 (2) 3x x≤0
(3) 4x2x为全体实数(4) 1 x 0 x
(5) x3 x≥0
(6)
1 x2
x0
初中数学
2.当 x 1 y 3 0时, x ( -1 ),y ( 3 )
3.已知 x 5 6 3y z 22 0
初中数学
(一)二次根式
a2 2500
b3
2
h
5
观察以上各式,它们有什么共同特点?
表示一些正数的算术平方根
初中数学
形如 a(a≥0)的式子叫做二次根式 1.表示a的算术平方根 2. a可以是数,也可以是式
3. 形式上含有二次根号
4. a≥0, a≥0
( 双重非负性)
5.既可表示开方运算,也可表示运算的结果
5
,用含有h的式子
.
初中数学
?米 50米
b-3
1.知识目标
(1)掌握二次根式的概念和性质,会确定被开方数的取值 范围;
(2)能利用积(或商)的算术平方根的性质进行二次根式 的化简和运算.
2.教学重点
二次根式的加减乘除运算.
3.教学难点
二次根式的乘除法与二次根式的积(或商)的算术平方根 的关系及应用.
A. 10 3 B.3 C. 3 D. 10 3
初中数学
初中数学
知识结构
三个概念
二次根式 最简二次根式
1、ab a ba 0,b 0
二 次
两个公式
2、
a b
a b
北师大版八年级上册2.7.2二次根式课件 (共26张PPT)

问题 你还记得单项式乘单项式法则吗?
试回顾如何计算3a2·2a3= 6a5 .
提示:可 类比上面
2. 计算:
(1)2 5 3 7;
的计算哦
(2)4
27
-
1 2
3 .
解:(1)2 5 3 7 2 3 5 7 =6 35;
(2)4
27
课堂小结(1分钟)
1、在实数范围内,有理数的运算法则及运算律仍然成立。
2、会正确运用公式: a b a b(a≥0,b≥0),
a a (a≥0, b>0).
bb 3、同类二次根式:几个被开方数相同的最简二次根式.
4、在二次根式的运算中, :
(1)最后结果一般要求写成最简的二次根式的形式. (2)加减法的运算步骤:“一化简二判断三合并” (3)合并的前提条件:只有被开方数相同的最简二次根 式(即同类二次根式)才能进行合并.
a b c n abc n a 0,b 0,c 0n 0
当二次根号外有因数(式)时,可以类比单项式乘单 项式的法则计算,即根号外的因数(式)的积作为根号 外的因数(式),被开方数的积作为被开方数,即
m a n b mn ab a 0,b 0
(2) 1 27 1 27 9 3.
3
3
可先用乘法结合 律,再运用二次 根式的乘法法则
(3) 2 3 5 ( 2 3) 5 6 5 30.
或者 2 3 5 2 3 5 30
归纳 (3)只需其中两个结合就可实现转化进行计算, 说明二次根式乘法法则同样适合三个及三个以上的二 次根式相乘,即 a b k a b k(a 0,b 0,k 0).
北师大版八年级上册 2.7.3 二次根式(共21张PPT)

号的先算括号内的.
(2)在运算过程中,每个二次根式都可以看做一 个“单项式”,多个不同的二次根式可以看做“ 多项式”,因此有理数中的运算律(交换律、结 合律、分配律等)和乘法公式(平方差公式、完
全平方公式)在二次根式的运算中仍然适用.
(3)二次根式的混合运算的结果应写成最简形
式,这个形式应该是最简二次根式,或几个非同
(பைடு நூலகம் 0,b 0, c 0, d 0).
(3)( a b)( a b)型,即
( a b)( a b) ( a )2 ( b )2 a b
(a 0,b 0),运用平方差公式.
(4)( a b)2型,即( a b)2 a 2 ab b
(a 0,b 0),运用完全平方公式.
第二章 实 数
2.7.3 二次根式
温故知新
(1)说一说什么是最简二次根式?
(2)二次根式化简过程中,你有哪些体会?
(3)上节课课后作业:已知 2 1.414, 3 1.732,
6 2.449,
你是怎样解决的?
3 计. 算
2
最简二次根式
一般地,被开方数不含分母,也不含能开得 尽方的因数或因式,这样的二次根式,叫做最简 二次根式
类二次根式的和或差,或有理式.
随堂练习
1、计算:
(1)( 80 90) 5
(2) 24 3 6 2 3
(3)( a3b 3ab ab3 ) ( ab) (a>0,b>0)(4)(2 6 5 2)( 2 6 5 2)
2.计算
(1)
x 1 ;(2)
2x 2
0.125a5b6c7
;(3)
解:(1) 28 4
1 -( 7 2
2)
(2)在运算过程中,每个二次根式都可以看做一 个“单项式”,多个不同的二次根式可以看做“ 多项式”,因此有理数中的运算律(交换律、结 合律、分配律等)和乘法公式(平方差公式、完
全平方公式)在二次根式的运算中仍然适用.
(3)二次根式的混合运算的结果应写成最简形
式,这个形式应该是最简二次根式,或几个非同
(பைடு நூலகம் 0,b 0, c 0, d 0).
(3)( a b)( a b)型,即
( a b)( a b) ( a )2 ( b )2 a b
(a 0,b 0),运用平方差公式.
(4)( a b)2型,即( a b)2 a 2 ab b
(a 0,b 0),运用完全平方公式.
第二章 实 数
2.7.3 二次根式
温故知新
(1)说一说什么是最简二次根式?
(2)二次根式化简过程中,你有哪些体会?
(3)上节课课后作业:已知 2 1.414, 3 1.732,
6 2.449,
你是怎样解决的?
3 计. 算
2
最简二次根式
一般地,被开方数不含分母,也不含能开得 尽方的因数或因式,这样的二次根式,叫做最简 二次根式
类二次根式的和或差,或有理式.
随堂练习
1、计算:
(1)( 80 90) 5
(2) 24 3 6 2 3
(3)( a3b 3ab ab3 ) ( ab) (a>0,b>0)(4)(2 6 5 2)( 2 6 5 2)
2.计算
(1)
x 1 ;(2)
2x 2
0.125a5b6c7
;(3)
解:(1) 28 4
1 -( 7 2
2)
北师大版八年级上册数学 2.7.1二次根式 课件(28张PPT)
• You have to believe in yourself. That's the secret of success. 人必须相信自己,这是成功的秘诀。
•
归纳:二次根式中字母的取值范围
?
必须满足被开方数大于等于零.
1、 a 1 表示什么?是平方根,还是算术平方根?
算术平方根
2、 a 1 的被开方式是什么?被开方式必须满足什 么条件,二次根式才有意义?
5.既可表示开方运算,也可表示运算的结果.
下列各式中哪些是二次根式?
?
7, 1, x6, x2y(y0), x2y2, 3
3 x2y2, a1 3
•9、要学生做的事,教职员躬亲共做;要学生学的知识,教职员躬亲共学;要学生守的规则,教职员躬亲共守。2021/9/52021/9/5Sunday, September 05, 2021 •10、阅读一切好书如同和过去最杰出的人谈话。2021/9/52021/9/52021/9/59/5/2021 12:21:42 AM •11、只有让学生不把全部时间都用在学习上,而留下许多自由支配的时间,他才能顺利地学习……(这)是教育过程的逻辑。2021/9/52021/9/52021/9/5Sep-215-Sep-21 •12、要记住,你不仅是教课的教师,也是学生的教育者,生活的导师和道德的引路人。2021/9/52021/9/52021/9/5Sunday, September 05, 2021
13、He who seize the right moment, is the right man.谁把握机遇,谁就心想事成。2021/9/52021/9/52021/9/52021/9/59/5/2021 •14、谁要是自己还没有发展培养和教育好,他就不能发展培养和教育别人。2021年9月5日星期日2021/9/52021/9/52021/9/5 •15、一年之计,莫如树谷;十年之计,莫如树木;终身之计,莫如树人。2021年9月2021/9/52021/9/52021/9/59/5/2021 •16、教学的目的是培养学生自己学习,自己研究,用自己的头脑来想,用自己的眼睛看,用自己的手来做这种精神。2021/9/52021/9/5September 5, 2021 •17、儿童是中心,教育的措施便围绕他们而组织起来。2021/9/52021/9/52021/9/52021/9/5
•
归纳:二次根式中字母的取值范围
?
必须满足被开方数大于等于零.
1、 a 1 表示什么?是平方根,还是算术平方根?
算术平方根
2、 a 1 的被开方式是什么?被开方式必须满足什 么条件,二次根式才有意义?
5.既可表示开方运算,也可表示运算的结果.
下列各式中哪些是二次根式?
?
7, 1, x6, x2y(y0), x2y2, 3
3 x2y2, a1 3
•9、要学生做的事,教职员躬亲共做;要学生学的知识,教职员躬亲共学;要学生守的规则,教职员躬亲共守。2021/9/52021/9/5Sunday, September 05, 2021 •10、阅读一切好书如同和过去最杰出的人谈话。2021/9/52021/9/52021/9/59/5/2021 12:21:42 AM •11、只有让学生不把全部时间都用在学习上,而留下许多自由支配的时间,他才能顺利地学习……(这)是教育过程的逻辑。2021/9/52021/9/52021/9/5Sep-215-Sep-21 •12、要记住,你不仅是教课的教师,也是学生的教育者,生活的导师和道德的引路人。2021/9/52021/9/52021/9/5Sunday, September 05, 2021
13、He who seize the right moment, is the right man.谁把握机遇,谁就心想事成。2021/9/52021/9/52021/9/52021/9/59/5/2021 •14、谁要是自己还没有发展培养和教育好,他就不能发展培养和教育别人。2021年9月5日星期日2021/9/52021/9/52021/9/5 •15、一年之计,莫如树谷;十年之计,莫如树木;终身之计,莫如树人。2021年9月2021/9/52021/9/52021/9/59/5/2021 •16、教学的目的是培养学生自己学习,自己研究,用自己的头脑来想,用自己的眼睛看,用自己的手来做这种精神。2021/9/52021/9/5September 5, 2021 •17、儿童是中心,教育的措施便围绕他们而组织起来。2021/9/52021/9/52021/9/52021/9/5
