2019届枣庄市中考《61圆的有关概念和性质》要题随堂演练有答案-(数学)-推荐
2019中考数学第六章圆第一节圆的有关概念和性质习题word版本

第六章圆第一节圆的有关概念和性质姓名:________ 班级:________ 用时:______分钟1.(2018·淮安中考)如图,点A,B,C都在⊙O上,若∠AOC=140°,则∠B的度数是( )A.70° B.80° C.110° D.140°2.(2018·杭州中考)如图,⊙O的半径OA=6,以A为圆心,OA为半径的弧交⊙O于点B,C,则BC=( )A.6 3 B.6 2 C.3 3 D.3 23.(2019·易错题)已知⊙O的半径为10,圆心O到弦AB的距离为5,则弦AB所对的圆周角的度数是( )A.30° B.60°C.30°或150° D.60°或120°4.(2018·凉山州中考)如图,⊙O是△ABC的外接圆,已知∠ABO=50°,则∠ACB的大小为( )A.40° B.30° C.45° D.50°5.(2018·随州中考)如图,点A,B,C在⊙O上,∠A=40度,∠C=20度,则∠B=________度.6.(2019·原创题)如图,Rt△ABC是⊙O的内接直角三角形,其中∠BCA=90°,若BC=3,AB=5,OD⊥BC于点D,则OD的长为______.7.(2018·黑龙江中考)如图,AB为⊙O的直径,弦CD⊥AB于点E,已知CD=6,EB=1,则⊙O的半径为______.8.(2019·易错题)等腰三角形ABC中,顶角A为40°,点P在以A为圆心,BC长为半径的圆上,且BP=BA,则∠PBC的度数为____________________.9.(2018·无棣一模)如图,△ABC是⊙O的内接三角形,AD是⊙O直径,若∠ABC=50°,则∠CAD=________.10.(2019·原创题)如图,在△ABC的外接圆⊙O中,∠A=60°,AB为直径,点D是AC 的中点,过点D作DE⊥AB交AB于点E,若DE=3,求BC的长.11.(2018·白银中考)如图,⊙A 过点O(0,0),C(3,0),D(0,1),点B 是x 轴下方⊙A 上的一点,连接BO ,BD ,则∠OBD 的度数是( )A .15°B .30°C .45°D .60°12.(2018·咸宁中考)如图,已知⊙O 的半径为5,弦AB ,CD 所对的圆心角分别是∠AOB ,∠COD ,若∠AOB 与∠COD 互补,弦CD =6,则弦AB 的长为( )A .6B .8C .5 2D .5 313.(2018·玉林中考)小华为了求出一个圆盘的半径,他用所学的知识,将一宽度为 2 cm 的刻度尺的一边与圆盘相切,另一边与圆盘边缘两个交点处的读数分别是“4”和“16”(单位:cm),请你帮小华算出圆盘的半径是________cm.14.(2019·易错题)已知⊙O 的半径为10 cm ,AB ,CD 是⊙O 的两条弦,AB ∥CD ,AB =16 cm ,CD =12 cm ,则弦AB 和CD 之间的距离是____________cm.15.(2018·宜宾中考)如图,AB 是半圆的直径,AC 是一条弦,D 是AC ︵的中点,DE ⊥AB 于点E ,且DE 交AC 于点F ,DB 交AC 于点G ,若EF AE =34,则CGGB=________.16.(2018·无锡中考)如图,四边形ABCD 内接于⊙O ,AB =17,CD =10,∠A =90°,cos B =35,求AD 的长.17.如图,在半径为5的⊙O 中,直径AB 的不同侧有定点C 和动点P ,已知BC ∶CA =4∶3,点P 在AB ︵上运动.(1)当点P 与点C 关于AB 对称时,求CP 的长; (2)当点P 运动到AB ︵的中点时,求CP 的长; (3)点P 在AB ︵上运动时,求CP 的长的取值范围.18.(2018·乐山中考)《九章算术》是我国古代第一部自成体系的数学专著,代表了东方数学的最高成就.它的算法体系至今仍在推动着计算机的发展和应用.书中记载:“今有圆材埋在壁中,不知大小,以锯锯之,深一寸,锯道长一尺,问径几何?”译为:“今有一圆柱形木材,埋在墙壁中,不知其大小,用锯去锯这木材,锯口深1寸(ED=1寸),锯道长1尺(AB=1尺=10寸),问这块圆柱形木材的直径是多少?”如图所示,请根据所学知识计算:圆柱形木材的直径AC是( )A.13寸 B.20寸C.26寸 D.28寸参考答案【基础训练】1.C 2.A 3.D 4.A5.60 6.2 7.5 8.30°或110°9.40°10.解:如图,连接OD.∵AB为直径,∴∠ACB=90°.∵在Rt△ADE中,∠A=60°,∴∠ADE=30°.∵点D是AC的中点,则OD⊥AC,∴∠ODE=∠ADO-∠ADE=60°.又∵DE=3,∴OD=2 3.又∵点O是AB的中点,根据中位线定理得BC=2OD=4 3.【拔高训练】11.B 12.B13.10 14.2或14 15.5 516.解:∵四边形ABCD内接于⊙O,∠A=90°,∴∠C=180°-∠A=90°,∠ABC+∠ADC=180°.如图,连接BD,作AE⊥BC于点E,DF⊥AE于点F,则四边形CDFE是矩形,EF=CD=10.在Rt△AEB中,∵∠AEB=90°,AB=17,cos ∠ABC =35,∴BE =AB·cos ∠ABE =515,∴AE =AB2-BE2=685,∴AF =AE -EF =685-10=185.∵∠ABC +∠ADC =180°,∠CDF =90°,∴∠ABC +∠ADF =90°.∵cos ∠ABC =35,∴sin ∠ADF =cos ∠ABC =35.在Rt △ADF 中,∵∠AFD =90°,sin ∠ADF =35,∴AD =AFsin∠ADF =18535=6.17.解:(1)∵点P 与点C 关于AB 对称,∴CP ⊥AB.如图,设垂足为点D.∵AB 为⊙O 的直径,∴∠ACB =90°.∵AB =10,BC ∶CA =4∶3,∴BC =8,AC =6.又∵△ACD ∽△ABC , ∴AC AB =CDBC,∴CD =4.8,∴CP =2CD =9.6.(2)如图,连接AP ,PB ,过点B 作BE ⊥PC 于点E.∵点P 是AB ︵的中点,∴AP =BP =52,∠ACP =∠BCP =45°.∵BC =8,∴CE =BE =4 2.又∵PB =52,∴PE =PB2-BE2=32,∴CP =CE +PE =7 2.(3)点P 在AB ︵上运动时,恒有CP ≥CA ,即CP ≥6.当CP 过圆心O 时,CP 取得最大值10,∴CP 的取值范围是6≤CP ≤10.【培优训练】18.C。
山东省滨州市2019中考数学第六章圆第一节圆的有关概念和性质要题随堂演练
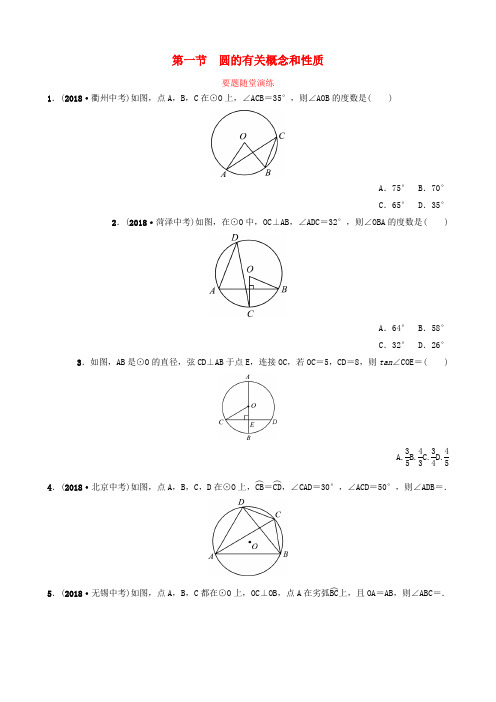
第一节 圆的有关概念和性质要题随堂演练1.(2018·衢州中考)如图,点A ,B ,C 在⊙O 上,∠ACB=35°,则∠AOB 的度数是( )A .75° B.70°C .65° D.35°2.(2018·菏泽中考)如图,在⊙O 中,OC⊥AB,∠ADC=32°,则∠OBA 的度数是( )A .64° B.58°C .32° D.26°3.如图,AB 是⊙O 的直径,弦CD⊥AB 于点E ,连接OC ,若OC =5,CD =8,则tan ∠COE=( )A.35B.43C.34D.454.(2018·北京中考)如图,点A ,B ,C ,D 在⊙O 上,CB ︵=CD ︵,∠CAD=30°,∠ACD=50°,则∠ADB=.5.(2018·无锡中考)如图,点A ,B ,C 都在⊙O 上,OC⊥OB,点A 在劣弧BC ︵上,且OA =AB ,则∠ABC=.6.(2018·泰安中考)如图,⊙O是△ABC的外接圆,∠A=45°,BC=4,则⊙O的直径为.7.(2018·烟台中考)如图,方格纸上每个小正方形的边长均为1个单位长度,点O,A,B,C在格点(两条网格线的交点叫格点)上,以点O为原点建立直角坐标系,则过A,B,C三点的圆的圆心坐标为.8.(2017·临沂中考)如图,∠BAC的平分线交△ABC的外接圆于点D,∠ABC的平分线交AD于点E.(1)求证:DE=DB;(2)若∠BAC=90°,BD=4.求△ABC外接圆的半径.参考答案1.B 2.D 3.B4.70° 5.15° 6.4 2 7.(-1,-2)8.(1)证明:∵AD 平分∠BAC,BE 平分∠ABC,∴∠BAD=∠CAD,∠ABE=∠CBE.又∵∠BED=∠ABE+∠BAD, ∠DBE=∠DBC+∠CBE,∠DBC=∠DAC, ∴∠BED=∠DBE,∴DE=DB. (2)解:如图,连接CD.∵∠BAC=90°,∴BC 是圆的直径,∴∠BDC =90°.∵∠BAD=∠CAD,∴BD ︵=CD ︵,∴BD=CD ,∴△BCD 是等腰直角三角形.∵BD=4,∴BC=42,∴△ABC 的外接圆的半径为2 2.。
2019届数学中考全程演练 第29课时 圆的有关性质

第九单元 圆第29课时 圆的有关性质(60分)一、选择题(每题5分,共30分)1.[2017·梧州]已知⊙O 的半径是5,点A 到圆心O 的距离是7,则点A 与⊙O 的位置关系是(C)A .点A 在⊙O 上B .点A 在⊙O 内C .点A 在⊙O 外D .点A 与圆心O 重合【解析】 ∵⊙O 的半径是5,点A 到圆心O 的距离是7,即点A 到圆心O 的距离大于圆的半径,∴点A 在⊙O 外.2.[2016·珠海]如图29-1,在⊙O 中,直径CD 垂直于弦AB ,若∠C =25°,则∠BOD 的度数是(D)A .25°B .30°C .40°D .50°【解析】 ∵在⊙O 中,直径CD 垂直于弦AB , ∴AD ︵=BD ︵,∴∠DOB =2∠C =50°.3.[2016·遂宁]如图29-2,在半径为5 cm 的⊙O 中,弦AB =6 cm ,OC ⊥AB 于点C ,则OC =(B)A .3 cmB .4 cmC .5 cmD .6 cm图29-2【解析】 显然利用垂径定理.如答图,连结OA ,图29-1∵AB =6 cm ,AC =12AB =3 cm ,又⊙O 的半径为5 cm ,所以OA =5 cm , 在Rt △AOC 中,OC =AO 2-AC 2=52-32=4(cm).4.[2016·宁波]如图29-3,⊙O 为△ABC 的外接圆,∠A =72°,则∠BCO 的度数为(B)A .15°B .18°C .20°D .28°图29-3【解析】 连结OB ,如答图,∠BOC =2∠A =2×72°=144°, ∵OB =OC ,∴∠CBO =∠BCO ,∴∠BCO =12(180°-∠BOC )=12×(180°-144°)=18°.5.[2016·巴中]如图29-4,在⊙O 中,弦AC ∥半径OB ,∠BOC =50°,则∠OAB 的度数为(A)A .25°B .50°C .60°D .30° 【解析】 ∵∠BOC =2∠BAC ,∠BOC =50°, ∴∠BAC =25°,∵AC ∥OB ,∴∠BAC =∠B =25°, ∵OA =OB ,∴∠OAB =∠B =25°.图29-4 图29-56.[2017·荆门]如图29-5,AB 是半圆O 的直径,D ,E 是半圆上任意两点,连结AD ,DE ,AE 与BD 相交于点C ,要使△ADC 与△ABD 相似,可以添加一个条件.下列添加的条件其中错误的是(D)第4题答图A .∠ACD =∠DAB B .AD =DEC .AD 2=BD ·CDD .AD ·AB =AC ·BD【解析】 由题意可知,∠ADC =∠ADB =90°, A .∵∠ACD =∠DAB , ∴△ADC ∽△BDA ,故A 正确; B .∵AD =DE , ∴AD ︵=DE ︵,∴∠DAE =∠B ,∴△ADC ∽△BDA ,故B 正确; C .∵AD 2=BD ·CD ,∴AD ∶BD =CD ∶AD , ∴△ADC ∽△BDA ,故C 正确;D .∵AD ·AB =AC ·BD ,∴AD ∶BD =AC ∶AB , 但∠ADC =∠ADB 不是夹角,故D 错误. 二、填空题(每题5分,共30分)7.[2016·贵州]如图29-6,A ,B ,C 三点均在⊙O 上,若∠AOB =80°,则∠ACB =__40°__.【解析】 ∠ACB =12∠AOB =12×80°=40°.图29-6 图29-78.[2016安徽]如图29-7,点A ,B ,C 在⊙O 上,⊙O 的半径为9,AB ︵的长为2π,则∠ACB 的大小是__20°__.9.[2016·娄底]如图29-8,在⊙O 中,AB 为直径,CD 为弦,已知∠ACD =40°,则∠BAD =__50__度.【解析】 ∵在⊙O 中,AB 为直径,∴∠ADB =90°, ∵∠B =∠ACD =40°,∴∠BAD =90°-∠B =50°.10.[2016·泰州]如图29-9,⊙O 的内接四边形ABCD 中,∠A =115°,则∠BOD 等于__130°__.【解析】 ∵∠A =115°,∴∠C =180°-∠A =65°,∴∠BOD =2∠C =130°.图29-8图29-9 图29-1011.[2016·绍兴]如图29-10,已知点A (0,1),B (0,-1),以点A 为圆心,AB 为半径作圆,交x 轴的正半轴于点C ,则∠BAC 等于__60__度. 【解析】 ∵A (0,1),B (0,-1), ∴AB =2,OA =1,∴AC =2, 在Rt △AOC 中,cos ∠BAC =OA AC =12, ∴∠BAC =60°.12.某居民区一处圆形下水管道破裂,修理人员准备更换一段与原管道同样粗细的新管道.如图29-11,水面宽度原有60 cm ,发现时水面宽度只有50 3 cm ,同时水位也下降65 cm ,则修理人员应准备的半径为__50__cm 的管道.图29-11【解析】 如答图所示:过点O 作EF ⊥AB 于点F ,交CD 于点E ,连结OC ,OA , ∵CD ∥AB ,∴EF ⊥CD , ∵CD =60 cm ,AB =50 3 cm ,∴CE =12CD =12×60=30 cm ,AF =12AB =12×503=25 3 cm ,第12题答图设⊙O 的半径为r ,OE =h cm ,则OF =65-h (cm), 在Rt △OCE 中,OC 2=CE 2+OE 2,即r 2=302+h 2,①在Rt △OAF 中,OA 2=AF 2+OF 2,即r 2=(253)2+(65-h )2,② ①②联立,解得r =50 cm. 三、解答题(共10分)13.(10分)[2017·湖州]如图29-12,已知在以点O 为圆心的两个同心圆中,大圆的弦AB 交小圆于点C ,D . (1)求证:AC =BD ;(2)若大圆的半径R =10,小圆的半径r =8,且圆心O 到直线AB 的距离为6,求AC 的长.图29-12解:(1)证明:如答图,过点O 作OE ⊥AB 于点E .则CE =DE ,AE =BE . ∴AE -CE =BE -DE ,即AC =BD ; (2)由(1)可知,OE ⊥AB 且OE ⊥CD , 如答图,连结OA ,OC ,∴CE =OC 2-OE 2=82-62=27.AE =OA 2-OE 2=102-62=8.∴AC =AE -CE =8-27.(18分)14.(8分)[2016·安顺]如图29-13,⊙O 的直径AB 垂直于弦CD ,垂足是E ,∠A =22.5°,OC =4,CD 的长为(C) A .2 2 B .4 C .4 2D .8【解析】 ∵∠A =22.5°,∴∠BOC =2∠A =45°, ∵⊙O 的直径AB 垂直于弦CD , ∴CE =DE ,△OCE 为等腰直角三角形, ∴CE =22OC =22,∴CD =2CE =4 2. 15.(10分)某地有一座圆弧形拱桥,圆心为O ,桥下水面宽度为7.2 m ,如图29-14,过O 作OC ⊥AB 于D ,交圆弧于C ,CD =2.4 m .现有一艘宽3 m ,船舱顶部为方形并高出水面第13题答图图29-13(AB )2 m 的货船要经过拱桥,此货船能否顺利通过这座拱桥?图29-14解:如答图,连结ON ,OB . ∵OC ⊥AB ,∴D 为AB 的中点. ∵AB =7.2 m , ∴BD =12AB =3.6 m.设OB =OC =ON =r ,则OD =OC -CD =r -2.4. 在Rt △BOD 中,根据勾股定理得r 2=(r -2.4)2+3.62, 解得r =3.9(m). ∵CD =2.4 m ,船舱顶部为方形并高出水面A B 为2 m , ∴CE =2.4-2=0.4(m),∴OE =r -CE =3.9-0.4=3.5(m). 在Rt △OEN 中,EN 2=ON 2-OE 2=3.92-3.52=2.96,∴EN = 2.96 m ,∴MN =2EN =2× 2.96≈3.44(m)>3(m), ∴此货船能顺利通过这座拱桥.(12分)16.(12分)[2016·台州]如图29-15,四边形ABCD 内接于⊙O ,点E 在对角线AC 上,EC =BC =DC . (1)若∠CBD =39°,求∠BAD 的度数; (2)求证:∠1=∠2. 解:(1)∵BC =DC ,第15题答图图29-15.∴BC ︵=DC ︵.∴∠BAC =∠CAD =∠CBD . ∵∠CBD =39°, ∴∠BAC =∠CAD =39°.∴∠BAD =∠BAC +∠DAC =78°; (2)证明:∵EC =BC , ∴∠CBE =∠CEB . ∵∠CBE =∠1+∠CBD , ∠CEB =∠2+∠BAC , ∴∠1+∠CBD =∠2+∠BAC . 又∵∠BAC =∠CBD , ∴∠1=∠2.。
河北省2019年中考数学一轮复习 第六章 圆 第一节 圆的基本性质好题随堂演练

第六章 圆好题随堂演练1.(2018·衢州)如图,点A ,B ,C 在⊙O 上,∠ACB=35°,则∠AOB 的度数 是( )A .75°B .70°C .65°D .35°2.(2018·盐城)如图,AB 为⊙O 的直径,CD 是⊙O 的弦,∠ADC=35°,则∠CAB 的度数为( ) A .35° B .45° C .55° D .65°3.(2017·宜昌改编)如图,已知点A ,B ,C ,D 在⊙O 上,AC 平分∠BAD,则下列结论正确的是( ) A .AB =AD B .BC =CD C.AB ︵=AD ︵D .∠BCA=∠DCA4. 如图,⊙O 的半径为13,弦AB 的长度是24,ON⊥AB,垂足为点N , 则ON = .5.如图,四边形ABCD 为⊙O 的内接四边形,已知∠C=∠D,则AB 与CD 的位置关系是 .6.(2017·牡丹江)如图,在⊙O 中,AC ︵=CB ︵,CD⊥OA 于D ,CE⊥OB 于E ,求证:AD =BE.7.(2017·安徽)如图,在四边形ABCD 中,AD =BC ,∠B=∠D,AD 不平行于BC ,过点C 作CE∥AD 交△ABC 的外接圆⊙O 于点E ,连接AE. (1)求证:四边形AECD 为平行四边形; (2)连接CO ,求证:CO 平分∠BCE.8.(2018·宜昌)如图,在△ABC 中,AB =AC ,以AB 为直径的圆交AC 于点D ,交BC 于点E ,延长AE 至点F ,使EF =AE ,连接FB ,FC. (1)求证:四边形ABFC 是菱形;(2)若AD =7,BE =2,求半圆和菱形ABFC 的面积.参考答案1.B 2.C 3.B 4.5 5.AB∥CD3 / 5第6题解图6.证明:如解图,连接OC. ∵AC ︵=CB ︵, ∴∠AOC=∠BOC.∵CD⊥OA 于点D ,CE⊥OB 于点E , ∴∠CDO=∠CEO=90°.在△COD 和△COE 中,⎩⎪⎨⎪⎧∠DOC=∠EOC,∠CDO=∠CEO,CO =CO ,∴△COD≌△COE(AA S ),∴OD=OE. ∵AO=BO ,∴AD=BE.7.证明:(1)∵∠B=∠D,∠B=∠E, ∴∠D=∠E.∵CE∥AD,∴∠E+∠DAE=180°, ∴∠D+∠DAE=180°,∴AE∥DC.又∵CE∥AD,∴四边形AECD 为平行四边形;(2)如解图,过点O 作OM⊥EC,ON⊥BC,垂足分别为M 、N.∴EM=MC ,BN =NC.∵四边形AECD 是平行四边形, ∴AD=EC ,又∵AD=BC ,∴EC=BC , ∴MC=NC ,∴OM=ON ,∴CO 平分∠BCE. 8.(1)证明:∵AB 是直径,5 / 5∴∠AEB=90°,即AE⊥BC, ∵AB=AC ,∴BE=CE ,∵AE=EF ,∴四边形ABFC 是平行四边形, ∵AC=AB ,∴四边形ABFC 是菱形;(2)解:设CD =x.如解图,连接BD. ∵AB 是直径,∴∠ADB=∠BDC=90°, ∴AB 2-AD 2=CB 2-CD 2,∴(7+x)2-72=42-x 2,解得x =1或-8(舍去), ∴AC=8,BD =82-72=15, ∴S 菱形ABFC =AC·BD=815. S 半圆=12·π·42=8π.。
潍坊专版2019中考数学复习第1部分第六章圆第一节圆的有关概念和性质要题随堂演练

圆的有关概念和性质要题随堂演练1.(2018·衢州中考)如图,点A ,B ,C 在⊙O 上,∠ACB=35°,则∠AOB 的度数是( )A .75°B .70° C.65° D.35°(第1题图) (第2题图)2.(2018·菏泽中考)如图,在⊙O 中,OC⊥AB,∠ADC=32°,则∠OBA 的度数是( )A .64°B .58°C .32°D .26°3.如图,AB 是⊙O 的直径,弦CD⊥AB 于点E ,连接OC ,若OC =5,CD =8,则tan ∠COE=( ) A.35 B.43 C.34 D.45(第3题图) (第4题图)4.(2018·北京中考)如图,点A ,B ,C ,D 在⊙O 上,CB ︵=CD ︵,∠CAD=30°,∠ACD=50°,则∠ADB = .5.(2018·无锡中考)如图,点A ,B ,C 都在⊙O 上,OC⊥OB,点A 在劣弧BC ︵上,且OA =AB ,则∠ABC = .6.(2018·临沂中考)如图,在△ABC 中,∠A=60°,BC =5 cm .能够将△ABC 完全覆盖的最小圆形纸片的直径是 cm .7.(2018·烟台中考)如图,方格纸上每个小正方形的边长均为1个单位长度,点O ,A ,B ,C 在格点(两条网格线的交点叫格点)上,以点O 为原点建立直角坐标系,则过A ,B ,C 三点的圆的圆心坐标为 .8.(2017·济南中考)如图,AB 是⊙O 的直径,∠ACD=25°,求∠BAD 的度数.参考答案1.B 2.D 3.B 4.70° 5.15° 6.1033 7.(-1,-2)8.解:∵∠ACD=25°,∴∠ABD=25°.∵AB 是⊙O 的直径,∴∠ADB=90°.在△ABD 中,∠BAD=180°-∠ABD-∠ADB=180°-25°-90°=65°.。
东营专版2019年中考数学复习第六章圆第一节圆的有关概念和性质要题随堂演练

第六章 圆要题随堂演练1.(xx·衢州中考)如图,点A ,B ,C 在⊙O 上,∠ACB=35°,则∠AOB 的度数是( )A .75° B.70° C.65° D.35°2.(xx·菏泽中考)如图,在⊙O 中,OC⊥AB,∠ADC=32°,则∠OBA 的度数是( )A .64° B.58° C.32° D.26°3.如图,AB 是⊙O 的直径,弦CD⊥AB 于点E ,连接OC ,若OC =5,CD =8,则tan∠COE=( )A.35B.43C.34D.454.(xx·北京中考)如图,点A ,B ,C ,D 在⊙O 上,CB ︵=CD ︵,∠CAD=30°,∠ACD=50°,则∠ADB=__________.5.(xx·无锡中考)如图,点A ,B ,C 都在⊙O 上,OC ⊥OB ,点A 在劣弧BC ︵上,且OA =AB ,则∠ABC=__________.6.(xx·临沂中考)如图,在△ABC 中,∠A=60°,BC =5 cm.能够将△ABC 完全覆盖的最小圆形纸片的直径是________ cm.7.(xx·烟台中考)如图,方格纸上每个小正方形的边长均为1个单位长度,点O ,A ,B ,C 在格点(两条网格线的交点叫格点)上,以点O 为原点建立直角坐标系,则过A ,B ,C 三点的圆的圆心坐标为_______________.8.(xx·济南中考)如图,AB 是⊙O 的直径,∠ACD=25°,求∠BAD 的度数.参考答案1.B 2.D 3.B4.70° 5.15° 6.10337.(-1,-2)8.解:∵∠ACD=25°,∴∠ABD=25°.∵AB是⊙O的直径,∴∠ADB=90°.在△ABD中,∠BAD=180°-∠ABD-∠ADB=180°-25°-90°=65°.。
(东营专用试题)2019年中考数学复习 第六章 圆 第一节 圆的有关概念和性质要题随堂演练
第六章 圆要题随堂演练1.(2018·衢州中考)如图,点A ,B ,C 在⊙O 上,∠ACB=35°,则∠AOB 的度数是( )A .75° B.70° C.65° D.35°2.(2018·菏泽中考)如图,在⊙O 中,OC⊥AB,∠ADC=32°,则∠OBA 的度数是( )A .64° B.58° C.32° D.26°3.如图,AB 是⊙O 的直径,弦CD⊥AB 于点E ,连接OC ,若OC =5,CD =8,则tan∠COE=( )A.35B.43C.34D.454.(2018·北京中考)如图,点A ,B ,C ,D 在⊙O 上,CB ︵=CD ︵,∠CAD=30°,∠ACD=50°,则∠ADB=__________.5.(2018·无锡中考)如图,点A ,B ,C 都在⊙O 上,OC ⊥OB ,点A 在劣弧BC ︵上,且OA =AB ,则∠ABC=__________.6.(2018·临沂中考)如图,在△ABC 中,∠A=60°,B C =5 cm.能够将△ABC 完全覆盖的最小圆形纸片的直径是________ cm.7.(2018·烟台中考)如图,方格纸上每个小正方形的边长均为1个单位长度,点O ,A ,B ,C 在格点(两条网格线的交点叫格点)上,以点O 为原点建立直角坐标系,则过A ,B ,C 三点的圆的圆心坐标为_______________.8.(2017·济南中考)如图,AB 是⊙O 的直径,∠AC D =25°,求∠BAD 的度数.参考答案1.B 2.D 3.B4.70° 5.15° 6.1033 7.(-1,-2)8.解:∵∠ACD=25°,∴∠ABD=25°.∵AB 是⊙O 的直径,∴∠ADB=90°.在△AB D 中,∠BAD=180°-∠ABD-∠ADB=180°-25°-90°=65°.。
全国通用版2019中考数学总复习 第六单元 圆 第23课时 圆的有关性质随堂小测
圆的有关性质1.如图Y -53,已知AB 为⊙O 的直径,弦CD ⊥AB ,垂足为E ,那么下列结论中错误的是( )图Y -53A .CE =DE B.BC ︵=BD ︵C .∠BAC =∠BAD D .AC <AD2.★如图Y -54,已知AB 是⊙O 的直径,CD 是⊙O 的弦,∠ABD =58°,则∠BCD =( )图Y -54A .116°B .32°C .58°D .64°3.如图Y -55,四边形ABCD 是圆内接四边形,E 是BC 延长线上一点,若∠BAD =105°,则∠DCE 的大小是( )图Y -55A .115°B .105°C .100°D .95°.★如图Y -56,AB 为⊙O 的直径,弦CD ⊥AB 于点E ,已知CD =12,BE =2,则⊙O 的直径为______.图Y -565.如图Y -57,AC 是⊙O 的直径,点B 在⊙O 上,∠ACB =30°.(1)利用尺规作∠ABC的平分线B D,交AC于点E,交⊙O于点D,连接CD(保留作图痕迹,不写作法);(2)在(1)所作的图形中,求△ABE与△CDE的面积之比.图Y-57参考答案1.D [解析] 根据垂径定理,可得CE =DE .又因为CD ⊥AB ,所以AC =AD .故选D.2.B [解析] 由AB 是⊙O 的直径知∠ADB =90°.又因为∠ABD =58°,所以∠BAD =∠BCD =90°-58°=32°.故选B.3.B [解析] 因为四边形ABCD 是圆内接四边形,E 是BC 延长线上一点,所以∠DCE 是圆内接四边形ABCD 的外角,所以∠DCE =∠BAD =105°.4.20 [解析] 连接OC ,设OC 的长为r .∵CD =12,由垂径定理可得CE =6,△OEC 是直角三角形.∵BE =2,∴OE =r -2,由勾股定理可得OC 2=OE 2+CE 2,即r 2=(r -2)2+62,解得r =10,∴直径AB =20.5.[解析] (1)尺规作图:作一个角的平分线;(2)这两个三角形是相似的,相似三角形面积之比等于相似比的平方,所以只要求出边之比即可.以圆半径为中间媒介即可计算出两边之比.解:(1)如图所示.(2)连接OD ,设⊙O 半径为r .在△ABE 和△DCE 中,⎩⎪⎨⎪⎧∠BAE =∠CDE ,∠AEB =∠DEC , ∴△ABE ∽△DCE . ∵AC 是⊙O 的直经,∴∠ABC =90°.在Rt △ABC 中,∠ABC =90°,∠ACB =30°,∴AB =12AC =r . ∵BD 平分∠ABC ,∴∠ABD =∠ACD =45°,∴∠DOC =90°.在Rt △ODC 中,DC =OD 2+OC 2=2r ,∴S △ABE S △CDE =⎝ ⎛⎭⎪⎫AB DC 2=⎝ ⎛⎭⎪⎫r 2r 2=12.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2019年北京中考数学习题精选:方案设计题要题随堂演练
1.(2018·衢州中考)如图,点A,B,C在⊙O上,∠ACB=35°,则∠AOB的度
数是( )
A.75° B.70° C.65° D.35°
2.(2018·菏泽中考)如图,在⊙O中,OC⊥AB,∠ADC=32°,则∠OBA的度数
是( )
A.64° B.58° C.32° D.26°
3.如图,AB是⊙O的直径,弦CD⊥AB于点E,连接OC,若OC=5,CD=8,则
tan∠COE=( )
A.35 B.43 C.34 D.45
4.(2018·北京中考)如图,点A,B,C,D在⊙O上,CB︵=CD︵,∠CAD=30°,
∠ACD=50°,则∠ADB= .
5.(2018·无锡中考)如图,点A,B,C都在⊙O上,OC⊥OB,点A在劣弧BC︵上,
且OA=AB,则∠ABC= .
6.(2018·临沂中考)如图,在△ABC中,∠A=60°,BC=5 cm.能够将△ABC
完全覆盖的最小圆形纸片的直径是 cm.
7.(2018·烟台中考)如图,方格纸上每个小正方形的边长均为1个单位长度,
点O,A,B,C在格点(两条网格线的交点叫格点)上,以点O为原点建立直角坐
标系,则过A,B,C三点的圆的圆心坐标为 .
8.(2017·济南中考)如图,AB是⊙O的直径,∠ACD=25°,求∠BAD的度数.
参考答案
1.B 2.D 3.B 4.70° 5.15° 6.1033 7.(-1,-2)
8.解:∵∠ACD=25°,∴∠ABD=25°.
∵AB是⊙O的直径,∴∠ADB=90°.
在△ABD中,∠BAD=180°-∠ABD-∠ADB=180°-25°-90°=65°.
