圆锥展开
ug圆锥面展开方法

ug圆锥面展开方法嘿,朋友们!今天咱就来讲讲 ug 圆锥面展开方法。
你想想看啊,圆锥面就好像是一个超级有趣的神秘物体。
要把它展开,就像是解开一个奇妙的谜题。
首先呢,咱得先了解圆锥的特点。
它就像是一个尖尖的帽子,有个高高的顶和一个圆圆的底。
那要把它展开,其实就是要把这个“帽子”给拆开来,看看它到底是由哪些部分组成的。
在 ug 里操作的时候,就好像是在和这个圆锥面玩游戏。
我们要找到合适的工具和步骤,才能顺利地把它展开。
比如说,我们得先确定好圆锥的各种参数,这就像是给这个“帽子”量尺寸一样。
高度多少呀,底面半径多大呀,这些都得弄得清清楚楚。
然后呢,就开始动手操作啦!就像一个小魔法师一样,在软件里施展魔法,让圆锥面一点点地展开。
哎呀,这过程可有意思啦!看着那个圆锥面在屏幕上慢慢地变成一个平面图形,你不觉得很神奇吗?这就好比是把一个立体的东西变成了一张纸一样。
你能想象吗?就好像是把一个复杂的迷宫一下子给铺平了,所有的路都一目了然。
在展开的过程中,可得细心点哦,不能出一点差错。
要不然,就像是走迷宫走错了路一样,得重新再来。
而且呀,这可不是一次就能成功的,得反复尝试,不断调整。
就像你学骑自行车一样,一开始可能会摔倒,但多练几次,不就会了嘛!当你终于成功地把圆锥面展开的时候,那种成就感,哇,简直没法形容!就好像你攻克了一座很难爬的山峰一样。
所以呀,朋友们,不要害怕困难,大胆去尝试吧!ug 圆锥面展开方法其实并不难,只要你有耐心,有细心,就一定能掌握它!相信自己,你一定可以的!加油哦!。
圆锥的侧面展开图

快速抢答:
1
2
3
4
快速抢答:
1.底面半径为5cm, 母线长为16cm的圆 锥,它的侧面展开图 80π 的面积是_____cm²
返回 前进
快速抢答:
2.圆锥的底面周长为58cm, 母线长30cm,则圆锥的侧 A 面积为___cm² . A.870 B.908 C.1125 D.1740
返回 前进
快速抢答:
3.圆锥侧面展开图是 一个弧长为36π的扇 形,则这个圆锥的底面 18 半径是____
2πr =36π
返回 前进
快速抢答:
4.一个圆心角为90°,半径为8
cm的扇形纸片,恰好围成一个 圆锥的侧面, (接缝忽略不计), 则该圆锥底面圆的半径为( C)
A.4cm B.3cm C.2cm D.1cm
返回 前进
本节课我们有什么收获?
1.认识了圆锥的侧面展开图: 圆锥的底面周长就是它侧面展开图 扇形的弧长,圆锥的母线就是它侧 面展开图扇形的半径. 2.学会计算圆锥的侧面积和全面积.
作业:
如图,圆锥的底面半径为1,母线长 为3,一只蚂蚁要从底面圆周上一点 B出发,沿圆锥侧面爬行一周再回到 B,问它爬行的最短路线是多少?
1、圆锥是由一个底面(圆) 和一个侧面围成的,我们 把连接圆锥顶点和底面圆 周上任意一点的线段叫做 圆锥的母线。
母线 高
2、连接圆锥的顶点和 底面圆心的线段叫做圆 锥的高。
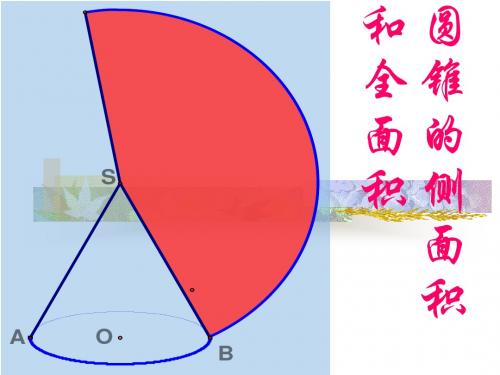
把圆锥沿一条母线剪开,它的侧面展开 图是怎样的图形呢?
12.exe
(1) 圆锥的侧面展开图是一个什么图形? 圆锥的侧面展开图是一个扇形. (2) 圆锥的底面周长与侧面展开图有什么关系? 圆锥的底面周长就是它侧面展开图扇形的弧长. (3) 圆锥的母线与侧面展开图有什么关系? 圆锥的母线就是它侧面展开图扇形的半径.
24.4.2圆锥的侧面展开图
P
h
l
2.圆锥的底面圆周长=侧面展 开后扇形的弧长,
A
O
r
B
3.圆锥的母线就是其侧面展开图扇形的半径。
圆锥侧面展开图
圆锥的侧面积和全面积
4.圆锥的侧面积就是弧长为圆锥底面的周长、 半径为圆锥的一条母线的长的扇形面积. 5.圆锥的全面积=圆锥的侧面积+底面积.
P
h A O r
a B
h a
r
P
例1. 圣诞节要到了,小明的妈妈想 做一顶圣诞老人的帽子,其帽身是 圆锥形(如图),若 (1)l = 20,r=12 A (2) h =12, r=5 (3)l = 10, h = 8 你能帮小明的妈妈算一算至少需多 少平方米的材料吗(不计接缝用料, 和余料,π取3.14,)?
A
B
C
例4. 如图,在直角三角形ABC 中,∠ABC=90°,∠A=30°,BC=2,将三角板作如 下运动
A
(1)若以AC为轴, (2)若以AB为轴, 把△ABC旋转一周 所得几何体的表面 积是多少?
C
┐
B
手工制作、已知一种圆锥模型的底 面半径为4cm ,高线长为3cm。你 能做出这个圆锥模型吗?
P
a h
A
O
r
B
小结
本节课我们有什么收获? 本节课我们认识了圆锥的侧面展开图, 学会计算圆锥的侧面积和全面积,在认识 圆锥的侧面积展开图时,应知道圆锥的底 面周长就是其侧面展开图扇形的弧长。圆 锥的母线就是其侧面展开图扇形的半径, 这样在计算侧面积和全面积时才能做到熟 练、准确。
l O .
r
B
例2.小明的妈妈做的圣诞老人的帽子满足以下条件,请你求出 帽子侧面展开图的圆心角 (r、h、l分别是圆锥的底பைடு நூலகம்半径、 高线、母线长)
圆锥的展开图课件定稿

这个公式是研究圆心角,母线,底面半径三者关系的, 非常的important,请做好笔记
n
R r
比一比,看谁反应快?
1、圆锥侧面展开图是一个半圆,其母线长为4,则该 圆锥底面半径为___________ 2 2、已知圆锥底面半径为10cm,母线长为40cm.则它 的侧面展开图的圆心角为__________ 90° 3、用圆心角为216°,半径为5的扇形,围成一个圆 4 锥,则该圆锥的高为__________
n R l 180 2
活动:抽查学生默写
圆锥知多少
圆锥相关概念
高
连结顶点与底面圆心的线段 叫做圆锥的高
h
R r
R h r
2 2
2
母线
圆锥底面圆周上的任意一点 与圆锥顶点的连线叫做圆锥的母线
动一动:
1.准备好的圆锥模型沿着母线剪开,观察圆锥的 侧面展开图.
R
图 23.3.6
问题: 1、沿着圆锥的母线,把一个圆锥的侧面展开,得 到一个扇形,这个扇形的弧长与底面的周长有什么 关系?
l h R r
S全=S侧+S底
rR
母线
底面圆半径
2 1 2 r R 2
lR
rR r
2
小试牛刀
(1)已知圆锥的底面直径为4,母线长为6,则它 12π 的侧面积为_________. (2)已知圆锥底面圆的半径为2 cm ,高为
6πcm2 5cm ,则这个圆锥的侧面积为_________;全面
图 23.3.7
有关圆锥展开图计算的两个重要公式

有关圆锥展开图计算的两个重要公式⼤家在解决有关圆锥侧⾯展开图的计算问题时,通常利⽤了两个等量关系,第⼀个是=×底⾯圆周长(或侧⾯的弧长)×母线长,第⼆个就是侧⾯的弧长等于底⾯的周长,但每次都直接利⽤这两个等量关系来计算还是很⿇烦,特别是同学们往往容易忘记乘以系数,基于此我们不妨把这两个等量关系进⼀步推导,得出实质性的乘积、⽐例公式。
我相信同学们在理解并运⽤这两个公式后,解题的思路可以变得清晰,速度和准确度也可以得到很⼤的提⾼。
⼀、推导公式:1.乘积式:侧⾯积:全⾯积:2.⽐例式:弧长等于⊙O1的周长∵∴⼜∵即:这两组公式的优点是避开了求底⾯圆周长,⽽直接建⽴了S侧与R、r的乘积关系,以及圆⼼⾓n与R、r的⽐例关系,减少了许多中间过程,特别是⽐例式给我们的计算带来了极⼤的便利。
⼆、运⽤乘积式:类型⼀:顺向使⽤公式【问题】(2009济南)在综合实践活动课上,⼩明同学⽤纸板制作了⼀个圆锥形漏⽃模型.如图所⽰,它的底⾯半径⾼则这个圆锥漏⽃的侧⾯积是()A. B. C. D.分析:从刚才推导出的可以看出,只与圆锥的母线长度以及底⾯圆半径有关,若题⽬没有直接给出母线长度以及底⾯圆半径,往往还可以利⽤R、r和h组成的直⾓三⾓形,求出未知的R 或r来,从⽽计算出侧⾯积。
结论:要求,就求R、r。
解答:此题由底⾯半径⾼可以求出母线BC为10cm,即R=10cm,r=6cm,再由,选C。
【练习】1. (2009铁岭)⼩丽想⽤⼀张半径为5cm的扇形纸⽚围成⼀个底⾯半径为4cm的圆锥,接缝忽略不计,则扇形纸⽚的⾯积是cm2.(结果⽤表⽰)202.(2009南昌)⼀个圆锥的底⾯直径是80cm,母线长是90cm,则它的侧⾯积是____ 。
3600cm23. (2008成都)⼩红同学要⽤纸板制作⼀个⾼4cm,底⾯周长是6πcm的圆锥形漏⽃模型,若不计接缝和损耗,则她所需纸板的⾯积是()BA.12πcm2 B.15πcm2 C.18πcm2 D.24πcm2类型⼆:逆向使⽤公式【问题】(2009义乌)如图,圆锥的侧⾯积为,底⾯半径为3,则圆锥的⾼AO为 .分析:从刚才推导出的可以看出,已知、R、r中任意两个量可以求出余下未知的量,若题⽬要求求出圆锥的⾼h,往往还可以利⽤R、r和h组成的直⾓三⾓形,从⽽求出。
圆锥的侧面展开图

例3. 已知圆锥底面半径为10cm,母线长为40cm.
(1)求它的侧面展开图的圆心角和全面积. (2)若一甲虫从圆锥底面圆上一点 A 出发,沿着 圆锥侧面绕行到母线 SA的中点 B,它所走的最短 路程是多少?
解:(1) r 10cm l 2r 20cm na 180l 180 20 0 B l S180 , a 40cm n a 40 90 1 2 S全=S侧+S底 20 40 10 500 2
一试 身手
如图,圆锥的底面半径为1,母线长为3,一只蚂蚁要从底面 圆周上一点B出发,沿圆锥侧面爬到过母线AB的轴截面上 另一母线AC上,问它爬行的最短路线是多少? A
解: 将圆锥沿AB展开成扇形ABB , 则点C
垂足为 D . , 解: 将圆锥沿AB展开成扇形ABB 则点 C是BB 的中点 ,解 过点 B 作 BD AC , : 将圆锥沿 AB 解 将圆锥沿 AB 展开成扇形 AB B 则点 , 解 : :将圆锥沿 AB 展开成扇形 AB B 则点 rD.BD AC,垂足为D. 垂足为 . 展开成扇形AB B ,D 则点 C是B B 的中点 , 过点 B 作 垂足为 垂足为 D . 360 BA B 120 C是BB 的中点, , 则点 解: 将圆锥沿AB 展开成扇形 AB B 解 : 将圆锥沿 AB 展开成扇形 ABB , 则点 l r r r r AB展开成扇形 解 : 将圆锥沿 AB B ,360 则点 BAB 360 垂足为 120 D. BA B , BA B 360 120 BA B 360 120 BAD 60 . 在 Rt ABC 中 , BAD 60 垂足为 D . l l ll 垂足为D. r 3 r 120 B BAD 60.在 BA ABC 中 BAD 60 , AB 3 ..在 CRt B , 360 120 BAD 60 .在 BAD 60 ABC 中 BAD BAD 60 . 在 ABC 中 ,, BAD 66 BD 3 BA B 360 Rt Rt 120 r l 2 l3 360 120 BAB 3 3 3. 3 BD 3 RtABC中, BAD 60, AB 3. 60. l BAD 在 Rt ABC 中 , BAD 60 , AB BD 3 60 BD 3 BD 3 3 BAD 60.在RtABC中, BAD 2 答: 它爬行的最短路线是 3 . 2 22 BAD 60.在RtABC 中, BAD 6 3 2 3 3 BD 3. BD 33 答: 它爬行的最短路线是 3 3 3 答 : 它爬行的最 答 : 它爬行的最短路线是 3. 2 答 : 它爬行的最短路线是 3. 2 2 3 BD 22 23 3 3 答: 它爬行的最短路线是 3. 短路线是 3. 答: 它爬行的最短路线是 3 3. 2 2 2 3. 答: 它爬行的最短路线是 2
圆锥的侧面展开图
圆锥的侧面展开图圆锥的侧面展开图圆锥是一种立体图形,由一个圆形底面和一个顶点连接的直线组成。
在几何学中,我们经常使用侧面展开图来描述立体图形的形状和结构。
侧面展开图是将立体图形展开,使我们能够更好地理解其构造和组成。
首先,我们来看一下圆锥的基本特征。
圆锥的底面是一个圆形,用于提供稳定的支撑面。
圆锥的侧面是由从顶点连接到底面边缘的直线组成,这些直线被称为母线。
圆锥的顶点是连接底面和侧面的中心点。
为了绘制圆锥的侧面展开图,我们需要将圆锥展开成一个平面图形。
这可以通过将侧面按照一定顺序剪开,并展开到一个平面上来实现。
在展开的过程中,我们需要保持底面的圆形形状不变,并确保侧面的母线与底面保持相对位置不变。
展开后的侧面图是由一系列直线段构成的。
这些直线段代表了圆锥的侧面母线。
从顶点开始,我们可以看到侧面的直线段逐渐向底面延伸,并最终连接到底面边缘上。
展开后的侧面图呈现出一种锥形的形状,底面呈圆形,顶点在图形的中心位置。
圆锥的侧面展开图能够帮助我们更好地理解圆锥的结构和构造。
通过展开图,我们可以清晰地看到圆锥的母线如何连接到底面,并形成一个锥形的形状。
展开图还可以帮助我们计算圆锥的表面积和体积,以及分析其特性和功能。
在实际应用中,圆锥的侧面展开图被广泛应用于制作纸模、设计建筑物、制作工艺品等领域。
通过将圆锥展开成一个平面图形,我们可以更方便地制作和操作这些物品,并确保其形状和结构的准确性。
总结一下,圆锥的侧面展开图是将圆锥展开成一个平面图形以展示其构造和形状的方法。
通过展开图,我们可以更好地理解圆锥的特征和结构,并在应用中应用展开图进行设计和制作。
展开图提供了一种直观和清晰的方式来描述圆锥的形状和组成,对于学习和应用圆锥的几何学非常有帮助。
7.4 圆锥的侧面展开图(新)
图中 R 是圆锥的母线 h 就是圆锥的高 r 是底面圆的半径
R h
r
合作探究:
圆锥的底面半径、高线、 母线长三者之间有什么 关系?
R h
r
把圆锥模型沿着母线剪开, 观察圆锥的侧面展开图.
图 23.3.7
A
BO
C
1.圆锥的侧面展开图是扇形 2.侧面展开图扇形的半径=母线的长 3.侧面展开图扇形的弧长=底面周长
7.4 圆锥的侧面展开图
第1ห้องสมุดไป่ตู้时
学习目标
1.了解圆锥的侧面展开图是扇形; 2.能利扇形的面积公式计算圆锥的侧面积及
表面积.
新课导入
圆的周长公式 圆的面积公式 弧长的计算公式
扇形面积计算公式
C=2πr
S=πr2
l
=
npR 180
S= npR2 或S = 1 lR
360
2
圆锥的侧面积与底面积的和叫做圆锥的全面积(或表面积).
S侧 =prl S全 = S侧+S 底 = prl + p r2
(r表示圆锥底面的半径, l表示圆锥的母线长 )
知识讲解
1.圆锥是由一个底面和一个侧面围成的,它的
底面是一个圆,侧面是一个曲面. 2.把圆锥底面圆周上的任意一点与圆锥顶点 的连线叫做圆锥的母线
问题:圆锥的母线有几条? 3.连接顶点与底面圆心的线段
圆锥的侧面积和全(表)面积
圆锥的底面周长就是其侧面展开图扇形的弧长, 圆锥的母线就是其侧面展开图扇形的半径.
S侧=S扇形
s侧
=
npR 2 360
n
即:360r= nR
R
S全=S侧+S底
例题讲解
圆锥的总结知识点
圆锥的总结知识点一、圆锥的定义及基本性质1. 圆锥的定义圆锥是由一个圆和一个点外侧全在同一平面内的直线段组成的几何体。
这个点称为圆锥的顶点,圆锥的底面为圆,顶点与底面圆上各点的连线称为母线,圆锥的高为顶点到底面的距离。
根据底面圆的尺寸,我们可以将圆锥分为很多种类,如直角圆锥、斜面圆锥等。
2. 圆锥的基本性质圆锥的底面积通常表示为S,高表示为h,底面周长表示为C。
其侧面积可表示为A,侧面积的计算方法为A=πrl,其中r为圆锥底面的半径,l为母线长。
圆锥的体积表示为V,计算方法为V=⅓Sh。
二、圆锥的展开与扇形面积1. 圆锥的展开圆锥的展开是指将圆锥侧面展开成一个扇形。
展开之后,我们可以计算得到这个扇形的面积,并进一步求解圆锥的表面积。
2. 扇形面积扇形是圆锥展开后的侧面形状。
扇形的面积计算方法为S=1/2r²θ,其中r为扇形的半径,θ为扇形的圆心角。
我们可以利用这个公式计算得到圆锥的表面积。
三、圆锥的立体几何计算1. 圆锥的表面积计算圆锥的表面积为底面圆的面积加上侧面积。
表面积的计算方法为A=πr²+πrl,其中r为底面圆的半径,l为母线长。
根据表面积的计算公式,我们可以计算得到不同种类圆锥的表面积。
2. 圆锥的体积计算圆锥的体积计算方法为V=1/3Sh,其中S为底面圆的面积,h为圆锥的高。
利用这个公式,我们可以计算得到不同种类圆锥的体积。
四、圆锥的应用1. 圆锥在建筑工程中的应用在建筑工程中,圆锥常常用来设计建筑物的锥形结构。
比如塔楼、尖塔等都是圆锥结构。
利用圆锥的计算公式,我们可以计算得到这些圆锥结构的表面积和体积,从而进行结构设计。
2. 圆锥在日常生活中的应用在日常生活中,圆锥也有很多应用,比如冰淇淋蛋筒、圆锥形帽子等都是圆锥的应用。
利用圆锥的面积和体积计算公式,我们可以计算得到这些物体的表面积和体积,从而进行制造和设计。
以上就是对圆锥的相关知识的总结,通过对圆锥的定义、基本性质、展开与扇形面积、立体几何计算以及应用等方面的总结,我们对圆锥有了更深入的了解。
圆锥的侧面展开图讲
S侧=S扇形
l弧
h l母 r
S全=S侧+S底
rl母 r
2
1 1 l l母 2 rl母 rl母 2 2
练习:填空 (1)已知圆锥的底面直径为4,母线长为6, 12π 则它的侧面积为_________. (2)已知圆锥底面圆的半径为2cm , 高为
r
r
4.若圆锥的母线l=10cm,高h=8cm,则其侧面展 开图中扇形的圆心角是 216 度。 ——
5.如图,若圆锥的侧面展开图是 半圆,那么这个展开图的圆心角 180 是___度;圆锥底半径 r与母线 l 1:2 的比r :l = ___ ;这个圆锥轴截 面的顶角是___度。 60
一试 身手
课堂小结:
圆锥的底面周长就是其侧面展开图扇形的弧长, 圆锥的母线就是其侧面展开图扇形的半径。
S侧=S扇形
L弧
h l母 r
S全=S侧+S底
rl母 r
2
1 1 l l母 2 rl母 rl母 2 2
结束寄语
•数学使人聪明,数学使人 陶醉,数学的美陶冶着你 ,我,他.
你会计算展开图中 的圆心角的度数吗?
l h l母 n r
Ql
n l母 180
180l 180 2 r r n 360 l母 l母 l母
1.圆锥的侧面积是底面积的2倍,这个圆锥的侧面
展开图扇形的圆心角是 180o 。 ____
2 .一个扇形,半径为30cm,圆心角为120度,用 它做成一个圆锥的侧面,那么这个圆锥的底面 半径为_____ 。 10cm
∴ △ABB’是等边三角形 ∴ BB’=AB=6
