2012年呼和浩特市中考数学试题及答案
内蒙古通辽市2012年中考数学真题试题(带解析)
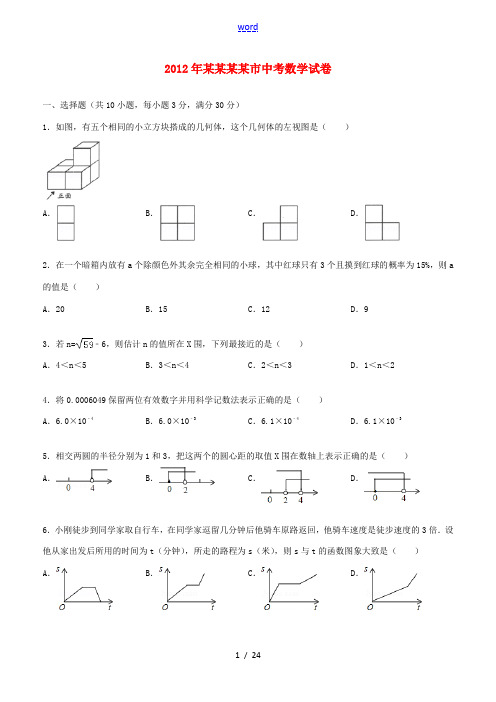
2012年某某某某市中考数学试卷一、选择题(共10小题,每小题3分,满分30分)1.如图,有五个相同的小立方块搭成的几何体,这个几何体的左视图是()A.B.C.D.2.在一个暗箱内放有a个除颜色外其余完全相同的小球,其中红球只有3个且摸到红球的概率为15%,则a 的值是()A.20 B.15 C.12 D.93.若n=﹣6,则估计n的值所在X围,下列最接近的是()A.4<n<5 B.3<n<4 C.2<n<3 D.1<n<24.将0.0006049保留两位有效数字并用科学记数法表示正确的是()A.6.0×10﹣4B.6.0×10﹣3C.6.1×10﹣4D .6.1×10﹣35.相交两圆的半径分别为1和3,把这两个的圆心距的取值X 围在数轴上表示正确的是()A.B.C.D.6.小刚徒步到同学家取自行车,在同学家逗留几分钟后他骑车原路返回,他骑车速度是徒步速度的3倍.设他从家出发后所用的时间为t(分钟),所走的路程为s(米),则s与t的函数图象大致是()A.B.C.D.7.美是一种感觉,当人体的下半身长与身高的比值越接近0.618时越给人一种美感.已知某女士身高160cm,下半身长与身高的比值是0.60,为尽可能达到好的效果,她应穿的高跟鞋的高度约为()A.6cm B.10cm C.4cm D.8cm8.4点10分,时针与分针所夹的小于平角的角为()A.55°B.65°C.70°D.以上结论都不对9.如图,过x轴正半轴上的任意一点P,作y轴的平行线,分别与反比例函数y=﹣和y=的图象交于A、B 两点.若点C是y轴上任意一点,连接AC、BC,则△ABC的面积为()A.3B.4C.5D.1010.为安置100名中考女生入住,需要同时租用6人间和4人间两种客房,若每个房间都住满,则租房方案共有()A.8种B.9种C.16种D.17种二、填空题(共7小题,每小题3分,满分21分)11.5的倒数是_________ ,|1﹣|= _________ ,﹣= _________ .12.2,3,4,5,6这五个数的平均数是4,则这组数据的方差是_________ .13.如图,梯形ABCD中,AD∥BC,DC⊥BC,将梯形沿对角线BD折叠,点A恰好落在DC边上的点A′处,若∠A′BC=15°,则∠A′BD的度数为_________ .14.一个扇形的弧长是20πcm,面积是240πcm2.则这个扇形的半径是_________ .15.已知方程x2﹣2x﹣1=0的两根分别是x1、x2,则= _________ .16.如图,△ABC的三边AB、BC、CA长分别为40、50、60.其三条角平分线交于点O,则S△ABO:S△BCO:S△CAO= _________ .17.观察下列等式:1×2=×(1×2×3﹣0×1×2)2×3=×(2×3×4﹣1×2×3)3×4=×(3×4×5﹣2×3×4)…计算:3×[1×2+2×3+3×4+…+n(n+1)]= _________ .三、解答题(共9小题,满分69分)18.先化简,再求值.()÷(其中x=)19.如图,小艳家(点A)在学校(点C)北偏东60°方向,AC=600(m).小颖家(点B)在小艳家正南,学校在小颖家北偏西45°方向.求:小颖家与小艳家的距离.(结果保留根号)20.洋洋九年级上学期的数学成绩如下表所示:测验类别平时期中考试期末考试测验1 测验2 测验3 测验4成绩106 102 115 109 112 110(1)计算洋洋该学期的数学平时平均成绩;(2)如果学期的总评成绩是根据如图所示的权重计算,请计算出洋洋该学期的数学总评成绩.21.某校学生乘车到距学校60千米的景区游玩,一部分学生乘慢车,另一部分学生乘快车,他们同时出发,结果乘慢车的同学晚到20分钟.已知快车速度是慢车速度的1.5倍,求慢车的速度.22.如图,AB是⊙O的直径,BC⊥AB于点B,连接OC交⊙O于点E,=.求证:(1)AD∥OC;(2)CD是⊙O的切线.23.如图,四边形ABCD与四边形ACED都是平行四边形,R是DE的中点,BR交AC、CD于点P、Q.若AD=,AB=AC=2.求:BP、PQ的长.24.甲口袋里装有2个相同的小球,它们分别写有数字1和2;乙口袋里装有3个相同的小球,它们分别写有数字3,4,5;丙口袋里有2个相同的小球,它们分别写有数字6,7.从三个口袋中各随机地取出1个小球,按要求解答下列问题:(1)画出“树形图”;(2)取出的3个小球上只有1个偶数数字的概率是多少?(3)取出的3个小球上全是奇数数字的概率是多少?25.已知直线y=2x+4与x轴交于点A,与y轴交于点B,点P在坐标轴上,且PO=240.求△ABP的面积.26.如图,在平面直角坐标系中,将一个正方形ABCD放在第一象限斜靠在两坐标轴上,且点A(0,2)、点B(1,0),抛物线y=ax2﹣ax﹣2经过点C.(1)求点C的坐标;(2)求抛物线的解析式;(3)在抛物线上是否存在点P与点Q(点C、D除外)使四边形ABPQ为正方形?若存在求出点P、Q两点坐标,若不存在说明理由.2012年某某某某市中考数学试卷参考答案与试题解析一、选择题(共10小题,每小题3分,满分30分)1.如图,有五个相同的小立方块搭成的几何体,这个几何体的左视图是()A.B.C.D.考点:简单组合体的三视图。
呼和浩特市中考数学试题及答案(通用)

呼和浩特市中考数学试题及答案(通用)一、选择题(每题4分,共40分)1. 下列选项中,既是有理数又是无理数的是()A. 0.333…B. √2C. 3.14D. -5答案:B2. 下列函数中,奇函数是()A. y = x²B. y = x³C. y = |x|D. y = 2x答案:B3. 若平行四边形ABCD的对角线交于点E,且AE=4,BE=6,则CE的长度是()A. 2B. 3C. 4D. 5答案:D4. 已知函数f(x) = (x-1)/(x+2),下列说法正确的是()A. 函数f(x)在x=-2处有定义B. 函数f(x)在x=1处有定义C. 函数f(x)在x=2处有定义D. 函数f(x)在x=0处有定义答案:D5. 下列选项中,是二次函数的是()A. y = 2x² + 3x + 1B. y = x² + 3/xC. y = 2x + 3D. y = √x答案:A6. 下列选项中,是等差数列的是()A. 1, 3, 5, 7, 9B. 2, 4, 8, 16, 32C. 1, 4, 9, 16, 25D. 1, 1/2, 1/4, 1/8, 1/16答案:A7. 下列选项中,是等比数列的是()A. 1, 3, 5, 7, 9B. 2, 4, 8, 16, 32C. 1, 4, 9, 16, 25D. 1, 1/2, 1/4, 1/8, 1/16答案:B8. 若两个平行线的斜率分别为k1和k2,则下列说法正确的是()A. k1 + k2 = 0B. k1 k2 = 1C. k1 = k2D. k1 k2 = 0答案:D9. 下列选项中,是锐角三角形的是()A. 30°, 60°, 90°B. 45°, 45°, 90°C. 60°, 70°, 50°D. 90°, 45°, 45°答案:C10. 下列选项中,是直角三角形的是()A. 30°, 60°, 90°B. 45°, 45°, 90°C. 60°, 70°, 50°D. 90°, 45°, 45°答案:A二、填空题(每题4分,共40分)11. 若a+b=5,a-b=3,求ab的值。
2012年内蒙古普通高中会考数学考试真题

2012年内蒙古普通高中会考数学考试真题第Ⅰ卷(选择题,计60分)一、选择题(本大题共12小题,每小题5分,共计60分。
在每小题所给出的四个选项中,只有一项是符合题目要求的)1、若是函数的导数,则的值是( ). ()x f '()13+-=x x x f ()()11f f 'A . B. C. D.01232、直线:3x-4y-9=0与圆:,(θ为参数)的位置关系是( ) ⎩⎨⎧==θθsin 2cos 2y x A.相切 B.相离 C.直线过圆心 D.相交但直线不过圆心3、若实数,满足,则的值是( )y x ,2)1()1(=-++y i x i xy A. 1 B. 2 C.-2 D.-34、若函数,且,则( ). ()x x f =()()41000lim =∆-∆+→∆x x f x x f x =0x A . B. C. D.12345、若动点(x ,y )在曲线(b >0)上变化,则x 2+2y 的最大值为 14222=+by x A 、; B 、; C 、 D 、2b 。
⎪⎩⎪⎨⎧≥<<+)4(2)40(442b b b b ⎪⎩⎪⎨⎧≥<<+)2(2)20(442b bb b 442+b6、已知动圆:,则),,(0sin 2cos 222是参数是正常数θθθb ,a b a by ax y x ≠=--+圆心的轨迹是( ) A 、直线 B 、圆 C 、抛物线的一部分 D 、椭圆7、曲线2x y x =-在点(1,1)-处的切线方程为( ). A . B. C. D.23+-=x y 12+-=x y 32-=x y 2-=x y 8、设函数2()()f x g x x =+,曲线()y g x =在点(1,(1))g 处的切线方程为21y x =+,则曲线()y f x =在点(1,(1))f 处切线的斜率为 ( ). A .2 B .12- C .4 D .14- 9、在复平面内,复数对应的点位于( )2(1)1i i ++A 、第一象限 B 、第二象限 C 、第三象限 D 、第四象限10、下列参数方程(t 为参数)中与普通方程x 2-y=0表示同一曲线的是11、已知过曲线上一点P ,原点为O ,直线PO 的倾斜角()⎩⎨⎧≤≤==πθθθθ0sin 4cos 3,y x 为参数为,则P 点坐标是 4πA 、(3,4) B 、 C 、(-3,-4) D 、 ⎪⎪⎭⎫ ⎝⎛22223,⎪⎭⎫ ⎝⎛512512,12、已知可导函数f(x)(x ∈R)的导函数f’(x),满足x·f’(x) >f(x),则当a >1时,f(a)和af(x)的大小关系为( )A 、f(a) ≤af(1) Bf(a) <af(1) C 、f(a) ≥af(1) D 、f(a) >af(1)第Ⅱ卷(非选择题,计90分)二、填空题(本大题共4小题,每小题5分,共计20分。
2024年内蒙古呼和浩特市中考数学真题(含答案)

2024年内蒙古呼和浩特市中考数学试题一、选择题(本大题共10小题,每小题3分,共30分.在每小题给出的四个选项中,只有一项是符合题目要求的)1.﹣2024的相反数是( )A.2024B.﹣2024C.D.2.如图,直线l1和l2被直线l3和l4所截,∠1=∠2=130°,∠3=75°,则∠4的度数为( )A.75°B.105°C.115°D.130°3.下列运算正确的是( )A.(3x)3=9x3B.(x﹣2)2=x2﹣4C.(﹣2ab2)2=4a2b4D.3a+4b=7ab4.如图所示的几何体,其主视图是( )A.B.C.D.5.我国南宋数学家杨辉在《田亩比类乘除算法》中记录了这样一个问题:“直田积八百六十四步,只云阔与长共六十步,问阔及长各几步?”其大意是:矩形面积是864平方步,其中宽与长的和为60步,问宽和长各几步?若设长为x步,则下列符合题意的方程是( )A.x•864B.x(60+x)=864C.x(60﹣x)=864D.x(30﹣x)=8646.为了解某小区居民的家庭月平均用水量的情况,物业公司从该小区1500户家庭中随机抽取150户家庭进行调查,统计了他们的月平均用水量,将收集的数据整理成如下的统计图表:月平均用水量x (吨)频数5≤x <7157≤x <9a 9≤x <113211≤x <134013≤x <1533总计150根据统计图表得出以下四个结论,其中正确的是( )A .本次调查的样本容量是1500B .这150户家庭中月平均用水量为7≤x <9的家庭所占比例是30%C .在扇形统计图中,月平均用水量为11≤x <13的家庭所对应圆心角的度数是95°D .若以各组组中值(各小组的两个端点的数的平均数)代表各组的实际数据,则这150户家庭月平均用水量的众数是127.如图,正四边形ABCD 和正五边形CEFGH 内接于⊙O ,AD 和EF 相交于点M ,则∠AMF 的度数为( )A .26°B .27°C .28°D .30°8.在同一平面直角坐标系中,函数y =ax ﹣b (a ≠0)和y (c ≠0)的图象大致如图所示,则函数y =ax 2+bx +c (a ≠0)的图象大致为( )A .B .C .D .9.如图,在△ABD 中,∠ABD =30°,∠A =105°,将△ABD 沿BD 翻折180°得到△CBD ,将线段DC 绕点D 顺时针旋转30°得到线段DF ,点E 为AB 的中点,连接EF ,ED .若EF =1,则△BED 的面积是( )A .B .C .D .10.下列说法中,正确的个数有( )①二次函数y =ax 2+bx +c (a >0)的图象经过(2,1),(﹣4,1)两点,m ,n 是关于x 的一元二次方程ax 2+bx +c ﹣k =0(0<k ≤1)的两个实数根,且m <n ,则﹣4<m <n <2恒成立.②在半径为r 的⊙O 中,弦AB ,CD 互相垂直于点P ,当OP =m 时,则AB 2+CD 2=8r 2﹣4m 2.③△ABC 为平面直角坐标系中的等腰直角三角形且∠ABC =90°,点A 的坐标为(1,0),点B的坐标为(0,5),点C是反比例函数y(k≠0)的图象上一点,则k=±30.④已知矩形的一组邻边长是关于x的一元二次方程x2﹣2(a+1)x+a2﹣1=0的两个实数根,且矩形的周长值与面积值相等,则矩形的对角线长是4.A.1个B.2个C.3个D.4个二、填空题(本大题共6小题,每题3分,共18分。
2012年内蒙古包头市中考真题及答案

2012年包头市高中招生考试试题卷数 学注意事项:1. 本试题卷满分为120分.考试时间为120分钟.2.答题前,考生务必先将自己的座位号、准考证号、姓名填写在试题卷和答题卡的指定位置.请认真核对条形码上的相关信息后,将条形码粘贴在答题卡的指定位置上.3.答选择题时,必须使用2B 铅笔将答题卡上对应题目的答案标号涂黑,修改时用橡皮擦干净,再选涂其他答案.4.答非选择题时,必须使用0.5毫米的黑色字迹签字笔书写,作图题可先用铅笔绘出,确认后再用0.5毫米的黑色字迹签字笔描清楚.要求字体工整,笔迹清晰.严格按题号所示的答题区域作答,超出答题区域书写的答案无效;在试题卷、草稿纸上答题无效.5.保持答题卡清洁、完整.严禁折叠、破损,严禁在答题卡上做任何标记,严禁使用涂改液、胶带纸、修正带.考试结束后,将本试题卷和答题卡一并交回.一、选择题:本大题共有12小题,每小题3分,共36分.每小题只有一个正确选项,请将答题卡上对应题目的答案标号涂黑. 1.9的算术平方根是( )(A )3± (B )3 (C )3- (D 2.联合国人口基金会的报告显示,世界人口总数在2011年10月31日达到70亿.将70亿用科学记数法表示为( )(A )9710⨯ (B )8710⨯ (C )87010⨯ (D )100.710⨯ 3.下列运算中,正确的是( )(A )32x x x -= (B )623x x x ÷=(C = (D =4.在Rt ABC △中,90C ∠=°,若2AB AC =,则sin A 的值是( )(A (B )12 (C (D 5.下列调查中,调查方式选择正确的是( )(A )为了了解1000个灯炮的使用寿命,选择全面调查 (B )为了了解某公园全年的游客流量,选择抽样调查 (C )为了了解生产的一批炮弹的杀伤半径,选择全面调查 (D )为了了解一批袋装食品是否含有防腐剂,选择全面调查6.如图,过ABCD Y 的对角线BD 上一点M 分别作平行四边形两边的平行线EF 与GH ,那么图中的AEMG Y 的面积1S 与HCFM Y 的面积2S 的大小关系是( )(A )12S S > (B )12S S < (C )12S S = (D )122S S =7.不等式组513(1)131722x x x x ->+⎧⎪⎨--⎪⎩,≤.的解集是( )(A )2x > (B )4x ≤(C )2x <或4x ≥ (D )24x <≤8.圆锥的底面直径是80cm ,母线长90cm ,则它的侧面展形图的圆心角是( ) (A )320° (B )40° (C )160° (D )80°9.随机掷一枚质地均匀的正方体骰子,骰子的六个面上分别刻有1到6的点数.掷两次骰子,掷得面朝上的点数之和是5的概率是( ) (A )16 (B )19 (C )118 (D )21510.已知下列命题: ①若0a ≤,则a a =-; ②若22ma na >,则m n >;③两组对角分别相等的四边形是平行四边形; ④垂直于弦的直径平分弦.其中原命题与逆命题均为真命题的个数是( )(A )1个 (B )2个 (C )3个 (D )4个 11.矩形ABCD 中,点O 是BC 中点,90AOD ∠=°,矩形ABCD 的周长为20cm ,则AB 的长为( )(A )1cm (B )2cm (C )5cm 2 (D )10cm 312.关于x 的一元二次方程25(5)0x mx m -+-=的两个正实数根分别为1x 、2x ,且1227x x +=,则m 的值是( )(A )2 (B )6 (C )2或6 (D )7二、填空题:本大题共有8小题,每小题3分,共24分.请把答案填在答题卡上对应的横线上. 1301)=____________. 14.化简:222142442a a a a a a a a ---⎛⎫-÷⎪++++⎝⎭=____________. 15.某校六个绿化小组一天植树的棵数如下:10,11,12,13,8,x .若这组数据的平均数是11,则这组数据的众数是____________.16.关于x 的两个方程220x x --=与121x x a=++有一个解相同,则a =____________.17.如图,ABC △内接于O ⊙,60BAC ∠=°,O ⊙的半径为2,则BC 的长为____________(保留根号). 18.如图,在平面直角坐标系中,点A 在x 轴上,ABO △三角形,90ABO ∠=°,点B 的坐标为(12)-,,将ABO △O 顺时针旋转90°得到11A B O △,则过1A 、B =____________.19.如图,直线122y x =-与x 轴、y 轴分别交于点A 和点B ,点C 在直线AB 上,且点C 的纵坐标为1-,点D 在反比例函数k y x =的图象上,CD 平行于y 轴,52OCD S =△,则k 的值为____________.20.如图,将ABC △纸片的一角沿DE 向下翻折,使点A 落在BC 边上的A '点处,且DE BC ∥,下列结论:①AED C ∠=∠;②A D A EDB EC''=; ③2BC DE =;④DBA EA C ADA E S S S '''=+△△四边形. 其中正确结论的个数是____________个.三、解答题:本大题共有6小题,共60分.请将必要的文字说明、计算过程或推理过程写在答题卡的对应位置. 21.(本小题满分8分)某年级组织学生参加夏令营活动,本次夏令营活动分为甲、乙、丙三组进行,下面条形统计图和扇形统计图反映了学生参加夏令营活动的报名情况,请你根据图中的信息回答下列问题:(1)该年级报名参加本次活动的总人数为_______人,报名参加乙组的人数为_______人; (2)补全条形统计图中乙组的空缺部分;(3)根据实际情况,需从甲组抽调部分学生到丙组,使丙组人数是甲组人数的3倍,应从甲组抽调多少名学生到丙组?如图,拦水坝的横断面为梯形ABCD ,坝顶宽5AD =米,斜坡AB 的坡度13i =:(指坡面的铅直高度AE 与水平宽度BE 的比),斜坡DC 的坡度11.5i =:,已知该拦水坝的高为6米.(1)求斜坡AB 的长;(2)求拦水坝的横断面梯形ABCD 的周长. (注意:本题中的计算过程和结果均保留根号)23.(本小题满分10分)某商场用36000元购进甲、乙两种商品,销售完后共获利6000元.其中甲种商品每件进价120元,售价138元;乙种商品每件进价100元,售价120元. (1)该商场购进甲、乙两种商品各多少件?(2)商场第二次以原进价购进甲、乙两种商品,购进乙种商品的件数不变,而购进甲种商品的件数是第一次的2倍,甲种商品按原售价出售,而乙种商品打折销售.若两种商品销售完毕,要使第二次经营活动获利不少于8160元,乙种商品最低售价为每件多少元?24.(本小题满分10分)如图,已知AB 为O ⊙的直径,过O ⊙上的点C 的切线交AB 的延长线于点E ,AD EC ⊥于点D 且交O ⊙于点F ,连接BC CF AC ,,. (1)求证:BC CF =;(2)若6AD =,8DE =,求BE 的长; (3)求证:2AF DF AB +=.如图,在Rt ABC △中,90C ∠=︒,AC =4cm ,BC =5cm ,点D 在BC 上,且CD =3cm ,现有两个动点P Q 、分别从点A 和点B 同时出发,其中点P 以1厘米/秒的速度沿AC 向终点C 运动;点Q 以 1.25厘米/秒的速度沿BC 向终点C 运动.过点P 作PE BC ∥交AD 于点E ,连接EQ .设动点运动时间为t 秒(0t >).(1)连接DP ,经过1秒后,四边形EQDP 能够成为平行四边形吗?请说明理由; (2)连接PQ ,在运动过程中,不论t 取何值时,总有线段PQ 与线段AB 平行.为什么? (3)当t 为何值时,EDQ △为直角三角形.26.(本小题满分12分)已知直线24y x =+与x 轴、y 轴分别交于A D 、两点,抛物线212y x bx c =-++经过点A D 、,点B 是抛物线与x 轴的另一个交点. (1)求这条抛物线的解析式及点B 的坐标;(2)设点M 是直线AD 上一点,且13AOM OMD S S =△△::,求点M 的坐标;(3)如果点(2)C y ,在这条抛物线上,在y 轴的正半轴上是否存在点P ,使BCP △为等腰三角形,若存在,请求出点P 的坐标;若不存在,请说明理由.2012年包头市高中招生考试 数学参考答案及评分标准二、填空题:共8小题,每小题3分,共24分.13.14.1(2)a a +或212a a+15.12 16.417.18.35y x =+19.3 20.4三、解答题:共6小题,共60分.21.(8分) 解:(1)60,12;(每空2分) (2)正确补全条形统计图; ························· (6分) (3)设应从甲组抽调x 名学生到丙组,可得方程:303(18)x x +=-,解得6x =,答:应从甲组抽调6名学生到丙组. ········································································· (8分) 22.(8分) 解:(1)163183AE i AE BE AE BE ===∴==,,, ··········································· (1分)在Rt ABE △中,根据勾股定理得AB =答:斜坡AB 的长为 ·················································································· (3分) (2)过点D 作DF BC ⊥于F ,∴四边形AEFD 是矩形.∴EF AD =,5AD = ,5EF ∴=,又263DF i DF AE CF ====,,392CF DF ∴==, 185932BC BE EF CF ∴=++=++=. ····························································· (5分)在Rt DCF △中,根据勾股定理得DC =∴梯形ABCD 的周长为:32537AB BC CD DA +++=+=+答:拦水坝的横断面梯形ABCD的周长为(37+米. ····················· (8分) 23.(10分) 解:(1)设该商场购进甲种商品x 件,乙种商品y 件,根据题意,得12010036000(138120)(120100)6000.x y x y +=⎧⎨-+-=⎩,······································································ (3分) 解得200120.x y =⎧⎨=⎩,答:该商场购进甲种商品200件,乙种商品120件. ·············································· (6分) (2)设乙种商品每件售价为z 元,根据题意,得120(100)2200(138120)8160z -+⨯⨯-≥. ······················································· (8分)解得z ≥108.答:乙种商品最低售价为每件108元. ··································································· (10分) 24.(10分) 解:(1)证明:连接OC ,ED 切O ⊙于点C ,OC ED ∴⊥. 又AD EC ⊥ ,OC AD ∴∥,OCA CAD ∴∠=∠.又OC OA ⊥ ,OAC OCA ∴∠∠=,OAC CAD ∴∠=∠.BCCF ∴=,BC CF ∴=.(3分) (2)在Rt ADE △中,68AD DE == ,,根据勾股定理得10AE =,又OC AD ∥,EOC EAD ∴△∽△,EO OCEA AD∴=. 设O ⊙的半径为r ,10OE r ∴=-,10106r r -∴=,154r ∴=,51022BE r ∴=-=. ··················································· (6分)(3)证明:过点C 作CG AB ⊥于点G ,OAC CAD AD EC ∠=∠⊥ ,,CG CD ∴=, Rt Rt AC AC AGC ADC AG AD =∴∴= ,△≌△,.又BC CF = , Rt Rt CGB CDF ∴△≌△,.GB DF AG GB AB AD DF AB ∴=+=∴+= ,, 2.AF DF AB ∴+= ·································································································· (10分)25.(12分)解:(1)能. 点P 的速度为1厘米/秒,点Q 的速度为1.25厘米/秒,1t =秒,1AP ∴=厘米,54BQ =厘米, 又4PE BC AC = ∥,厘米,5BC =厘米,3CD =厘米, 2AEP ADC BD ∴=△∽△,厘米,EP AP DC AC ∴=,即134EP =,34EP ∴=, 又53244QD BD BQ QD =-∴=-= ,, EP QD ∴=∴,四边形EQDP 能够成为平行四边形. ·············································· (2分) (2)554544AP t BQ t CP t CQ t ==∴=-=- ,,,. 55444454tCP t CQ t CA CB ---=== ,, CP CQ CA CB∴=.又C C CPQ CAB ∠=∠∴ ,△∽△, CPQ CAB PQ AB ∴∠=∠∴,∥.∴不论t 取何值时,总有线段PQ 与线段AB 平行. ················································ (5分) (3)①当90EQD ∠=°时,四边形EQCP 是矩形,4EQ PC t ∴==-,又EQ AC ∥,DEQ DAC ∴△∽△.EQ DQAC DC∴=, 即524443t t --=,解得 2.5.t = ························· (8分) ②当90DEQ ∠=°时,90EDQ CDA DEQ C ∠=∠∠=∠= ,°,EDQ CDA ∴△∽△,DQ DEDA DC∴=. 在Rt ACD △中,43AC CD == ,,5AD ∴=.EP DC ∥,AEP ADC ∴△∽△,AE APAD AC∴=,即54AE t =, 54AE t ∴=,554DE t ∴=-.55254453t t--∴=,解得 3.1t =. 综上所述,当 2.5t =秒或3.1秒时,EDQ △为直角三角形. ······························ (12分) 26.(12分)解:(1)当0x =时,4y =,(04)D ∴,.当0y =时,2x =-,(20)A ∴-,.抛物线212y x bx c =-++经过点A D 、,4220c b c =⎧∴⎨--+=⎩,.解得1b =,4c =. ∴这条抛物线的解析式为2142y x x =-++. ···························································· (2分) 当0y =时,整理得2280x x --=,解得12x =-,24x =,∴点(40)B ,. ····································································· (3分) (2)①当点M 在线段AD 上时,过点M 作ME x ⊥轴于E ,13AOM OMD S S = △△::,13AM MD ∴=::,又ME y ∥轴,Rt Rt AME ADO ∴△∽△,14ME AM DO AD ∴==,又(04)41D OD ME ∴=∴= ,,,, 133241(1)22x x M ∴+=∴=-∴-,,,. ···································································· (5分)②当点M 在DA 的延长线上时,过点M 作MF x ⊥轴于F ,13AOM OMD S S = △△::,13AM MD ∴=::,12AM AD ∴=::,又MF y ∥轴,Rt Rt AMF ADO ∴△∽△,12MF AM DO AD ∴==. 2422423(32)OD MF x x M =∴=∴+=-∴=-∴-- ,,,,,. ··························· (7分) (3)在y 轴的正半轴上存在符合条件的点P .点(2)C y ,在这条抛物线上,4y ∴=,∴点()24C ,, 连接CD ,(04)D ,,90CDO ∴∠=°, ①设11(0)P y ,,满足11PB PC =,其中10y >.在1Rt BOP △中,22211PB OB OP =+;在1Rt CDP △中,22211PC DC DP =+.222211OB DP DC DP ∴+=+,即22221142(4)y y +=+-.解得112y =,即11(0)2P ,,符合题意.②设22(0)P y ,,满足2P B BC =,其中20y >. 点(24)C ,,点(40)B ,,2224220BC ∴=+=, 在2Rt BOP △中,22222P B OB OP =+,22220OB OP ∴+=,即222420y +=,解得22y =-(舍去)或22y =,即2(02)P ,,符合题意. ③设33(0)P y ,,满足3PC BC =,其中30y >. 在3Rt CDP △中,22233PC DP CD =+,22320DP CD ∴+=,即223(4)220y -+=,解得30y =(舍去)或38y =,即3(08)P ,. 直线3P B 的解析式为28y x =-+,而(24)C ,在直线3P B 上, ∴3P 不符合题意,舍去.∴在y 轴的正半轴上存在符合条件的点P ,点1(0)2P ,或(02)P ,. ····················· (12分) 注;各题的其它解法或证法可参照该评分标准给分.。
内蒙古呼和浩特市中考数学试卷含答案解析版

2017年内蒙古呼和浩特市中考数学试卷一、选择题(本大题共10小题,每小题3分,共30分)1.(3分)我市冬季里某一天的最低气温是﹣10℃,最高气温是5℃,这一天的温差为( )A .﹣5℃B .5℃C .10℃D .15℃2.(3分)中国的陆地面积约为9600000km 2,将这个数用科学记数法可表示为( )A .×107km 2B .960×104km 2C .×106km 2D .×105km 23.(3分)图中序号(1)(2)(3)(4)对应的四个三角形,都是△ABC 这个图形进行了一次变换之后得到的,其中是通过轴对称得到的是( )A .(1)B .(2)C .(3)D .(4)4.(3分)如图,是根据某市2010年至2014年工业生产总值绘制的折线统计图,观察统计图获得以下信息,其中信息判断错误的是( )A .2010年至2014年间工业生产总值逐年增加B .2014年的工业生产总值比前一年增加了40亿元C .2012年与2013年每一年与前一年比,其增长额相同D .从2011年至2014年,每一年与前一年比,2014年的增长率最大5.(3分)关于x 的一元二次方程x 2+(a 2﹣2a )x +a ﹣1=0的两个实数根互为相反数,则a 的值为( )A .2B .0C .1D .2或06.(3分)一次函数y=kx +b 满足kb >0,且y 随x 的增大而减小,则此函数的图象不经过( )A .第一象限B .第二象限C .第三象限D .第四象限7.(3分)如图,CD 为⊙O 的直径,弦AB ⊥CD ,垂足为M ,若AB=12,OM :MD=5:8,则⊙O 的周长为( )A .26πB .13πC .96π5D .39√10π58.(3分)下列运算正确的是( )A .(a 2+2b 2)﹣2(﹣a 2+b 2)=3a 2+b 2B .a 2+1a−1﹣a ﹣1=2a a−1C .(﹣a )3m ÷a m =(﹣1)m a 2mD .6x 2﹣5x ﹣1=(2x ﹣1)(3x ﹣1)9.(3分)如图,四边形ABCD 是边长为1的正方形,E ,F 为BD 所在直线上的两点,若AE=√5,∠EAF=135°,则下列结论正确的是( ) A .DE=1 B .tan ∠AFO=13C .AF=√102D .四边形AFCE 的面积为9410.(3分)函数y=x 2+1|x|的大致图象是( ) A . B . C .D .二、填空题(本大题共6小题,每小题3分,共18分)11.(3分)若式子√1−2x有意义,则x 的取值范围是 . 12.(3分)如图,AB ∥CD ,AE 平分∠CAB 交CD 于点E ,若∠C=48°,则∠AED 为 °.13.(3分)如图是某几何体的三视图,根据图中数据,求得该几何体的表面积为 .14.(3分)下面三个命题:①若{x =a y =b 是方程组{|x|=22x −y =3的解,则a +b=1或a +b=0; ②函数y=﹣2x 2+4x +1通过配方可化为y=﹣2(x ﹣1)2+3;③最小角等于50°的三角形是锐角三角形,其中正确命题的序号为 .15.(3分)如图,在?ABCD 中,∠B=30°,AB=AC ,O 是两条对角线的交点,过点O 作AC 的垂线分别交边AD ,BC 于点E ,F ,点M 是边AB 的一个三等分点,则△AOE 与△BMF 的面积比为 .16.(3分)我国魏晋时期数学家刘徽首创“割圆术”计算圆周率.随着时代发展,现在人们依据频率估计概率这一原理,常用随机模拟的方法对圆周率π进行估计,用计算机随机产生m个有序数对(x,y)(x,y是实数,且0≤x≤1,0≤y≤1),它们对应的点在平面直角坐标系中全部在某一个正方形的边界及其内部.如果统计出这些点中到原点的距离小于或等于1的点有n个,则据此可估计π的值为.(用含m,n的式子表示)三、解答题(本大题共9小题,共72分)17.(10分)(1)计算:|2﹣√5|﹣√2(√18﹣√102)+32;(2)先化简,再求值:x−2x+2x÷x2−4x+4x−4+12x,其中x=﹣65.18.(6分)如图,等腰三角形ABC中,BD,CE分别是两腰上的中线.(1)求证:BD=CE;(2)设BD与CE相交于点O,点M,N分别为线段BO和CO的中点,当△ABC的重心到顶点A的距离与底边长相等时,判断四边形DEMN的形状,无需说明理由.19.(10分)为了解某地某个季度的气温情况,用适当的抽样方法从该地这个季度中抽取30天,对每天的最高气温x(单位:℃)进行调查,并将所得的数据按照12≤x<16,16≤x<20,20≤x<24,24≤x<28,28≤x<32分成五组,得到如图频数分布直方图.(1)求这30天最高气温的平均数和中位数(各组的实际数据用该组的组中值代表);(2)每月按30天计算,各组的实际数据用该组的组中值代表,估计该地这个季度中最高气温超过(1)中平均数的天数;(3)如果从最高气温不低于24℃的两组内随机选取两天,请你直接写出这两天都在气温最高一组内的概率.20.(7分)某专卖店有A,B两种商品,已知在打折前,买60件A商品和30件B商品用了1080元,买50件A商品和10件B商品用了840元,A,B两种商品打相同折以后,某人买500件A商品和450件B商品一共比不打折少花1960元,计算打了多少折?21.(6分)已知关于x的不等式2m−mx2>12x﹣1.(1)当m=1时,求该不等式的解集;(2)m取何值时,该不等式有解,并求出解集.22.(7分)如图,地面上小山的两侧有A,B两地,为了测量A,B两地的距离,让一热气球从小山西侧A地出发沿与AB成30°角的方向,以每分钟40m的速度直线飞行,10分钟后到达C 处,此时热气球上的人测得CB 与AB 成70°角,请你用测得的数据求A ,B 两地的距离AB 长.(结果用含非特殊角的三角函数和根式表示即可)23.(7分)已知反比例函数y=−k 2−1x(k 为常数). (1)若点P 1(1−√32,y 1)和点P 2(﹣12,y 2)是该反比例函数图象上的两点,试利用反比例函数的性质比较y 1和y 2的大小;(2)设点P (m ,n )(m >0)是其图象上的一点,过点P 作PM ⊥x 轴于点M .若tan∠POM=2,PO=√5(O 为坐标原点),求k 的值,并直接写出不等式kx +k 2+1x>0的解集.24.(9分)如图,点A ,B ,C ,D 是直径为AB 的⊙O 上的四个点,C 是劣弧BD̂的中点,AC 与BD 交于点E .(1)求证:DC 2=CE?AC ;(2)若AE=2,EC=1,求证:△AOD 是正三角形;(3)在(2)的条件下,过点C 作⊙O 的切线,交AB 的延长线于点H ,求△ACH 的面积.25.(10分)在平面直角坐标系xOy 中,抛物线y=ax 2+bx +c 与y 轴交于点C ,其顶点记为M ,自变量x=﹣1和x=5对应的函数值相等.若点M 在直线l :y=﹣12x +16上,点(3,﹣4)在抛物线上.(1)求该抛物线的解析式;(2)设y=ax 2+bx +c 对称轴右侧x 轴上方的图象上任一点为P ,在x 轴上有一点A (﹣72,0),试比较锐角∠PCO 与∠ACO 的大小(不必证明),并写出相应的P 点横坐标x 的取值范围.(3)直线l 与抛物线另一交点记为B ,Q 为线段BM 上一动点(点Q 不与M 重合),设Q 点坐标为(t ,n ),过Q 作QH ⊥x 轴于点H ,将以点Q ,H ,O ,C 为顶点的四边形的面积S 表示为t 的函数,标出自变量t 的取值范围,并求出S 可能取得的最大值.2017年内蒙古呼和浩特市中考数学试卷参考答案与试题解析一、选择题(本大题共10小题,每小题3分,共30分)1.(3分)(2017?呼和浩特)我市冬季里某一天的最低气温是﹣10℃,最高气温是5℃,这一天的温差为( )A.﹣5℃B.5℃C.10℃D.15℃【考点】1A:有理数的减法.【分析】用最高温度减去最低温度,再根据减去一个数等于加上这个数的相反数进行计算即可得解.【解答】解:5﹣(﹣10),=5+10,=15℃.故选D.【点评】本题考查了有理数的减法,熟记减去一个数等于加上这个数的相反数是解题的关键.2.(3分)(2017?呼和浩特)中国的陆地面积约为9600000km2,将这个数用科学记数法可表示为()A.×107km2B.960×104km2C.×106km2D.×105km2【考点】1I:科学记数法—表示较大的数.【分析】科学记数法的表示形式为a×10n的形式,其中1≤|a|<10,n为整数.确定n 的值时,要看把原数变成a时,小数点移动了多少位,n的绝对值与小数点移动的位数相同.当原数绝对值大于10时,n是正数;当原数的绝对值小于1时,n是负数.【解答】解:将9600000用科学记数法表示为:×106.故选:C.【点评】此题考查科学记数法的表示方法.科学记数法的表示形式为a×10n的形式,其中1≤|a|<10,n为整数,表示时关键要正确确定a的值以及n的值.3.(3分)(2017?呼和浩特)图中序号(1)(2)(3)(4)对应的四个三角形,都是△ABC这个图形进行了一次变换之后得到的,其中是通过轴对称得到的是()A.(1)B.(2)C.(3)D.(4)【考点】P3:轴对称图形.【专题】17 :推理填空题.【分析】轴对称是沿着某条直线翻转得到新图形,据此判断出通过轴对称得到的是哪个图形即可.【解答】解:∵轴对称是沿着某条直线翻转得到新图形,∴通过轴对称得到的是(1).【点评】此题主要考查了轴对称图形的性质和应用,要熟练掌握,解答此题的关键是要明确:轴对称是沿着某条直线翻转得到新图形,观察时要紧扣图形变换特点,进行分析判断.4.(3分)(2017?呼和浩特)如图,是根据某市2010年至2014年工业生产总值绘制的折线统计图,观察统计图获得以下信息,其中信息判断错误的是()A.2010年至2014年间工业生产总值逐年增加B.2014年的工业生产总值比前一年增加了40亿元C.2012年与2013年每一年与前一年比,其增长额相同D.从2011年至2014年,每一年与前一年比,2014年的增长率最大【考点】VD:折线统计图.【分析】根据题意结合折线统计图确定正确的选项即可.【解答】解:A、2010年至2014年间工业生产总值逐年增加,正确,不符合题意;B、2014年的工业生产总值比前一年增加了40亿元,正确,不符合题意;C、2012年与2013年每一年与前一年比,其增长额相同,正确,不符合题意;D、从2011年至2014年,每一年与前一年比,2012年的增长率最大,故D符合题意;故选:D.【点评】本题考查了折线统计图,计算增长率是解题关键.5.(3分)(2017?呼和浩特)关于x的一元二次方程x2+(a2﹣2a)x+a﹣1=0的两个实数根互为相反数,则a的值为()A.2 B.0 C.1 D.2或0【考点】AB:根与系数的关系.【专题】11 :计算题.【分析】设方程的两根为x1,x2,根据根与系数的关系得a2﹣2a=0,解得a=0或a=2,然后利用判别式的意义确定a的取值.【解答】解:设方程的两根为x1,x2,根据题意得x1+x2=0,所以a2﹣2a=0,解得a=0或a=2,当a=2时,方程化为x2+1=0,△=﹣4<0,故a=2舍去,所以a的值为0.【点评】本题考查了根与系数的关系:若x 1,x 2是一元二次方程ax 2+bx +c=0(a ≠0)的两根时,x 1+x 2=﹣b a ,x 1x 2=c a.也考查了根的判别式. 6.(3分)(2017?呼和浩特)一次函数y=kx +b 满足kb >0,且y 随x 的增大而减小,则此函数的图象不经过( )A .第一象限B .第二象限C .第三象限D .第四象限【考点】F7:一次函数图象与系数的关系.【分析】根据y 随x 的增大而减小得:k <0,又kb >0,则b <0.再根据k ,b 的符号判断直线所经过的象限.【解答】解:根据y 随x 的增大而减小得:k <0,又kb >0,则b <0,故此函数的图象经过第二、三、四象限,即不经过第一象限.故选A .【点评】能够根据k ,b 的符号正确判断直线所经过的象限.7.(3分)(2017?呼和浩特)如图,CD 为⊙O 的直径,弦AB ⊥CD ,垂足为M ,若AB=12,OM :MD=5:8,则⊙O 的周长为( )A .26πB .13πC .96π5D .39√10π5【考点】M2:垂径定理. 【分析】连接OA ,根据垂径定理得到AM=12AB=6,设OM=5x ,DM=8x ,得到OA=OD=13x ,根据勾股定理得到OA=12×13,于是得到结论. 【解答】解:连接OA ,∵CD 为⊙O 的直径,弦AB ⊥CD ,∴AM=12AB=6, ∵OM :MD=5:8,∴设OM=5x ,DM=8x ,∴OA=OD=13x ,∴AM=12x=6,∴x=12,∴OA=12×13, ∴⊙O 的周长=2OA?π=13π,故选B .【点评】本题考查的是垂径定理,根据题意作出辅助线,构造出直角三角形,利用勾股定理求解是解答此题的关键.8.(3分)(2017?呼和浩特)下列运算正确的是( )A .(a 2+2b 2)﹣2(﹣a 2+b 2)=3a 2+b 2B .a 2+1a−1﹣a ﹣1=2a a−1C .(﹣a )3m ÷a m =(﹣1)m a 2mD .6x 2﹣5x ﹣1=(2x ﹣1)(3x ﹣1) 【考点】6B :分式的加减法;4I :整式的混合运算;57:因式分解﹣十字相乘法等.【分析】直接利用分式的加减运算法则以及结合整式除法运算法则和因式分解法分别分析得出答案.【解答】解:A 、(a 2+2b 2)﹣2(﹣a 2+b 2)=3a 2,故此选项错误;B 、a 2+1a−1﹣a ﹣1=a 2+1−(a+1)(a−1)a−1=2a−1,故此选项错误; C 、(﹣a )3m ÷a m =(﹣1)m a 2m ,正确;D 、6x 2﹣5x ﹣1,无法在实数范围内分解因式,故此选项错误;故选:C .【点评】此题主要考查了分式的加减运算以及整式除法运算和因式分解等知识,正确掌握运算法则是解题关键.9.(3分)(2017?呼和浩特)如图,四边形ABCD 是边长为1的正方形,E ,F 为BD 所在直线上的两点,若AE=√,∠EAF=135°,则下列结论正确的是( )A .DE=1B .tan ∠AFO=13C .AF=√102D .四边形AFCE 的面积为94【考点】LE :正方形的性质;T7:解直角三角形.【分析】根据正方形的性质求出AO 的长,用勾股定理求出EO 的长,然后由∠MAN=135°及∠BAD=90°可以得到相似三角形,根据相似三角形的性质求出BF 的长,再一一计算即可判断.【解答】解:∵四边形ABCD 是正方形,∴AB=CB=CD=AD=1,AC ⊥BD ,∠ADO=∠ABO=45°,∴OD=OB=OA=√22,∠ABF=∠ADE=135°, 在Rt △AEO 中,EO=√AE 2−OA 2=√5−12=32√2, ∴DE=√2,故A 错误.∵∠EAF=135°,∠BAD=90°,∴∠BAF +∠DAE=45°,∵∠ADO=∠DAE +∠AED=45°,∴∠BAF=∠AED ,∴△ABF ∽△EDA ,∴BF DA =AB DE , ∴BF 1=√2, ∴BF=√22, 在Rt △AOF 中,AF=√OA 2+OF 2=√(22)2+(√2)2=√102,故C 正确, tan ∠AFO=OA OF =√22√2=12,故B 错误, ∴S 四边形AECF =12?AC?EF=12×√2×52√2=52,故D 错误, 故选C .【点评】本题考查的是相似三角形的判定与性质,根据正方形的性质,运用勾股定理求出相应线段的长,再根据∠EAF=135°和∠BAD=90°,得到相似三角形,用相似三角形的性质求出BF 的长,然后根据对称性求出四边形的面积. 10.(3分)(2017?呼和浩特)函数y=x 2+1|x|的大致图象是( )A.B.C.D.【考点】E6:函数的图象.【分析】本题可用排除法解答,根据y始终大于0,可排除D,再根据x≠0可排除A,根据函数y=x2+1|x|和y=32x有交点即可排除C,即可解题.【解答】解:①∵|x|为分母,∴|x|≠0,即|x|>0,∴A错误;②∵x2+1>0,|x|>0,∴y=x2+1|x|>0,∴D错误;③∵当直线经过(0,0)和(1,32)时,直线解析式为y=32x,当y=32x=x2+1|x|时,x=√2,∴y=32x与y=x2+1|x|有交点,∴C错误;④∵当直线经过(0,0)和(1,1)时,直线解析式为y=x,当y=x=x2+1|x|时,x无解,∴y=x与y=x2+1|x|没有有交点,∴B正确;故选B.【点评】此题主要考查了函数图象的性质,考查了平方根和绝对值大于等于0的性质,本题中求得直线与函数的交点是解题的关键.二、填空题(本大题共6小题,每小题3分,共18分)11.(3分)(2017?呼和浩特)若式子√1−2x 有意义,则x的取值范围是x<12.【考点】72:二次根式有意义的条件;62:分式有意义的条件.【分析】根据二次根式有意义的条件:被开方数为非负数,再结合分式有意义的条件:分母≠0,可得不等式1﹣2x>0,再解不等式即可.【解答】解:由题意得:1﹣2x>0,解得:x<1 2,故答案为:x<1 2,【点评】此题主要考查了二次根式有意义的条件;用到的知识点为:二次根式有意义,被开方数为非负数.12.(3分)(2017?呼和浩特)如图,AB∥CD,AE平分∠CAB交CD于点E,若∠C=48°,则∠AED为114°.【考点】JA:平行线的性质;IJ:角平分线的定义.【分析】根据平行线性质求出∠CAB的度数,根据角平分线求出∠EAB的度数,根据平行线性质求出∠AED的度数即可.【解答】解:∵AB∥CD,∴∠C+∠CAB=180°,∵∠C=48°,∴∠CAB=180°﹣48°=132°,∵AE平分∠CAB,∴∠EAB=66°,∵AB∥CD,∴∠EAB+∠AED=180°,∴∠AED=180°﹣66°=114°,故答案为:114.【点评】本题考查了角平分线定义和平行线性质的应用,解题时注意:两条平行线被第三条直线所截,同旁内角互补.13.(3分)(2017?呼和浩特)如图是某几何体的三视图,根据图中数据,求得该几何体的表面积为(225+25√2)π.【考点】U3:由三视图判断几何体.【分析】根据给出的几何体的三视图可知几何体是由圆柱体和圆锥体构成,从而根据三视图的特点得知高和底面直径,代入表面积公式计算即可.【解答】解:由三视图可知,几何体是由圆柱体和圆锥体构成,故该几何体的表面积为:20×10π+π×82+12×10π×√52+52=(225+25√2)π 故答案是:(225+25√2)π.【点评】本题考查了由三视图判断几何体,该三视图中的数据确定圆锥的底面直径和高是解本题的关键;本题体现了数形结合的数学思想,注意圆锥的高,母线长,底面半径组成直角三角形.14.(3分)(2017?呼和浩特)下面三个命题:①若{x =a y =b 是方程组{|x|=22x −y =3的解,则a +b=1或a +b=0; ②函数y=﹣2x 2+4x +1通过配方可化为y=﹣2(x ﹣1)2+3;③最小角等于50°的三角形是锐角三角形,其中正确命题的序号为 ②③ .【考点】O1:命题与定理.【分析】①根据方程组的解的定义,把{x =a y =b 代入{|x|=22x −y =3,即可判断; ②利用配方法把函数y=﹣2x 2+4x +1化为顶点式,即可判断;③根据三角形内角和定理以及锐角三角形的定义即可判断.【解答】解:①把{x =a y =b 代入{|x|=22x −y =3,得{|a|=22a −b =3, 如果a=2,那么b=1,a +b=3;如果a=﹣2,那么b=﹣7,a +b=﹣9.故命题①是假命题;②y=﹣2x 2+4x +1=﹣2(x ﹣1)2+3,故命题②是真命题;③最小角等于50°的三角形,最大角不大于80°,一定是锐角三角形,故命题③是真命题.所以正确命题的序号为②③.故答案为②③.【点评】主要考查命题的真假判断,正确的命题叫真命题,错误的命题叫做假命题.判断命题的真假关键是要熟悉课本中的定义以及性质定理等知识.15.(3分)(2017?呼和浩特)如图,在?ABCD 中,∠B=30°,AB=AC ,O 是两条对角线的交点,过点O 作AC 的垂线分别交边AD ,BC 于点E ,F ,点M 是边AB 的一个三等分点,则△AOE 与△BMF 的面积比为 3:4 .【考点】S9:相似三角形的判定与性质;L5:平行四边形的性质.【分析】作MH ⊥BC 于H ,设AB=AC=m ,则BM=13m ,MH=12BM=16m ,根据平行四边形的性质求得OA=OC=12AC=12m ,解直角三角形求得FC=√33m ,然后根据ASA 证得△AOE ≌△COF ,证得AE=FC=√33m ,进一步求得OE=12AE=√36m ,从而求得S △AOE =√324m 2,作AN ⊥BC 于N ,根据等腰三角形的性质以及解直角三角形求得BC=√3m ,进而求得BF=BC ﹣FC=√3m ﹣√33m=2√33m ,分别求得△AOE 与△BMF 的面积,即可求得结论. 【解答】解:设AB=AC=m ,则BM=13m , ∵O 是两条对角线的交点,∴OA=OC=12AC=12m , ∵∠B=30°,AB=AC ,∴∠ACB=∠B=30°,∵EF ⊥AC ,∴cos ∠ACB=OC FC ,即cos30°=12m FC , ∴FC=√33m , ∵AE ∥FC ,∴∠EAC=∠FCA ,又∵∠AOE=∠COF ,AO=CO ,∴△AOE ≌△COF ,∴AE=FC=√33m , ∴OE=12AE=√36m , ∴S △AOE =12OA?OE=12×12m ×√36m=√324m 2, 作AN ⊥BC 于N ,∵AB=AC ,∴BN=CN=12BC , ∵BN=√32AB=√32m , ∴BC=√3m ,∴BF=BC ﹣FC=√3m ﹣√33m=2√33m , 作MH ⊥BC 于H ,∵∠B=30°,∴MH=12BM=16m , ∴S △BMF =12BF?MH=12×2√33m ×16m=√318m 2, ∴S △AOE S △BMF =√324m 2√318m =34. 故答案为3:4.【点评】本题考查了平行四边形的性质、全等三角形的判定和性质以及解直角三角形等,熟练掌握性质定理是解题的关键.16.(3分)(2017?呼和浩特)我国魏晋时期数学家刘徽首创“割圆术”计算圆周率.随着时代发展,现在人们依据频率估计概率这一原理,常用随机模拟的方法对圆周率π进行估计,用计算机随机产生m 个有序数对(x ,y )(x ,y 是实数,且0≤x ≤1,0≤y ≤1),它们对应的点在平面直角坐标系中全部在某一个正方形的边界及其内部.如果统计出这些点中到原点的距离小于或等于1的点有n 个,则据此可估计π的值为 4nm .(用含m ,n 的式子表示)【考点】X8:利用频率估计概率;D2:规律型:点的坐标.【分析】根据落在扇形内的点的个数与正方形内点的个数之比等于两者的面积之比列出14?π1=nm ,可得答案. 【解答】解:根据题意,点的分布如图所示:则有14?π1=n m, ∴π=4n m ,故答案为:4n m. 【点评】此题主要考查了利用频率估计概率,大量反复试验下频率稳定值即概率.用到的知识点为:频率=所求情况数与总情况数之比.三、解答题(本大题共9小题,共72分)17.(10分)(2017?呼和浩特)(1)计算:|2﹣√5|﹣√2(√18﹣√102)+32; (2)先化简,再求值:x−2x 2+2x ÷x 2−4x+4x 2−4+12x ,其中x=﹣65. 【考点】6D :分式的化简求值;2C :实数的运算.【专题】11 :计算题;513:分式.【分析】(1)原式利用绝对值的代数意义化简,去括号合并即可得到结果;(2)原式第一项利用除法法则变形,约分后利用同分母分式的加法法则计算得到最简结果,把x 的值代入计算即可求出值.【解答】解:(1)原式=√5﹣2﹣12+√5+32=2√5﹣1; (2)原式=x−2x(x+2)?(x+2)(x−2)(x−2)2+12x =1x +12x =32x, 当x=﹣65时,原式=﹣54. 【点评】此题考查了分式的化简求值,以及实数的运算,熟练掌握运算法则是解本题的关键.18.(6分)(2017?呼和浩特)如图,等腰三角形ABC 中,BD ,CE 分别是两腰上的中线.(1)求证:BD=CE ;(2)设BD 与CE 相交于点O ,点M ,N 分别为线段BO 和CO 的中点,当△ABC 的重心到顶点A 的距离与底边长相等时,判断四边形DEMN 的形状,无需说明理由.【考点】KD :全等三角形的判定与性质;K5:三角形的重心;KH :等腰三角形的性质.【分析】(1)根据已知条件得到AD=AE ,根据全等三角形的性质即可得到结论;(2)根据三角形中位线的性质得到ED ∥BC ,ED=12BC ,MN ∥BC ,MN=12BC ,等量代换得到ED ∥MN ,ED=MN ,推出四边形EDNM 是平行四边形,由(1)知BD=CE ,求得DM=EN ,得到四边形EDNM 是矩形,根据全等三角形的性质得到OB=OC ,由三角形的重心的性质得到O 到BC 的距离=12BC ,根据直角三角形的判定得到BD ⊥CE ,于是得到结论. 【解答】(1)解:由题意得,AB=AC ,∵BD ,CE 分别是两腰上的中线,∴AD=12AC ,AE=12AB , ∴AD=AE ,在△ABD 和△ACE 中{AB =AC ∠A =∠A AD =AE,∴△ABD ≌△ACE (ASA ).∴BD=CE ;(2)四边形DEMN 是正方形,证明:∵E 、D 分别是AB 、AC 的中点,∴AE=12AB ,AD=12AC ,ED 是△ABC 的中位线, ∴ED ∥BC ,ED=12BC , ∵点M 、N 分别为线段BO 和CO 中点,∴OM=BM ,ON=CN ,MN 是△OBC 的中位线,∴MN ∥BC ,MN=12BC , ∴ED ∥MN ,ED=MN ,∴四边形EDNM 是平行四边形,由(1)知BD=CE ,又∵OE=ON ,OD=OM ,OM=BM ,ON=CN ,∴DM=EN ,∴四边形EDNM 是矩形,在△BDC 与△CEB 中,{BE =CDCE =BD BC =CB,∴△BDC ≌△CEB ,∴∠BCE=∠CBD ,∴OB=OC ,∵△ABC 的重心到顶点A 的距离与底边长相等,∴O 到BC 的距离=12BC , ∴BD ⊥CE ,∴四边形DEMN 是正方形.【点评】本题考查了等腰三角形的性质、三角形中位线定理、矩形的判定、平行四边形的判定与性质、全等三角形的判定与性质;熟练掌握等腰三角形的性质和三角形中位线定理,并能进行推理论证是解决问题的关键.19.(10分)(2017?呼和浩特)为了解某地某个季度的气温情况,用适当的抽样方法从该地这个季度中抽取30天,对每天的最高气温x (单位:℃)进行调查,并将所得的数据按照12≤x <16,16≤x <20,20≤x <24,24≤x <28,28≤x <32分成五组,得到如图频数分布直方图.(1)求这30天最高气温的平均数和中位数(各组的实际数据用该组的组中值代表);(2)每月按30天计算,各组的实际数据用该组的组中值代表,估计该地这个季度中最高气温超过(1)中平均数的天数;(3)如果从最高气温不低于24℃的两组内随机选取两天,请你直接写出这两天都在气温最高一组内的概率.【考点】X6:列表法与树状图法;V5:用样本估计总体;V8:频数(率)分布直方图;W2:加权平均数;W4:中位数.【分析】(1)根据30天的最高气温总和除以总天数,即可得到这30天最高气温的平均数,再根据第15和16个数据的位置,判断中位数;(2)根据30天中,最高气温超过(1)中平均数的天数,即可估计这个季度中最高气温超过(1)中平均数的天数;(3)从6天中任选2天,共有15种等可能的结果,其中两天都在气温最高一组内的情况有6种,据此可得这两天都在气温最高一组内的概率.【解答】解:(1)这30天最高气温的平均数为:14×8+18×6+22×10+26×2+30×430=℃; ∵中位数落在第三组内,∴中位数为22℃;(2)∵30天中,最高气温超过(1)中平均数的天数为16天,∴该地这个季度中最高气温超过(1)中平均数的天数为1630×90=48(天); (3)从6天中任选2天,共有15种等可能的结果,其中两天都在气温最高一组内的情况有6种,故这两天都在气温最高一组内的概率为615=25.【点评】本题主要考查了频数分布直方图,平均数以及中位数的计算,一般来说,用样本去估计总体时,样本越具有代表性、容量越大,这时对总体的估计也就越精确.解题时注意:如果一组数据的个数是偶数,则中间两个数据的平均数就是这组数据的中位数.20.(7分)(2017?呼和浩特)某专卖店有A,B两种商品,已知在打折前,买60件A 商品和30件B商品用了1080元,买50件A商品和10件B商品用了840元,A,B两种商品打相同折以后,某人买500件A商品和450件B商品一共比不打折少花1960元,计算打了多少折?【考点】9A:二元一次方程组的应用.【分析】设打折前A商品的单价为x元/件、B商品的单价为y元/件,根据“买60件A 商品和30件B商品用了1080元,买50件A商品和10件B商品用了840元”,即可得出关于x、y的二元一次方程组,解之即可得出x、y的值,再算出打折前购买500件A 商品和450件B商品所需钱数,结合少花钱数即可求出折扣率.【解答】解:设打折前A商品的单价为x元/件、B商品的单价为y元/件,根据题意得:{60x+30y=1080 50x+10y=840,解得:{x=16 y=4,500×16+450×4=9800(元),9800−19609800=.答:打了八折.【点评】本题考查了二元一次方程组的应用,找准等量关系,列出二元一次方程组是解题的关键.21.(6分)(2017?呼和浩特)已知关于x的不等式2m−mx2>12x﹣1.(1)当m=1时,求该不等式的解集;(2)m取何值时,该不等式有解,并求出解集.【考点】C3:不等式的解集.【专题】11 :计算题;524:一元一次不等式(组)及应用.【分析】(1)把m=1代入不等式,求出解集即可;(2)不等式去分母,移项合并整理后,根据有解确定出m的范围,进而求出解集即可.【解答】解:(1)当m=1时,不等式为2−x2>x2﹣1,去分母得:2﹣x>x﹣2,解得:x <2;(2)不等式去分母得:2m ﹣mx >x ﹣2,移项合并得:(m +1)x <2(m +1),当m ≠﹣1时,不等式有解,当m >﹣1时,不等式解集为x <2;当x <﹣1时,不等式的解集为x >2.【点评】此题考查了不等式的解集,熟练掌握不等式的基本性质是解本题的关键.22.(7分)(2017?呼和浩特)如图,地面上小山的两侧有A ,B 两地,为了测量A ,B 两地的距离,让一热气球从小山西侧A 地出发沿与AB 成30°角的方向,以每分钟40m 的速度直线飞行,10分钟后到达C 处,此时热气球上的人测得CB 与AB 成70°角,请你用测得的数据求A ,B 两地的距离AB 长.(结果用含非特殊角的三角函数和根式表示即可)【考点】T8:解直角三角形的应用.【分析】过点C 作CM ⊥AB 交AB 延长线于点M ,通过解直角△ACM 得到AM 的长度,通过解直角△BCM 得到BM 的长度,则AB=AM ﹣BM .【解答】解:过点C 作CM ⊥AB 交AB 延长线于点M ,由题意得:AC=40×10=400(米).在直角△ACM 中,∵∠A=30°,∴CM=12AC=200米,AM=√32AC=200√3米. 在直角△BCM 中,∵tan20°=BM CM, ∴BM=200tan20°,∴AB=AM ﹣BM=200√3﹣200tan20°=200(√3﹣tan20°),因此A ,B 两地的距离AB 长为200(√3﹣tan20°)米.【点评】本题考查解直角三角形的应用、三角函数等知识,解题的关键是添加辅助线,构造直角三角形,记住三角函数的定义,以及特殊三角形的边角关系,属于中考常考题型.23.(7分)(2017?呼和浩特)已知反比例函数y=−k 2−1x(k 为常数).(1)若点P 1(1−√32,y 1)和点P 2(﹣12,y 2)是该反比例函数图象上的两点,试利用反比例函数的性质比较y 1和y 2的大小;(2)设点P (m ,n )(m >0)是其图象上的一点,过点P 作PM ⊥x 轴于点M .若tan∠POM=2,PO=√5(O 为坐标原点),求k 的值,并直接写出不等式kx +k 2+1x>0的解集.【考点】G6:反比例函数图象上点的坐标特征;T7:解直角三角形.【分析】(1)先根据反比例函数的解析式判断出函数图象所在的象限及其增减性,再根据P 1、P 2两点的横坐标判断出两点所在的象限,故可得出结论.(2)根据题意求得﹣n=2m ,根据勾股定理求得m=1,n=﹣2,得到P (1,﹣2),即可得到﹣k 2﹣1=﹣2,即可求得k 的值,然后分两种情况借助反比例函数和正比例函数图象即可求得.【解答】解:(1)∵﹣k 2﹣1<0,∴反比例函数y=−k 2−1x在每一个象限内y 随x 的增大而增大, ∵﹣12<1−√32<0, ∴y 1>y 2;(2)点P (m ,n )在反比例函数y=−k 2−1x的图象上,m >0, ∴n <0,∴OM=m ,PM=﹣n ,∵tan ∠POM=2,∴PM OM =−n m=2, ∴﹣n=2m ,∵PO=√5,∴m 2+(﹣n )2=5,∴m=1,n=﹣2,∴P (1,﹣2),∴﹣k 2﹣1=﹣2,解得k=±1,①当k=﹣1时,则不等式kx+k2+1x>0的解集为:x<﹣√2或0<x<√2;②当k=1时,则不等式kx+k2+1x>0的解集为:x>0.【点评】本题考查的是反比例函数图象上点的坐标特点,即反比例函数图象上各点的坐标一定适合此函数的解析式;也考查了反比例函数和一次函数的交点.24.(9分)(2017?呼和浩特)如图,点A,B,C,D是直径为AB的⊙O上的四个点,C是劣弧BD̂的中点,AC与BD交于点E.(1)求证:DC2=CE?AC;(2)若AE=2,EC=1,求证:△AOD是正三角形;(3)在(2)的条件下,过点C作⊙O的切线,交AB的延长线于点H,求△ACH的面积.【考点】MR:圆的综合题.【分析】(1)由圆周角定理得出∠DAC=∠CDB,证明△ACD∽△DCE,得出对应边成比例,即可得出结论;(2)求出DC=√3,连接OC、OD,如图所示:证出BC=DC=√3,由圆周角定理得出∠ACB=90°,由勾股定理得出AB=√AC2+BC2=2√3,得出OB=OC=OD=DC=BC=√3,证出△OCD、△OBC是正三角形,得出∠COD=∠BOC=∠OBC=60°,求出∠AOD=60°,即可得出结论;(3)由切线的性质得出OC⊥CH,求出∠H=30°,证出∠H=∠BAC,得出AC=CH=3,求出AH和高,由三角形面积公式即可得出答案.【解答】(1)证明:∵C是劣弧BD̂的中点,∴∠DAC=∠CDB,∵∠ACD=∠DCE,∴△ACD∽△DCE,∴ACDC=CDCE,∴DC2=CE?AC;(2)证明:∵AE=2,EC=1,∴AC=3,∴DC2=CE?AC=1×3=3,。
呼和浩特市中考数学试题及答案(通用)
呼和浩特市中考数学试题及答案(通用)一、选择题(每题4分,共40分)1. 以下哪个数是最小的?A. -1B. 0.5C. -0.5D. 1答案:C2. 一个等边三角形的周长是15cm,求其高(精确到小数点后两位)?A. 2.60cmB. 3.46cmC. 4.24cmD. 5.20cm答案:B3. 以下哪个图形的面积最小?A. 边长为2的正方形B. 半径为2的圆C. 长为4,宽为3的矩形D. 边长为2的等边三角形答案:D4. 一个数的平方根是3,那么这个数的平方是?A. 6B. 9C. 12D. 18答案:B5. 以下哪个图形的面积公式正确?A. 圆的面积公式是πr²B. 矩形的面积公式是πl²C. 三角形的面积公式是1/2πr²D. 正方形的面积公式是1/2a²答案:A---二、填空题(每题4分,共40分)6. 一个二次方程x² - 5x + 6 = 0的解是______。
答案:x = 2 或 x = 37. 一个立方体的体积是64立方厘米,它的边长是______厘米。
答案:4厘米8. 一个圆的直径是8cm,它的半径是______cm。
答案:4cm9. 一个长方体的长为10cm,宽为6cm,高为4cm,它的体积是______立方厘米。
答案:240立方厘米10. 一个直角三角形的两条直角边分别是3cm和4cm,它的斜边长是______cm。
答案:5cm---三、解答题(每题20分,共80分)11. 已知一个等差数列的前三项分别是2,5,8,求第10项的值。
解答过程:首先确定公差d = 5 - 2 = 3。
利用等差数列的通项公式a_n = a_1 + (n - 1)d,代入n = 10,a_1 = 2,d = 3,得到a_10 = 2 + (10 - 1) 3 = 29。
答案:第10项的值是29。
12. 已知一个正方形的对角线长度是10cm,求它的面积。
2012年内蒙古包头市中考数学试卷-答案
数学答案解析
第Ⅰ卷
一、选择题
1.【答案】B
【解析】∵ ,∴9的算术平方根是3.故选B.
【提示】根据算术平方根的定义:一个非负数的正的平方根,即为这个数的算术平方根.所以结果必须为正数,由此即可求出9的算术平方根.
【考点】算术平方根.
2.【答案】A
【解析】 .故选:A.
【提示】先将括号里面的分式的分子分母分解因式,再通分进行分式加减计算后,最后进行分式的除法计算就可以得出结论.
【考点】分式的混合运算.
15.【答案】12
【解析】∵数据10,11,12,13,8,x的平均数是11,∴ ,
∵数据12出现的次数最多,∴众数为12.故答案为12
【提示】首先根据平均数的定义求得x的值,然后利用众数的定义求得答案即可.
【提示】根据矩形性质求出 ,可证 ,求出 ,求出 ,即可求出答案.
【考点】矩形的性质,全等三角形的判定与性质,等腰直角三角形
12.【答案】B
【解析】根据题意得 , ,则 ,∵ ,∴ ,
即 ,∴ ,∴ ,整理得 , ,解得 ,∵ ,∴ .故选B.
【提示】根据一元二次方程 ( )的根与系数的关系和两根都为正根得到 ,
【提示】根据合并同类项法则对A进行判断;根据同底数幂的除法法则对B进行判断;根据同类二次根式的定义对C进行判断;根据二次根式的乘法法则对D进行判断.
【解析】A. 与 不是同类项,不能合并,所以A选项错误;
B. ,,所以B选项错误;
C. 与 不是同类二次根式,不能合并,所以C选项错误;
D. ,所以D选项正确.故选D.
【考点】众数,算术平均数
16.【答案】4
【解析】 , , 或 , , ,∵ ,∴ ,把 代入 中得: ,解得: ,故答案为:4.
内蒙古呼和浩特市中考数学试卷含答案解析版
2017年内蒙古呼和浩特市中考数学试卷一、选择题(本大题共10小题,每小题3分,共30分)1.(3分)我市冬季里某一天的最低气温是﹣10℃,最高气温是5℃,这一天的温差为()A.﹣5℃B.5℃C.10℃D.15℃2.(3分)中国的陆地面积约为9600000km2,将这个数用科学记数法可表示为()A.0.96×107km2B.960×104km2C.9.6×106km2 D.9.6×105km2 3.(3分)图中序号(1)(2)(3)(4)对应的四个三角形,都是△ABC这个图形进行了一次变换之后得到的,其中是通过轴对称得到的是()A.(1)B.(2)C.(3)D.(4)4.(3分)如图,是根据某市2010年至2014年工业生产总值绘制的折线统计图,观察统计图获得以下信息,其中信息判断错误的是()A.2010年至2014年间工业生产总值逐年增加B.2014年的工业生产总值比前一年增加了40亿元C.2012年与2013年每一年与前一年比,其增长额相同D.从2011年至2014年,每一年与前一年比,2014年的增长率最大5.(3分)关于x的一元二次方程x2+(a2﹣2a)x+a﹣1=0的两个实数根互为相反数,则a的值为()A .2B .0C .1D .2或06.(3分)一次函数y=kx +b 满足kb >0,且y 随x 的增大而减小,则此函数的图象不经过( )A .第一象限B .第二象限C .第三象限D .第四象限7.(3分)如图,CD 为⊙O 的直径,弦AB ⊥CD ,垂足为M ,若AB=12,OM :MD=5:8,则⊙O 的周长为( )A .26πB .13πC .96π5D .39√10π58.(3分)下列运算正确的是( )A .(a 2+2b 2)﹣2(﹣a 2+b 2)=3a 2+b 2B .a 2+1a−1﹣a ﹣1=2a a−1C .(﹣a )3m ÷a m =(﹣1)m a 2mD .6x 2﹣5x ﹣1=(2x ﹣1)(3x ﹣1) 9.(3分)如图,四边形ABCD 是边长为1的正方形,E ,F 为BD 所在直线上的两点,若AE=√5,∠EAF=135°,则下列结论正确的是( )A .DE=1B .tan ∠AFO=13C .AF=√102D .四边形AFCE 的面积为9410.(3分)函数y=x 2+1|x|的大致图象是( )A .B .C .D .二、填空题(本大题共6小题,每小题3分,共18分)11.(3分)若式子√1−2x有意义,则x 的取值范围是 . 12.(3分)如图,AB ∥CD ,AE 平分∠CAB 交CD 于点E ,若∠C=48°,则∠AED 为 °.13.(3分)如图是某几何体的三视图,根据图中数据,求得该几何体的表面积为 .14.(3分)下面三个命题:①若{x =a y =b 是方程组{|x|=22x −y =3的解,则a +b=1或a +b=0;②函数y=﹣2x2+4x+1通过配方可化为y=﹣2(x﹣1)2+3;③最小角等于50°的三角形是锐角三角形,其中正确命题的序号为.15.(3分)如图,在▱ABCD中,∠B=30°,AB=AC,O是两条对角线的交点,过点O作AC的垂线分别交边AD,BC于点E,F,点M是边AB的一个三等分点,则△AOE与△BMF的面积比为.16.(3分)我国魏晋时期数学家刘徽首创“割圆术”计算圆周率.随着时代发展,现在人们依据频率估计概率这一原理,常用随机模拟的方法对圆周率π进行估计,用计算机随机产生m个有序数对(x,y)(x,y是实数,且0≤x≤1,0≤y≤1),它们对应的点在平面直角坐标系中全部在某一个正方形的边界及其内部.如果统计出这些点中到原点的距离小于或等于1的点有n个,则据此可估计π的值为.(用含m,n的式子表示)三、解答题(本大题共9小题,共72分)17.(10分)(1)计算:|2﹣√5|﹣√2(√18﹣√102)+32;(2)先化简,再求值:x−2x2+2x÷x2−4x+4x2−4+12x,其中x=﹣65.18.(6分)如图,等腰三角形ABC中,BD,CE分别是两腰上的中线.(1)求证:BD=CE;(2)设BD与CE相交于点O,点M,N分别为线段BO和CO的中点,当△ABC 的重心到顶点A的距离与底边长相等时,判断四边形DEMN的形状,无需说明理由.19.(10分)为了解某地某个季度的气温情况,用适当的抽样方法从该地这个季度中抽取30天,对每天的最高气温x (单位:℃)进行调查,并将所得的数据按照12≤x <16,16≤x <20,20≤x <24,24≤x <28,28≤x <32分成五组,得到如图频数分布直方图.(1)求这30天最高气温的平均数和中位数(各组的实际数据用该组的组中值代表);(2)每月按30天计算,各组的实际数据用该组的组中值代表,估计该地这个季度中最高气温超过(1)中平均数的天数;(3)如果从最高气温不低于24℃的两组内随机选取两天,请你直接写出这两天都在气温最高一组内的概率.20.(7分)某专卖店有A ,B 两种商品,已知在打折前,买60件A 商品和30件B 商品用了1080元,买50件A 商品和10件B 商品用了840元,A ,B 两种商品打相同折以后,某人买500件A 商品和450件B 商品一共比不打折少花1960元,计算打了多少折?21.(6分)已知关于x 的不等式2m−mx 2>12x ﹣1. (1)当m=1时,求该不等式的解集;(2)m 取何值时,该不等式有解,并求出解集.22.(7分)如图,地面上小山的两侧有A ,B 两地,为了测量A ,B 两地的距离,让一热气球从小山西侧A 地出发沿与AB 成30°角的方向,以每分钟40m 的速度直线飞行,10分钟后到达C 处,此时热气球上的人测得CB 与AB 成70°角,请你用测得的数据求A ,B 两地的距离AB 长.(结果用含非特殊角的三角函数和根式表示即可)23.(7分)已知反比例函数y=−k 2−1x(k 为常数). (1)若点P 1(1−√32,y 1)和点P 2(﹣12,y 2)是该反比例函数图象上的两点,试利用反比例函数的性质比较y 1和y 2的大小; (2)设点P (m ,n )(m >0)是其图象上的一点,过点P 作PM ⊥x 轴于点M .若tan ∠POM=2,PO=√5(O 为坐标原点),求k 的值,并直接写出不等式kx +k 2+1x>0的解集.24.(9分)如图,点A ,B ,C ,D 是直径为AB 的⊙O 上的四个点,C 是劣弧BD̂的中点,AC 与BD 交于点E .(1)求证:DC 2=CE•AC ;(2)若AE=2,EC=1,求证:△AOD 是正三角形;(3)在(2)的条件下,过点C 作⊙O 的切线,交AB 的延长线于点H ,求△ACH 的面积.25.(10分)在平面直角坐标系xOy 中,抛物线y=ax 2+bx +c 与y 轴交于点C ,其顶点记为M ,自变量x=﹣1和x=5对应的函数值相等.若点M 在直线l :y=﹣12x +16上,点(3,﹣4)在抛物线上.(1)求该抛物线的解析式;(2)设y=ax 2+bx +c 对称轴右侧x 轴上方的图象上任一点为P ,在x 轴上有一点A(﹣72,0),试比较锐角∠PCO 与∠ACO 的大小(不必证明),并写出相应的P 点横坐标x 的取值范围.(3)直线l 与抛物线另一交点记为B ,Q 为线段BM 上一动点(点Q 不与M 重合),设Q 点坐标为(t ,n ),过Q 作QH ⊥x 轴于点H ,将以点Q ,H ,O ,C 为顶点的四边形的面积S表示为t的函数,标出自变量t的取值范围,并求出S可能取得的最大值.2017年内蒙古呼和浩特市中考数学试卷参考答案与试题解析一、选择题(本大题共10小题,每小题3分,共30分)1.(3分)(2017•呼和浩特)我市冬季里某一天的最低气温是﹣10℃,最高气温是5℃,这一天的温差为()A.﹣5℃B.5℃C.10℃D.15℃【考点】1A:有理数的减法.【分析】用最高温度减去最低温度,再根据减去一个数等于加上这个数的相反数进行计算即可得解.【解答】解:5﹣(﹣10),=5+10,=15℃.故选D.【点评】本题考查了有理数的减法,熟记减去一个数等于加上这个数的相反数是解题的关键.2.(3分)(2017•呼和浩特)中国的陆地面积约为9600000km2,将这个数用科学记数法可表示为()A.0.96×107km2B.960×104km2C.9.6×106km2 D.9.6×105km2【考点】1I:科学记数法—表示较大的数.【分析】科学记数法的表示形式为a×10n的形式,其中1≤|a|<10,n为整数.确定n的值时,要看把原数变成a时,小数点移动了多少位,n的绝对值与小数点移动的位数相同.当原数绝对值大于10时,n是正数;当原数的绝对值小于1时,n是负数.【解答】解:将用科学记数法表示为:9.6×106.故选:C.【点评】此题考查科学记数法的表示方法.科学记数法的表示形式为a×10n的形式,其中1≤|a|<10,n为整数,表示时关键要正确确定a的值以及n的值.3.(3分)(2017•呼和浩特)图中序号(1)(2)(3)(4)对应的四个三角形,都是△ABC这个图形进行了一次变换之后得到的,其中是通过轴对称得到的是()A.(1)B.(2)C.(3)D.(4)【考点】P3:轴对称图形.【专题】17 :推理填空题.【分析】轴对称是沿着某条直线翻转得到新图形,据此判断出通过轴对称得到的是哪个图形即可.【解答】解:∵轴对称是沿着某条直线翻转得到新图形,∴通过轴对称得到的是(1).故选:A.【点评】此题主要考查了轴对称图形的性质和应用,要熟练掌握,解答此题的关键是要明确:轴对称是沿着某条直线翻转得到新图形,观察时要紧扣图形变换特点,进行分析判断.4.(3分)(2017•呼和浩特)如图,是根据某市2010年至2014年工业生产总值绘制的折线统计图,观察统计图获得以下信息,其中信息判断错误的是()A.2010年至2014年间工业生产总值逐年增加B.2014年的工业生产总值比前一年增加了40亿元C.2012年与2013年每一年与前一年比,其增长额相同D.从2011年至2014年,每一年与前一年比,2014年的增长率最大【考点】VD:折线统计图.【分析】根据题意结合折线统计图确定正确的选项即可.【解答】解:A、2010年至2014年间工业生产总值逐年增加,正确,不符合题意;B、2014年的工业生产总值比前一年增加了40亿元,正确,不符合题意;C、2012年与2013年每一年与前一年比,其增长额相同,正确,不符合题意;D、从2011年至2014年,每一年与前一年比,2012年的增长率最大,故D符合题意;故选:D.【点评】本题考查了折线统计图,计算增长率是解题关键.5.(3分)(2017•呼和浩特)关于x的一元二次方程x2+(a2﹣2a)x+a﹣1=0的两个实数根互为相反数,则a的值为()A.2 B.0 C.1 D.2或0【考点】AB:根与系数的关系.【专题】11 :计算题.【分析】设方程的两根为x1,x2,根据根与系数的关系得a2﹣2a=0,解得a=0或a=2,然后利用判别式的意义确定a的取值.【解答】解:设方程的两根为x1,x2,根据题意得x1+x2=0,所以a2﹣2a=0,解得a=0或a=2,当a=2时,方程化为x2+1=0,△=﹣4<0,故a=2舍去,所以a的值为0.故选B.【点评】本题考查了根与系数的关系:若x1,x2是一元二次方程ax2+bx+c=0(a≠0)的两根时,x1+x2=﹣ba,x1x2=ca.也考查了根的判别式.6.(3分)(2017•呼和浩特)一次函数y=kx +b 满足kb >0,且y 随x 的增大而减小,则此函数的图象不经过( )A .第一象限B .第二象限C .第三象限D .第四象限【考点】F7:一次函数图象与系数的关系.【分析】根据y 随x 的增大而减小得:k <0,又kb >0,则b <0.再根据k ,b 的符号判断直线所经过的象限.【解答】解:根据y 随x 的增大而减小得:k <0,又kb >0,则b <0, 故此函数的图象经过第二、三、四象限,即不经过第一象限.故选A .【点评】能够根据k ,b 的符号正确判断直线所经过的象限.7.(3分)(2017•呼和浩特)如图,CD 为⊙O 的直径,弦AB ⊥CD ,垂足为M ,若AB=12,OM :MD=5:8,则⊙O 的周长为( )A .26πB .13πC .96π5D .39√10π5【考点】M2:垂径定理. 【分析】连接OA ,根据垂径定理得到AM=12AB=6,设OM=5x ,DM=8x ,得到OA=OD=13x ,根据勾股定理得到OA=12×13,于是得到结论. 【解答】解:连接OA ,∵CD 为⊙O 的直径,弦AB ⊥CD ,∴AM=12AB=6, ∵OM :MD=5:8,∴设OM=5x ,DM=8x ,∴OA=OD=13x ,∴AM=12x=6,∴x=12, ∴OA=12×13, ∴⊙O 的周长=2OA•π=13π,故选B .【点评】本题考查的是垂径定理,根据题意作出辅助线,构造出直角三角形,利用勾股定理求解是解答此题的关键.8.(3分)(2017•呼和浩特)下列运算正确的是( )A .(a 2+2b 2)﹣2(﹣a 2+b 2)=3a 2+b 2B .a 2+1a−1﹣a ﹣1=2a a−1C .(﹣a )3m ÷a m =(﹣1)m a 2mD .6x 2﹣5x ﹣1=(2x ﹣1)(3x ﹣1) 【考点】6B :分式的加减法;4I :整式的混合运算;57:因式分解﹣十字相乘法等.【分析】直接利用分式的加减运算法则以及结合整式除法运算法则和因式分解法分别分析得出答案.【解答】解:A 、(a 2+2b 2)﹣2(﹣a 2+b 2)=3a 2,故此选项错误;B 、a 2+1a−1﹣a ﹣1=a 2+1−(a+1)(a−1)a−1=2a−1,故此选项错误; C 、(﹣a )3m ÷a m =(﹣1)m a 2m ,正确;D 、6x 2﹣5x ﹣1,无法在实数范围内分解因式,故此选项错误;故选:C .【点评】此题主要考查了分式的加减运算以及整式除法运算和因式分解等知识,正确掌握运算法则是解题关键.9.(3分)(2017•呼和浩特)如图,四边形ABCD 是边长为1的正方形,E ,F 为BD 所在直线上的两点,若AE=√5,∠EAF=135°,则下列结论正确的是( )A .DE=1B .tan ∠AFO=13C .AF=√102D .四边形AFCE 的面积为94【考点】LE :正方形的性质;T7:解直角三角形.【分析】根据正方形的性质求出AO 的长,用勾股定理求出EO 的长,然后由∠MAN=135°及∠BAD=90°可以得到相似三角形,根据相似三角形的性质求出BF 的长,再一一计算即可判断.【解答】解:∵四边形ABCD 是正方形,∴AB=CB=CD=AD=1,AC ⊥BD ,∠ADO=∠ABO=45°,∴OD=OB=OA=√22,∠ABF=∠ADE=135°, 在Rt △AEO 中,EO=√AE 2−OA 2=√5−12=32√2, ∴DE=√2,故A 错误.∵∠EAF=135°,∠BAD=90°,∴∠BAF +∠DAE=45°,∵∠ADO=∠DAE +∠AED=45°,∴∠BAF=∠AED ,∴△ABF ∽△EDA ,∴BF DA =AB DE , ∴BF 1=√2, ∴BF=√22, 在Rt △AOF 中,AF=√OA 2+OF 2=√(√22)+(√2)=√102,故C 正确,tan ∠AFO=OA OF =√22√2=12,故B 错误, ∴S 四边形AECF =12•AC•EF=12×√2×52√2=52,故D 错误, 故选C .【点评】本题考查的是相似三角形的判定与性质,根据正方形的性质,运用勾股定理求出相应线段的长,再根据∠EAF=135°和∠BAD=90°,得到相似三角形,用相似三角形的性质求出BF 的长,然后根据对称性求出四边形的面积.10.(3分)(2017•呼和浩特)函数y=x 2+1|x|的大致图象是( ) A . B . C .D .【考点】E6:函数的图象.【分析】本题可用排除法解答,根据y 始终大于0,可排除D ,再根据x ≠0可排除A ,根据函数y=x 2+1|x|和y=32x 有交点即可排除C ,即可解题. 【解答】解:①∵|x |为分母,∴|x |≠0,即|x |>0,∴A 错误;②∵x 2+1>0,|x |>0,∴y=x 2+1|x|>0,∴D 错误; ③∵当直线经过(0,0)和(1,32)时,直线解析式为y=32x , 当y=32x=x 2+1|x|时,x=√2, ∴y=32x 与y=x 2+1|x|有交点,∴C 错误; ④∵当直线经过(0,0)和(1,1)时,直线解析式为y=x ,当y=x=x 2+1|x|时,x 无解, ∴y=x 与y=x 2+1|x|没有有交点,∴B 正确; 故选B .【点评】此题主要考查了函数图象的性质,考查了平方根和绝对值大于等于0的性质,本题中求得直线与函数的交点是解题的关键.二、填空题(本大题共6小题,每小题3分,共18分)11.(3分)(2017•呼和浩特)若式子√1−2x 有意义,则x 的取值范围是 x <12 .【考点】72:二次根式有意义的条件;62:分式有意义的条件.【分析】根据二次根式有意义的条件:被开方数为非负数,再结合分式有意义的条件:分母≠0,可得不等式1﹣2x >0,再解不等式即可.【解答】解:由题意得:1﹣2x >0, 解得:x <12, 故答案为:x <12,【点评】此题主要考查了二次根式有意义的条件;用到的知识点为:二次根式有意义,被开方数为非负数.12.(3分)(2017•呼和浩特)如图,AB ∥CD ,AE 平分∠CAB 交CD 于点E ,若∠C=48°,则∠AED为114°.【考点】JA:平行线的性质;IJ:角平分线的定义.【分析】根据平行线性质求出∠CAB的度数,根据角平分线求出∠EAB的度数,根据平行线性质求出∠AED的度数即可.【解答】解:∵AB∥CD,∴∠C+∠CAB=180°,∵∠C=48°,∴∠CAB=180°﹣48°=132°,∵AE平分∠CAB,∴∠EAB=66°,∵AB∥CD,∴∠EAB+∠AED=180°,∴∠AED=180°﹣66°=114°,故答案为:114.【点评】本题考查了角平分线定义和平行线性质的应用,解题时注意:两条平行线被第三条直线所截,同旁内角互补.13.(3分)(2017•呼和浩特)如图是某几何体的三视图,根据图中数据,求得该几何体的表面积为(225+25√2)π.【考点】U3:由三视图判断几何体.【分析】根据给出的几何体的三视图可知几何体是由圆柱体和圆锥体构成,从而根据三视图的特点得知高和底面直径,代入表面积公式计算即可.【解答】解:由三视图可知,几何体是由圆柱体和圆锥体构成,故该几何体的表面积为:20×10π+π×82+12×10π×√52+52=(225+25√2)π 故答案是:(225+25√2)π.【点评】本题考查了由三视图判断几何体,该三视图中的数据确定圆锥的底面直径和高是解本题的关键;本题体现了数形结合的数学思想,注意圆锥的高,母线长,底面半径组成直角三角形.14.(3分)(2017•呼和浩特)下面三个命题:①若{x =a y =b 是方程组{|x|=22x −y =3的解,则a +b=1或a +b=0; ②函数y=﹣2x 2+4x +1通过配方可化为y=﹣2(x ﹣1)2+3;③最小角等于50°的三角形是锐角三角形,其中正确命题的序号为 ②③ .【考点】O1:命题与定理.【分析】①根据方程组的解的定义,把{x =a y =b 代入{|x|=22x −y =3,即可判断; ②利用配方法把函数y=﹣2x 2+4x +1化为顶点式,即可判断;③根据三角形内角和定理以及锐角三角形的定义即可判断.【解答】解:①把{x =a y =b 代入{|x|=22x −y =3,得{|a|=22a −b =3, 如果a=2,那么b=1,a +b=3;如果a=﹣2,那么b=﹣7,a +b=﹣9.故命题①是假命题;②y=﹣2x 2+4x +1=﹣2(x ﹣1)2+3,故命题②是真命题;③最小角等于50°的三角形,最大角不大于80°,一定是锐角三角形,故命题③是真命题.所以正确命题的序号为②③.故答案为②③.【点评】主要考查命题的真假判断,正确的命题叫真命题,错误的命题叫做假命题.判断命题的真假关键是要熟悉课本中的定义以及性质定理等知识.15.(3分)(2017•呼和浩特)如图,在▱ABCD 中,∠B=30°,AB=AC ,O 是两条对角线的交点,过点O 作AC 的垂线分别交边AD ,BC 于点E ,F ,点M 是边AB 的一个三等分点,则△AOE 与△BMF 的面积比为 3:4 .【考点】S9:相似三角形的判定与性质;L5:平行四边形的性质.【分析】作MH ⊥BC 于H ,设AB=AC=m ,则BM=13m ,MH=12BM=16m ,根据平行四边形的性质求得OA=OC=12AC=12m ,解直角三角形求得FC=√33m ,然后根据ASA 证得△AOE ≌△COF ,证得AE=FC=√33m ,进一步求得OE=12AE=√36m ,从而求得S △AOE =√324m 2,作AN ⊥BC 于N ,根据等腰三角形的性质以及解直角三角形求得BC=√3m ,进而求得BF=BC ﹣FC=√3m ﹣√33m=2√33m ,分别求得△AOE 与△BMF 的面积,即可求得结论.【解答】解:设AB=AC=m ,则BM=13m , ∵O 是两条对角线的交点,∴OA=OC=12AC=12m , ∵∠B=30°,AB=AC ,∴∠ACB=∠B=30°,∵EF ⊥AC ,∴cos ∠ACB=OC FC ,即cos30°=12m FC , ∴FC=√33m , ∵AE ∥FC ,∴∠EAC=∠FCA ,又∵∠AOE=∠COF ,AO=CO ,∴△AOE ≌△COF ,∴AE=FC=√33m , ∴OE=12AE=√36m , ∴S △AOE =12OA•OE=12×12m ×√36m=√324m 2, 作AN ⊥BC 于N ,∵AB=AC ,∴BN=CN=12BC , ∵BN=√32AB=√32m , ∴BC=√3m ,∴BF=BC ﹣FC=√3m ﹣√33m=2√33m , 作MH ⊥BC 于H ,∵∠B=30°, ∴MH=12BM=16m , ∴S △BMF =12BF•MH=12×2√33m ×16m=√318m 2, ∴S △AOE S △BMF =√324m 2√318m =34. 故答案为3:4.【点评】本题考查了平行四边形的性质、全等三角形的判定和性质以及解直角三角形等,熟练掌握性质定理是解题的关键.16.(3分)(2017•呼和浩特)我国魏晋时期数学家刘徽首创“割圆术”计算圆周率.随着时代发展,现在人们依据频率估计概率这一原理,常用随机模拟的方法对圆周率π进行估计,用计算机随机产生m 个有序数对(x ,y )(x ,y 是实数,且0≤x ≤1,0≤y ≤1),它们对应的点在平面直角坐标系中全部在某一个正方形的边界及其内部.如果统计出这些点中到原点的距离小于或等于1的点有n 个,则据此可估计π的值为 4n m .(用含m ,n 的式子表示)【考点】X8:利用频率估计概率;D2:规律型:点的坐标.【分析】根据落在扇形内的点的个数与正方形内点的个数之比等于两者的面积之比列出14⋅π1=n m,可得答案. 【解答】解:根据题意,点的分布如图所示:则有14⋅π1=n m, ∴π=4n m, 故答案为:4n m. 【点评】此题主要考查了利用频率估计概率,大量反复试验下频率稳定值即概率.用到的知识点为:频率=所求情况数与总情况数之比.三、解答题(本大题共9小题,共72分)17.(10分)(2017•呼和浩特)(1)计算:|2﹣√5|﹣√2(√18﹣√102)+32; (2)先化简,再求值:x−2x 2+2x ÷x 2−4x+4x 2−4+12x ,其中x=﹣65. 【考点】6D :分式的化简求值;2C :实数的运算. 【专题】11 :计算题;513:分式.【分析】(1)原式利用绝对值的代数意义化简,去括号合并即可得到结果;(2)原式第一项利用除法法则变形,约分后利用同分母分式的加法法则计算得到最简结果,把x 的值代入计算即可求出值.【解答】解:(1)原式=√5﹣2﹣12+√5+32=2√5﹣1; (2)原式=x−2x(x+2)•(x+2)(x−2)(x−2)2+12x =1x +12x =32x, 当x=﹣65时,原式=﹣54. 【点评】此题考查了分式的化简求值,以及实数的运算,熟练掌握运算法则是解本题的关键.18.(6分)(2017•呼和浩特)如图,等腰三角形ABC 中,BD ,CE 分别是两腰上的中线.(1)求证:BD=CE ;(2)设BD 与CE 相交于点O ,点M ,N 分别为线段BO 和CO 的中点,当△ABC 的重心到顶点A 的距离与底边长相等时,判断四边形DEMN 的形状,无需说明理由.【考点】KD :全等三角形的判定与性质;K5:三角形的重心;KH :等腰三角形的性质.【分析】(1)根据已知条件得到AD=AE ,根据全等三角形的性质即可得到结论;(2)根据三角形中位线的性质得到ED ∥BC ,ED=12BC ,MN ∥BC ,MN=12BC ,等量代换得到ED ∥MN ,ED=MN ,推出四边形EDNM 是平行四边形,由(1)知BD=CE ,求得DM=EN ,得到四边形EDNM 是矩形,根据全等三角形的性质得到OB=OC ,由三角形的重心的性质得到O 到BC 的距离=12BC ,根据直角三角形的判定得到BD ⊥CE ,于是得到结论.【解答】(1)解:由题意得,AB=AC ,∵BD ,CE 分别是两腰上的中线,∴AD=12AC ,AE=12AB , ∴AD=AE ,在△ABD 和△ACE 中{AB =AC ∠A =∠A AD =AE,∴△ABD ≌△ACE (ASA ).∴BD=CE ;(2)四边形DEMN 是正方形,证明:∵E 、D 分别是AB 、AC 的中点,∴AE=12AB ,AD=12AC ,ED 是△ABC 的中位线, ∴ED ∥BC ,ED=12BC , ∵点M 、N 分别为线段BO 和CO 中点,∴OM=BM ,ON=CN ,MN 是△OBC 的中位线,∴MN ∥BC ,MN=12BC , ∴ED ∥MN ,ED=MN ,∴四边形EDNM 是平行四边形,由(1)知BD=CE ,又∵OE=ON ,OD=OM ,OM=BM ,ON=CN ,∴DM=EN ,∴四边形EDNM 是矩形,在△BDC 与△CEB 中,{BE =CD CE =BD BC =CB,∴△BDC ≌△CEB ,∴∠BCE=∠CBD ,∴OB=OC ,∵△ABC 的重心到顶点A 的距离与底边长相等,∴O 到BC 的距离=12BC , ∴BD ⊥CE ,∴四边形DEMN是正方形.【点评】本题考查了等腰三角形的性质、三角形中位线定理、矩形的判定、平行四边形的判定与性质、全等三角形的判定与性质;熟练掌握等腰三角形的性质和三角形中位线定理,并能进行推理论证是解决问题的关键.19.(10分)(2017•呼和浩特)为了解某地某个季度的气温情况,用适当的抽样方法从该地这个季度中抽取30天,对每天的最高气温x(单位:℃)进行调查,并将所得的数据按照12≤x<16,16≤x<20,20≤x<24,24≤x<28,28≤x<32分成五组,得到如图频数分布直方图.(1)求这30天最高气温的平均数和中位数(各组的实际数据用该组的组中值代表);(2)每月按30天计算,各组的实际数据用该组的组中值代表,估计该地这个季度中最高气温超过(1)中平均数的天数;(3)如果从最高气温不低于24℃的两组内随机选取两天,请你直接写出这两天都在气温最高一组内的概率.【考点】X6:列表法与树状图法;V5:用样本估计总体;V8:频数(率)分布直方图;W2:加权平均数;W4:中位数.【分析】(1)根据30天的最高气温总和除以总天数,即可得到这30天最高气温的平均数,再根据第15和16个数据的位置,判断中位数;(2)根据30天中,最高气温超过(1)中平均数的天数,即可估计这个季度中最高气温超过(1)中平均数的天数;(3)从6天中任选2天,共有15种等可能的结果,其中两天都在气温最高一组内的情况有6种,据此可得这两天都在气温最高一组内的概率.【解答】解:(1)这30天最高气温的平均数为:14×8+18×6+22×10+26×2+30×430=20.4℃;∵中位数落在第三组内,∴中位数为22℃;(2)∵30天中,最高气温超过(1)中平均数的天数为16天,∴该地这个季度中最高气温超过(1)中平均数的天数为1630×90=48(天);(3)从6天中任选2天,共有15种等可能的结果,其中两天都在气温最高一组内的情况有6种,故这两天都在气温最高一组内的概率为615=25.【点评】本题主要考查了频数分布直方图,平均数以及中位数的计算,一般来说,用样本去估计总体时,样本越具有代表性、容量越大,这时对总体的估计也就越精确.解题时注意:如果一组数据的个数是偶数,则中间两个数据的平均数就是这组数据的中位数.20.(7分)(2017•呼和浩特)某专卖店有A,B两种商品,已知在打折前,买60件A商品和30件B商品用了1080元,买50件A商品和10件B商品用了840元,A,B两种商品打相同折以后,某人买500件A商品和450件B商品一共比不打折少花1960元,计算打了多少折?【考点】9A :二元一次方程组的应用.【分析】设打折前A 商品的单价为x 元/件、B 商品的单价为y 元/件,根据“买60件A 商品和30件B 商品用了1080元,买50件A 商品和10件B 商品用了840元”,即可得出关于x 、y 的二元一次方程组,解之即可得出x 、y 的值,再算出打折前购买500件A 商品和450件B 商品所需钱数,结合少花钱数即可求出折扣率.【解答】解:设打折前A 商品的单价为x 元/件、B 商品的单价为y 元/件,根据题意得:{60x +30y =108050x +10y =840, 解得:{x =16y =4,500×16+450×4=9800(元),9800−19609800=0.8. 答:打了八折.【点评】本题考查了二元一次方程组的应用,找准等量关系,列出二元一次方程组是解题的关键.21.(6分)(2017•呼和浩特)已知关于x 的不等式2m−mx 2>12x ﹣1. (1)当m=1时,求该不等式的解集;(2)m 取何值时,该不等式有解,并求出解集.【考点】C3:不等式的解集.【专题】11 :计算题;524:一元一次不等式(组)及应用.【分析】(1)把m=1代入不等式,求出解集即可;(2)不等式去分母,移项合并整理后,根据有解确定出m 的范围,进而求出解集即可.【解答】解:(1)当m=1时,不等式为2−x 2>x 2﹣1, 去分母得:2﹣x >x ﹣2,解得:x <2;(2)不等式去分母得:2m ﹣mx >x ﹣2,移项合并得:(m +1)x <2(m +1),当m ≠﹣1时,不等式有解,当m >﹣1时,不等式解集为x <2;当x <﹣1时,不等式的解集为x >2.【点评】此题考查了不等式的解集,熟练掌握不等式的基本性质是解本题的关键.22.(7分)(2017•呼和浩特)如图,地面上小山的两侧有A ,B 两地,为了测量A ,B 两地的距离,让一热气球从小山西侧A 地出发沿与AB 成30°角的方向,以每分钟40m 的速度直线飞行,10分钟后到达C 处,此时热气球上的人测得CB 与AB 成70°角,请你用测得的数据求A ,B 两地的距离AB 长.(结果用含非特殊角的三角函数和根式表示即可)【考点】T8:解直角三角形的应用.【分析】过点C 作CM ⊥AB 交AB 延长线于点M ,通过解直角△ACM 得到AM 的长度,通过解直角△BCM 得到BM 的长度,则AB=AM ﹣BM .【解答】解:过点C 作CM ⊥AB 交AB 延长线于点M ,由题意得:AC=40×10=400(米).在直角△ACM 中,∵∠A=30°,∴CM=12AC=200米,AM=√32AC=200√3米. 在直角△BCM 中,∵tan20°=BM CM, ∴BM=200tan20°,∴AB=AM ﹣BM=200√3﹣200tan20°=200(√3﹣tan20°),因此A ,B 两地的距离AB 长为200(√3﹣tan20°)米.【点评】本题考查解直角三角形的应用、三角函数等知识,解题的关键是添加辅助线,构造直角三角形,记住三角函数的定义,以及特殊三角形的边角关系,属于中考常考题型.23.(7分)(2017•呼和浩特)已知反比例函数y=−k 2−1x(k 为常数). (1)若点P 1(1−√32,y 1)和点P 2(﹣12,y 2)是该反比例函数图象上的两点,试利用反比例函数的性质比较y 1和y 2的大小;(2)设点P (m ,n )(m >0)是其图象上的一点,过点P 作PM ⊥x 轴于点M .若tan ∠POM=2,PO=√5(O 为坐标原点),求k 的值,并直接写出不等式kx +k 2+1x>0的解集.【考点】G6:反比例函数图象上点的坐标特征;T7:解直角三角形.【分析】(1)先根据反比例函数的解析式判断出函数图象所在的象限及其增减性,再根据P 1、P 2两点的横坐标判断出两点所在的象限,故可得出结论.(2)根据题意求得﹣n=2m ,根据勾股定理求得m=1,n=﹣2,得到P (1,﹣2),即可得到﹣k 2﹣1=﹣2,即可求得k 的值,然后分两种情况借助反比例函数和正比例函数图象即可求得.【解答】解:(1)∵﹣k 2﹣1<0,∴反比例函数y=−k 2−1x在每一个象限內y 随x 的增大而增大, ∵﹣12<1−√32<0, ∴y 1>y 2;(2)点P (m ,n )在反比例函数y=−k 2−1x的图象上,m >0, ∴n <0,∴OM=m ,PM=﹣n ,∵tan∠POM=2,∴PMOM =−nm=2,∴﹣n=2m,∵PO=√5,∴m2+(﹣n)2=5,∴m=1,n=﹣2,∴P(1,﹣2),∴﹣k2﹣1=﹣2,解得k=±1,①当k=﹣1时,则不等式kx+k2+1x>0的解集为:x<﹣√2或0<x<√2;②当k=1时,则不等式kx+k2+1x>0的解集为:x>0.【点评】本题考查的是反比例函数图象上点的坐标特点,即反比例函数图象上各点的坐标一定适合此函数的解析式;也考查了反比例函数和一次函数的交点.24.(9分)(2017•呼和浩特)如图,点A,B,C,D是直径为AB的⊙O上的四个点,C是劣弧BD̂的中点,AC与BD交于点E.(1)求证:DC2=CE•AC;(2)若AE=2,EC=1,求证:△AOD是正三角形;(3)在(2)的条件下,过点C作⊙O的切线,交AB的延长线于点H,求△ACH 的面积.【考点】MR:圆的综合题.【分析】(1)由圆周角定理得出∠DAC=∠CDB,证明△ACD∽△DCE,得出对应边成比例,即可得出结论;(2)求出DC=√3,连接OC、OD,如图所示:证出BC=DC=√3,由圆周角定理得。
【数学】内蒙古呼和浩特市中考真题(解析版)
A. 0.96 107 km2
B. 960 104 km2 C. 9.6 106 km2 D. 9.6 105 km2
3.如图中序号(1)(2)(3)(4)对应的四个三角形,都是 ABC 这个图形进行了一次变换
之后得到的,其中是通过轴对称得到的是( )
A.(1)
B.(2)
C.(3)
D.(4)
4.如图,是根据某市 2010 年至 2014 年工业生产总值绘制的折线统计图,观察统计图获得 以下信息,其中信息判断错误的是( )
③最小角等于 50 的三角形是锐角三角形.
其中正确命题的序号为
.
15.如图,在 ABCD 中, B 30 , AB AC , O 是两条对角线的交点,过点 O 作 AC 的垂线分别交边 AD , BC 于点 E , F ,点 M 是边 AB 的一个三等分点,则 AOE 与 BMF 的面积比为 .
x
24.如图,点 A , B , C , D 是直径为 AB 的 O 上的四个点, C 是劣弧 BD 的中点, AC 与 BD 交于点 E .
(1)求证: DC 2 CE AC ; (2)若 AE 2 , EC 1,求证: AOD 是正三角形; (3)在(2)的条件下,过点 C 作 O 的切线,交 AB 的延长线于点 H ,求 ACH 的面
()
A. 2
B. 0
C.1
D. 2 或 0
6.一次函数 y kx b 满足 kb 0 ,且 y 随 x 的增大而减小,则此函数的图象不经过(
)
A.第一象限
B.第二象限
C.第三象限
D.第四象限
7.如图, CD 是 O 的直径,弦 AB CD ,垂足为 M ,若 AB 12 , OM : MD 5 : 8 ,则 O 的周长为( )
