哈夫曼树构造方法
哈夫曼树结点数和叶子结点数的关系

哈夫曼树结点数和叶子结点数的关系哈夫曼树是一种用来压缩信息的数据结构,它的关键在于能够将出现频率高的字符用较短的编码表示,从而达到节省空间的目的。
在构造哈夫曼树时,我们需要知道它的结点数和叶子结点数之间的关系,这是本文将要探讨的问题。
一、哈夫曼树的定义哈夫曼树(Huffman Tree)又称最优二叉树,是一种带权路径长度最短的树。
它的构造基于贪心算法,通过不断合并权值最小的两个子树来构造出最终的哈夫曼树。
在哈夫曼树中,树的每一个叶子结点都对应着一个字符,并且权值越大的叶子结点距离根结点越近。
二、哈夫曼树的结点数对于给定的n个字符(字符的出现概率已知),构造哈夫曼树时所需要的结点数是2n-1个。
这个结论可以通过归纳法证明。
首先,当n=1时,哈夫曼树只有一个结点,结论成立。
其次,当n=2时,哈夫曼树有3个结点。
假设当n=k时结论成立,考虑当n=k+1时的情况。
我们先对n个字符进行排序,找出权值最小的两个字符,将它们的权值相加得到一个新的权值,并构造一棵新的子树。
这样就将原来的n 个字符缩减成了n-1个字符,并且引入了一个新的结点。
在接下来的n-2次合并中,每次都引入了一个新的结点,所以总共需要2n-3个结点来构造出这n个字符对应的哈夫曼树。
此时,还需要引入一个新的根结点,作为两个结点(n个字符对应的两个子树)的父结点,并将两个子树连接到这个新的根结点上。
因此,总结点数为2n-3+1=2n-2。
最后,将新的根结点变为虚拟结点,并将n个叶子结点作为其子结点,就得到了结点数为2n-1的哈夫曼树。
三、哈夫曼树的叶子结点数在哈夫曼树中,每个叶子结点都对应着一个字符,因此叶子结点数就等于字符的个数n。
这个结论显然成立。
综上所述,哈夫曼树的结点数和叶子结点数之间存在如下关系:- 结点数 = 2n-1- 叶子结点数 = n这个结论可以帮助我们更好地理解哈夫曼树的构造过程,并且可以在实际应用中帮助我们提前估算哈夫曼树的大小。
判定树
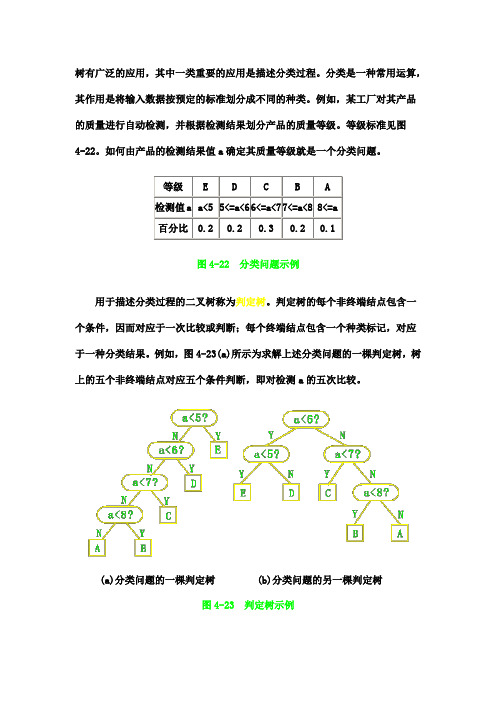
树有广泛的应用,其中一类重要的应用是描述分类过程。
分类是一种常用运算,其作用是将输入数据按预定的标准划分成不同的种类。
例如,某工厂对其产品的质量进行自动检测,并根据检测结果划分产品的质量等级。
等级标准见图4-22。
如何由产品的检测结果值a 确定其质量等级就是一个分类问题。
图4-22 分类问题示例用于描述分类过程的二叉树称为判定树。
判定树的每个非终端结点包含一个条件,因而对应于一次比较或判断;每个终端结点包含一个种类标记,对应于一种分类结果。
例如,图4-23(a)所示为求解上述分类问题的一棵判定树,树上的五个非终端结点对应五个条件判断,即对检测a 的五次比较。
(a)分类问题的一棵判定树(b)分类问题的另一棵判定树图4-23 判定树示例易知一棵判定树描述了一种分类方法。
图4-23(a)中判定树对应的分类算法如下:char classify1(float x)/ * 依给定标准将检测值x区分成相应的质量等级作为返回值 */{ if(x<5) return ('E');else if(x<6) return('D');else if(x<7)return('C');else if(x<8) return('B');else return('A');}利用这个算法,可由产品的检测结果值x确定其质量等级。
当一个分类算法需要反复使用时,其时间性能就值得进一步考虑。
假如进行上述产品质量自动分类(定等级)的工厂的产量很大,上述分类算法就将被频繁地重复使用,这时就需要考虑其时间性能。
假设需要分级的产品有N=100000件,并且这批产品的等级分布如图4-22中表格的第三行所示。
某等级产品总比较次数=某等级的“产品数”X单个检测的“比较次数”比如,D级产品数为N*20%个,为区分出一件产品是D级的,需进行2次比较。
那么,D级产品总比较次数=N*20%*2=100000*0.2*2=40000。
数据结构课程设计(哈夫曼编码)

┊┊┊┊┊┊┊┊┊┊┊┊┊装┊┊┊┊┊订┊┊┊┊┊线┊┊┊┊┊┊┊┊┊┊┊┊┊目录目录 (1)1 课程设计的目的和意义 (2)2 需求分析 (3)3 系统设计 (4)(1)设计思路及方案 (4)(2)模块的设计及介绍 (4)(3)主要模块程序流程图 (6)4 系统实现 (10)(1)主调函数 (10)(2)建立HuffmanTree (10)(3)生成Huffman编码并写入文件 (13)(4)电文译码 (14)5 系统调试 (16)小结 (18)参考文献 (19)附录源程序 (20)┊┊┊┊┊┊┊┊┊┊┊┊┊装┊┊┊┊┊订┊┊┊┊┊线┊┊┊┊┊┊┊┊┊┊┊┊┊1 课程设计的目的和意义在当今信息爆炸时代,如何采用有效的数据压缩技术来节省数据文件的存储空间和计算机网络的传送时间已越来越引起人们的重视。
哈夫曼编码正是一种应用广泛且非常有效的数据压缩技术。
哈夫曼编码的应用很广泛,利用哈夫曼树求得的用于通信的二进制编码称为哈夫曼编码。
树中从根到每个叶子都有一条路径,对路径上的各分支约定:指向左子树的分支表示“0”码,指向右子树的分支表示“1”码,取每条路径上的“0”或“1”的序列作为和各个对应的字符的编码,这就是哈夫曼编码。
通常我们把数据压缩的过程称为编码,解压缩的过程称为解码。
电报通信是传递文字的二进制码形式的字符串。
但在信息传递时,总希望总长度尽可能最短,即采用最短码。
作为软件工程专业的学生,我们应该很好的掌握这门技术。
在课堂上,我们能过学到许多的理论知识,但我们很少有过自己动手实践的机会!课程设计就是为解决这个问题提供了一个平台。
在课程设计过程中,我们每个人选择一个课题,认真研究,根据课堂讲授内容,借助书本,自己动手实践。
这样不但有助于我们消化课堂所讲解的内容,还可以增强我们的独立思考能力和动手能力;通过编写实验代码和调试运行,我们可以逐步积累调试C程序的经验并逐渐培养我们的编程能力、用计算机解决实际问题的能力。
6-10+哈夫曼树

哈夫曼--编码
按A B C D E F G H 这八个字母出现的频率构造哈夫曼树。
A:0110,B:10,C:1110,D:1111, E:110,F:00,G:0111,H:010
树的带权路径长度的含义是各个字符的编码长与 其出现次数的乘积之和,也就是电文的代码总长, 所以采用哈夫曼树构造的编码是一种能使电文代码 总长最短的不等长编码。
对于同一组给定叶结点所构造的哈夫曼树,树的形状可 能不同,但带权路径长度值是相同的,一定是最小的
哈夫曼树—示例 叶结点权值集合为W = W = {7,5,3,1}构造哈夫曼树三种形态:
给定n个权值,需经过n-1次合并最终能得到一棵哈夫曼树。 经过n-1次合并得到n-1个新结点,这n-1个新结点都是具有两个孩子结点的分支 结点。也就是说哈夫曼树中没有度为1的结点。 构造的哈夫曼树共有2n-1个结点。
这样的编码不能保证译码的唯一性,我们称之为具有二义性的译码。
哈夫曼--编码
哈夫曼树可用于构造使电文的编码总长最短的编码方案,且不会产生二义性。
设需要编码的字符集合为{d1,d2,…,dn}, 它们在电文中出现的次数或频率集合为{w1,w2,…,wn}, 以d1,d2,…,dn作为叶结点,w1,w2,…,wn作为它们的权值, 构造一棵哈夫曼树,然后,规定哈夫曼树中的左分支代表0,右分支代表1, 则从根结点到每个叶结点所经过的路径分支组成的0和1的序列便为该结点对应 字符的编码,我们称之为哈夫曼编码。
哈夫曼树--基本概念
给定一组权值,用以作为叶结点可以构造出不同形状的二叉树。 例如,设有4个权值分别为1,3,5,7,作为4个叶结点,构造二叉树。
(a)
(b)
(c)
(d)
(e)
树的遍历和哈夫曼树

2021/4/18 北京化工大学信息学院 数据结构 33
求二叉树高度的递归算法
int Height ( BinTreeNode * T ) { if ( T == NULL ) return -1; else { int m = Height ( T->leftChild ); int n = Height ( T->rightChild ) ); return (m > n) ? m+1 : n+1;
中序遍历 (Inorder Traversal)
中序遍历二叉树算法的框架是:
若二叉树为空,则空操作;
-
否则 中序遍历左子树 (L);
+
/
访问根结点 (V);
a *e f
中序遍历右子树 (R)。
遍历结果
b-
a+b*c-d-e/f
cd
2021/4/18 北京化工大学信息学院 数据结构 20
二叉树递归的中序遍历算法
如果 n = 0,称为空树;如果 n > 0,则 ▪ 有一个特定的称之为根(root)的结点,
它只有直接后继,但没有直接前驱; ▪ 除根以外的其它结点划分为 m (m 0)
个 互不相交的有限集合T0, T1, …, Tm-1,每 个集合又是一棵树,并且称之为根的子树。
2021/4/18 北京化工大学信息学院 数据结构 3
typedef struct node { //树结点定义
TreeData data;
//结点数据域
struct node * leftChild, * rightchild;
//子女指针域
} BinTreeNode;
typedef BinTreeNode * BinTree; //树定义,代表树的根指针
哈夫曼时间复杂度

哈夫曼时间复杂度哈夫曼编码是一种常用的数据压缩算法,它通过构建最优的二叉树来实现对数据的高效编码。
在实际应用中,我们需要对哈夫曼编码的时间复杂度进行分析,以评估算法的性能和效率。
本文将讨论哈夫曼编码的时间复杂度,并对其进行详细解释。
一、哈夫曼编码的基本原理哈夫曼编码是一种变长编码方式,其基本原理是根据不同字符的出现频率构建一颗最优的二叉树,使得出现频率高的字符拥有较短的编码,而出现频率低的字符拥有较长的编码。
通过这种方式,我们可以实现对数据的高效压缩和解压缩。
二、哈夫曼编码的时间复杂度1. 构建哈夫曼树的时间复杂度:O(nlogn)构建哈夫曼树的过程主要包括以下几个步骤:(1)根据字符的出现频率构建小顶堆:O(nlogn)。
(2)通过不断合并堆顶的两个节点构建哈夫曼树:O(nlogn)。
因此,构建哈夫曼树的总时间复杂度为O(nlogn)。
2. 生成哈夫曼编码的时间复杂度:O(n)生成哈夫曼编码的过程是在哈夫曼树的基础上通过遍历每个叶子节点来得到对应的编码。
由于哈夫曼树中每个叶子节点都是对应一个字符,因此遍历每个叶子节点的时间复杂度为O(n)。
3. 压缩和解压缩数据的时间复杂度:O(n)在得到了字符对应的哈夫曼编码后,对于压缩和解压缩数据的操作,其时间复杂度主要取决于数据的长度,即O(n)。
综上所述,哈夫曼编码的总时间复杂度为O(nlogn),其中n为数据的长度。
值得注意的是,由于构建哈夫曼树的过程中涉及到了对频率进行排序的操作,因此时间复杂度比较高。
三、哈夫曼编码的应用哈夫曼编码在实际应用中被广泛使用,尤其是在数据压缩领域。
通过使用哈夫曼编码,我们可以大幅度减少数据的存储空间和传输带宽,提高数据的传输效率。
此外,哈夫曼编码还可以应用于图像压缩、音频压缩等领域。
通过对图像或音频数据进行编码,我们可以将其压缩为较小的文件大小,从而节省存储空间和提高传输效率。
总结:哈夫曼编码是一种高效的数据压缩算法,通过构建最优的二叉树实现对数据的编码和解码。
霍夫曼树

2.6.2 图的存储结构
(1)图的连接矩阵表示法 (2)图的邻接表示法
2014-6-24
30
图的连接矩阵表示法
V1 V2 V3 V4 V1 0 0 1 0
V1
V3
V2
V3 V2 V4 V4
0
0 1
0
0 0
0
0 0
1
1 0
V1 V2 V3 V4 V1 V1 V3 V2 V3 V2 V4
2014-6-24
28
权:与图的边或弧相关的数。 网:带权的图。 顶点的度:依附于该顶点的边数或弧数。 出度:(仅对有向图)以该顶点为尾的弧数。 入度:(仅对有向图)以该顶点为头的弧数。 路径:顶点A与顶点C之间存在一条路径。路 径上边或弧的数目称为该路径的路径长度。
3 2 5
A
1
B D
C
6
2014-6-24
29
B D
5
C
6
V表示顶点的非空有限集合。
VR表示两个顶点之间关系的集合。
2014-6-24
24
有向图
图
无向图
若<v,w>属于VR,则<v,w>表示从v到w的一条 弧,且称v为弧尾,w为弧头。此时的图称为 有向图。 若<v,w>属于VR,必有<w,v>,即VR是对称的, 则以无序对(v,w)代替这两个有序对,表示v 和w之间的一条边。此时的图称为有向图。
WPL最小的二叉树就称作最优二叉树或哈夫曼树 。
2014-6-24
6
哈夫曼树 (最优树)
加权路径长度最小的二叉树就 是哈夫曼树。
n
公式:
WPL
k 1
WK LK
浅析基于哈夫曼树与哈夫曼编码的数据压缩

4 . 将哈夫曼树信息写入输 出文件, 以各解压缩使用 。 5 . 再度扫描源文件, 将源 文件 的数据生成对应哈夫曼编码 , 写入到输 出 文件。对文件做标示, 最终完成源文件 的压缩。 上面这一算法是根据经典 的哈夫曼编码思想引出,压缩时首先扫描源
2 . 在F 中选 出两棵根结点权值 最小的树作 为一棵新 的二叉树 的左右子 树, 且置新二叉树根结点的权值为两棵子树根结点的权值之和 。 3 . 从F 中删去这两棵树, 同时把新二叉树加入F 中 4 . 重复2 和3 , 直到F 中只有一棵树 为止 , 此树便是哈夫曼树 。 从哈夫曼树 的构造方法,我们可以推导 出构造哈夫曼树 的算法实现原 理: 基于哈夫曼树没有度 为1 的结点, 根据二叉树性质 , 可 推导知一棵有n 个 叶子的哈夫曼树共有2 n - 1 个结点, 我们可定义大 小为2 n - 1 的一维数组存储 哈夫曼树。这个数组 的前n 个位 置存放 的为已知 的叶子结点 , 后( n 一 1 ) 个位 置存放 的为动态生成的树 内结点。在算法的大循环 过程中, 就是根据位置i 前面的已知结点找出结点权值最小的两个结 点,然后根据这两个结点构造
科 学研 究
嗨 与赋
浅析基于哈夫曼树与哈夫曼编码的数据压缩
李 玮 琦
( 达州职业技术 学院 四川 达州 6 3 5 0 0 1 )
摘 要: 哈夫曼编码作为一种最常用 的不等长无损压缩编码方法 , 在数据压缩程序 中具有非常重要 的应用 。本文是基于哈夫曼树与哈弗曼编码 的数 据压缩算法。 关键词: 哈夫曼树 哈弗曼编码 数据压缩 算法
出 位 置i 的新 的父 结 点 , 即一 棵 新 树 的根 结 点 。 三、 哈 夫 曼 编 码
文件, 根据源文件中数据 出现频率生成字符频率表 , 据此构造哈夫曼树并生 成长短不~ 的编码 , 再将 哈夫曼编码写入压缩文件 , 对文件做出标示后完成 压缩过程, 解压缩时只要逆转编码过程即可 。 这样 的压缩算法能够 以较高压缩率完成文件的压缩,不过分析算法步 骤后发现 , 这一算法有明显缺 陷, 在于需要对源文件进行两次扫描, 第一次 扫描 目的在 于统计并建立频率表 , 以便解压缩使用, 第二次扫描 目的在于得 到哈夫曼编码 。如果源文件较大, 扫描两次所引发的低效率不容忽视 , 同时 重复扫描也增加 了磁盘访 问, 再次降低压缩效率。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
哈夫曼树构造方法
哈夫曼树(Huffman Tree)是一种广泛应用于数据压缩和编码
的二叉树结构。
它是一种最优二叉树,即带权路径长度最短的二叉树。
哈夫曼树的构造方法主要有两种:贪心算法和分治算法。
1. 贪心算法:
哈夫曼树的贪心算法是一种自底向上(从叶子节点到根节点)的构造方法。
首先,根据给定的权值列表,将每个权值看作一个独立的节点,并按照权值从小到大的顺序构建一个森林。
然后,从森林中选择权值最小的两个节点(可以使用最小堆来实现),将它们合并为一个新的节点,并将新节点的权值设为两个被合并节点的权值之和。
将新节点插入到森林中,并移除原来的两个节点。
重复上述步骤,直到森林中只有一个节点为止,该节点就是哈夫曼树的根节点。
贪心算法构造哈夫曼树的时间复杂度为O(nlogn),n为节点数量。
2. 分治算法:
哈夫曼树的分治算法是一种自顶向下(从根节点到叶子节点)的构造方法。
首先,将给定的权值列表按照权值从小到大的顺序排序。
然后,将权值最小的两个节点合并为一个新的节点,并将新节点的权值设为两个被合并节点的权值之和。
将新节点插入到排序后的列表中,并移除原来的两个节点。
重复上述步骤,直到列表中只有一个节点为止,该节点就是哈夫曼树的根
节点。
分治算法构造哈夫曼树的时间复杂度为O(n^2),n为节点数量。
无论是贪心算法还是分治算法,构造出的哈夫曼树都具有最优性质,即带权路径长度最短。
由于贪心算法的时间复杂度较低,因此在实际应用中更为常用。
另外,构造哈夫曼树的方法除了贪心算法和分治算法外,还可以使用动态规划等其他方法。
对于哈夫曼树的应用,最常见的是数据压缩和编码。
哈夫曼树可以根据字符出现的频率构建对应的编码表,将频率高的字符用较短的编码表示,将频率低的字符用较长的编码表示,从而实现对数据的压缩。
在压缩的过程中,利用哈夫曼树可以实现对数据的高效编码和解码。
此外,哈夫曼树还有其他应用,比如在路由表的构建和图像压缩等领域也有广泛应用。
总结起来,哈夫曼树是一种最优二叉树,可以通过贪心算法或分治算法构造。
贪心算法是一种自底向上的构造方法,时间复杂度为O(nlogn);分治算法是一种自顶向下的构造方法,时间复杂度为O(n^2)。
哈夫曼树主要用于数据压缩和编码,是一
种高效的数据压缩算法。
通过构造哈夫曼树,可以实现对数据的高效编码和解码,从而实现数据的压缩和解压缩。
