数值分析第四章数值积分与数值微分习题答案

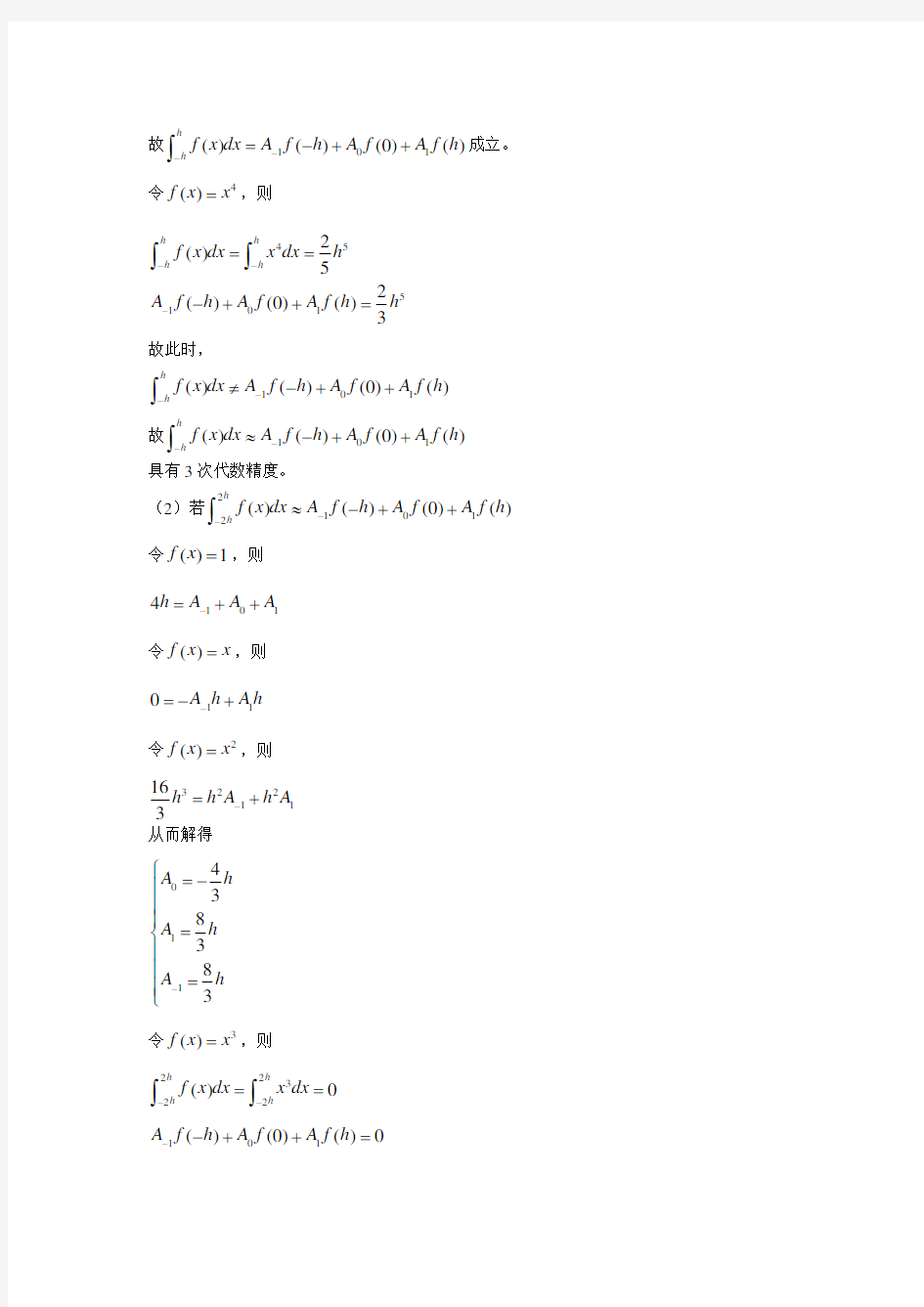
第四章 数值积分与数值微分
1.确定下列求积公式中的特定参数,使其代数精度尽量高,并指明所构造出的求积公式所具有的代数精度:
101210121
12120
(1)()()(0)();
(2)()()(0)();
(3)()[(1)2()3()]/3;
(4)()[(0)()]/2[(0)()];
h
h
h
h h
f x dx A f h A f A f h f x dx A f h A f A f h f x dx f f x f x f x dx h f f h ah f f h -----≈-++≈-++≈-++''≈++-??
??
解:
求解求积公式的代数精度时,应根据代数精度的定义,即求积公式对于次数不超过m 的多项式均能准确地成立,但对于m+1次多项式就不准确成立,进行验证性求解。 (1)若101(1)
()()(0)()h
h
f x dx A f h A f A f h --≈-++?
令()1f x =,则
1012h A A A -=++
令()f x x =,则
110A h Ah -=-+
令2
()f x x =,则
3
221123
h h A h A -=+ 从而解得
011431313A h A h A h -?=??
?
=??
?=??
令3
()f x x =,则
3()0h
h
h
h
f x dx x dx --==?
?
101()(0)()0A f h A f A f h --++=
令4()f x x =,则
455
1012()5
2
()(0)()3
h
h
h
h
f x dx x dx h A f h A f A f h h ---==
-++=?
?
故此时,
101()()(0)()h
h
f x dx A f h A f A f h --≠-++?
故
101()()(0)()h h
f x dx A f h A f A f h --≈-++?
具有3次代数精度。 (2)若
21012()()(0)()h
h
f x dx A f h A f A f h --≈-++?
令()1f x =,则
1014h A A A -=++
令()f x x =,则
110A h Ah -=-+
令2
()f x x =,则
3
2211163
h h A h A -=+ 从而解得
1143
8383A h A h A h -?=-??
?
=??
?=??
令3
()f x x =,则
22322()0h
h
h
h
f x dx x dx --==?
?
101()(0)()0A f h A f A f h --++=
令4()f x x =,则
2245
2264()5
h
h
h
h
f x dx x dx h --==
?
?
5
10116()(0)()3
A f h A f A f h h --++=
故此时,
21012()()(0)()h
h
f x dx A f h A f A f h --≠-++?
因此,
21012()()(0)()h h
f x dx A f h A f A f h --≈-++?
具有3次代数精度。 (3)若
1
121
()[(1)2()3()]/3f x dx f f x f x -≈-++?
令()1f x =,则
1
121
()2[(1)2()3()]/3f x dx f f x f x -==-++?
令()f x x =,则
120123x x =-++
令2
()f x x =,则
2212
2123x x =++ 从而解得
120.28990.5266x x =-??
=?或120.68990.1266
x x =??=? 令3
()f x x =,则
1
1
31
1
()0f x dx x dx --==?
?
12[(1)2()3()]/30f f x f x -++≠
故
1
121
()[(1)2()3()]/3f x dx f f x f x -=-++?
不成立。
因此,原求积公式具有2次代数精度。 (4)若
20
()[(0)()]/2[(0)()]h
f x dx h f f h ah f f h ''≈++-?
令()1f x =,则
(),h
f x dx h =?
2[(0)()]/2[(0)()]h f f h ah f f h h ''++-=
令()f x x =,则
20
22
1()2
1
[(0)()]/2[(0)()]2
h
h
f x dx xdx h h f f h ah f f h h ==
''++-=?
?
令2()f x x =,则
23
0232
1
()3
1
[(0)()]/2[(0)()]22
h
h f x dx x dx h h f f h ah f f h h ah ==''++-=-?
?
故有
33
211232
112
h h ah a =-=
令3
()f x x =,则
3
400
2444
1()4
1111[(0)()]/2[(0)()]12244h
h f x dx x dx h h f f h h f f h h h h
==''++-=-=??
令4
()f x x =,则
4
500
2555
1()5
1111[(0)()]/2[(0)()]12236h
h f x dx x dx h h f f h h f f h h h h
==''++-=-=??
故此时,
2
1()[(0)()]/2[(0)()],12
h
f x dx h f f h h f f h ''≠++
-?
因此,
2
1()[(0)()]/2[(0)()]12
h
f x dx h f f h h f f h ''≈++
-?
具有3次代数精度。
2.分别用梯形公式和辛普森公式计算下列积分:
1
2
01
2
101
(1),8;4(1)
(2),10;
(3),4;
(4),6;
x x
dx n x e dx n x
n n ?-=+-===?
??
解:
2
1(1)8,0,1,,()84x
n a b h f x x =====+
复化梯形公式为
7
81
[()2()()]0.111402k k h
T f a f x f b ==++=∑
复化辛普森公式为
7781012
[()4()2()()]0.111576k k k k h
S f a f x f x f b +===+++=∑∑
1
2
1(1)(2)10,0,1,,()10x e n a b h f x x
--====
= 复化梯形公式为
9
101
[()2()()] 1.391482k k h
T f a f x f b ==++=∑
复化辛普森公式为
99101012
[()4()2()()] 1.454716k k k k h
S f a f x f x f b +===+++=∑∑
(3)4,1,9,2,()n a b h f x =====
复化梯形公式为
3
41
[()2()()]17.227742k k h
T f a f x f b ==++=∑
复化辛普森公式为
33
41012
[()4()2()()]17.32222
6(4)6,0,,,()6
36
k k k k h
S f a f x f x f b n a b h f x π
π
+===+++====
=
=∑∑
复化梯形公式为
5
61
[()2()()] 1.035622k k h
T f a f x f b ==++=∑
复化辛普森公式为
5561012
[()4()2()()] 1.035776k k k k h
S f a f x f x f b +===+++=∑∑
3。直接验证柯特斯教材公式(2。4)具有5交代数精度。
证明:
柯特斯公式为
01234()[7()32()12()32()7()]90
b
a
b a
f x dx f x f x f x f x f x -=
++++?
令()1f x =,则
01234()90
[7()32()12()32()7()]90
b
a
b a f x dx b a
f x f x f x f x f x b a -=
-++++=-?
令()f x x =,则
22
2
2012341()()2
1[7()32()12()32()7()]()902b
b a a
f x dx xdx b a b a f x f x f x f x f x b a ==--++++=-??
令2
()f x x =,则
2333
3012341()()3
1[7()32()12()32()7()]()903b
b a a
f x dx x dx b a b a f x f x f x f x f x b a ==--++++=-??
令3
()f x x =,则
344
44012341()()4
1
[7()32()12()32()7()]()904b
b a a
f x dx x dx b a b a f x f x f x f x f x b a ==--++++=-??
令4()f x x =,则
45555012341()()5
1
[7()32()12()32()7()]()905b
b a a
f x dx x dx b a b a f x f x f x f x f x b a ==--++++=-??
令5()f x x =,则
5666
6012341()()6
1[7()32()12()32()7()]()906b
b a a
f x dx x dx b a b a f x f x f x f x f x b a ==--++++=-??
令6()f x x =,则
012340
()[7()32()12()32()7()]90
h
b a
f x dx f x f x f x f x f x -≠
++++?
因此,该柯特斯公式具有5次代数精度。 4。用辛普森公式求积分1
x e dx -?
并估计误差。
解:
辛普森公式为
[()4()()]62
b a a b
S f a f f b -+=
++ 此时,
0,1,(),x a b f x e -===
从而有
1
121
(14)0.632336
S e e --=++=
误差为
4(4)
04()()()1802
11
0.00035,(0,1)1802
b a b a R f f e ηη--=-≤
??=∈
5。推导下列三种矩形求积公式:
223()
()()()();2()
()()()();
2()
()()()();
224b
a b
a b
a
f f x dx b a f a b a f f x dx b a f b b a a b f f x dx b a f b a ηηη'=-+
-'=---''+=-+-???
证明:
(1)()()()(),(,)f x f a f x a a b ηη'=+-∈
两边同时在[,]a b 上积分,得
()()()()()b
b
a
a
f x dx b a f a f x a dx η'=-+-?
?
即
2
()()()()()2
(2)()()()(),(,)
b
a
f f x dx b a f a b a f x f b f b x a b ηηη'=-+
-'=--∈? 两边同时在[,]a b 上积分,得
()()()()()b
b
a
a
f x dx b a f a f b x dx η'=---?
?
即
2
2
()
()()()()2
()(3)()()()()(),(,)
22222
b
a
f f x dx b a f b b a a b a b a b f a b f x f f x x a b ηηη'=--
-''++++'=+-+-∈?
两连边同时在[,]a b 上积分,得
2
()()()(
)()()()22222b
b b a
a a a
b a b a b f a b f x dx b a f f x dx x dx η''++++'=-+-+-???
即
3()
()()(
)();224
b a
a b f f x dx b a f b a η''+=-+-?
6。若用复化梯形公式计算积分1
x I e dx =?
,问区间[0,1]应人多少等分才能使截断误差不超
过
51
102
-??若改用复化辛普森公式,要达到同样精度区间[0,1]应分多少等分? 解:
采用复化梯形公式时,余项为
2
()(),(,)12
n b a R f h f a b ηη-''=-
∈
又1
x
I e dx =
?
故(),(),0, 1.x x f x e f x e a b ''====
221()()1212n e R f h f h η''∴=
≤ 若5
1()102n R f -≤?,则
256
10h e
-≤?
当对区间[0,1]进行等分时,
1,h n
=
故有
212.85n ≥
= 因此,将区间213等分时可以满足误差要求 采用复化辛普森公式时,余项为
4(4)
()()(),(,)1802
n b a h R f f a b ηη-=-
∈ 又(),x f x e =
(4)4(4)4
(),
1()|()|28802880x n f x e e R f h f h
η∴=∴=-≤ 若51
()102
n R f -≤
?,则 451440
10h e
-≤
? 当对区间[0,1]进行等分时
1n h
=
故有
1
54
1440(10) 3.71n e
≥?=
因此,将区间8等分时可以满足误差要求。
7。如果()0f x ''>,证明用梯形公式计算积分()b
a I f x dx =?所得结果比准确值I 大,并说
明其几何意义。
解:采用梯形公式计算积分时,余项为
3()
(),[,]12
T f R b a a b ηη''=-
-∈ 又()0f x ''> 且b a >
0T R ∴<
又1T R T =-
I T ∴<
即计算值比准确值大。
其几何意义为,()0f x ''>为下凸函数,梯形面积大于曲边梯形面积。 8。用龙贝格求积方法计算下列积分,使误差不超过5
10-
.
1
20
3
(2)sin (3).
x
e dx
x xdx π
-??
解:
1
(1)x I e dx -=
因此
20
(2)sin I x xdx π
=?
因此
3
(3)I =?
因此
9。用2,3n =的高斯-勒让德公式计算积分
3
1
sin .x e xdx ?
解:
3
1
sin .x I e xdx =?
[1,3],x ∈ 令2t x =-,则[1,1]t ∈-
用2n =的高斯—勒让德公式计算积分
0.5555556[(0.7745967)(0.7745967)]0.8888889(0)10.9484
I f f f ≈?-++?≈
用3n =的高斯—勒让德公式计算积分
0.3478548[(0.8611363)(0.8611363)]0.6521452[(0.3399810)(0.3399810)]10.95014
I f f f f ≈?-++?-+≈ 10 地球卫星轨道是一个椭圆,椭圆周长的计算公式是
,S a θ=
这是a 是椭圆的半径轴,c 是地球中心与轨道中心(椭圆中心)的距离,记h 为近地点距离,
H 为远地点距离,R=6371(km )为地球半径,则
(2)/2,()/2.a R H h c H h =++=-
我国第一颗地球卫星近地点距离h=439(km),远地点距离H=2384(km )。试求卫星轨道的周长。 解:
6371,439,2384R h H ===
从而有。
(2)/27782.5()/2972.54a R H h c H h S a θ
=++==-==
1.56464648708()
I S km ≈≈
即人造卫星轨道的周长为48708km
11。证明等式 3
5
2
4
sin
3!5!n n
n
n
π
πππ=-
+
-
试依据sin()(3,6,12)n n n
π
=的值,用外推算法求π的近似值。
解
若()sin
,f n n n
π
=
又35
11sin 3!5!
x x x x =-+-
∴此函数的泰勒展式为
353
5
2
4
()sin
11[()()]3!5!3!5!f n n n
n n n n
n n π
πππ
πππ==-+-=-
+
-
()k n T π≈
当3n =时, sin 2.598076n n
π
= 当6n =时, sin
3n n
π
=
当12n =时, sin 3.105829n n
π
=
由外推法可得
故 3.14158π≈
12。用下列方法计算积分
3
1
dy
y
?
,并比较结果。 (1)龙贝格方法;
(2)三点及五点高斯公式;
(3)将积分区间分为四等分,用复化两点高斯公式。 解
3
1
dy I y
=?
故有 1.098613I ≈ (2)采用高斯公式时
3
1
dy I y
=?
此时[1,3],y ∈
令,x y z =-则[1,1],x ∈-
1
11,2
1
(),
2
I dx x f x x -=+=+?
利用三点高斯公式,则
0.5555556[(0.7745967)(0.7745967)]0.8888889(0)1.098039
I f f f =?-++?≈
利用五点高斯公式,则
0.2369239[(0.9061798)(0.9061798)]
0.4786287[(0.5384693)(0.5384693)]0.5688889(0)1.098609
I f f f f f ≈?-++?-++?≈ (3)采用复化两点高斯公式 将区间[1,3]四等分,得
12341.52 2.531
1.52
2.5I I I I I dy dy dy dy y y y
y =+++=+++?
??? 作变换5
4
x y +=
,则 1
1111,5
1
(),5
(0.5773503)(0.5773503)0.4054054I dx x f x x I f f -=+=+≈-+≈?
作变换7
4
x y +=
,则 1
2121,7
1
(),7
(0.5773503)(0.5773503)0.2876712I dx x f x x I f f -=+=+≈-+≈?
作变换9
4
x y +=
,则 1
3131,9
1
(),9
(0.5773503)(0.5773503)0.2231405I dx x f x x I f f -=+=+≈-+≈?
作变换11
4
x y +=
,则 1
4141
,
11
1
(),11
(0.5773503)(0.5773503)0.1823204I dx x f x x I f f -=+=+≈-+≈?
因此,有
1.098538I ≈
13.用三点公式和积分公式求2
1
()(1)f x x =
+在 1.0,1.1x =,和1.2处的导数值,并估计误差。
()f x 的值由下表给出:
2
1
()(1)
f x x =
+ 由带余项的三点求导公式可知
2
00122
1022
20121()[3()4()()]()
231()[()()]()261()[()4()3()]()
23
h f x f x f x f x f h h f x f x f x f h h f x f x f x f x f h ξξξ''''=-+-+''''=-+-''''=-++
又012()0.2500,()0.2268,()0.2066,f x f x f x ===
001210220121
()[3()4()()]0.24721
()[()()]0.217
21
()[()4()3()]0.187
2f x f x f x f x h
f x f x f x h f x f x f x f x h
'∴≈-+-='≈
-+=-'=-+=- 又2
1
()(1)
f x x =
+ 5
24
()(1)f x x -'''∴=
+
又[1.0,1.2]x ∈
()0.75f ξ'''∴≤
故误差分别为
2
3
02
312
3
2()() 2.5103()() 1.25106()() 2.5103
h R x f h R x f h R x f ξξξ---'''=≤?'''=≤?'''=≤?
利用数值积分求导, 设()()x f x ?'=
1
1()()()k k
x k k x f x f x x dx ?++=+?
由梯形求积公式得
1
1()[()()]2
k k
x k k x h x dx x x ???++=+?
从而有
11()()[()()]2
k k k k h
f x f x x x ??++=++
故
011012212()()[()()]
2
()()[()()]
x x f x f x h
x x f x f x h
????+=-+=-
又1
1
11()()()k k x k k x f x f x x dx ?+-+-=+?
且
1
1
11()[()()]k k x k k x x dx h x x ???+--+=+?
从而有
1111()()[()()]k k k k f x f x h x x ??+--+=++
故02201
()()[()()]x x f x f x h
??+=- 即
01120
2()()0.464()()0.404()()0.434
x x x x x x ??????+=-??
+=-??+=-? 解方程组可得
012
()0.247
()0.217()0.187x x x ???=-??
=-??=-?
数值分析第四章数值积分与数值微分习题答案
第四章 数值积分与数值微分 1.确定下列求积公式中的特定参数,使其代数精度尽量高,并指明所构造出的求积公式所具有的代数精度: 101210121 12120 (1)()()(0)(); (2)()()(0)(); (3)()[(1)2()3()]/3; (4)()[(0)()]/2[(0)()]; h h h h h f x dx A f h A f A f h f x dx A f h A f A f h f x dx f f x f x f x dx h f f h ah f f h -----≈-++≈-++≈-++''≈++-?? ?? 解: 求解求积公式的代数精度时,应根据代数精度的定义,即求积公式对于次数不超过m 的多项式均能准确地成立,但对于m+1次多项式就不准确成立,进行验证性求解。 (1)若101(1) ()()(0)()h h f x dx A f h A f A f h --≈-++? 令()1f x =,则 1012h A A A -=++ 令()f x x =,则 110A h Ah -=-+ 令2 ()f x x =,则 3 221123 h h A h A -=+ 从而解得 011431313A h A h A h -?=?? ? =?? ?=?? 令3 ()f x x =,则 3()0h h h h f x dx x dx --==? ? 101()(0)()0A f h A f A f h --++=
令4()f x x =,则 455 1012()5 2 ()(0)()3 h h h h f x dx x dx h A f h A f A f h h ---== -++=? ? 故此时, 101()()(0)()h h f x dx A f h A f A f h --≠-++? 故 101()()(0)()h h f x dx A f h A f A f h --≈-++? 具有3次代数精度。 (2)若 21012()()(0)()h h f x dx A f h A f A f h --≈-++? 令()1f x =,则 1014h A A A -=++ 令()f x x =,则 110A h Ah -=-+ 令2 ()f x x =,则 3 2211163 h h A h A -=+ 从而解得 1143 8383A h A h A h -?=-?? ? =?? ?=?? 令3 ()f x x =,则 22322()0h h h h f x dx x dx --==? ? 101()(0)()0A f h A f A f h --++=
数值分析习题与答案
第一章绪论 习题一?1.设x>0,x*的相对误差为δ,求f(x)=ln x的误差限。 解:求lnx的误差极限就是求f(x)=lnx的误差限,由公式(1.2.4)有 已知x*的相对误差满足,而 ,故 即 2.下列各数都是经过四舍五入得到的近似值,试指出它们有几位有效数字,并给出其误差限与相对误差限。 解:直接根据定义和式(1.2.2)(1.2.3)则得?有5位有效数字,其误差限,相对误差限 有2位有效数字, 有5位有效数字, 3.下列公式如何才比较准确? (1)?(2) 解:要使计算较准确,主要是避免两相近数相减,故应变换所给公式。
(1)?(2) 4.近似数x*=0.0310,是 3 位有数数字。 5.计算取,利用 :式计算误差最小。 四个选项: 第二、三章插值与函数逼近 习题二、三 1. 给定的数值表 用线性插值与二次插值计算ln0.54的近似值并估计误差限. 解:仍可使用n=1及n=2的Lagrange插值或Newto n插值,并应用误差估计(5.8)。线性插值时,用0.5及0.6两点,用Newton插值??误差限 ,因,
故? 二次插值时,用0.5,0.6,0.7三点,作二次Newton插值 ?误差限,故? 2. 在-4≤x≤4上给出的等距节点函数表,若用二次插值法求的近似值,要使误差不超过,函数表的步长h应取多少? 解:用误差估计式(5.8), ?令 因?得 3. 若,求和.
解:由均差与导数关系 ?于是 4. 若互异,求 的值,这里p≤n+1. 解:,由均差对称性 可知当有?而当P=n +1时 ?于是得 5. 求证. 解:解:只要按差分定义直接展开得 ? 6. 已知的函数表
数值积分与数值微分实验报告
实验三 数值积分程序设计算法 1)实验目的 通过本次实验熟悉并掌握各种数值积分算法及如何在matlab 中通过设计程序实现这些算法,从而更好地解决实际中的问题。 2)实验题目 给出积分 dx x I ? -= 3 2 2 1 1 1.用Simpson 公式和N=8的复合Simpson 公式求积分的近似值. 2.用复合梯形公式、复合抛物线公式、龙贝格公式求定积分,要求绝对误差为 7 10*2 1-= ε,将计算结果与精确解做比较,并对计算结果进行分析。 3)实验原理与理论基础 Simpson 公式 )]()2 ( 4)([6 b f b a f a f a b S +++-= 复化梯形公式 将定积分? = b a dx x f I )(的积分区间],[b a 分隔为n 等分,各节点为 n j jh a x j ,,1,0, =+= n a b h -= 复合梯形(Trapz)公式为 ])()(2)([21 1 ∑-=++-= n j j n b f x f a f n a b T 如果将],[b a 分隔为2n 等分,而n a b h /)(-=不变, 则 )]()(2)(2)([41 2 111 2b f x f x f a f n a b T n j j n j j n +++-= ∑∑-=+-= 其中 h j a h x x j j )2 1(2 12 1+ +=+ =+ ,)]()(2)(2)([41 2 11 1 2b f x f x f a f n a b T n j j n j j n +++-= ∑∑-=+ -= ∑ -=-++-+ =1 )2) 12((22 1n j n n a b j a f n a b T n=1时,a b h -=,则)]()([2 1b f a f a b T +-= )0(0T = )2 1(2 2 112h a f a b T T + -+ =)1(0T = 若12-=k n ,记)1(0-=k T T n , ,2,1=k 1 2 --= k a b h jh a x j +=1 2 --+=k a b j a h x x j j 2 12 1+ =+ k a b j a 2 ) 12(-++=,则可得如下递推公式
数值分析习题解答4
第四章 数值积分方法与数值微分 (习 题) 1.直接验证梯形公式(1.2)与中矩形公式(1.3)具有1次代数精度,而辛甫生公式(1.4)则具有3次代数精度. 解 梯形公式: ?+-≈ b a b f a f a b dx x f )]()([2 )(. 矩形公式: ?+-≈b a b a f a b dx x f )2 ()()(. 以上两求积公式以 ,1)(=x f x 代入公式两边,结果相等,而以2 )(x x f = 代入公式两边,其结果不相等.故梯形公式的代数精度等于1. Simpson 公式: ? +++-≈ b a b f b a f a f a b dx x f )]()2 (4)([6)(. 容易验证:以2 ,,1)(x x x f =分别代入Simpson 公式两边,结果相等。 以3 )(x x f =代入 左边= )(444 13a b dx x b a -=? 右边=[ ] 32 322322332 3 3 3 36246b ab b a a a b b b a a a b +++-=??? ?????+??? ??++- = ).(4 144 a b - Simpson 公式两边,结果相等。而以4 x 代入Simpson 公式两边,其结果 不相等。故Simpson 求积公式的代数精度为3. □ 3.对于? =h dx x f I 30 )(的数值积分公式? = h h dx x p I 30 )(,其中)(x p 为对)(x f 在 h h x 2,,0=进行插值的2次多项式.证明:)()0(8 354h O f h I I h +'''?=-. 证明: )(x P 为)(x f 于h h x 2,,0=进行插值的二次多项式,则: )()()(x R x P x f += 其中: )2()(! 3) ()(h x h x x f x R --'''=ξ. 求积分公式误差 ? ?-= h h dx x P dx x f f E 3030 )()()( ? --'''=h dx h x h x x f 30 )2()(! 3) (ξ
数值分析第4章答案
第四章 数值积分与数值微分 1.确定下列求积公式中的特定参数,使其代数精度尽量高,并指明所构造出的求积公式所具有的代数精度: 101210121 12120 (1)()()(0)(); (2)()()(0)(); (3)()[(1)2()3()]/3; (4)()[(0)()]/2[(0)()]; h h h h h f x dx A f h A f A f h f x dx A f h A f A f h f x dx f f x f x f x dx h f f h ah f f h -----≈-++≈-++≈-++''≈++-?? ?? 解: 求解求积公式的代数精度时,应根据代数精度的定义,即求积公式对于次数不超过m 的多项式均能准确地成立,但对于m+1次多项式就不准确成立,进行验证性求解。 (1)若101(1) ()()(0)()h h f x dx A f h A f A f h --≈-++? 令()1f x =,则 1012h A A A -=++ 令()f x x =,则 110A h Ah -=-+ 令2 ()f x x =,则 3 221123 h h A h A -=+ 从而解得 01 1431313A h A h A h -?=?? ?=?? ?=?? 令3 ()f x x =,则 3()0h h h h f x dx x dx --==? ? 101()(0)()0A f h A f A f h --++= 故 101()()(0)()h h f x dx A f h A f A f h --=-++? 成立。 令4 ()f x x =,则
数值积分与数值微分知识题课
数值积分与 数值微分 习题课
一、已知012113,,424x x x ===,给出以这 3个点为求积节 点在[]0.1上的插值型求积公式 解:过这3个点的插值多项式基函数为 ()()()()()()()()()()()()()()()()1202010202121012012220211 20,0,1,2 k k x x x x l x x x x x x x x x l x x x x x x x x x l x x x x x A l x dx k --= ----= ----= --==?
()()()()()()()()()()()()111200001021102100101210120202113224111334244131441113324241142x x x x x x A dx dx x x x x x x x x x x A dx dx x x x x x x x x x x A dx x x x x ????-- ???--????=== --????-- ??? ???? ????-- ???--????===- --????-- ??? ???? ????-- ??--???==--?????102313134442dx ??= ????-- ??? ???? ? 故所求的插值型求积公式为 ()1 211 123343234f x dx f f f ??????≈- + ? ? ??????? ?
二、确定求积公式 ( )( )(1 1158059f x dx f f f -? ?≈++?? ? 的代数精度,它是Gauss 公式吗? 证明:求积公式中系数与节点全部给定,直接检验 依次取()23451,,,,,f x x x x x x =,有 [ ](1 1111 215181519 1058059dx xdx --==?+?+???==?+?+?? ???
数值分析习题集及答案
(适合课程《数值方法A 》和《数值方法B 》) 第一章 绪 论 1. 设x >0,x 的相对误差为δ,求ln x 的误差. 2. 设x 的相对误差为2%,求n x 的相对误差. 3. 下列各数都是经过四舍五入得到的近似数,即误差限不超过最后一位的半个单位,试指出它们是几位 有效数字: ***** 123451.1021,0.031,385.6,56.430,7 1.0.x x x x x =====? 4. 利用公式(3.3)求下列各近似值的误差限: * * * * * * * * 12412324(),(),()/,i x x x ii x x x iii x x ++其中* * * * 1234,,,x x x x 均为第3题所给的数. 5. 计算球体积要使相对误差限为1%,问度量半径R 时允许的相对误差限是多少? 6. 设028,Y =按递推公式 11783 100 n n Y Y -=- ( n=1,2,…) 计算到100Y .若取783≈27.982(五位有效数字),试问计算100Y 将有多大误差? 7. 求方程2 5610x x -+=的两个根,使它至少具有四位有效数字(783≈27.982). 8. 当N 充分大时,怎样求 2 11N dx x +∞+?? 9. 正方形的边长大约为100㎝,应怎样测量才能使其面积误差不超过1㎝2 ? 10. 设2 12S gt = 假定g 是准确的,而对t 的测量有±0.1秒的误差,证明当t 增加时S 的绝对误差增加, 而相对误差却减小. 11. 序列{}n y 满足递推关系1101 n n y y -=-(n=1,2,…),若02 1.41y =≈(三位有效数字),计算到10 y 时误差有多大?这个计算过程稳定吗? 12. 计算6 (21)f =-,取 2 1.4≈,利用下列等式计算,哪一个得到的结果最好? 3 6 3 11,(322), ,9970 2. (21) (322) --++ 13. 2 ()ln(1)f x x x =- -,求f (30)的值.若开平方用六位函数表,问求对数时误差有多大?若改用另一等 价公式 2 2 ln(1)ln(1)x x x x - -=-+ + 计算,求对数时误差有多大? 14. 试用消元法解方程组{ 10 10 12121010; 2. x x x x +=+=假定只用三位数计算,问结果是否可靠? 15. 已知三角形面积 1sin , 2 s ab c = 其中c 为弧度, 02c π << ,且测量a ,b ,c 的误差分别为,,.a b c ???证 明面积的误差s ?满足 . s a b c s a b c ????≤ ++ 第二章 插值法 1. 根据( 2.2)定义的范德蒙行列式,令
Matlab数值积分与数值微分
M a t l a b数值积分与数值微分 Matlab数值积分 1.一重数值积分的实现方法 变步长辛普森法、高斯-克朗罗德法、梯形积分法 1.1变步长辛普森法 Matlab提供了quad函数和quadl函数用于实现变步长 辛普森法求数值积分.调用格式为: [I,n]=Quad(@fname,a,b,tol,trace) [I,n]=Quadl(@fname,a,b,tol,trace) Fname是函数文件名,a,b分别为积分下限、积分上限; tol为精度控制,默认为1.0×10-6,trace控制是否展 开积分过程,若为0则不展开,非0则展开,默认不展开. 返回值I为积分数值;n为调用函数的次数. --------------------------------------------------------------------- 例如:求 ∫e0.5x sin(x+π )dx 3π 的值. 先建立函数文件 fesin.m function f=fesin(x) f=exp(-0.5*x).*sin(x+(pi/6));再调用quad函数
[I,n]=quad(@fesin,0,3*pi,1e-10) I= 0.9008 n= 365 --------------------------------------------------------------------- 例如:分别用quad函数和quadl函数求积分 ∫e0.5x sin(x+π 6 )dx 3π 的近似值,比较函数调用的次数. 先建立函数文件 fesin.m function f=fesin(x) f=exp(-0.5*x).*sin(x+(pi/6)); formatlong [I,n]=quadl(@fesin,0,3*pi,1e-10) I= n= 198 [I,n]=quad(@fesin,0,3*pi,1e-10) I= n= 365 --------------------------------------------------------------------- 可以发现quadl函数调用原函数的次数比quad少,并 且比quad函数求得的数值解更精确. 1.2高斯-克朗罗德法
数值分析1-4习题及答案
1、 0.1%,要取几位有效数字? ( c ) (a) 2 (b) 3 (c) 4 (d) 5 2、若* 12.30x =是经过四舍五入得到的近似数,则它有几位有效数字? ( c ) (a) 2 (b) 3 (c) 4 (d) 5 3、已知n +1个互异节点(x 0,y 0), (x 1,y 1),…, (x n ,y n )和过这些点的拉格朗日插值基函数l k (x )(k =0,1,2,…,n ),且ω(x )=(x -x 0) (x -x 1)… (x -x n ).则n 阶差商f (x 0,x 1,…, x n )= ( ) (a) ∑=n k k k y x l 0 )( (b) ∑='n k k k k x l y 0)( (c) ∑=n k k k x y 0)(ω (d) ∑='n k k k x y 0)(ω 4、已知由数据(0,0),(0.5,y ),(1,3),(2,2)构造出的三次插值多项式 33()6 P x x y 的 的系数是,则 等于 ( ) (a) -1.5 (b) 1 (c) 5.5 (d) 4.25 5、设(0,1,2,3,4)i x i =为互异结点,()i l x 为拉格朗日插值基函数,则 4 2 () ()i i i x x l x =-∑等于 ( a ) (a) 0 (b) 1 (c) 2 (d) 4 4()[,],()()(),()(),( )(), ' () ' (),22 ()()_________________________f x C a b H x a b a b H a f a H b f b H f H a f a f x H x ∈++====-=设是满足下列插值条件的三次多项式:则插值余项 1、 是以0,1,2为节点的三次样条函数,则b=-2,c=3 2、 已知(1)0,(1)3,(2)4,f f f =-=-=写出()f x 的牛顿插值多项式 2()P x =___2537 623x x +-__,其余项表达式 R(x)=__() (1)(1)(4) [1,4]6 f x x x ξξ'''-+-∈-_______________________ 3、 确定求积公式1 0121 ()(1)(0)'(1)f x dx A f A f A f -≈-++? 中的待定参数,使其代数精度 尽量高,则A 0=_ 29__________, A 1=__169________, A 2=_29 _______,代数精度=__2_________。
数值微分与数值积分练习题
第五章 数值微分与数值积分 一.分别用向前差商,向后差商和中心差商公式计算()f x =2x =的导数的近似值。其中,步长0.1h =。 【详解】 00()()(20.1)(2)=0.349 2410.10.1 f x h f x f f h +?+?===向前差商 00()()(2)(20.1)=0.358 0870.10.1 f x f x h f f h ????===向后差商 00()()(20.1)(20.1)= 0.353 664220.10.2f x h f x h f f h +??+??===×中心差商 二.已知数据 x 2.5 2.55 2.60 2.65 2.70 ()f x 1.58114 1.59687 2 1.62788 1.64317 求( 2.50),(2.60),(2.70)f f f ′′′的近似值。 【详解】 0.05h =,按照三点公式 3(2.50)4(2.55)(2.60)3 1.581144 1.59687 1.61245(2.50)0.316 10020.050.1 f f f f ?+??×+×?′≈==×(2.65)(2.55)1.627881.59687(2.60)0.310 10020.050.1 f f f ??′≈==× (2.60)4(2.65)3(2.70)241.6278831.64317(2.70) 4.179 90020.050.1 f f f f ?+?×+×′≈==× 三.已知如下数据 x 3 4 5 6 7 8 ()f x 2.937 6 6.963 213.600 0 23.500 8 37.318 4 55.705 6
郑州大学数值分析重点考察内容及各章习题
《数值分析》 重点考察内容及各章作业答案 学院: 学号: 姓名:
重点考察内容 基本概念(收敛阶,收敛条件,收敛区域等), 简单欧拉法。 第一章基础 掌握:误差的种类,截断误差,舍入误差的来源,有效数字的判断。 了解:误差限,算法及要注意的问题。 第二章插值 掌握:Hermite插值,牛顿插值,差商计算,插值误差估计。 了解:Lagrange插值 第三章数据拟合 掌握:给出几个点求线性拟合曲线。 了解:最小二乘原理 第四章数值积分微分 掌握:梯形公式,Simpson公式,代数精度,Gauss积分,带权Gauss积分公式推导,复化梯形公式推导及算法。 了解:数值微分,积分余项 第五章直接法 掌握:LU分解求线性方程组,运算量 了解:Gauss消去法,LDL,追赶法 第六章迭代法 掌握:Jacobi,Gauss-Seidel迭代格式构造,敛散性分析,向量、矩阵的范数、谱半径 了解:SOR迭代 第七章Nolinear迭代法 掌握:牛顿迭代格式构造,简单迭代法构造、敛散性分析,收敛阶。 了解:二分法,弦截法 第八章ODE解法 掌握:Euler公式构造、收敛阶。 了解:梯形Euler公式、收敛阶,改进Euler公式 题目类型:填空,计算,证明综合题
第一章 误差 1. 科学计算中的误差来源有4个,分别是________,________,________,________。 2. 用Taylor 展开近似计算函数000()()'()()f x f x f x x x ≈+-,这里产生是什么误差? 3. 0.7499作 3 4 的近似值,是______位有效数字,65.380是舍入得到的近似值,有____几位有效数字,相对误差限为_______. 0.0032581是四舍五入得到的近似值,有_______位有效数字. 4. 改变下列表达式,使计算结果比较精确: (1)11,||1121x x x x --++ (2 ||1x (3) 1cos ,0,|| 1.x x x x -≠ (4)sin sin ,αβαβ-≈ 5. 采用下列各式计算61)时,哪个计算效果最好?并说明理由。 (1) (2 )99-3 )6 (3-(4 6. 已知近似数*x 有4位有效数字,求其相对误差限。 上机实验题: 1、利用Taylor 展开公式计算0! k x k x e k ∞ ==∑,编一段小程序,上机用单精度计算x e 的函数 值. 分别取x =1,5,10,20,-1,-5,-10,-15,-20,观察所得结果是否合理,如不合理请分析原因并给出解决方法. 2、已知定积分1 ,0,1,2,,206 n n x I dx n x ==+? ,有如下的递推关系 111 110 0(6)61666 n n n n n x x x x I dx dx I x x n ---+-===++-? ? 可建立两种等价的计算公式 (1) 1016,0.154n n I I I n -= -=取; (2) 12011),0.6n n I nI I n -=-=(取
数值分析习题
习题1 1. 填空题 (1) 为便于算法在计算机上实现,必须将一个数学问题分解为 的 运算; (2) 在数值计算中为避免损失有效数字,尽量避免两个 数作减法运算;为避免 误差的扩大,也尽量避免分母的绝对值 分子的绝对值; (3) 误差有四大来源,数值分析主要处理其中的 和 ; (4) 有效数字越多,相对误差越 ; 2. 用例1.4的算法计算10,迭代3次,计算结果保留4位有效数字. 3. 推导开平方运算的误差限公式,并说明什么情况下结果误差不大于自变量误差. 4. 以下各数都是对准确值进行四舍五入得到的近似数,指出它们的有效数位、误差限和相对误差限. 95123450304051104000003346087510., ., , ., .x x x x x -==?===? 5. 证明1.2.3之定理1.1. 6. 若钢珠的的直径d 的相对误差为1.0%,则它的体积V 的相对误差将为多少。(假定钢珠为标准的球形) 7. 若跑道长的测量有0.1%的误差,对400m 成绩为60s 的运动员的成绩将会带来多大的误差和相对误差. 8. 为使20的近似数相对误差小于0.05%,试问该保留几位有效数字. 9. 一个园柱体的工件,直径d 为10.25±0.25mm,高h 为40.00±1.00mm,则它的体积V 的近似值、误差和相对误差为多少. 10 证明对一元函数运算有 r r xf x f x k x k f x εε'≈= () (())(),() 其中 并求出157f x x x ==()tan ,.时的k 值,从而说明f x x =()tan 在2 x π ≈时是病态问题. 11. 定义多元函数运算 1 1 1,,(),n n i i i i i i S c x c x εε====≤∑∑其中 求出S ε()的表达式,并说明i c 全为正数时,计算是稳定的,i c 有正有负时,误差难以控制. 12. 下列各式应如何改进,使计算更准确:
数值分析第四版习题及答案
第四版 数值分析习题 第一章 绪 论 1. 设x >0,x 的相对误差为δ,求ln x 的误差. 2. 设x 的相对误差为2%,求n x 的相对误差. 3. 下列各数都是经过四舍五入得到的近似数,即误差限不超过最后一位的半个单位,试指 出它们是几位有效数字: *****123451.1021,0.031,385.6,56.430,7 1.0.x x x x x =====? 4. 利用公式求下列各近似值的误差限: ********12412324(),(),()/,i x x x ii x x x iii x x ++其中**** 1234 ,,,x x x x 均为第3题所给的数. 5. 计算球体积要使相对误差限为1%,问度量半径R 时允许的相对误差限是多少? 6. 设028,Y =按递推公式 1n n Y Y -=…) 计算到100Y .(五位有效数字),试问计算100Y 将有多大误差? 7. 求方程2 5610x x -+=的两个根,使它至少具有四位有效数字. 8. 当N 充分大时,怎样求 2 11N dx x +∞ +? ? 9. 正方形的边长大约为100㎝,应怎样测量才能使其面积误差不超过1㎝2 ? 10. 设 212S gt = 假定g 是准确的,而对t 的测量有±秒的误差,证明当t 增加时S 的绝对误 差增加,而相对误差却减小. 11. 序列 {}n y 满足递推关系1101n n y y -=-(n=1,2,…),若0 1.41y =≈(三位有效数字), 计算到 10y 时误差有多大?这个计算过程稳定吗? 12. 计算61)f =, 1.4≈,利用下列等式计算,哪一个得到的结果最好? 3 -- 13. ()ln(f x x =,求f (30)的值.若开平方用六位函数表,问求对数时误差有多大?若改用另一等价公式 ln(ln(x x =- 计算,求对数时误差有多大?
实验4_数值积分与数值微分
数值分析实验报告四 数值积分与数值微分实验(2学时) 一 实验目的 1.掌握复化的梯形公式、Simpson 公式等牛顿-柯特斯公式计算积分。 2. 掌握数值微分的计算方法。 二 实验内容 1. 用复化梯形公式计算积分。 ?9 0dx x M=8 2. 用复化Simpson 公式计算积分。 ? 90dx x M=8 3. 给定下列表格值 利用四点式(n=3)求)50()50('''f f 和的值。 三 实验步骤(算法)与结果 1复化梯形公式 用C 语言编程如下: #include
float y; y=sqrt(x); return y; } void main() { int i,m; float a,b,h,r; printf("输入等分数m:" ); scanf("%d",&m); printf("输入区间左端点a的值:"); scanf("%f",&a); printf("输入区间右端点b的值:"); scanf("%f",&b); float x[m+1]; h=(b-a)/m; for(i=0;i<=m;i++) x[i]=a+i*h; r=0; for(i=0;i<=m;i++) {if(i==0) r=r+h*0.5*f(x[i]); if(i>0&&i if(i==m) r=r+0.5*h*f(x[i]); } printf("输出区间[%3.1f %3.1f]的积分值:%f\n",a,b,r); } 求解结果如下: 输入等分数m:8 输入区间左端点a的值:0 输入区间右端点b的值:9 输出区间[0.0 9.0]的积分值:17.769514 2复化Simpson公式 用C语言编程如下: #include ()()()()()()()()()收敛较慢 代入上式得:将解: 收敛速度次并分析该迭代公式的迭代的根求方程 取试用迭代公式∴≠<<*'*+++-='∴+*+*=*∴=+?+?? ? ??===++= =∴++= ==-++=++=++014.01022220||10 2202613381013202132020 132010212010220. 2.0 20102110220 4.1222 222212012123021x x x x x x x x x x x x x x x x x x x x x x x x k k k k k k k ?????? )))()()()[]()()[])49998.0cos 215.0cos 2 1,022,00cos 2 102 12,0210,2,0.cos 2 10sin 2 11,cos 2 113cos 2 12; 1.0cos 2 12.4120101==== ==->-=<-=-=>+='-===-+x x x x x x x f f x x x f x x f x x x f x x x x k k 则 取上有一个根在所以上在为单调递增函数故则令解: 位有效数字求出这些根,精确到用迭代公式分析该方程有几个根给定方程ππππ 500 .0105.0102.0||3412≈*? 第七章数值积分与数值微分 积分问题最早来自于几何形体的面积、体积计算,也是经典力学中的重要问题(例如计算物体的重心位置). 在现实应用中,很多积分的结果并不能写成解析表达式,因此需要通过数值方法来计算. 数值微分是利用一些离散点上的函数值近似计算某一点处的函数导数,它针对表达式未知的函数. 本章介绍一元函数积分(一重积分)和微分的各种数值算法,它们也是数值求解积分方程、微分方程的基础. 7.1数值积分概论 7.1.1基本思想 考虑如下定积分的计算: I(f)≡∫f(x)dx b a ,(7.1) 其中函数f: ?→?,首先应想到的是微积分中学习过的牛顿-莱布尼兹(Newton-Leibniz)公式: ∫f(x)dx b a =F(b)?F(a) , 其中F′(x)=f(x),即F(x)为f(x)的原函数. 但是,诸如e x2,sinx x ,sinx2等表达式很简单的函数却找不到用初等函数表示的原函数,因此必须研究数值方法来近似计算积分. 另一方面,某些函数的原函数虽然可以解析表示,但其推导、计算非常复杂,此时也需要使用数值积分方法. 一般考虑连续的、或在区间[a,b]上可积①的函数f(x),则根据积分的定义有: lim n→∞,?→0∑(x i+1?x i)f(ξi) n i=0 =I(f) , (7.2) 其中a=x0 数值积分与微分 摘要 本文首先列举了一些常用的数值求积方法,一是插值型求积公式,以N e w t o n C o t e s -公式为代表,并分析了复合型的Newton Cotes -公式;另一个是Gauss Ledendre -求积公式,并给出几个常用的Gauss Ledendre -求积公式。其次,本文对数值微分方法进行分析,主要是差分型数值微分和插值型数值微分,都给出了几种常用的微分方法。然后,本文比较了数值积分与微分的关系,发现数值积分与微分都与插值或拟合密不可分。 本文在每个方法时都分析了误差余项,并且在最后都给出了MATLAB 的调用程序。 关键词:插值型积分Gauss Ledendre -差分数值微分插值型数值微分 MATLAB 一、常用的积分方法 计算积分时,根据Newton Leibniz -公式, ()()()b a f x dx F b F a =-? 但如果碰到以下几种情况: 1)被积函数以一组数据形式表示; 2)被积函数过于特殊或者原函数无法用初等函数表示 3)原函数十分复杂难以计算 这些现象中,Newton Leibniz -公式很难发挥作用,只能建立积分的近似计算方法,数值积分是常用的近似计算的方法。 1.1 插值型积分公式 积分中的一个常用方法是利用插值多项式来构造数值求积公式,具体的步骤如下: 在积分区间上[,]a b 上取一组节点:01201,,,,()n n x x x x a x x x b ≤<<≤ 。已知()k x f 的函数值,作()x f 的n 次插值多项式,则 (1) ()10()()()()() (1)!n n x n n k k n k f f L x R x f x l x w x n ++==+=++∑ 其中,()k l x 为n 次插值基函数,则得 (1)+10()(()())1 =[()]()[()](1)!b b n n a a n b b n k k n a a k f x dx L x R x dx l x dx f x f x w x dx n ξ+==+++? ?∑??() 公式写成一般形式: ()()[]n b k k n a k f x dx A f x R f ==+∑? 其中, 01100110 ()()()() ()()()()()b b k k k k a a k k k k k k x x x x x x x x A l x dx dx x x x x x x x x -+-+----==----?? (1)+11 [][()](1)!b n n n a R f f x w x dx n ξ+=+?() 显然,当被积函数f 为次数小于等于n 的多项式时,其相应的插值型求积公式为准确公式,即: ()() n b k k a k f x dx A f x ==∑? 1.1.1 求积公式的代数精度 定义:求积公式对于任何次数不大于m 的代数多项式()f x 均精确成立,而对于 1()m f x x +=不精确成立,则称求积公式具有m 次代数精度。 定理:含有1n +个节点(0,1,,)k x k n = 的插值型求积公式的代数精度至少为n 。 数值分析习题集 (适合课程《数值方法A 》和《数值方法B 》) 长沙理工大学 第一章 绪 论 1. 设x >0,x 的相对误差为δ,求ln x 的误差. 2. 设x 的相对误差为2%,求n x 的相对误差. 3. 下列各数都是经过四舍五入得到的近似数,即误差限不超过最后一位的半个单位,试指 出它们是几位有效数字: *****123451.1021,0.031,385.6,56.430,7 1.0.x x x x x =====? 4. 利用公式(3.3)求下列各近似值的误差限: ********12412324(),(),()/,i x x x ii x x x iii x x ++其中**** 1234 ,,,x x x x 均为第3题所给的数. 5. 计算球体积要使相对误差限为1%,问度量半径R 时允许的相对误差限是多少? 6. 设028,Y =按递推公式 1n n Y Y -=…) 计算到100Y .27.982(五位有效数字),试问计算100Y 将有多大误差? 7. 求方程2 5610x x -+=的两个根,使它至少具有四位有效数字27.982). 8. 当N 充分大时,怎样求2 1 1N dx x +∞+?? 9. 正方形的边长大约为100㎝,应怎样测量才能使其面积误差不超过1㎝2 ? 10. 设 212S gt = 假定g 是准确的,而对t 的测量有±0.1秒的误差,证明当t 增加时S 的绝对 误差增加,而相对误差却减小. 11. 序列 {}n y 满足递推关系1101n n y y -=-(n=1,2,…),若0 1.41y =≈(三位有效数字), 计算到 10y 时误差有多大?这个计算过程稳定吗? 12. 计算6 1)f =, 1.4≈,利用下列等式计算,哪一个得到的结果最好? 3 -- 13. ()ln(f x x =,求f (30)的值.若开平方用六位函数表,问求对数时误差有多大? 第5章数值积分与数值微分方法关于定积分计算,已经有较多方法,如公式法、分步积分法等,但实际问题中,经常出现不能用通常这些积分方法计算的定积分问题。怎样把这些通常方法失效的定积分在一定精度下快速计算出来,特别是通过计算机编程计算出来就是本章研究的内容。 此外,怎样根据函数在若干个点处的函数值去求该函数的导数近似值也是本章介绍的内容。 本章涉及的方法有Newton-Cotes求积公式、Gauss求积公式、复化求积公式、Romberg求积公式和数值微分。 5.1 引例 人造地球卫星轨道可视为平面上的椭圆。我国的第一颗人造地球卫星近地点距离地球表面439km ,远地点距地球表面2384km ,地球半径为6371km ,求该卫星的轨道长度。 本问题可用椭圆参数方程 cos ,,0sin x a t a b y b t π=?≤≤>?=? (0t 2) 来描述人造地球卫星的轨道,式中a, b 分别为椭圆的长短轴,该轨道的长度L 就是如下参数方程弧长积分 但这个积分是椭圆积分,不能用解析方法计算。 5.2问题的描述与基本概念 要想用计算机来计算()b a f x dx ?,应对其做离散化处 理。注意到定积分是如下和式的极限 1 ()lim ()n b i i a i f x dx f x λξ→==?∑? 要离散化,做 1) 去掉极限号lim 2) 将i ξ取为具体的i x 值 3) 为减少离散化带来的误差,将i x ?用待定系数i A 代替 于是就得到 定义 5.1 若存在实数1212,,,;,, ,,n n x x x A A A 且任 取()[,],f x C a b ∈都有 1 ()()n b i i a i f x dx A f x =≈∑? (5.1)数值计算第四章课后习题答案
第7章 数值积分与数值微分
数值积分与微分方法
数值分析习题集及答案Word版
数值积分与数值微分
