3个技巧 9道经典题 24个几何模型 拿下几何中考最难题资料
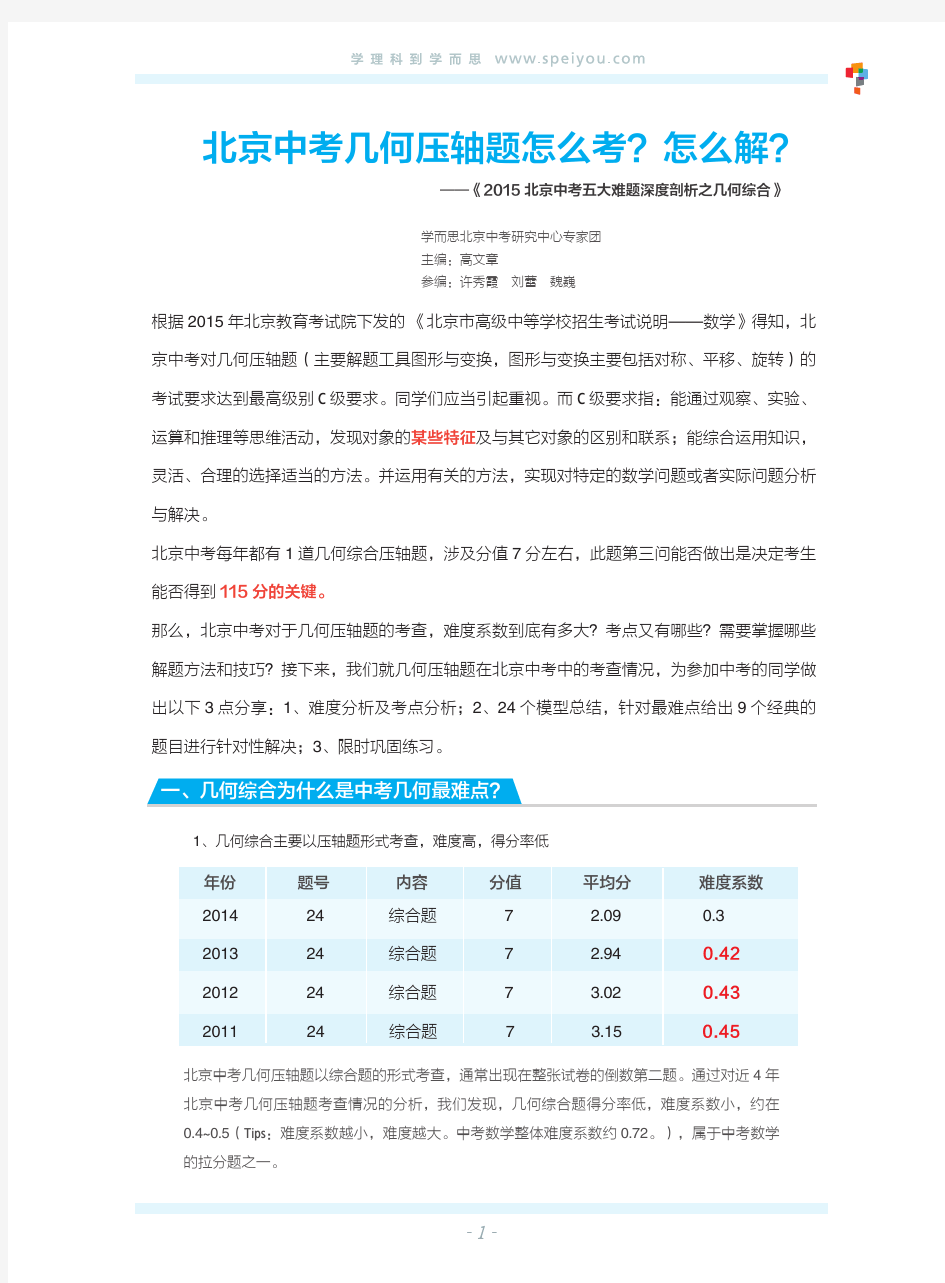

2018年中考常见几何模型分析
中考直通车·数学广州分册 第八章专题拓展 第24讲常见几何模型
【考点解读】 常见几何模型是广州市中考的压轴题常考题型,主要以考察选择、填空最后一题和几何压轴题为主。几何模型类型较多,综合性强,属于中考中重点但同样是难点的一个考点。 【考点分析】 2011年 考查三角形全等和三角形中位线性质,标准的手拉手模型。 2014年 考查三角形全等的判断和性质,根据手拉手模型找出全等三角形,再应用其性质 2016年 本年度模型思想明显,分值占比大,主要考查三角形全等的判定及其性质、图像的旋转,利用模型思想作为解题突破口顺利完成辅助线。 【模型介绍】 手拉手模型: 1、 【条件】 如图两个等边三角形ABD ?与BCE ?,连结 AE 与CD , 【结论】(1)DBC ABE ??? (2)DC AE = (3)AE 与DC 之间的夹角为? 60 (4)AE 与DC 的交点设为H , BH 平分AHC ∠
C D A B F E C D 2、 【条件】如图两个等腰直角三角形ADC 与EDG ,连结CE AG ,,二者相交于点H 。 【结论】 (1)CDE ADG ???是否成立? (2)AG =CE (3)AG 与CE 之间的夹角为 90 (4)HD 是否平分AHE ∠? 旋转模型: 一、邻角相等对角互补模型 【条件】如图,四边形ABCD 中,AB =AD ,90BAD BCD ?∠=∠= 【结论】45ACB ACD BC CD ? ∠=∠=+= ① ② 二、角含半角模型:全等 角含半角要旋转:构造两次全等 F E D C B A G F E D C B A A C D E A C D E F
中考数学几何模型能力 共顶点模型(解析版)
中考数学几何模型2:共顶点模型 共顶点模型,亦称“手拉手模型”,是指两个顶角相等的等腰或者等边三角形的顶点重合,两个三角形的两条腰分别构成的两个三角形全等或者相似。寻找共顶点旋转模型的步骤如下: (1)寻找公共的顶点 (2)列出两组相等的边或者对应成比例的边 (3)将两组相等的边分别分散到两个三角形中去,证明全等或相似即可。 两等边三角形 两等腰直角三角形 两任意等腰三角形 *常见结论: 连接BD 、AE 交于点F ,连接CF ,则有以下结论: (1)BCD ACE ?△△ (2)AE BD = (3)AFB DFE ∠=∠ (4)FC BFE ∠平分 例题1. 以点A 为顶点作等腰Rt △ABC ,等腰Rt △ADE ,其中∠BAC =∠DAE =90°,如图1所示放置,使 得一直角边重合,连接BD 、CE . (1)试判断BD 、CE 的数量关系,并说明理由; (2)延长BD 交CE 于点F 试求∠BFC 的度数; (3)把两个等腰直角三角形按如图2放置,(1)、(2)中的结论是否仍成立?请说明理由.
变式练习>>> 1. 已知:如图,△ABC和△DCE都是等腰直角三角形,∠ACB=∠DCE=90°. (1)求证:BD=AE. (2)若∠ABD=∠DAE,AB=8,AD=6,求四边形ABED的面积. 例题2. 如图,等边△ABC,等边△ADE,等边△DBF分别有公共顶点A,D,且△ADE,△DBF都在△ADB内,求证:CD与EF互相平分.
变式练习>>> 2. 已如图,已知等边三角形ABC,在AB上取点D,在AC上取点E,使得AD=AE,作等边三角形PCD,QAE和RAB,求证:P、Q、R是等边三角形的三个顶点. 例题3. 在等边△ABC与等边△DCE中,B,C,E三点共线,连接BD,AE交于点F,连接CF. (1)如图1,求证:BF=AF+FC,EF=DF+FC;
初中数学经典几何难题及答案39256
1、已知:如图,O 是半圆的圆心,C 、E 是圆上的两点,CD ⊥AB ,EF ⊥AB ,EG ⊥CO . 求证:CD =GF .(初二) 第1题图 第2题图 2、已知:如图,P 是正方形ABCD 内点,∠PAD =∠PDA =150 . 求证:△PBC 是正三角形.(初二) 3、如图,已知四边形ABCD 、A 1B 1C 1D 1都是正方形,A 2、B 2、C 2、D 2分别是AA 1、BB 1、CC 1、DD 1的中点.求证:四边形A 2B 2C 2D 2是正方形.(初二) 第3题图 第4 题图 4、已知:如图,在四边形ABCD 中,AD =BC ,M 、N 分别是AB 、CD 的中点,AD 、BC 的延长线交MN 于E 、F .求证:∠DEN =∠F . B D 2 C 2 B 2 A 2 D 1 C 1 B 1 C B D A A 1 A P C D B A F G C E B O D
1、已知:△ABC 中,H 为垂心(各边高线的交点),O 为外心,且OM ⊥BC 于M . (1)求证:AH =2OM ; (2)若∠BAC =600 ,求证:AH =AO .(初二) 第1题图 第2题图 2、设MN 是圆O 外一直线,过O 作OA ⊥MN 于A ,自A 引圆的两条直线,交圆于B 、C 及D 、E ,直线EB 及CD 分别交MN 于P 、Q .求证:AP =AQ .(初二) 3、如果上题把直线MN 由圆外平移至圆内,则由此可得以下命题: 设MN 是圆O 的弦,过MN 的中点A 任作两弦BC 、DE ,设CD 、EB 分别交MN 于P 、Q . 求证:AP =AQ .(初二) 第3题图 第4题图 F
平面几何经典难题及解答
经典难题(一) 1、已知:如图,O就是半圆的圆心,C、E就是圆上的两点,CD⊥AB,EF⊥AB,EG⊥CO. 求证:CD=GF. 求证:△PBC就是正三角形. 3、如图,已知四边形ABCD、A1 CC1、DD1的中点. 求证:四边形A2B2C2D2 4、已知:如图,在四边形ABCD中 线交MN于E、F. 求证:∠DEN=∠F. 1、已知:△ABC中,H为垂心( (1)求证:AH=2OM; (2)若∠BAC=600,求证:AH= 2、设MN就是圆O外一直线,过 D、E,直线EB及CD分别交 求证:AP=AQ.(初二) 3、如果上题把直线MN 设MN就是圆O的弦,过 P、Q. 求证:AP=AQ.(初二) 4、如图,分别以△ABC的AC与 点P就是EF的中点. 求证:点P到边AB 1、如图,四边形ABCD为正方形 求证:CE=CF.(初二) 2、如图,四边形ABCD为正方形 求证:AE=AF.(初二) 3、设P就是正方形ABCD一边 求证:PA=PF.(初二) 4、如图,PC切圆O于C,AC 求证:AB=DC,BC=AD.(初三 1、已知:△ABC就是正三角形,P 求:∠APB的度数.(初二) 2、设P就是平行四边形ABCD 求证:∠PAB=∠PCB.(初二)
3、设ABCD 为圆内接凸四边形,求证:AB ·CD +AD ·BC =AC · 4、平行四边形ABCD 中,设E 、F 分别就是BC 、AB 上的一点,AE AE =CF.求证:∠DPA =∠DPC.(初二) 经典难题(五) 1、设P 就是边长为1的正△ABC 内任一点证: ≤L <2. 2、已知:P 就是边长为1的正方形ABCD 内的一点,求PA +PB +PC 3、P 为正方形ABCD 内的一点,并且PA =a,PB =2a,PC =3a, 4、如图,△ABC 中,∠ABC =∠ACB =800,D 、E 分别就是AB 、AC =200,求∠BED 的度数. 经典难题解答: 经典难题(一) 1、如下图做GH ⊥AB,连接EO 。由于GOFE 四点共圆,所以∠GFH 即△GHF ∽△OGE,可得 EO GF =GO GH =CO CD ,又CO=EO,所以CD=GF
【猿辅导几何模型】中考必会几何模型:相似模型
中考必考几何模型(猿辅导) 最 新 讲 义
相似模型 模型1:A、8模型 已知∠1=∠2 结论:△ADE∽△ABC 模型分析 如图,在相似三角形的判定中,我们通过做平行线,从而得出A型或8型相似.在做题使,我们也常常关注题目由平行线所产生的相似三角形. 模型实例 【例1】如图,在ABC中,中线AF、BD、CE相交于点O,求证: 1 2 OF OE OD OA OC OB ===. 解答:证法一:如图①,连接DE.∵D、E是中点,∴ 1 2 DE BC =.,DE//BC ∴△EOD∽△COB(8模型)∴ 1 2 OE DE OC BC ==.同理: 1 2 OF OA =, 1 2 OD OB =. ∴ 1 2 OF OE OD OA OC OB ===.
证法二:如图②,过F作FG//AC交BD于点G,∵F是中点,∴ 1 2 GF BF AD BC ==. ∵AD=CD, ∴ 1 2 GF AD =.∵FG//AD,∴△GOF∽△DOA(8模型) ∴ 1 2 OF GF OA AD ==.同理 1 2 OE OC =, 1 2 OD OB =.∴ 1 2 OF OE OD OA OC OB ===. 【例2】如图,点E、F分别在菱形ABCD的边AB、AD上,且AE=DF,BF交DE于点G, 延长BF交CD的延长线于H,若AF DF =2,求 HF BG 的值. 解答:∵四边形ABCD是菱形,∴AB=BC=CD=AD. 设DF=a,则DF=AE=a,AF=EB=2a.∵HD//AB,∴△HFD∽△BF A ∴ 1 2 HD DF HF AB AF FB ===,∴HD=1.5a, 1 3 FH BH =,∴FH= 1 3 BH ∵HD//EB,∴△DGH∽△EGB,∴ 1.53 24 HG HD a GB EB a ===,∴ 4 7 BG HB = ∴BG=4 7 HB,∴ 1 7 3 412 7 BH HF BG BH == 跟踪练习: 1.如图,D、E分别是△ABC的边AB、BC上的点,且DE//AC,AE、CD相交于点O,若S△DOE:S△COA=1:25.则S△BD E与S△CDE的比是____________.
初中数学经典几何难题及答案
经典难题(一) 1、已知:如图,O 是半圆的圆心,C 、E 是圆上的两点,CD ⊥AB ,EF ⊥AB ,EG ⊥CO . 求证:CD =GF .(初二) 第1题图 第2题图 2、已知:如图,P 是正方形ABCD 内点,∠PAD =∠PDA =150. 求证:△PBC 是正三角形.(初二) 3、如图,已知四边形ABCD 、A 1B 1C 1D 1都是正方形,A 2、B 2、C 2、D 2分别是AA 1、BB 1、CC 1、DD 1的中点.求证:四边形A 2B 2C 2D 2是正方形.(初二) 第3题图 第 4题图 4、已知:如图,在四边形ABCD 中,AD =BC ,M 、N 分别是AB 、CD 的中点,AD 、BC 的延 B D 2 C 2 B 2 A 2 D 1 C 1 B 1 C B D A A 1 A P C D B A F G C E B O D
长线交MN于E、F.求证:∠DEN=∠F. 经典难题(二) 1、已知:△ABC中,H为垂心(各边高线的交点),O为外心,且OM⊥BC于M. (1)求证:AH=2OM; (2)若∠BAC=600,求证:AH=AO.(初二) 第1题图第2题图 2、设MN是圆O外一直线,过O作OA⊥MN于A,自A引圆的两条直线,交圆于B、C及 D、E,直线EB及CD分别交MN于P、Q.求证:AP=AQ.(初二) 3、如果上题把直线MN由圆外平移至圆内,则由此可得以下命题: 设MN是圆O的弦,过MN的中点A任作两弦BC、DE,设CD、EB分别交MN于P、Q.求证:AP=AQ.(初二)
第3题图 第4题图 4、如图,分别以△ABC 的AC 和BC 为一边,在△ABC 的外侧作正方形ACDE 和正方形CBFG ,点P 是EF 的中点. 求证:点P 到边AB 的距离等于AB 的一半.(初二) 经典难题(三) 1、如图,四边形ABCD 为正方形,DE ∥AC ,AE =AC ,AE 与CD 相交于F . 求证:CE =CF .(初二) 第1题图 第2题图 2、如图,四边形ABCD 为正方形,DE ∥AC ,且CE =CA ,直线EC 交DA 延长线于F . 求证:AE =AF .(初二)
(完整word版)初二几何证明整理(经典题型)
如何做几何证明题 【知识梳理】 1、几何证明是平面几何中的一个重要问题,它对培养学生逻辑思维能力有着很大作用。几何证明有两种基本类型:一是平面图形的数量关系;二是有关平面图形的位置关系。这两类问题常常可以相互转化,如证明平行关系可转化为证明角等或角互补的问题。 2、掌握分析、证明几何问题的常用方法: (1)综合法(由因导果),从已知条件出发,通过有关定义、定理、公理的应用,逐步向前推进,直到问题的解决; (2)分析法(执果索因)从命题的结论考虑,推敲使其成立需要具备的条件,然后再把所需的条件看成要证的结论继续推敲,如此逐步往上逆求,直到已知事实为止; (3)两头凑法:将分析与综合法合并使用,比较起来,分析法利于思考,综合法易于表达,因此,在实际思考问题时,可合并使用,灵活处理,以利于缩短题设与结论的距离,最后达到证明目的。 3、掌握构造基本图形的方法:复杂的图形都是由基本图形组成的,因此要善于将复杂图形分解成基本图形。在更多时候需要构造基本图形,在构造基本图形时往往需要添加辅助线,以达到集中条件、转化问题的目的。 【例题精讲】 【专题一】证明线段相等或角相等 两条线段或两个角相等是平面几何证明中最基本也是最重要的一种相等关系。很多其它问题最后都可化归为此类问题来证。证明两条线段或两角相等最常用的方法是利用全等三角形的性质,其它如线段中垂线的性质、角平分线的性质、等腰三角形的判定与性质等也经常用到。 【例1】已知:如图所示,?A B C 中,∠=?===C AC BC AD DB AE CF 90,,,。 求证:DE =DF F E D C B A
【巩固】如图所示,已知?A B C 为等边三角形,延长BC 到D ,延长BA 到E ,并且使AE =BD ,连结CE 、DE 。 求证:EC =ED 【例2】已知:如图所示,AB =CD ,AD =BC ,AE =CF 。 求证:∠E =∠F 【专题二】证明直线平行或垂直 在两条直线的位置关系中,平行与垂直是两种特殊的位置。证两直线平行,可用同位角、内错角或同旁内角的关系来证,也可通过边对应成比例、三角形中位线定理证明。证两条直线垂直,可转化为证一个角等于90°,或利用两个锐角互余,或等腰三角形“三线合一”来证。 【例3】如图所示,设BP 、CQ 是?A B C 的内角平分线,AH 、AK 分别为A 到BP 、CQ 的 垂线。 求证:KH ∥BC A C E D F B A B D C E A B Q P H C K
平面几何经典难题
经典难题(一) 1、已知:如图,O 是半圆的圆心,C 、E 是圆上的两点,CD ⊥AB ,EF ⊥AB ,EG ⊥CO . 求证:CD =GF . 2、已知:如图,P 是正方形ABCD 内一点,∠PAD =∠PDA =150. 求证:△PBC 是正三角形. 3、如图,已知四边形ABCD 、A 1B 1C 1D 1都是正方形,A 2、B 2、C 2、D 2分别是AA 1、BB 1、CC 1、 DD 1的中点. 求证:四边形A 2B 2C 2D 2是正方形.(初二) 4、已知:如图,在四边形ABCD 中,AD =BC ,M 、N 分别是AB 、CD 的中点,AD 、BC 的延 长线交MN 于E 、F . 求证:∠DEN =∠F . A P C D B A F G C E B O D D 2 C 2 B 2 A 2 D 1 C 1 B 1 C B D A A 1 B
F 1、已知:△ABC 中,H 为垂心(各边高线的交点),O 为外心,且 (1)求证:AH =2OM ; (2)若∠BAC =600,求证:AH =AO .(初二) 2、设MN 是圆O 外一直线,过 O 作OA ⊥MN 于A ,自A D 、E ,直线EB 及CD 分别交MN 于P 、Q . 求证:AP =AQ .(初二) 3、如果上题把直线MN 由圆外平移至圆内,则由此可得以下命题: 设MN 是圆O 的弦,过MN 的中点A 任作两弦BC 、DE ,设CD 、EB 分别交MN 于P 、 Q . 求证:AP =AQ .(初二) 4、如图,分别以△ABC 的AC 和BC 为一边,在△ABC 的外侧作正方形ACDE 和正方形CBFG , 点P 是EF 的中点. 求证:点P 到边AB 的距离等于AB 的一半.
中考数学必会几何模型:半角模型
半角模型 已知如图:①∠2=1 2 ∠AOB;②OA=OB. O A B E F 1 23 连接FB,将△FOB绕点O旋转至△FOA的位置,连接F′E,FE,可得△OEF≌△OEF′ 43 2 1 F' F E B A O 模型分析 ∵△OBF≌△OAF′, ∴∠3=∠4,OF=OF′. ∴∠2=1 2 ∠AOB, ∴∠1+∠3=∠2 ∴∠1+∠4=∠2 又∵OE是公共边, ∴△OEF≌△OEF′. (1)半角模型的命名:存在两个角度是一半关系,并且这两个角共顶点; (2)通过先旋转全等再轴对称全等,一般结论是证明线段和差关系; (3)常见的半角模型是90°含45°,120°含60°. 模型实例 例1 已知,正方形ABCD中,∠MAN=45°,它的两边分别交线段CB、DC于点M、N.(1)求证:BM+DN=MN. (2)作AH⊥MN于点H,求证:AH=AB.
证明:(1)延长ND 到E ,使DE=BM , ∵四边形ABCD 是正方形,∴AD=AB . 在△ADE 和△ABM 中, ?? ? ??=∠=∠=BM DE B ADE AB AD ∴△ADE ≌△ABM . ∴AE=AM ,∠DAE=∠BAM ∵∠MAN=45°,∴∠BAM+∠NAD=45°. ∴ ∠MAN=∠EAN=45°. 在△AMN 和△AEN 中, ?? ? ??=∠=∠=AN AN EAN M AN EA M A ∴△AMN ≌△AEN . ∴MN=EN . ∴BM+DN=DE+DN=EN=MN . (2)由(1)知,△AMN ≌△AEN . ∴S △AMN =S △AEN . 即EN AD 2 1 MN AH 21?=?. 又∵MN=EN , ∴AH=AD . 即AH=AB .
平面几何经典难题及解答之令狐文艳创作
平面几何 令狐文艳 经典难题(一) 1、已知:如图,O 是半圆的圆心,C 、E 是圆上的两点,CD ⊥AB ,EF ⊥AB ,EG ⊥CO . 求证:CD =GF . 2、已知:如图,P 是正方形ABCD 内一点,∠PAD =∠PDA =150 . 求证:△PBC 是正三角形. 3、如图,已知四边形ABCD 、A 1B 1C 1D 1 D 2分别是AA 1、BB 1、CC 1、DD 1的中点. 求证:四边形A 2B 2C 2D 24、已知:如图,在四边形ABCD 中,AD AB 、CD 的中点,AD 、BC 的延长线交求证:∠DEN =∠F . 经典难题(二) 1、已知:△ABC 中,H 心,且OM ⊥BC 于M . (1)求证:AH =2OM ; (2)若∠BAC =600 ,求证:AH =AO 2、设MN 是圆O 外一直线,过O 作OA ⊥MN 于A G C E B
两条直线,交圆于B 、C 及D 、E ,直线EB 及CD 分别交MN 于P 、Q . 求证:AP =AQ .(初二) 3、如果上题把直线MN 由圆外平移至圆内,则由此可得以下命题: 设MN 是圆O 的弦,过MN CD 、EB 分别交MN 于P 、Q . 求证:AP =AQ .(初二) 4、如图,分别以△ABC 的AC 和BC 正方形ACDE 和正方形CBFG ,点P 是求证:点P 到边AB 的距离等于AB 经典难1、如图,四边形ABCD 为正方形,DE 相交于F . 求证:CE =CF 2、如图,四边形ABCD EC 交DA 延长线于F . 求证:AE =AF 3、设P 是正方形ABCD ∠DCE . 求证:PA =PF 4、如图,PC 切圆O 于AE 、AF 与直线PO
(完整版)中考数学常见几何模型简介
初中几何常见模型解析 模型一:手拉手模型-旋转型全等 (1)等边三角形 ?条件:均为等边三角形 ?结论:①;②;③平分。 (2)等腰 ?条件:均为等腰直角三角形 ?结论:①;②; ?③平分。 (3)任意等腰三角形 ?条件:均为等腰三角形 ?结论:①;②; ?③平分 模型二:手拉手模型-旋转型相似 (1)一般情况 ?条件:,将旋转至右图位置 ?结论: ?右图中①; ?②延长AC交BD于点E,必有 (2)特殊情况 ?条件:,,将旋转至右图位置 ?结论:右图中①;②延长AC交BD于点E,必有; ③; ④; ⑤连接AD、BC,必有; ⑥(对角线互相垂直的四边形)
模型三:对角互补模型 (1)全等型-90° ?条件:①;②OC平分 ?结论:①CD=CE; ②;③ ?证明提示: ①作垂直,如图,证明; ②过点C作,如上图(右),证明; ?当的一边交AO的延长线于点D时: 以上三个结论:①CD=CE(不变); ②;③ 此结论证明方法与前一种情况一致,可自行尝试。 (2)全等型-120° ?条件:①; ?②平分; ?结论:①;②; ?③ ?证明提示:①可参考“全等型-90°”证法一; ②如图:在OB上取一点F,使OF=OC,证明 为等边三角形。 (3)全等型-任意角 ?条件:①;②; ?结论:①平分;②; ?③. ?当的一边交AO的延长线于点D时(如右上图): 原结论变成:①; ②; ③; 可参考上述第②种方法进行证明。请思考初始条件的变化对模型的影响。 ?对角互补模型总结: ①常见初始条件:四边形对角互补;注意两点:四点共圆及直角三角形斜边中线; ②初始条件“角平分线”与“两边相等”的区别; ③两种常见的辅助线作法; ④注意平分时,相等如何推导?
初中数学几何经典难题精选
初三数学总复习辅导学习资料(6)——几何经典难题 1.已知:如图,O 是半圆的圆心,C 、E 是圆上的两点,CD ⊥AB ,EF ⊥AB ,EG ⊥CO .求证:CD =GF . 2.已知:如图,P 是正方形ABCD 内点,∠PAD =∠PDA =150 .求证:△PBC 是正三角形. 3.如图,已知四边形ABCD 、A 1B 1C 1D 1都是正方形,A 2、B 2、 C 2、 D 2分别是AA 1、BB 1、CC 1、DD 1的中点. 求证:四边形A 2B 2 C 2 D 2是正方形. 4、已知:如图,在四边形ABCD 中,AD =BC ,M 、N 分别是AB 、CD 的中点,AD 、BC 的延长线交MN 于E 、F . 求证:∠DEN =∠F . 5.已知:△ABC 中,H 为垂心(各边高线的交点),O 为外心,且OM ⊥BC 于M .(1)求证:AH =2OM ;(2)若∠BAC =600 ,求证:AH =AO . A P C D B A F G C E B O D D 2 C 2 B 2 A 2 D 1 C 1 B 1 C B D A A 1
F 6.设MN 是圆O 外一直线,过O 作OA ⊥MN 于A ,自A 引圆的两条直线,交圆于B 、C 及D 、E ,直线EB 及 CD 分别交MN 于P 、Q .求证:AP =AQ . 7.如果上题把直线MN 由圆外平移至圆内,则由此可得以下命题:设MN 是圆O 的弦,过MN 的中点A 任作 两弦BC 、DE ,设CD 、EB 分别交MN 于P 、Q .求证:AP =AQ . 8.如图,分别以△ABC 的AC 和BC 为一边,在△ABC 的外侧作正方形ACDE 和正方形CBFG ,点P 是EF 的中点.求证:点P 到边AB 的距离等于AB 的一半. 9.如图,四边形ABCD 为正方形,DE ∥AC ,AE =AC ,AE 与CD 相交于 10.如图,四边形ABCD 为正方形,DE ∥AC ,且CE =CA ,直线EC 交DA 延长线于F .求证:AE =AF . E
平面几何经典难题及解答
经典难题(一) 1、已知:如图, 0是半圆的圆心, C E 是圆上的两点, CD 丄AB, EF 丄AB, EGL CO 求证:CD= GF. 4、已知:如图,在四边形 ABCD 中, AD= BC, M N 分别是AB CD 的中点,AD BC 的延长线 交MN 于E 、F . 求证:/ DEN=Z F . 2、已知:如图,P 是正方形 ABCD 内一点, 求 证:△ PBC 是正三角形 . PAD=Z PDA= 150. 3、如图,已知四边形 ABCD AiBCD 都是正方形, 的中 点. 求证:四边形A e B 2C 2C 2是正方形.(初二) A 、E 2、C 2、D 2 分别是 AA 、BB 、CG 、DD D C D C M
经典难题(二) 1、已知:△ ABC 中,H 为垂心(各边高线的交点),0为外心,且 OM L BC 于M. (1) 求证:AH= 20M (2) 若/ BAC= 600,求证: 2、设MN 是圆O 外一直线,过0作OAL MN 于A 自A 引圆的两条直线, 交圆于B 、C 及D E , 直线EB 及CD 分别交MN 于P 、Q. 求证:AP = AQ (初二) 3、如果上题把直线 MN 由圆外平移至圆内,则由此可得以下命题: 设MN 是圆O 的弦,过MN 的中点A 任作两弦BC DE 设CD EB 分别交MN 于P 、Q. 求证:AP = AQ (初二) 4、如图,分别以厶 ABC 的AC 和BC 为一边,在△ ABC 的外侧作正方形 ACDE 和正方形CBFG AH= AO (初二) H E B C M D G E C A M N P O
平面几何经典难题及解答
平面几何 经典难题(一) 1、已知:如图,O 是半圆的圆心,C 、E 是圆上的两点,CD ⊥AB ,EF ⊥AB ,EG ⊥CO . 求证:CD =GF . 2、已知:如图,P 是正方形ABCD 内一点,∠PAD =∠PDA =150 . 求证:△PBC 是正三角形. 3、如图,已知四边形ABCD 、A 1B 1C 1D 1都是正方形,A 2、B 2、C 2、D 2分别是AA 1、BB 1、CC 1、DD 1 的中点. 求证:四边形A 2B 2C 2D 2是正方形.(初二) 4、已知:如图,在四边形ABCD 中,AD =BC ,M 、N 分别是AB 、CD 的中点,AD 、BC 的延长线 交MN 于E 、F . 求证:∠DEN =∠F . A P C D B A F G C E B O D D 2 C 2 B 2 A 2 D 1 C 1 B 1 C B D A A 1 B
F 经典难题(二) 1、已知:△ABC 中,H 为垂心(各边高线的交点),O 为外心,且 (1)求证:AH =2OM ; (2)若∠BAC =600 ,求证:AH =AO .(初二) 2、设MN 是圆O 外一直线, 过O 作OA ⊥MN 于A ,自A 引圆的两条直线,交圆于B 、C 及D 、E ,直线EB 及CD 分别交MN 于P 、Q . 求证:AP =AQ .(初二) 3、如果上题把直线MN 由圆外平移至圆内,则由此可得以下命题: 设MN 是圆O 的弦,过MN 的中点A 任作两弦BC 、DE ,设CD 、EB 分别交MN 于P 、Q . 求证:AP =AQ .(初二) 4、如图,分别以△ABC 的AC 和BC 为一边,在△ABC 的外侧作正方形ACDE 和正方形CBFG , 点P 是EF 的中点. 求证:点P 到边AB 的距离等于AB 的一半.
初中数学经典几何难题及答案
初中数学经典几何难题及答案
经典难题(一) 1、已知:如图,O 是半圆的圆心,C 、E 是圆上的两点,CD ⊥AB ,EF ⊥AB ,EG ⊥CO . 求证:CD =GF .(初二) 2、已知:如图,P 是正方形ABCD 内一点,∠PAD =∠PDA =150. 求证:△PBC 是正三角形.(初二) A P C D B A F G C E B O D
3、如图,已知四边形ABCD 、A 1B 1C 1D 1都是正 方形,A 2、B 2、C 2、D 2分别是AA 1、BB 1、CC 1、DD 1的中点. 求证:四边形A 2B 2C 2D 2是正方形.(初二) 4、已知:如图,在四边形ABCD 中,AD =BC , M 、N 分别是AB 、CD 的中点,AD 、BC 的延长线交MN 于E 、F . 求证:∠DEN =∠F . D 2 C 2 B 2 A 2 D 1 C 1 B 1 C D A A 1 A N F E C D M B
经典难题(二) 1、已知:△ABC 中,H 为垂心(各边高线的交点),O 为外心,且OM ⊥BC 于M . (1)求证:AH =2OM ; (2)若∠BAC =600,求证:AH =AO .(初 二) 2、设MN 是圆O 外一直线,过O 作OA ⊥MN 于A ,自A 引圆的两条直线,交圆于B 、C 及D 、E ,直线EB 及CD 分别交MN 于P 、Q . 求证:AP =AQ .(初二) · A D H E M C B O · G A O D B E C Q P N M
C G D E 3、如果上题把直线MN 由圆外平移至圆内,则由此可得以下命题: 设MN 是圆O 的弦,过MN 的中点A 任作两弦BC 、DE ,设CD 、EB 分别交MN 于P 、Q . 求证:AP =AQ .(初二) 4、如图,分别以△ABC 的AC 和BC 为一边, 在△ABC 的外侧作正方形ACDE 和正方形CBFG ,点P 是EF 的中点. · O Q P B D E C N M · A
平面几何经典难题及解答
经典难题(一) 1、已知:如图,O是半圆的圆心,C、E是圆上的两点,CD⊥AB,EF⊥AB,EG⊥CO. 求证:CD=GF. 求证:△PBC是正三角形. 3、如图,已知四边形ABCD、A1B 点. 求证:四边形A2B2C2D2 4、已知:如图,在四边形ABCD 于E、F. 求证:∠DEN=∠F. 1、已知:△ABC中,H (1)求证:AH=2OM; (2)若∠BAC=600,求证: 2、设MN是圆O外一直线,过O EB及CD分别交MN于P、Q 求证:AP=AQ.(初二) 3、如果上题把直线MN 设MN是圆O的弦,过 求证:AP=AQ 4、如图,分别以△ABC的AC和是 EF的中点. 求证:点P到边AB 1、如图,四边形ABCD 求证:CE=CF.(初二) 2、如图,四边形ABCD 求证:AE=AF.(初二) 3、设P是正方形ABCD一边BC 求证:PA=PF.(初二) 4、如图,PC切圆O于C,AC AB=DC,BC=AD.(初三) 1、已知:△ABC是正三角形,P 求:∠APB的度数.(初二) 2、设P是平行四边形ABCD 求证:∠PAB=∠PCB
3、设ABCD 为圆内接凸四边形,求证:AB ·CD +AD ·BC =AC · 4、平行四边形ABCD 中,设E 、F 分别是BC 、AB 上的一点,AE AE =CF .求证:∠DPA =∠DPC .(初二) 经典难题(五)1、设P 是边长为1的正△ABC 内任一点,L =PA +PB +PC ,求证:≤L <2. 2、已知:P 是边长为1的正方形ABCD 内的一点,求PA +PB +PC 3、P 为正方形ABCD 内的一点,并且PA =a ,PB =2a ,PC =3a 4、如图,△ABC 中,∠ABC =∠ACB =800,D 、E 分别是AB 、AC 200,求∠BED 的度数. 经典难题解答: 经典难题(一) 1.如下图做GH ⊥AB,连接EO 。由于GOFE 四点共圆,所以∠GFH =∠即△GHF ∽△OGE,可得 EO GF =GO GH =CO CD ,又CO=EO ,所以CD=GF 2. 如下图做△DGC 使与△ADP 全等,可得△PDG 为等边△,从而可得△DGC ≌△APD ≌△CGP,得出PC=AD=DC,和∠DCG=∠PCG =150 所以∠DCP=300 ,从而得出△PBC 是正三角形 3.如下图连接BC 1和AB 1分别找其中点F,E.连接C 2F 与A 2E 并延长相交于Q 点, 连接EB 2并延长交C 2Q 于H 点,连接FB 2并延长交A 2Q 于G 点, 由A 2E=12A 1B 1=12B 1C 1= FB 2 ,EB 2=12AB=1 2BC=F C 1 ,又∠GFQ+∠Q=900和 ∠GE B 2+∠Q=900,所以∠GE B 2=∠GFQ 又∠B 2FC 2=∠A 2EB 2 , 可得△B 2FC 2≌△A 2EB 2 ,所以A 2B 2=B 2C 2 , 又∠GFQ+∠HB 2F=900和∠GFQ=∠EB 2A 2 , 从而可得∠A 2B 2 C 2=900 , 同理可得其他边垂直且相等, 从而得出四边形A 2B 2C 2D 2是正方形。 4.如下图连接AC 并取其中点Q ,连接QN 和QM ,所以可得∠QMF=∠F ,∠QNM=∠DEN 和∠QMN=∠QNM ,从而得出∠DEN =∠F 。 经典难题(二) D
初中数学几何经典例题目及解题技巧
初中几何证明技巧及经典试题 证明两线段相等 1.两全等三角形中对应边相等。 2.同一三角形中等角对等边。 3.等腰三角形顶角的平分线或底边的高平分底边。 4.平行四边形的对边或对角线被交点分成的两段相等。 5.直角三角形斜边的中点到三顶点距离相等。 6.线段垂直平分线上任意一点到线段两段距离相等。 7.角平分线上任一点到角的两边距离相等。 8.过三角形一边的中点且平行于第三边的直线分第二边所成的线段相等。 *9.同圆(或等圆)中等弧所对的弦或与圆心等距的两弦或等圆心角、圆周角所对的弦相等。 *10.圆外一点引圆的两条切线的切线长相等或圆内垂直于直径的弦被直径分成的两段相等。 11.两前项(或两后项)相等的比例式中的两后项(或两前项)相等。 *12.两圆的内(外)公切线的长相等。 13.等于同一线段的两条线段相等。 证明两个角相等 1.两全等三角形的对应角相等。 2.同一三角形中等边对等角。 3.等腰三角形中,底边上的中线(或高)平分顶角。 4.两条平行线的同位角、内错角或平行四边形的对角相等。 5.同角(或等角)的余角(或补角)相等。 *6.同圆(或圆)中,等弦(或弧)所对的圆心角相等,圆周角相等,弦切角等于它所夹的弧对的圆周角。*7.圆外一点引圆的两条切线,圆心和这一点的连线平分两条切线的夹角。 8.相似三角形的对应角相等。 *9.圆的内接四边形的外角等于内对角。 10.等于同一角的两个角相等。 证明两条直线互相垂直 1.等腰三角形的顶角平分线或底边的中线垂直于底边。 2.三角形中一边的中线若等于这边一半,则这一边所对的角是直角。 3.在一个三角形中,若有两个角互余,则第三个角是直角。 4.邻补角的平分线互相垂直。 5.一条直线垂直于平行线中的一条,则必垂直于另一条。 6.两条直线相交成直角则两直线垂直。 7.利用到一线段两端的距离相等的点在线段的垂直平分线上。 8.利用勾股定理的逆定理。 9.利用菱形的对角线互相垂直。 *10.在圆中平分弦(或弧)的直径垂直于弦。 *11.利用半圆上的圆周角是直角。 证明两直线平行 1.垂直于同一直线的各直线平行。 2.同位角相等,内错角相等或同旁内角互补的两直线平行。 3.平行四边形的对边平行。 4.三角形的中位线平行于第三边。
最新中考数学必会几何模型
目录 将军饮马模型 (3) 模型1:直线与两定点 (3) 模型2/角与定点 (10) 模型3两定点一定长 (15) 第十二章辅助圆 (20) 模型1 共端点,等线段模型 (20) 模型2 直角三角形共斜边模型 (23) 半角模型 (32) 模型实例 (33) 8字模型与飞镖模型 (50) 模型1:角的8字模型 (50) 模型2:角的飞镖模型 (54) 模型3 边的“8”字模型 (57) 模型4 边的飞镖模型 (58) 中点四大模型 (63) 模型1 倍长中线或类中线(与中点有关的线段)构造全等三角形 (63) 模型2 已知等腰三角形底边中点,可以考虑与顶点连接用“三线合一”. (66) 模型3 已知三角形一边的中点,可考虑中位线定理 (71) 模型4 已知直角三角形斜边中点,可以考虑构造斜边中线 (78) 二次函数 (85) 圆中的辅助线 (91) 模型1 连半径构造等腰三角形 (91) 模型2 构造直角三角形 (94) 模型3 与圆的切线有关的辅助线 (100) 相似模型 (111) 模型1:A、8模型 (111) 模型2 共边共角型 (116) 模型3 一线三等角型 (121) 模型4 倒数型 (127) 模型5 与圆有关的简单相似 (132) 模型6 相似和旋转 (136) 1.2空间几何体的三视图和直观图 (145)
1.3 空间几何体的表面积与体积 (145) 手拉手模型 (147) 模型手拉手 (147) 三垂直全等模型 (158) 模型三垂直全等模型 (158) 蚂蚁行程 (170) 模型立体图形展开的最短路径 (170) 截长补短辅助线模型 (180) 模型:截长补短 (180) 角平分线四大模型 (192) 模型1 角平分线的点向两边作垂线 (192) 模型2 截取构造对称全等 (194) 模型3 角平分线+垂线构造等腰三角形 (198) 模型4 角平分线+平行线 (200)
中考数学九大几何模型标准版
初中数学九大几何模型 一、手拉手模型----旋转型全等 (1)等边三角形 【条件】:△OAB 和△OCD 均为等边三角形; 【结论】:①△OAC ≌△OBD ;②∠AEB=60°;③OE 平分∠AED (2)等腰直角三角形 【条件】:△OAB 和△OCD 均为等腰直角三角形; 【结论】:①△OAC ≌△OBD ;②∠AEB=90°;③OE 平分∠AED (3)顶角相等的两任意等腰三角形 【条件】:△OAB 和△OCD 均为等腰三角形; 且∠COD=∠AOB 【结论】:①△OAC ≌△OBD ; ②∠AEB=∠AOB ; ③OE 平分∠AED O A B C D E 图 1 O A B C D E 图 2 O A B C D E 图 1 O A C D E 图 2 O A B C D E O A B C D E 图 1 图 2
二、模型二:手拉手模型----旋转型相似 (1)一般情况 【条件】:CD ∥AB , 将△OCD 旋转至右图的位置 【结论】:①右图中△OCD ∽△OAB →→→△OAC ∽△OBD ; ②延长AC 交BD 于点E ,必有∠BEC=∠BOA (2)特殊情况 【条件】:CD ∥AB ,∠AOB=90° 将△OCD 旋转至右图的位置 【结论】:①右图中△OCD ∽△OAB →→→△OAC ∽△OBD ; ②延长AC 交BD 于点E ,必有∠BEC=∠BOA ; ③ ===OA OB OC OD AC BD tan ∠OCD ;④BD ⊥AC ; ⑤连接AD 、BC ,必有22 22CD AB B C AD +=+;⑥BD AC 21 S △BCD ?= 三、模型三、对角互补模型 (1)全等型-90° 【条件】:①∠AOB=∠DCE=90°;②OC 平分∠AOB 【结论】:①CD=CE ;②OD+OE=2OC ;③2△OCE △OCD △DCE OC 2 1 S S S =+= 证明提示: ①作垂直,如图2,证明△CDM ≌△CEN ②过点C 作CF ⊥OC ,如图3,证明△ODC ≌△FEC ※当∠DCE 的一边交AO 的延长线于D 时(如图4): 以上三个结论:①CD=CE ;②OE-OD=2OC ; ③2△OCD △OCE OC 21 S S =- O B C O A C D E O B C D E O A C D A O B C D E 图 1 A O B C D E M N 图 2 A O B C D E F 图 3 A O B C D E M N 图 4
初中数学经典几何难题, 附答案
初二数学几何经典难题 初二数学几何经典难题(一) 1、已知:如图,O 是半圆的圆心,C 、E 是圆上的两点,CD ⊥AB ,EF ⊥AB ,EG ⊥CO . 求证:CD =GF .(初二) 2、已知:如图,P 是正方形ABCD 内点,∠PAD =∠PDA =150. 求证:△PBC 是正三角形.(初二) 3、如图,已知四边形ABCD 、A 1B 1C 1D 1都是正方形,A 2、B 2、C 2、D 2分别是AA 1、BB 1、 CC 1、DD 1的中点. 求证:四边形A 2B 2C 2D 2是正方形.(初二) 4、已知:如图,在四边形ABCD 中,AD =BC ,M 、N 分别是AB 、CD 的中点,AD 、BC 的延长线交MN 于E 、F . A P C D B A F G C E B O D D 2 C 2 B 2 A 2 D 1 C 1 B 1 C B D A A 1 F
G D 求证:∠DEN =∠F . 经典难题(二) 1、已知:△ABC 中,H 为垂心(各边高线的交点),O 为外心,且OM ⊥BC 于M . (1)求证:AH =2OM ; (2)若∠BAC =600,求证:AH =AO .(初二) 2、设MN 是圆O 外一直线,过O 作OA ⊥MN 于A ,自A 引圆的两条直线,交圆于B 、C 及D 、E ,直线EB 及CD 分别交MN 于P 、Q . 求证:AP =AQ .(初二) 3、如果上题把直线MN 由圆外平移至圆内,则由此可得以下命题: 设MN 是圆O 的弦,过MN 的中点A 任作两弦BC 、DE ,设CD 、EB 分别交MN 于P 、Q . 求证:AP =AQ .(初二) 4、如图,分别以△ABC 的AC 和BC 为一边,在△ABC 的外侧作正方形ACDE 和正方形 CBFG ,点P 是EF 的中点. 求证:点P 到边AB 的距离等于AB 的一半.(初二) · A D H E M C B O · G A O D B E C Q P N M · O Q P B D E C N M · A
初中几何经典难题
经典难题(一)1、已知:如图,O是半圆的圆心,C、E是圆上的两点,CD⊥AB,EF⊥AB,EG⊥CO.求证:CD=GF.(初二) 2、已知:如图,P是正方形ABCD内点,∠PAD=∠PDA=15度求证:△PBC 是正三角形.(初二) 3、如图,已知四边形ABCD、A1B1C1D1都是正方形,A2、B2、C2、D2分别是AA1、BB1、CC1、DD1的中点.求证:四边形A2B2C2D2是正方形.(初二) 4、已知:如图,在四边形ABCD中,AD=BC,M、N分别是AB、CD的中点,AD、BC的延长线交MN于E、F.求证:∠DEN=∠F.
经典难题(二)1、已知:△ABC中,H为垂心(各边高线的交点),O为外心,且OM⊥BC于M.(1)求证:AH=2OM;(2)若∠BAC=600,求证:AH=AO.(初二) 2、设MN是圆O外一直线,过O作OA⊥MN于A,自A引圆的两条直线,交圆于B、C及D、E,直线EB及CD分别交MN于P、Q.求证:AP=AQ.(初二) 3、如果上题把直线MN由圆外平移至圆内,则由此可得以下命题:设MN是圆O的弦,过MN的中点A任作两弦BC、DE,设CD、EB分别交MN于P、Q.求证:AP=AQ.(初二)
4、如图,分别以△ABC的AC和BC为一边,在△ABC的外侧作正方形ACDE 和正方形CBFG,点P是EF的中点.求证:点P到边AB的距离等于AB的一半.(初二) 经典难题(三)1、如图,四边形ABCD为正方形,DE∥AC,AE=AC,AE与CD相交于F.求证:CE=CF.(初二) 2、如图,四边形ABCD为正方形,DE∥AC,且CE=CA,直线EC交DA延长线于F.求证:AE=AF.(初二)
