第4章续 多变量寻优方法

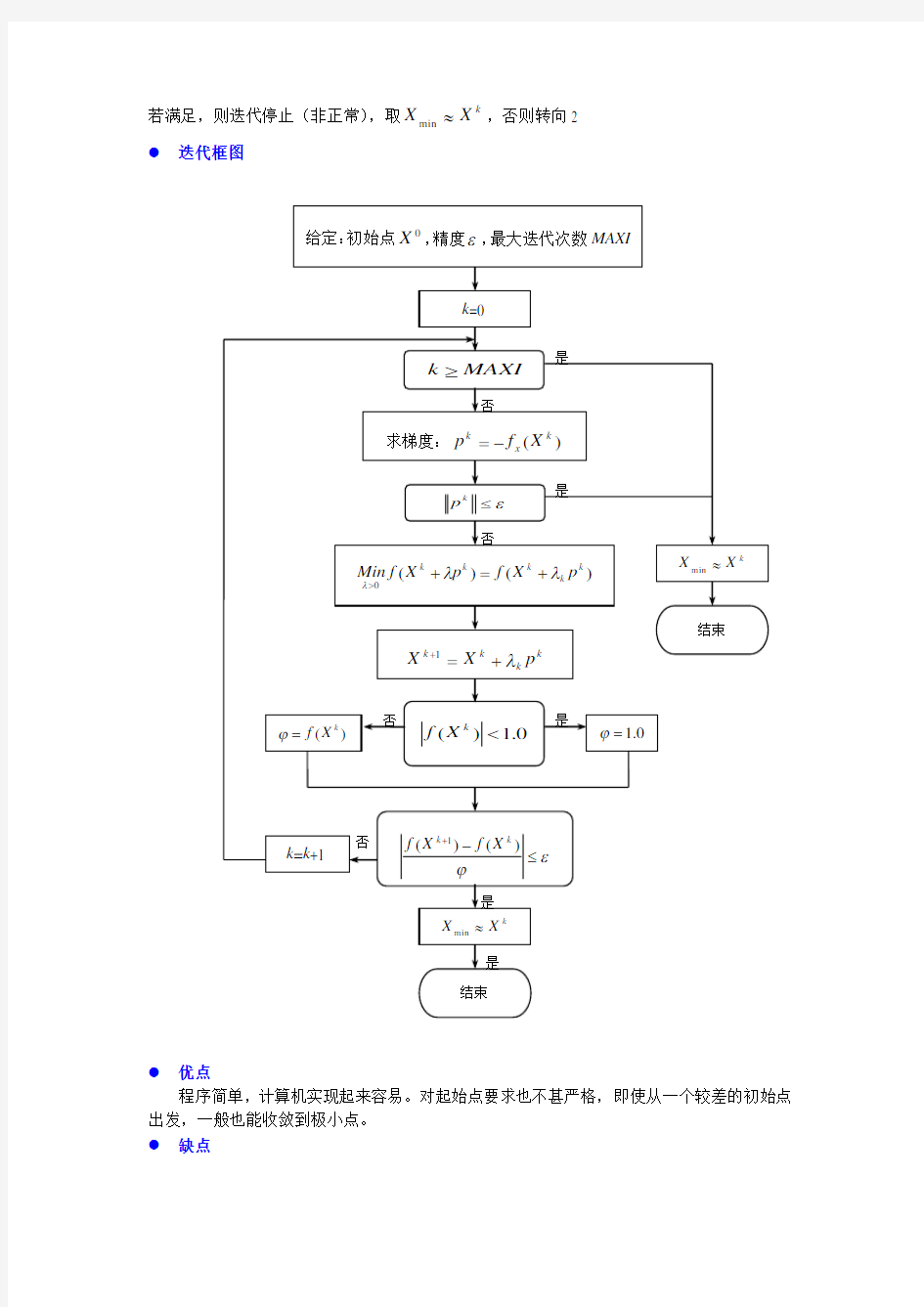
4.4:梯度法
解析法(间接法):在确定搜索方向时,需要计算目标函数导数的方法。 梯度法,共轭梯度法,变尺度法,牛顿法。 ● 方法
又称最速下降法,它是在n
X 点附近沿负梯度方向一维搜索,并按负梯度方向逐步进行寻优的方法。最简单最基本的无约束优化问题方法 ● 收敛性判别准则
给定允许误差0>ε,如果)(k x k X f p -=满足
ε≤k p
则搜索停止,从而得到问题的近似解。 ● 迭代步骤
1:取初始点0
X ,梯度模的允许误差ε,最大迭代次数MAXI ,令k =0; 2:计算梯度
)(k x k X f p -=
3:检验是否满足收敛性判别准则
ε≤k p
若满足,则迭代停止,得到k
X X ≈min ;否则进行4 4:求单变量极值问题的最优解k λ
)()(0
k k k k k p X f p X f Min λλλ+=+>
5:令k k k k p X X λ+=+1 6:判断是否满足
ε?
≤-+)
()(1k k X f X f
)
(0.1)(0.10.1)(k
k k X f X f X f =≥=
若满足,则迭代停止,得到k
X X ≈min ;否则进行7 7:令 k =k+1 8:判断迭代次数
MAXI k ≥
若满足,则迭代停止(非正常),取k X X ≈min ,否则转向2 ● 迭代框图
● 优点
程序简单,计算机实现起来容易。对起始点要求也不甚严格,即使从一个较差的初始点出发,一般也能收敛到极小点。 ● 缺点
在极小点附近收敛得很慢,对于目标函数而言,在起始点远离极小点时,开头几步下降较快,到了极值点时,下降便开始变缓慢,甚至在极小点附近出现来回摆动的情况。
它的收敛快慢与变量尺度关系很大。
2221)(x x X f += 一次迭代 [0,0]
22
219)(x x X f += 十次迭代
]10165.6,10276.5[66--??
对于小扰动会出现不稳定。舍入误差或者一维搜索步长的确定不准确,带来小扰动,这
些小扰动在个别情况下甚至可能使实际下降方向与理论下降方向成正交的荒谬结论,破坏了方法的收敛性。
4.5:共轭梯度法(FR 法)
找到某一个方向的共轭方向,可以一步直接达极值点。 ● 计算方法
正定二次函数X Z CX X X f T T
+=
2
1)(,C 为n n ?对称正定阵。 若n p p ,,1 为任意一组C 的共轭向量,则由任意初始点1
X 出发,按如下格式迭代 )()(k k k k k p X f p X f Min λλλ
+=+
n k p X X k
k k k ,,11 =+=+λ
则至多迭代n 步即收敛。 ● 找共轭方向
取1
X 处的目标函数负梯度方向作为第一个搜索方向
)(1)1(1X f g p x -=-=
然后沿着1p 方向作一维搜索
)()(11111p X f p X f Min λλ+=+
由此得到一个新的点2
X ,并计算出相应的梯度方向 1112p X X λ+=
)(2)2(X f g x =
因为梯度方向和前一搜索方向在1λ处正交
0)()()()2()1(21=-=-g g X f X f T x T x
为了在)
1(g 和)
2(g
构成的正交系中寻求共轭方向2
p ,令
11)2(2p g p υ+-=
即,共轭方向为2
X 处的负梯度方向与前一个搜索方向的线性组合,这里的关键是选择1υ使得1p 和2p 共轭。
对于正定二次函数有
k
k T k k k k T T k k k k T
T k k x k Cp C p g g Z C p X g Z C X X f g λλλ或)()()()()()1()1()(=-++=+==++
于是得到如下关系
1+k p 为)1(+-k g 与k p 的线性组合 k k k k p g p υ+-=++)1(1 1+k p 与k p 共轭
0)(!=+k T k Cp p
二次正定函数)
1(+k g 与)
(k g
关系
k k T k k k k Cp C p g g λλ或)()()1(=-+
从而
2
2
12
)(2)1()
()
(k
x k x k k k X f X
f g
g
++=
=
υ
),2,1()1(1 =+-=++k p g p k
k k k υ
迭代步骤
1:给定起始点1
X ,梯度的模允许误差0>ε,维数n ,最大迭代轮次MAXI ,令k =1
2:检验是否满足收敛性判别准则
ε≤)(1X f x
若满足,迭代停止,得到1
min X X ≈,否则转向3 3:令)(1)1(1X f g p x -=-= 4:求单变量极值问题的最优解
)()(k k k k k p X f p X f Min λλλ
+=+
k k k k p X X λ+=+1
5:判断是否满足
ε?
≤-+)
()(1k k X f X f
)
(0.1)(0.10.1)(k
k
k X f X f X f =≥=
若满足,迭代停止,得到1min +≈k X X ,否则转向6 6:判断k =n 是否成立。若成立,令1
1
+=k X X ,转向10;否则,转向7
7:检验是否满足收敛性准则
ε≤+)(1k x X f
若满足,迭代停止,得到1min +≈k X X ,否则转向8 8:计算
2
2
1)
()
(k
x k x k X f X
f +=
υ
k k k x k p X f p υ+-=++)(11
k =k +1
9:正定性检查
gb <0, gb 为)(k x X f 与k
p 的内积
若满足,则转向4;否则,令k
X X =1
转向10 10:判断迭代轮次J 是否达到规定的最大值
MAXI J ≥ 若满足,则迭代停止,取1
min X X ≈,否则转向2
“再开始”:n 步迭代后,为了避免舍入误差造成的不良后果,以加快收敛速度,由起始点1
X
出发,每进行n 步迭代以后,如果不满足收敛性判别准则,再由
1111),(++==n n x X X X f p 重新开始,也就是进行n 步以后的第一次迭代取负梯
度方向。
“正定性检查”:即检查寻查方向k
p 与梯度方向)
(k g
的夹角是否为钝角,若不为钝角,则取
负梯度方向重新开始迭代。
迭代框图
迭代程序简单,储存量小。
● 缺点
)(k x X f 较小时,计算k υ可能会带来较大的舍入误差,甚至可能引起不稳定。
4.6:变度量法(DFP 法及BFGS 法)
DFP 法是由Davidon 于1959年提出的,Flethei-Powell 于1963年改进的一种算法。比共轭梯度法有更快的收敛速度,在高维问题求解中有着明显优势。 ● 广义牛顿法
对二次严格凸函数
X Z CX X X f T T
+=
2
1)( 从初始点1
X 出发,沿着方向
)()()(1111111Z C X Z CX C X f C p T x ---+-=+-=-=
沿着此方向搜索,只需要一次迭代可以直接得到最优解 Z C p X X 1112--=+=
0)()()(122=+-=+=-T T T T x Z C Z C Z C X X f
广义牛顿法迭代公式
k k k p X X +=+1
牛顿法中每次迭代都必须计算搜索方向
T k x k xx T k x k X f X f X f C p )())(()(11---=-=
引进一组矩阵121,,,,+n n H H H H 来替代111))((,,))((--n xx xx X f X f
k k k H H H ?+=+1
修正矩阵k H ?不断修正,每次迭代都能逼近1))((-k xx X f 。 DFP 法中修正矩阵为
)
()()()()()()()()(k k T k k
T k k k k T k T k k k g
H g H g g H g X X X H ????-=????=?
BFGS 法中修正矩阵为
)
()()()()()()()()()()()(1k T k k
T
k k T k k k T k k k T k k k T k k g
X H g X X g H X X g X g H g H ????-??-????????????+=? 其中
k
k k k k k k x k k k k X X X g
g
g
X f g g H p -=?-=?=-=++1)
()
1()
()()
()(
一维搜索
k
k k k k k k k k p
X X
p X f p X f Min λλλλ
+=+=++1
)
()(
迭代步骤
1:给定起始点1
X ,允许误差0>ε,维数n ,最大迭代轮次MAXI ,初始矩阵I H =1,令
J =0
2:检验是否满足收敛性判别准则
ε≤)(1X f x
若满足,迭代停止,得到1min X X ≈,否则转向3 3:判断迭代轮次J 是否达到规定的最大值
MAXI J ≥ 若满足,则迭代停止,取1min X X ≈,否则转向4 4:令
)(1)1(X f g x =
k =1
5:令
)(k k k g H p -=
当k =1时,转向7,否则转向6 6:正定性检查
gb <0, gb 为)(k x X f 与k
p 的内积
若满足,则转向7;否则,令I H k =)
(k k
g p -=转向7
7:求单变量极值问题的最优解
)()(k k k k k p X f p X f Min λλλ
+=+
k k k k p X X λ+=+1
8:检验是否满足收敛性准则
ε≤+)(1k x X f
若满足,迭代停止,得到1
min +≈k X
X ,否则转向9
9:判断是否满足
ε?
≤-+)
()(1k k X f X f
)
(0.1)(0.10.1)(k
k k X f X f X f =≥=
若满足,迭代停止,得到1min +≈k X X 否则,当k =n 时,令1
1
+=k X
X ,I H k =,J =J +1令转向3
当k k k k k k k x k X X X g g g X f g -=?-=?=++++1)()1()(1)1() ( 10:若取L =0,则选用DFP 法计算 ) ()()()()()()()()(k k T k k T k k k k T k T k k k g H g H g g H g X X X H ????-=????=? 若L ≠0,则选用BFGS 法计算 ) ()()() ()()()()()()()()(1k T k k T k k T k k k T k k k T k k k T k k g X H g X X g H X X g X g H g H ????-??-??????? ?????+=? 转向11 11:令k =k +1,转向5 迭代框图 ● 优点 保留了广义牛顿法的优点,克服其计算不便的缺点。收敛速度快,避开牛顿法的繁琐计算,不必计算赫森矩阵的逆。 ● 缺点 此方法对一维搜索的精度要求比较高,当舍入误差较大时,就不易保证度量矩阵k H 的正定性,会出现数值不稳定。(正定性检查) BFGS 法较为成功,k H 不易成为病态矩阵,具有较好的数值稳定性。 4.7:关于寻优方法的几个问题 ● 梯度的差分逼近 1:梯度的差分逼近公式 简单差分:计算n 次目标函数值,精度低 i k i i k i k d X f e d X f x X f ) ()()(-+≈ ?? T i e ]0,,0,1,0,,0,0[ =,其中第i 个变量为1,其余均是0 i d 为第i 个坐标轴上的步长 中心差分:计算2n 次目标函数值,精度高 i i i k i i k i k d e d X f e d X f x X f 2) ()()(--+≈ ?? 2:Stewert 选择差分法 d f d f d ) 0()(-= γ 22 1 )0()(ad d f d f ++=γ )0(x f =γ,)0(xx f a = 相对截断误差(公式本身产生的误差) γ γγγad d 21= - 相对舍入误差(当d 很小时,计算)0()(f d f -时产生的误差) )0()() 0(2)0()()]0()([)]0()([f d f f f d f f d f f d f -≤----**η )1)(()(ε+=*d f d f )1)(0()0(ε+=*f f 确定步长的思想 ) 0()() 0(221f d f f ad -=η γ 0)0(42 123 2=?-?+ηγγf d a d a 略去三次项(ηγ)0(2af ≥) 2 1 2)0(2431?? ?? ??=? ? ????+-=ητγτττf a a d 略去二次项(ηγ)0(2 af <) 3 1 2 )0(24321?? ? ? ??=? ? ????+-=a f a d ηγτγτγτ 若 εγ ≤ad 21,用简单差分公式,否则用中心差分公式 ● 目标函数的形态及全局最优解 线性规划:单纯形法 非线性规划:没有一种方法普遍有效 全局最优问题:改变初始点 用某种寻优方法求的最优解后,以此为起始点,用随机方向法座大步长搜索 用某种寻优方法求得最优解后,固定其他变量,逐级改变其中一个变量 ● 判断收敛性的准则 梯度向量的模小于给定精度 某两点间的距离小到一定程度 某两点的目标函数值之差小到一定程度 迭代次数大于某规定值 ● 步长、精度、迭代次数的选取 步长选取:成功失败法、模式法、单纯性边长等。在0—1区间寻查时,多取为0.2—0.25, 定区间搜索时,取为1.0,差分步长取为10-4—10-6 精度:两点距离或目标函数值差精度取0.01 步长加速法最小步长0.01 随机方向法取最大调优矢长度0.01 渐进式随机取点法概率0.99,精度0.000125 单纯形法,0.0001 解析法10-5—10-9 最大迭代次数 关于应用寻优方法的评价 可用性,调用目标函数的次数多少,耗费计算机时间多少。 4.4:梯度法 解析法(间接法):在确定搜索方向时,需要计算目标函数导数的方法。 梯度法,共轭梯度法,变尺度法,牛顿法。 ● 方法 又称最速下降法,它是在n X 点附近沿负梯度方向一维搜索,并按负梯度方向逐步进行寻优的方法。最简单最基本的无约束优化问题方法 ● 收敛性判别准则 给定允许误差0>ε,如果)(k x k X f p -=满足 ε≤k p 则搜索停止,从而得到问题的近似解。 ● 迭代步骤 1:取初始点0 X ,梯度模的允许误差ε,最大迭代次数MAXI ,令k =0; 2:计算梯度 )(k x k X f p -= 3:检验是否满足收敛性判别准则 ε≤k p 若满足,则迭代停止,得到k X X ≈min ;否则进行4 4:求单变量极值问题的最优解k λ )()(0 k k k k k p X f p X f Min λλλ+=+> 5:令k k k k p X X λ+=+1 6:判断是否满足 ε? ≤-+) ()(1k k X f X f ) (0.1)(0.10.1)(k k k X f X f X f =≥= 若满足,则迭代停止(非正常),取k X X ≈min ,否则转向2 ● 迭代框图 ● 优点 程序简单,计算机实现起来容易。对起始点要求也不甚严格,即使从一个较差的初始点出发,一般也能收敛到极小点。 ● 缺点 在极小点附近收敛得很慢,对于目标函数而言,在起始点远离极小点时,开头几步下降较快,到了极值点时,下降便开始变缓慢,甚至在极小点附近出现来回摆动的情况。 它的收敛快慢与变量尺度关系很大。 2221)(x x X f += 一次迭代 [0,0] 22 219)(x x X f += 十次迭代 ]10165.6,10276.5[66--?? 对于小扰动会出现不稳定。舍入误差或者一维搜索步长的确定不准确,带来小扰动,这 些小扰动在个别情况下甚至可能使实际下降方向与理论下降方向成正交的荒谬结论,破坏了方法的收敛性。 4.5:共轭梯度法(FR 法) 找到某一个方向的共轭方向,可以一步直接达极值点。 ● 计算方法 正定二次函数X Z CX X X f T T += 2 1)(,C 为n n ?对称正定阵。 若n p p ,,1 为任意一组C 的共轭向量,则由任意初始点1 X 出发,按如下格式迭代 )()(k k k k k p X f p X f Min λλλ +=+ n k p X X k k k k ,,11 =+=+λ 则至多迭代n 步即收敛。 ● 找共轭方向 取1 X 处的目标函数负梯度方向作为第一个搜索方向 )(1)1(1X f g p x -=-= 然后沿着1p 方向作一维搜索 )()(11111p X f p X f Min λλ+=+ 由此得到一个新的点2 X ,并计算出相应的梯度方向 1112p X X λ+= )(2)2(X f g x = 因为梯度方向和前一搜索方向在1λ处正交 0)()()()2()1(21=-=-g g X f X f T x T x 为了在) 1(g 和) 2(g 构成的正交系中寻求共轭方向2 p ,令 寻北仪的方位引出方法 陀螺寻北仪的寻北测量结果需要传递给使用者,这就需要解决寻北方位引出问题。早期的摆式-液浮的和吊丝式寻北仪-都与经纬仪相连,以经纬仪望远镜光轴为寻北方位输出。 理论上讲,寻北方位输出应该以敏感地速水平分量的陀螺敏感轴为寻北方位输出轴,但是由于理论上的陀螺敏感轴难以直接观测或者引出不便因此通常以陀螺的安装基面或通过标定,将敏感轴传递到寻北仪的某个固定轴线例如经纬仪的水平光轴或者某个固定垂直基面的法线作为寻北结果的输出轴。 根据使用方法的不同采用不同的引出方法,此时需要考虑的是:标定和引出方便、易于检测和常数标定、与理论敏感轴之间的关系稳定、使用过程中易于保护等。 1.车载寻北仪 车体本身是机动的但是车载寻北仪是直接安装在车上的,寻北仪的寻北测量结果需要传递给车载导航仪或者车载雷达、火炮、火箭发射装置等,因此通常是以寻北仪外壳的侧向安装基面(法线)与车载导航仪建立固定的关系,经过标定测量来确定两者之间的固定安装角。为了防止传递关系的变化需要定期检测。见图1 自寻北航向仪是具有自寻北功能的惯性航向保持装置其航向仪的水平安装基面既是航向仪的输出基面也是寻北结果的输出基面。 2摆式(吊丝)陀螺寻北仪 2.1.普通吊丝式寻北仪 最初的摆式陀螺寻北仪MW10为半液浮的宝石轴承定位,相当于质心下移的悬浮式自由陀螺。陀螺房上安装的侧向平面镜其法线大致平行于陀螺H轴。 大约在1975年德国研制出上挂摆式(陀螺敏感部安装在经纬仪之上)吊丝式陀螺经纬仪,简称为吊丝式陀螺经纬仪,这是摆式陀螺寻北仪发展的一个里程碑。后来出现下挂式,而上挂式被淘汰。 这些寻北仪与普通经纬仪连接在一起,称为陀螺经纬仪。通过标定,将陀螺H轴与经纬仪望远镜光轴建立稳定的方位角关系,将其寻北结果从经纬仪传递出去。见图2 2.2.美国ALINE陀螺寻北仪(陀螺经纬仪) ALINE寻北仪的方位引出方法是在方位跟踪转台上固定一片倾斜45°的平面镜,其法线的水平投影即为寻北方位引出线。转台上的小型准直经纬仪向下俯45°来准直平面镜即完成寻北方位向经纬仪光轴的传递。经纬仪仰角45°回到水平位置再向用户传递。见图3 此时望远镜的俯仰偏差被带入了,为此需要计入经纬仪的俯仰偏差。 由于每次方位引出都需要经纬仪重新准直倾斜平面镜因此,经纬仪可以临时安置在转台上。 ALINE和下面的MARCS寻北仪中的陀螺房摆动传感器都是感应式的而不是光学的。 2.3.美国MARCS高精度吊丝式寻北仪 MARCS高精度寻北仪是世界最高精度的吊丝式寻北仪(2″级),作为野战条件下校正普通寻北仪的方位基准。其方位转台上没有安装经纬仪因此不能称为陀螺经纬仪。它的方位引出方法是:在方位跟踪转台上安装一个直角棱镜,其法线即为寻北方位引出线。用户通过准直这个直角棱镜得到寻北方位。由于减少了一些方位传递环节因此具有更高的稳定性。其实,就经纬仪本身来说,从底部的安装面到上部的经纬仪望远镜之间以及度盘与上下回转机 多元变量的最值与范围问题 热点一:消元 1.已知z y x ,,为正数,满足032=+-z y x ,则xz y 2 的最小值为 2.已知222c b a =+,c ≠0;求c a b 2-的取值范围. 3.已知实数c b a ,,满足0>a ,ac b a 442 2≤+;求222 c a b +的最大值. 热点二:构造(基本)不等式 4.已知z y x ,,均为正数,且xy y x =+,xyz z y x =++,求z 的取值范围. 5.已知z y x ,,为正数,求 y x z z x y z y x +++++的最小值. 6.已知实数c b a ,,均为正数,求bc ab c b a 32 22+++的最小值. 热点三:多次运用基本不等式 7.已知A,B,C 是同一平面内的三个点,AB =c ,BC =a ,CA =b ,求 c b b a c ++的最小值. 8.对于实数0>c ,当非零实数b a ,满足052222=-+-c b ab a 且使b a +最大时,求c b a +-8的最小值. 1. 不等式22()a mb b a b λ+≥+对于,a b R ?∈,存在R λ∈恒成立,则实数m 的范围为 . 2.已知y x ,为正实数,则 x y y x x ++22的最小值为 3.设0))(3(2≤-+b x ax 对任意),0[+∞∈x 恒成立,其中b a ,是整数,则b a +的取值的集合为 4.已知函数f (x )=ax 2+x -b (a ,b 均为正数),不等式f (x )>0的解集记为P ,集合Q ={x |-2-t <x <-2+t }.若 对于任意正数t ,P ∩Q ≠?,则1a -1b 的最大值是 5. 已知函数f (x )=2x -1 +a ,g (x )=bf (1-x ),其中a ,b ∈R ,若关于x 的不等式f (x )≥g (x )的解的最小值为2,则a 的取值范围是________. 6.已知在ABC ?中,A C B sin 3sin 2sin ≤+,B A C sin 3sin 2sin ≤+,A B sin sin 的取值范围是_______. 7.已知在等差数列{a n }中,a 1≥1,a 2≥2,a 3≤4.实数a 2015的取值范围是________. 8.若实数c b a ,,满足b a b a +=+222,c b a c b a ++=++2222,则c 最大值是________. 9.已知12 22=++z y x ,则xyz z 2)1(2 +的最小值是________. 10.已知1)(=++z y x xyz ,则))((z y y x ++的最小值是________. 11.已知正数c b a ,,满足a c b a 3≤+≤,225)(3b c a a b ≤+≤;则a c b 2-的最小值是________. 12.若函数,,24,1x y R y x x ∈≤≤-≥,则222221 x y x y xy x y ++-+-+-的最大值为________. 13.设实数,x y 满足2 214 x y -=,则232x xy -的最小值是________. 14.已知实数c b a ,,满足0=++c b a ,1222=++c b a ;则实数a 的取值范围是________. 15.已知22=+++bc ac ab a ,则c b a 23++的最小值是________. 16.已知函数),(32)(2R b a b ax x f ∈+=.若对于任意]1,1[-∈x ,都有1|)(|≤x f 成立,则ab 的最大值是 17.已知0b a ≥>,若存在,x y R ∈,满足2222220,0,()()x a y b x a y b x b y a ≤≤≤≤-+-=+=+,则b a 的最大值是________. 18.若函数22()(1)(0)f x ax a x a a =++->的一个零点为0x ,则0x 的最大值为________. 多元变量的最值 最值问题,特别是多元变量的最值问题是近几年高考的热点.这类最值问题因为变量多,结构式复杂,相互之间的制约关系较难把握,导致处理难度大. 一、利用基本不等式 求二元解析式的最值时,若关于两个变元的和式或积式为定值,可用基本不等式求最值. 例1 已知x>0,y>o ,lg2x +lg8y =1g2,则 113x y +的最小值是 二、构造方程 牵涉多个变量,通过设立主元,其他看成系数,构造一元二次方程,运用根的判别式求解. 例2 已知实数a ,b ,c 满足a+b+c=9,ab+ac+bc=24,则b 的取值范围是 . 三、转化为函数问题 有时变量虽多,但巧妙利用两个等式之间的关系,构造出函数,再利用函数求最值是处理中学最值问题的一个常规手段. 例3 已知x,y,z ∈R ,且x+y+z=1,x 2+y 2+z 2=3,则xyz 的最大值是 . 四、降元化归思想 题中变量较多时,可以利用不等关系将三元变量降为二元,利用齐次结构式将二元转换为一元,体现数学中的化归思想。 例4 已知三次函数32()()32a b f x x x cx d a b = +++<在R 上单调递增,则a b c b a ++-的最小值为 五、三角换元法 形如“约束条件f(x,y)=0的二次式下求解w=g(x,y)的最值、值域"等问题,利用三角代换来求解一样有它自己的特色和魅力.利用三角求解一样有别致新颖、干净利落一面,而且学生也易于掌握. 例5 若实数x,y 满足221,x y xy ++=,则x+y 的最大值是 . 六、运用式子的几何意义 在解题时充分利用好题目中的原始条件,结合一些常见的思想方法,从不同角度、用不同的知识处理这类问题(不是简单的重复或类比),既可以充分利用所学的知识,又不失创造性。 例6 已知点P(x ,y)到原点的距离为1,则m 22 x y x y +-= -+的最大值为 . 练习 1.已知正数x ,y 满足xy +x +2y =6,则xy 的最大值为 . 2.已知a b ∈R ,,45222=+-b ab a ,则a b +的取值范围为 ab 的最小值为 .. 3. 已知正实数,x y 满足ln ln 0x y +=,且22 (2)4k x y x y +≤+恒成立,则k 的最大值是________. 多元数据处理 ---因子分析方法 多元数据处理主要包括多元随机变量,协方差分析,趋势面分析,聚类分析,判别分析,主成分分析,因子分析,典型相关分析,回归分析以及各个分析方法的相互结合等等。本文主要针对其中的因子分析方法展开了论述,并举了一个因子分析法在我国房地产市场绩效评价中的应用实例。 第一章因子分析方法概述 1.1因子分析的涵义 为了更全面和准确的测量和评估对象的特征,在实际的应用中,我们往往尽可能多的选用特征指标进行系统评估,选取的指标越多,就越能全面、客观的反映评价对象的特征。选取众多指标的同时也带来了统计分析的困难:一、不同的指标,不同重要程度需要赋予不同的权重,而靠主观的评价避免不了一些失误与错误。二、收集到的指标之间可能存在较大的相关性,大量收集指标带来了人力、物力和财力的浪费。而因子分析方法则较好的解决了上述问题。 因子分析[1]是一种多元统计方法,该方法起源于20世纪初Karl Pearson 和Charles Spearman 等人关于心理测试的统计分析,它的核心是用最少的相互独立的因子反映原有变量的绝大部分信息。[2]通过分析事物内部的因果关系来找出其主要矛盾,找出事物内在的基本规律。 因子分析的基本思想是通过变量的相关系数矩阵内部结构的研究,找出能控制所有变量的少数几个随机变量去描述多个变量之间的相关关系,但是,这少数几个随机变量是不可观测的,通常称为因子。然后根据相关性的大小把变量分组,使得同组内的变量之间相关性较高,使不同组内的变量相关性较低[3]。对于所研究的问题就可试图用最少个数的所谓因子的线性函数与特殊因子之和来描述原来观测的每一变量[4]。因子变量的特点:第一,因子变量的数量远小于原指标的数量,对因子变量的分析能够减少分析的工作量;第二,因子变量不是原有变量的简单取舍,而是对原有变量的 第十章约束条件下多变量函数 的寻优方法 ●将非线性规划→线性规划 ●将约束问题→无约束问题 ●将复杂问题→较简单问题 10.1约束极值问题的最优性条件 非线性规划:min f(X) h i(X)=0 (i=1,2,…,m) (10.1.1) g j(X)≥0 (j=1,2,…,l) 一、基本概念 1.起作用约束 设X(1)是问题(10.1.1)的可行点。对某g j(X)≥0而言: 或g j(X(1))=0:X(1)在该约束形成的可行域边界上。 该约束称为X(1)点的起作用约束。 或g j(X(1))>0:X(1)不在该约束形成的可行域边界上。 该约束称为X(1)点的不起作用约束。 X(1)点的起作用约束对X(1)点的微小摄动有某种限制作用。等式约束对所有可行点都是起作用约束。 () θcos ab b a =? 2.正则点 对问题(10.1.1),若可行点X (1)处,各起作用约束的梯度线性无关,则X (1)是约束条件的一个正则点。 3.可行方向(对约束函数而言) 用R 表示问题(10.1.1)的可行域。设X (1)是一个可行点。对某方向D 来说,若存在实数λ1>0,使对于任意λ(0<λ<λ1)均有X (1)+λD ∈R ,则称D 是点X (1)处的一个可行方向。 经推导可知,只要方向D 满足: ▽g j (X (1))T D>0 (j ∈J ) (10.1.3) 即可保证它是点X (1)的可行方向。J 是X (1)点起作用约束下标的集合。 在X (1)点,可行方向D 与各起作用约束的梯度方向的夹角为锐角 。 4.下降方向(对目标函数而言) 设X (1)是问题(10.1.1)的一个可行点。对X (1)的任一方向D 来说,若存在实数λ1>0,使对于任意λ(0<λ<λ1)均有f(X (1)+λD) 毕业论文 题目多元回归分析中的变量选取 ——SPSS的应用 院(系)数学与统计学院 专业年级 2010级统计学 指导教师职称副教授 多元回归分析中的变量选取——SPSS的应用 殷婷 摘要 本文不仅对于复杂的统计计算通过常用的计算机应用软件SPSS来实现,同时通过对两组数据的实证分析,来研究统计学中多元回归分析中的变量选取,让大家对统计中的多元回归数据的选取和操作方法有更深层次的了解。一组数据是对于淘宝交易额的未来发展趋势的研究,一组数据时对于我国财政收入的研究。本文通过两个实证从不同程度上对数据选取的研究运用通俗的语言和浅显的描述将SPSS在多元回归分析中的统计分析方法呈现在大家面前,让大家对多元回归分析以及SPSS软件都可以有更深一步的了解。通过SPSS软件对数据进行分析,对数据进行处理的方法进行总结,找出SPSS对于数据处理和分析的优缺点,最后得在对变量的选取和软件的操作提出建议。 关键词:统计学 SPSS 变量的选取多元回归分析 Abstract In this paper, not only for complex statistical calculations done by the commonly used computer application software of SPSS, through the empirical analysis of the two groups of data at the same time, to study the statistics of the variables in the multivariate regression analysis, let everybody to select multiple regression in statistical data and operation methods have a deeper understanding. Is a set of data for the future development trend of taobao transactions of research, a set of data for the research of our country's financial income. In this paper, through two empirical to select data from different extent research using a common language and plain the SPSS statistical analysis method in multiple regression analysis of present in front of everyone, let everyone to multiple regression analysis and SPSS software can have a deeper understanding. Through the SPSS software to analyze data, and summarizes method of data processing, find out the advantages and disadvantages of SPSS for data processing and analysis, finally had to put forward the proposal to the operation of the selection of variables and software. Keywords: Statistical SPSS The selection of variables multiple regression analysis 目录 摘要 (1) 英文摘要 (1) 引言 (3) 第一章回归分析 (3) 1.1自变量的选择 (4) 2017版导数题型归类 第五讲 多变量问题 一、学习目标 1.了解常见的多变量问题的处理思路。 2.掌握主元法、消元法。 二、重难点 重点:主元法 难点:怎么根据特征判断用对应的方法 三、引入 多元变量问题的处理思路:消元,那么消元的方法有哪些? 四、过程 例题1.已知函数0,20,ln 2 {)(<++>=x a x x x x x f 其中a 为实数,设))(,()),(,(2211x f x B x f x A 为该函数图像上的两点,且21x x <。 1)求函数f(x)的单调区间、 2)若函数f(x)的图像在点A,B 处的切线互相垂直,且02 例题2.已知x x x g x x x f ln )(,)1ln()(=-+= 1)求函数)(x f 的最大值 2)设,0b a <<证明:2ln )()2 (2)()(0a b b a g b g a g -<+-+< 方法:两个变量,可以把其中一个当常数,另外一个当自变量 特征:小问中两个变量没有明确的数量等式关系。 例题3.已知函数0,2 1)(,ln )(2≠+==a bx ax x g x x f 1)若b=2,且)()()(x g x f x h -=存在单调递减区间,求a 的取值范围。 2)设函数f(x)的图像1c 与图像g(x)的图像 2c 交于点P.Q ,过PQ 的中点做x 轴的垂线分别交1c ,2c 于点M,N,证明:1c 在点M 处的切线与2c 在点N 处的切线不平行。 方法:通过变量的四则运算后,把整体处理为一个变量,从而达到消元的目的。 特征:这种题一般是两个以上的变元或是两个量的确定关系在解题过程中反复出现。 2021年新高考数学总复习第二章《函数与基本初等函数》 多元变量的最值问题 一、代入减元 例1 设x ,y ∈R +,且2x +8y -xy =0,求x +y 的最小值. 解 由2x +8y -xy =0得y =2x x -8 ,因为x ,y ∈R +,所以x >8,所以 x +y =x +2x x -8=x +2(x -8)+16x -8=x +2+16x -8 =(x -8)+16x -8+10≥2(x -8)·16x -8 +10=18, 当且仅当x -8=16x -8 ,即x =12时,取“=”号. 所以,当x =12,y =6时,x +y 取得最小值18. 点评 此题是一道学生经常见到的求多变量最值的试题,虽然此解法不是最优的解法,但可 能是学生比较容易想到的解法.它的优点是由前面的等式可以得到y =2x x -8 ,代入x +y 中,从而使二元变量变为一元变量,从而达到解题的目的. 二、等量减元 例2 设正实数x ,y ,z 满足x 2-3xy +4y 2-z =0,则当xy z 取得最大值时,2x +1y -2z 的最大值为( ) A .0 B .1 C.94 D .3 答案 B 解析 由已知得z =x 2-3xy +4y 2(*) 则xy z =xy x 2-3xy +4y 2=1x y +4y x -3≤1,当且仅当x =2y 时取等号,把x =2y 代入(*)式,得z =2y 2,所以2x +1y -2z =1y +1y -1y 2=-????1y -12+1≤1. 点评 此题是2013年山东高考理科第12题,作为选择题压轴题,其难度在于如何寻求多元 变量x ,y ,z 之间的关系,进而达到减元的目的.其实,由xy z 变到xy x 2-3xy +4y 2 就已经应用到了代入消元,再由xy x 2-3xy +4y 2变到1x y +4y x -3仍然用到了整体消元的思想(把x y 当做整体), 第十章:多元线性回归与曲线拟合―― Regression菜单详解(上) (医学统计之星:张文彤) 回归分析是处理两个及两个以上变量间线性依存关系的统计方法。在医学领域中,此类问题很普遍,如人头发中某种金属元素的含量与血液中该元素的含量有关系,人的体表面积与身高、体重有关系;等等。回归分析就是用于说明这种依存变化的数学关系。 §10.1Linear过程 10.1.1 简单操作入门 调用此过程可完成二元或多元的线性回归分析。在多元线性回归分析中,用户还可根据需要,选用不同筛选自变量的方法(如:逐步法、向前法、向后法,等)。 例10.1:请分析在数据集Fat surfactant.sav中变量fat对变量spovl的大小有无影响? 显然,在这里spovl是连续性变量,而fat是分类变量,我们可用用单因素方差分析来解决这个问题。但此处我们要采用和方差分析等价的分析方法--回归分析来解决它。 回归分析和方差分析都可以被归入广义线性模型中,因此他们在模型的定义、计算方法等许多方面都非常近似,下面大家很快就会看到。 这里spovl是模型中的因变量,根据回归模型的要求,它必须是正态分布的变量才可以,我们可以用直方图来大致看一下,可以看到基本服从正态,因此不再检验其正态性,继续往下做。 10.1.1.1 界面详解 在菜单中选择Regression==>liner,系统弹出线性回归对话框如下: 除了大家熟悉的内容以外,里面还出现了一些特色菜,让我们来一一品尝。 【Dependent框】 用于选入回归分析的应变量。 【Block按钮组】 由Previous和Next两个按钮组成,用于将下面Independent框中选入的自变量分组。由于多元回归分析中自变量的选入方式有前进、后退、逐步等方法,如果对不同的自变量选入的方法不同,则用该按钮组将自变量分组选入即可。下面的例子会讲解其用法。 【Independent框】 用于选入回归分析的自变量。 【Method下拉列表】 用于选择对自变量的选入方法,有Enter(强行进入法)、Stepwise(逐步法)、Remove(强制剔除法)、Backward(向后法)、Forward(向前法)五种。该选项对当前Independent框中的所有变量均有效。 五种最优化方法 1.最优化方法概述 1.1最优化问题的分类 1)无约束和有约束条件; 2)确定性和随机性最优问题(变量是否确定); 3)线性优化与非线性优化(目标函数和约束条件是否线性); 4)静态规划和动态规划(解是否随时间变化)。 1.2最优化问题的一般形式(有约束条件): min f(X) XeΩ h√X)= OJ = U1 L s.t S i(X)≥ OJ = l9‰u,m 式中f(X)称为目标函数(或求它的极小,或求它的极大),Si(X)称为不等式约束,hj(X)称为等式约束。化过程就是优选X ,使目标函数达到最优值。 2.牛顿法 2.1简介 1)解决的是无约束非线性规划问题; 2)是求解函数极值的一种方法; 3)是一种函数逼近法。 2.2原理和步骤 ■1:顿法的直本思想显*在扱小点附近用-阶T吓1小多顶式近似[3标函数['、宀进而求出极小点的估计值, 老億问题 min FWHElRl < 9i 3. 1 } 令 祕Jr) = /(√i,) +/(J iit Xx-J ut) +y∕(j't,K4T-J01 }' . 耳令 √(+f > - ∕t d时)+ j f* 微专题5多元变量的最值和范围问题(1) 1. 掌握用代数的方法(消元法、函数思想、基本不等式、1的代换)和几何的方法(线性规划、几何意义、平面几何、解析几何)等方法解决一般情形的多元变量的最值和范围问题. 2. 掌握用消元(代入消元、整体换元、三角换元、选择主元)的方法解决三元变量的最值和范围问题,特别注意齐次分式、齐次多项式,还有和式、积式、平方和的结构关系以及公式的几何意义. 考题导航 2. 在△ABC中,A=π 3,角A,B,C 所对的边长分别是a,b,c.若三角形的外接圆直径 为2,则b+c的取值范围是________. 1. 已知正实数x,y满足x+2 x+3y+ 4 y=10,则xy的取值范围为________. 2. 若△ABC的内角满足sin A+2sin B=2sin C,则cos C的最小值是________. 3. 已知a>0,b>0,c>2,且a+b=2,则ac b+ c ab- c 2+ 5 c-2的最小值为________. 微专题5多元变量的最值和范围问题(2) 1. 已知ab=1 4,a,b∈(0,1),则 1 1-a+ 2 1-b的最小值为________. 2. 在锐角三角形ABC中,若sin A=2sin BsinC,则tan Atan Btan C的最小值是________. 1. 已知A,B,C是平面上任意三点,BC=a,CA=b,AB=c,则y=c a+b+b c的最小值为 ________. 2. 若实数x,y满足2x2+xy-y2=1,则 x-2y 5x2-2xy+2y2的最大值为________. 第五章:带约束的寻优方法 ● 问题:{} ???=≥==m i X g X R x x x X X f Min i n ,,2,1,0)(|} ,,,{)(21 ● 约束函数:等式约束、不等式约束 ● 内点、外点、边界点 ● 约束非线性规划问题:方法:直接处理约束的方法:约束随机法、复合形法 线性规划去逐次逼近非线性规划问题 有约束化为无约束方法:罚函数法(外点、内点) 5.1:有约束最优化问题化为无约束最优化问题的方法(罚函数法) 附加一项修正函数(惩罚、障碍) 外点法:由外点开始寻优收敛至最优解 内点法:由内点开始寻优收敛至最优解 ● 外点法 原理 设 )(X g u i = ?? ?<∞+≥=0 00 )(u u u p 当当 则: ()∑=+=m i i X g p X f X 1 )()()(? 当R X ∈时, ()0)(1=∑=m i i X g p 当R X ?时, ()+∞=∑=m i i X g p 1 )( ()∑=m i i X g p 1 )(为惩罚项 则: {} ?? ?=≥==m i X g X R x x x X X f Min i n ,,2,1,0)(|} ,,,{)(21 )(X Min ?? 方法: ()∑=+=m i i X g p X f X 1 )()()(?,因为当+∞=)(u p 时,数据溢出,因此在其上进行改进 1:取充分大的罚因子 )(X g u i = ???<+≥=0 100 )(2 u u u u p 当当 ()∑=+=m i i X g p M X f M X 1 )()(),(? 分析:p (u )不连续,当u =0时,导数不存在。 寻优:只能用直接法,不能用方向加速法。 2:一次外点法(1-UMT ) )(X g u i = ?? ?<-≥=0 00)(u u u u p 当当 () () ∑∑==-=+=m i i m i i X g Min M X f X g p M X f M X 1 1)(,0)()()(),(? 分析:p (u )连续,但不可微。 寻优:只能用直接寻优法 3:外点罚函数法 )(X g u i = ???<≥=0 00)(2 u u u u p 当当 () ()[] ∑∑==+=+=m i i m i i X g Min M X f X g p M X f M X 1 2 1)(,0)()()(),(? 分析:p (u )连续,又可微。 寻优:可以用直接寻优法和间接寻优法。 M 的选取 取01>M ,若R M X ?)(1,说明1M 不够大 再取12M M >,若R M X ∈)(1,则停止迭代 迭代步骤: 1:取01>M ,给定允许误差0>ε,令k =1 2:求无约束问题 热点问题3 基本不等式(含多元变量) 一、填空题 1.已知2()log (2)f x x =-,若实数,m n 满足()(2)3f m f n +=,则m n +的最小值为________. 2.设实数,x y 满足2210x xy +-=,则22x y +的最小值是________. 3.已知y x ,为正实数且满足y x +≤1,则 111++y x 的最小值为________. 4.若不等式xy x 22+≤)(22y x a +对于一切正数x ,y 恒成立,则实数a 的最小值为________. 5.设∈m R ,过定点A 的动直线0x my +=和过定点B 的动直线03=+--m y mx 交于点(,)P x y , 则PB PA ?的最大值是________. 6.国际上钻石的重量计量单位为克拉.已知某种钻石的价值V 美元与其重量ω克拉的平方成正比, 若把一颗钻石切割成重量分别为m ,n (m ≥n )的两颗钻石,且价值损失的百分率为 原有价值-现有价值原有价值 ×100%(切割中重量损耗不计),则价值损失的百分率的最大值为________. 7.已知0,0>>y x ,且满足y x y x xy 4++= ,则y x 4+的最小值为________. 8.已知c b a ,,为正实数且满足c b +≥a ,则 b a c c b ++的最小值为________. 二、解答题 9.已知0,0>>y x 且满足8=++y x xy ,求x + y 的最小值. 变式1.已知0,0< 多元变量的最值问题 一、热身练习: 1.函数()()9122 f x x x x =+ >-的最小值是________. xx+k.Co 2.已知实数x ,y 满足,2,0,y x x y x ≥??+≤??≥? 则93x y z =?的最大值是 . 3. 设ab b a b a =+>>2,0,0,则b a 2+的最小值为 4.已知正实数,x y 满足xy y x =+,则1 213-+-y y x x 的最小值为 . 5.设实数y x ,满足1)1(22=-+y x ,当0≥++c y x 时,c 的取值范围为 . 6.设正实数,,x y z 满足22340x xy y z -+-=,则当 z xy 取得最大值时,2x y z +-的最大值为 二、典例研究: 例.已知正实数x ,y 满足2221x xy y +-=,则5x ?2y 的最小值为 . 三、巩固训练: 1.已知0,0>>y x ,且 112=+y x ,若m m y x 222+>+恒成立,则实数m 的取值范围是 . 2.已知x <0,且x -y =1,则121++ y x 的最大值是 . 3.已知0,0,8,a b ab >>= 则当a 的值为 时()22log log 2a b ?取得最大值. 4.已知正数a ,b ,c 满足3a -b +2c =0,则 ac b 错误!未找到引用源。的最大值为 . 5.若不等式2222()y x c x xy -≥-对任意满足0x y >>的实数,x y 恒成立,则实数c 的最大值为 6.若实数y x ,满足,0>>y x 且 ,1241=++-y x y x 则y x +的最小值为_________ 7.若,x y ∈R ,22231x xy y +-=,则22z x y =+的最小值为 8.设c b a ,,是正实数,满足a c b ≥+,则 b a c c b ++的最小值为 . 9.对一切实数,x 二次函数)()(2b a c bx ax x f <++=的值均为非负数,则 c b a a b ++-的最大值为_____ 10.已知)15)(1()12(2+-=-y y xy ,求y x 21+ 的最小值______________ 统计学多元回归分析方法 ————————————————————————————————作者:————————————————————————————————日期: 多元线性回归分析 在数量分析中,经常会看到变量与变量之间存在着一定的联系。要了解变量之间如何发生相互影响的,就需要利用相关分析和回归分析。回归分析的主要类型:一元线性回归分析、多元线性回归分析、非线性回归分析、曲线估计、时间序列的曲线估计、含虚拟自变量的回归分析以及逻辑回归分析等。 1.1 回归分析基本概念 相关分析和回归分析都是研究变量间关系的统计学课题。在应用中,两种分析方法经常相互结合和渗透,但它们研究的侧重点和应用面不同。 在回归分析中,变量y称为因变量,处于被解释的特殊地位;而在相关分析中,变量y与变量x处于平等的地位,研究变量y与变量x的密切程度和研究变量x与变量y的密切程度是一样的。 在回归分析中,因变量y是随机变量,自变量x可以是随机变量,也可以是非随机的确定变量;而在相关分析中,变量x和变量y都是随机变量。 相关分析是测定变量之间的关系密切程度,所使用的工具是相关系数;而回归分析则是侧重于考察变量之间的数量变化规律,并通过一定的数学表达式来描述变量之间的关系,进而确定一个或者几个变量的变化对另一个特定变量的影响程度。 具体地说,回归分析主要解决以下几方面的问题。 (1)通过分析大量的样本数据,确定变量之间的数学关系式。 (2)对所确定的数学关系式的可信程度进行各种统计检验,并区分出对某一特定变量影响较为显著的变量和影响不显著的变量。 (3)利用所确定的数学关系式,根据一个或几个变量的值来预测或控制另一个特定变量的取值,并给出这种预测或控制的精确度。 作为处理变量之间关系的一种统计方法和技术,回归分析的基本思想和方法以及“回归(Regression)”名称的由来都要归功于英国统计学F·Galton(1822~1911)。 在实际中,根据变量的个数、变量的类型以及变量之间的相关关系,回归分析通常分为一元线性回归分析、多元线性回归分析、非线性回归分析、曲线估计、时间序列的曲线估计、含虚拟自变量的回归分析和逻辑回归分析等类型。 1.2 多元线性回归 1.2.1 多元线性回归的定义 一元线性回归分析是在排除其他影响因素或假定其他影响因素确定的条件下,分析某一个因素(自变量)是如何影响另一事物(因变量)的过程,所进行的分析是比较理想化的。其实,在现实社会生活中,任何一个事物(因变量)总是受到其他多种事物(多个自变量)的影响。 一元线性回归分析讨论的回归问题只涉及了一个自变量,但在实际问题中,影响因变量的因素往往有多个。例如,商品的需求除了受自身价格的影响外,还要受到消费者收入、其他商品的价格、消费者偏好等因素的影响;影响水果产量的外界因素有平均气温、平均日照 一、 真题再现 1(2008江苏卷11)设,,x y z 为正实数,满足230x y z -+=,则2 y xz 的最小值是 3 【解析】本小题考查二元基本不等式的运用.由230x y z -+=得32x z y +=,代入2y xz 得229666344x z xz xz xz xz xz +++≥=,当且仅当x =3z 时取“=”. 感悟方法: 2.(2010江苏卷12)设实数x,y 满足3≤2 xy ≤8,4≤y x 2≤9,则43 y x 的最大值是 27 .[解析] 2 2()[16,81]x y ∈,2111[,]83xy ∈,32 2421()[2,27]x x y y xy =?∈,43y x 的最大值是27. 感悟方法: 3.(2012江苏14)已知正数a b c , ,满足:4ln 53ln b c a a c c c a c b -+-≤≤≥,,则b a 的取值范围是 [,7]e . [解析] 感悟方 法: 二、考 点剖析 不 等式中 多元变量问题是近几年江苏高考的热点,如2008第11题,2010年第12题,2012年第14题,其他省的高考试卷也多有涉及;这类问题涉及到的变量多,方法处理灵活,是一个难点;这类问题一般是放在填空题最后两题位置,或者和函数导数结合,放在解答题最后两题位置,考查的重点是求最值问题或者是不等式的证明.解决这类问题的基本方法是:通过换元、消元、选择主元、重组变量构造新元等手段减少变量,转化为一元或二元问题,或是根据题设 条件转化为线性规划或其它问题,常用到数形结合、转化化归、函数与方程思想. 三、典题剖析 1. 若错误!未找到引用源。则2a+b+c的最小值为 4 . 2.若错误!未找到引用源。为正数,且错误!未找到引用源。,则错误!未找到引用源。的最小值为 2 . 3.已知实数错误!未找到引用源。满足错误!未找到引用源。,则的取值范围[1,5] . 4.若实数错误!未找到引用源。满足错误!未找到引用源。,则错误!未找到引用源。的最小值为错误!未找到引用源。 5.错误!未找到引用源。 求证:错误!未找到引用源。 解:错误!未找到引用源。是f(x)=0的两根 2错误!未找到引用源。错误!未找到引用源。 两式相减得:错误!未找到引用源。 又错误!未找到引用源。, 错误!未找到引用源。 令错误!未找到引用源。 则原式=错误!未找到引用源。 令错误!未找到引用源。 四、感悟总结: 五、巩固提高: 1.已知正数错误!未找到引用源。满足错误!未找到引用源。则错误!未找到引用源。的最小值为错误!未找到引用源。. 2.已知错误!未找到引用源。错误!未找到引用源。. 3.已知实数x,y满足错误!未找到引用源。则x+2y的取值范围为错误!未找到引用源。] . 4.已知实数错误!未找到引用源。且错误!未找到引用源。,则错误!未找到引用源。的最小值错误!未找到引用源。. 选编说明: 不等式中多元变量问题是近几年江苏高考的热点,如2008第11题,2010年第12题,2012年第14题,其他省的高考试卷也多有涉及;这类问题涉及到的变量多,方法处理灵活,对学生来说是一个难点;这类问题一般是放在填空题最后两题位置,或和函数导数结合,放在解答题最后两题位置,考查的重点是求最值问题或不等式的证明.解决这类问题的基本方法是:通过换元、消元、选择主元、重组变量构造新元等手段减少变量,转化为一元或二元问题,或是根据题设条件转化为线性规划或其它问题,常用到数形结合、转化化归、函数与方程思想.通过一轮复习,学生对二元变量求最值问题和利用线性规划或转化为线性规划的第4章续 多变量寻优方法
寻北仪的方位引出方法
多元变量的最值与范围问题
多元变量的最值
多元数据处理——因子分析法
约束条件下多变量函数的寻优方法
(完整版)多元回归分析中变量的选择——SPSS的应用毕业论文
(2017版)导数题型归类第五讲:多变量问题
多元变量的最值问题
多元回归拟合
五种最优化方法
微专题5多元变量的最值和范围问题
第5章 带约束的寻优方法
热点问题3 不等式(含多元变量)(学生版)
多元变量的最值问题
统计学多元回归研究分析方法
2015年高考数学复习学案:不等式中多元变量问题的处理
