八年级初二数学勾股定理知识点总结附解析

一、选择题
1.如图,已知ABC 中,4AB AC ==,6BC =,在BC 边上取一点P (点P 不与点B 、C 重合),使得ABP △成为等腰三角形,则这样的点P 共有( ).
A .1个
B .2个
C .3个
D .4个
2.在ABC ?中,D 是直线BC 上一点,已知15AB =,12AD =,13AC =,5CD =,
则BC 的长为( ) A .4或14
B .10或14
C .14
D .10
3.已知:△ABC 中,BD 、CE 分别是AC 、AB 边上的高,BQ =AC ,点F 在CE 的延长线上,CF =AB ,下列结论错误的是( ).
A .AF ⊥AQ
B .AF=AQ
C .AF=AD
D .F BAQ ∠=∠
4.“勾股图”有着悠久的历史,它曾引起很多人的兴趣.1955年希腊发行了以“勾股图”为背景的邮票(如图1),欧几里得在《几何原本》中曾对该图做了深入研究.如图2,在ABC 中,90ACB ∠=?,分别以ABC 的三条边为边向外作正方形,连结EB ,
CM ,DG ,CM 分别与AB ,BE 相交于点P ,Q .若30ABE ∠=?,则
DG
QM
的值为( )
A 3
B 5
C .
45
D 31
5.已知等边三角形的边长为a ,则它边上的高、面积分别是( )
A .2,24a a
B .2
3,24a a
C .2
33,
24a a D .2
33,
44
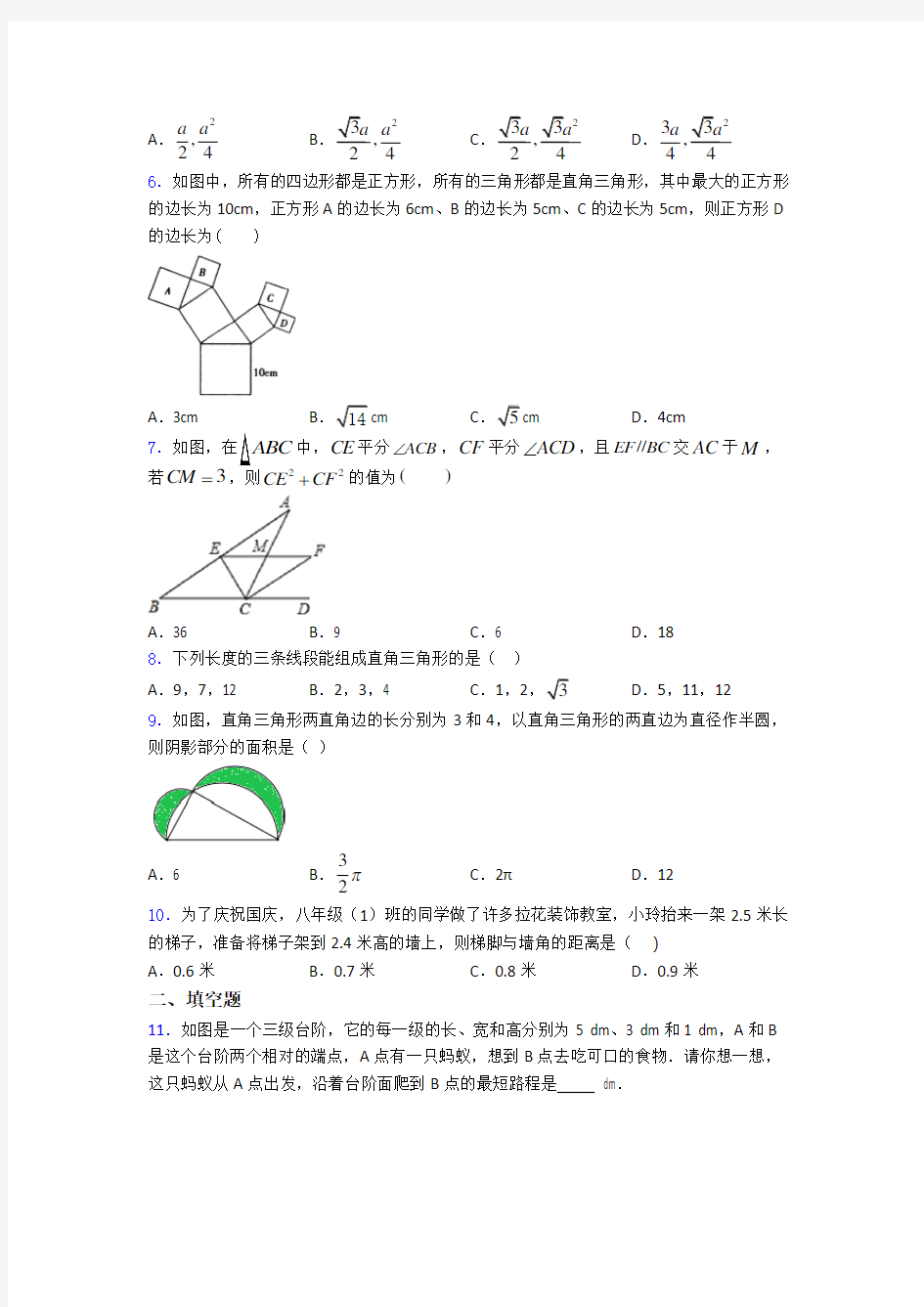
a a 6.如图中,所有的四边形都是正方形,所有的三角形都是直角三角形,其中最大的正方形的边长为10cm ,正方形A 的边长为6cm 、B 的边长为5cm 、C 的边长为5cm ,则正方形D 的边长为( )
A .3cm
B .14cm
C .5cm
D .4cm
7.如图,在ABC 中,CE 平分ACB ∠,CF 平分ACD ∠,且//EF BC 交AC 于M ,若3CM =,则22CE CF +的值为( )
A .36
B .9
C .6
D .18 8.下列长度的三条线段能组成直角三角形的是( )
A .9,7,12
B .2,3,4
C .1,2,3
D .5,11,12
9.如图,直角三角形两直角边的长分别为3和4,以直角三角形的两直边为直径作半圆,则阴影部分的面积是( )
A .6
B .
3
2
π C .2π D .12
10.为了庆祝国庆,八年级(1)班的同学做了许多拉花装饰教室,小玲抬来一架2.5米长的梯子,准备将梯子架到2.4米高的墙上,则梯脚与墙角的距离是( ) A .0.6米
B .0.7米
C .0.8米
D .0.9米
二、填空题
11.如图是一个三级台阶,它的每一级的长、宽和高分别为5 dm 、3 dm 和1 dm ,A 和B 是这个台阶两个相对的端点,A 点有一只蚂蚁,想到B 点去吃可口的食物.请你想一想,这只蚂蚁从A 点出发,沿着台阶面爬到B 点的最短路程是 dm .
12.在△ABC 中,AB =6,AC =5,BC 边上的高AD =4,则△ABC 的周长为__________. 13.如图,在ABC △中8,4,AB AC BC AD BC ===⊥于点D ,点P 是线段AD 上一个动点,过点P 作PE AB ⊥于点E ,连接PB ,则PB PE +的最小值为________.
14.已知Rt △ABC 中,AC =4,BC =3,∠ACB =90°,以AC 为一边在Rt △ABC 外部作等腰直角三角形ACD ,则线段BD 的长为_____.
15.以直角三角形的三边为边向外作正方形P ,Q ,K ,若S P =4,S Q =9,则K S =___ 16.如图所示,“赵爽弦图”是由8个全等的直角三角形拼接而成的,记图中正方形ABCD ,正方形EFGH ,正方形MNKT 的面积分别为123,,S S S ,已知12310S S S ++=,则2S 的值是____.
17.如图,在锐角ABC ?中,2AB =,60BAC ∠=,BAC ∠的平分线交BC 于点D ,
M ,N 分别是AD 和AB 上的动点,则BM MN +的最小值是______.
18.如图,正方体的底面边长分别为2cm 和3cm ,高为5cm .若一只蚂蚁从P 点开始经过四个侧面爬行一圈到达Q 点,则蚂蚁爬行的最短路径长为_____cm .
19.如图,在矩形ABCD 中,AD >AB ,将矩形ABCD 折叠,使点C 与点A 重合,折痕为
MN ,连接CN .若△CDN 的面积与△CMN 的面积比为1:3,则2
2
MN BM
的值为______________.
20.如图的实线部分是由Rt ABC ?经过两次折叠得到的.首先将Rt ABC ?沿高CH 折叠,使点B 落在斜边上的点B '处,再沿CM 折叠,使点A 落在CB '的延长线上的点A '处.若图中
90ACB ∠=?,15cm BC =,20cm AC =,则MB '的长为______.
三、解答题
21.如图,已知ABC ?中,90B ∠=?,8AB cm =,6BC cm =,P 、Q 是ABC ?边上的两个动点,其中点P 从点A 开始沿A B →方向运动,且速度为每秒1cm ,点Q 从点B 开始沿B C →方向运动,且速度为每秒2cm ,它们同时出发,设出发的时间为t 秒.
(1)当2t =秒时,求PQ 的长;
(2)求出发时间为几秒时,PQB ?是等腰三角形?
(3)若Q 沿B C A →→方向运动,则当点Q 在边CA 上运动时,求能使BCQ ?成为等腰三角形的运动时间.
22.如图1,在△ABC 中,AB =AC ,∠BAC =90°,D 为AC 边上一动点,且不与点A 点C 重合,连接BD 并延长,在BD 延长线上取一点E ,使AE =AB ,连接CE .
(1)若∠AED =20°,则∠DEC = 度;
(2)若∠AED =a ,试探索∠AED 与∠AEC 有怎样的数量关系?并证明你的猜想; (3)如图2,过点A 作AF ⊥BE 于点F ,AF 的延长线与EC 的延长线交于点H ,求证:EH 2+CH 2=2AE 2.
23.已知ABC ?中,如果过项点B 的一条直线把这个三角形分割成两个三角形,其中一个为等腰三角形,另一个为直角三角形,则称这条直线为ABC ?的关于点B 的二分割线.例如:如图1,Rt ABC ?中,90A ?∠=,20C ?∠=,若过顶点B 的一条直线BD 交AC 于点D ,若20DBC ?∠=,显然直线BD 是ABC ?的关于点B 的二分割线.
(1)在图2的ABC ?中,20C ?∠=,110ABC ?∠=.请在图2中画出ABC ?关于点B 的二分割线,且DBC ∠角度是 ;
(2)已知20C ?∠=,在图3中画出不同于图1,图2的ABC ?,所画ABC ?同时满足:①C ∠为最小角;②存在关于点B 的二分割线.BAC ∠的度数是 ;
(3)已知C α∠=,ABC ?同时满足:①C ∠为最小角;②存在关于点B 的二分割线.请求出BAC ∠的度数(用α表示).
24.如图,将一长方形纸片OABC 放在平面直角坐标系中,(0,0)O ,(6,0)A ,(0,3)C ,动点F 从点O 出发以每秒1个单位长度的速度沿OC 向终点C 运动,运动
2
3
秒时,动点E 从点A 出发以相同的速度沿AO 向终点O 运动,当点E 、F 其中一点到达终点时,另一点也停止运动.
设点E 的运动时间为t :(秒)
(1)OE =_________,OF =___________(用含t 的代数式表示)
(2)当1t =时,将OEF ?沿EF 翻折,点O 恰好落在CB 边上的点D 处,求点D 的坐标及直线DE 的解析式;
(3)在(2)的条件下,点M 是射线DB 上的任意一点,过点M 作直线DE 的平行线,与x 轴交于N 点,设直线MN 的解析式为y kx b =+,当点M 与点B 不重合时,设
MBN ?的面积为S ,求S 与b 之间的函数关系式.
25.如图所示,已知ABC ?中,90B ∠=?,16AB cm =,20AC cm =,P 、Q 是
ABC ?的边上的两个动点,其中点P 从点A 开始沿A B →方向运动,且速度为每秒1cm ,点Q 从点B 开始沿B C A →→方向运动,且速度为每秒2cm ,它们同时出发,设出发的时间为ts .
(1)则BC =____________cm ;
(2)当t 为何值时,点P 在边AC 的垂直平分线上?此时CQ =_________? (3)当点Q 在边CA 上运动时,直接写出使BCQ ?成为等腰三角形的运动时间.
26.如图,在ABC ?中,90ACB ∠=?,2BC AC =.
(1)如图1,点D 在边BC 上,1CD =,5AD =,求ABD ?的面积.
(2)如图2,点F 在边AC 上,过点B 作BE BC ⊥,BE BC =,连结EF 交BC 于点
M ,过点C 作CG EF ⊥,垂足为G ,连结BG .求证:2EG BG CG =+.
27.如图,在△ABC 中,∠C =90°,把△ABC 沿直线DE 折叠,使△ADE 与△BDE 重合.
(1)若∠A =35°,则∠CBD 的度数为________; (2)若AC =8,BC =6,求AD 的长;
(3)当AB =m(m>0),△ABC 的面积为m +1时,求△BCD 的周长.(用含m 的代数式表示) 28.如图,△ABC 中,90BAC ∠=?,AB=AC ,P 是线段BC 上一点,且045BAP ?<∠
(2)设∠BAP 的大小为α.求∠ADC 的大小(用含α的代数式表示).
(3)延长CD 与AP 交于点E,直接用等式表示线段BD 与DE 之间的数量关系.
29.如图1,在正方形ABCD 中,点E ,F 分别是AC ,BC 上的点,且满足DE ⊥EF ,垂足为点E ,连接DF .
(1)求∠EDF= (填度数);
(2)延长DE 交AB 于点G ,连接FG ,如图2,猜想AG ,GF ,FC 三者的数量关系,并给出
(3)①若AB=6,G 是AB 的中点,求△BFG 的面积;
②设AG=a ,CF=b ,△BFG 的面积记为S ,试确定S 与a ,b 的关系,并说明理由.
30.如图,在△ABC 中,D 是边AB 的中点,E 是边AC 上一动点,连结DE,过点D 作DF ⊥DE 交边BC 于点F(点F 与点B 、C 不重合),延长FD 到点G,使DG=DF,连结EF 、AG.已知AB=10,BC=6,AC=8. (1)求证:△ADG ≌△BDF ; (2)请你连结EG,并求证:EF=EG ;
(3)设AE=x ,CF=y ,求y 关于x 的函数关系式,并写出自变量x 的取值范围; (4)求线段EF 长度的最小值.
【参考答案】***试卷处理标记,请不要删除
一、选择题 1.B 解析:B 【分析】
在BC 边上取一点P (点P 不与点B 、C 重合),使得ABP △成为等腰三角形,分三种情况分析:AP BP =、AB BP =、AB AP =;根据等腰三角形的性质分别对三种情况逐个分析,即可得到答案. 【详解】
根据题意,使得ABP △成为等腰三角形,分AP BP =、AB BP =、AB AP =三种情况
当AP BP =时,点P 位置再分两种情况分析: 第1种:点P 在点O 右侧,AO BC ⊥于点O
∴2
2
172AO AB BC ??=-= ???
设OP x = ∴2227AP AO OP x =
+=+
∵4AB AC ==
∴1
32
BO BC =
= ∴3BP BO OP x =+=+
∴27=3x x ++ ∴2x =-,不符合题意;
第2种:点P 在点O 左侧,AO BC ⊥于点O
设OP x = ∴2227AP AO OP x ++∴3BP BO OP x =-=- 273x x +=-
∴2x =,点P 存在,即1BP =;
当AB BP =时,4BP AB ==,点P 存在;
当AB AP =时,4AP AB ==,即点P 和点C 重合,不符合题意; ∴符合题意的点P 共有:2个 故选:B . 【点睛】
本题考查了等腰三角形、勾股定理、一元一次方程的知识;解题的关键是熟练掌握等腰三角形、勾股定理、一元一次方程的性质,从而完成求解.
2.A
解析:A
根据AC =13,AD =12,CD =5,可判断出△ADC 是直角三角形,在Rt △ADB 中求出BD ,继而可得出BC 的长度. 【详解】
∵AC =13,AD =12,CD =5, ∴222AD CD AC +=, ∴△ABD 是直角三角形,AD ⊥BC , 由于点D 在直线BC 上,分两种情况讨论: 当点D 在线段BC 上时,如图所示,
在Rt △ADB 中,229BD AB AD =-=,
则14BC BD CD =+=;
②当点D 在BC 延长线上时,如图所示,
在Rt △ADB 中,229BD AB AD =-=,
则4BC BD CD =-=.
故答案为:A. 【点睛】
本题考查勾股定理和逆定理,需要分类讨论,掌握勾股定理和逆定理的应用为解题关键.
3.C
解析:C 【分析】
根据BD 、CE 分别是AC 、AB 边上的高,推导出EBH DCH ∠=∠;再结合题意,可证明
FAC AQB △≌△,由此可得F BAQ ∠=∠,AF AQ =;再经90AEF ∠=得
90F FAE ∠+∠=,从而证明AF ⊥AQ ;最后由勾股定理得222
AQ AD QD =+,从而得
到AF AD ≠,即可得到答案. 【详解】
如图,CE 和BD 相较于H
∵BD 、CE 分别是AC 、AB 边上的高 ∴CE AB ⊥,BD AC ⊥
∴90BEC BDC AEF ADQ ∠=∠=∠=∠= ∴90EBH EHB DHC DCH ∠+∠=∠+∠=
∵EHB DHC ∠=∠ ∴EBH DCH ∠=∠ 又∵BQ =AC 且CF =AB ∴FAC AQB △≌△
∴F BAQ ∠=∠,AF AQ =,故B 、D 结论正确; ∵90AEF ∠= ∴90F FAE ∠+∠=
∴90BAQ FAE F FAE ∠+∠=∠+∠= ∴AF ⊥AQ 故A 结论正确;
∵90ADQ ∠= ∴2
2
2
AQ AD QD =+ ∵0QD ≠ ∴AQ AD ≠ ∴AF AD ≠ 故选:C . 【点睛】
本题考查了全等三角形、直角三角形、勾股定理、三角形的高等知识;解题的关键是熟练掌握全等三角形、直角三角形、勾股定理、三角形的高的性质,从而完成求解.
4.D
解析:D 【分析】
先用已知条件利用SAS 的三角形全等的判定定理证出△EAB ≌△CAM ,之后利用全等三角形的性质定理分别可得30EBA CMA ==?∠∠,60BPQ APM ==?∠∠,
12PQ PB =
,然后设1AP =,继而可分别求出2PM =,31PQ -=,所以33
QM QP PM +=+=
;易证Rt △ACB ≌Rt △DCG (HL ),从而得3DG AB ==
然后代入所求数据即可得DG
QM
的值. 【详解】
解:∵在△EAB 和△CAM 中 ,
AE AC EAB CAM AB AM =??
=??=?
∠∠, ∴△EAB ≌△CAM (SAS ), ∴30EBA CMA ==?∠∠, ∴60BPQ APM ==?∠∠, ∴90BQP ∠=?,
1
2
PQ PB =
, 设1AP =
,则AM =2PM =
,1PB =
,1
2
PQ =
,
∴13
222
QM QP PM +=+=
+=
; ∵ 在Rt △ACB 和Rt △DCG 中,
CG BC
AC CD
=??
=?, Rt △ACB ≌Rt △DCG (HL ),
∴DG AB ==
∴1
DG
GM
=
=. 故选D . 【点睛】
本题主要考查了勾股定理,三角形全等的判定定理和性质定理等知识.
5.C
解析:C 【分析】
作出等边三角形一边上的高,利用直角三角形中,30°角所对的直角边等于斜边的一半,得出BD ,利用勾股定理即可求出AD ,再利用三角形面积公式即可解决问题. 【详解】
解:如图作AD ⊥BC 于点D . ∵△ABC 为等边三角形,
∴∠B =60°,∠B AD =30° ∴1122
BD AB a =
= 由勾股定理得,2222213
()22
AD AB BD a a a =
-=-=
∴边长为a 的等边三角形的面积为12×a ×3a =3a 2
, 故选:C .
【点睛】
本题考点涉及等边三角形的性质、含30°角的直角三角形、勾股定理以及三角形面积公式,熟练掌握相关性质定理是解题关键.
6.B
解析:B 【解析】 【分析】
先求出S A 、S B 、S C 的值,再根据勾股定理的几何意义求出D 的面积,从而求出正方形D 的边长. 【详解】
解∵S A =6×6=36cm 2,S B =5×5=25cm 2,Sc=5×5=25cm 2, 又∵1010A B C D S S S S +++=? , ∴36+25+25+S D =100, ∴S D =14,
∴正方形D 14 故选:B. 【点睛】
本题考查了勾股定理,熟悉勾股定理的几何意义是解题的关键.
7.A
解析:A 【分析】
先根据角平分线的定义、角的和差可得90ECF ∠=?,再根据平行线的性质、等量代换可得,ACE CEF ACF F ∠=∠∠=∠,然后根据等腰三角形的定义可得
,EM CM FM CM ==,从而可得6EF =,最后在Rt CEF 中,利用勾股定理即可
得. 【详解】
CE 平分ACB ∠,CF 平分ACD ∠,
,11
22
ACB ACD BCE ACE DCF ACF ∴∠∠=∠=∠=∠∠=,
111
(90222
)ACB AC E D ACB ACD CF ACE ACF ∠=∠+∴∠+∠=∠∠∠=+=?,
//EF BC ,
,BCE CEF DCF F ∠=∴∠∠=∠, ,ACE CEF ACF F ∴∠=∠∠=∠, 3,3EM CM FM CM ∴====,
6EF EM FM ∴=+=,
在Rt CEF 中,由勾股定理得:2222636CE CF EF +===, 故选:A . 【点睛】
本题考查了角平分线的定义、平行线的性质、等腰三角形的定义、勾股定理等知识点,熟练掌握等腰三角形的定义是解题关键.
8.C
解析:C 【分析】
利用勾股定理的逆定理:如果三角形两条边的平方和等于第三边的平方,那么这个三角形就是直角三角形.最长边所对的角为直角.由此判定即可. 【详解】
解:A 、因为92+72≠122,所以三条线段不能组成直角三角形; B 、因为22+32≠42,所以三条线段不能组成直角三角形;
C 、因为12= 22,所以三条线段能组成直角三角形;
D 、因为52+112≠122,所以三条线段不能组成直角三角形. 故选C . 【点睛】
此题考查勾股定理逆定理的运用,注意数据的计算.
9.A
解析:A 【分析】
分别求出以AB 、AC 、BC 为直径的半圆及△ABC 的面积,再根据S 阴影=S 1+S 2+S △ABC -S 3即可得出结论. 【详解】 解:如图所示:
∵∠BAC=90°,AB=4cm ,AC=3cm ,BC=5cm , ∴以AB 为直径的半圆的面积S 1=2π(cm 2); 以AC 为直径的半圆的面积S 2=9
8
π(cm 2); 以BC 为直径的半圆的面积S 3=25
8
π(cm 2); S △ABC =6(cm 2);
∴S 阴影=S 1+S 2+S △ABC -S 3=6(cm 2); 故选A . 【点睛】
本题考查的是勾股定理,熟知在任何一个直角三角形中,两条直角边长的平方之和一定等于斜边长的平方是解答此题的关键.
10.B
解析:B 【解析】
试题解析:依题意得:梯子、地面、墙刚好形成一直角三角形,梯高为斜边,利用勾股定理得:梯脚与墙角距离:222.5 2.4-=0.7(米). 故选B .
二、填空题
11.【解析】
试题分析:将台阶展开,如图,
331312,5,AC BC =?+?==222169,AB AC BC ∴=+=13,AB ∴=即蚂蚁爬行的最
短线路为13.dm
考点:平面展开:最短路径问题. 12.1425+或825+【分析】
分两种情况考虑:如图1所示,此时△ABC 为锐角三角形,在直角三角形ABD 与直角三角
形ACD 中,利用勾股定理求出BD 与DC 的长,由BD+DC 求出BC 的长,即可求出周长;如图2所示,此时△ABC 为钝角三角形,同理由BD -CD 求出BC 的长,即可求出周长. 【详解】
解:分两种情况考虑:
如图1所示,此时△ABC 为锐角三角形,
在Rt △ABD 中,根据勾股定理得:BD=22226425AB AD -=-=, 在Rt △ACD 中,根据勾股定理得:CD=2222543AC AD -=-=,
∴BC=253+,
∴△ABC 的周长为:652531425+++=+; 如图2所示,此时△ABC 为钝角三角形,
在Rt △ABD 中,根据勾股定理得:22226425AB AD -=-= 在Rt △ACD 中,根据勾股定理得:2222543AC AD --=,
∴BC=253-,
∴△ABC 的周长为:65253825++=+ 综合上述,△ABC 的周长为:145+85+ 故答案为:145+825+ 【点睛】
此题考查了勾股定理,利用了分类讨论的思想,熟练掌握勾股定理是解本题的关键.
1315【分析】
根据题意点B 与点C 关于AD 对称,所以过点C 作AB 的垂线,与AD 的交点即点P ,求出CE 即可得到答案 【详解】
∵8,AB AC AD BC ==⊥ ∴点B 与点C 关于AD 对称
过点C 作CE ⊥AB 于一点即为点P ,此时PB PE +最小 ∵8,4,AB AC BC AD BC ===⊥ ∴BD=2
在Rt △A BC 中, 222282215AD AB BD =-=-=
∵S △ABC=
11
22
BC AD AB CE ??=?? ∴42158CE ?= 得15CE = 故此题填15
【点睛】
此题考察最短路径,根据题意找到对称点,作直角三角形,利用勾股定理解决问题 14.72965【分析】
分三种情形讨论:(1)如图1中,以点C 所在顶点为直角时;(2)如图2中,以点D 所在顶点为直角时;(3)如图3中,以点A 所在顶点为直角时. 【详解】
(1)如图1中,以点C 所在顶点为直角时. ∵AC =CD =4,BC =3,∴BD =CD +BC =7;
(2)如图2中,以点D 所在顶点为直角时,作DE ⊥BC 与E ,连接BD . 在Rt △BDE 中DE =2,BE =5,∴BD 2229DE BE + (3)如图3中,以点A 所在顶点为直角时,作DE ⊥BC 于E , 在Rt △BDE 中,DE =4.BE =7,∴BD 2265DE BE +
故答案为:72965
【点睛】
本题考查了勾股定理、等腰直角三角形等知识,解题的关键是学会用分类讨论的思想思考问题.
15.5或13
【分析】
根据已知可得题意中的图是一个勾股图,可得S P+S Q=S K为从而易求S K.
【详解】
解:如下图所示,
若A=S P=4.B=S Q=9,C=S K,
根据勾股定理,可得
A+B=C,
∴C=13.
若A=S P=4.C=S Q=9,B=S K,
根据勾股定理,可得
A+B=C,
∴B=9-4=5.
∴S K为5或13.
故答案为:5或13.
【点睛】
本题考查了勾股定理.此题所给的图中,以直角三角形两直角边为边所作的正方形的面积和等于以斜边为边所作的正方形的面积.
16.
103. 【分析】
根据八个直角三角形全等,四边形ABCD ,EFGH ,MNKT 是正方形,得出CG=NG ,
CF=DG=NF ,再根据()21S CG DG =+,2
2S GF =,()2
3S NG NF =-,
12310S S S ++=,即可得出答案.
【详解】
∵八个直三角形全等,四边形ABCD ,EFGH ,MNKT 是正方形 ∴CG=NG ,CF=DG=NF
∴()2
222122S CG DG CG DG CG DG GF CG DG =+=++=+
22S GF =
()2
2232S NG NF NG NF NG NF =-=+-
∴22222
12322310S S S GF CG DG GF NG NF NG NF GF ++=+?+++-?==
∴2
103
GF = 故2103
S =
故答案为
103
. 【点睛】
本题主要考查了勾股定理的应用,用到的知识点由勾股定理和正方形、全等三角形的性质. 17.3. 【分析】
作点B 关于AD 的对称点B′,过点B′作B′N ⊥AB 于N 交AD 于M ,根据轴对称确定最短路线问题,B′N 的长度即为BM+MN 的最小值,根据∠BAC=60°判断出△ABB′是等边三角形,再根据等边三角形的性质求解即可. 【详解】
如图,作点B 关于AD 的对称点B′,
由垂线段最短,过点B′作B′N ⊥AB 于N 交AD 于M ,B′N 最短, 由轴对称性质,BM=B′M , ∴BM+MN=B′M+MN=B′N ,
由轴对称的性质,AD 垂直平分BB′, ∴AB=AB′, ∵∠BAC=60°, ∴△ABB′是等边三角形, ∵AB=2, ∴B′N=2×
3
=3, 即BM+MN 的最小值是3. 故答案为3. 【点睛】
本题考查了轴对称确定最短路线问题,等边三角形的判定与性质,确定出点M 、N 的位置是解题的关键,作出图形更形象直观. 18.55 【解析】 【分析】
要求长方体中两点之间的最短路径,最直接的作法,就是将长方体展开,然后利用两点之间线段最短解答. 【详解】 展开图如图所示:
由题意,在Rt △APQ 中,PD=10cm ,DQ=5cm ,
∴蚂蚁爬行的最短路径长2222105PD QD +=+5cm ), 故答案为:5 【点睛】
本题考查了平面展开﹣最短路径问题,解答此类问题时要先根据题意把立体图形展开成平面图形后,再确定两点之间的最短路径.一般情况是两点之间,线段最短.在平面图形上构造直角三角形解决问题. 19.12 【解析】
如图,过点N 作NG ⊥BC 于点G ,连接CN ,根据轴对称的性质有: MA=MC ,NA=NC ,∠AMN=∠CMN.
