二次插值算法

二次插值法亦是用于一元函数在确定的初始区间搜索极小点的一种方法。它属于曲线拟合方法的畴。
一、基本原理
在求解一元函数的极小点时,常常利用一个低次插值多项式来逼近原目标函数,
然后求该多项式的极小点(低次多项式的极小点比较容易计算),并以此作为目标函数
的近似极小点。如果其近似的程度尚未达到所要求的精度时,可以反复使用此法,逐次拟合,直到满足给定的精度时为止。
常用的插值多项式为二次或三次多项式,分别称为二次插值法和三次插值法。这里我们主要介绍二次插值法的计算公式。
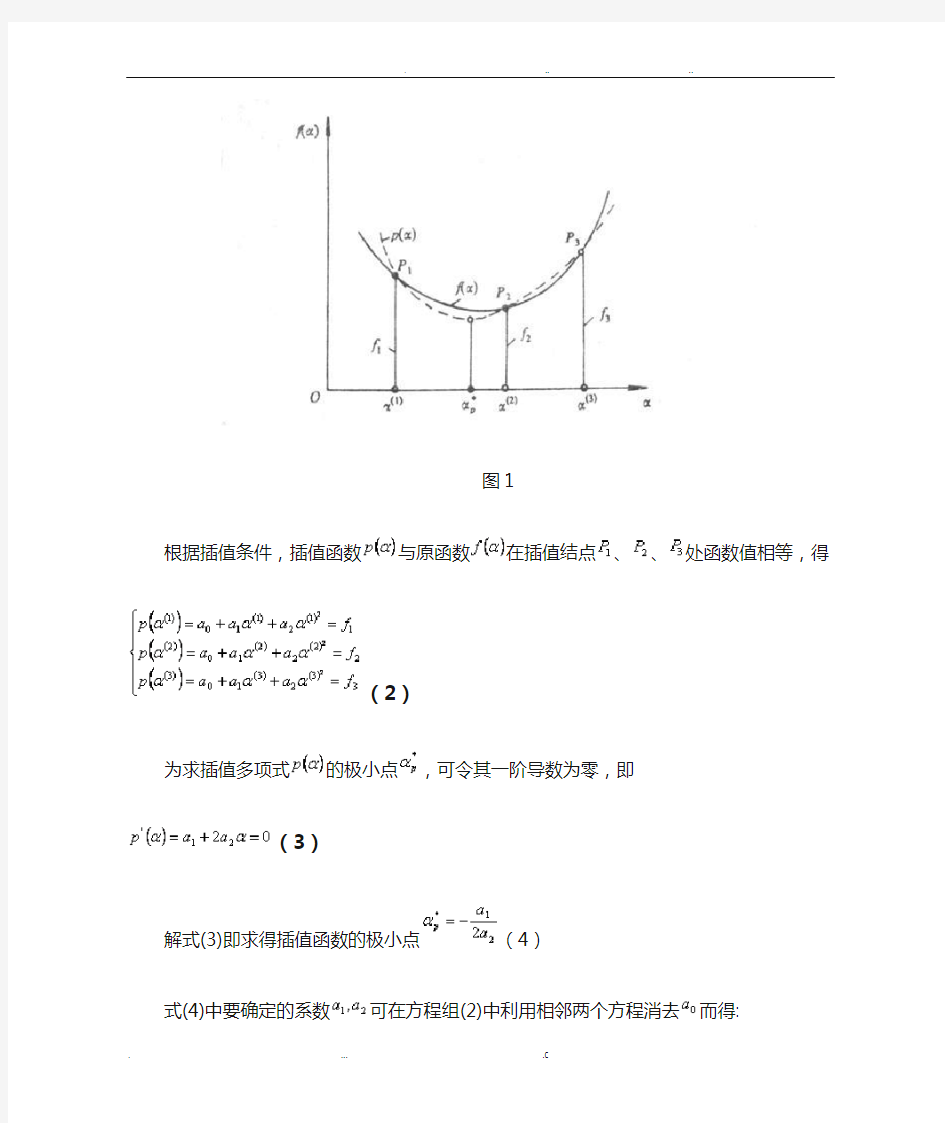
假定目标函数在初始搜索区间中有三点、和
,其函数值分别为、和(图1},且满足,,即满足函数值为两头大中间小的性质。利用这三点及相应的函数值作一条二次曲线,其函数为一个二次多项式
(1)
式中、、为待定系数。
图1
根据插值条件,插值函数与原函数在插值结点、、处函数值相等,得
(2)
为求插值多项式的极小点,可令其一阶导数为零,即
(3)
解式(3)即求得插值函数的极小点(4)
式(4)中要确定的系数可在方程组(2)中利用相邻两个方程消去而得:
(5)
(6)
将式(5)、(6)代入式(4)便得插值函数极小值点的计算公式:
(7)
把取作区间的另一个计算点,比较与两点函数值的大小,在保持
两头大中间小的前提下缩短搜索区间,从而构成新的三点搜索区间,再继续按上述方法进行
三点二次插值运算,直到满足规定的精度要求为止,把得到的最后的作为的近似极小值点。上述求极值点的方法称为三点二次插值法。
为便于计算,可将式(7)改写为
(8)
式中:
(9)
(10)
二、迭代过程及算法框图
(1)确定初始插值结点
通常取初始搜索区间的两端点及中点为,,。计算函数值,,,构成三个初始插值结点、、。
(2)计算二次插值函数极小点
按式(8)计算,并将记作点,计算。若本步骤为对初始搜索区间的第一次插值或点仍为初始给定点时,则进行下一步(3);否则转步骤(4)
(3)缩短搜索区间
缩短搜索区间的原则是:比较函数值、,取其小者所对应的点作为新的点,并以此点左右两邻点分别取作新的和,构成缩短后的新搜索区间。其具体方法则如图2所示,根据原区间中和的相对位置以及函数值和之比较有a、b、c、d四种情况,图中阴影线部分表示丢去的区间。在对新区间三个新点的代号作依次、
、的一般化处理后,计算其函数值,并令,,,返回步骤(2)。
图2(a)
图2(b)
图2(c)
图2(d)
(4)判断迭代终止条件
在一般情况下,因是前一次插值函数的极小值点,是本次插值函数的极小值点,若和的距离足够小时,即满足,或和两者原函数值已很接近,即满足,则停止迭代,这时,若,输出极小值点,
极小值;否则,即时,输出极小值点,极小值。如不满足上述迭代终止条件,则返回步骤(3),再次缩短搜索区间,直至最后满足终止条件。
按上述步骤设计的二次插值法算法框图见图3。
图3
算法框图中有几点需作些说明。
1.判别框?若成立,按式(9)和式(10)则有
说明三个插值结点、、在一条直线上;
2.判别框?若不成立,说明落在区间之外。
上述两种情况只是在区间已缩得很小,由于三个插值结点已十分接近,计算机的舍入误差才可能使其发生。此时取和作为最优解应是合理的。
3.在初始搜索区间第一次插值或仍为初始给定点时,和并不代表前后二次插值函数极小点,因而判别式并不能确切地反映该不该终止迭代,这时应进行步骤(3)缩短搜索区间,直至初始点第一次由代替,使用判别式?进行终止判别才具意义。为此,算法框图中设置开关K=0和K=1分别表示初始点第一次由代替前和后的状态。
二次插值算法
二次插值法亦是用于一元函数在确定的初始区间内搜索极小点的一种方法。它属于曲线拟合方法的范畴。 一、基本原理 在求解一元函数的极小点时,常常利用一个低次插值多项式来逼近原目标函数,然后求该多项式的极小点(低次多项式的极小点比较容易计算),并以此作为目标函数的近似极小点。如果其近似的程度尚未达到所要求的精度时,可以反复使用此法,逐次拟合,直到满足给定的精度时为止。 常用的插值多项式为二次或三次多项式,分别称为二次插值法和三次插值法。这里我们主要介绍二次插值法的计算公式。 假定目标函数在初始搜索区间中有三点、和 ,其函数值分别为、和(图1},且满足,,即满足函数值为两头大中间小的性质。利用这三点及相应的函数值作一条二次曲线,其函数为一个二次多项式 (1) 式中、、为待定系数。
图1 根据插值条件,插值函数与原函数在插值结点、、处函数值相等,得 (2) 为求插值多项式的极小点,可令其一阶导数为零,即 (3) 解式(3)即求得插值函数的极小点(4) 式(4)中要确定的系数可在方程组(2)中利用相邻两个方程消去而得: (5)
(6)将式(5)、(6)代入式(4)便得插值函数极小值点的计算公式: (7)把取作区间内的另一个计算点,比较与两点函数值的大小,在保持两头大中间小的前提下缩短搜索区间,从而构成新的三点搜索区间,再继续按上述 方法进行三点二次插值运算,直到满足规定的精度要求为止,把得到的最后的作为 的近似极小值点。上述求极值点的方法称为三点二次插值法。 为便于计算,可将式(7)改写为 (8) 式中: (9) (10) 二、迭代过程及算法框图 (1)确定初始插值结点 通常取初始搜索区间的两端点及中点为,, 。计算函数值,,,构成三个初始插值结点、、。
两种空间插值方法的比较研究
两种空间插值方法的比较研究 摘要:距离倒数加权法算法简单,容易实现,适合分布较均匀的采样点集,但容易出现“牛眼”现象;克里金法是一种无偏最优估计法,精度较高,适合空间自相关程度高的数据,但其算法复杂,实现较难。这两种 方法各有其适用情形,本文比较了这两种方法的优劣并提出算法优化的思路。 关键字:距离倒数加权,克里金,优化 1引言 空间插值是根据一组已知的离散数据或分区数据,按照某种假设推求出其他未知点或未知区域的数据的过程,简单的说就是由已知空间特性推求未知空间特性。它是地学研究中的基本问题,也是GIS 数据处理的重要内容。在利用GIS 处理空间数据的过程中,需要进行空间插值的场合很多,如采样密度不够、采样分布不合理、采样存在空白区、等值线的自动绘制、数字高程模型的建立、区域边界分析、曲线光滑处理、空间趋势预测、采样结果的2.5维可视化等[1]。通过归纳,空间插值可以简化为以下三种情形:(1)现有离散曲面的分辨率、像元大小或方向与所要求的不符,需要重新插值。例如将一个扫描影像(航空像片、遥感影像)从一种分辨率或方向转换为另一种分辨率或方向的影像。(2)现有连续曲面的数据模型与所需的数据模型不符,需要重新插值。如将一个连续曲面从一种空间切分方式变为另一种空间切分方式,从TIN 到栅格、栅格到TIN 或矢量多边形到栅格。(3)现有数据不能完全覆盖所要求的区域范围,需要插值。如将离散的采样点数据内插为连续的数据表面[2]。。 现有的空间插值方法多种多样,但每一种方法都有其适用情形和无法避免的缺陷,本文分析了距离倒数加权法和克里金法的插值结果,并提出改进的思路。 2方法 距离倒数加权法和克里金法都是建立在地理学第一定律之上的,即:空间距离越近,地理事物的相似性越大[3]。它们都是通过确定待插点周围采样点的权重来求取待插点的估计值,可统一表示。设n x x ,,1 为区域上的一系列观测点,)(,),(1n x Z x Z 为相应的观测值。待插点0x 处的值)(0x Z 可采用一个线性组合来估计: ∑==n i i i x Z x Z 10)()(λ (1)
黄金分割法、二次插值法C语言编程
已知:F(x)=x4-4x3-6x2-16x+4,求极小值,极小值点,区间,迭代次数?用进退法确定区间,用黄金分割法求极值。 #include
二次插值算法
二次插值法亦是用于一元函数在确定的初始区间搜索极小点的一种方法。它属于曲线拟合方法的畴。 一、基本原理 在求解一元函数的极小点时,常常利用一个低次插值多项式来逼近原目标函数, 然后求该多项式的极小点(低次多项式的极小点比较容易计算),并以此作为目标函数 的近似极小点。如果其近似的程度尚未达到所要求的精度时,可以反复使用此法,逐次拟合,直到满足给定的精度时为止。 常用的插值多项式为二次或三次多项式,分别称为二次插值法和三次插值法。这里我们主要介绍二次插值法的计算公式。 假定目标函数在初始搜索区间中有三点、和 ,其函数值分别为、和(图1},且满足,,即满足函数值为两头大中间小的性质。利用这三点及相应的函数值作一条二次曲线,其函数为一个二次多项式 (1) 式中、、为待定系数。
图1 根据插值条件,插值函数与原函数在插值结点、、处函数值相等,得 (2) 为求插值多项式的极小点,可令其一阶导数为零,即 (3) 解式(3)即求得插值函数的极小点(4) 式(4)中要确定的系数可在方程组(2)中利用相邻两个方程消去而得: (5)
(6) 将式(5)、(6)代入式(4)便得插值函数极小值点的计算公式: (7) 把取作区间的另一个计算点,比较与两点函数值的大小,在保持 两头大中间小的前提下缩短搜索区间,从而构成新的三点搜索区间,再继续按上述方法进行 三点二次插值运算,直到满足规定的精度要求为止,把得到的最后的作为的近似极小值点。上述求极值点的方法称为三点二次插值法。 为便于计算,可将式(7)改写为 (8) 式中: (9) (10) 二、迭代过程及算法框图 (1)确定初始插值结点 通常取初始搜索区间的两端点及中点为,,。计算函数值,,,构成三个初始插值结点、、。
arcgis空间内插值教程
GIS空间插值(局部插值方法)实习记录 一、空间插值的概念和原理 当我们需要做一幅某个区域的专题地图,或是对该区域进行详细研究的时候,必须具备研究区任一点的属性值,也就是连续的属性值。但是,由于各种属性数据(如降水量、气温等)很难实施地面无缝观测,所以,我们能获取的往往是离散的属性数据。例如本例,我们现有一幅山东省等降雨量图,但是最终目标是得到山东省降水量专题图(覆盖全省,统计完成后,各地均具有自己的降雨量属性)。 空间插值是指利用研究区已知数据来估算未知数据的过程,即将离散点的测量数据转换为连续的数据曲面。利用空间插值,我们就可以通过离散的等降雨量线,来推算出山东省各地的降雨量了。 二、空间插值的几种方法及本次实习采用的原理和方法 –整体插值方法 ?边界内插方法 ?趋势面分析 ?变换函数插值 –局部分块插值方法 ?自然邻域法 ?移动平均插值方法:反距离权重插值 ?样条函数插值法(薄板样条和张力样条法) ?空间自协方差最佳插值方法:克里金插值 ■局部插值方法的控制点个数与控制点选择问题 局部插值方法用一组已知数据点(我们将其称为控制点)样本来估算待插值点(未知点)的值,因此控制点对该方法十分重要。 为此,第一要注意的是控制点的个数。控制点的个数与估算结果精确程度的关系取决于控制点的分布与待插值点的关系以及控制点的空间自相关程度。为了获取更精确的插值结果,我们需要着重考虑上述两点因素(横线所示)。 第二需要注意的是怎样选择控制点。一种方法是用离估算点最近的点作为控制点;另一种方法是通过半径来选择控制点,半径的大小必须根据控制点的分布来调整。 S6、按照不同方法进行空间插值,并比较各自优劣 打开ArcToolbox——Spatial Analyst 工具——插值,打开插值方法列表,如下图:
ArcGIS中几种空间插值方法
ArcGIS 中几种空间插值方法 1. 反距离加权法(IDW) ArcGIS 中最常用的空间内插方法之一,反距离加权法是以插值点与样本点之间的距离为权重的插值方法,插值点越近的样本点赋予的权重越大,其权重贡献与距离成反比。可表示为: 1111() ()n n i p p i i i i Z Z D D ===∑∑ 其中Z 是插值点估计值,Z i (i=1Λn)是实测样本值,n 为参与计算的实测样本数,D i 为插值点与第i 个站点间的距离,p 是距离的幂,它显著影响内插的结果,它的选择标准是最小平均绝对误差。 2.多项式法 多项式内插法(Polynomial Interpolation)是根据全部或局部已知值,按研究区域预测数据的某种特定趋势来进行内插的方法,属统计方法的范畴。在GA 模块中,有二种类型的多项式内插方法,即全局多项式内插和局部多项式内插。前者多用于分析数据的全局趋势;后者则是使用多个平面来拟合整个研究区域,能表现出区域内局部变异的情况。 3.样条函数内插法 样条函数是一个分段函数,进行一次拟合只有少数点拟合,同时保证曲线段连接处连续,这就意味着样条函数可以修改少数数据点配准而不必重新计算整条曲线。样条函数的一些缺点是:样条内插的误差不能直接估算,同时在实践中要
解决的问题是样条块的定义以及如何在三维空间中将这些“块”拼成复杂曲面,又不引入原始曲面中所没有的异常现象等问题。 4.克里格插值法 克里格法是GIS 软件地理统计插值的重要组成部分。这种方法充分吸收了地理统计的思想,认为任何在空间连续性变化的属性是非常不规则的,不能用简单的平滑数学函数进行模拟,可以用随机表面给予较恰当的描述。这种连续性变化的空间属性称为“区域性变量”,可以描述象气压、高程及其它连续性变化的描述指标变量。地理统计方法为空间插值提供了一种优化策略,即在插值过程中根据某种优化准则函数动态的决定变量的数值。Kriging 插值方法着重于权重系数的确定,从而使内插函数处于最佳状态,即对给定点上的变量值提供最好的线性无偏估计。 对于普通克里格法,其一般公式为 01()()n i i i Z x Z x λ==∑,其中,Z(x i )(i=1, Λ,n)为n 个样本点的观测值,Z(x 0)为待定点值,i λ为权重,权重由克立格方程组: 011 (,)(,)1n i i j i i n i i C x y C x x λμλ==?-=????=??∑∑ 决定,其中,C(x i ,x j )为测站样本点之间的协方差,C(x i ,x 0)为测站样本点与插值点之间的协方差,μ为拉格朗日乘子。 插值数据的空间结构特性由半变异函数描述,其表达式为: () 21 1()(()())2()N h i i i h Z x Z x h N h ν==-+∑ 其中,N(h)为被距离区段分割的试验数据对数目,根据试验变异函数的特性,选
三次样条插值方法的应用
CENTRAL SOUTH UNIVERSITY 数值分析实验报告
三次样条插值方法的应用 一、问题背景 分段低次插值函数往往具有很好的收敛性,计算过程简单,稳定性好,并且易于在在电子计算机上实现,但其光滑性较差,对于像高速飞机的机翼形线船体放样等型值线往往要求具有二阶光滑度,即有二阶连续导数,早期工程师制图时,把富有弹性的细长木条(即所谓的样条)用压铁固定在样点上,在其他地方让他自由弯曲,然后沿木条画下曲线,称为样条曲线。样条曲线实际上是由分段三次曲线并接而成,在连接点即样点上要求二阶导数连续,从数学上加以概括就得到数学样条这一概念。下面我们讨论最常用的三次样条函数及其应用。 二、数学模型 样条函数可以给出光滑的插值曲线(面),因此在数值逼近、常微分方程和偏微分方程的数值解及科学和工程的计算中起着重要的作用。 设区间[]b ,a 上给定有关划分b x x n =<<<= 10x a ,S 为[]b ,a 上满足下面条件的函数。 ● )(b a C S ,2∈; ● S 在每个子区间[]1,+i i x x 上是三次多项式。 则称S 为关于划分的三次样条函数。常用的三次样条函数的边界条件有三种类型: ● Ⅰ型 ()()n n n f x S f x S ''0'',==。 ● Ⅱ型 ()()n n n f x S f x S ''''0'''',==,其特殊情况为()()0''''==n n x S x S 。 ● Ⅲ型 ()() 3,2,1,0,0==j x S x S n j j ,此条件称为周期样条函数。 鉴于Ⅱ型三次样条插值函数在实际应用中的重要地位,在此主要对它进行详细介绍。 三、算法及流程 按照传统的编程方法,可将公式直接转换为MATLAB 可是别的语言即可;另一种是运用矩阵运算,发挥MATLAB 在矩阵运算上的优势。两种方法都可以方便地得到结果。方法二更直观,但计算系数时要特别注意。这里计算的是方法一的程序,采用的是Ⅱ型边界条件,取名为spline2.m 。 Matlab 代码如下: function s=spline2(x0,y0,y21,y2n,x) %s=spline2(x0,y0,y21,y2n,x) %x0,y0 are existed points,x are insert points,y21,y2n are the second
空间插值算法-反距离加权法
Show Inverse Distance Weighted Interpolation One of the most commonly used techniques for interpolation of scatter points is inverse distance weighted (IDW) interpolation. Inverse distance weighted methods are based on the assumption that the interpolating surface should be influenced most by the nearby points and less by the more distant points. The interpolating surface is a weighted average of the scatter points and the weight assigned to each scatter point diminishes as the distance from the interpolation point to the scatter point increases. Several options are available for inverse distance weighted interpolation. The options are selected using the Inverse Distance Weighted Interpolation Options dialog. This dialog is accessed through the Options button next to the Inverse distance weighted item in the 2D Interpolation Options dialog. SMS uses Shepard's Method for IDW: Shepard's Method The simplest form of inverse distance weighted interpolation is sometimes called "Shepard's method" (Shepard 1968). The equation used is as follows: where n is the number of scatter points in the set, fi are the prescribed function values at the scatter points (e.g. the data set values), and wi are the weight functions assigned to each scatter point. The classical form of the weight function is: where p is an arbitrary positive real number called the power parameter (typically, p=2) and hi is the distance from the scatter point to the interpolation point or where (x,y) are the coordinates of the interpolation point and (xi,yi) are the coordinates of each scatter point. The weight function varies from a value of unity at the scatter point to a value approaching zero as the distance from the scatter point increases. The weight functions are normalized so that the weights sum to unity.
优化设计VC6.0二次插值法
题目:利用二次插值法求()f sin αα=在4≤α≤5上的极小点。 利用VC++6.0进行编程,求得极小点。具体程序如下说明。 一、 二次插值法 求解原理:在求解一元函数的极小点时,常常利用一个低次插值多项式 来逼近原目标函数,然后求该多项式的极小点(低次多项式的极小点比较容易计算),并以此作为目标函数的近似极小点。如果其近似的程度尚未达到所要求的精度时,可以反复使用此法,逐次拟合,直到满足给定的精度时为止。二次差值的程序流程图
程序如下: #include "stdio.h" #include "math.h" #define f(x) sin(x)//宏定义函数f(x) int main() { //////////////////////////////////////////////////////////////////////////二次插值法 printf("*************************************二次插值法************************************\n"); float m1=4,m2=4.5,m3=5,w=1,s; float h1,h2,h3,hp,c1,c2,mp; s=1e-5; int i=0; h1=f(m1); h2=f(m2); h3=f(m3); c1=(h3-h1)/(m3-m1); c2=((h2-h1)/(m2-m1)-c1)/(m2-m3); mp=(m1+m3-(c1/c2))/2; hp=f(mp); while (fabs((m2-mp)/m2)>=s) { i++; if ((mp-m2)*w>0) { if (h2>=hp) { m1=m2; h1=h2; m2=mp; h2=hp; } else { m3=mp; h3=hp; } } else { if (h2>=hp) { m3=m2;
空间插值算法汇总
空间插值算法: 1、距离倒数乘方法(Inverse Distance to a Power)距离倒数乘方格网化方法是一个加权平均插值法,可以进行确切的或者圆滑的方式插值。方次参数控制着权系数如何随着离开一个格网结点距离的增加而下降。对于一个较大的方次,较近的数据点被给定一个较高的权重份额,对于一个较小的方次,权重比较均匀地分配给各数据点。计算一个格网结点时给予一个特定数据点的权值与指定方次的从结点到观测点的该结点被赋予距离倒数成比例。当计算一个格网结点时,配给的权重是一个分数,所有权重的总和等于1.0。当一个观测点与一个格网结点重合时,该观测点被给予一个实际为 1.0 的权重,所有其它观测点被给予一个几乎为0.0 的权重。换言之,该结点被赋给与观测点一致的值。这就是一个准确插值。距离倒数法的特征之一是要在格网区域内产生围绕观测点位置的"牛眼"。用距离倒数格网化时可以指定一个圆滑参数。大于零的圆滑参数保证,对于一个特定的结点,没有哪个观测点被赋予全部的权值,即使观测点与该结点重合也是如此。圆滑参数通过修匀已被插值的格网来降低"牛眼"影响。 2、克里金法(Kriging)克里金法是一种在许多领域都很有用的地质统计格网化方法。克里金法试图那样表示隐含在你的数据中的趋势,例如,高点会是沿一个脊连接,而不是被牛眼形等值线所孤立。克里金法中包含了几个因子:变化图模型,漂移类型和矿块效应。 3、最小曲率法(Minimum Curvature)最小曲率法广泛用于地球科学。用最小曲率法生成的插值面类似于一个通过各个数据值的,具有最小弯曲量的长条形薄弹性片。最小曲率法,试图在尽可能严格地尊重数据的同时,生成尽可能圆滑的曲面。使用最小曲率法时要涉及到两个参数:最大残差参数和最大循环次数参数来控制最小曲率的收敛标准。 4、多元回归法(Polynomial Regression)多元回归被用来确定你的数据的大规模的趋势和图案。你可以用几个选项来确定你需要的趋势面类型。多元
插值法-第二次程序题
插值法 题目1:对Runge 函数2 2511 )(x x R += 在区间[-1,1]作下列插值逼近, 并和R(x)的图像进行比较,并对结果进行分析。 (1)用等距节点,200,1.0,-1≤≤=+=i h ih x i 绘出它的20次Newton 插值多项式的图像。 (2)用节点)20,,2,1,0(,)42 1 2cos( ???=+=i i x i π,绘出它的20次Lagrange 插值多项式的图像。 (3)用等距节点,200,1.0,-1≤≤=+=i h ih x i 绘出它的分段线性插 值函数的图像。 (4)用等距节点,200,1.0,-1≤≤=+=i h ih x i 绘出它的三次自然样 条插值函数的图像。 程序及分析: (1)用等距节点,200,1.0,-1≤≤=+=i h ih x i 绘出它的20次Newton 插值多项式的图像。 Matlab 程序如下: %计算均差 x=[-1::1];
n=length(x); syms z for i=1:n y(i)=1/(1+25*x(i)*x(i)); end N=zeros(n,n); N(:,1)=y'; for j=2:n for k=j:n N(k,j)=(N(k,j-1)-N(k-1,j-1))/(x(k)-x(k-j+1)); end end for t=1:n c(t)=N(t,t) end
%构造插值多项式 f=N(1,1); for k=2:n a=1; for r=1:(k-1) a=a*(z-x(r)); end f=f+N(k,k)*a; end %作图 a=[-1::1]; n=length(a); for i=1:n b(i)=1/(1+25*a(i)*a(i)); end
ArcGIS中的空间插值和面积计算
说明:本文阐述了空间插值和污染面积估算的方法,供群内交流学习用,若要用于商业用途或转载,请与原作者联系。本文若有不正确之处,敬请指出! 一、空间插值 插值方法种类很多,每种插值方法里参数也很多,至于哪种最好,没有定论,只能根据需求以及制图的效果来选定。建议:插值效果图与网格图进行对比,哪种效果最接近网格图(能体现局部)而且又能反映整体趋势就取哪种。 1.1、 1.2、以“反距离权重法,1次方”为例:
请问:此处有可选smooth ,可以做进行平滑处理吗? 可以,但精度会受到影响,看平滑后的效果来决定是否进行平滑处理。建议不做
3、扩展研究区域 4、至此可以制作分层设色图filled contours/等值线图contours 为减少误差,还可以对分级进行设置 请问:此处分级该如何设置?有无相应依据? 含量图主要根据百分含量,如果作图效果不好,适当调整 评价图根据污染等级
5、这是采用“反距离权重法,1次方”来插值的。 可选用“局部多项式”或“普通克里格插值”方法来试试,看哪种和网格分级图更接近些。但无论哪种方法聚类误差可能都较大,一部分高值可能被掩盖。 二、下面转成栅格图层再进行分层设色图制作,这样精度较高,且图层可用来进行面积估算 2.1、导出成栅格图层
2.2、设置格网大小,一般在50到100左右(本次都设为100)
(2.3和2.4均非必要步骤,只是为了另外的处理或制图的美观性。如果是为了制图的美观性有可能这两个步骤会弄巧成拙,是否须要请根据具体需要和效果来定) 2.3、并可对栅格图层重分类,生成新的栅格图层如(ah_cd)
机械优化设计外推法,黄金分割法,二次插值法
机械优化设计课程作业 外推法 #include 黄金分割法 #include 数值计算方法期末论文 ————同等要求下三次样条插值法与最小二值法的分析及比较。 引言 在实际中,常常要处理由实验或测量所得到的一批离散数据.插值与拟合方法就是要通过这些数据去确定某一类已知函数的参数或寻找某个近似函数,使所得到的近似函数与已知数据有较高的拟合程度.如果要求这个近似函数(曲线或曲面)经过已知的所有数据点,则称此类问题为插值问题。 当所给的数据较多时,用插值方法所得到的插值函数会很复杂,所以,通常插值方法用于数据较少的情况.但数据一般都是由观测或试验得到的,往往会带有一定的随机误差,因而,要求近似函数通过所有的数据点也是不必要的.如果不要求近似函数通过所有数据点,而是要求它能较好地反应数据的整体变化趋势,则解决这类问题的方法称为数据拟合. 插值和拟合都是要根据一组数据构造一个函数作为近似,由于近似的要求不同,二者的数学方法上是完全不同的。而面对一个实际问题,究竟应该用插值还是拟合,有时容易确定,有时则并不明显。 本文由具体题目为基础,主要论述了在同等要求下三次样条插值法与最小二值法的分析及比较。 关键词:数值计算方法、三次样条插值法、最小二值法 目录 引言--------------------------------------------------- 2 第一章三次样条插值------------------------------------ 4 1.1三次样条插值函数--------------------------------- 4 1.2 分段线性插值------------------------------------ 5 1.3插值理论----------------------------------------- 6 第二章最小二乘法--------------------------------------- 7 2.1 线性最小二乘拟合法------------------------------ 7 2.2 一般线性最小二乘拟合法--------------------------- 8 2.3非线性最小二乘拟合法------------------------------ 9 第三章算法对比与实现------------------------------------ 10 3.1对比实例一---------------------------------------- 10 3.2对比实例二---------------------------------------- 11 3.3结果及分析---------------------------------------- 15 第四章总结---------------------------------------------- 16 Matlab 实践 1、 二次插值法无约束最优化 算法说明:在包含f (x )极小值x0的区间【a b 】,给定三点x1、x2、x3,其对应的函数值分别为 f1、f2、f3,且满足x1 算法举例: f (x )=(x 2-2)2/2-1,x ∈[0,5] 2、拉压杆系的静不定问题。求各杆的轴力Ni 及节点C 的位移,已知桁架结构如图所示,各杆横截面积分别为Ai ,材料的弹性模量为E 。 算法说明:假设各杆均受拉力,C 点因各杆变形而引起的x 方向位移△x ,y 方向位移△y ,由几何 关系,的变形方程: i i i i i i y x EA L N L ααsin cos ?+?== ? i=1,……,n 令K i = i i EA L , 故 0sin cos =?-?-i i i i y x N K αα, 四川理工学院 《最优化方法》课程论文 姓名:陈晓容 专业:统计 班级:1班 学号:11071050130 完成日期:2014-6-25 无约束最优化方法——三点二次插值法 摘要 在生产过程、科学实验以及日常生活中,人们总希望用最少的人力、物力、财力和时间去办更多的事,获得最大的效益,在管理学中被看作是生产者的利润最大化和消费者的效用最大化,如果从数学的角度来看就被看作是“最优化问题”。最优化问题分为无约束最优化和约束最优化,本文主要拟就无约束最优化进行分析。 无约束最优化计算方法是数值计算领域中十分活跃的研究课题之一,快速的求解无约束最优化问题,除了自身的重要性以外,还体现在它也构成一些约束最优化问题的子问题。因此,对于无约束最优化问题,如何快速有效的求解一直是优化工作者十分关心的事。本文研究求解无约束最优化问题的精确线性搜索方法——三点二次插值法,并且讨论了这种方法的优缺点以及适用范围,同时论文中对这种方法给出了具体实例,并对例子进行了matlab软件实现。 关键词:三点二次插值法、插值多项式、目标函数 目录 一、问题的提出 (3) 二、设计思路和步骤 (3) 3.1设计思路 (3) 3.2 设计步骤 (3) 三、程序设计 (5) 3.1问题分析 (5) 3.2 算法设计 (5) 3.3 算法框图 (5) 3.4 程序编制 (7) 四、结果分析 (8) 四、结果分析 3.1理论结果 .......................................................... 8 3.2 编程结果 .......................................................... 9 五、收获提高 (11) 5.1设计的优缺点 ..................................................... 11 5.2收获与启发 ....................................................... 11 参考文献 . (11) 一、问题的提出 用精确线性搜索方法求 ()23m i n 30 +-=≥ααα?α 的近似最优解(精确极小点为*α=1)。设已确定其初始搜索区间为[0,3],取初始插值点为0α=2,终止误差ε=0.05。 二、设计思路和步骤 2.1设计思路 在求解一元函数()α?的极小点时,在搜索区间中用低次(通常不超过三次)插值多项式()αq 来近似目标函数,后求该多项式的极小点(比较容易计算),并以此作为目标函数()α?的近似极小点。如果其近似的程度尚未达到所要求的精度时,反复使用此法,逐次拟合,直到满足给定的精度时为止。 2.2设计步骤 考虑二次多项式 ()c b a q ++=ααα2 则 b a q +='αα2)( 二次插值法C语言程序 #include"stdio.h" #include"math.h" #include"conio.h" void main() { float*area(float a1,float p,float a[3]); float f(float x); float ar,fr; float a1=10,p=0.01,e=0.000001; float pa[3]; area(a1,p,pa); a1=pa[0]; float a2=pa[1]; float a3=pa[2]; float f1=f(a1); float f2=f(a2); float f3=f(a3); do { ar=((a3*a3-a2*a2)*f1+(a1*a1-a3*a3)*f2+(a2*a2-a1*a1)*f3); ar=ar/2/((a3-a2)*f1+(a1-a3)*f2+(a2-a1)*f3); fr=f(ar); if(ar>a2) { if(fr>f2) { a3=ar; f3=fr; } else if(fr 文小编收集文档之二次插值法亦是用于一元函数在确定的初始区间内搜索极小点的一种方法。它属于曲线拟合方法的范畴。' 一、基本原理 在求解一元函数的极小点时,常常利用一个低次插值多项式来逼近原目标函数,然后求该多项式的极小点(低次多项式的极小点比较容易计算),并以此作为目标函数的近似极小点。如果其近似的程度尚未达到所要求的精度时,可以反复使用此法,逐次拟合,直到满足给定的精度时为止。 常用的插值多项式为二次或三次多项式,分别称为二次插值法和三次插值法。这里我们主要介绍二次插值法的计算公式。 假定目标函数在初始搜索区间中有三点、和 ,其函数值分别为、和(图1},且满足,,即满足函数值为两头大中间小的性质。利用这三点及相应的函数值作一条二次曲线,其函数为一个二次多项式 (1) 式中、、为待定系数。 图1 根据插值条件,插值函数与原函数在插值结点、、处函数值相等,得 (2) 为求插值多项式的极小点,可令其一阶导数为零,即 (3) 解式(3)即求得插值函数的极小点(4) 式(4)中要确定的系数可在方程组(2)中利用相邻两个方程消去而得: (5) (6) 将式(5)、(6)代入式(4)便得插值函数极小值点的计算公式: (7) 把取作区间内的另一个计算点,比较与两点函数值的大小,在 保持两头大中间小的前提下缩短搜索区间,从而构成新的三点搜索区间,再继续按上述方法进行三点二次插值运算,直到满足规定的精度要求为止,把得到的最后的作为的近似极小值点。上述求极值点的方法称为三点二次插值法。为便于计算,可将式(7)改写为 (8) 式中: (9) (10) 二、迭代过程及算法框图 (1)确定初始插值结点 通常取初始搜索区间的两端点及中点为,, 。计算函数值,,,构成三个初始插值结点、、。 (2)计算二次插值函数极小点 按式(8)计算,并将记作点,计算。若本步骤为对初始搜索区间的第一次插值或点仍为初始给定点时,则进行下一步(3);否则转步骤(4) (3)缩短搜索区间 缩短搜索区间的原则是:比较函数值、,取其小者所对应的点作为新的点,并以此点左右两邻点分别取作新的和,构成缩短后的新搜索区间 。其具体方法则如图2所示,根据原区间中和的相对位置以及函数值和之比较有a、b、c、d四种情况,图中阴影线部分表示丢去的区间。在 数值分析--第2章插值法 第2章 插值法 在科学研究与工程技术中,常常遇到这样的问题:由实验或测量得到一批离散样点,要求作出一条通过这些点的光滑曲线,以便满足设计要求或进行加工。反映在数学上,即已知函数在一些点上的值,寻求它的分析表达式。此外,一些函数虽有表达式,但因式子复杂,不易计算其值和进行理论分析,也需要构造一个简单函数来近似它。 解决这种问题的方法有两类:一类是给出函数)(x f 的一些样点,选定一个便于计算的函数)(x ?形式,如多项式、分式线性函数及三角多项式等,要求它通过已知样点,由此确定函数)(x ?作为)(x f 的近似,这就是插值法;另一类方法在选定近似函数的形式后,不要求近似函数过已知样点,只要求在某种意义下在这些样点上的总偏差最小。这类方法称为曲线(数据)拟合法。 设已知函数f 在区间],[b a 上的1+n 个相异点i x 处的函数值(),0,,i i f f x i n ==,要求构造一个简单函数()x ?作为函数()f x 的近似表达式()()f x x ?≈,使得 ()(),0,1,,i i i x f x f i n ?=== (2-1) 这类问题称为插值问题。称f 为被插值函数;()x ?为插值函数;n x x ,,0 为插值节点;(2-1)为插值条件。 若插值函数类{()}x ?是代数多项式,则相应的插值问题为代数插值。若{()}x ?是三角多项式,则相应的插值问题称为三角插值。若{()}x ?是有理分式,则相应的插值问题称为有理插值。 §1 Lagrange 插值 1.1 Lagrange 插值多项式 设函数f 在1+n 个相异点0 1 ,,,n x x x 上的值n i x f f i i ,,1,0),( ==是已知的,在次数不超过n 的多项式集合n P 中,求()n L x 使得 (),0,1,,n i i L x f n n == (2-2) 定理2.1 存在惟一的多项式n n P L ∈满足插值条件(2-2)。 证明 我们采用构造性的证明方法。假如我们能够构造出n 次多项式()i l x ,使得 1,(),0,1,,0,i j ij i j l x i j n i j δ=?===?≠? , (2-3) 那么 ∑==n i i i n x l f x L 0) ()( (2-4) 是满足插值条件(2-2)的插值多项式。 余下的问题就是如何构造出满足式(2-3)的n 次多项式(),0,1,,i l x i n =。由于当j i ≠时,()0,0,1,,i j l x i j n ==,,即111,,,,,i i n x x x x -+是()i l x 的零点,因此()i l x 必然具有形式 ∏≠=+--=----=n i j j j i n i i i i x x c x x x x x x x x c x l 0110)()())(()()( 又因1)(=i i x l ,故∏≠=-=n i j j j i i x x c 0)(,因此 ∏ ∏∏≠=≠=≠=--=--= n i j j j i j n i j j j i n i j j j i x x x x x x x x x l 000) () () () ()( (2-5)三次样条插值法与最小二值 法的分析及比较
二次插值法无约束最优化
最优化课程论文-三点二次插值法
二次插值法C语言程序
文小编收集文档之二次插值算法
数值分析--第2章 插值法
