非线性数学模型的线性化

非线性数学模型的线性化
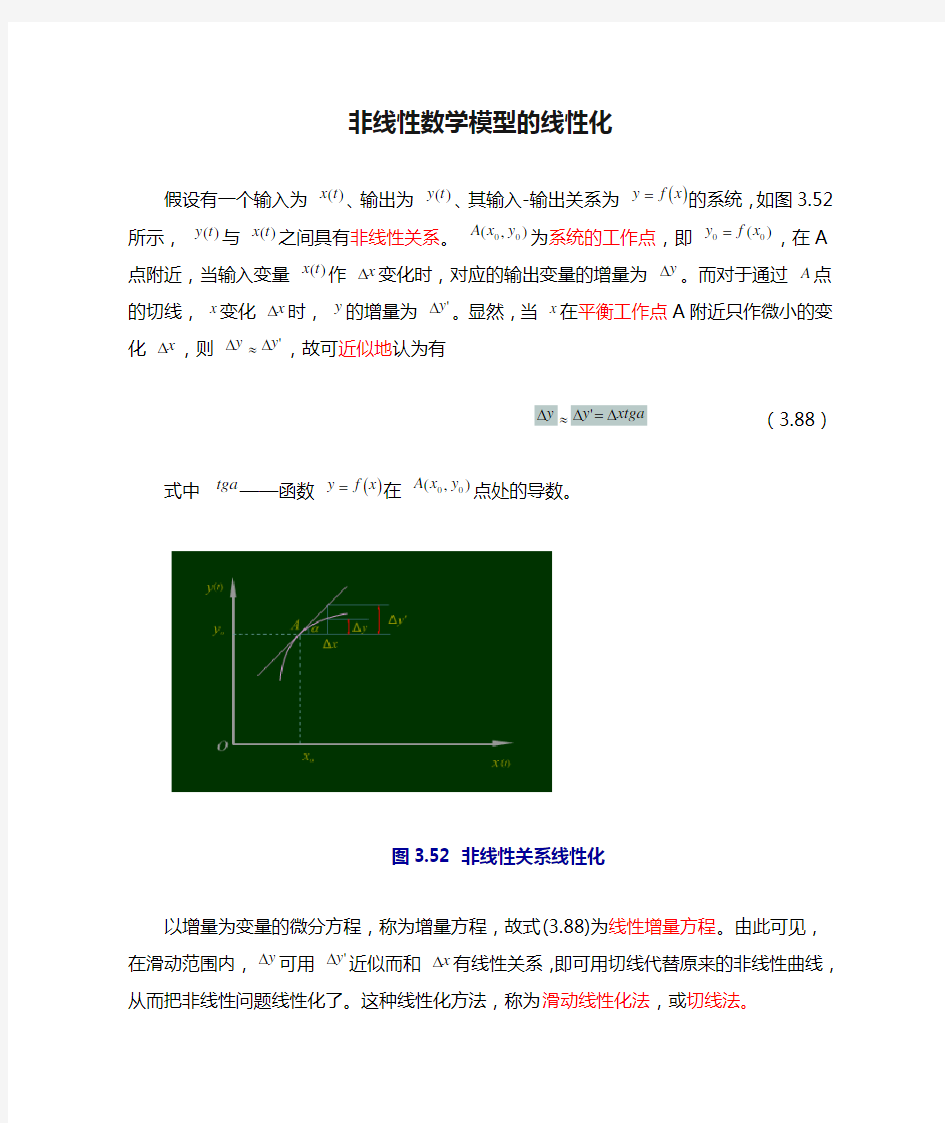
假设有一个输入为 )(t x 、输出为 )(t y 、其输入-输出关系为 ()x f y =的系统,如图3.52所示, )(t y 与 )(t x 之间具有非线性关系。 ),(00y x A 为系统的工作点,即 )(00x f y =,在A 点附近,当输入变量 )(t x 作 x ?变化时,对应的输出变量的增量为 y ?。而对于通过 A 点的切线, x 变化 x ?时, y 的增量为 'y ?。显然,当 x 在平衡工作点A 附近只作微小的变化 x ?,则 y ?≈'y ?,故可近似地认为有 y ?≈xtga y ?=?' (3.88)
式中 tga ——函数 ()x f y =在 ),(00y x A 点处的导数。
图3.52 非线性关系线性化
以增量为变量的微分方程,称为增量方程,故式(3.88)为线性增量方程。由此可见,在滑动范围内, y ?可用 'y ?近似而和 x ?有线性关系,即可用切线代替原来的非线性曲线,从而把非线性问题线性化了。这种线性化方法,称为滑动线性化法,或切线法。
滑动线性化的这种近似,对大多数控制系统来说都是可行的。首先,控制系统在通常情况下,都有一个正常的稳定的工作状态,称为平衡工作点。例如,恒温控制系统的正常工作状态是输入、输出为常值(输出为被控温度,输入为期望值)。其次,当系统的输入或输出相对于正常工作状态发生微小偏差时,系统会立即进行控制调节,力图去消除此偏差,因此可以看出,这种偏差是“小偏差”,不会很大。
滑动线性化这种近似,用数学方法来处理,就是将变量的非线性函数展开成泰勒级数,分解成这些变量在某工作状态附近的小增量的表达式,然后略去高于一次小增量的项,就获得近似的线性函数。
对于以一个自变量作为输入量的非线性函数 ()x f y =,在平衡工作点 ),(00y x 附近展开成泰勒级数,则有
()()()()()()()0002323000023d d d 11()d 2!d 3!d x x x x x x f x f x f x y f x f x x x x x x x x x x =====+-+-+-+
略去高于一次增量 0x x x -=?的项,便有
()()()000d d x x f x y f x x x x ==+- (3.89)
或
(3.90)
式中, )(00x f y =称为系统的静态方程; 0d ()d x x f x K x ==。
式(3.89)或式(3.90)就是非线性系统的线性化数学模型。式(3.90)为增量方程式。
若输出变量 y 与输入变量 1x 、 2x 有非线性关系,即 ),(21x x f y =,那么同样地将这个方程式在工作点 ),(2010x x 附近展开成泰勒级数,并忽略二阶和高阶导数项,便可得到 y 的线性化方程为
)()(),(202210112010202101202101x x x f x x x f
x x f y x x x x x x x x -??+-??+=====(3.91)
写成增量方程式,则有 22110x K x K y y y ?+?=?=- (3.92)
式中, ),(20100x x f y =为系统静态方程,
2021012021012211;x x x x x x x x x f K x f
K ====??=??=
数学模型课程设计一
课程设计名称: 设计一:MATLAB 软件入门 指导教师: 张莉 课程设计时数: 8 课程设计设备:安装了Matlab 、C ++软件的计算机 课程设计日期: 实验地点: 第五教学楼北902 课程设计目的: 1. 熟悉MA TLAB 软件的用户环境; 2. 了解MA TLAB 软件的一般目的命令; 3. 掌握MA TLAB 数组操作与运算函数; 4. 掌握MATLAB 软件的基本绘图命令; 4. 掌握MA TLAB 语言的几种循环、条件和开关选择结构。 课程设计准备: 1. 在开始本实验之前,请回顾相关内容; 2. 需要一台准备安装Windows XP Professional 操作系统和装有数学软件的计算机。 课程设计内容及要求 要求:设计过程必须包括问题的简要叙述、问题分析、实验程序及注释、实验数据及结果分析和实验结论几个主要部分。 1. 采用向量构造符得到向量[1,4,7,,31] 。 //a=[1:3:31] 2. 随机产生一向量x ,求向量x 的最大值。 // a=rand(1,6) max(a) 3. 利用列向量(1,2,3,,6)T 建立一个范德蒙矩阵A ,并利用位于矩阵A 的奇数行偶数列的元素建立一个新的矩阵B ,须保持这些元素的相对位置不变。 4. 按水平和竖直方向分别合并下述两个矩阵: 100234110,5670018910A B ????????==???????????? 5. 当100n =时,求1121n i y i ==-∑的值。 6. 一个三位整数各位数字的立方和等于该数本身则称该数为水仙花数。输出全部水仙花数。 7. 求[1000,2000]之间第一个被17整除的整数。 8. 用MATLAB 绘制两条曲线,[0,2]x π∈,以10 π为步长,一条是正弦曲线,一条是余弦曲线,线宽为6个象素,正弦曲线为绿色,余弦曲线为红色,线型分别为实线和虚线,并给所绘的两条曲线增添图例,分别为“正弦曲线”和“余弦曲线”。
常见非线性回归模型
常见非线性回归模型 1.简非线性模型简介 非线性回归模型在经济学研究中有着广泛的应用。有一些非线性回归模型可以通 过直接代换或间接代换转化为线性回归模型,但也有一些非线性回归模型却无 法通过代换转化为线性回归模型。 柯布—道格拉斯生产函数模型 y AKL 其中L和K分别是劳力投入和资金投入, y是产出。由于误差项是可加的, 从而也不能通过代换转化为线性回归模型。 对于联立方程模型,只要其中有一个方程是不能通过代换转化为线性,那么这个联立方程模型就是非线性的。 单方程非线性回归模型的一般形式为 y f(x1,x2, ,xk; 1, 2, , p) 2.可化为线性回归的曲线回归 在实际问题当中,有许多回归模型的被解释变量y与解释变量x之间的关系都不是线性的,其中一些回归模型通过对自变量或因变量的函数变换可以转化为
线性关系,利用线性回归求解未知参数,并作回归诊断。如下列模型。 (1)y 0 1e x (2)y 0 1x2x2p x p (3)y ae bx (4)y=alnx+b 对于(1)式,只需令x e x即可化为y对x是线性的形式y01x,需要指出的是,新引进的自变量只能依赖于原始变量,而不能与未知参数有关。 对于(2)式,可以令x1=x,x2=x2,?,x p=x p,于是得到y关于x1,x2,?, x p 的线性表达式y 0 1x12x2 pxp 对与(3)式,对等式两边同时去自然数对数,得lnylnabx ,令 y lny, 0 lna, 1 b,于是得到y关于x的一元线性回归模型: y 0 1x。 乘性误差项模型和加性误差项模型所得的结果有一定差异,其中乘性误差项模型认为yt本身是异方差的,而lnyt是等方差的。加性误差项模型认为yt是等 方差的。从统计性质看两者的差异,前者淡化了y t值大的项(近期数据)的作用, 强化了y t值小的项(早期数据)的作用,对早起数据拟合得效果较好,而后者则 对近期数据拟合得效果较好。 影响模型拟合效果的统计性质主要是异方差、自相关和共线性这三个方面。 异方差可以同构选择乘性误差项模型和加性误差项模型解决,必要时还可以使用 加权最小二乘。
优化设计数学建模
一、问题重述 1、利用优化设计相关理论计算法,对某设计问题做优化设计。要求如下: ①列出优化数学模型; ②选择所用优化算法; ③画出程序框图; ④程序编写; ⑤程序调试运算结果。 现根据以上条件,结合生活实际,准备以铁板为材料设计一鱼缸,为了能使鱼儿有更大的生存空间,要求鱼缸容积最大。 现有边长为5米长的方形铁板,预备在四个角减去四个相等的方形面积,用以制成方形鱼缸,如何减能使鱼缸的容积最大。 二、问题分析 2.1、对于此问题,我采用的数学模型包括三部分,即设计变量、目标函数和约束条件。 模型如下: 其中,设裁去铁块的边长为:x(0 四、程序编写及函数图像 4.1求极值所用程序如下: function q=line_s(a,b) N=10000;r=0.01; a=0;b=1.5; for k=1:N; v=a+0.382*(b-a); u=a+0.618*(b-a); fv=-25*v+20*v^2-4*v^3; fu=-25*u+20*u^2-4*u^3; if fv>fu if b-v<=r u fu break; else a=v;v=u; u=a+0.618*(b-a); end else if u-a<=r v -fv break; else b=u;u=v; v=a+0.382*(b-a); end k=k+1 end end 4.2 函数曲线图程序如下: 如下曲线所得y值为负,前面(1*)已作解释。 x=0:0.1:2.5; y=-25*x+20*x.^2-4*x.^3; plot(x,y); 五、程序调试运行结果 5.1 如图所示: 当k执行5或7或10或12次时,均有x=0.8329时,有最大y=9.2593(函数中已做处理,变负为正,可以对照曲线图)。 非线性数学模型的线性化 假设有一个输入为 )(t x 、输出为 )(t y 、其输入-输出关系为 ()x f y =的系统,如图3.52所示, )(t y 与 )(t x 之间具有非线性关系。 ),(00y x A 为系统的工作点,即 )(00x f y =,在A 点附近,当输入变量 )(t x 作 x ?变化时,对应的输出变量的增量为 y ?。而对于通过 A 点的切线, x 变化 x ?时, y 的增量为 'y ?。显然,当 x 在平衡工作点A 附近只作微小的变化 x ?,则 y ?≈'y ?,故可近似地认为有 y ?≈xtga y ?=?' (3.88) 式中 tga ——函数 ()x f y =在 ),(00y x A 点处的导数。 图3.52 非线性关系线性化 以增量为变量的微分方程,称为增量方程,故式(3.88)为线性增量方程。由此可见,在滑动范围内, y ?可用 'y ?近似而和 x ?有线性关系,即可用切线代替原来的非线性曲线,从而把非线性问题线性化了。这种线性化方法,称为滑动线性化法,或切线法。 滑动线性化的这种近似,对大多数控制系统来说都是可行的。首先,控制系统在通常情况下,都有一个正常的稳定的工作状态,称为平衡工作点。例如,恒温控制系统的正常工作状态是输入、输出为常值(输出为被控温度,输入为期望值)。其次,当系统的输入或输出相对于正常工作状态发生微小偏差时,系统会立即进行控制调节,力图去消除此偏差,因此可以看出,这种偏差是“小偏差”,不会很大。 滑动线性化这种近似,用数学方法来处理,就是将变量的非线性函数展开成泰勒级数,分解成这些变量在某工作状态附近的小增量的表达式,然后略去高于一次小增量的项,就获得近似的线性函数。 对于以一个自变量作为输入量的非线性函数 ()x f y =,在平衡工作点 ),(00y x 附近展开成泰勒级数,则有 ()()()()()()()0002323000023d d d 11()d 2!d 3!d x x x x x x f x f x f x y f x f x x x x x x x x x x =====+-+-+-+ 略去高于一次增量 0x x x -=?的项,便有 ()()()000d d x x f x y f x x x x ==+- (3.89) 或 (3.90) 式中, )(00x f y =称为系统的静态方程; 0d ()d x x f x K x ==。 式(3.89)或式(3.90)就是非线性系统的线性化数学模型。式(3.90)为增量方程式。 《数学建模》课程设计 报告 课题名称:___常染色体遗传模型 系(院):理学院 专业:数学与应用数学 班级: 学生姓名:巫荣 学号: 指导教师:陈宏宇 开课时间:2011-2012 学年二学期 常染色体遗传模型摘要 为了揭示生命的奥秘, 遗传特征的逐代传播, 愈来愈受到人们更多的注意。我们通过问题分析,模型的建立,去解决生物学的问题。为了去研究理想状态下常染色体遗传的情况,我们通过建立随机组合时常染色体的遗传模型,可以计算出各种情况随机出现的百分率,并且可以通过常染色体遗传模型,算出各个情况的概率分布,并且通过模型,分析情况出现的稳定性。揭示了常染色体遗传的分布规律,揭示了下一代各情形变化的规律性和稳定性。 关键词:遗传; 随机; 百分率; 概率分布; 稳定 一、问题重述 问题产生背景 常染色体遗传中,后代从每个亲体的基因对中各继承一个基因,形成自己的基因对,基因对也称为基因型。如果我们所考虑的遗传特征是由两个基因A和a控制的,那么就有三种基因对,记为AA, Aa,aa 。例如,金鱼草由两个遗传基因决定花的颜色,基因型是AA的金鱼草开红花,Aa 型的开粉红色花,而aa型的开白花。又如人类眼睛的颜色也是通过常染色体遗传控制的。基因型是AA或Aa 的人,眼睛为棕色,基因型是aa的人,眼睛为蓝色。这里因为AA和Aa 都表示了同一外部特征,我们认为基因A支配基因a,也可以认为基因a对于A来说是隐性的。当一个亲体的基因型为Aa ,而另一个亲体的基因型是aa时,那么后代可以从aa型中得到基因a,从Aa 型中或得到基因A,或得到基因a。这样,后代基因型为Aa或aa的可能性相等。下面给出双亲体基因型的所有可能的结合,以及其后代形成每种基因型的概率,如下表所示。 父体—母体的基因型 AA ??AA AA ??Aa AA ??aa Aa ??Aa Aa ??aa aa ??aa 后代AA 1 1/2 0 1/4 0 0 基因Aa 0 1/2 1 1/2 1/2 0 型aa 0 0 0 1/4 1/2 1 问题描述 题目:农场的植物园中某种植物的基因型为AA, Aa和aa。农场计划采用AA型的植物与每种基因型植物相结合的方案培育植物后代。那么经过若干年后,这种植物的任一代的三种基因型分布如何? 二、问题分析 在本问题中要知道每一代的基因分布,首先要知道上一代的基因型分布,在自由组合后的所有子代可能出现的基因型(上面已经给出)。为了求出每一代的基因型分布,第一步写出第一代的基因型分布;第二步推出第n+1代的基因型分布与第n代的基因型分布的关系;第三步利用差分方程求出每一代的每种基因型分布通项从而求得任一子代三种基因型的概率分布。 现该农场的植物园中某种植物的基因型为AA,Aa和aa.采用AA型基因的植物相结合培育后代,求若干年后这种植物的任一代的三种基因型分布,首先分析出初始里,AA,Aa,aa这三种基因型植物的大致分布,首先必须分析出初 2.非线性回归模型 教学目标 班级____姓名________ 1.进一步体会回归分析的基本思想. 2.通过非线性回归分析,判断几种不同模型的拟合程度. 教学过程 一、非线性回归模型. 非线性回归分析的步骤:(1)确定研究对象;(2)采集数据;(3)作散点图;(4)选取函数模型,并转化成线性回归模型,并转化数据;(5)求线性回归方程;(6)建线性回归模型,求残差,画残差图;(7)求2R ,刻画拟合效果. 二、例题分析. 例1:研究红铃虫产卵数与温度的关系. (例见教科书2P ) 1.确定研究对象:红铃虫产卵数与温度的关系. 2.采集数据: 3.作散点图: 4.选取函数模型,并转化成线性回归模型,并转化数据: (1)根据样本点的变化趋势,选取函 数模型:x c e c y 21=(指数函数模 型); (2)令y z ln =,将指数函数 模型转化成一次函数模型a bx z +=(1ln c a =,2c b =); (3)数据转化: (4)新散点图: 5.求线性回归方程: 温度C x ο/ 21 23 25 27 29 32 35 产卵数/y 个 7 11 21 24 66 115 325 21 23 25 27 29 32 35 1.946 2.398 3.045 3.178 4.190 4.745 5.784 运用公式求得272.0?=b ,849.3?=a ,线性回归方程为849.3272.0?-=x z , 而红铃虫的产卵数对温度的非线性回归方程为849.3272.0)1(?-=x e y . 6.建线性回归模型,求残差,画残差图; 残差849.3272.0)1() 1(??--=-=i x i i i i e y y y e 7.求2R ,刻画拟合效果. 注意事项: (1)根据样本点的变化趋势,选取函数模型时,可能的选择不止一个; (2)本例可选取二次函数模型423c x c y +=, (3)令2x t =,将二次函数模型转化成一次函数模型43c t c y +=; (4)不同模型拟合效果不同,可根据2R 来判断,2R 越大,拟合效果越好. 作业:为了研究某种细菌随时间x 变化时,繁殖个数y 的变化,收集数据如下: 天数x /天 1 2 3 4 5 6 繁殖个数y / 个 6 12 25 49 95 190 (1)用天数x 作解释变量,繁殖个数y 作预报变量,作出这些数据的散点图; (2)描述解释变量x 与预报变量y 之间的关系; (3)计算相关指数 2R . 数学模型课程设计 文档仅供参考,不当之处,请联系改正。 攀枝花学院 学生课程设计(论文) 题目:蔬菜的运输问题 学生姓名:孟蕾 学号: 1080 所在院(系):数学与计算机学院 专业:信息与计算科学 班级:级信本 指导教师:李思霖 6 月 29 日 攀枝花学院教务处制 攀枝花学院本科学生课程设计任务书 课程设计(论文)指导教师成绩评定表 摘要 本文针对蔬菜的运输问题进行分析,针对蔬菜运输时所需要注意的蔬菜供应量,需求量,运输距离,运输补贴,短缺补偿等约束性条件,运用lingo编程的方法解决如何进行蔬菜运输来分别使各类要求的支出最少的问题。 问题一中,要求如果不考虑短缺补偿,只考虑运费补贴最少,请为该市设计最优蔬菜运输方案。我们将供货商和销售点需求分别编号a和b,数量是从1~8和1~35。从题中能够看出其约束条件,所有销售点从第 A基地获得的蔬菜数量应该等于该基地所 i 生产的蔬菜数量;所有基地给 B销售点提供的蔬菜数量要大于等 j 于0,而且应该小于或等于该点的需求量。 问题二中,增添了对短缺补缺的考虑,规定各蔬菜销售点的短缺量一律不超过需求量的30%,在同时考虑短缺补偿和运费补贴的情况下再次设计最有蔬菜方案。由题意即是要求总费用,具体步骤仍同问题一,需要变化的分别是总费用w的表示式和关于销售点需求的约束条件。w变为原运输补贴的公式再加上每个销售点每吨短缺蔬菜的数量乘上各个销售点不同的短缺补偿,短缺数量需要用各个销售点的需求减去所有基地供给给这个的销售点的蔬菜数量之和。 问题三中,要求增加任意两个基地的生产数量,使得不存在短缺情况出现,然后视运费补贴最小的情况来确定哪两个基地分 EViews非线性模型参数估计方法步骤 1.新建EViews工作区,并将时间序列X、P1和P0导入到工作区; 2.设定参数的初始值全部为1,其方法是在工作区中其输入下列命令 并按回车键 param c(1) 1 c(2) 1 c(3) 1 c(4) 1 3.估计非线性模型参数,其方法是在工作区中其输入下列命令并按 回车键 nls q=exp(c(1))*x^c(2)*p1^c(3)*p0^c(4) 4.得到结果见table01(91页表3. 5.4结果)(案例一结束) Dependent Variable: Q Method: Least Squares Date: 03/29/15 Time: 21:44 Sample: 1985 2006 Included observations: 22 Convergence achieved after 9 iterations Q=EXP(C(1))*X^C(2)*P1^C(3)*P0^C(4) Coefficient Std. Error t-Statistic Prob. C(1) 5.567708 0.083537 66.64931 0.0000 C(2) 0.555715 0.029067 19.11874 0.0000 C(3) -0.190154 0.143823 -1.322146 0.2027 C(4) -0.394861 0.159291 -2.478866 0.0233 R-squared 0.983631 Mean dependent var 1830.000 Adjusted R-squared 0.980903 S.D. dependent var 365.1392 S.E. of regression 50.45954 Akaike info criterion 10.84319 Sum squared resid 45830.98 Schwarz criterion 11.04156 Log likelihood -115.2751 Hannan-Quinn criter. 10.88992 Durbin-Watson stat 0.672163 (92页表3.5.5结果)(案例二过程) 5.新建EViews工作区,并将时间序列X、P1和P0导入到工作区; 在手机普遍流行的今天,建设基站的问题分析对于运营商来说很有必要。本文针对现有的条件和题目的要求进行讨论。在建设此模型中,核心运用到了0-1整数规划模型,且运用lingo 软件求解。 对于问题一: 我们引入0-1变量,建立目标函数:覆盖人口最大数=所有被覆盖的社区人口之和,即max=15 1j j j p y =∑,根据题目要求建立约束条件,并用数学软件LINGO 对其模型求解,得到最优解。 对于问题二: 同样运用0-1整数规划模型,建立目标函数时,此处假设每个用户的正常资费相同,所以68%可以用减少人口来求最优值,故问题二的目标函数为:max=∑=15 1j j j k p 上述模型得到最优解结果如下: 关键字:基站; 0-1整数规划;lingo 软件 1 问题的重述.........................3 2 问题的分析.........................4 3 模型的假设与符号的说明...................5 3.1模型的假设...................... 5 3.2符号的说明...................... 5 4 模型的建立及求解...................... 5 4.1模型的建立...................... 5 4.2 模型的求解...................... 6 5 模型结果的分析.......................7 6 优化方向..........................7 7 参考文献..........................8 8、附录........................... 9 工业中截断切割的优化设计 一摘要 本文讨论了加工业中截断切割的优化排序策略我们对于不同的切割 方式总数用穷举法得到720 种所可行解及其费用并对于原问题建立了决策 并对所给出的算法进行了分析和检验 1.当e=0时我归纳出解决问题的最优法则, 从而提出了将面间距统一成判断权重来作为排 序准则的算法,同时证明 了e = 0 的情况下根据这种最优准则能够实现题目所要求的优化目标 2.对于e 1 0 时我们提出了实用准则 最后我结合实际问题将本问题进行了拓展讨论了当最终产品(成品) 在毛坯(待加工长方体)中位置不预定时应如何实施加工方案以达到节省费用 和节约资源的目的,使我们的方案适用于更为广阔的领域 二问题的重述、 在工业生产中,常需要采取将物理一分为二的截断切割方式从一块长方体材料中切出一个小长方体,其加工费用取决于水平切割和垂直切割的截面面积,以及调整刀具时的额外费用。对本题所给出的问题我们首先面临的对加工次序的排序策略然后我们考虑当毛坯和产品位置不预定的时候如何采取策略以达到我们的优化目的 问题: 1> 需考虑的不同切割方式的总数。 2> 给出上述问题的数学模型和求解方法。 3> 试对某部门用的如下准则做出评价,每次选择一个加工费用最少的切割面进行切割。 4> 对于e=0 的情况有无简明的优化准则。 5> 用以下实例验证你的方法: 待加工长方体和成品长方体的长,宽,高分别为10,14.5,19 和3,2,4,两者左侧面,正面,底面之间的距离分别为6,7,5(单位为厘米,垂直切割费用为每平方厘米1 元,r 和e 的数据有 4 组: 1) r=1,e=0; 2) r=1.5,e=0; 3) r=8,e=0; 4) r=1.5, 2 £ e £15 ; 三模型的假设和符号说明 1 切割刀具为两个一个水平放置一个为垂直放置 2 目标长方体所在位置不与毛坯任一表面重合 3 水平方向只需平行移动水平刀具垂直方向只平行移动或调整后再平行 移动刀具因此调整费用e 是否付出仅取决于先后两次垂直切割是否平行而 不记是否穿插着水平切割 4毛坯与工作台接触的底面是事先指定的 营销生产策略的制定 姓名:xxxxxxx 时间:xxxxxxx 问题描述: 现有企业(甲)想在杭州市场上推销某种新产品A,请你用所学知识,根 据下设情形,分别为企业(甲)制定一个合理的营销生产策略。 1、假定杭州市场上还没有出现过产品A或类似的产品; 2、假定杭州市场上有类似的产品,且市场占有率已达到15%; 3、假定杭州市场上还没有产品A或类似的产品,但新产品A有一个服从均值为5(年)的寿命分布。 摘要: 在数学建模中,产品营销问题是一类常见的典型问题。对于产品的销售情况 一般都用Logistic模型去描述,所以本实验都用了Logistic销售模型的建模思路。Logistic回归模型,主要是用来对多因素影响的事件进行概率预测,它是普通多元线性回归模型的进一步扩展,Logistic模型是非线性模型。对于题中的三种假定,结合微分方程基本理论对在杭州市场上推销的新产品A进行研究,并为企业(甲)制定一个合理的营销生产策略。 问题1:设定新产品A价格、质量以及销售人员的销售情况等其他影响新产品销售的外在因素是相对稳定,杭州市场对产品的需求量有限,产品的销售速度与销售量和剩余需求量的积成正比三个假设,建立了Logistic销售模型并求解。得出结论,在销售量达到最大销售量的一半时,产品最为畅销。 问题2:设定类似产品A的销售速度与销售量和剩余需求量的积成正比,新产品A的需求量、类似产品的需求量、剩余需求量之和为总需求量,在假定一和假定二下,不考虑新产品A的使用寿命三个假设,不考虑消费者同时拥有新产品A 和其类似产品,建立了微分方程组销售模型并求解。得出结论,问题2中的微分方程组的驻定解不稳定。 问题3:设定了新产品A服从均值为5(年)的指数寿命分布,其的报废量与新产品A的销售量成正比,新产品A报废后,人们仍愿意进行购买三个假设,参照Logistic销售模型,建立了微分方程销售模型并求解。给出了最大需求量A及销售速度的曲线。 问题分析与解题思路 在杭州市场还没有出现过A产品或类似产品的条件下,A产品刚刚进入市场,人们对A产品不熟悉,A产品的销售速度较慢,但在逐渐的增加,人们对A产品的熟悉度增加,此时A产品的销售速度逐渐增快,当产品销售到一定数量时,人们就会停滞购买,A的销售速度减慢。 在杭州市场上有类似的产品,且市场占有率已达到15%的条件下,不考虑消费者同时拥有新产品A和其类似产品的情况,认为类似产品的市场占有率会影响新产品A的销售,且类似产品的销售模型与新产品A的销售模型相同。 在杭州市场上还没有出现过产品A或类似的产品时,考虑新产品A的寿命是有限的,即新产品A有一个服从均值为5(年)的寿命分布,新产品A的报废会使市场上的剩余销售量增加,所以,有理由认为新产品的销售速度不仅受销售量,剩余量的影响,还受到新产品A的寿命的影响。 -32- 第三章 非线性规划 §1 非线性规划 1.1 非线性规划的实例与定义 如果目标函数或约束条件中包含非线性函数,就称这种规划问题为非线性规划问题。一般说来,解非线性规划要比解线性规划问题困难得多。而且,也不象线性规划有单纯形法这一通用方法,非线性规划目前还没有适于各种问题的一般算法,各个方法都有自己特定的适用范围。 下面通过实例归纳出非线性规划数学模型的一般形式,介绍有关非线性规划的基本概念。 例1 (投资决策问题)某企业有n 个项目可供选择投资,并且至少要对其中一个项目投资。已知该企业拥有总资金A 元,投资于第),,1(n i i L =个项目需花资金i a 元,并预计可收益i b 元。试选择最佳投资方案。 解 设投资决策变量为 ?? ?=个项目 决定不投资第,个项目 决定投资第i i x i 0,1,n i ,,1L =, 则投资总额为 ∑=n i i i x a 1,投资总收益为 ∑=n i i i x b 1 。因为该公司至少要对一个项目投资,并 且总的投资金额不能超过总资金A ,故有限制条件 ∑=≤< n i i i A x a 1 另外,由于),,1(n i x i L =只取值0或1,所以还有 .,,1,0)1(n i x x i i L ==? 最佳投资方案应是投资额最小而总收益最大的方案,所以这个最佳投资决策问题归结为总资金以及决策变量(取0或1)的限制条件下,极大化总收益和总投资之比。因此,其数学模型为: ∑∑=== n i i i n i i i x a x b Q 11max s.t. ∑=≤< n i i i A x a 1 .,,1,0)1(n i x x i i L ==? 上面例题是在一组等式或不等式的约束下,求一个函数的最大值(或最小值)问题,其中至少有一个非线性函数,这类问题称之为非线性规划问题。可概括为一般形式 )(min x f q j x h j ,,1, 0)(s.t. L =≤ (NP) p i x g i ,,1, 0)(L == 案例16 停车场的优化设计 随着城市车辆的增加,停车位的需求量也越来越大,停车困难已逐渐成为市民们头疼的问题。要解决停车难问题,除了尽可能的增加停车场以外,对停车场进行优化设计也能在一定程度上缓解这一供需矛盾。停车场的优化设计就是在停车场大小确定的情况下,对停车区域进行优化设计,以便容纳更多的车辆。本文的目的就是希望分析一下这一情况,找出缓解停车困难的有效办法。 假设某公共场所附近有一块空地,如果不考虑建设地下或多层结构,我们该如何有效的设计停车位置呢?一般来说,想尽可能的把车塞进停车场,最好的办法就是以垂直停靠的方式将车一辆挤一辆地排成行,但是这样停放的后果就是车辆不能自由出入,只有后进入的车辆全部先出去了,先进入的车才可以离开停车场,显然不符合实际的需求。因而,为了使汽车能够自由地出入停车场,必须设立一定数量具有足够宽度的通道,并且每个通道都应该有足够大的“转弯半径”, 而通道越宽越多,就会使得容纳的车辆数越少。所以我们的问题就是要确定在满足车辆能够自由进出的实际需求下,如何进行停车位置和车行通道的设计,才能够停放更多的车辆,从而做到既方便停车又能获得最大的经济效益。 我们先来看看生活中非货运车辆大小的种类。根据实际调查和经验数据,这类车辆一般可分为小轿车,中型客车和大型客车三类。其中小轿车约占九成,大型客车约占一成,而中型客车一般不多于1%。根据这样的情况,我们可以免去对中型客车的车位设计,即便有中型客车停车的需要,可以使用大型车的车位,这也符合现实生活中绝大多数停车场的车位设计情况。我们设小轿车所占的比例为0.9α=,大型客车所占的比例为10.1α-=,当然现实中也有不少全为小轿车设计的停车场,例如小区的地下车库。 再来看看车位的大小。根据实际的调查,城市内比较普通的小轿车长度一般不超过4.7米,宽度一般不超过1.7米,而一般大型客车长度不超过12米,宽度不超过2.2米。另外,经实际考察可知,停车场中标志线的宽度大约为0.1米,所以我们可以假设停车场中停放轿车需要的车位长5L C =米,宽 2.5W C =米,这其中包括了0.1米的标志线宽度和至少0.3米的汽车间的横向间距。设停放大客车需要长12.5L B =米,宽3W B =米,其中包括0.1米的标志线宽度和必要的汽 数学建模课程设计 题目:最佳捕鱼方案 第九组:组员一组员二组员三 姓名:崔健萍王晓琳吴晓潇 学号: 021340712 021341009 021341014 专业:数学与应用数学数学与应用数学数学与应用数学成绩: 湖北民族学院理学院 二零一五年五月三十一日 最佳捕鱼方案问题 摘要 捕鱼方案问题在实际生活中应用广泛,如何捕鱼投放市场效益最佳这是一个一直需要讨论的问题。 本文通过建立一个数学模型的方式把捕鱼方案问题这种实际问题转化为数学模型的方式进行解答。 在本文中,首先我们对于这个问题进行了分析假设,排除了一些实际生活中不可避免但是我们又无法预计的实际情况,然后对本题进行了分析,选择了最合适的建模方式。在已知鱼的总量、水位、水位随时间的变化关系、鱼损失的变化率随水位的变化关系、捕鱼成本随水位的变化关系及不同供应量时鱼的价格的情况如下,要求下面几个问题: 问题一:建立草鱼的销售收益随供应量变化的函数关系,主要是考虑当随捕鱼量取不同值时,鱼的价格,然后再把其联系在一块,做出其函数关系。 问题二:建立草鱼的捕捞成本随时间变化的函数关系,由于是自然放水,所以水的深度和时间是一个一次函数的关系,但水的深度降低时,捕捞成本越来越低,并且降低的速度越来越快。经过一系列的模型建立与求解最终得出捕捞成本随时间的函数关系。 问题三:当水位下降时捕鱼的损失率会越来越大,并且其损失率会加速增大,据查询的可靠资料,最后得出水位和损失率的关系跟反函数图像最接近,最后就采用以水位为自变量,损失率为因变量建立模型,最终得出其函数模型,然后再联系水位与时间的关系,最终可以得出草鱼的损失率与时间变化的函数关系。问题四:为取得最大的总经济效益,保证在放水的过程中,每一天都达到了最大的经济效益,其中要考虑到捕鱼成本随水深的变化和损失率随水深的变化,同时水深又是随时间的变化,建立相应的目标规划模型。 关键词:0-1变量规划问题多目标 LINGO 攀枝花学院学生课程设计(论文) 题目: 学生姓名:学号: 所在院(系):数学与计算机学院 专业:信息与计算科学 班级: 指导教师:职称:讲师 2014年 12月 19 日 攀枝花学院教务处制 攀枝花学院本科学生课程设计任务书 年 注:任务书由指导教师填写。 摘要 按照人们的职位或职位划分为许多等级,如大学教师分为教授,讲师,助教,工厂技术员分为高级工程师,工程师,技术员,学生有大学生,研究生,中学生等。不同等级人员比例不一样的等级结构。合适的,稳定的等级结构有利于教学,研究,生产等各个方面工作顺利进行,因此希望建立一个模型来描述等级结构变化情况,预知未来的结构。 引起等级结构变化的因素有两个,一是系统中等级间转移,即是升级或降级。二是系统外的交流,即是调入或退出。系统变化本是一个确定转移问题,但是当我们的人员时期按照一定比例成员提升,降级或退出,就转化为马氏链模型等级描述变化。 关键词等级结构、预知,变化,转移,马氏链 目录 摘要 (4) 1问题重述与问题分析 (5) 问题重述 (5) 问题分析: (6) 2模型假设与符号解释 (6) 模型假设 (6) 符号说明 (6) 3建立模型与分析 (9) 建立模型 (9) 模型1 (9) ..................................... 错误!未定义书签。 模型二 (10) 用调入比例进行动态调节 (10) 4模型结果 (12) 模型解释 (12) 结束语 (12) 参考文献 (12) 1问题重述与问题分析 问题重述 随着经济全球化的发展,推动生活节奏的加快,社会上常常要求按照人们的职位或职位划分为许多等级,如大学教师分为教授,讲师,助教,工厂技术员分为高级工程师,工程师,技术员,学生有大学生,研究生,中学生等。不同等级人员比例不一样的等级结构。合适的,稳定的等级结构有利于教学,研究,生产等各个方面工作顺利进行,因此希望建立一个模型来描述等级结构变化情况,预知未来的结构. 社会系统中的等级结构,适当的、稳定的结构的意义,描述等级结构的演变过程,预测未来的结构,确定为达到某个理想结构应采取相应 第2章 优化设计的数学模型及基本要素 Chapter 2 Mathematical Modeling for Optimization 2-1 数学模型的建立 (mathematical modeling) 建立数学模型,就是把实际问题按照一定的格式转换成数学表达式的过程。数学模型建立的合适、正确与否,直接影响到优化设计的最终结果。 建立数学模型,通常是根据设计要求,应用相关基础和专业知识,建立若干个相应的数学表达式。如机械结构的优化设计,主要是根据力学、机械设计基础等专业基础知识及机械设备等专业知识来建立数学模型的。 当然,要建立能够反映客观实际的、比较准确的数学模型并非容易之事。数学模型建的过于复杂,涉及的因素太多,数学求解时可能会遇到困难;而建的太简单,又不接近实际情况,解出来也无多大意义。因此,建立数学模型的原则:抓主要矛盾,尽量使问题合理简化。Principle :The problem is simplified as much as possible. 由于设计对象千变万化,即使对同一个问题,由于看问题的角度不同,数学模型建的可能也不一样。建立数学模型不可能遵循一个不变的规则,本课也不准备把大量的时间花在数学模型的建立上。仅想以几个例子来演示一下数学模型的建立过程,使学生从中得到一些启发。 Exp. 2-1 例2-1 用宽度为cm 24,长度cm 100的薄 铁皮做成cm 100长的梯形槽,确定折边的尺寸 x 和折角θ(如图 2-1所示) ,使槽的容积最大。 解: 由于槽的长度就是板的长度,槽的梯形 截面积最大就意味着其容积最大。因此,该问题 就由,求体积最大变成求截面积最大。槽的梯形 截面积为: 图 2-1 ?= 2 1S 高 ?(上底边+下底边) 其中,上底边=x 224-;下底边=θcos 2224x x +-;高=θsin x 定义:该优化设计问题的目标函数是槽的梯形截面积S ,设计变量为θ,x 。问题可以简单地归结为:选择适当的设计变量θ,x ,在一定的限制条件下,使目标函数S 达到最大,限制条件为: 120,20<<< 重庆交通大学学生实验报告 实验课程名称数学模型课程设计 开课实验室数学实验室 学院XXX级XXX 专业 1 班 开课时间2013 至2014 学年第 2 学期设计题目大学生就业问题 2013 年12月 大学生就业问题 摘要:近年来,我国高校毕业生数量逐年增多,加之当前金融危机的影响,毕业生的就业形势受到前 所未有的挑战,甚至出现了所谓“毕业即失业”的说法。因此大学生毕业后能否顺利就业,已成为全社会普遍关注的热点问题。大学生就业难不仅有社会原因,也有大学生自身的原因。如何解决大学生就业难的问题不仅关系到大学生的切身利益,更关系到社会的与谐稳定,需要政府、企业、高校与大学生共同的努力。本文从大学生自身,企业与社会三个大方面方面进行了分析与论述,从而总结出相关的结论及解决大学生就业难题的可行方法。 关键词大学生就业 Matlab 数据拟合 一、问题重述 据中国媒体援引人力与社会保障部的最新统计数据,二零一零年全国高校毕业生为630万人,比去年的611万多19万人,加上往届未能就业的,需要就业的毕业生数量很大,高校毕业生就业形势十分严峻。 随着九十年代末大学扩招与教育产业化政策推行以来,大学生人数的增幅远远超过经济增长所需要的人才增长,大学生就业不难才就是怪事,"毕业即失业"成为中国大学生的普遍现象。 尽管如此,中国教育部决定继续扩大全日制专业学位硕士研究生招生规模,努力培养更多高层次、应用型人才。表面上瞧,研究生扩招能提高大学生学历层次,可以缓解就业难。但就是,如果不清理高等教育积弊,扩招研究生来应对就业难将就是饮鸩止渴,使就业矛盾更加突出。 现在大学生就业难的问题,就是由许多原因造成的,既有社会原因,也有历史原因。 请用数学建模的方法从以下几个侧面探讨大学生就业问题: (1)利用网上大学生就业统计数据建立大学生就业供需预测模型,利用所建模型对2012年就业形势进行预测; (2)分析影响大学生就业的主要因素,建立就业竞争力评价模型,利用所建模型评估您的竞争力; (3)利用定量分析的结果,给相关政府部门提出增加就业的建议以及您个人提高就业竞争力的打算。 二、基本假设与符号说明 基本假设: 1、假设政府在近几年内没有出台什么对大学生就业影响很大的政策与措施。 2、假设高校毕业生就业人数的变化率与社会的劳动力需求呈正相关。 3、假设高校毕业生就业人数的变化率与毕业生的综合素质呈正相关。 4、假设部分毕业生的自身主观原因影响了自身的就业。 5、假设相应的网络数据为真实的就业情况。 6、假设影响大学生就业的因素没有很大的变化。 7、国家经济的发展对大学生的需求在一定时期就是稳定的。 浅谈非线性回归模型的线性化 广东省惠州市惠阳区崇雅中学高中部 卢瑞勤(516213) 回归分析在各个领域中都有十分重要的作用,比如:在财务中可以用回归分析进行财务预测;在医疗检验中可以用回归分析进行病理预报等等。高中新课标教材就在《必修3》和《选修2-3》中分别增加了《线性回归》和《回归分析》的内容,介绍了求线性回归方程的方法。但在实际问题中,变量间的关系并非总是线性关系,本文结合本人的教学实践,对教材中的这两部分内容进行适当延伸,谈谈对一些可线性化的非线性回归模型的线性化问题,供各位同行在教学时参考。 一、什么是可线性化的非线性回归模型 线性回归模型的基本特征是预报变量可以表示成解释变量和一个系数相乘的和,即预报变量y 可以表示成解释变量i x (i =1,2,3,……)的如下形式:0112233y a a x a x a x =++++ ,其中变量i x 是以其原型(而不是以n i x 或其它)的形式出现,变量y 是各变量i x 的线性函数。而有些回归模型不具备这个特点,但是可以通过适当的代数变换转化成这种形式,我们称这类回归模型为可线性化的回归模型。 在本文中,我们只讨论只有一个解释变量可线性化的非线性回归模型的线性化。 二、非线性回归模型的线性化的基本思路 非线性回归模线性化的基本思路是:由已知数据,确定解释变量和预报变量,作出散点图,根据经验,确定回归曲线的类型,然后作适当的代数变换,若变换后散点图体现较好的线性关系,即可将其化成线性形式求解,最后还原到原来的回归曲线。如果回归曲线可用多种形式表示,可以各自将其线性化后求解,再用相关系数2 R 进行拟合效果分析,2 R 越大,拟合效果越好,所求的回归方程也就越精确。 三、非线性回归模型的线性化的常用方法 可线性化的非线性回归模型有以下几种常见类型: (1)双曲线型,其形式为 1a b y x =+,其变换为1y y '=, 1 x x '=,变换后的形式为y b ax ''=+ (2)幂函数型,其形式为b y ax = ,可以变形为ln ln ln y a b x =+,作变换ln y y '= ,ln x x '= ,变换后的形式为y a bx ''=+ (3)指数函数型,其形式为bx y ae = ,以变形为ln ln y a bx =+,作变换ln y y '=,ln a a '= ,变换后的形式为y a bx ''=+ (4)对数函数型,其形式为ln y a b x =+,作变换ln x x '=,变换后的形式为y a bx '=+ 下面以高中新课标数学教材《选修2-3》一道习题为例加以说明 【例】在某地区的一段时间内观察到的不小于某震级x 的地震个数y 数据如下表,试建立回归方程表述二者之间的关系。 摘要 汽车刹车距离 1.问题提出 司机在驾驶过程中遇到突发事件会紧急刹车,从司机决定刹车到车完全停住,汽车行驶的距离称为刹车距离,车速越快,刹车距离越长,请问刹车距离与车速之间具有怎样的数量关系? 2.问题分析 问题要求建立刹车距离与车速之间的数量关系,一方面车速是刹车距离的主要影响因素,车速越快,刹车距离越长;另一方面,还有很多其他的因素会影响刹车距离,包括车型、车重、刹车系统的机0械状况、轮胎类型的状况、路面类型的状况、天气的状况、驾驶员的操作技术和身体状况等。若果所有可能的因素都考虑到,就无法建立车速与刹车距离之间的数量关系,所以需要对问题提出合理的简化假设,使得问题可以仅仅考虑车速对刹车距离的影响,从而建立刹车距离与车速之间的函数关系。 需要提出哪几条合理的简化假设? 可以假设车型、轮胎类型、路面条件都相同;假设汽车没有超载;假设刹车系统的机械状况、轮胎状况、天气状况以及驾驶员状况都良好;假设汽车在平直道路上行驶,驾驶员紧急刹车,一脚把刹车踏板踩到底,汽车在刹车过程没有转方向。 这些假设都是为了使得问题可以仅仅考虑车速对刹车距离的影响,这些假设是初步的和粗糙的,在下面的建立数学模型的过程中,还可能随着问题的深入理解而提出新的假设,或者修改原有的假设。至于假设的合理性,一方面可以根据题意和常识来判断,另一方面,还可以等模型建立和求解完毕以后,对其进行检验分析, 首先,仔细分析刹车的过程,发现刹车决定经历两个阶段。 在第一阶段,司机意识到危险,做出刹车决定,并踩下刹车踏板使刹车系统开始起作用,这一瞬间可以称为“反应时间”,非常短暂,但是对于高速行驶的汽车而言,汽车在这一瞬间行驶的距离却不容忽略,汽车在反应时间行驶的距离称为“反应距离”。 在第二阶段,从刹车踏板被踩下、刹车系统开始起作用,到汽车完全停住,这是汽车的制动过程,汽车在制动过程“行驶”(轮胎滑动摩擦地面)的距离为“制动距离”。 根据以上分析,得到刹车距离的初步的数量关系如下: 刹车距离=反应距离+制动距离(1.1) 引入以下符号,并说明单位: v车速(m/s); ~ d刹车距离(m); ~ d反应距离(m); ~ 1 ~ k反应时间(s); 1 ~ d制动距离(m); 2非线性数学模型的线性化
《数学建模》课程设计报告--常染色体遗传模型
高中数学 选修 非线性回归模型
数学模型课程设计
非线性模型参数估计方法步骤
数学建模课程设计——优化问题
数学建模截断切割的优化设计
数学建模课程设计
数学建模-非线性规划
数学建模案例_停车场的优化设计(1)
数学建模课程设计论文
数学模型等级结构
优化设计的数学模型及基本要素
大学生就业问题数学模型
浅谈非线性回归模型的线性化
数学建模课设
