微积分 经管类 第四版 吴赣昌 习题全解 第六章定积分的应用
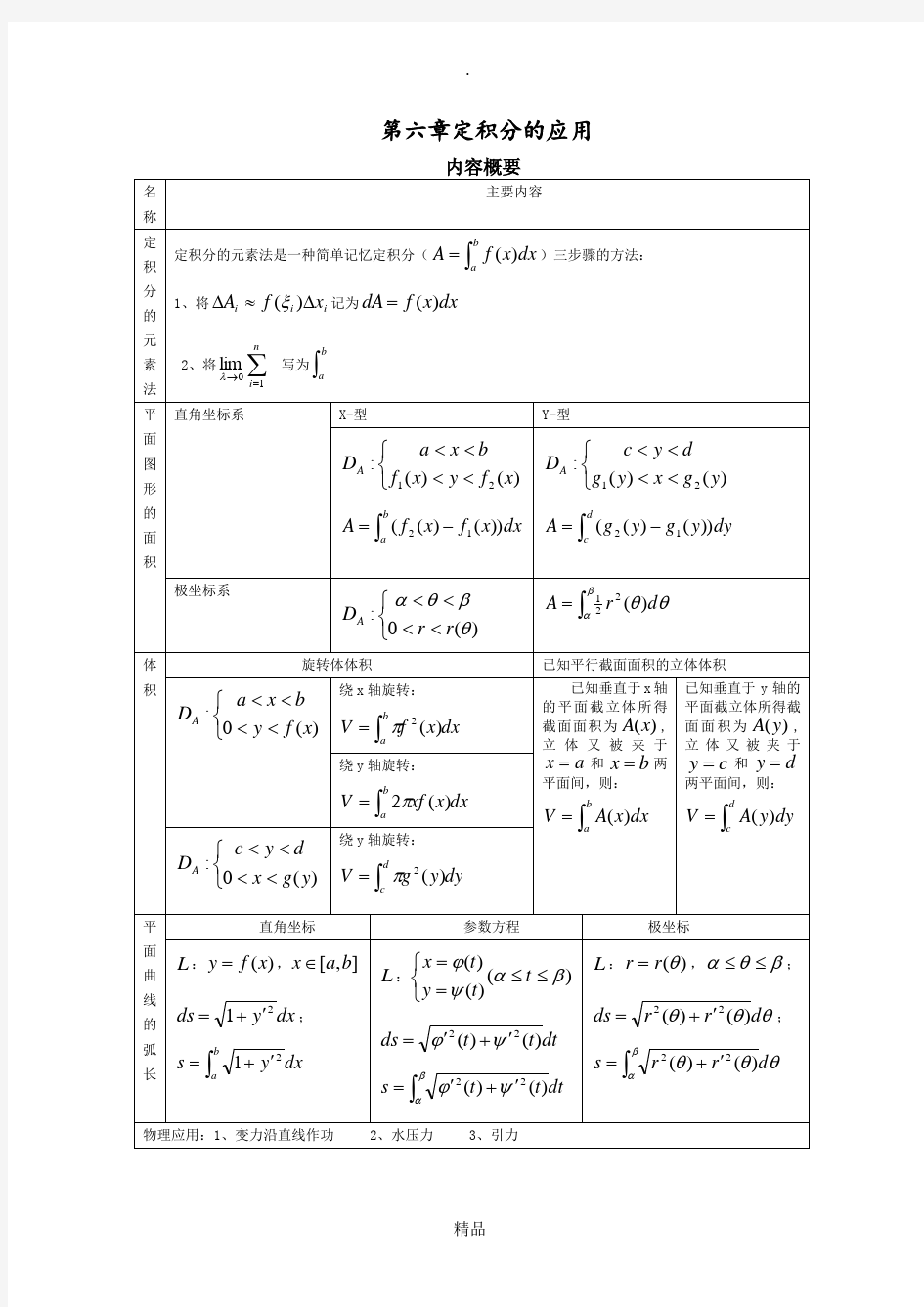

第六章定积分的应用
课后习题全解
习题6-2
★ 1.求由曲线
x
y =与直线
x y =所围图形的面积。
知识点:平面图形的面积
思路:由于所围图形无论表达为X-型还是Y-型,解法都较简单,所以选其一做即可 解: 见图6-2-1
∵所围区域D 表达为X-型:???<<< ??<<< 0) ∴?-=1 0)(dx x x S D 61 )2132(1 22 3 =-=x x (?= -=1 26 1 )(dy y y S D ) ★ 2.求在区间[0, π/2]上,曲线x y sin =与直线0=x 、1=y 所围图形的面积 知识点:平面图形面积 思路:由于所围图形无论表达为X-型还是Y-型,解法都较简单,所以选其一做即可 解:见图6-2-2 ∵所围区域D 表达为X-型:?????<<< <1 sin 2 0y x x π, (或D 表达为Y-型:???<<< )cos ()sin 1(202 -= +=-=?π π π x x dx x S D ( 12 arcsin 1 -= =?π ydy S D ) ★★3.求由曲线 x y =2与42+-=x y 所围图形的面积 知识点:平面图形面积 思路:由于所围图形表达为Y-型时解法较简单,所以用Y-型做 解:见图6-2-3 ∵两条曲线的交点:???±==?? ??+-==22 42 2y x x y x y , ∴所围区域D 表达为Y-型:?? ?-<<<<-2 2 422y x y y , ∴23 16 )32 4()4(2 2 32 22 2 = -=--=- - ? y y dy y y S D (由于图形关于X 轴对称,所以也可以解为: 2316 )324(2)4(22 32 22=-=--=? y y dy y y S D ) ★★4.求由曲线 2x y =、24x y =、及直线1=y 所围图形的面积 知识点:平面图形面积 思路:所围图形关于Y 轴对称,而且在第一象限内的图形表达为Y-型时,解法较简单 解:见图6-2-4 ∵第一象限所围区域1D 表达为Y-型:?? ?<<< x y y 21 0, ∴3 43 22)2(2210 231 1= ? =-==?y dy y y S S D D (若用X-型做,则第一象限内所围区域=1D b a D D ,其中a D :?????<<<<22 4 10x y x x , b D :?????<<<<14 212y x x ;∴122122 01422[()(1]443D D x x S S x dx dx ==-+-=??) ★★5.求由曲线x y 1 =与直线x y =及2=x 所围图形的面积 知识点:平面图形面积 思路:由于所围图形表达为X-型,解法较简单,所以用X-型做 解:见图6-2-5 ∵两条曲线 x y = 和x y =的交点为(1,1)、(-1,-1),又这两条线和2=x 分别交于 )2 1 ,2(、2) ,2( ∴所围区域D 表达为X-型:?????<<< x 1 21, ∴2 2 21 1 113 ((ln )ln 222D S x dx x x x =-=-=-? ★★★6.抛物线 x y 22=分圆822=+y x 的面积为两部分,求这两部分的面积 知识点:平面图形面积 思路:所围图形关于X 轴对称,而且在第一象限内的图形表达为Y-型时,解法较简单 解:见图6-2-6,设阴影部分的面积为1D S ,剩余面积为2D S ∵两条曲线 x y 22=、822=+y x 的交于(2,2)±(舍去4-=x 的解), ∴所围区域1D 表达为Y-型:?????-<<<<-2 2 82 22y x y y ;又图形关于x 轴对称, ∴342)342(2)68(2)28(22 03202 2 0221 +=-+=--=--=??ππy y dy y y S D (其中 22 2cos 18cos 22cos 2284 4 sin 222 2 +=+=?= -? ?? =πππ dt t tdt t dy y t y ) ∴3 4634282 -=- -=πππD S ★★★7.求由曲线 x e y =、x e y -=与直线1=x 所围图形的面积 知识点:平面图形面积 思路:由于所围图形表达为X-型时,解法较简单,所以用X-型做 解:见图6-2-7 ∵两条曲线 x e y =和x e y -=的交点为(0,1),又这两条线和1=x 分别交于 ) ,1(e 和) ,1(1 -e ∴所围区域D 表达为X-型:?? ?<<<<-x x e y e x 10, ∴2)()(110 1 -+=+=-=---?e e e e dx e e S x x x x D ★★★8.求由曲线 x y ln =与直线a y ln =及b y ln =所围图形的面积)0(>>a b 知识点:平面图形面积 思路:由于所围图形表达为Y-型时,解法较简单,所以用Y-型做 解:见图6-2-8 ∵在x ln 的定义域范围内所围区域D :? ??<<< e x b y a 0ln ln , ∴a b e dy e S b a y b a y D -===?ln ln ln ln ★★★★9.求通过(0,0),(1,2)的抛物线,要求它具有以下性质:(1)它的对称轴平行于y 轴,且 向下弯;(2)它与x轴所围图形面积最小 知识点:平面图形面积和求最值 思路:首先根据给出的条件建立含参变量的抛物线方程,再求最值时的参变量 解:由于抛物线的对称轴平行于y 轴,又过(0,0),所以可设抛物线方程为bx ax y +=2 ,(由于下 弯,所以0 ),将(1,2)代入bx ax y +=2,得到2=+b a ,因此x a ax y )2(2-+= 该抛物线和X 轴的交点为0=x 和a a x 2 -= , ∴所围区域D :2200(2)a x a y ax a x -? < ??<<+-? ∴2 32 2 32 2 6)2() 223(])2([a a x a x a dx x a ax S a a a a D -= -+=-+=--? )4()2(6 1)]2()2()2(3[61)(233322+-=-?-+-?=' ---a a a a a a a a S D 得到唯一极值点:4-=a , ∴所求抛物线为: x x y 642+-= ★★★★10.求位于曲线 x e y =下方,该曲线过原点的切线的左方以及x 轴上方之间的图形的面积 知识点:切线方程和平面图形面积 思路:先求切线方程,再作出所求区域图形,然后根据图形特点,选择积分区域表达类型 解:x e y =?x e y =',∴在任一点0x x =处的切线方程为)(000 x x e e y x x -=- 而过(0,0)的切线方程就为:)1(-=-x e e y ,即ex y = 所求图形区域为21D D D =,见图6-2-10 X-型下的1D :?? ?<<<<∞-x e y x 00,2D :???<<< e y ex x 1 ∴2 22 )(1 211 e e e x e e dx ex e dx e S x x x D =- =-=-+=∞ -∞ -?? ★★★11.求由曲线θcos 2a r =所围图形的面积 知识点:平面图形面积 思路:作图可知该曲线是半径为a 、圆心(0 ,a )的圆在极坐标系下的表达式,可直接求得面积为2 a π, 也可选择极坐标求面积的方法做。 解:∵作图6-1-11 知所求图形区域D :?????<<<<-θ πθπcos 2022a r ∴222 22 2 2) 2sin 2121(2)cos 2(21a a d a S D πθθθθπ ππ π=+==--? ★★★12.求三叶玫瑰线θ3sin a r =的面积S 知识点:平面图形面积 思路: 三叶玫瑰由三瓣面积相等的叶片组成 图6-2-12中所画是三叶玫瑰中的一叶, 而一叶图形又关于6 πθ = 对称, 因此选择其中一叶的一半区域1D 求其面积 解:∵1D :????? <<< <θ πθ3cos 06 0a r 图6-2-13 )cos 2(2θ+=a r r a 6 a 4 a 3 图6-2-14 θ ae r = r a 2 /πae π ae π-ae D ∴260 26 241 )6sin 6121(3)3cos (21661 a a d a S S D D πθθθθπ π =+===? ★★★13.求由曲线)cos 2(2θ+=a r 所围图形的面积 知识点:平面图形面积 思路:作图可知该曲线围成的图形关于极轴对称,因此选择其中一半区域1D 求其面积 解:∵1D :? ?? +<<<<)cos 2(200θπθa r ∴ 12220 1411 22[2(2cos3)]4[4(sin 3sin 6)1823212D D S S a d a a π π θθπθθθπ==+=+++=? ★★★14.求对数螺线 θρae =)(πθπ≤≤-及射线πθ=所围图形的面积 知识点:平面图形面积 思路:作图可知该曲线围成的图形是由θ ρae =,θ从π-到π一段曲线及射线πθ=所围,由此可 确定θ、ρ的范围 解:∵所围区域D :?? ?<<<<-θ ρπ θπae ∴)(4 2 12)(2122222 2ππ π π θπ π θθ----=?==? e e a e a d ae S D ★★★★15.求由曲线θcos 3=r 及θcos 1+=r 所围图形的面积 知识点:平面图形面积 思路:作图可知两条闭围线围成的图形由三部分组成,其中一部分为两图形重叠部分D ,而D 又关于极 轴对称,设θ在(0, 2 π )内的曲线和极轴围成的半个D 为1D 区域 解:两条曲线θcos 3=r 、θcos 1+=r 交于3 π θ± =处, 因此分割区域b a D D D +=1,其中a D :?????+<<<<θπθcos 1030r ,b D :?????<<< <θ πθπcos 302 3r 1223203320 3 11 22[(1cos )(3cos )] 2 2 319115 2[(2sin sin 2)(sin 2)]23422644D D S S d d π π ππππθθθθππθθθπ ==++=?+++?+=?? ★★★16.求由曲线θsin 2=r 及θ2cos 2=r 所围图形的面积 知识点:平面图形面积 思路:作图可知两条闭围线围成的图形由三部分 组成,其中一部分为两图形重叠部分D ,而D 又关于射线2 π θ= 对称,设两条曲线 在(0, 2 π )围成的半个D 为 1D 区域 解:两条曲线θsin 2= r 、θ2cos 2=r 交于6 π θ= 及6 5πθ= 因此分割区域b a D D D +=1,其中a D :?????<<<<θπθsin 2060r ,b D :??? ??<<<<θ πθπ 2cos 02 6r 2 3 6)2sin 412sin 4 1 621(2]2cos 21 )sin 2(21[2226 60 26 6 21- =+-?=+==??πθθ πθθθθπππ π ππ d d S S D D (和书后答案不同) ★★★17.求由摆线 )sin (t t a x -=,)cos 1(t a y -=)20(π≤≤t 及x 轴所围图形的面积 知识点:平面图形面积 思路:在直角坐标系下作图可知所围图形的 x 、y 变化范围,先求出直角坐标系下积分表达式,再将积分变量代换成t 解:∵所围区域D :? ? ?<<<<)(020x y y a x π, ( )(x y y =为摆线) ∴20 ()a D S y x dx π=? , 作代换)sin (t t a x -=, 则22202220322 3 )cos 1(])sin ([)cos 1(a a dt t a t t a d t a S D πππ π =?=-=--=?? 习题6-3 1. 求下列平面图形分别绕x 轴、y 轴旋转产生的立体体积: ★(1).曲线 x y =与直线1=x 、4=x 、0=y 所围成的图形; 知识点:旋转体体积 思路:作出平面图形(或求出该平面区域的x 、y 范围), 代入相应的公式。 解:平面图形D :?? ?≤≤≤≤x y x 04 1,见图6-3-1-1 绕x 轴旋转产生的立体体积: ππ2 15)(24 1= =?dx x V ; 绕y 轴旋转产生的立体体积:ππ5 124 241 = =?dx x x V (和书上答案不同) ★★(2).在区间2 ,0[π 上,曲线x y sin =与直线2 π= x 、 0=y 所围成的图形; 解:平面图形D :?????≤≤≤ ≤x y x sin 020π,见图6-3-1-2, 绕x 轴旋转产生的立体体积: 22204 1 )(sin πππ ==?dx x V ; 绕y 轴旋转产生的立体体积: 方法一:?? -== 20 2 cos )(2sin 2π π ππx d x dx x x V π ππ π2)sin cos (22020 =+-=x x x 方法二:V 可看作由1D (矩形2 0π≤ ≤x ,10≤≤y )绕 y 轴旋转而成的体积1V ,减去由2 D (10≤≤ y ,y x arcsin 0≤≤)绕y 轴旋转而成的立体体积2V 所得 ∴π ππ π2)(arcsin )2 (1 022=-=?dy y V ★(3).曲线 3x y =与直线2=x 、0=y 所围成的图形。 解:平面图形D :?? ?≤≤≤≤3020x y x ,绕x 轴旋转产生的立体体积: ππ7128)(202 3==?dx x V ; 绕y 轴旋转产生的立体体积:ππ5 64 22 3= =?dx xx V (绕y 轴旋转产生的立体体积如同(2)也有两种计算法) ★★2.求由曲线 2x y =、2y x =所围成的图形绕y 轴旋转一周所产生的旋转体体积。 知识点:旋转体体积 思路:该平面图形绕y 轴旋转而成体积V 可看作1D :? ? ?≤≤≤≤y x y 01 0绕y 轴旋转而成的体积1V ,减去 2D :? ??≤≤≤≤2 01 0y x y 绕y 轴旋转而成的立体体积2V 所得,见图6-3-2 解: πππ10 3)()(1 2 22 1 21= -= -=??dy y dy y V V V ★★3.求由曲线 x y sin =(π ≤≤x 0)与x 轴围成的平面图形绕y 轴旋转一周所产生的旋转体体积。 知识点:旋转体体积 思路:作出平面图形(或求出该平面区域的x 、y 范围),代入相应的公式 解:平面图形D :?? ?≤≤≤≤x y x sin 00π,绕y 轴旋转产生的立体体积: 2 2sin 2πππ==?dx x x V (绕y 轴旋转产生的立体体积如同1(2)也有两种计算法) ★★★4.求由曲线 a x ach y =,0=x ,a x =,0=y (0>a )所围成的图形绕x 轴旋转而成的立体体积。 知识点:旋转体体积 思路:作出平面图形(或求出该平面区域的x 、y 范 围),代入相应的公式 解:平面图形D :?? ???≤≤≤≤a x ach y a x 00,见图6-3-4, 绕x 轴旋转产生的立体体积: )22(4 )224(21 2(3020220sh a a a x sh a a dx a x ch a dx a x ch a V a a a +=+=+==??ππππ ★★★5.求摆线 )sin (t t a x -=,)cos 1(t a y -=的一拱与0=y 所围图形绕直线a y 2=轴旋转而 成的旋转体体积。 知识点:旋转体体积 思路:若设所围区域为D ,则该平面图形绕a y 2=旋转而成体积V 可看作矩形区域1D :?? ?≤≤≤≤a y x 2020π 绕 a y 2=旋转而成的体积1V ,减去区域2D :02()2x y x y a π ≤≤?? ≤≤? 绕a y 2=旋转而成的立体体积2V 所得,(其中,()y x 表示摆线的函数式,见图6-3-5 解:? -- ?=-=a dx y a a a V V V ππππ20 22 21)2(2)2(,作代换)sin (t t a x -=,则 2232222320 8(cos )(sin )8sin (1cos )V a a a t ad t t a a t t dt π πππππ=-+-=--?? =22223 223 01cos 28(sin sin )72 t a a dt td t a π ππππ---=? ? ★★★★6.求 222a y x ≤+绕b x -=(0>>a b )旋转而成的旋转体体积。 知识点:旋转体体积 思路:由图形的对称性可知所求体积12V V =,其中1V 是由2 2 2 a y x ≤+(0≥y )部分,绕b x -=旋转而成的旋转体体积,又根据元素法,1V 是由图形中的线段y (2 20x a y -≤≤)绕b x -=旋 转一周所得的圆柱面叠加而成,见图6-3-6 解:12V V =b a dx x a b dx x a b x a a a a 22222224)(22 πππ=-=-+=? ? -- ★★★★7.由心形线 )cos 1(4θρ+=和射线0=θ及2 π θ= 所围图形绕极轴旋转而成的旋转体体积。 知识点:旋转体体积 思路:极坐标中的此平面图形绕极轴旋转相当于直角坐标系下的该图形绕x 轴旋转 解:平面区域D :04(1cos ) ρθ≤≤+(2 0πθ≤ ≤),见图6-3-7 ∵心形线)cos 1(4θρ +=的直角坐标表示: ?? ?+=+=θ θθθsin )cos 1(4cos )cos 1(4y x (80≤≤x ),根据直角坐标下的体积计算及222 x y ρ+=,得: ???-=-==8 03 8 02 8 02 2 2 3 8)(ππρρππdx dx x dx y V 微积分(经管类复习题)2011.5 一、选择题 1. 二元函数) 3ln(1),(2 2 y x y x f --= 的定义域为( ) .A 222<+y x .B 222≤+y x .C 322<+y x .D 322≤+y x 2. 点),(00y x 使0),(='y x f x 且0),(=' y x f y 成立,则( ) .A ),(00y x 是),(y x f 的极值点 .B ),(00y x 是),(y x f 的最小值点 .C ),(00y x 是),(y x f 的最大值点 .D ),(00y x 可能是),(y x f 的极值点 3. 级数 ∑∞ =1 n n aq 收敛的充分条件是( ) .A 1>q .B 1=q .C 1 一、教学目标:1. 理解定积分的基本概念并能利用定积分的几何意义解决一些简单的积分计算问题. 2. 理解微积分的基本定理,并会用定积分公式解决简单函数的定积分问题. 二、知识要点分析 1. 定积分的概念:函数)(x f 在区间[a ,b ]上的定积分表示为:?b a dx x f )( 2. 定积分的几何意义: (1)当函数f (x )在区间[a ,b]上恒为正时,定积分?b a dx x f )(的几何意义是:y=f (x )与x=a ,x= b 及x 轴围成的曲边梯形面积,在一般情形下.?b a dx x f )(的几何意义是介于x 轴、函数f (x )的图象、以及直线x=a ,x= b 之间的各部分的面积代数和,在x 轴上方的面积取正号,x 轴下方的面积取负号. 在图(1)中:0s dx )x (f b a >=?,在图(2)中:0s dx )x (f b a <=?,在图(3)中:dx )x (f b a ?表示 函数y=f (x )图象及直线x=a ,x=b 、x 轴围成的面积的代数和. 注:函数y=f (x )图象与x 轴及直线x=a ,x=b 围成的面积不一定等于?b a dx x f )(,仅当在区间[a ,b]上f (x )恒正时,其面积才等于?b a dx x f )(. 3. 定积分的性质,(设函数f (x ),g (x )在区间[a ,b ]上可积) (1)???±=±b a b a b a dx )x (g dx )x (f dx )]x (g )x (f [ (2)??=b a b a dx x f k dx x kf )()(,(k 为常数) (3)???+=b c b a c a dx x f dx x f dx x f )()()( (4)若在区间[a , b ]上,?≥≥b a dx x f x f 0)(,0)(则 推论:(1)若在区间[a ,b ]上,??≤≤b a b a dx x g dx x f x g x f )()(),()(则 (2)??≤b a b a dx x f dx x f |)(||)(| (3)若f (x )是偶函数,则??=-a a a dx x f dx x f 0)(2)(,若f (x )是奇函数,则0)(=?-a a dx x f 4. 微积分基本定理: 一般地,若)()()(],[)(),()('a F b F dx x f b a x f x f x F b a -==?上可积,则在且 注:(1)若)()('x f x F =则F (x )叫函数f (x )在区间[a ,b ]上的一个原函数,根据 定积分与微积分基本定理练习题及答案 1.(2011·宁夏银川一中月考)求曲线y =x2与y =x 所围成图形的面积,其中正确的是( ) A .S =??01(x2-x)dx B .S =??01(x -x2)dx C .S =??01(y2-y)dy D .S =??01(y -y)dy [答案] B [分析] 根据定积分的几何意义,确定积分上、下限和被积函数. [解读] 两函数图象的交点坐标是(0,0),(1,1),故积分上限是1,下限是0,由于在[0,1]上,x≥x2,故函数y =x2与y =x 所围成图形的面积S =??0 1(x -x2)dx. 2.(2010·山东日照模考)a =??02xdx ,b =??02exdx ,c =??02sinxdx ,则a 、b 、c 的大小关系 是( ) A .a 一. 单项选择题(共45分,每题3分) 请务必将选择题答案填入下面的答题卡 1. 数列{}n x 有界就是数列{}n x 收敛的( ) A 、 充分条件 B 、 充要条件 C 、 必要条件 D 、 非充分又非必要 条件 2.设极限0(1)(12)(13)a lim 6x x x x x →++++=,则a =( ) A 、 1 B 、 2 C 、 3 D 、 -1 3.当1x →时,函数 1 2111 x x e x ---的极限就是( ) A 、 2 B 、 不存在也不就是∞ C 、 ∞ D 、 0 4.如果函数()y f x =在点0x x =处取得极大值,则( ) A 、 0()0f x '= B 、 0()0f x ''< C 、 0()0f x '=且0()0f x ''< D 、 0()0f x '=或0()f x '不存在 5.若两曲线2 y x ax b =++与3 21y xy =-+在点(1,1)-处相切,则,a b 的值为( ) A 、 0,2a b ==- B 、 1,3a b ==- C 、 3,1a b =-= D 、 1,1a b =-=- 6.某商品的价格P 与需求量Q 的关系为100.01P Q =-,则4P =时的边际收益为( ) A 、 300 B 、 200 C 、 100 D 、 0 7.设函数()f x 可导,且0 lim ()1x f x →'=,则(0)f ( ) A 、 就是()f x 的极大值 B 、 就是()f x 的极小值 C 、 不就是()f x 的极值 D 、 不一定就是()f x 的极值 8.设()f x 就是连续函数,则下列计算正确的就是( ) A 、 11 221 ()2()f x dx f x dx -=? ? B 、 131 ()0f x dx -=? 《高等数学》经管类期末考试 ————————————————————————————————作者:————————————————————————————————日期: 一、 填空题(本大题共5题,每题2分,共10分。请直接将正确结果填 入各题的空格处) 1. 函数221y x z --=的定义域 ; 2. 由方程z e xz yz xy =+-所确定的隐函数),(y x z z =在点()1,1处的全微分11==y x dz = ; 3. 变换二重积分 ??==b a x a I dy y x f dx I 的积分次序后),( ; 4. 将函数()2cos x x f =展开成x 的幂级数为 ; 5. 微分方程0='-''y y 的通解是 。 二、 选择题(本大题共5题,每题2分,共10分。每小题有四个选项, 其中有且只有一个选项正确,请将正确选项的代号字母填入括号内) 6. 在空间解析几何中方程422=+y x 表示( )。 A .圆 B .平面 C .圆柱面 D .球 面 7. 设函数22y x z =,则=??22x z ( )。 A. 22y B. xy 4 C. y 4 D. 0 8. 设(){}01,01,≤≤-≤≤-=y x y x D ,则??D dxdy 等于( ) 。 A .-1 B .1 C .2 D .-2 9. 级数∑ ∞=121n n ( )。 A. 发散 B.收敛,其和为2 C.收敛,其和为1 D.收敛,其和为3 10. 下列方程中,( )是二阶线性齐次微分方程。 A .y y dx y d ='+22 B .y x y '+=''2)( C .y y x y '+=''2 D . x y y y +'=''2)( 三、 计算题(本大题共9题,每题7分,共63分。解答须有主要解题步 骤,说明必要的理由) 11. 设),(v u f z =,y x u 2 =,y x v =,求y z x z ????,。 12. 求函数 122++=y x z 在条件03=-+y x 下的极值。 13. ??D xyd σ,其中D 是由抛物线 x y =2及直线2-=x y 所围成的 闭区域。 14. 计算??D dxdy y 2,其中D 为:4122≤+≤y x 。(要求画草图。提示:在极 坐标下计算) 15. 计算由y x z ++=1,1=+y x ,0=x ,0=y 及0=z 所围成 立体的体积(第一卦限). 16. 判断级数∑∞ =1 2sin n n n α的敛散性; 17. 求幂级数n n x n ∑∞=11的收敛区间与和函数。 高中数学~~定积分和微积分基本原理 1、求曲线、直线、坐标轴围成的图形面积 ? [ 高三数学] ? 题型:单选题 由曲线y =x ,直线y =x -2及y 轴所围成的图形的面积为( ) A. 310 B. 4 C. 3 16 D. 6 问题症结:大概知道解题方向了,但没有解出来,请老师分析 考查知识点: ? 定积分在几何中的应用 ? 用微积分基本定理求定积分值 难度:难 解析过程: 联立方程组,2 ???-==x y x y 得到两曲线的交点坐标为(4,2), 因此曲线y =x ,直线y =x -2及y 轴所围成的图形的面积为: 3 16)]2([4 = --? dx x x . 答案:C 规律方法: 首先求出曲线y=和直线y=x-2的交点,确定出积分区间和被积函数,然后利用导数和积分的关 系求解. 利用定积分知识求解该区域面积是解题的关键. 高二数学问题 ? [ 高一数学] ? 题型:简答题 曲线y=sinx (0≤x ≤π)与直线y=?围成的封闭图形面积是? 问题症结:找不到突破口,请老师帮我理一下思路 考查知识点: ? 用定义求定积分值 难度:中 解析过程: 规律方法: 利用定积分的知识求解。 知识点:定积分和微积分基本原理 概述 所属知识点: [导数及其应用] 包含次级知识点: 定积分的概念、定积分的性质、用定义求定积分值、用微积分基本定理求定积分值、用几何意义求定积分的值、定积分在几何中的应用、定积分在物理中的应用、微积分基本原理的含义、微积分基本原理的应用 知识点总结 本节主要包括定积分的概念、定积分的性质、用定义求定积分值、用微积分基本定理求定积分值、用几何意义求定积分的值、定积分在几何中的应用、定积分在物理中的应用、微积分基本原理的含义、微积分基本原理的应用等知识点。对于定积分和微积分基本原理的理解和掌握一定要通过数形结合理解,不能死记硬背。只有理解了定积分的概念,才能理解定积分的几何意义。 高等数学经管类-CAL-FENGHAI-(2020YEAR-YICAI)_JINGBIAN 一. 单项选择题(共45分,每题3分) 请务必将选择题答案填入下面的答题卡 1. 数列{}n x 有界是数列{}n x 收敛的( ) A. 充分条件 B. 充要条件 C. 必要条件 D. 非充分 又非必要条件 2.设极限0(1)(12)(13)a lim 6x x x x x →++++=,则a =( ) A. 1 B. 2 C. 3 D. -1 3.当1x →时,函数 1 2111 x x e x ---的极限是( ) A. 2 B. 不存在也不是∞ C. ∞ D. 0 4.如果函数()y f x =在点0x x =处取得极大值,则( ) A. 0()0f x '= B. 0()0f x ''< C. 0()0f x '=且0()0f x ''< D. 0()0f x '=或0()f x '不存在 5.若两曲线2y x ax b =++与321y xy =-+在点(1,1)-处相切,则,a b 的值为( ) A. 0,2a b ==- B. 1,3a b ==- C. 3,1a b =-= D. 1,1a b =-=- 6.某商品的价格P 和需求量Q 的关系为100.01P Q =-,则4P =时的边际收益为( ) A. 300 B. 200 C. 100 D. 7.设函数()f x 可导,且0 lim ()1x f x →'=,则(0)f ( ) A. 是()f x 的极大值 B. 是()f x 的极小值 C. 不是()f x 的极值 D. 不一定是()f x 的极值 8.设()f x 是连续函数,则下列计算正确的是( ) A. 1 1 221 ()2()f x dx f x dx -=?? B. 1 31 ()0f x dx -=? C. 0+∞-∞ =? D. 11 221 0()2()f x dx f x dx -=? ? 9.设2sin ()sin x t x F x e tdt π+=? ,则()F x ( ) A. 为正常数 B. 为负常数 C. 恒为零 D. 不为常数 10.设直线1158 :121x y z L --+== -,20:23 x y L y z -=??+=?,则12,L L 的夹角为( ) A. 6 π B. 4π C. 3 π D. 2 π 11.设()f x,y 在点()a,b 处偏导数存在,则极限()() n f a x,b f a x,b lim x →+∞ +--= ( ) A. ()x f a,b B. ()2x f a,b C. ()2x f a,b D. ()1 2 x f a,b 12.设函数()f x 连续,则22 0()dt x d tf x t dx -=?( ) A. ()2xf x B. ()2xf x - C. ()22xf x D. ()22xf x - 13.设二次积分2sin 0 d (cos ,sin )d I f r r r r π θθθθ=??,则I 可写成( ) A. 2 2d (,)d x f x y y -? B. 2 20 d (,)d y f x y x -? C. 2 0d (,)d x f x y y ? D. 2 d (,)d y f x y x ? 14.点(0,0)是函数z xy =的( ) A. 极大值点 B. 极小值点 C. 驻点 D. 非驻点 2020年全国高考数学 第15讲 定积分和微积分基本定理 考纲解读 1.了解定积分的实际背景、基本思想及概念. 2.了解微积分基本定理的含义. 命题趋势探究 定积分的考查以计算为主,其应用主要是求一个曲边梯形的面积,题型主要为选择题和填空题. 知识点精讲 基本概念 1.定积分的极念 一般地,设函效()f x 在区间[a ,b]上连续.用分点0121i i a x x x x x -=<<<< 定积分与微积分基本定理习题 一、选择题 1. a =??02x d x ,b =??02e x d x ,c =??0 2sin x d x ,则a 、b 、c 的大小关系是( ) A .a 《有机化学》考试大纲 (201409修改) 一、考试目的 有机化学是一门研究有机物的组成、结构、性质、合成以及与此相关的理论、规律的科学。通过考试,使同学们系统地掌握有机化学的基本概念、基本理论,熟练掌握有机化合物分子结构与性质之间的关系,有机化合物的合成及相互转化的方法和规律,具有基本科学的思维方法和理论联系实际独立分析问题解决问题的能力。 二、考试内容 第一章绪论 1.1有机化合物和有机化学 有机化合物的定义 1.2 有机化合物的特征 1.3 分子结构和结构式 短线式、缩简式、键线式 1.4 共价键 1.4.1 共价键的形成 Lewis 结构式、价键理论、轨道杂化(sp、sp2、sp3 杂化) 1.4.2 共价键的属性 键长、键能、键角、键的极性、诱导效应 1.4.3 共价键的断裂和有机反应的类型 均裂(产生自由基)、异裂(形成正、负离子)、自由基反应、离子型反应 1.5 分子间的相互作用力 偶极-偶极相互作用、范德华力、氢键 1.6 酸碱的概念 1.6.1 Br? nsted 酸碱理论 Br? nsted 酸、Br? nsted 碱、共轭酸碱 1.6.2 Lewis 酸碱理论 Lewis 酸、Lewis 碱 1.7 有机化合物的分类 1.7.1 按碳架分类 脂肪族化合物、脂环族化合物、杂环化合物 1.7.2 按官能团分类 官能团 第二章饱和烃:烷烃和环烷烃 烃、脂肪烃、脂环烃、饱和烃 2.1烷烃和环烷烃的通式和构造异构 烷烃:CnH2n+2 环烷烃:CnH2n 构造异构体 2.2 烷烃和环烷烃的命名 伯、仲、叔、季碳原子;伯、仲、叔氢原子;烷基、环烷基烷烃的命名、单环环烃的命名 2.3烷烃和环烷烃的结构 2.3.1 σ键的形成及其特征 2.3.2 环烷烃的结构与环的稳定性 角张力 2.5 烷烃和环烷烃的物理性质 2.6 烷烃和环烷烃的化学性质 2.6.1 自由基取代反应 卤化反应、自由基的稳定性次序、卤素的活性次序 2.6.2 氧化反应 2.6.5 小环环烷烃的加成反应 加氢、加溴、加溴化氢 第三章不饱和烃: 烯烃和炔烃 3.1烯烃和炔烃的结构 碳碳双键的组成、碳碳叁键的组成、π键的特性 3.2烯烃和炔烃的同分异构 第三节定积分和微积分基本定理 考纲解读 1?了解定积分的实际背景、基本思想及概念 ? 2?了解微积分基本定理的含义 . 命题趋势探究 定积分的考查以计算为主, 其应用主要是求一个曲边梯形的面积, 题型主要为选择题和填空 题? 知识点精讲 一、基本概念 1.定积分的极念 一般地,设函效 f (x )在区间[a , b ]上连续.用分点a = x 0 < x 2< L < x — < x b - a < L < X n 二b 将区间[a,b ]等分成n 个小区间,每个小区间长度为 D x ( D x = ), n n 在每个小区间[X i -^X i ]上任取一点\ i =1,2J||,n ,作和式:S^v f(i)C x =: i 二 n b _a f ( i ),当D x 无限接近于0 (亦即n —; ? ?)时,上述和式S n 无限趋近于常数 S , i i n b 那么称该常数S 为函数f (x)在区间[a,b ]上的定积分?记为: S 二 f (x)dx , f (x)为 * a 被积函数,X 为积分变量, 需要注意以下几点: [a, b ]为积分区间,b 为积分上限,a 为积分下限. b (1) 定积分 f(x)dx 是一个常数,即S n 无限趋近的常数S (n 时),称为 a b f (x)dx ,而不是 S n . a (2) 用定义求定积分的一般方法 . b n ? b -^a a f(x)dx 二[imj f i -" a - i n b t 2 b (3)曲边图形面积:S = f x dx ;变速运动路程s 二 v(t)dt ;变力做功S = F(x) dx 2 ?定积分的几何意义 b 从几何上看,如果在区间[a ,b ]上函数f (x )连续且恒有f(x)_0,那么定积分a f x dx 表 示由直线 X =a,x =b(a =b), y =0和曲线y = f (x )所围成的曲边梯形(如图3-13中的阴影 ①分割:n 等分区间[a ,b ];②近似代替:取点 n b — a i ?〔x 」,X i 丨;③求和:、? 口 f(i ); ◎ n ④取极限: 考点13 定积分与微积分基本定理 一、定积分 1.曲边梯形的面积 (1)曲边梯形:由直线x =a 、x =b (a ≠b )、y =0和曲线()y f x =所围成的图形称为曲边梯形(如图①). (2)求曲边梯形面积的方法与步骤: ①分割:把区间[a ,b ]分成许多小区间,进而把曲边梯形拆分为一些小曲边梯形(如图②); ②近似代替:对每个小曲边梯形“以值代曲”,即用矩形的面积近似代替小曲边梯形的面积,得到每个小曲边梯形面积的近似值(如图②); ③求和:把以近似代替得到的每个小曲边梯形面积的近似值求和; ④取极限:当小曲边梯形的个数趋向无穷时,各小曲边梯形的面积之和趋向一个定值,即为曲边梯形的面积. 2.求变速直线运动的路程 3.定积分的定义和相关概念 (1)如果函数f (x )在区间[a ,b ]上连续,用分点a =x 0 ()d b a f x x ? =1 lim ()n i n i b a f n ξ→∞ =-∑ . (2)在 ()d b a f x x ? 中,a 与b 分别叫做积分下限与积分上限,区间[a ,b ]叫做积分区间,函数()f x 叫做被 积函数,x 叫做积分变量,f (x )d x 叫做被积式. 4.定积分的性质 (1)()()d d b b a a kf x x k f x x =??(k 为常数); (2)[()()]d ()d ()d b b b a a a f x g x x f x x g x x ±=±? ??; (3) ()d =()d +()d b c b a a c f x x f x x f x x ? ??(其中a 经管类《微积分》(上)习题参考答案 第一章 函数、极限与连续 习题一 一、1.否; 2.是; 3.是; 4.否. 二、1.)[()5,33,2?; 2.()πππ+k k 2,2;3. 2,24>-<<-x x 或; 4.[]a a -1,;。5.[]2,0; 6.222+-x x . 三、1.奇函数;2.奇函数. 3.(略) 四、1(略);2.2 12+x ; 3.11 -+x x . 五、1.x v v u u y sin ,,ln 2===;2.x x u e y u ln ,==;3.1525++?x x . 六、50 500,,)50(8.050)(>≤=<-=x x x x x f 为()x f 的跳跃间断点。 物流班高数复习重点 题型:选择题3'X 5=15 填空3'X 5=15 解答题 ? X8 =60 应用10'X1=10 #1、P15判断二元函数在某点处的极限例5 例6 2、P20偏导数的计算例5 P27 1(1)(5) 3、P29 7.4.2可微于连续、偏导数存在之间的关系两个定理 P51 5 ,6 # 4、P35 多元复合求偏导例4 P31 全微分计算例3 例4 #5 P44 求二元函数的极值例4 #6 P49 拉格朗日乘数发求各种极值问题例9 P50 6 , 7 7、P60交换积分次序例2 例3 #8、P61 直角坐标下的二重积分例4 Y型积分区域 #9、P65求坐标系下二重积分计算例1 10、P73常见的级数敛散性1)等比级数2)调和收敛3)P级数 11、P73常数项级数性质1——3 P75级数收敛必要条件 12、P82比值判断法1、(5) 13、任意项级数、绝对收敛、条件收敛、例3 P86 1、(1) 14、P90求幂级数的收敛性例2 #15、P92求幂级数的和函数例4 P92 2、(1) =1+x+x2+……+x n(|x|<1) 16、P98 将f(x) 展开成幂级数4个e x sin x1 1?x ln(1+x) 17、P111可分变量的微分方程例1----例4 18、P115齐次方程求解例7 19、P120 一阶线性方程例1 例2 #20、P125可降阶的高阶微分方程类型II(不含y)例3 例4 #21、P132 表10—1 例7、例8、例9 P134 2、指数函数情形f(x)=A e ax 这时二阶常系数线性非齐次方程为y′′+p y′+qy=A e ax微积分(经管类复习题)
高中数学高考总复习定积分与微积分基本定理习题及详解
定积分与微积分基本定理练习题及答案
高等数学经管类
《高等数学》经管类期末考试
高中数学~定积分和微积分基本原理
高等数学经管类
2020年全国高考数学·第15讲 定积分和微积分基本定理
高中数学高考总复习定积分与微积分基本定理习题及详解教学内容
微积分经管类考试大纲
定积分和微积分基本定理
专题13 定积分与微积分基本定理知识点
经管类微积分(上)参考答案
高等数学经管类(下)复习重点
(完整版)高中数学高考总复习定积分与微积分基本定理习题及详解()
