数学建模模拟赛题

数学建模模拟赛题

吊车问题

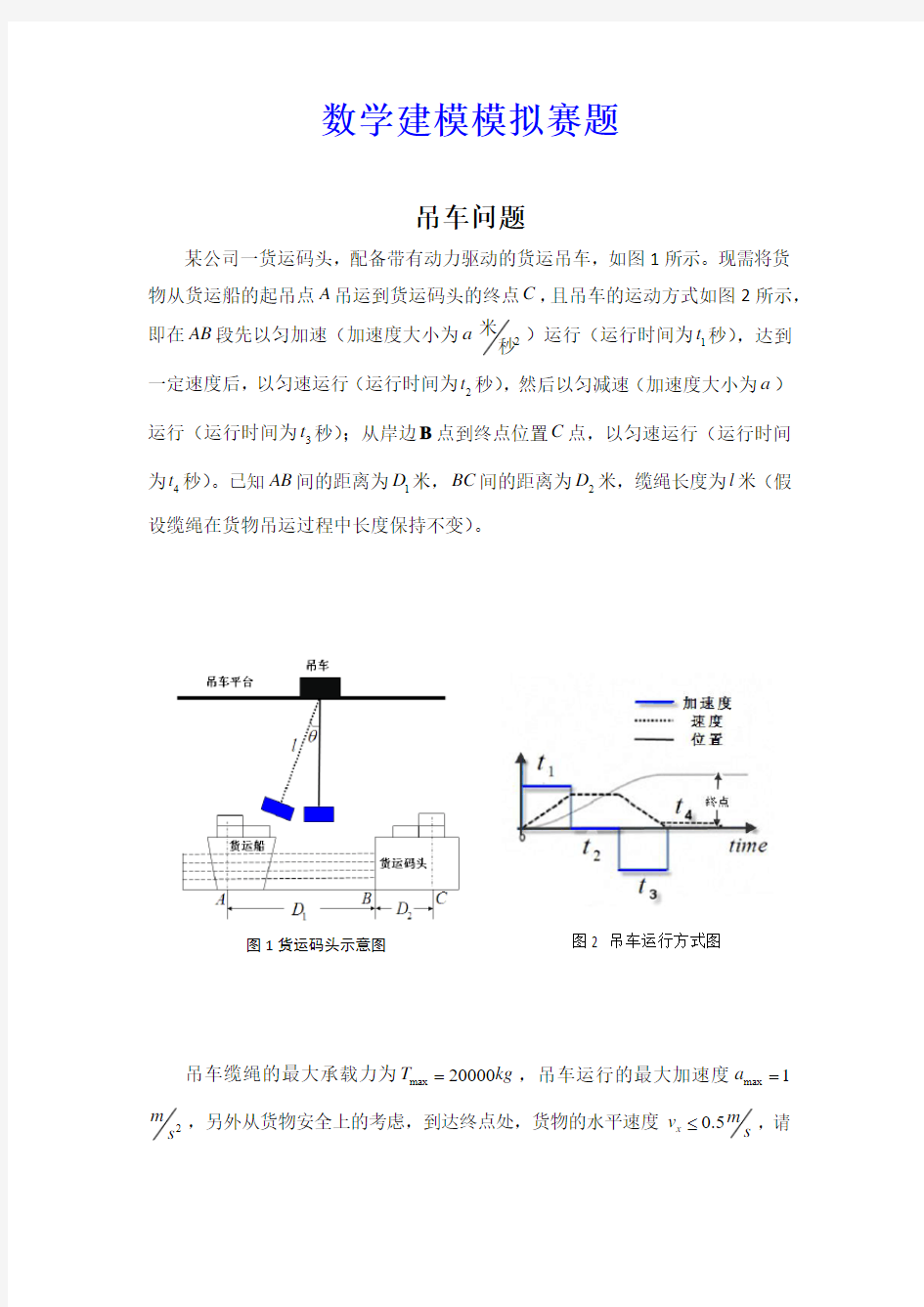
某公司一货运码头，配备带有动力驱动的货运吊车，如图1所示。现需将货物从货运船的起吊点A 吊运到货运码头的终点C ，且吊车的运动方式如图2所示，即在AB 段先以匀加速（加速度大小为a 2米

秒）运行（运行时间为1t 秒），达到

一定速度后，以匀速运行（运行时间为2t 秒），然后以匀减速（加速度大小为a ）运行（运行时间为3t 秒）；从岸边B 点到终点位置C 点，以匀速运行（运行时间为4t 秒）。已知AB 间的距离为1D 米，BC 间的距离为2D 米，缆绳长度为l 米（假设缆绳在货物吊运过程中长度保持不变）。

吊车缆绳的最大承载力为max 20000T kg =，吊车运行的最大加速度max 1a =2

m s ，另外从货物安全上的考虑，到达终点处，货物的水平速度0.5x m v s ≤，请 图2 吊车运行方式图

图1货运码头示意图

解决如下问题：

（1） 已知加速度a 的大小为20.5m s ，距离12D 60m D 10m =＝，，15l m =，

货物质量6000m =公斤，在不考虑吊车缆绳承载力的情况下，确定吊车运行方式，即建立模型，确定时间,1,2,3,4i t i =的大小，使得货物从岸边B 点到终点C ，其间摆动最小。

（2） 在第一问假设条件下，如果同时计及吊运效率，建立模型确定时间

,1,2,3,4i t i =的大小，使货物从岸边B 点到终点C 不仅摆动幅度小而且整体效率高。

（3） 考虑缆绳的最大承载力，并兼顾摆动大小和效率，请建立模型，确定

吊车运行方式,即确定加速度a 的大小、时间,1,2,3,4i t i =，并确定最大起吊货物重量max m 。