优化方法大作业

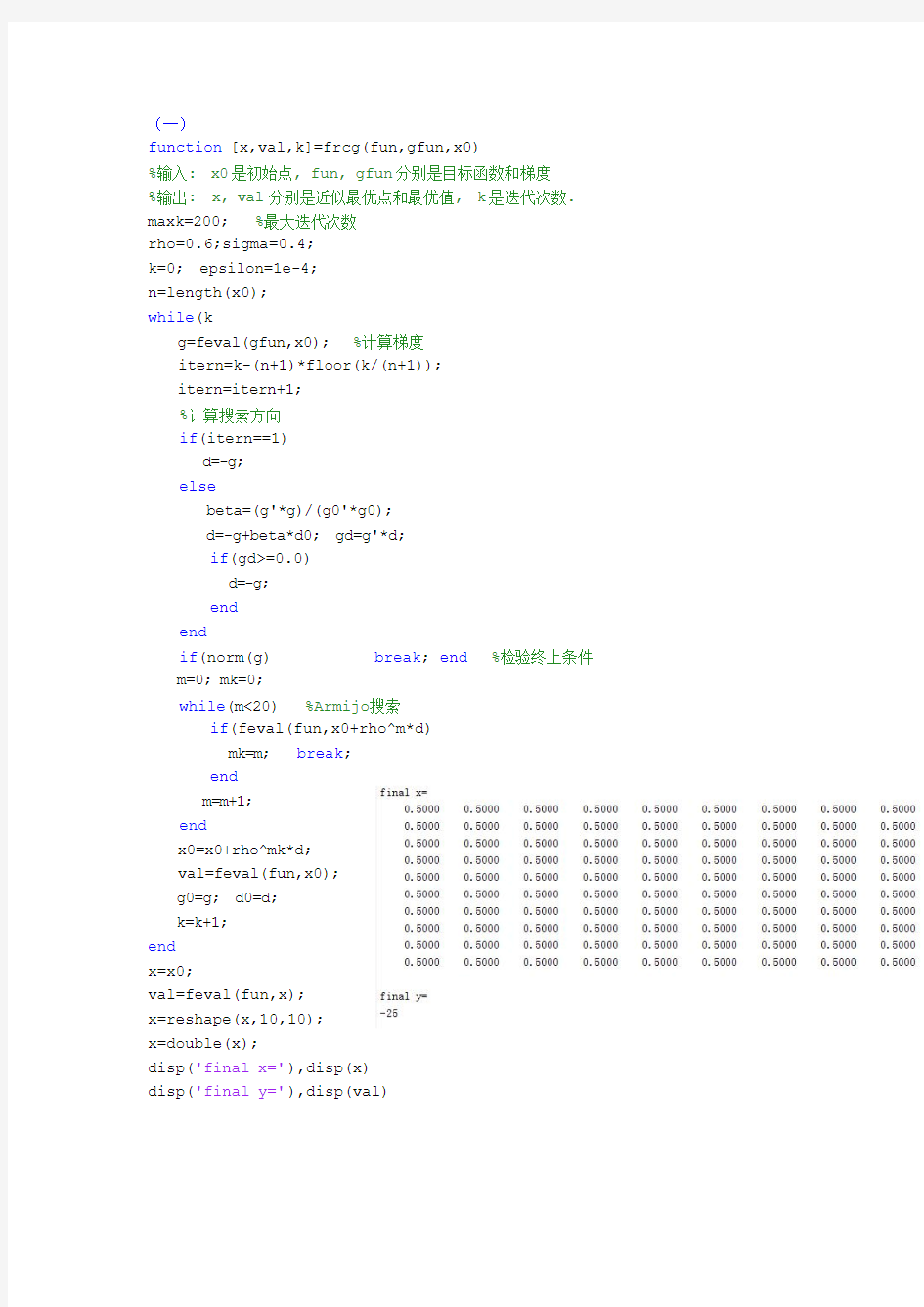
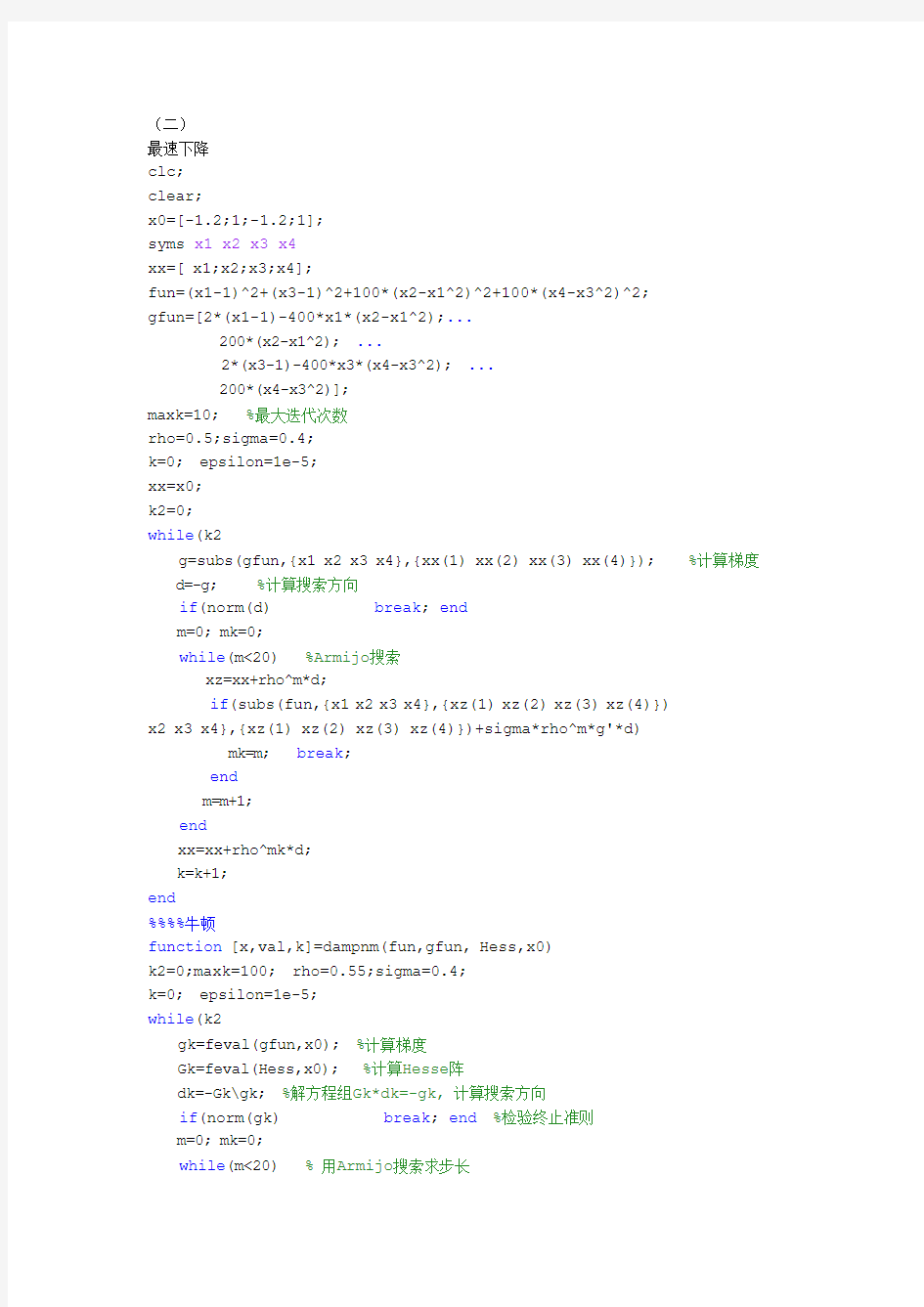
function [x,val,k]=frcg(fun,gfun,x0)

%输入: x0是初始点, fun, gfun分别是目标函数和梯度

%输出: x, val分别是近似最优点和最优值, k是迭代次数.

maxk=200; %最大迭代次数

rho=0.6;sigma=0.4;

k=0; epsilon=1e-4;

n=length(x0);

while(k

g=feval(gfun,x0); %计算梯度

itern=k-(n+1)*floor(k/(n+1));

itern=itern+1;

%计算搜索方向

if(itern==1)

d=-g;

else

beta=(g'*g)/(g0'*g0);

d=-g+beta*d0; gd=g'*d;

if(gd>=0.0)

d=-g;

end

end

if(norm(g)

m=0; mk=0;

while(m<20) %Armijo搜索

if(feval(fun,x0+rho^m*d)

end

m=m+1;

end

x0=x0+rho^mk*d;

val=feval(fun,x0);

g0=g; d0=d;

k=k+1;

end

x=x0;

val=feval(fun,x);

x=reshape(x,10,10);

x=double(x);

disp('final x='),disp(x)

disp('final y='),disp(val)

最速下降

clc;

clear;

x0=[-1.2;1;-1.2;1];

syms x1x2x3x4

xx=[ x1;x2;x3;x4];

fun=(x1-1)^2+(x3-1)^2+100*(x2-x1^2)^2+100*(x4-x3^2)^2;

gfun=[2*(x1-1)-400*x1*(x2-x1^2);...

200*(x2-x1^2);...

2*(x3-1)-400*x3*(x4-x3^2);...

200*(x4-x3^2)];

maxk=10; %最大迭代次数

rho=0.5;sigma=0.4;

k=0; epsilon=1e-5;

xx=x0;

k2=0;

while(k2

g=subs(gfun,{x1 x2 x3 x4},{xx(1) xx(2) xx(3) xx(4)}); %计算梯度

d=-g; %计算搜索方向

if(norm(d)

m=0; mk=0;

while(m<20) %Armijo搜索

xz=xx+rho^m*d;

if(subs(fun,{x1 x2 x3 x4},{xz(1) xz(2) xz(3) xz(4)})

mk=m; break;

end

m=m+1;

end

xx=xx+rho^mk*d;

k=k+1;

end

%%%%牛顿

function [x,val,k]=dampnm(fun,gfun, Hess,x0)

k2=0;maxk=100; rho=0.55;sigma=0.4;

k=0; epsilon=1e-5;

while(k2

gk=feval(gfun,x0); %计算梯度

Gk=feval(Hess,x0); %计算Hesse阵

dk=-Gk\gk; %解方程组Gk*dk=-gk, 计算搜索方向

if(norm(gk)

m=0; mk=0;

while(m<20) % 用Armijo搜索求步长

if(feval(fun,x0+rho^m*dk)

mk=m; break;

end

m=m+1;

end

x0=x0+rho^mk*dk;

k2=k2+1;

end

x2=x0;

%%%%BFGS

Bk=eye(n);

K3=0;

while(k3

gk=feval(gfun,x0); %计算梯度

if(norm(gk)

break;

end%检验终止准则

dk=-Bk\gk; m=0; mk=0;

while(m<20) % 用Armijo搜索求步长

newf=feval(fun,x0+rho^m*dk);

oldf=feval(fun,x0);

if(newf

mk=m; break;

end

m=m+1;

end

x=x0+rho^mk*dk;

det_xk=x-x0;

det_gk=feval(gfun,x)-gk;

if(det_gk'*det_xk>0)

Bk=Bk-(Bk*det_xk*det_xk'*Bk)/(det_xk'*Bk*det_xk)+(det_gk*det_gk')/(de t_gk'*det_xk);

end

k3=k3+1; x0=x;

End

x3=x;

disp('the solution for gradient is '); disp(xx');

disp(' gradient iteration is '); disp(k);

disp('the solution for newton is '); disp(x2');

disp('newton iteration is'); disp(k2);

disp('the solution for BGFS is '); disp(x3’);

disp('BFGS iteration is'); disp(k3);

（三）惩罚函数法

clc

clear

m=zeros(1,50);

a=zeros(1,50);

b=zeros(1,50);

f0=zeros(1,50); syms x1

syms x2

syms e

m(1)=1;

c=10;

a(1)=6;

b(1)=6;

imax=100；

for k=1:imax xi=a(k);yi=b(k);e=m(k);

fx=4*x1-x2^2-12;

hx=25-x1^2-x2^2;

gx=-10*x1+x1^2-10*x2+x2^2+34;

gx1=subs(gx,{x1 x2},{xi yi});

if gx1<=0

f=fx+M*hx^2;

else

f=fx+M*(hx^2+gx^2);

end

fx1=diff(f,'x1');fx2=diff(f,'x2');

fx1x1=diff(fx1,'x1');fx1x2=diff(fx1,'x2');

fx2x1=diff(fx2,'x1');fx2x2=diff(fx2,'x2');

for n=1:100

f1=subs(fx1,{x1 x2},{xi yi}); f2=subs(fx2,{x1 x2},{xi yi});

f11=subs(fx1x1,{x1 x2},{xi yi});

f12=subs(fx1x2,{x1 x2},{xi yi});

f21=subs(fx2x1,{x1 x2},{xi yi});

f22=subs(fx2x2,{x1 x2},{xi yi});

if(double(sqrt(f1^2+f2^2))<=1e-6) %

a(k+1)=double(x1);b(k+1)=double(x2);f0(k+1)=double(subs(f));

break;

else

X=[x1 x2]'-inv([f11 f12;f21 f22])*[f1 f2]';

xi=X(1);yi=X(2);

end

end

end

ffinal=double(subs(fi,{x1 x2},{xi yi}));

disp('x1='),disp(xi)

disp('x2='),disp(yi)

disp('objective function value f='),disp(ffinal)

乘子法

function [x,mu,lambda,output]=multphr(fun,hf,gf,dfun,dhf,dgf,x0)

maxk=500; %最大迭代次数

sigma=2.0; %罚因子

eta=2.0; theta=0.8; %PHR算法中的实参数

k=0; ink=0; %k, ink分别是外迭代和内迭代次数

epsilon=1e-5; %终止误差值

x=x0; he=feval(hf,x); gi=feval(gf,x);

n=length(x); l=length(he); m=length(gi);

%选取乘子向量的初始值

mu=0.1*ones(l,1); lambda=0.1*ones(m,1);

btak=10; btaold=10; %用来检验终止条件的两个值

while(btak>epsilon & k

%调用BFGS算法程序求解无约束子问题

[x,ival,ik]=bfgs('mpsi','dmpsi',x0,fun,hf,gf,dfun,dhf,dgf,mu,lambda,s igma);

ink=ink+ik;

he=feval(hf,x); gi=feval(gf,x);

btak=0.0;

for (i=1:l), btak=btak+he(i)^2; end

for i=1:m

temp=min(gi(i),lambda(i)/sigma);

btak=btak+temp^2;

end

btak=sqrt(btak);

if btak>epsilon

if(k>=2 & btak > theta*btaold)

sigma=eta*sigma;

end

%更新乘子向量

for (i=1:l), mu(i)=mu(i)-sigma*he(i); end

for (i=1:m)

lambda(i)=max(0.0,lambda(i)-sigma*gi(i));

end

end

k=k+1;

btaold=btak;

x0=x;

end

f=feval(fun,x);

disp('x1='),disp(x(1))

disp('x2='),disp(x(2))

disp('objective function value f='),disp(f)