计算方法上机实验指导

计算方法上机实验指导

一、非线性方程求解

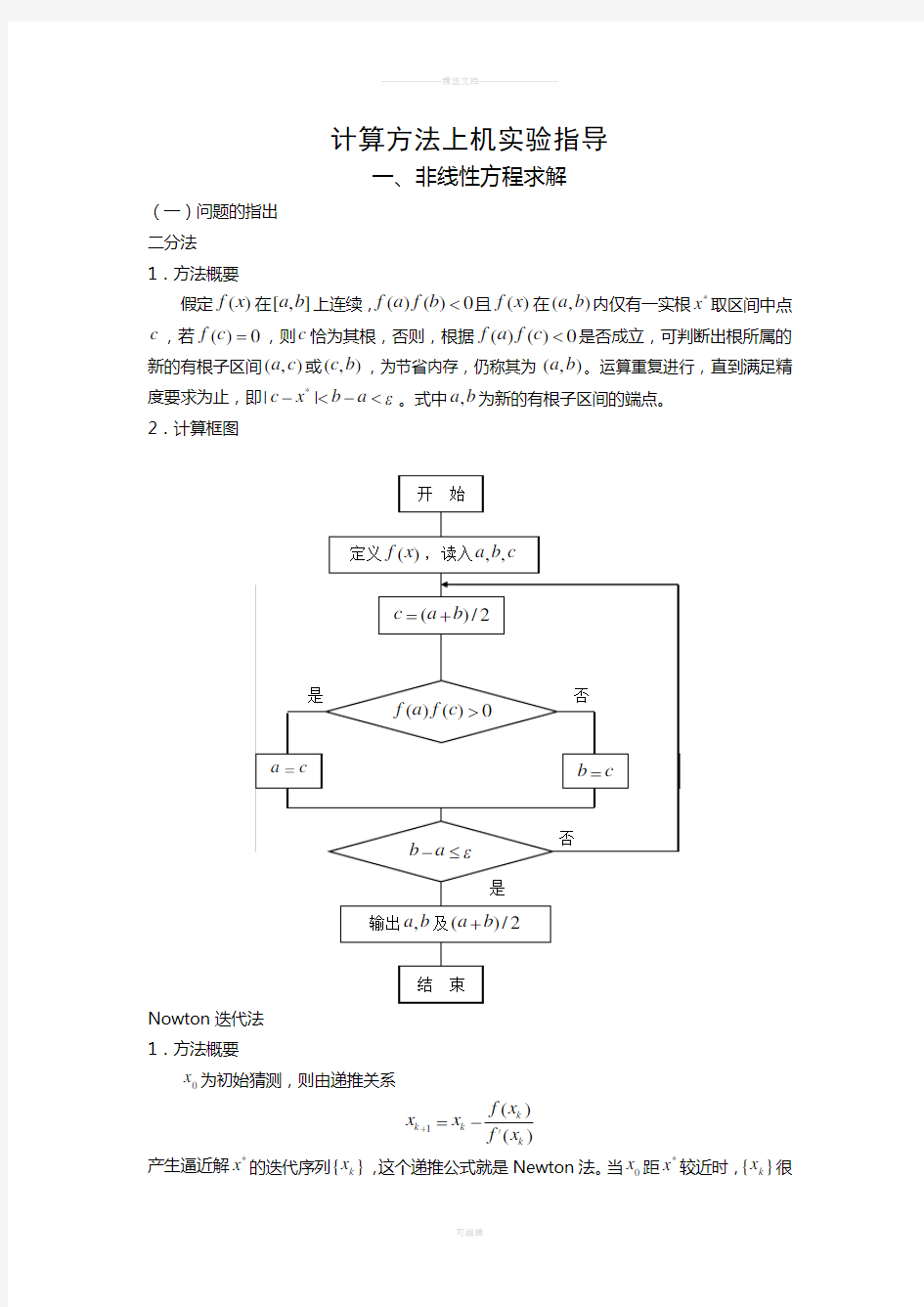
（一）问题的指出 二分法 1．方法概要

假定()f x 在[,]a b 上连续，()()0f a f b <且()f x 在(,)a b 内仅有一实根*

x 取区间中点

c ，若()0f c =，则c 恰为其根，否则，根据()()0f a f c <是否成立，可判断出根所属的

新的有根子区间(,)a c 或(,)c b ，为节省内存，仍称其为(,)a b 。运算重复进行，直到满足精度要求为止，即*

||c x b a ε-<-<。式中,a b 为新的有根子区间的端点。 2．计算框图

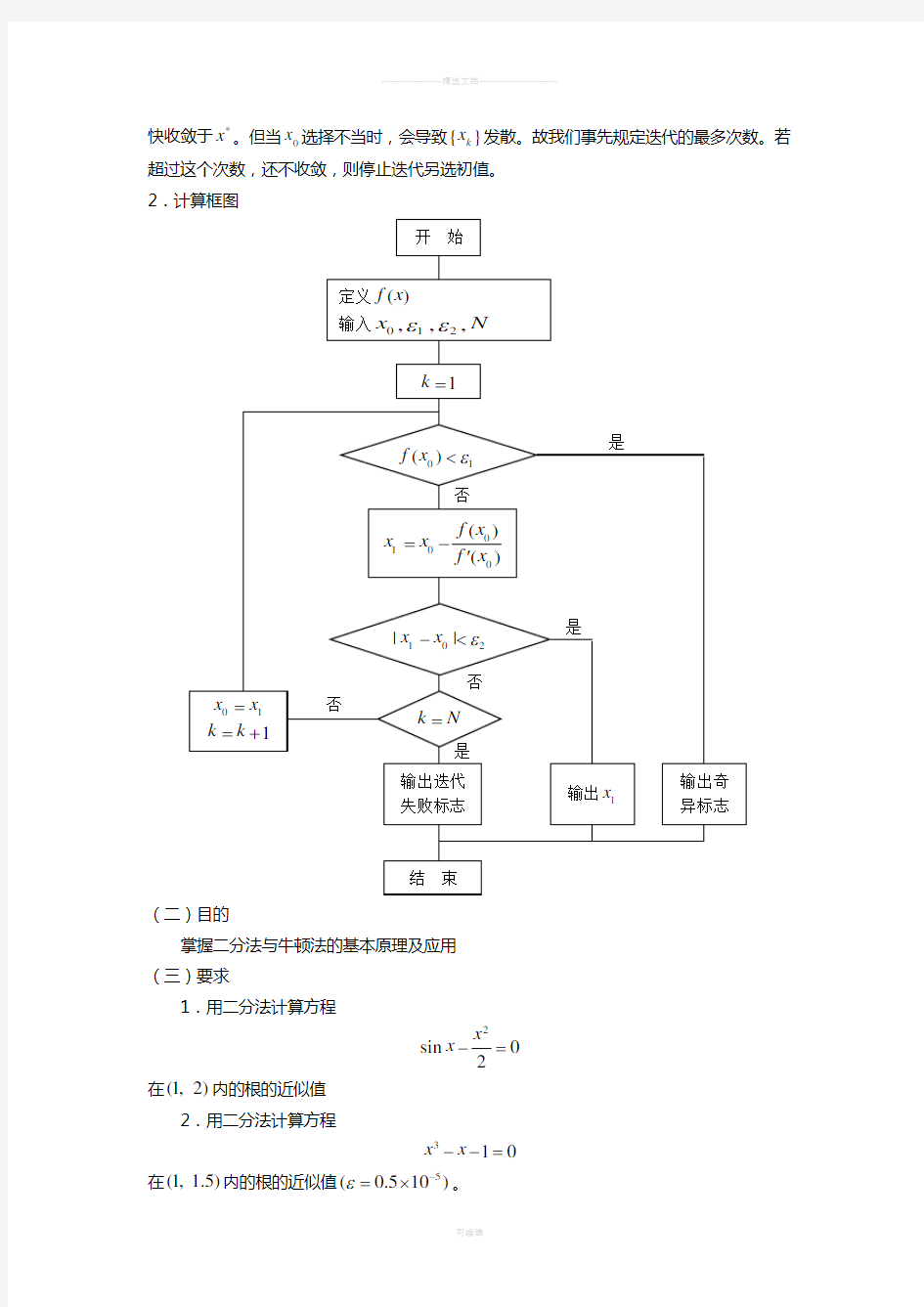
Nowton 迭代法 1．方法概要

0x 为初始猜测，则由递推关系

1()

()

k k k k f x x x f x +=-

' 产生逼近解*

x 的迭代序列{}k x ，这个递推公式就是Newton 法。当0x 距*

x 较近时，

{}k x 很

快收敛于*

x 。但当0x 选择不当时，会导致{}k x 发散。故我们事先规定迭代的最多次数。若超过这个次数，还不收敛，则停止迭代另选初值。 2．计算框图

（二）目的

掌握二分法与牛顿法的基本原理及应用 （三）要求

1．用二分法计算方程

2

sin 02

x x -=

在(1,2)内的根的近似值 2．用二分法计算方程

310x x --=

在(1,1.5)内的根的近似值5

(0.510)ε-=?。

3．用牛顿法求下列非线性方程的近似根。

① 10x

xe -= 00.5x = ② 3

10x x --= 01x =

③ 2

(1)(21)0x x --= 00.45x = 00.65x =

4．用改进的牛顿法

12()

()

k k k k f x x x f x +=-

'

计算方程

20(1)(21)0

0.55x x x --==

的近似根，并与要求3.中的③的结果进行比较。

二、Gauuss 列主元消去法

（一）问题的提出

由地一般线性方程组在使用Gauss 消去法求解时，从求解过程中可以清楚地看到，若

(1)0k kk a -=，必须施以行交换的手续，才能使消去过程继续下去。有时既使(1)0k kk a -≠，但其

绝对值很小，由于舍入误差的影响，消去过程也会出现不稳定现象。因此，为使这种不稳定现象发生的可能性减至最小，在施行消去过程时每一步都要选主元素，即要寻找行r ，使

(1)(1)

||max ||k k rk ik i k

a a -->=

并将第r 行与第k 行交换，以使(1)

k kk a -的当前值（即(1)

k ik

a -的数值）远大于0。

这种列主元消去法的主要步骤如下：

1．消元过程

对1,2,,1k n =-L ，做 1o 选主元，记

||max ||rk ik i k

a a >=

若0rk a =，说明方程组系数矩阵奇异，则停止计算，否则进行2o。 2o 交换A （增广矩阵）的,r k 两行元素

,,1rj kj

a a j k n ?=+L

3o 计算

/ij ij ik kj kk a a a a a =-

1,,i k n =+L

1,,1j k n =++L

2．回代过程

对,1,,2,1k n n =-L ，计算

,11

(/)n

k k n kj

j kk j k x a a

x a +=-=-

∑

其计算框图如下：

（二）目的

1．熟悉Gauss 列主元消去法，编出实用程序。 2．认识选主元技术的重要性。

3．明确对于哪些系数矩阵A ，在求解过程中不需使用选主元技术。

（三）要求

1．编制程序，用Gauss 列主元消去法求解线性方程组Ax b =，并打印结果，其中

（1）810231 3.712 4.6232 1.072 5.643A -????=-????-??

， 123b ????=??

????

（2）424217104109A -????=-????-??， 1037b ????=????-??

2．与不选主元的Gauss 消去法结果比较并分析原因。

三、Runge 现象的产生和克服

（一）问题的提出

在给定1n +个插值节点和相应的函数值以后构造n 次插值多项式的方法。从余项的表达式看出，插值多项式与被插函数逼近的程度是同分点的数目及位置有关的。能不能说，分点越多，插值多项式对函数的逼近程度越好呢？答案是否定的，在本世纪初Runge 指出了这种多项式插值的缺点。 什么是Runge 现象呢？ 例：给定函数

2

1

()11125f x x x =

-≤≤+

取等距节点2

1(0,1,,10)10

i x i i =-+=L ，试建立插值多项式10()x φ，并研究它与()f x 的误差。

插值多项式的次数为10，用拉格朗日插值公式有

10

100

()()()i i i x f x l x φ==∑

其中

21

()125i i f x x =

+

2

1,0,1,,1010

i x i i =-+=L

0111001110()()()()

()()()()()

i i i i i i i i i x x x x x x x x l x x x x x x x x x -+-+----=

----L L L L

画出它们的图形，从图中可以看出，在[0.20,0]-区间内10()x φ能较好地逼近()f x ，但在其他部分10()x φ与()f x 的差异较大，越靠近端点，逼近的效果越差。事实上可以证明，对

2

1

125x

+这个函数在[1,1]-区间内用1n +个等距节点作插值多项式10()x φ，当n →∞时()n x φ只能在||0.73x <内收敛，而在这个区间之外是发散的，这一现象称为Runge 现象。

从上面例子看到，在区间上给定等距插值节点，过这些插值节点作拉格朗日插值多项式，节点不断加密时，构造的插值多项式的次数也不断提高，但是，尽管被插值函数是连续的，高次插值多项式也不一定收敛到相应的被插值函数。

解决Runge 现象有分段线性插值，三次样条插值等方法。 分段线性插值：

设在区间[,]a b 上，给定1n +插值节点

01n a x x x b =<<<=L

和相应的函数值01,,,n y y y L ，求作一个插值函数()x φ，具有下面性质： （1）(),0,1,2,,j j x y j n φ==L

（2）()x φ在每个小区间1[,]j j x x +上是线性函数。

插值函数()x φ叫做区间[,]a b 上对数据(,)(0,1,,)i i x y i n =L 的分段线性插值函数。 三次样条插值

给定区间[,]a b 一个分划

01:N a x x x b ?=<<<=L

若函数()S x 满足下述两条件：

1）()S x 在每个小区间1[,](1,2,,)j j x x j N -=L 上是3次多项式。

2）()S x 及其直到2阶导数在[,]a b 连续。则称()S x 是关于分划?的三次样条函数。

（二）目的

1．深刻认识多项式插值的缺点； 2．明确插值的不收敛性怎样克服； 3．明确精度与节点、插值方法的关系。

（三）要求 给定函数21(),11125f x x x =

-≤≤+，及节点2

1(1),1,2,,1j

x j j N N

=-+-?=+L ，试用如下插值方法如何克服Runge 现象 1．用多项式插值计算出下列插值

(0),(0.060.1),(0.060.1)N N N S S k S k +--

0,1,,9k =L ，观察是否会产生Runge 现象。

2．用下列方法进行计算，并且比较它们克服Runge 现象的效果。 （1）分段线性插值

（2）三次样条函数插值（一），条件为：

()(),1,,1()(),1,,1N j j N

i j S x f x j N S x f x i N ?==+??''''==+??L L

（3）三次样条函数插值（二），条件为

()(),1,,1

()(),1,,1N j j N

i i S x f x j N S x f x i N ?==-??''==-??L L

3．编程序，打印结果分析。

（1）编写计算程序，调试计算，比较每种插值在插值点上与精确值的误差是多少。 （2）同一种插值法，当节点增多时，精度怎样？ （3）打印程序、结果，写出实验报告。

四、多项式最小二乘法

（一）问题的提出

对于给定的测量数据(,)(1,2,,)i i x f i n =L 设函数分布为

()()m

j j j y x a x ?==∑

特别地，取()j x ?为多项式形式

()0,1,2,,j

j x x j m ?==L

则根据最小二乘原理，可构造泛函

2011

(,,,)(())n

n

m i j j i i j H a a a f a x ?===-∑∑L

令

00,1,2,,k

H

k m a ?==?L

则可得到法方程

01

1

()()()m n

n

j

i k i j i k i j i i x x a f x ?

??====∑∑∑

0,1,2,,k m =L

求解该方程组，则可得到解012,,,,m a a a a L ，因此可得到数据的最小二乘解

()()m

j j j f x a x ?=≈∑

（二）目的

1．学习使用最小二乘原理 2．了解法方程的特性 （三）要求

用最小二乘方法处理实验数据。

3456789

2.01 2.98

3.50 5.02 5.47 6.027.05

i i

x f

并作出()f x 的近似分布图。

五、龙贝格积分法

（一）问题的提出 考虑积分

()()b a

I f f x dx =?

欲求其近似值，可以采用如下公式：

（复化）梯形公式 1

10[()()]2n i i i h

T f x f x -+==

+∑ 2

()12b a E h f η-''=- [,]a b η∈

（复化）辛卜生公式 1

1102

[()4()()]6n i i i i h

S f x f x f x -++

==++∑

4

(4)

()1802b a h E f η-??=- ??? [,]a b η∈

（复化）柯特斯公式 1

11042

[7()32()12()90n i i i i h

C f x f x f x -++

==+++∑

3

14

32()7()]i i f x

f x +++

6

(6)

2()()9454b a h E f η-??=- ???

[,]a b η∈

这里，梯形公式显得算法简单，具有如下递推关系

1

2102

1()22n n n i i h T T f x -+==+∑

因此，很容易实现从低阶的计算结果推算出高阶的近似值，而只需要花费较少的附加函数计算。但是，由于梯形公式收敛阶较低，收敛速度缓慢。所以，如何提高收敛速度，自然是人们极为关心的课题。为此，记0,k T 为将区间[,]a b 进行2k

等份的复化梯形积分结果，1,k T 为将区间[,]a b 进行2k

等份的复化辛卜生积分结果，2,k T 为将区间[,]a b 进行2k

等份的复化柯

特斯积分结果。根据李查逊（Richardson ）外推加速方法，可得到

1,11,,0,1,2,40,1,2,41

m m k m k

m k m k T T T m -+-=-??=

?=-??

L L 可以证明，如果()f x 充分光滑，则有

,lim ()m k k T I f →∞

= （m 固定）

,0lim ()m m T I f →∞

=

这是一个收敛速度更快的一个数值求积公式，我们称为龙贝格积分法。 该方法的计算可按下表进行

0,0T 0,1T 0,2T … 0,m T 1,0T 1,1T … 1,1m T - 2,0T … 2,2m T - … … ,0m T

很明显，龙贝格计算过程在计算机上实现时，只需开辟一个一维数组，即每次计算的结果

,m k T ，可存放在0,k T 位置上，其最终结果,0m T 是存放在0,0T 位置上。具体的计算过程为：

1．准备初值，计算

0,0[()()]2

a b

T f a f b -=

+ 且0k ←（k 为等份次数）

2．按梯形公式的递推关系，计算

210,10,10

11

(())2222k

k k k k i b a b a T T f a i -++=--=+++∑

3．按龙贝格公式计算加速值

1,11,0,,40,1,2,,41

m m k m m k m

k m m k m m

T T T T m k -+------←=

=-L

4．精度控制。对给定的精度ε，若

,01,0||m m T T ε--<

则终止计算，并取0,,s m s T T ←作为所求结果；否则1k k ←+，重复2~4步，直到满足精度为止。 （二）目的

1．理解和掌握龙贝格积分法的原理； 2．学会使用龙贝格积分法；

3．明确龙贝格积分法的收敛速度及应用时容易出现的问题。 （三）要求

1．用龙贝格积分法计算下列积分的近似值 （1）

10036

x dx ?； （2）1

0sin x

dx x ?

； （3）120sin x dx ? 2．打印龙贝格积分法的函数表，使积分结果更加清楚。 3．分析所出现的问题并加以讨论。

六、常微分方程初值问题的数值解法

（一）问题的提出

一阶常微分方程初值问题

0(,)

()dy

f x y dx

y x y

?=???=? （6.1） 的数值解法是近似计算中很重要的部分。

常微分方程初值问题的数值解法是求方程（6.1）的解在点列1(0,1,)n n n x x h n -=+=L 上的近似值n y ，这里n h 是1n x -到n x 的步长，一般略去下标记为h 。 常微分方程初值问题的数值解法一般分为两大类：

（1）单步法：这类方法在计算n y 时，只用到1n x +、n x 和n y ，即前一步的值。因此，在有了初值以后就可以逐步往下计算。典型方法如龙格–库塔()R K -方法。

（2）多步法：这类方法在计算1n y +时，除用到1n x +、n x 和n y 以外，还要用

(1,2,,;0)n p y p k k -=>L ，即前面k 步的值。典型方法如Adams 方法。

经典的R K -方法是一个四阶的方法，它的计算公式是：