三角函数、解三角形习题精选

三角函数、解三角形习题精选
1.设函数.cos )
cos(2)
2
3cos(
)2cos 1()(2
ααπαπαα++-+=
f
(I )设ABC A ?∠是的内角,且为钝角,求)(A f 的最小值; (II )设B A ∠∠,是锐角ABC ?的内角,且,2,1)(,12
7===∠+∠BC A f B A π
求ABC ? 的三个内角的大小和AC 边的长.
2.已知函数()sin
sin(
)22
2
x x f x π
=+
⑴求函数()f x 在[,0π-]上的单调区间; ⑵已知角α满足(0,)2
π
α∈,2(2)4(
2)12
f f π
αα+-=,求()f α的值。
3. 已知.02cos
22sin
=-x x
(1) 求x tan 的值;(2) 求
x
x x
sin 4cos 22cos ??
?
??+π的值。
4.已知函数().
33cos
323cos 3sin 22
-
??? ?
?
-+??? ?
?
-??? ??-=
πππx x x x f
(1) 求()x f 的单调递增区间;
(2) 求()x f 的最大值及取得最大值时相应的x 的值。
5.已知A B C ?的三个内角,,A B C 所对的边分别为a b c 、、
,向量
(4,
1m =-
2(c o s
,c o s 2)2A
n A =
,且7
2
m n ?= .
(1)求角A 的大小; (2
)若a =b c ?取得最大值时A B C ?形状.
6.已知角A 、B 、C 是ABC ?的三个内角,若向量(1cos(),cos )2
A B m A B -=-+u r
,
5(,cos )82A B
n -=r ,且
98m n ?=u r r . (1)求tan tan A B 的值; (2)求
2
2
2
sin ab C a b c
+-的最大值
7.在锐角△ABC 中,角,,A B C 的对边的长分别为,,,a b c 已知5b =
,sin 4
A =
,
4
ABC S ?=
.
(I )求c 的值; (II )求sin C 的值.
8. 已知ABC ?的周
长为1)
,且sin sin B C A +=.
(I ) 求边长a 的值;
(II ) 若3sin ABC S A ?=,求cos A 的值
9.已知向量,)8(sin ),8
cos(2
???
??
+
+
=ππ
x x a ,1),8sin(??? ?
?
+=πx b 函数()12-?=b a x f 1)求函数()x f 的解析式,并求其最小正周期;
2)求函数)(x f 图象的对称中心坐标与对称轴方程. 3)求函数??
?
??
-
=x f y 21
的单调递增区间;
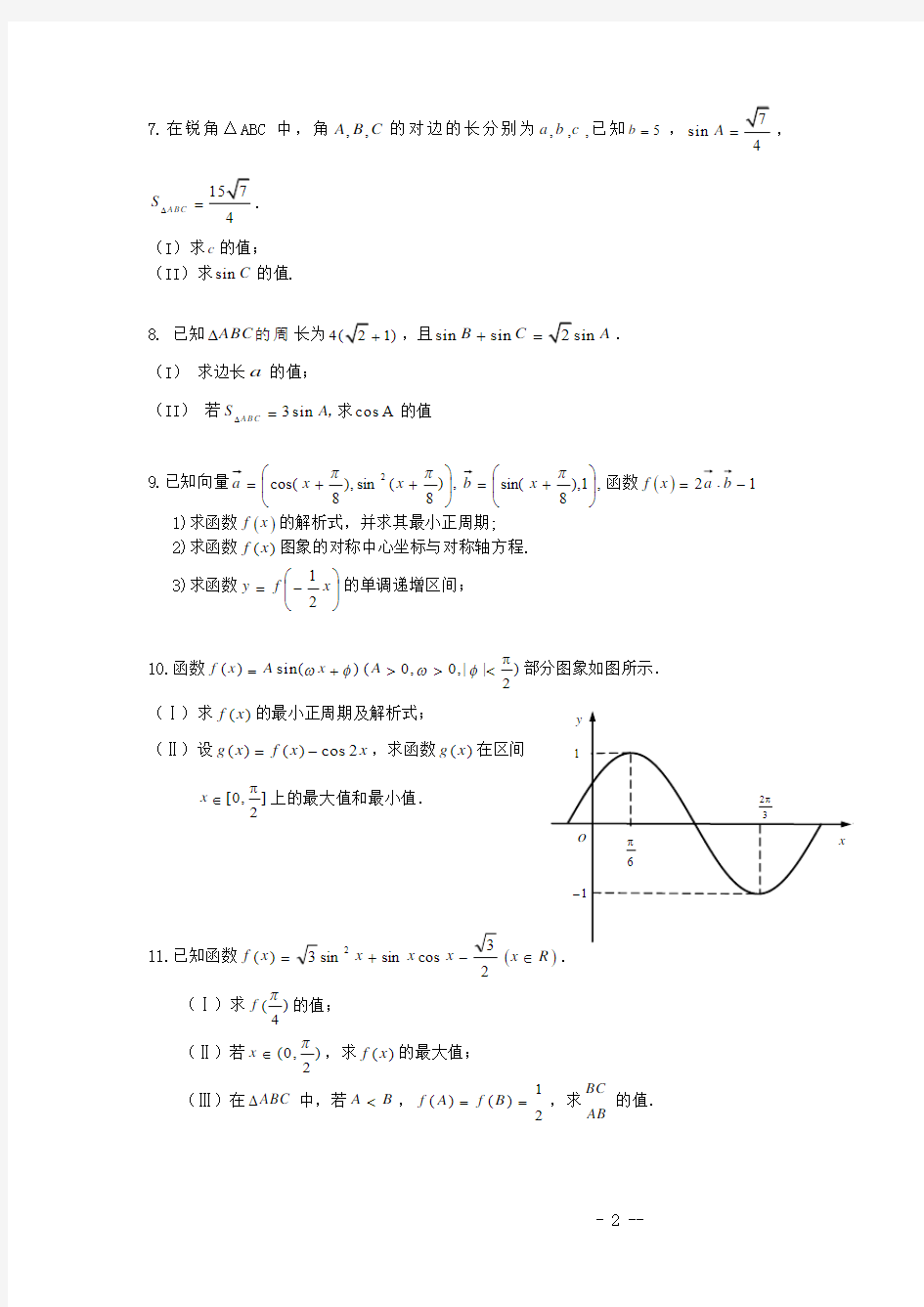
10.函数()sin()(0,0,||)2
f x A x A ωφωφπ=+>><部分图象如图所示.
(Ⅰ)求()f x 的最小正周期及解析式;
(Ⅱ)设()()cos 2g x f x x =-,求函数()g x 在区间 [0,]2x π
∈上的最大值和最小值.
11.已知函数2
3cos sin sin
3)(2
-
+=
x x x x f (R x ∈.
(Ⅰ)求)4
(
π
f 的值;
(Ⅱ)若)2
,
0(π
∈x ,求)(x f 的最大值;
(Ⅲ)在ABC ?中,若B A <,2
1)()(==B f A f ,求
AB
BC 的值.
12.
已知函数2
()22sin f x x x =-.
(Ⅰ)若点(1,P 在角α的终边上,求()f α的值; (Ⅱ)若[,
]6
3
x π
π
∈-,求()f x 的值域.
13.在A B C ?中,角A 、B 、C
所对的边分别为2a b c a b ==、、,,1cos 2
A =-.
(I ) 求角B 的大小;
(Ⅱ)若2()cos 2sin ()f x x c x B =++,求函数()f x 的最小正周期和单增区间.
14.在△ABC 中,角A ,B ,C 的对边分别为a ,b ,c 分,且满足2cos cos c b B a
A
-=.
(Ⅰ)求角A 的大小;
(Ⅱ)若a =ABC 面积的最大值.
15.
已知πsin()410
A +
=
,ππ
(
,)42
A ∈. (Ⅰ)求cos A 的值; (Ⅱ)求函数5()cos 2sin sin 2
f x x A x =+的值域.
16.已知函数cos 2()sin()
4
x f x x π
=
+
.
(Ⅰ)求函数()f x 的定义域; (Ⅱ)若4()3
f x =
,求s i n 2
x 的值. 17.已知函数()4cos sin()16
f x x x π=+-.(1)求()f x 的最小正周期;
(2)求()f x 在区间[,]64
ππ
-上的最大值和最小值。
18.已知等比数列{}n a 的公比3q =,前3项和3133
S =.
(Ⅰ) 求数列{}n a 的通项公式;
(Ⅱ) 若函数()sin(2)(0,0)f x A x A ??π=+><<在6
x π
=
处取得最大值,且最大值
为3a ,求函数()f x 的解析式.
19.设函数f (θ)=3sin θ +cos θ,其中,角θ的顶点与坐标原点重合,始边与x 轴非负半轴重合,终边经过点P (x ,y ),且0≤θ≤π。
(Ⅰ)若P 的坐标是(12,3
2
),求f (θ)的值;
(Ⅱ)若点P (x ,y )为平面区域????
?x +y ≥1x ≤1 y ≤1
上的一个动点,试确定角θ的取值范围,并求函
数f (θ)的最小值和最大值。
20.1
()2sin(),3
6
f x x x R π
=-
∈已知函数
5(1)(
)4
f π求的值;
106(2),0,
,(3),(32),cos()22135f f π
παβαβπαβ??
∈+=+=+????
设求的值.
21.已知函数()12sin 3
6f
x x π??=- ???,x R ∈.
(1)求()0f 的值;
(2)设10,0,,3,2213f ππαβα???
?∈+=
???????()632,5f βπ+=求()sin αβ+的值.
22.在△ABC 中,角A 、B 、C 所对应的边为c b a ,, (1)若,cos 2)6sin(A A =+π
求A 的值; (2)若c b A 3,3
1cos ==,求C sin 的值.
23.已知函数73()sin()cos()4
4
f x x x ππ=+
+-
,x ∈R .
(Ⅰ)求()f x 的最小正周期和最小值; (Ⅱ)已知4cos()5
βα-=
,4cos()5
βα+=-
,02
παβ<<≤
,求证:2[()]20f β-=.
24.已知函数()2cos 2cos 1f x x x x =+-()x ∈R . (Ⅰ)求函数()f x 的最小正周期及在区间0,
2π?
?
?
??
?
上的最大值和最小值.
(Ⅱ)若()06
5f x =,0,42x ππ??
∈????
.求0cos 2x 的值.
25.在A B C ?中,
cos cos A C B A B
C
=
.
(Ⅰ)证明:B C =. (Ⅱ)若1cos 3
A =-.求sin 43
B π?
?
+
??
?
的值.
26.已知函数2
π
()2sin 24f x x x ??=+-
???
,ππ,42x ??
∈????
.ks**5u
(Ⅰ)求()f x 的最大值和最小值;
(Ⅱ)若不等式()2f x m -<在ππ,42x ??∈???
?
上恒成立,求实数m 的取值范围
27.已知函数()sin cos ,'()f x x x f x =+是()f x 的导函数. (1)求函数2
()()'()()F x f x f x f x =+的最大值和最小正周期; (2)若()2'()f x f x =,求22
1sin cos sin cos x x x x
+-的值.
参考答案
1.解:(1)2
223
(cos 21)cos()cos sin 2()cos cos 2cos()cos A A A A f A A A A A
ππ+-=+=++
.2
1)4
2sin(2
2)12cos 2(sin 2
1cos
2sin 2
12
+
+
=
++=+=π
A A A A A
∵角A 为钝角,.4
94
24
5,2
ππ
πππ
<
+
<<<∴
A A
)(,2
34
2A f A 时当ππ
=+∴取值最小值,其最小值为
.2
2
1-
(2)由.2
2)4
2sin(,12
1)4
2sin(2
21)(=
+
∴=+
+
=π
π
A A A f 得
524
A A π
π
π∴<+
<
为锐角,4
4
,
.12
5.3
,12
7.4
,4
34
2ππ
ππ
ππ
=
∴=
∴=
+=
=
+
∴C B B A A A 又 在△ABC
中,由正弦定理得:
sin .sin sin sin B C
A C
B C B A C A B
A
=
∴=
=
2.解:1
()sin sin()sin cos sin 222222
x x x x f x x π=+==
⑴函数()f x 在区间[,]2
π
π--单调递减,在区间[,0]2
π
-
单调递增。(6分)
⑵2(2)4(
2)12
f f π
αα+-=
sin 22sin(
2)12
π
αα?+-=
2
2
2sin cos 2(cos sin )1αααα?+-=
22
cos 2sin cos 3sin 0αααα?+-=(cos 3sin )(cos sin )0αααα?+-= ∵(0,
)2
π
α∈
,∴cos sin 0tan 1sin 2
αααα-=?=?=
∴1()sin 2
4
f αα==
。(12分)
3.(1).3
4tan ,22
tan
-
=∴=x x (2)原式=.4
1tan 11sin
sin cos sin
cos
2
2
2
=
+=--x
x
x x x
x
4.(1)().32sin 2322cos 3322sin ??? ?
?
-=??? ??-+???
?
?
-
=πππx x x x f
令,
2
23
22
2π
ππ
π
π+
≤-
≤-
k x k 则()x f 的单调递增区间为
?
????
?
+-∈125,12ππππk k x
)(Z k ∈
(2)当,
2
23
2π
ππ
+
=-
k x 即()Z k k x
∈+
=12
5ππ时,().2max
=x f
5.解:(1)由2(4,1),(cos ,cos 2)2
A
m n A =-=
24cos cos 22A m n A ?=- 21cos 4(2cos 1)2A A +=?-- 2
2cos 2cos 3A A =-++
又因为77,2cos 322m n A A ?=++= 2所以-2cos 解得1
cos 2
A =…………2分
0,3
A A π
π<<∴=
………………………………………2分
(2)在2222cos ,ABC a b c bc A a ?=+-=中,且
2
2
2
122
b c bc ∴=+-?
22b c bc =+-。…………………2分
2
22,32b c bc bc bc +≥∴≥- ,
即3,bc ≤当且仅当b c b c ==?,取得最大值,…………………2分
又由(Ⅰ)知,,3
3
A B C π
π
=
∴==
故b c ?取得最大值时,A B C ?为等边三角形.2分
6.解:(理)(1)255
cos()cos 882
A B
m n A B -?=-++
9199cos cos sin sin 8
8
8
8
A B A B =
-
+
=
cos cos 9sin sin A B A B ∴=,1tan tan 9
A B =
得……………………5分
(2)tan tan tan()1tan tan A B A B A B
++=-
993(tan tan )8
8
4
A B =+≥
?=…………8分
(∴>=
09
1tan tan B A A,B 均是锐角,即其正切均为正)
2
2
2
sin sin 113tan (11) tan()2cos 2
2
8
ab C C C A B a b c
C
=
==-+≤-
+-分
所求最大值为8
3-
。…………………………………………12分
7.解:(I )由1sin 2
4
ABC S bc A ?=
=
…………...……..…2分
可得,6c = ………….….4分
(II )由锐角△ABC
中sin 4
A =
3cos 4
A =
……………….…….....6分
由余弦定理可得:22232cos 253660164
a b c bc A =+-?=+-?
=, ……….….8分
有:4a = …….. ……………….9分
由正弦定理:
sin sin c a C
A
=
, …….. ……..…….10分
即6sin 4sin 48
c A C a
?=
=
= .................12分 8.解:(I)
根据正弦定理,sin sin B C +=
可化为b c +=.
。。。。。。2分
联立方程组1)
a b c b c ?++=+??+=??,解得4a =.所以,边长4a =. 。。。。。。5分
(II)3sin ABC S A ?= , ∴
1sin 3sin 62
bc A A bc ==,. 。。。。。。7分
又由(I)
可知,b c +=
∴2
2
2
22
()21cos 223
b c a
b c bc a
A bc
bc
+-+--==
=
。。。。。。10分
9. 解:1)()=-?=12b a x f 1)8
(sin 2)8
sin()8
cos(22
-+
++
+π
π
π
x x x
x x x 2sin 242cos )42sin(=??? ?
?
+-+
=ππ
---- 4分
ππ==
∴2
2T ---- 5分
2)令0=y ,即02sin 2=x ,得πk x =2,2
πk x =,Z k ∈
∴对称点为??
?
??0,2π
k ,Z k ∈ ---- 7分 由22sin 2±=x , 22ππ+=∴k x ,4
2π
π+=k x ,Z k ∈
∴对称轴方程是直线4
2π
π+=k x ,Z k ∈ ---- 9分 3) ??
?
?
?-
=x f y 21
=x x sin 2)sin(2-=- 的单调递增区间
x sin ∴递减∴z k k x k ∈+
≤≤+,2
322
2πππ
π ---- 11分
∴??? ??
-
=x f y 21
的单调递增区间是z k k k ∈??
????
++,232,22ππππ -- 12
10.解:(Ⅰ)由图可得1A =,
22362
T πππ=-=,所以T =π. …………2分
所以2ω=.
当6
x π=
时,()1f x =,可得 sin(2)16
?π?
+=,
因为||2
?π<,所以6
?π=
. …………5分
所以()f x 的解析式为()sin(2)6
f x x π=+
. ……………………6分
(Ⅱ)()()cos 2sin(2)cos 26g x f x x x x π
=-=+
-
sin 2cos
cos 2sin cos 26
6
x x x ππ=+-
12cos 22
2
x x =-
sin(2)6
x π=-
. ………………………………10分
因为02x π≤≤
,所以526
6
6
x πππ-≤-≤.
当262
x ππ-=,即3
x π=
时,()g x 有最大值,最大值为1;
当26
6
x ππ-=-,即0x =时,()g x 有最小值,最小值为12
-
.……13分
11.解:(Ⅰ)2
34
cos
4
sin
4
sin
3)4
(
2
-
+=π
π
π
π
f
2
1=. ……………4分
(Ⅱ)2)
2cos 1(3)(x x f -=+
2
32sin 21-
x
x x 2cos 2
32sin 2
1-
=
)3
2sin(π
-
=x . ……………6分
2
0π
<
23 23 ππ π < - <- ∴x . ∴当23 2 x π π - = 时,即12 5π=x 时,)(x f 的最大值为1. …………8分 (Ⅲ) )3 2sin()(π- =x x f , 若x 是三角形的内角,则π< 5323π<π- <π- x . 令21)(=x f ,得2 1)32sin(= π- x , ∴6 3 2π=π- x 或6 53 2π= π- x , 解得4 π=x 或12 7π=x . ……………10分 由已知,B A ,是△ABC 的内角,B A <且2 1)()(==B f A f , ∴4 π= A ,12 7π= B , ∴6 π=--π=B A C . ……………11分 又由正弦定理,得 22 1226 sin 4sin sin sin = =ππ== C A AB BC . ……………13分 12.解: (Ⅰ)因为点(1,P 在角α的终边上, 所以sin 2 α=-,1cos 2 α=, ………………2分 所以2 2 ()22sin cos 2sin f αααααα= -=- ………………4分 2 1(2(32 2 2 =- ? -?- =-. ………………5分 (Ⅱ)2 ()22sin f x x x = -2cos 21x x = +- ………………6分 2sin(2)16 x π =+ -, ………………8分 因为[, ]6 3 x π π ∈-,所以6 56 26 ππ π ≤ + ≤- x , ………………10分 所以1sin(2)12 6 x π - ≤+ ≤, ………………11分 所以()f x 的值域是[2,1]-. ………………13分 13.解:(Ⅰ)sin 2 A = ……………2分 由 sin sin a b A B = 得1sin 2 B = , 6 B π = (5) 分 (Ⅱ) 2c = ………………6分 2 ()cos 22sin ()6 f x x x π =++ =cos 2cos(2)13 x x π -+ + 1cos 2cos 2212 2 x x x =- + +sin(2)16 x π =+ + ………………10分 所以,所求函数的最小正周期为π 由222,26 2 k x k k Z π π π ππ- ≤+ ≤+ ∈ 得,3 6 k x k k Z π π ππ- ≤≤+ ∈ 所以所求函数的单增区间为 [,],3 6 k k k Z π π ππ- + ∈ ……………………………13分 14.解:(Ⅰ)因为2cos cos c b B a A -=, 所以(2)cos cos c b A a B -?=? 由正弦定理,得(2sin sin )cos sin cos C B A A B -?=?. 整理得2sin cos sin cos sin cos C A B A A B ?-?=?. 所以2sin cos sin()sin C A A B C ?=+=. 在△ABC 中,sin 0C ≠. 所以1cos 2 A = ,3 A π∠= . (Ⅱ)由余弦定理2 2 2 1cos 22 b c a A bc +-= = ,a = 所以22 20220b c bc bc +-=≥- 所以20bc ≤,当且仅当b c =时取“=” . 所以三角形的面积1sin 2 S bc A = ≤ 所以三角形面积的最大值为. 15.解:(Ⅰ)因为 ππ4 2 A << ,且πsin()410A + = 所以ππ3π2 4 4 A <+< ,πcos()4 10A + =-. 因为ππππππcos cos[()]cos()cos sin()sin 4 4 4 4 4 4 A A A A =+ -=+++ 310 2 10 2 5 =- ? + = . 所以3cos 5 A =. ……………………6分 (Ⅱ)由(Ⅰ)可得4sin 5A =.新 课 标 第一 网 所以5()cos 2sin sin 2 f x x A x =+ 212sin 2sin x x =-+ 2 132(sin )22 x =-- + ,x ∈R . 因为sin [1,1]x ∈-,所以,当1sin 2 x =时,()f x 取最大值 32 ; 当sin 1x =-时,()f x 取最小值3-. 所以函数()f x 的值域为3 [3,]2-. ……………………13分 16.解:(Ⅰ)由题意,sin()04 x π+ ≠, ………2分 所以()4 x k k π+ ≠π∈Z , ………………3分 所以()4 x k k π≠π- ∈Z , ………………4分 函数()f x 的定义域为{x x ≠,4 k k ππ-∈Z }. ………………5分 (Ⅱ)cos 2cos 2()sin()sin cos cos sin 44 4 x x f x x x x = = πππ+ + ………………7分 2sin cos x x x = + ………………8分 22 sin )sin )sin cos x x x x x x -= =-+. ………………10分 因为4()3 f x =,所 以cos sin 3 x x -= . ………………11分 所以,2sin 21(cos sin )x x x =-- ………………12分 81199 =- = . ………………13分 17.解:(1)()2sin(2)6 f x x π =+,函数()f x 的最小正周期为π; (2)226 6 3 x π π π-≤+≤ ,当26 2 x π π += 即6 x π = 时,函数()f x 取得最大值2; 当26 6 x π π +=- 即6 x π =-时,函数()f x 取得最小值1-; 18.解:(Ⅰ)由3133,3 q S == 得113 a = ,所以2 3n n a -=; (Ⅱ)由(Ⅰ)得33a =,因为函数()f x 最大值为3,所以3A =, 又当6 x π = 时函数()f x 取得最大值,所以sin( )13 π ?+=,因为0?π<<,故6 π ?= , 所以函数()f x 的解析式为()3sin(2)6 f x x π =+。 19.(Ⅰ)f (θ)=2;(Ⅱ) θ=0时f (θ)min =1,θ=π 3时f (θ)min =2。 20. . 65165413 55 31312sin sin cos cos )cos(. 5 4sin ],2 [0,,53cos ,5 6cos 2)2 sin(2)23(; 13 12cos ],2 [0,,13 5sin ,13 10sin 2)2 3()2(.24 sin 2)6 12 5sin( 2)4 5( )1(:=? -?= -=+∴= ∴∈=∴==+ =+=∴∈= ∴==+ ==- =βαβαβαβπβββπβπβαπαααπαππππ f f f 解 21.解:(1)(0)2sin()2sin 16 6 f π π =-=-=- (2) 101(3)2sin[(3)]2sin ,13 2326 61(32)2sin[(32)]2sin()2cos 5362 53sin ,cos ,13 5 12cos , 13 4sin 5 5312463sin()sin cos cos sin 13513565 f f π ππ αααππ βπβπββαβαβαβαβαβ=+ =?+-==+=?+-=+=∴== ∴== = = ∴+=+= ?+?= 22. (1)sin()2cos ,sin ,cos 0,tan 06 3 A A A A A A A A π π π+ =∴= ≠= <<∴= (2)在三角形中 ,2 2 2 2 1cos ,3,2cos 8,3 A b c a b c bc A c a = =∴=+-== 由正弦定理得:sin sin c A C = ,而sin 3 A == 1sin 3 C ∴= .(也可以先 推出直角三角形) ( 也能根据余弦定理得到1cos 0sin 3 3 C C C π=< ) 23.(Ⅰ)解析:7733()sin cos cos sin cos cos sin sin 4 4 4 4 f x x x x x ππππ=+++ x x = - 2sin()4 x π=- ,∴()f x 的最小正周期2T π =,最小值min ()2f x =-. (Ⅱ)证明:由已知得4cos cos sin sin 5 αβαβ+=,4cos cos sin sin 5 αβαβ-=- 两式相加得2cos cos 0αβ=,∵02 παβ<<≤,∴cos 0β=,则2 πβ=. ∴22 [()]24sin 20 4f πβ-=-=. 24.(Ⅰ)由( )2 cos 2cos 1f x x x x =+-得 ( ))( )2 2sin cos 2cos 12cos 22sin 26f x x x x x x x π? ?= +-= +=+ ?? ?. 所以函数的最小正周期为22T π π= =.因为0,2x π?? ∈???? ,所以72,666x πππ??+∈????. 所以2,662x π ππ??+ ∈????,即0,6x π?? ∈???? 时,函数()f x 为增函数,而在,62x ππ?? ∈? ??? 时,函数()f x 为减函数,所以2sin 262f ππ??== ???为最大值,72sin 126f ππ?? ===- ? ?? 为最小值. (Ⅱ)由(Ⅰ)知,()002sin 26f x x π? ? =+ ?? ? ,又由已知()065 f x = ,则 03s i n 265x π? ?+= ?? ?. 因为0,42x ππ?? ∈????,则0272,636x πππ??+∈???? ,因此0cos 206x π??+< ???, 所以04 cos 265x π? ? + =- ?? ?,于是00 cos 2cos 266x x ππ????=+- ???? ???, 00cos 2cos sin 2sin 6666x x ππππ??? ?=+++ ? ????? 4313525210-=-?+?=. 25.(Ⅰ)在A B C ?中,由 cos cos A C B A B C = 及正弦定理得 sin cos sin cos B B C C = , 于是sin cos cos sin 0B C B C -=,即()sin 0B C -=, 因为0B π<<,0C π<<,则B C ππ-<-<, 因此0B C -=,所以B C =. (Ⅱ)由A B C π++=和(Ⅰ)得2A B π=-, 所以()1cos 2cos 2cos 3 B B A π=--=-= , 又由B C =知02B π<<,所以sin 23 B = .sin 42sin 2cos 29 B B B ==. 2 2 7cos 4cos 2sin 29 B B B =-=- . 所以sin 4sin 4cos cos 4sin 333 18 B B B ππ π ? ? + =+= ?? ?. 26.解:(Ⅰ)π()1cos 221sin 222f x x x x x ????=-+- =+- ?????? ?∵ π12sin 23x ? ?=+- ?? ?. (3) 分 又ππ,42x ?? ∈? ?? ?∵,ππ2π26 3 3 x - ∴ ≤≤ ,即π212sin 233x ? ? +- ?? ? ≤≤, max min ()3,()2 f x f x ==∴.……………………………………………………………7分 (Ⅱ)()2()2()2f x m f x m f x - ∈? ?? ?,……………………………9分 max ()2 m f x >-∴且min ()2m f x <+,14 m < <∴,即m 的取值范围是(1,4).……14分 27.略 1.已知函数f(x)=sin(ωx)﹣2sin2+m(ω>0)的最小正周期为3π,当x∈[0,π]时,函数f(x)的最小值为0. (1)求函数f(x)的表达式; (2)在△ABC中,若f(C)=1,且2sin2B=cosB+cos(A﹣C),求sinA的值. 解:(Ⅰ). 依题意:函数. 所以. , 所以f(x)的最小值为m.依题意,m=0. . (Ⅱ)∵,∴ .. 在Rt△ABC中,∵, ∴. ∵0<sinA<1,∴. 2.已知函数(其中ω>0),若f(x)的一条对称轴离最近的对称中心的距离为. (I)求y=f(x)的单调递增区间; (Ⅱ)在△ABC中角A、B、C的对边分别是a,b,c满足(2b﹣a)cosC=c?cosA,则f(B)恰是f(x)的最大值,试判断△ABC的形状. 【解答】解:(Ⅰ)∵ , =, ∵f(x)的对称轴离最近的对称中心的距离为, ∴T=π,∴,∴ω=1,∴. ∵得:, ∴函数f(x)单调增区间为; (Ⅱ)∵(2b﹣a)cosC=c?cosA,由正弦定理, 得(2sinB﹣sinA)cosC=sinC?cosA2sinBcosC=sinAcosC+sinCcosA=sin(A+C), ∵sin(A+C)=sin(π﹣B)=sinB>0,2sinBcosC=sinB, ∴sinB(2cosC﹣1)=0,∴,∵0<C<π,∴,∴, ∴.∴, 根据正弦函数的图象可以看出,f(B)无最小值,有最大值y max=1, 此时,即,∴,∴△ABC为等边三角形. 3.已知函数f(x)=sinωx+cos(ωx+)+cos(ωx﹣)﹣1(ω>0),x∈R,且函数的最小正周期为π: (1)求函数f(x)的解析式; (2)在△ABC中,角A、B、C所对的边分别是a、b、c,若f(B)=0,?=,且a+c=4,试求b的值. 【解答】解:(1)f(x)=sinωx+cos(ωx+)+cos(ωx﹣)﹣1 ==. ∵T=,∴ω=2. 则f(x)=2sin(2x)﹣1; (2)由f(B)==0,得. ∴或,k∈Z. ∵B是三角形内角,∴B=. 而=ac?cosB=,∴ac=3. 三角函数及解三角形练习题 一.解答题(共16小题) 1.在△ABC中,3sinA+4cosB=6,4sinB+3cosA=1,求C的大小. 2.已知3sinθtanθ=8,且0<θ<π. (Ⅰ)求cosθ; (Ⅱ)求函数f(x)=6cosxcos(x﹣θ)在[0,]上的值域. 3.已知是函数f(x)=2cos2x+asin2x+1的一个零点. (Ⅰ)数a的值; (Ⅱ)求f(x)的单调递增区间. 4.已知函数f(x)=sin(2x+)+sin2x. (1)求函数f(x)的最小正周期; (2)若函数g(x)对任意x∈R,有g(x)=f(x+),求函数g(x)在[﹣,]上的值域. 5.已知函数f(x)=2sinωxcosωx+cos2ωx(ω>0)的最小正周期为π.(1)求ω的值; (2)求f(x)的单调递增区间. 6.已知函数f(x)=sin(ωx+φ)(ω>0,﹣≤φ<)的图象关于直线x=对称,且图象上相邻两个最高点的距离为π. (Ⅰ)求ω和φ的值; (Ⅱ)若f()=(<α<),求cos(α+)的值. 7.已知向量=(cosx,sinx),=(3,﹣),x∈[0,π]. (1)若∥,求x的值; (2)记f(x)=,求f(x)的最大值和最小值以及对应的x的值. 8.已知函数的部分图象如图所示. (1)求函数f(x)的解析式; (2)在△ABC中,角A,B,C的对边分别是a,b,c,若(2a﹣c)cosB=bcosC,求的取值围. 9.函数f(x)=2sin(ωx+φ)(ω>0,0<φ<)的部分图象如图所示,M 为最高点,该图象与y轴交于点F(0,),与x轴交于点B,C,且△MBC的面积为π. (Ⅰ)求函数f(x)的解析式; (Ⅱ)若f(α﹣)=,求cos2α的值. 10.已知函数. (Ⅰ)求f(x)的最大值及相应的x值; (Ⅱ)设函数,如图,点P,M,N分别是函数y=g(x)图象的零值点、最高点和最低点,求cos∠MPN的值. 11.设函数f(x)=sin(ωx﹣)+sin(ωx﹣),其中0<ω<3,已知f ()=0. 三角函数高考试题精选 一.选择题(共18小题) 1.(2017?山东)函数y=sin2x+cos2x的最小正周期为( ) A. B.?C.πD.2π 2.(2017?天津)设函数f(x)=2sin(ωx+φ),x∈R,其中ω>0,|φ|<π.若f()=2,f()=0,且f(x)的最小正周期大于2π,则() A.ω=,φ=B.ω=,φ=﹣ C.ω=,φ=﹣D.ω=,φ= 3.(2017?新课标Ⅱ)函数f(x)=sin(2x+)的最小正周期为()A.4πB.2π?C.π?D. 4.(2017?新课标Ⅲ)设函数f(x)=cos(x+),则下列结论错误的是()A.f(x)的一个周期为﹣2π B.y=f(x)的图象关于直线x=对称 C.f(x+π)的一个零点为x= D.f(x)在(,π)单调递减 5.(2017?新课标Ⅰ)已知曲线C :y=cosx,C2:y=sin(2x+),则下面结论 1 正确的是() A.把C1上各点的横坐标伸长到原来的2倍,纵坐标不变,再把得到的曲线向右平移个单位长度,得到曲线C2 B.把C 上各点的横坐标伸长到原来的2倍,纵坐标不变,再把得到的曲线向左平1 移个单位长度,得到曲线C2 C.把C1上各点的横坐标缩短到原来的倍,纵坐标不变,再把得到的曲线向右平移个单位长度,得到曲线C2 D.把C1上各点的横坐标缩短到原来的倍,纵坐标不变,再把得到的曲线向左 平移个单位长度,得到曲线C2 6.(2017?新课标Ⅲ)函数f(x)=sin(x+)+cos(x﹣)的最大值为()A.?B.1?C.D. 7.(2016?上海)设a∈R,b∈[0,2π),若对任意实数x都有sin(3x﹣)=sin(ax+b),则满足条件的有序实数对(a,b)的对数为( ) A.1 B.2 C.3?D.4 8.(2016?新课标Ⅲ)若tanα=,则cos2α+2sin2α=() A.? B.C.1 D. 9.(2016?新课标Ⅲ)若tanθ=﹣,则cos2θ=() A.﹣B.﹣C.D. 10.(2016?浙江)设函数f(x)=sin2x+bsinx+c,则f(x)的最小正周期() A.与b有关,且与c有关B.与b有关,但与c无关 C.与b无关,且与c无关? D.与b无关,但与c有关 11.(2016?新课标Ⅱ)若将函数y=2sin2x的图象向左平移个单位长度,则平移后的图象的对称轴为() A.x=﹣(k∈Z)?B.x=+(k∈Z)?C.x=﹣(k∈Z)D.x=+(k∈Z) 12.(2016?新课标Ⅰ)已知函数f(x)=sin(ωx+φ)(ω>0,|φ|≤),x=﹣ 为f(x)的零点,x=为y=f(x)图象的对称轴,且f(x)在(,)上单调,则ω的最大值为( ) A.11 B.9 C.7 D.5 13.(2016?四川)为了得到函数y=sin(2x﹣)的图象,只需把函数y=sin2x 的图象上所有的点() A.向左平行移动个单位长度?B.向右平行移动个单位长度 三角函数、解三角形 1.弧长公式:r l α= 扇形面积公式:22 121r lr S α== 2.同角三角函数的基本关系式: 平方关系:1cos sin 2 2 =+αα 商数关系:sin tan cos α αα = 3.三角函数的诱导公式: 诱导公式(把角写成απ ±2 k 形式,利用口诀:奇变偶不变,符号看象限) 公式一()()()?????=?+=?+=?+απααπααπαtan 2tan cos 2cos sin 2sin k k k 公式二()()()?????=+=+=+ααπααπααπtan tan cos -cos -sin sin 公式三()()()?? ? ??=-=-=-ααααααtan -tan cos cos -sin sin 公式四()()()?????=-=-=-ααπααπααπtan -tan cos -cos sin sin 公式五???????=??? ??-=??? ??-ααπααπsin 2cos cos 2sin 公式六???????=??? ??+=?? ? ??+ααπααπsin -2 cos cos 2sin 4.两角和与差的正弦、余弦、正切公式: βαβαβαcos sin cos sin )sin(+=+ βαβαβαcos sin cos sin )sin(-=- βαβαβαsin sin cos cos )cos(-=+ βαβαβαsin sin cos cos )cos(+=- βαβαβαtan tan 1tan tan )tan(-+= + β αβαβαtan tan 1tan tan )tan(+-=- 5.二倍角公式: a a a cos sin 22sin = 1cos 2sin 21sin cos 2cos 2222-=-=-=a a a a a a a a 2tan 1tan 22tan -= 6.辅助角公式: sin cos a b αα+ )α?+( 其中sin tan b a ???= = = ). 比如: x x y cos 3sin += ) cos ) 3(13sin ) 3(11( )3(12 2 2 2 22x x ++ ++= )cos 23sin 21(2x x += )3 sin cos 3cos (sin 2ππx x +=)3sin(2π+=x 7.正弦定理: 2sin sin sin a b c R C ===A B (R 为△ABC 外接圆的半径) 8.余弦定理:2 2 2 2cos a b c bc =+-A ,2 2 2 2cos b a c ac =+-B ,2 2 2 2cos c a b ab C =+- 推论:222cos 2b c a bc +-A =,222cos 2a c b ac +-B =,222 cos 2a b c C ab +-=. 学思堂教育个性化教程教案 数学科教学设计 学生姓名教师姓名刘梦凯班主任日期时间段年级课时教学内容 教学目标 重点 难点 教学过程 命题点二解三角形 难度:高、中、低命题指数:☆☆☆☆☆ 1.(2015·安徽高考)在△ABC中,AB=6,∠A=75°,∠B=45°,则 AC=________. 2.(2015·广东高考改编)设△ABC的内角A,B,C的对边分别为a,b, c.若a=2,c=2 3,c os A= 3 2 且b<c,则b=________. 3.(2015·北京高考)在△ABC中,a=3,b=6,∠A= 2π 3 ,则∠B= ________. 4.(2015·福建高考)若△ABC中,A C=3,A=45°,C=75°,则 BC=________. 5.(2015·全国卷Ⅰ)已知a,b,c分别为△ABC内角A,B,C的对边, sin2B=2sin A sin C. (1)若a=b,求cos B;[来源:学科网ZXXK] (2)设B=90°,且a=2,求△ABC的面积. 教 学 效 果 分 析 教学过程 6.(2015·山东高考)△ABC中,角A,B,C所对的边分别为a,b,c. 已知cos B= 3 3 ,sin(A+B)= 6 9 ,ac=23,求sin A和c的值. 7.(2015·全国卷Ⅱ)△ABC中,D是BC上的点,AD平分∠BAC,BD= 2DC. (1)求 sin B sin C ; (2)若∠BAC=60°,求∠B. 8.(2015·浙江高考)在△ABC中,内角A,B,C所对的边分别为a,b, c,已知tan ? ? ?? ? π 4 +A=2. (1)求 sin 2A sin 2A+cos2A 的值; (2)若B= π 4 ,a=3,求△ABC的面积.[来源:学科 教 学 效 果 分 析 三角函数与解三角形 一、选择题 (2016·7)若将函数y =2sin 2x 的图像向左平移 12 π个单位长度,则平移后图象的对称轴为( ) A .()26k x k Z ππ =-∈ B .()26k x k Z ππ =+∈ C .()212 k x k Z ππ =-∈ D .()212 k x k Z ππ =+∈ (2016·9)若3 cos( )45 π α-=,则sin 2α =( ) A . 725 B .15 C .1 5 - D .7 25 - (2014·4)钝角三角形ABC 的面积是12 ,AB =1,BC ,则AC =( ) A .5 B C .2 D .1 (2012·9)已知0>ω,函数)4sin()(π ω+ =x x f 在),2(ππ 单调递减,则ω的取值范围是() A. 15 [,]24 B. 13[,]24 C. 1(0,]2 D. (0,2] (2011·5)已知角θ的顶点与原点重合,始边与x 轴的正半轴重合,终边在直线y =2x 上,则cos2θ =( ) A .45 - B .35 - C .35 D .45 (2011·11)设函数()sin()cos()(0,||)2 f x x x π ω?ω?ω?=+++>< 的最小正周期为π,且()()f x f x -=, 则( ) A .()f x 在(0,)2π 单调递减 B .()f x 在3(,)44 ππ 单调递减 C .()f x 在(0,)2π 单调递增 D .()f x 在3(,)44 ππ 单调递增 二、填空题 (2017·14)函数()23sin 4f x x x =- (0,2x π?? ∈???? )的最大值是 . (2016·13)△ABC 的内角A 、B 、C 的对边分别为a 、b 、c ,若cos 4 5 A = ,1cos 53C =,a = 1,则b = . (2014·14)函数()sin(2)2sin cos()f x x x ???=+-+的最大值为_________. (2013·15)设θ为第二象限角,若1 tan()42 πθ+=,则sin cos θθ+=_________. (2011·16)在△ABC 中,60,B AC ==o 2AB BC +的最大值为 . 三、解答题 初三三角函数试题精选 一.选择题(共10小题) 1.(2016?安顺)如图,在网格中,小正方形的边长均为1,点A,B,C都在格点上,则∠ABC的正切值是() A.2 B.C.D. 2.(2016?乐山)如图,在Rt△ABC中,∠BAC=90°,AD⊥BC于点D,则下列结论不正确的是() A.B.C.D. 3.(2016?攀枝花)如图,点D(0,3),O(0,0),C(4,0)在⊙A上,BD是⊙A的一条弦,则sin∠OBD=() A.B.C.D. 4.(2016?西宁)如图,在△ABC中,∠B=90°,tan∠C=,AB=6cm.动点P从点A开始 沿边AB向点B以1cm/s的速度移动,动点Q从点B开始沿边BC向点C以2cm/s的速度移动.若P,Q两点分别从A,B两点同时出发,在运动过程中,△PBQ的最大面积是() A.18cm2B.12cm2C.9cm2 D.3cm2 5.(2016?绵阳)如图,△ABC中AB=AC=4,∠C=72°,D是AB中点,点E在AC上,DE⊥AB,则cosA的值为() A.B.C.D. 6.(2016?福州)如图,以圆O为圆心,半径为1的弧交坐标轴于A,B两点,P是上一点(不与A,B重合),连接OP,设∠POB=α,则点P的坐标是() A.(sinα,sinα) B.(cosα,cosα)C.(cosα,sinα) D.(sinα,cosα) 7.(2016?重庆)如图所示,某办公大楼正前方有一根高度是15米的旗杆ED,从办公楼顶端A测得旗杆顶端E的俯角α是45°,旗杆底端D到大楼前梯坎底边的距离DC是20米,梯坎坡长BC是12米,梯坎坡度i=1:,则大楼AB的高度约为()(精确到0.1米,参考数据:≈1.41,≈1.73,≈2.45) A.30.6 B.32.1 C.37.9 D.39.4 8.(2016?苏州)如图,长4m的楼梯AB的倾斜角∠ABD为60°,为了改善楼梯的安全性能,准备重新建造楼梯,使其倾斜角∠ACD为45°,则调整后的楼梯AC的长为() A.2m B.2m C.(2﹣2)m D.(2﹣2)m 课程标题三角函数与解三角形 求三角函数得定义域实质就就就是解三角不等式(组)、一般可用三角函数得图象或三角函数线确定三角不等式得解、列三角不等式,既要考虑分式得分母不能为零;偶次方根被开方数大于等于零;对数得真数大于零及底数大于零且不等于1,又要考虑三角函数本身得定义域; 求三角函数得值域得常用方法:1、化为求得值域; ,引入辅助角,化为求解方法同类型。 2、化为关于(或)得二次函数式; ,设,化为二次函数在上得最值求之; 周期问题一般将函数式化为(其中为三角函数,)、 ) ②y=tanx图象得对称中心(,0) (二)主要方法: 1、函数得单调增区间可由 解出,单调减区间可由解出; 周期 2、函数得单调减区间可由 解出,单调增区间呢。(自己导出)周期 3、函数得单调增区间可由 解出。(无增区间,重点掌握) 周期 课堂练习: 1.已知函数得定义域为,值域为,求常数得值 (化为求得值域)、 2、函数得单调递减区间就就是 3、函数得单调增区间为 2、函数,、 (Ⅰ)求函数得最小正周期;(Ⅱ)求函数在区间上得最小值与最大值、(化为求得值域)、 3、函数得一个单调增区间就就是 ???? 4、若函数,则就就是 最小正周期为得奇函数最小正周期为得奇函数 最小正周期为得偶函数最小正周期为得偶函数 5、函数得最大值 6、当函数得最大值为时,求得值、 7、函数得最大值就就是 8、已知函数,、 (1)求得最大值与最小值;(2)f(x)得最小正周期。 (3)若不等式在上恒成立,求实数得取值范围、 解三角形 正弦定理:, 余弦定理: 推论:正余弦定理得边角互换功能 ① ,, ②,, ③== ④ (4)面积公式:S=ab*sinC=bc*sinA=ca*sinB 课堂练习: 1、在中,角得对边分别为,已知,则( ) A、1 ?B.2 C、???D、 2、在△ABC中,AB=3,BC=,AC=4,则边AC上得高为( ) A、B、 C、D、 3、在ΔABC中,已知a=,b=,B=45°,求角A,角C得大小及边c得长度。 4、得内角A、B、C得对边分别为a、b、c,若a、b、c成等比数列,且,则() A、 B、 C、D、 【填空题】 5、在中,分别就就是、、所对得边。若,,,则__________ 6、在锐角△ABC中,边长a=1,b=2,则边长c得取值范围就就是_______、 7、已知锐角得面积为,,则角得大小为( ) ?A、75°?B、60° ?C、45°D、30° 8、在△中,若,则等于、 9、在中,已知,则得大小为 ( ) ??? 【解答题】 10、在中,分别就就是三个内角得对边、若,,求得面积、 11、如图,就就是等边三角形,就就是等腰直角三角形,∠=,交于,、 ?(1)求∠得得值; (2)求、 12、在中,角A、B、C所对得边分别为a,b,c,且满足 必修四三角函数与解三角形综合测试题 (本试卷满分150分,考试时间120分) 第Ⅰ卷(选择题 共40分) 一.选择题(本大题共12小题,每小题5分,共60分。在每小题给出的四个选项中,只有一项是符合题目要求的) 1.若点P 在3 2π的终边上,且OP=2,则点P 的坐标( ) A .)3,1( B .)1,3(- C .)3,1(-- D .)3,1(- 2.已知=-=-ααααcos sin ,4 5cos sin 则( ) A .47 B .169- C .329- D .32 9 3.下列函数中,最小正周期为 2 π的是( ) A .)32sin(π-=x y B .)32tan(π-=x y C .)62cos(π+=x y D .)6 4tan(π+=x y 4.等于则)2cos(),,0(,31cos θππθθ+∈=( ) A .924- B .924 C .9 7- D .97 5.函数y =sin (π4 -2x )的单调增区间是 ( ) A.[kπ-3π8 ,kπ+π8 ](k ∈Z ) B.[kπ+π8 ,kπ+5π8 ](k ∈Z ) C.[kπ-π8 ,kπ+3π8 ](k ∈Z ) D.[kπ+3π8 ,kπ+7π8 ](k ∈Z ) 6.将函数x y 4sin =的图象向左平移12 π个单位,得到)4sin(?+=x y 的图象,则?等于( ) A .12π- B .3π- C .3 π D .12π 7.οοοο50tan 70tan 350tan 70tan -+的值等于( ) A .3 B .33 C .33- D .3- 8.在△ABC 中,sinA >sinB 是A >B 的( ) A .充分不必要条件 B .必要不充分条件 C .充要条件 D .既不充分也不必要条件 9.ABC ?中,π= A ,BC =3,则ABC ?的周长为( ) 2018-2019学年高三一模理分类---三角函数和解三角形 海淀(理) (15)(本小题满分13分) 已知函数()cos()cos 4 f x x x a π =-+ (Ⅱ)求a 的值; (Ⅱ)求函数()f x 的单调递增区间. 文)已知函数()cos()cos 4 f x x x a π =-+的图象经过点(O,l),部分图象如图所示. (I)求a 的值; (Ⅱ)求图中0x 的值,并直接写出函数()f x 的单调递增区间. 朝阳 (理)15.(本小题满分13分) 在ABC △中,a ,120A ∠=?,ABC △b c <. (Ⅰ)求b 的值; (Ⅱ)求cos 2B 的值. (文)15.(本小题满分13分) 已知函数2 ()cos cos f x x x x =. (Ⅰ)求( )3 f π 的值及()f x 的最小正周期; (Ⅱ)若函数()f x 在区间[0,]m 上单调递增,求实数m 的最大值. 石景山 (文 理)15. (本小题13分) 在ABC △中,角A B C , ,的对边分别为a b c ,, ,b=3c =,1 cos 3 B=-. (Ⅰ)求sin C 的值; (Ⅱ)求ABC △的面积. 丰台 (理)15.(本小题13分) 已知函数2()cos(2)2sin ()3f x x x a a π =--+∈R ,且()03 f π=. (Ⅰ)求a 的值; (Ⅱ)若()f x 在区间[0,]m 上是单调函数,求m 的最大值. 延庆 (理)15.(本小题满分13分) 如图,在ABC ?中,点D 在BC 边上,cos ADB ∠=,3cos =5 C ∠,7AC =. sin CA D ∠(求Ⅰ)的值; (Ⅱ)若10BD =, 求AD 的长及ABD ?的面积. 怀柔 15.(本小题满分13分) 在 中,角,,所的对边分别是a ,b ,c , , . (Ⅰ)求边c 的值; (Ⅱ)若,求 的面积. 门头沟 A D B C 三角函数题解 1.(2003上海春,15)把曲线y cos x +2y -1=0先沿x 轴向右平移 2 π个单位,再沿y 轴向 下平移1个单位,得到的曲线方程是( ) A.(1-y )sin x +2y -3=0 B.(y -1)sin x +2y -3=0 C.(y +1)sin x +2y +1=0 D.-(y +1)sin x +2y +1=0 2.(2002春北京、,5)若角α满足条件sin2α<0,cos α-sin α<0,则α在( ) A.第一象限 B.第二象限 C.第三象限 D.第四象限 3.(2002上海春,14)在△ABC 中,若2cos B sin A =sinC ,则△ABC 的形状一定是( ) A.等腰直角三角形 B.直角三角形 C.等腰三角形 D.等边三角形 4.(2002京皖春文,9)函数y =2sin x 的单调增区间是( ) A.[2k π- 2 π,2k π+ 2 π](k ∈Z ) B.[2k π+ 2 π ,2k π+ 23π](k ∈Z ) C.[2k π-π,2k π](k ∈Z ) D.[2k π,2k π+π](k ∈Z ) 5.(2002全国文5,理4)在(0,2π),使sin x >cos x 成立的x 取值范围为( ) A.( 4π , 2 π )∪(π, 45π) B.( 4 π,π) C.( 4π , 4 5π ) D.( 4 π,π)∪( 45π,2 3π) 6.(2002北京,11)已知f (x )是定义在(0,3)上的函数,f (x )的图象如图4—1所示,那么不等式f (x )cos x <0的解集是( ) A.(0,1)∪(2,3) B.(1, 2 π )∪( 2 π,3) 图4—1 高中数学必修五 第一章 解三角形知识点归纳 1、三角形三角关系:A+B+C=180°;C=180°—(A+B); 2、三角形三边关系:a+b>c; a-b 三角函数的概念、诱导公式与三角恒等变换 6.(2019浙江18)设函数()sin ,f x x x =∈R . (1)已知[0,2),θ∈π函数()f x θ+是偶函数,求θ的值; (2)求函数22[()][()]124 y f x f x ππ =+ ++ 的值域. 解析(1)因为()sin()f x x θθ+=+是偶函数,所以,对任意实数x 都有 sin()sin()x x θθ+=-+, 即sin cos cos sin sin cos cos sin x x x x θθθθ+=-+, 故2sin cos 0x θ=, 所以cos 0θ=. 又[0,2π)θ∈,因此π2θ= 或3π2 . (2)2 2 22ππππsin sin 124124y f x f x x x ? ???????????=+++=+++ ? ? ? ???????????? ????? ππ1cos 21cos 213621cos 2sin 222222x x x x ??? ?-+-+ ? ? ??????=+=-- ? ??? π123x ? ?=+ ?? ?. 因此,函数的值域是[1- +. 27.(2018江苏)已知,αβ为锐角,4 tan 3 α= ,cos()5αβ+=-. (1)求cos2α的值; (2)求tan()αβ-的值. 【解析】(1)因为4tan 3α= ,sin tan cos ααα=,所以4 sin cos 3 αα=. 因为22sin cos 1αα+=,所以29 cos 25 α= , 因此,27cos22cos 125 αα=-=- . (2)因为,αβ为锐角,所以(0,π)αβ+∈. 又因为cos()αβ+=,所以sin()αβ+=, 因此tan()2αβ+=-. 因为4tan 3α=,所以22tan 24 tan 21tan 7 ααα==--, 因此,tan 2tan()2 tan()tan[2()]1+tan 2tan()11ααβαβααβααβ-+-=-+==-+. 28.(2018浙江)已知角α的顶点与原点O 重合,始边与x 轴的非负半轴重合,它的终边过 点3 4(,)55 P --. (1)求sin()απ+的值; (2)若角β满足5 sin()13 αβ+= ,求cos β的值. 【解析】(1)由角α的终边过点34(,)55P --得4 sin 5α=-, 所以4 sin()sin 5απα+=-=. (2)由角α的终边过点34(,)55P --得3 cos 5 α=-, 由5sin()13αβ+=得12 cos()13 αβ+=±. 由()βαβα=+-得cos cos()cos sin()sin βαβααβα=+++, 所以56cos 65β=-或16 cos 65 β=-. 29.(2017浙江)已知函数22 ()sin cos cos f x x x x x =--()x ∈R . (Ⅰ)求2( )3 f π 的值; (Ⅱ)求()f x 的最小正周期及单调递增区间. 【解析】(Ⅰ)由2sin 32π=,21 cos 32 π=-, 解三角形3 一、选择题 1.在ABC ?中,6=a , 30=B , 120=C ,则ABC ?的面积是( ) A .9 B .18 C .39 D .318 2.在ABC ?中,若 b B a A cos sin =,则B 的值为( ) A . 30 B . 45 C . 60 D . 90 3.在ABC ?中,若B a b sin 2=,则这个三角形中角A 的值是( ) A . 30或 60 B . 45或 60 C . 60或 120 D . 30或 150 4.在ABC ?中,根据下列条件解三角形,其中有两个解的是( ) A .10=b , 45=A , 70=C B .60=a ,48=c , 60=B C .7=a ,5=b , 80=A D .14=a ,16=b , 45=A 5.已知三角形的两边长分别为4,5,它们夹角的余弦是方程02322 =-+x x 的根,则第三边长是( ) A .20 B .21 C .22 D .61 二、填空题 1.在ABC ?中,若6:2:1::=c b a ,则最大角的余弦值等于_________________. 2.在ABC ?中,5=a , 105=B , 15=C ,则此三角形的最大边的长为____________. 3.在△ABC 中,若=++=A c bc b a 则,2 22_________。 4.在△ABC 中,若====a C B b 则,135,30,20 _________。 5.在△ABC 中,若sin A ∶sin B ∶sin C=7∶8∶13,则C=_____________。 6.若A 、B 是锐角三角形的两内角,则B A tan tan _____1(填>或<) 7.若在△ABC 中,∠A=,3,1,600==ABC S b 则C B A c b a sin sin sin ++++=_______。 1. 任意角的三角函数的定义: 设〉是任意一个角,p (x, y )是〉的终 边上的任意一点(异于原点),它与原点的距离是「“x 2r 2.o , 位置无关。 2. 三角函数在各象限的符号:(一全二正弦,三切四余弦) + L i + —— L + _ - + ------ ■ —— + - ■ sin : cos : tan : 3. 同角三角函数的基本关系式: 4. 三角函数的诱导公式 k 二.一 诱导公式(把角写成2 …形式,利用口诀:奇变偶不变,符 (2)商数关 系: tan-E 屮一、 cos 。(用于切化弦) (1)平方关 系: 2 2 2 sin 工 cos ■■ -1,1 tan : 1 cos 2: ※平方关系一般为隐含条件,直接运用。注意“ 1”的代换 si …y,cos 」 那么 r 三角函数值只与角的大小有关,而与终边上点 5. 特殊角的三角函数值 度 0s 30c A 45“ A 60“ 90 120c A 135“ 150s 180c 270° 360 弧 31 JI JI 2n 3兀 5兀 JI 3兀 2兀 度 6 4 3 2 3 4 6 2 si n 。 0 1 竝 迈 1 旦 1 0 1 2 2 2 2 2 2 cosa 亦 1 1 念 力 1 2 _1 1 2 2 2 2 2 号看象限) sin (2k .亠 x ) = sin x cos (2k ■亠 x ) = cosx [)tan (2k ,亠 x )二 tanx sin ( -x ) - - sin x cos (-x ) =cosx H )tan (-x ) - - tanx m ) |sin (,亠 x ) = -sin x cos (m ) = - cosx tan (二 x ) IV ) Sin (兀 _x ) =sin x cos (兀—x ) = —cosx tan (兀一 sin (— -〉)= cos ..z sin (二:)=cos : V ) -?) = sin : 2020年高考数学三角函数与解三角形大题精做例题一:在△ ABC中,内角A , B , C所对的边分别为a , b , c,已知m n cosC,cos A,且m n . (1)求角A的大小; (2 )若b c 5 , △ ABC的面积为3,求a . n,AB 4 , BC .17,点D 在AC 边上,且cos (1 )求BD的长; (2)求△ BCD的面积. 例题三:△ ABC的内角A , B , C的对边分别为a , b , c,已知a 2c cosB bcosA 0 .a,c 2b , 例题二:如图,在厶ABC中, (1 )求B ; (2)若b 3 , △ ABC的周长为3 2 3,求△ ABC的面积. 例题四:已知函数f x cos2 x 2 3 sin xcosx sin2 x . (1)求函数y f x的最小正周期以及单调递增区间; (2)已知△ ABC的内角A、B、C所对的边分别为a、b、c,若fC 1,c 2,sinC sin B A 2sin 2A,求△ ABC 的面积. 例题一:【答案】(1) A -; (2) a .13 . 3 【解析】(1)由m n ,可得 m n 0 ,艮卩2b cos A acosC ccosA , 即 2sin B cos A sin AcosC sin C cosA ,即 2sin BcosA sin A C , ?/ sin A C sin n B sin B , / ? 2sin B cosA sin B ,即 sin B 2cos A 1 0 , ?/ 0 B n, ? sin B 0 , ? cosA 1 2 ?/ 0 A n, ? A n . 3 (2) 由S A ABC J /3,可得 S A ABC 1 - bcsin A 3 , ? bc 4 , 2 又b c 5 , 由余弦定理得 2 .2 a b 2 2 c 2bccosA b c 3bc 13 ? a 13 . 例题二:【答案】(1) 3; ( 2) 4 2 . 【解析】(1)在△ ABD 中, ■/ cos ADB 1 ,? sin ADB 3 22 3 , BD AB ABsi n BAD 4 2 -Z 3 由正弦疋理一 ,? BD sin BAD sin ADB ' sin ADB 2 2 3 (2) ?/ ADB CDB n, 1 cos ADB -. 3 2 1 得 17 9 CD 2 2 3CD -,解得 CD 4或 CD 2 (舍). 3 2 例题三:【答案】(1) B 2 n; (2) S\ABC ??? △ BCD 的面积S -BD CD sin CDB 2 22 3 3.3 4 二 cos CDB cos n ADB 二 sin CDB sin n ADB sin ADB CDB 在厶BCD 中,由余弦定理 BC 2 3 2 BD 2 2 CD 2 2BD CD cos CDB , 任意角的三角函数 一、选择题 1.以下四个命题中,正确的是( ) A .在定义域内,只有终边相同的角的三角函数值才相等 B .{α|α=k π+6 π,k ∈Z }≠{β|β=-k π+6 π ,k ∈Z } C .若α是第二象限的角,则sin2α<0 D .第四象限的角可表示为{α|2k π+2 3π<α<2k π,k ∈Z } 2.若角α的终边过点(-3,-2),则( ) A .sin α tan α>0 B .cos α tan α>0 C .sin α cos α>0 D .sin α cot α>0 3.角α的终边上有一点P (a ,a ),a ∈R ,且a ≠0,则sin α的值是( ) A . 2 2 B .- 2 2 C .± 2 2 D .1 4.α是第二象限角,其终边上一点P (x ,5),且cos α=42 x ,则sin α的值为 ( ) A .410 B .46 C .42 D .-410 5.使lg (cos θ·tan θ)有意义的角θ是( ) A .第一象限角 B .第二象限角 C .第一或第二象限角 D .第一、二象限角或终边在y 轴上 6.设角α是第二象限角,且|cos 2α|=-cos 2α,则角2α 是( ) A .第一象限角 B .第二象限角 C .第三象限角 D .第四象限角 7.点P 是角α终边上的一点,且 ,则b 的值是( ) A 3 B -3 C ±3 D 5 8.在△ABC 中,若最大的一个角的正弦值是 ,则△ABC 是( ) A 锐角三角形 B 钝角三角形 C 直角三角形 D 等边三角形 9.若α是第四象限角,则 是( ) A 第二象限角 B 第三象限角 C 第一或第三象限角 D 第二或第四象限角 10.已知sin α=4 5 ,且α为第二象限角,那么tan α的值等于 ( ) 1. 任意角的三角函数的定义:设α是任意一个角,P (,)x y 是α的终边上的任意一点(异 于原点),它与原点的距离是 0r =>,那么 sin ,cos y x r r αα= =, () tan ,0y x x α=≠ 三角函数值只与角的大小有关,而与终边上点P 的位置无关。 2.三角函数在各象限的符号: (一全二正弦,三切四余弦) + + - + - + - - - + + - sin α cos α tan α 3. 同角三角函数的基本关系式: (1)平方关系: 22221sin cos 1,1tan cos αααα+=+= (2)商数关系: sin tan cos α αα= (用于切化弦) ※平方关系一般为隐含条件,直接运用。注意“1”的代换 4.三角函数的诱导公式 诱导公式(把角写成α π±2k 形式,利用口诀:奇变偶不变,符号看象限) Ⅰ)?????=+=+=+x x k x x k x x k tan )2tan(cos )2cos(sin )2sin(πππ Ⅱ)?????-=-=--=-x x x x x x tan )tan(cos )cos(sin )sin( Ⅲ) ?????=+-=+-=+x x x x x x tan )tan(cos )cos(sin )sin(πππ Ⅳ)?????-=--=-=-x x x x x x tan )tan(cos )cos(sin )sin(πππ Ⅴ)???????=-=-ααπααπsin )2cos(cos )2sin( Ⅵ)???????-=+=+ααπααπsin )2cos(cos )2sin( 题型练3大题专项(一) 三角函数、解三角形综合问题 1.(优质试题浙江,18)已知角α的顶点与原点O重合,始边与x轴的非负半轴重合,它的终边过点P. (1)求sin(α+π)的值; (2)若角β满足sin(α+β)=,求cos β的值. 2.(优质试题北京,理15)在△ABC中,a=7,b=8,cos B=-. (1)求A; (2)求AC边上的高. 3.△ABC的内角A,B,C的对边分别为a,b,c.已知△ABC的面积为. (1)求sin B sin C; (2)若6cos B cos C=1,a=3,求△ABC的周长. 4.已知函数f(x)=4tan x sin cos. (1)求f(x)的定义域与最小正周期; (2)讨论f(x)在区间上的单调性. 5.已知函数f(x)=a cos2a sin ωx-a(ω>0,a>0)在一个周期内的图象如图所示,其中点A为图象上的最高点,点B,C为图象与x轴的两个相邻交点,且△ABC是边长为4的正三角形. (1)求ω与a的值; (2)若f(x0)=,且x0∈,求f(x0+1)的值. 6.在平面直角坐标系xOy中,已知向量m=,n=(sin x,cos x),x∈. (1)若m⊥n,求tan x的值; (2)若m与n的夹角为,求x的值. 题型练3大题专项(一) 三角函数、解三角形综合问题 1.解(1)由角α的终边过点P, 得sin α=-,所以sin(α+π)=-sin α= (2)由角α的终边过点P,得cos α=-, 由sin(α+β)=,得cos(α+β)=± 由β=(α+β)-α,得cos β=cos(α+β)cos α+sin(α+β)sin α,所以cos β=-或cos β= 2.解(1)在△ABC中,∵cos B=-,∴B, ∴sin B= 由正弦定理,得, ∴sin A= ∵B,∴A,∴A= (2)在△ABC中,sin C=sin(A+B)=sin A cos B+sin B cos A= 如图所示,在△ABC中,过点B作BD⊥AC于点D. ∵sin C=,∴h=BC·sin C=7, ∴AC边上的高为 3.解(1)由题设得ac sin B=,即c sin B= 由正弦定理得sin C sin B= 故sin B sin C= (2)由题设及(1)得cos B cos C-sin B sin C=-, 即cos(B+C)=- 所以B+C=,故A= 由题设得bc sin A=,即bc=8. 由余弦定理得b2+c2-bc=9,即(b+c)2-3bc=9,得b+c= 故△ABC的周长为3+三角函数解三角形综合
三角函数与解三角形练习题
三角函数高考试题精选(含详细答案)
高中数学三角函数、解三角形知识点
三角函数-解三角形的综合应用
高考数学三角函数与解三角形练习题
初三三角函数试题精选
三角函数与解三角形
必修四三角函数与解三角形综合测试题(基础含答案)
2019年三角函数和解三角形大题
高中三角函数习题解析精选(含详细解答)
最新解三角形知识点归纳(附三角函数公式)
高考真题:三角函数及解三角形综合
三角函数习题及答案
三角函数及解三角形知识点总结
2020年高考数学三角函数与解三角形大题精做
(完整版)任意角的三角函数练习题及答案详解
三角函数与解三角形知识点总结
高考专题; 三角函数、解三角形综合问题
