整数线性规划

整数线性规划

【数学模型】

m in

T

x

f

x st.

A x b

?≤

A eq x b eq ?=

lb x ub ≤≤

i x 取值为整数

其中f , x , b , beq , lb 和ub 为向量，A 和Aeq 为矩阵。 【函数】

intprog 【说明】

在Matlab 中无求解整数线性规划的现成函数，利用Matlab 的线性规划函数linprog 来编写整数线性规划函数，输入与输出与linprog 类似，采用分枝定界法来实现。

Matlab 主程序intprog 如下：

function [x,fval,status] = intprog(f,A,B,I,Aeq,Beq,lb,ub,e) %整数规划求解函数 intprog() % 其中 f 为目标函数向量

% A 和B 为不等式约束 Aeq 与Beq 为等式约束 % I 为整数约束

% lb 与ub 分别为变量下界与上界 % x 为最优解，fval 为最优值 % 控制输入参数 if nargin < 9, e = 0.00001; if nargin < 8, ub = []; if nargin < 7, lb = []; if nargin < 6, Beq = []; if nargin < 5, Aeq = [];

if nargin < 4, I = [1:length(f)]; end , end , end , end , end , end %求解整数规划对应的线性规划,判断是否有解 options = optimset('display','off');

[x0,fval0,exitflag] = linprog(f,A,B,Aeq,Beq,lb,ub,[],options); if exitflag < 0

disp('没有合适整数解'); x = x0; fval = fval0; status = exitflag; return ; else

%采用分支定界法求解

bound = inf;

[x,fval,status] = branchbound(f,A,B,I,x0,fval0,bound,Aeq,Beq,lb,ub,e);

end

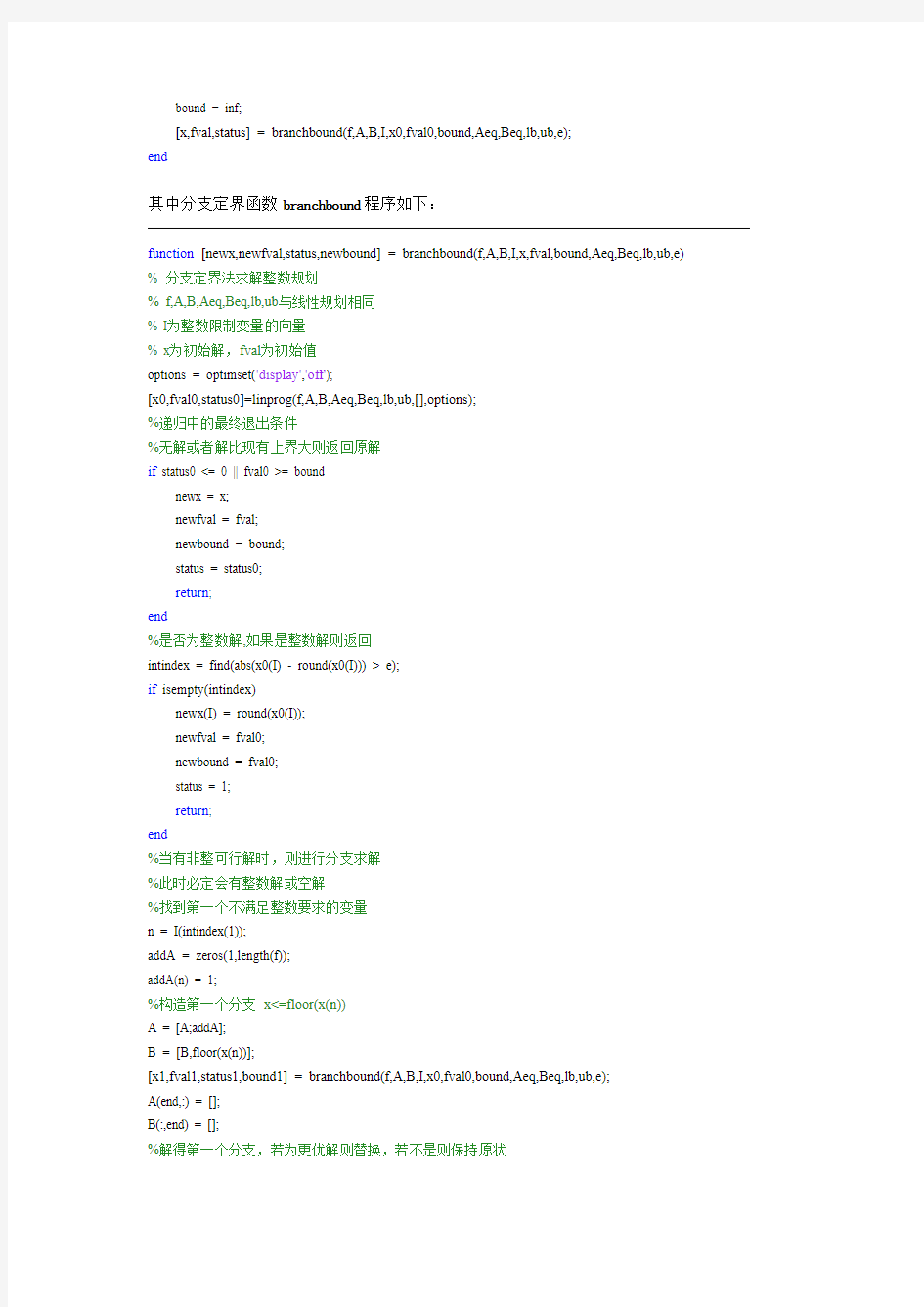
其中分支定界函数branchbound程序如下：

function [newx,newfval,status,newbound] = branchbound(f,A,B,I,x,fval,bound,Aeq,Beq,lb,ub,e) % 分支定界法求解整数规划

% f,A,B,Aeq,Beq,lb,ub与线性规划相同

% I为整数限制变量的向量

% x为初始解，fval为初始值

options = optimset('display','off');

[x0,fval0,status0]=linprog(f,A,B,Aeq,Beq,lb,ub,[],options);

%递归中的最终退出条件

%无解或者解比现有上界大则返回原解

if status0 <= 0 || fval0 >= bound

newx = x;

newfval = fval;

newbound = bound;

status = status0;

return;

end

%是否为整数解,如果是整数解则返回

intindex = find(abs(x0(I) - round(x0(I))) > e);

if isempty(intindex)

newx(I) = round(x0(I));

newfval = fval0;

newbound = fval0;

status = 1;

return;

end

%当有非整可行解时，则进行分支求解

%此时必定会有整数解或空解

%找到第一个不满足整数要求的变量

n = I(intindex(1));

addA = zeros(1,length(f));

addA(n) = 1;

%构造第一个分支x<=floor(x(n))

A = [A;addA];

B = [B,floor(x(n))];

[x1,fval1,status1,bound1] = branchbound(f,A,B,I,x0,fval0,bound,Aeq,Beq,lb,ub,e);

A(end,:) = [];

B(:,end) = [];

%解得第一个分支，若为更优解则替换，若不是则保持原状

status = status1;

if status1 > 0 && bound1 < bound newx = x1; newfval = fval1; bound = fval1; newbound = bound1; else

newx = x0; newfval = fval0; newbound = bound; end

%构造第二分支 A = [A;-addA]; B = [B,-ceil(x(n))];

[x2,fval2,status2,bound2] = branchbound(f,A,B,I,x0,fval0,bound,Aeq,Beq,lb,ub,e); A(end,:) = []; B(:,end) = [];

%解得第二分支，并与第一分支做比较，如果更优则替换 if status2 > 0 && bound2 < bound status = status2; newx = x2; newfval = fval2; newbound = bound2; end

【实例】

例11.13 汽车厂生产三种类型的汽车，已知各类型每辆车对钢材、劳动时间的需求，利润及工厂每月的现有量如下表11.1所示，若每月生产的汽车必须为整车，试制订月生产计划，使工厂的利润最大。

设每月生产小、中、大型汽车的数量分别为123,,x x x ，工厂的月利润为z ，在题目所给参数均不随生产数量变化的假设下，立即可得整数线性规划模型：

123

m ax 234z x x x =++ st. 1231.535600

x x x ++≤

1

2328025040060000

x x x ++≤

123,,0x x x ≥ 且为整数

将目标函数改为求最小值，求解的MATLAB 代码如下

f = [-2 -3 -4];

A = [1.5 3 5;280 250 400];

B = [600 60000];

I = [1:length(f)];

lb = [0 0 0];

[x,fval,status]=intprog(f,A,B,I,[],[],lb)

【输出】

x =

64 168 0

fval =

-632.0000

status =

1

由此可知，汽车厂的最优月生产计划为生产小型车64辆，中型车168辆，不生产大型车，最大利润为632。