欧拉运动微分方程各项单位

第四章
1 欧 拉 运 动 微 分 方 程
d d u
f t p =-?1
ζ
各 项 的 单 位 是: (1) 单 位 质 量 力 (2) 单 位 重 能 量
(3) 单 位 重 的 力
(4) 上 述 回 答 都 不 对
2. 欧 拉 运 动 微 分 方 程 在 每 点 的 数 学 描 述 是:
(1)流入的质量流量等于流出的质量流量(2) 单 位 质 量 力 等 于 加 速 度 (3) 能 量 不 随 时 间 而 改 变 (4) 服 从 牛 顿 第 二 定 律
3. 欧 拉 运 动 微 分 方 程:
(1) 适 用 于 不 可 压 缩 流 体, 不 适 用 于 可 压 缩 流 体 (2) 适 用 于 恒 定 流, 不 适 用 非 恒 定 流 (3) 适 用 于 无 涡 流, 不 适 用 于 有 涡 流
(4) 适 用 于 上 述 所 提 及 的 各 种 情 况 下 流 体 流 动
4. 水 流 一 定 方 向 应 该 是( )
(1) 从 高 处 向 低 处 流;
(2) 从 压 强 大 处 向 压 强 小 处 流;
(3) 从 流 速 大 的 地 方 向 流 速 小 的 地 方 流;
(4) 从 单 位 重 量 流 体 机 械 能 高 的 地 方 向 低 的 地 方 流。 5. 理 想 流 体 流 经 管 道 突 然 放 大 断 面 时, 其 测 压 管 水 头 线( )
(1) 只 可 能 上 升; (2) 只 可 能 下 降;
(3) 只 可 能 水 平;
(4) 以 上 三 种 情 况 均 有 可 能。
6 在应用恒定总流的能量方程时,可选用图中的(
) 断 面, 作为计算断面。
(a )1,2,3,4,5 (b )1,3,5
(c )2,4
(d )2,3,4
1
122
3
3
4
4
5
5
7. 设有一恒定汇流,如图所示,Q Q Q 312=+, 根据总流伯努力方程式,则有(
)
()12221111
2
2222
2
3333
2
13
23
z p g
V g
z p g
V g
z p g
V g
h h w
w +
+
++
+
=+
+
++--ραραρα
()()()
22211111
2
22222
2
ρραρραgQ z p g
V g
gQ z p g
V g
+
+
++
+
=++
+
++--ρραρρg Q Q z p g
V g
gQ h gQ h w
w ()()123333
2
12213
23
(3) 上 述 两 式 均 不 成 立, 都 有 错 误;
(4) 上 述 两 式 均 成 立。
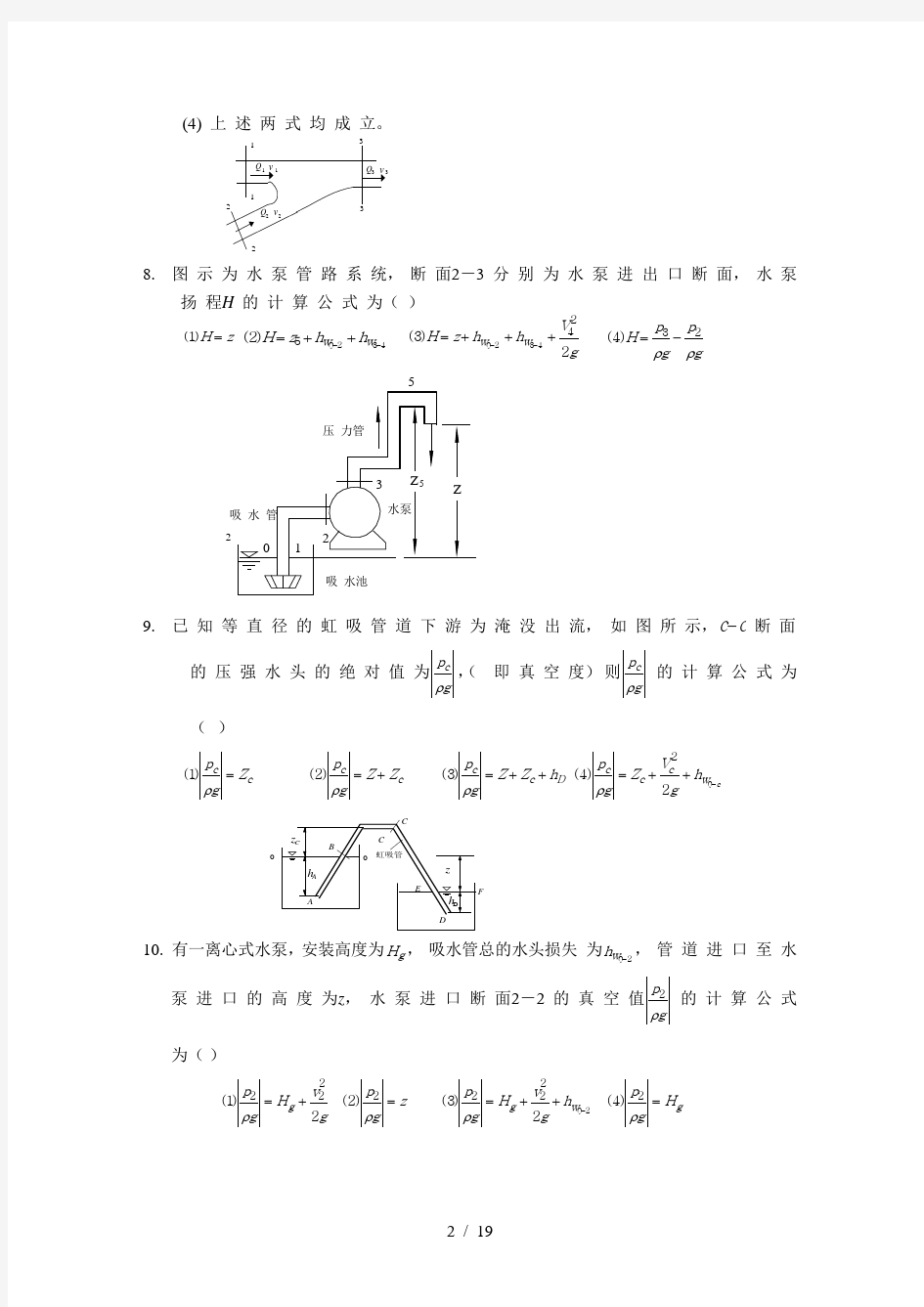
8. 图 示 为 水 泵 管 路 系 统, 断 面2-3 分 别 为 水 泵 进 出 口 断 面, 水 泵
扬 程H 的 计 算 公 式 为( )
()1H z = ()250234H z h h w w =++--
()3202344
2
H z h h V g
w w =+++
--
()432H p g
p g
=
-
ρρ
2
9. 已 知 等 直 径 的 虹 吸 管 道 下 游 为 淹 没 出 流, 如 图 所 示,c c - 断 面
的 压 强 水 头 的 绝 对 值 为p g
c ρ,( 即 真 空 度) 则
p g
c ρ 的 计 算 公 式 为
( )
()
1p g
Z c c ρ=
()
2p g
Z Z c c ρ=+
()
3p g
Z Z h c c D ρ=++ ()
422
0p g
Z V g
h c c c
w c
ρ=+
+-
10. 有一离心式水泵,安装高度为H g , 吸水管总的水头损失 为h w 02-, 管 道 进 口 至 水
泵 进 口 的 高 度 为z , 水 泵 进 口 断 面2-2 的 真 空 值p g
2ρ 的 计 算 公 式
为( )
()
1222
2
p g
H v g
g ρ=+
()
22p g
z ρ=
()
3222
2
02
p g
H v g
h g w ρ=+
+- ()
42p g
H g ρ=
11. 设有一恒定分流,如 图 所 示,Q Q Q 123=+, 根据总流伯努利方程, 可 列( )
()12221111
2
2222
2
3333
2
12
13
Z p g
V g
Z p g
V g
Z p g
V g
h h w
w +
+
=+
+
++
+
++--ραραρα
()()()()222211111
2
22222
2
33333
2
2312
13
ρραρραρραρρgQ Z p g V g
gQ Z p g V g
gQ Z p g
V g
gQ h gQ h w
w +
+
=+
+
++
+
++--
()()()32211111
2
22222
2
212
ρραρραρgQ Z p g
V g
gQ Z p g
V g
gQ h w +
+
=+
+
+-
()()()42211111
2
33333
3
313
ρραρραρgQ Z p g
V g
gQ Z p g
V g
gQ h w +
+
=+
+
+-
3
2
2
3
12. 总 流 能 量 方 程Z p g
V g
Z p g
V g
h l
1111
2
2222
2
2212
+
+
=+
+
+-ραρα 用 于 压 缩 性 可 忽 略 的
气 体 中 时, 下 述 论 述 中 正 确 者 为( )
(1)p 1 及p 2 分 别 为 第 一 断 面 及 第 二 断 面 的 相 对 压 强; (2)p 1 及p 2 分 别 为 第 一 及 第 二 断 面 的 绝 对 压 强;
(3)p 1、p 2 用 相 应 断 面 的 相 对 压 强 或 绝 对 压 强, 不 影 响 计 算 结 果;
(4) 上 述 方 程 只 适 用 于 液 体, 不 适 用 于 气 体。 13 不可压缩气体总流能量方程p V g Z Z p V p a l
112
21222
2
2
12
++--=+
+-ρρρρ()() 中的p p 12,分别
代表( )
(1)1 和2 断 面 上 的 绝 对 压 强;
(2)1 断 面 上 的 绝 对 压 强 及2 动 能 上 的 相 对 压 强; (3)1 和2 断 面 上 的 相 对 压 强;
(4)1 断 面 上 的 相 对 压 强 及2 断 面 上 的 绝 对 压 强。
14. 当 空 气 密 度ρa 大 于 气 体 的 密 度ρ, 且 气 体 由 位 于 低 处 的1 断 面
流 向2 断 面 时, 气 体 总 流 能 量 方 程 中 的g Z Z a ()()ρρ--21 代 表( )
(1) 单 位 重 量 气 体 在 流 动 过 程 中 损 失 的 位 能; (2) 单 位 重 量 气 体 在 流 动 过 程 中 增 加 的 位 能; (3) 单 位 体 积 气 体 在 流 动 过 程 中 损 失 的 位 能; (4) 单 位 体 积 气 体 在 流 动 过 程 中 增 加 的 位 能。
15. 若 空 气 密 度 为ρa , 不 可 压 缩 气 体( 密 度 为ρ), 流 动 时, 则( )
(1) 当ρρa > 时, 位 置 升 高, 位 压 最 大; (2) 当ρρa < 时, 位 置 升 高, 位 压 最 大; (3) 当ρρa > 时, 位 置 升 高, 位 压 减 小; (4) 当ρρa < 时, 位 置 升 高, 位 压 减 小。
16. 不 可 压 缩 气 体 流 动 时, 下 述 论 述 中 正 确 的 为(
)
(1) 总 压 线、 势 压 线 及 位 压 线 总 是 沿 程 下 降 的; (2) 总 压 线、 势 压 线 及 位 压 线 均 可 能 沿 程 有 升 有 降; (3) 总 压 线 及 位 压 线 总 是 沿 程 下 降 的, 势 压 线 沿 程 可 能 有 升 有 降;
(4) 总 压 线 沿 程 总 是 下 降 的, 势 压 线 与 位 压 线 沿 程 可 能 有 升 有 降。
17. 射流从管道出口垂直下线流入放在磅秤上的一水箱,经水箱侧壁孔口出流而保持水箱水
位恒定, 水重和箱重共为G ,若管道出口流量为Q ,出口流速为V 0,水股人射流速为V 1, 如图示,则磅秤上的重量读数为( )
(1)G
(2)G QV +ρ0
(3)G QV +ρ1
(4)G gh
d +ρπ0
2
4
18. 射 流 从 直 径 为d 的 圆 形 喷 嘴 以 速 度V 射 出, 冲 击 在 出 口 角 度 为
β2 的 轴 对 称 曲 线 叶 片 上 , 该 叶 片 的 运 动 速 度 为u , 如 图 所 示。
V u >, 若 忽 略 摩 擦 阻 力 和 水 头 损 失, 射 流 对 运 动 叶 片 的 冲 击 力
F x 为( )
(1)ρπd V 2
2
4
(2)ρ
πβd
V 2
2
24
1(cos )-(3)ρ
πβd
V V u 2
24
1()(cos )--(4)ρ
πβd
V u 2
2
24
1()(cos )--
x
19. 设水槽中固定装置一水泵,如图所示。水泵将水流经管嘴射
向光滑平板后回落到水槽内。已知管嘴直径为d,射流速度为V0,平板折角为θ,射流进入水槽的角度为α,若能量损失、空气阻力、轮子与地面的摩擦阻力都不计,试问水槽的运动方向是〔〕图:
(1)向左;(2)向右;(3)静止不动;(4)不能确定。
20. 一消防水枪以V046
=m s的速度向水平距离为30m,高也为30m 的着火点喷水,当水枪的最小仰角为()时,喷水方能达到目的地。
(1)32?;(2)495.?;(3)573.?;(4)75?。
21. 选择:管流的测压管水头线沿程的变化是
(1)沿程下降;(2)沿程上升;
(3)保持水平;(4)前三种情况都可能。
22.水由喷口水平射出,冲击在固定的垂直光滑平板上,喷口直径d=01.m,喷射流量Q=04.m s
3,空气对射流的阻力及射流与平板间的摩擦阻力不计,射流对平板的冲击力等于
().kN 12038;(
).kN
31435;(4)49.6kN
23. 实际流体在等直径管道中流动,在过流地面I I I
,上有1、2、3 点,则有下列关系
(A )Z p r Z p r 1122+=+ (B )Z p r
Z p r
1133+=+
(C )Z p r
Z p r
2233+
=+
(D )Z p r
Z p r
Z p r
112233+
≠+
≠+
I II
24. 重力场中理想不可压缩恒定势流的流动中两点A 、B ,A 点的流速u A 大于B 点的流速u B ,
则
(a )A 点 的 测 压 管 水 头>B 点 的 测 压 管 水 头; (b )A 点 的 测 压 管 水 头B 点 的 压 强 水 头; (d )A 点 的 压 强 水 头
25. 重力场中理想不可压缩恒定流动中同一条流线上两点A 、B ,A 点的流速u A 大于B 点的流
速u B ,则
(a )A 点 的 测 压 管 水 头>B 点 的 测 压 管 水 头; (b )A 点 的 测 压 管 水 头B 点 的 压 强 水 头; (d )A 点 的 压 强 水 头
A 流速有方向,作用力没有方向。
B 流速没有方向,作用力有方向。
C 都没有方向。
D 都有方向。
27.动能修正系数是反映过流断面上实际流速分布不均匀性的系数,流速分布_____,系数值 _______,当流速分布_____时,则动能修正系数的值接近于____. A 越不均匀 ;越小;均匀;1。 B 越均匀 ;越小;均匀;1。 C 越不均匀 ;越小;均匀;零 D 越均匀 ;越小;均匀;零 28. 实际流体总流能量方程应用条件是:
A 不可压缩液体
B 恒定流(或定常流)
C 重力流体
D 沿程流量不变 29. 动 力 粘 度 的 量 纲 是
()FL T 21-; ()FL T 211--; ()FLT 23-; ()FLT 42
30.将下列各物理量分别用:(a)力F 、长度L 、时间T ,(b)质量M 、长度L 、时间T ,两种基本量纲表示。
(1)、质量 m ,(2)、速度v ,(3)、力F ,(4)、密 度ρ,(5)、压 强p 31 由功率P 、流量Q 、密度ρ、重力加速度g 和作用水头H 组 成一个无量纲数是
()
a P Q gH
ρ;
()
b PQ gH
ρ;
()
c Q P gH
ρ;
()
d H PQ g
ρ
32. 对于二力相似的孔口出流, 正 确 的 时 间 比 尺 与 水 头 比 尺 的 关 系 为
(1)λλt H =2
; (2)λλt H =05.
; (3)λλλt H
v =
2
;
(4)λλλλρt H
k
=
33. 流体运动粘度ν的量纲是
()
[FL ]12-;
()
[L T ]121
M --;
()
[L T ]232
-; ()
[L T ]241
-
34. 将 正 确 答 案 的 序 号( 一 个 或 几 个) 填 入 括 号 内。
鱼雷所受阻力F D 与它的尺寸L 、速度v 以及水的密度ρ 和粘度μ 有关,则F D 可以表示为
(1)0,22=???
?
??vL v L F f D
ρμρ;
(2))(Re f F D =;
(3)Re v L F D 22ρ=;
(4)F L v f Re
D =ρ22
1
();
(5)
)(2
2Re f v
L F D
=ρ
35. 将 正 确 答 案 的 序 号( 一 个 或 几 个) 填 入 括 号 内
单位长电线杆受风吹的作用力F 与风速v 、电线杆直径d 、空气的密度ρ以及粘度μ有关,F 可表示为
(1)
F v f Re ρα
2
=();
(2)F v dRe =ρ2;(3)F v d f Re =ρ22();
(4)F f Re =(); (5)0,2=???
?
??vd d v F f ρμρ 36. 下面各种模型试验分别应采用(1)雷诺准则;(2)欧拉准则;(3)佛劳德准则中的哪一个准则,将其序号填入括号内:
a. 测 定 管 路 沿 程 阻 力 系 数; ( )
b. 堰 流 模 型 实 验;
( )
c. 水 库 经 水 闸 放 水 实 验; ( )
d. 气 体 从 静 压 箱 中 流 至 同 温 大 气 中; ( )
e. 船 的 波 浪 阻 力 实 验。
( )
37. 将 正 确 答 案 的 序 号( 一 个 或 几 个) 填 入 括 号 内
水轮机输出功率P 取决于轮叶直径D 、旋转角速度ω、效率η、流量Q 、水的密度ρ 及上游水面高H 。则功率P 的表达式为
??
?
??=ωρω353,)
1(D Q D H f D P ;
??
? ??
=ωηρω353,)
2(D Q f D P ;
???
? ??=-ηωρ,,)
3(343Q D D H f D Q P
; ??
?
??=ηωρω,,)
4(3
53D Q D H f D P ; ??
?
??=ηωρω,,)
5(353H Q H D f H P
38.将 正 确 答 案 的 序 号( 一 个 或 几 个) 填 入 括 号 内:
薄 壁 矩 形 堰 流 量Q 与 下 列 因 素 有 关: 堰 宽b 、 堰 顶 水 头H 、 流 体 密 度ρ、 粘 度μ 及 重 力 加 速 度g , 则 流 量Q 可 以 表 示 为
??
?
??=H b Re f gb H
Q ,1)
1(2; 0,,)
2(2=???
?
??H b
Re gH H Q f ;
)()
3(2/12/3Re f g bH Q =;
0,,)
4(2=???
? ??b H gb b gb b Q f ρμ 各 式 中 为Re 雷 诺 数, 其 特 征 长 度 为H , 特 征 速 度 为gH 。 39. 水深为4m 的宽浅河道,实验室中与之相似的模型河道水深为1m ,如果河道中的平均流速为1m/s ,那么模型河道中的流速为
(a)、0.25m/s ;
(b)、0.50m/s ;
(c)、1.0m/s ; (d)、2.0m/s
40. 某 溢 流 堰 原 型 坝 高P p =12m , 最 大 泄 流 量Q p =60m 3/s , 拟 采 用 模 型 进 行 水 力 试 验, 设 计 模 型 坝 高P m =0.48m , 则 模 型 最 大 泄 流 量 为 (a)、2.4m 3/s ;
(b)、0.0192m 3/s ;
(c)、0.192m 3/s ;
(d)、0.24m 3/s
41.长度比尺λl=50的船舶模型,在水池中以1m/s 的速度牵引前进,测得波浪阻力为0.02N ,则原型中需要的功率Np=_______。 A.2.17kw; B.32.4kw; C.17.8kw; D.13.8kw
42.设模型比尺为1:100 ,符合重力相似准则,如果模型流量为1000m/s,则原型流量为_____m/s.
A 0.01
B 1*10^8
C 10
D 10000
43.设模型比尺为1:100 ,符合重力相似准则,如果模型流速6m/s,则原型流速_______m/s. A 600 B 0.06 C 60 D 600000
44.如模型比尺为1:20, 考虑粘滞离占主要因素,采用的模型中流体与原型中相同,模型中流速为50m/s,则原型中流速为______m/s 。 A 11.1 B 1000 C 2.5 D 223 45.运动黏度系数的基本量纲表示为:
A F*T/L 2
或 M/(L*T) B F*T/L 或 M/(L*T) C L 2
/T 2
或 L 2
/T 2
D L 2
/T 或 L 2
/T
46.动力黏度系数的基本量纲表示为:
A F*T/L 2
或 M/(L*T) B F*T/L 或 M/(L*T) C F*T/L 2
或 M/(L 2
*T) D F/(T*L 2
)或 M/(L*T) 47.对于二相似的孔口出流,正确的时间比尺 λt 与水头比尺λH 的关系为: A λt=λH 2
B λt=λH 0.5
C λt=λH 2
/λv D λt=λH*(λp/ λk)0.5
48.对于两液流力学相似满足条件中,非恒定流比恒定流多一个条件是: A 几何相似 B 运动相似 C 动力相似 D 初始条件相似 49.动力黏度的量纲是:
A F*L -2
*T B F*L -1
*T -1
C F*L*T -2
D F*L*T 2
50.满足 Fr 准则时,原型的功率Pv 可按______ 来计算。 A Pp=Pm*λl 0.5
B Pp=Pm*λl 5/2
C Pp=λp*λl 5/2
D Pp=λp*λl 1.5
51.满足雷诺准则时,其流量比尺λQ 的表达式是: A λQ=λA*λl B λQ=λl*λv C λQ=λl D λQ=λA*λV
计算题:
1.图示为水自压力容器定常出流,压力表读数为10atm ,H=3.5m ,管嘴直径D 1=0.06m ,D 2=0.12m ,试求管嘴上螺钉群共受多少拉力?计算时管嘴内液体本身重量不计,忽略一切损失。
解:对容器液面和管嘴出口截面列伯努利方程:
选管嘴表面和管嘴进出口断面所围成的体积为控制体,列动量方程:
对管嘴的进出口断面列伯努利方程,得
g v H g P e 22
1=
+ρ)/(77.455
.38.92100010013.1102225
1s m gH P v e
=??+???=+=ρ
)
/(44.1177.4512.006.0212212s m v D D v =????
??=???
? ??=()x e x x v pnx F A P v v q F +=-=∑
2221ρ()2
221A P v v q F e v x --=ρg v g P g v e 222122
2
=
+ρ)
(77.9819862Pa P e =
∴
2.如图示,水流经弯管流入大气,已知d 1=100mm ,d 2=75mm ,v 2=23m/s ,不计水头损失,求弯管上所受的力。
解:由连续方程: 得:
对弯管的进、出口截面列伯努利方程:
其中,P 2 b = 0,z 1 = z 2,代入得:
选弯管所围成的体积为控制体,对控制体列动量方程:
求得:F pnbx = - 710.6 (N) ∴ F x = - F pnbx = 710.6 (N) F pnby = 1168.5 (N) F y = - F pnby = -1168.5 (N)
3.已知油的密度ρ=850 kg/m 3,粘度μ=0.06 Pa.s ,在图示连接两容器的光滑管中流动,已知H=3 m 。当计及沿程和局部损失时,求:(1)管内的流量为多少?(2)在管路中安一阀门,当调整阀门使得管内流量减小到原来的一半时,问阀门的局部损失系数等于多少?(水力光滑流动时,λ= 0.3164/Re 0.25)。 解:(1)对两容器的液面列伯努利方程,得:
())(6.666312.04
77.98198644.1177.4506.0477.45100022N F x -=??--????=π
π)(6.6663N F F x =-=2
22211d v d v =)/(94.12231007522
212221s m d d v v =?==g
v z g P g v z g P b b 222
2
222111++=++ρρ()
)
(10808.194.12232
100022522
212
21Pa g v v P b ?=-=-=ρρ()()
pnby pnby y pn y pn y y v pnbx b pnbx x pn x pn x x v F F F F v v q F A P F F F v v q =++=-+=++=-2112112112ρρ()()pnby
pnbx
F v F v v =-????+???=-????030sin 075.042310001.04
10808.130cos 075.042310002225122π
π
π)(6.136722N F F F y x =+=g
v g
v d l h h h H j f w 25.122
2+=+==∑
λ
即: (1)
设λ= 0.03,代入上式,得 v = 3.27 m/s ,则
故,令λ=λ’=0.0291,代入(1)得:v=3.306(m/s )
则
∴
(2)
则
求得:
7.为确定鱼雷阻力,可在风洞中进行模拟试验。模型与实物的比例尺为1/3,已知实际情况下鱼雷速度v p =6 km/h ,海水密度ρp =1200 kg/m 3,粘度νp =1.145×10-6 m 2/s ,空气的密度ρ
m =1.29 kg/m 3,粘度νm =1.45×10-5 m 2
/s ,试求:
(1)风洞中的模拟速度应为多大?(2)若在风洞中测得模型阻力为1000N ,则实际阻力为多少? 解:已知 g v g v 25.123.04032
2+=λ5.1389706
.03.027.3850Re =??==μρvd 0291
.0138973164.0Re 3164.0'25.025.0===λ%
2%303
.00291
.003.0'>=-=-λλλ5
.1405006
.03.0306.3850Re =??==μρvd λλ====0291.05.140503164.0Re 3164.0'25
.025.0)/(234.0306.33.044322s m v d q v =??==ππ)
/(117.02234.02
1'3s m q q v v ===)
/(655.13.014.34
117.04
'22s m d q v v =??==π75
.703306.03.0655.1850Re =??==μρvd 0345.075.70333164.0Re 3164.025
.025.0===λg
v d l h h h H v j f w 2)5.1(2
ξλ++=+==∑
8.92655.1)5.13.0400345.0(32
?++=v ξ37.15=v ξ3
1
=
=p
m l l l k
(1)由Re p = Re m 得, k ν = k v k l , ∴
v m = k v v p = 38×6 =228 (km/h)
(2)由k F = k ρk l 2 k v 2 得
∴ F P = F m /k F = 1000/0.1725 = 5798 (N)
4.流体通过孔板流量计的流量q v 与孔板前、后的压差ΔP 、管道的内径d 1、管内流速v 、孔板的孔径d 、流体密度ρ和动力粘度μ有关。试用π定理导出流量q v 的表达式。 (dim ΔP =ML -1T -2, dim μ=ML -1T -1)。
解:设q v = f (ΔP, d 1, v, d,ρ,μ)
选d, v, ρ为基本变量
上述方程的量纲方程为:
由量纲一致性原则,可求得:
a 1=0 a 2=1 a 3=0 a 4=1
b 1=1 b 2=2 b 3=0 b 4=1
c 1=2 c 2=0 c 3=1 c 4=1
∴
38310
145.11045.165
=???===--l p m l v k k k k ννν()()1725.03831120029.138312222=??
? ??=??? ??==p m p m F F F k ρρ1
111c b a v d v q ρπ=2
222c b a d v P ρπ=?33331c b a d v d ρπ=4
444c b a d v ρπμ=(
)()11
11313c b a L LT ML T L ---=()()2
221321c b a L LT ML T ML ----=()()
3
331311c b a L LT ML T ML ----=(
)()33
313c b a L LT ML L --=21vd q v =π22v P ρπ?=d d
1
3=πvd ρμπ=4???? ???=vd d d v P f vd q v ρμρ,,122
5.如图所示,由上下两个半球合成的圆球,直径d=2m ,球中充满水。当测压管读数H=3m 时,不计球的自重,求下列两种情况下螺栓群A-A 所受的拉力。(1)上半球固定在支座上;(2)下半球固定在支座上。 解:(1)上半球固定在支座上时
(2)下半球固定在支座上时
9. 新设计的汽车高1.5m ,最大行驶速度为108km/h ,拟在风洞中进行模型试验。已知风洞试验段的最大风速为45m/s ,试求模型的高度。在该风速下测得模型的风阻力为1500N ,试求原型在最大行驶速度时的风阻。
解:
根据粘性力相似准则,
又
10. 连续管系中的90o渐缩弯管放在水平面上,管径d 1=15 cm ,d 2=7.5 cm ,入口处水平均流速v 1=2.5 m/s ,静压p 1e =6.86×104 Pa (计示压强)。如不计能量损失,试求支撑弯管在其位置所需的水平力。
解:由连续方程:
())
(89.1123/114.323114.38.9100032432kN r H d g gV F p =??+????=???
?
??+==ππρρ())
(84.713/114.323114.38.9100032432kN r H d g gV F p =??-????=???
?
??-==ππρρ15
.16.310845
====ρk v v k p
m v )
(15.15.11
11Re Re m h h h h k k k k p m p
m
v l l v p m ======∴=)(150011500
2
222N k k k F F F F
k k k k l v m p p m
l v F ===∴==ρρ
由能量方程:
X 方向动量方程:
Y 方向动量方程:
合力为:
11. 小球在不可压缩粘性流体中运动的阻力F D 与小球的直径D 、等速运动的速度v 、流体的密度ρ、动力粘度μ有关,试导出阻力的表达式。 (dimF =MLT -2, dim μ=ML -1T -1)。(15分)
解:设F D = f (D, v, ρ,μ)
选D 、v 、ρ为基本变量
上述方程的量纲方程为:
)/(105.2)5.715(21222
121122
211s m v d d A A v v A v A v =?====)(21725)
105.2(210001086.6)(2222242
221122
22211Pa v v p p g v g p g v g p e e e e =-+?=-+=+=+ρρρ)(76.537075.0421725)010(15.045.21000)()(2
22
2122
212N A p v v q F A p F v v q e x x v x e x x x v =??+-????=+-=-=-ππρρ)(71.132215.041086.6)5.20(15.045.21000)()(2
421
1121
112N A p v v q F A p F v v q e y y v y e y y y v =???++????=+-=-=-π
πρρ)(85.142771.132276.5372222N F F F y x =+=+=1
111c b a D D v F ρπ=2
224c b a D v ρπμ=
由量纲一致性原则,可求得:
a 1=1 a 2=1
b 1=2 b 2=1
c 1=2 c 2=1
∴
12. 如图所示,一封闭容器内盛有油和水,油层厚h 1=40 cm ,油的密度ρo =850 kg/m 3,盛有水银的U 形测压管的液面距水面的深度h 2=60 cm ,水银柱的高度低于油面h=50 cm ,水银的密度ρhg = 13600 kg/m 3,试求油面上的计示压强(15分)。
解:
13. 额定流量q m =35.69 kg/s 的过热蒸汽,压强p e =981 N/cm 2,蒸汽的比体积为v=0.03067 m 3/kg ,经内径为227mm 的主蒸汽管道铅垂向下,再经90o弯管转向水平方向流动。如不计能量损失,试求蒸汽作用给弯管的水平力。
解:由连续方程: 得: ()()
1
11132c b a L LT ML MLT ---=()()
2
221311c b a L LT ML T ML ----=221d v F D ρπ=vd
ρμ
π=2
???? ??=vd f d v F D ρμρ22)
(21212h h h g gh gh P P hg w o e e -+=++=ρρρ)
(574286
.08.910004.08.9850)5.06.04.0(8.913600)(2121Pa gh gh h h h g P w o hg e =??-??--+??=---+=∴ρρ
ρ227.04
03067.069.352
2
d
v q A
q V VA q m m
m ???=
=
=
=ππρρ
选弯管所围成的体积为控制体,对控制体列x 方向动量方程:
14. Water flows over the spillway of constant section. Given that y 1 = 4.2m and y 2 = 0.7m, determine the resultant horizontal force on the spillway per meter of spillway width (perpendicular to the spillway section). Assume ideal flow. (10分)
Solution:
将y 1 = 4.2m, y 2 = 0.7m, p 1 = p 2 , γ=9810 N/m 2 , 代入得
解得:v 1 =1.4 , v 2 =8.4
To the right
15. A diverging nozzle that discharges an 8-in-diameter water jet into the air is on the right end of a horizontal 6-in-diameter pipe. If the velocity in the pipe is 12fps, find the magnitude and direction of the resultant axial force the water exerts on the nozzle. Neglect fluid friction. (10分)
()())(1098.34
227.010981)0047.27(69.35524
2212222112N A P V V q F F A P F F F V V q e x x m pnbx pnbx
e pnbx x pn x pn x x v ?=???+-?=+-=+-=++=-πρg
v y p g v y p y v y v 2222
2221112
211++=++=γγ81.927.081.922.47.02.422212
1?+=?+=v v v v )
(96.42)/(42960)4.14.8(2.44.110002
7.0981022.49810)
(22)()
(2
21211221112112112kN F F m N B F v v B y v B y y B y y F v v B y v F F F v v Q F b b b b x x x =-=-=-???+?+?-=-++-=-=+--=∑
ργγρρ
Solution:
to the right
16. A horizontal 100-mm-diameter pipe (f=0.027) projects into a body of water (k e =0.8) 1m below the surface. Considering all losses, find the pressure at a point 5 m from the end of the pipe if the velocity is 4 m/s and the flow is (a) into the body of water; (b) out of the body of water. (10分)
Solution: (a)
(b)
17. A rectangular plate 5 ft by 4 ft is at an angle of 30°with the horizontal, and the 5-ft side is horizontal. Find the magnitude of the force on one side of the plate and the depth of its center of pressure when the top edge is (a) at the water surface; (b) 1 ft below the water surface. (10分)
Solution:
)
/(75.6128
622
1212s ft v A A v =?==g
v z p g v z p 2222
222111++=++γγ )/(38.95)1275.6(2.3224.62)(222221221ft lb v v g p -=-?=-=∴γbx x F A P V V Q F +=-=∑
1112)(ρ )(24.5)
1275.6()126(4122.324.62)126(438.95)(221
211lb V V Q A P F F bx x =-????-??-=--=-=∴ππ
ρ)/(6.208.9241.05027.0198002)'(2222212
12121122112
2222111m kN p p g v k g v d l f z z g v p h g v z p g v z p L
=??+=++-=++++=++γγγ)/(4.158.9248.18.9241.05027.0198002222221221212
1122112
2
222111m kN p p g
v k g v d l f z z g v p h g v z p g v z p e L
-=??-??-=---=+-++=++γγγ
(a)
(b)
18. Water in a reservoir is discharged from a vertical pipe. If a=25 ft, b= 60 ft, c=40 ft, d= 2ft. All the losses of energy are to be ignored when the stream discharging into the air at E has a diameter of 4 in. What are pressure heads at B, C and D, if the diameter of the vertical pipe is 5 in? (10分)
19. A nozzle that discharges a 60-mm-diamater water jet into the air is on the right end of a
)(1248)45(30sin 2
44.62lb A h F c =?????==γ)(333.130sin 43
232ft h h p =???==)(2496)45()30sin 2
41(4.62lb A h F c =????+?==γ)(333.4)54(4451214)2
430sin 1(121)2430sin 1(33ft A bl A y I y y c c c
p =????+=+?++?=+=)(17.25.0333.430sin ft y h p p =?=?
=g
v z p g v z p E
E E A A A 222
2++=++γγ g
v E
2000)406025(02
++=++++)/(72.891252.322s ft v E =??=∴)/(42.5772.895
422
s ft v A A v v v E B E D C B =?====∴g v z p g v z p B
B B A A A 222
2+
+=++γγ )
(2.262.32242.572522
2
ft g v a P B B -=?-=-=∴γg v z p g v z p C C C B
B B 2222
++=++γγ )
(8.33602.26)(ft z z P
P C B B C =+-=-+=∴γγg v z p g v z p D
D D B B B 2222+
+=++γγ )
(8.71240602.26)(ft z z P
P D B B D =-++-=-+=∴γγ
horizontal 120-mm-diameter pipe. In the pipe the water has a velocity of 4 m/s and a gage pressure of 400 kPa. Find the magnitude and direction of the resultant axial force the water exerts on the nozzle, and the head loss in the nozzle. (10分)
Solution:
to the right
)
/(164601202
2
1212s m v A A v =?==bx
x F A P V V Q F +=-=∑
1112)(ρ )(39819.5429.4523)416(12.044100012.04400000)(221
211N V V Q A P F F bx x =-=-????-??=--=-=∴ππρ)(57.288.92168.92498004000022222
2211m g v g v p h L =?-?+=-+=∴γL h g
v z p g v z p +++=++2222
222111γγ
常微分方程作业欧拉法与改进欧拉法
P77 31.利用改进欧拉方法计算下列初值问题,并画出近似解的草图:dy + =t = t y y ≤ ≤ ,2 ;5.0 0,3 )0( )1(= ,1 ? dt 代码: %改进欧拉法 function Euler(t0,y0,inv,h) n=round(inv(2)-inv(1))/h; t(1)=t0; y(1)=y0; for i=1:n y1(i+1)=y(i)+h*fun(t(i),y(i)); t(i+1)=t(i)+h; y(i+1)=y(i)+1/2*h*(fun(t(i),y(i))+ fun(t(i+1),y1(i+1))) end plot(t,y,'*r') function y=fun(t,y); y=y+1; 调用:Euler(0,3,[0,2],0.5) 得到解析解:hold on; y=dsolve('Dy=y+1','(y(0)=3)','t'); ezplot(y,[0,2]) 图像:
dy y =t - t y ;2.0 t = ≤ )0( 0,5.0 ,4 )2(2= ≤ ? ,2 dt 代码: function Euler1(t0,y0,inv,h) n=round(inv(2)-inv(1))/h; t(1)=t0; y(1)=y0; for i=1:n y1(i+1)=y(i)+h*fun(t(i),y(i)); t(i+1)=t(i)+h; y(i+1)=y(i)+1/2*h*(fun(t(i),y(i))+ fun(t(i+1),y1(i+1))) end plot(t,y,'*r') function y=fun(t,y); y=y^2-4*t; 调用: Euler1(0,0.5,[0,2],0.2) 图像:
对于欧拉方程的理解
关于欧拉方程的理解 1755年,瑞士数学家L.欧拉在《流体运动的一般原理》一书中首先提出这个方程。 形如:)(1)1(11)(x f y x p y x p y x n n n n n ='+++--- (1) 的方程称为欧拉方程, 其中n p p p ,,,21 为常数。 欧拉方程的特点是: 方程中各项未知函数导数的阶数与其乘积因子自变量的幂次相同。 现阶段欧拉方程的应用领域很广,现只结合流体力学来探讨我对于欧拉方程的理解。 欧拉方程提出采用了连续介质的概念,把静力学中压力的概念推广到了运动流体中。 流体静力学着重研究流体在外力作用下处于平衡状态的规律及其在工程实际中的应用。 这里所指的静止包括绝对静止和相对静止两种。以地球作为惯性参考坐标系,当流体相对于惯性坐标系静止时,称流体处于绝对静止状态;当流体相对于非惯性参考坐标系静止时,称流体处于相对静止状态。 流体处于静止或相对静止状态,两者都表现不出黏性作用,即切向应力都等于零。所以,流体静力学中所得的结论,无论对实际流体还是理想流体都是适用的。 流体静压强的特性 1静压强的方向—沿作用面的内法线方向 2任一点的流体静压强的大小与作用面的方向无关,只与该点的位置有关
由上图可以推到出流体平衡微分方程式,即欧拉平衡方程 x y z p f x p f y p f z ρρρ??=?????=?????=??? 当流体处于平衡状态时,单位体积质量力在某一轴向上的分力,与压强沿该轴的递增率相平衡。 这里的fx 、fy 、fz 是流体质量力在x 、y 、z 轴上的投影,且质量力中包含以下两项:重力和惯性力。在这里如果假定fx 、fy 、fz 仅仅是重力在三个坐标轴上的投影,那么惯性力在x 、y 、z 轴上的投影分别为:-du/dt ,-dv/dt 和-dw/dt 。于是,上式便可写成 d d d d d d x y z u p f t x v p f t y w p f t z ρρρ????-= ???? ??????-=? ??? ??????-=? ??? ?? 上式整理后可得:
常微分方程的Euler解法
毕业论文 题目:常微分方程的Euler解法 及其程序设计 学院:数学与信息科学学院 专业:数学与应用数学 毕业年限: 2011年6月 学生: 学号: 指导教师:
常微分方程的Euler解法及其程序设计 摘要本文总结了常微分方程的Euler解法,对各种格式给出了误差估计,设计了这些格式的计算程序. 关键词常微分方程;Euler解法;误差分析;程序设计 Euler Method of Ordinary Differential Equation and Its Programming Abstract Euler method of ordinary differential equation is summarized,the error of each format is analyzed and its programming is designed in this paper. Keywords Ordinary differential equation; Euler method; Error analysis; Programming
科学技术中常常需要求解常微分方程的定解问题,这类问题最简单的形式,即为微分方程 (,)dy f x y dx = (1) 的初值问题 00(,),(). dy f x y dx y x y ?=???=? (2) 定理 (存在与唯一性定理)如果方程(1)的右端函数(,)f x y 在闭矩形域 000000:,R x a x x a y b y y b -≤≤+-≤≤+ 上满足如下条件: (1)在R 上连续; (2)在R 上关于变量y 满足利普希茨(Lipschitz )条件,即存在常数L ,使 对于R 上任何一对点(,)x y 和(,)x y 有不等式: (,)(,)f x y f x y L y y -≤-, 则初值问题(2)在区间00000x h x x h -≤≤+上存在唯一解 00(),()y y x y x y ==, 其中0(,)min(,),max (,)x y R b h a M f x y M ∈==. 根据存在与唯一性定理,只要(,)f x y 关于y 满足Lipschitz 条件 (,)(,)f x y f x y L y y -≤-, 即可保证其解()y y x =存在并唯一. 然而解析方法只能用来求解少数较简单和典型的常微分方程,例如线性常系数微分方程等,对于变系数常微分方程的解析求解就比较困难,而一般的非线性常微分方程就更不用说,因此,在大多数情况下,实际问题中归结出来的微分方程主要靠数值解法求解.
《图解刚体力学——欧拉运动学方程》
本科生毕业论文 论文题目:图解刚体力学——欧拉运动学方程 学生姓名:罗加宽 学号: 2008021152 专业名称:物理学 论文提交日期: 2012年05月17日 申请学位级别:理学学士 论文评审等级: 指导教师姓名:陈洛恩 职称:教授 工作单位:玉溪师范学院 学位授予单位:玉溪师范学院 玉溪师范学院理学院物理系 2012年05月
图解刚体力学—欧拉运动学方程 罗加宽 (玉溪师范学院理学院物理系 08级物理1班云南玉溪 653100) 指导教师:陈洛恩、杨春艳 摘要:本文阐述了描述刚体定点转动的欧拉角及欧拉运动学方程的图解,以期让复杂的问题转 化得简单清晰而易于学习者的理解,抽象的概念变得直观具体而易于学习者的掌握;并能在一 定程度上对提高学习者的空间思维能力、引导和培养学习者的创新思维能力有一定的帮助。 关键字:图解;刚体;欧拉角;欧拉运动学方程 1.引言 理论力学是研究物体机械运动一般规律的科学;依照牛顿的说法,理论力学“是关于力产生的运动和产生任何运动的力的理论,是精确的论述和证明” [1]。理论力学作为使用数学方法的自然知识的一部分,不仅研究实际物体,而且研究其模型—质点、质点系、刚体和连续介质。从研究次序来看,通常先研究描述机械运动现象的运动学,然后再进一步研究机械运动应当遵循哪些规律的动力学。至于研究平衡问题的静力学,对理科来讲可以作为动力学的一部分来处理,但在工程技术上,静力学却是十分的重要,因此,常把它和动力学分开,自成一个系统[2]。本文图解的内容为刚体力学运动学问题之一的刚体的绕定点的转动。 “图解”的方法,较早见于上海科学技术出版社1988年翻译出版的《图解量子力学》,原书名为The Picture Book of Quantum Mechanics,由Springer-Verlag 出版;类似的书还有Springer-Verlag出版的Visual Quantum Mechanics。其特点是通过将理论物理与数值计算相结合实现可视化来讲解物理知识。国外对物理的可视化教学十分重视,早在1995-1996年间Wiley出版社出版了9本有关物理多媒体教学的丛书,是由大学高等物理软件联盟(The Consortium for Upper-Level Physics Software,CUPS)编写该丛书及其所用的教学软件[3]。如今,图解法已经广泛应用于力学、电磁学、模拟电子技术等方面,理论力学方面同样也有不少人已经采用了图解法。如赵宗杰使用3dsmax建立质点外弹道运动规律的虚拟模型和场景[4];乐山师范学院王峰等利用Matlab分别对质点受力仅为位置、速度或时间的函数进行了图解,并说明了Matlab在理论力学中的应用[5];阜阳师范学院孙美娟、韩修林利用Mathematica进行编程作出了落体的位移—时间图像[6]。通过图解,使很多抽象繁难的物理问题在解析时达到空间立体直观,概念形成清晰,逻辑链路晓畅明朗,数式转换准确易见。 理论力学因理论性较强,与高等数学联系密切,一些概念的形成、公式的推导、逻辑推理等较抽象、繁难、复杂,往往使教授者感到教学很难达到预期的效果,学
欧拉及改进的欧拉法求解常微分方程
生物信息技术0801 徐聪U200812594 #include
对流体力学欧拉运动方程式的修正
第9节 对流体力学欧拉运动方程式的修正(探讨) 内容提要:本文是探讨性的论文。观念正确如否有待学界审视及实践的检验。流体力学的欧拉运动方程式有修正的必要吗?首先,欧拉运动方程式是在《场论》只具有散度和旋度的数学基础为背景的产物;其次,人们注意到,航天器在飞行运动中存在一未知的莫铭的力。这个莫铭的力应该是欧拉方程尚未虑及的因素造成的。作者在研究《超变函数论》过程中揭示了在三维向量场中除了散度、旋度外尚存在一个为目前所未知的副冲量度【见文献3】。 我们所提出的修正意见就是从这里切入的,即在考虑存在副冲量度这一因素后,欧拉运动方程式应该发生怎样的变化。 关键词:理想流体,时变加速度,位变加速度,欧拉运动方程式,副冲量度,冲量力,压扁的四维空间. 分类号: 一,现在的欧拉运动方程式[见文献4,第77页] 在理想流体场中取出一微小六面体流体微团。微团中心的压力为P ,速度为,,x y z ωωω。微团所受的力有表面力(压力)和体积力(质量力)。六面体各面所受的表面力如下图所示。体积力为,,x y z F F F 。设单位质量的的体积力为X,Y,Z ,则在x 轴方向微团所受的力为 ()()22 ()??+-+???=-?dx dx X dxdydz dydz dydz x x X dxdydz x P P ρP - P P ρ 在x 轴方向微团产生加速度的运动力为 x d dxdydz dt ωρ 【注:其中,总加速度 ???????=+++???????????=+++????y x x x z y x x z x y z d x y z dt t x t y t z t t x y z ωωωωωωωωωωωω 该式右侧第一项称为时变加速度;第二、三、四项总称为位变加速度。】
微分方程常用的两种数值解法:欧拉方法与龙格—库塔法
四川师范大学本科毕业论文 微分方程常用的两种数值解法:欧拉方法与龙 格—库塔法 学生姓名XXX 院系名称数学与软件科学学院 专业名称信息与计算科学 班级2006级 4 班 学号20060640XX 指导教师Xxx 四川师范大学教务处 二○一○年五月
微分方程常用的两种数值解法:欧拉方法与龙格—库塔法 学生姓名:xxx 指导教师:xx 【内容摘要】微分方程是最有生命力的数学分支,在自然科学的许多领域中,都 会遇到常微分方程的求解问题。当前计算机的发展为常微分方程的应用及理论研究提供了非常有力的工具,利用计算机解微分方程主要使用数值方法,欧拉方法和龙格——库塔方法是求解微分方程最典型常用的数值方法。本文详细研究了这两类数值计算方法的构造过程,分析了它们的优缺点,以及它们的收敛性,相容性,及稳定性。讨论了步长的变化对数值方法的影响和系数不同的同阶龙格—库塔方法的差别。通过编制C程序在计算机上实现这两类方法及对一些典型算例的结果分析比较,能更深切体会它们的功能,优缺点及适用场合,从而在实际应用中能对不同类型和不同要求的常微分方程会选取适当的求解方法。 关键词:显式单步法欧拉(Euler)方法龙格—库塔(Runge—Kutta)方法截断误差收敛性 Two commonly used numerical solution of differential equations:Euler method and Runge - Kutta method Student Name: Xiong Shiying Tutor:Zhang Li 【Abstract】The differential equation is the most vitality branch in mathematics. In many domains of natural science, we can meet the ordinary differential equation solution question. Currently, the development of computer has provided the extremely powerful tool for the ordinary differential equation application and the fundamental research, the computer solving differential equation mainly uses value method. The Euler method and the Runge—Kutta method are the most typical commonly value method to solve the differential equation. This article dissects the structure process of these two kinds of values commonly value method to solve the analyses their good and bad points, to their astringency, the compatibility, and the stability has made the proof. At the same time, the article discuss the length of stride to the numerical method changing influence and the difference of the coefficient different same step Runge—kutta method. Through establishing C program on the computer can realize these two kind of methods, Anglicizing some models of calculate example result can sincerely realize their function, the advantage and disadvantage points and the suitable situation, thus the suitable solution method can be selected to solve the different type and the
MATLAB Euler法解常微分方程
Euler 法解常微分方程 Euler 法解常微分方程算法: Step 1 分别取积分上限、积分下限、步长 Step 2计算h n n +=判断b n ≤是否成立,成立转到Step 3,否则继续进行Step 4 Step 3 计算),(1n n n n y x hf y y +=+ Step 4 ),(1n n n n y x hf y y +=+ Euler 法解常微分方程算程序: function euler2(fun,y0,A,h) %fun--y' %y0---初值 %A----x 取值范围 %a----x 左区间端点值 %b----x 右区间端点值 %h----给定步长 x=min(A); b=max(A); y=y0; while x 0.4613 指导教师: 年 月 日 改进Euelr 法解常微分方程 改进Euler 法解常微分方程算法: Step 1 分别取积分上限、积分下限、步长 Step 2 取一个以h 为步长,a ,b 分别为左右端点的矩阵 Step 3 (1)做显性Euler 预测),( 1n n i i y x hf y y +=+ (2)将1+i y 带入,(),([2h 11++++=i i i i i x f y x f y y Step 4计算h n n +=判断b n ≤是否成立,成立返回Step 5 )],(),([2h 111+++++=i i i i i i y x f y x f y y 改进Euler 法解常微分方程算程序: function gaijineuler2(fun,y0,A,h) %fun--y' %y0---初值 %A----x 取值范围 %a----x 左区间端点值 %b----x 右区间端点值 %h----给定步长 a=min(A); b=max(A); x=a:h:b; y(1)=y0; for i=1:length(x)-1 w1=feval(fun,x(i),y(i)); y(i+1)=y(i)+h*w1; w2=feval(fun,x(i+1),y(i+1)); y(i+1)=y(i)+h*(w1+w2)/2; end x=x' 牛顿-欧拉方程 欧拉方程(Euler equations),是欧拉运动定律的定量描述,欧拉运动定律是牛顿运动定律的延伸,在牛顿发表牛顿运动定律超过半个世纪后,于1750年,欧拉才成功的用欧拉方程表述了该定律: 该方程是建立在角动量定理的基础上的描述刚体的旋转运动时刚体所受外力矩与角加速度的关系式,大多时候可简写成: 其中,分别为刚体坐标系下三个轴的所受的外力矩,分别为刚体三个坐标轴的转动惯量(刚体坐标系下)。 欧拉方程通常与牛顿的平移运动方程被一起写出,称为牛顿-欧拉方程(Newton-Euler equations): 这里对牛顿的平移运动方程不赘述,只对欧拉方程进行讨论。 1.单质点角动量定理 质点旋转时,有动量定理: 对两边叉乘质点位置矢量: 观察: 因为: 故有: 定义角动量,可以看出为外力矩 故有单质点的角动量定理: 2.刚体的角动量定理 定义刚体的角动量为: 其中:下标G表示该向量为大地坐标系下的,的下标i表示该向量为大地坐标下各个质量元的向量。刚体旋转运动参考的惯性系是大地坐标系,不能把采用刚体的本身坐标系作为参考系,本身坐标系的提出只是方便我们某些量的分析与表述,如角速度、惯性张量。 (这里需要特别说明的是因为刚体质量分布不均匀的原因,角动量的方向往往不与刚体角速度方向一致,这也是无力矩进动的原因,即很多时候刚体角速度不守恒但刚体的角动量守恒了,宏观来看就是因为要保证角动量和动量守恒所以才要产生内力作用使角速度变化达到守恒的效果。) 由牛顿第三定律易知内力矩产生的角动量变化相抵,故有刚体的角动量定理: 其中:为外力矩 把上式展开有: 其中:称为惯性矩阵 常微分方程欧拉算法 Company Document number:WUUT-WUUY-WBBGB-BWYTT-1982GT 常微分方程欧拉算法 摘要:本文主要论述了常微分方程的欧拉算法的算法原理,误差分析,实例,程序,以及算法比较等内容。 关键词:常微分方程 显式欧拉法 隐式欧拉法 引言:微分方程初值问题模型是常见的一类数学模型。对于一些简单而典型的微分方程模型,譬如线性方程、某些特殊的一阶非线性方程等是可以设法求出其解析解的,并有理论上的结果可资利用。但在数学建模中碰到的常微分方程初值问题模型,通常很难,甚至根本无法求出其解析解,而只能求其近似解。因此,研究其数值方法,以便快速求得数值鳃有其重大意义。 一、欧拉算法原理 对于微分方程初值问题 的解在xy 平面上是一条曲线,称为该微分方程的积分曲线。积分曲线上一点(),x y 的切线斜率等于函数f 在点(),x y 的值,从初始点()000,P x y 出发,向该点的切线方向推进到下一个点()111,P x y ,然后依次做下去,得到后面的未知点。一般地,若知道(),n n n P x y 依上述方法推进到点()111,n n n P x y +++,则两点的坐标关系为: 即 这种方法就是欧拉(Euler )方法(也叫显式欧拉法或向前欧拉法)。当初值0y 已知,则n y 可以逐步算出 对微分方程()=x y dy f dx ,从n x 到1n x +积分,那么有 现在用左矩形公式()(),n n hf x y x 代替()()1 ,n n x x f t y t dt +?,n y 代替()n y x ,1n y +代替() 1n y x +就得到了欧拉方法。如果用右矩形公式()()11,n n hf x y x ++去代替右端积分,则得到另外一 个公式,该方法就称为隐式欧拉法(或后退欧拉法),其公式为 欧拉公式与隐式欧拉公式的区别在于欧拉公式是关于1n y +的一个直接计算公式,然而隐式欧拉公式右端含有1n y +,所以它实际上是关于1n y +的一个函数方程。 二、实例 例 取h=,用Euler 方法解 第8章 常微分方程数值解法 本章主要内容: 1.欧拉法、改进欧拉法. 2.龙格-库塔法。 3.单步法的收敛性与稳定性。 重点、难点 一、微分方程的数值解法 在工程技术或自然科学中,我们会遇到的许多微分方程的问题,而我们只能对其中具有较简单形式的微分方程才能够求出它们的精确解。对于大量的微分方程问题我们需要考虑求它们的满足一定精度要求的近似解的方法,称为微分方程的数值解法。本章我们主要 讨论常微分方程初值问题?????==00 )() ,(y x y y x f dx dy 的数值解法。 数值解法的基本思想是:在常微分方程初值问题解的存在区间[a,b]内,取n+1个节点a=x 0<x 1<…<x N =b (其中差h n = x n –x n-1称为步长,一般取h 为常数,即等步长),在这些节点上把常微分方程的初值问题离散化为差分方程的相应问题,再求出这些点的上的差分方程值作为相应的微分方程的近似值(满足精度要求)。 二、欧拉法与改进欧拉法 欧拉法与改进欧拉法是用数值积分方法对微分方程进行离散化的一种方法。 将常微分方程),(y x f y ='变为() *+=?++1 1))(,()()(n x n x n n dt t y t f x y x y 1.欧拉法(欧拉折线法) 欧拉法是求解常微分方程初值问题的一种最简单的数值解法。 欧拉法的基本思想:用左矩阵公式计算(*)式右端积分,则得欧拉法的计算公式为:N a b h N n y x hf y y n n n n -= -=+=+)1,...,1,0(),(1 欧拉法局部截断误差 11121 )(2 ++++≤≤''=n n n n n x x y h R ξξ或简记为O (h 2)。 Euler法解常微分方程 Euler法解常微分方程算法: Step 1 分别取积分上限、积分下限、步长 Step 2计算判断是否成立,成立转到Step 3,否则继续进行Step 4 Step 3 计算 Step 4 Euler法解常微分方程算程序: function euler2(fun,y0,A,h) %fun--y' %y0---初值 %A----x取值范围 %a----x左区间端点值 %b----x右区间端点值 %h----给定步长 x=min(A); b=max(A); y=y0; while x Step 3 (1)做显性Euler预测 (2)将带入 Step 4计算判断是否成立,成立返回Step 3,否则继续进行Step 5 Step 5 改进Euler法解常微分方程算程序: function gaijineuler2(fun,y0,A,h) %fun--y' %y0---初值 %A----x取值范围 %a----x左区间端点值 %b----x右区间端点值 %h----给定步长 a=min(A); b=max(A); x=a:h:b; y(1)=y0; for i=1:length(x)-1 w1=feval(fun,x(i),y(i)); y(i+1)=y(i)+h*w1; w2=feval(fun,x(i+1),y(i+1)); y(i+1)=y(i)+h*(w1+w2)/2; end x=x' y=y' 例:用改进Euler法计算下列初值问题(取步长h=0.25) 输入:fun=inline('-x*y^2') gaijineuler2(fun,2,[0 5],0.25) 得到: x = 0.2500 0.5000 0.7500 1.0000 1.2500 1.5000 1.7500 2.0000 2.2500 2.5000 2.7500 常微分方程欧拉算法 Prepared on 22 November 2020 常微分方程欧拉算法 摘要:本文主要论述了常微分方程的欧拉算法的算法原理,误差分析,实例,程序,以及算法比较等内容。 关键词:常微分方程 显式欧拉法 隐式欧拉法 引言:微分方程初值问题模型是常见的一类数学模型。对于一些简单而典型的微分方程模型,譬如线性方程、某些特殊的一阶非线性方程等是可以设法求出其解析解的,并有理论上的结果可资利用。但在数学建模中碰到的常微分方程初值问题模型,通常很难,甚至根本无法求出其解析解,而只能求其近似解。因此,研究其数值方法,以便快速求得数值鳃有其重大意义。 一、欧拉算法原理 对于微分方程初值问题 的解在xy 平面上是一条曲线,称为该微分方程的积分曲线。积分曲线上一点(),x y 的切线斜率等于函数f 在点(),x y 的值,从初始点()000,P x y 出发,向该点的切线方向推进到下一个点()111,P x y ,然后依次做下去,得到后面的未知点。一般地,若知道(),n n n P x y 依上述方法推进到点()111,n n n P x y +++,则两点的坐标关系为: 即 这种方法就是欧拉(Euler )方法(也叫显式欧拉法或向前欧拉法)。当初值0y 已知,则n y 可以逐步算出 对微分方程()=x y dy f dx ,从n x 到1n x +积分,那么有 现在用左矩形公式()(),n n hf x y x 代替()()1 ,n n x x f t y t dt +?,n y 代替()n y x ,1n y +代替() 1n y x +就得到了欧拉方法。如果用右矩形公式()()11,n n hf x y x ++去代替右端积分,则得到另外一 个公式,该方法就称为隐式欧拉法(或后退欧拉法),其公式为 欧拉公式与隐式欧拉公式的区别在于欧拉公式是关于1n y +的一个直接计算公式,然而隐式欧拉公式右端含有1n y +,所以它实际上是关于1n y +的一个函数方程。 二、实例 例 取h=,用Euler 方法解 第四章 1 欧 拉 运 动 微 分 方 程 d d u f t p =-?1 ζ 各 项 的 单 位 是: (1) 单 位 质 量 力 (2) 单 位 重 能 量 (3) 单 位 重 的 力 (4) 上 述 回 答 都 不 对 2. 欧 拉 运 动 微 分 方 程 在 每 点 的 数 学 描 述 是: (1)流入的质量流量等于流出的质量流量(2) 单 位 质 量 力 等 于 加 速 度 (3) 能 量 不 随 时 间 而 改 变 (4) 服 从 牛 顿 第 二 定 律 3. 欧 拉 运 动 微 分 方 程: (1) 适 用 于 不 可 压 缩 流 体, 不 适 用 于 可 压 缩 流 体 (2) 适 用 于 恒 定 流, 不 适 用 非 恒 定 流 (3) 适 用 于 无 涡 流, 不 适 用 于 有 涡 流 (4) 适 用 于 上 述 所 提 及 的 各 种 情 况 下 流 体 流 动 4. 水 流 一 定 方 向 应 该 是( ) (1) 从 高 处 向 低 处 流; (2) 从 压 强 大 处 向 压 强 小 处 流; (3) 从 流 速 大 的 地 方 向 流 速 小 的 地 方 流; (4) 从 单 位 重 量 流 体 机 械 能 高 的 地 方 向 低 的 地 方 流。 5. 理 想 流 体 流 经 管 道 突 然 放 大 断 面 时, 其 测 压 管 水 头 线( ) (1) 只 可 能 上 升; (2) 只 可 能 下 降; (3) 只 可 能 水 平; (4) 以 上 三 种 情 况 均 有 可 能。 6 在应用恒定总流的能量方程时,可选用图中的( ) 断 面, 作为计算断面。 (a )1,2,3,4,5 (b )1,3,5 (c )2,4 (d )2,3,4 1 122 3 3 4 4 5 5 7. 设有一恒定汇流,如图所示,Q Q Q 312=+, 根据总流伯努力方程式,则有( ) ()12221111 2 2222 2 3333 2 13 23 z p g V g z p g V g z p g V g h h w w + + ++ + =+ + ++--ραραρα ()()() 22211111 2 22222 2 ρραρραgQ z p g V g gQ z p g V g + + ++ + =++ + ++--ρραρρg Q Q z p g V g gQ h gQ h w w ()()123333 2 12213 23 (3) 上 述 两 式 均 不 成 立, 都 有 错 误; [收稿日期]2005-02-28 [基金项目]安徽省高等学校自然科学研究项目(2005K J051) 第22卷第3期大 学 数 学 V ol .22,№.3 2006年6月 COLLEGE M A TH EM A TICS Jun .2006 随机微分方程欧拉格式算法分析 郭小林 (安徽财经大学计算机系,蚌埠233041) [摘 要]首先给出了线性随机微分方程的欧拉格式算法,然后给出了非线性随机微分方程变步长的欧拉格式算法,接着讨论了其对初值的连续依赖性和收敛性. [关键词]随机微分方程;欧拉格式;对初值的连续依赖性;收敛性 [中图分类号]O 211.63 [文献标识码]A [文章编号]1672-1454(2006)03-0094-06 1 引 言 随机微分方程在描述现象中起着重要的作用.当使用随机微分方程解决问题时,我们常常是先把随机微分方程离散化为随机差分方程,然后利用随机差分方程进行计算或模拟.在所有离散化的方法中,欧拉格式是最基本且最重要的一种[1-7].在文[3]中,Vlad Bally 和Denis Talay 研究了关于随机微分方程 d x t =b (x t )d t +σ(x t )d w t 的欧拉格式,其算法格式为 x n (p +1)h =x n ph +b (x n ph )h +σ(x n ph )(w (p +1)h -w ph ), 其中h 为固定步长,p =0,1,2,….当ph ≤t ≤(p +1)h 时,x n t 被定义为 x n t =x n ph +b (x n ph )(t -ph )+σ(x n ph )(w t -w p h ), 其中w t 是布朗运动.在文[7]中,No rbert H ofmann 给出了随机微分方程(1)的欧拉格式 y n +1=y n +a (t n ,y n )h +b (t n ,y n )h ξn , 其中h 是固定步长,ξn 满足P (ξn =±1)= 1 2 ,且当i ≠j 时,ξi 与ξj 相互独立,i ,j =1,2,…,n .然而,维纳过程不能用一个两点分布很好地近似,因此,在本文中,我们将给出变步长的欧拉格式. 下文结构如下:在第二节中给出线性随机微分方程的欧拉格式;第三节中给出非线性随机微分方程的变步长欧拉格式. 2 线性随机微分方程的欧拉格式 考虑线性随机微分方程 d x t =[a (t )x t +f (t )]d t +[b (t )x t +g (t )]d B t , (1)其中a (t ),b (t ),f (t )和g (t )均可积,B t 为一维布朗运动,则其欧拉格式为 y t n +1=y t n +[a (t n )y t n +f (t n )]h +[b (t n )y t n +g (t n )]h ξn , (2) 其中ξn ~N (0,1)满足:当i ≠j 时,ξi 与ξj 相互独立,对任意n ∈N ,h ≡Δt n =t n +1-t n . 数学与计算科学学院 实验报告 实验项目名称 Eular 方法求解一阶常微分方程数值解 所属课程名称 偏微分方程数值解 _________________ 实验类型 ________________ 验证性 _______________________ 实验日期 ___________ 2015-3-26 _____________________ 级 __________ 号 _________ 名 ________________ 绩 ______________________ 一、实验概述: 【实验目的】 纟沙理工久 班 学 姓 成 熟练掌握应用显性Eular法和隐式Eular法求解一般一阶常微分方程的近似数值解。 【实验原理】 虽然求解常微分方程有各种各样的解析方法,但解析方法只能用来求解一些特殊类型的方程。求解从实际问题当中归结出来的微分方程主要靠数值解法。欧拉方法是一类重要的数值解法。这类方法回避解y(x)的函数表达式,而是寻求它在一系 列离散节点上的近似值,相邻的两个节点的间距称作步长。假定步长为定数。 欧拉方法是一类离散化方法,这类方法将寻求解y(x)的分析问题转化为计算离 散值值的代数问题,从而使问题获得了实质性的简化。然而随之带来的困难是,由于数据量往往很大,差分方法所归结出的可能是个大规模的代数方程组。 【实验环境】 1.硬件环境 22软件环境 MATLAB7.0 、实验内容: 【实验过程】(实验步骤) (一)实验任务 描述某种化学反应过程的方程,利用显性和隐形 Eualar 方法求解下列一阶线性 微分方程组的近似数值解: y i (0) 5(0) 0, y a (0) 0 (二)求解过程 Eular 方法: 一阶线性微分方程初值问题 y' f (x,y ),a x b y (a ) y 。 a x 0 x., .... x n b ( 1) X n x nh, h 为步长 方程离散化:差分和差商 y'g y1 y0 y1 y0 x 1 x 0 h 愀必)y/0 h y 1 y ° hf (x °,y °) (2) y n 1 y n hf (X °,y °) 通过初始值y ,依据递推公式(2)逐步算出Y 1,Y 2,....,y n 就为显性的Eular 方 法。 隐形Eular 方法: y 1 y ° hf(X 1,yJ y n 1 y n hf(X n1,y n1) 公式(3)即为隐式Eular 公式 (3) 4 0.04y 1 10 y 1y 2 0.04% 104 y-i y 2 3 1O 7y 2 牛顿-欧拉方程 欧拉方程(Eulerequations),是欧拉运动定律的定量描述,欧拉运动定律是牛顿运动定律的延伸,在牛顿发表牛顿运动定律超过半个世纪后,于1750年,欧拉才成功的用欧拉方程表述了该定律: 该方程是建立在角动量定理的基础上的描述刚体的旋转运动时刚体所受外力矩与角加速度的关系式,大多时候可简写成: 其中,分别为刚体坐标系下三个轴的所受的外力矩,分别为刚体三个坐标轴的转动惯量(刚体坐标系下)。 欧拉方程通常与牛顿的平移运动方程被一起写出,称为牛顿-欧拉方程(Newton-Euler equations): 这里对牛顿的平移运动方程不赘述,只对欧拉方程进行讨论。 1.单质点角动量定理 质点旋转时,有动量定理: 对两边叉乘质点位置矢量: 观察: 因为: 故有: 定义角动量,可以看出为外力矩 故有单质点的角动量定理: 2.刚体的角动量定理 定义刚体的角动量为: 其中:下标G表示该向量为大地坐标系下的,的下标i 表示该向量为大地坐标下各个质量元的向量。刚体旋转运动参考的惯性系是大地坐标系,不能把采用刚体的本身坐标系作为参考系,本身坐标系的提出只是方便我们某些量的分析与表述,如角速度、惯性张量。 (这里需要特别说明的是因为刚体质量分布不均匀的原因,角动量的方向往往不与刚体角速度方向一致,这也是无力矩进动的 原因,即很多时候刚体角速度不守恒但刚体的角动量守恒了,宏观来看就是因为要保证角动量和动量守恒所以才要产生内力作用使角速度变化达到守恒的效果。) 由牛顿第三定律易知内力矩产生的角动量变化相抵,故有刚体的角动量定理: 其中:为外力矩 把上式展开有: 其中:称为惯性矩阵 刚体旋转时,是变化的,但刚体在刚体坐标系下的惯性矩阵不会变,且容易分析得到: 某师X大学本科毕业论文 微分方程常用的两种数值解法:欧拉方法与龙 格—库塔法 学生某XXX 院系名称数学与软件科学学院 专业名称信息与计算科学 班级2006级 4 班 学号20060640XX 指导教师Xxx 某师X大学教务处 二○一○年五月 微分方程常用的两种数值解法:欧拉方法与龙格—库塔法 学生某:xxx 指导教师:xx 【内容摘要】微分方程是最有生命力的数学分支,在自然科学的许多领域中,都 会遇到常微分方程的求解问题。当前计算机的发展为常微分方程的应用及理论研究提供了非常有力的工具,利用计算机解微分方程主要使用数值方法,欧拉方法和龙格——库塔方法是求解微分方程最典型常用的数值方法。本文详细研究了这两类数值计算方法的构造过程,分析了它们的优缺点,以及它们的收敛性,相容性,及稳定性。讨论了步长的变化对数值方法的影响和系数不同的同阶龙格—库塔方法的差别。通过编制C程序在计算机上实现这两类方法及对一些典型算例的结果分析比较,能更深切体会它们的功能,优缺点及适用场合,从而在实际应用中能对不同类型和不同要求的常微分方程会选取适当的求解方法。 关键词:显式单步法欧拉(Euler)方法龙格—库塔(Runge—Kutta)方法截断误差收敛性 Two monly used numerical solution of differential equations:Euler method and Runge - Kutta method Student Name: Xiong Shiying Tutor:Zhang Li 【Abstract】The differential equation is the most vitality branch in mathematics. In many domains of natural science, we can meet the ordinary differentialequation solution question. Currently, the development of puter has provided the extremely powerful tool for the ordinary differential equation application and the fundamental research, the puter solving differential equation mainly uses value method.The Euler method and the Runge—Kutta method are the most typical monly value method to solve the differential equation. This article dissects the structure process of these two kinds of values monly value method to solve the analyses their good and bad points, to their astringency, the patibility, and the stability has made the proof. At the same time, the article discuss the length of stride to the numerical method changing influence and the difference of the coefficient different same step Runge—kutta method. Through establishing C program on the puter can realize these two kind of methods, Anglicizing some models of calculate example result can sincerely realize their function, the advantage and disadvantage points and the suitable situation, thus the suitable solution method can be selected to solve the different type and the different request ordinary牛顿—欧拉方程
常微分方程欧拉算法
第8章 常微分方程数值解法 本章主要内容: 1.欧拉法、改进欧拉法 2
MATLABEuler法解常微分方程
常微分方程欧拉算法
欧拉运动微分方程各项的单位
机微分方程的欧拉算法_郭小林
欧拉法解常微分方程
牛顿—欧拉方程
微分方程常用的两种数值解法:欧拉方法和龙格库塔法
