最新圆的相关定理及其几何证明(含答案)

O A

圆的相关定理及其几何证明

典题探究

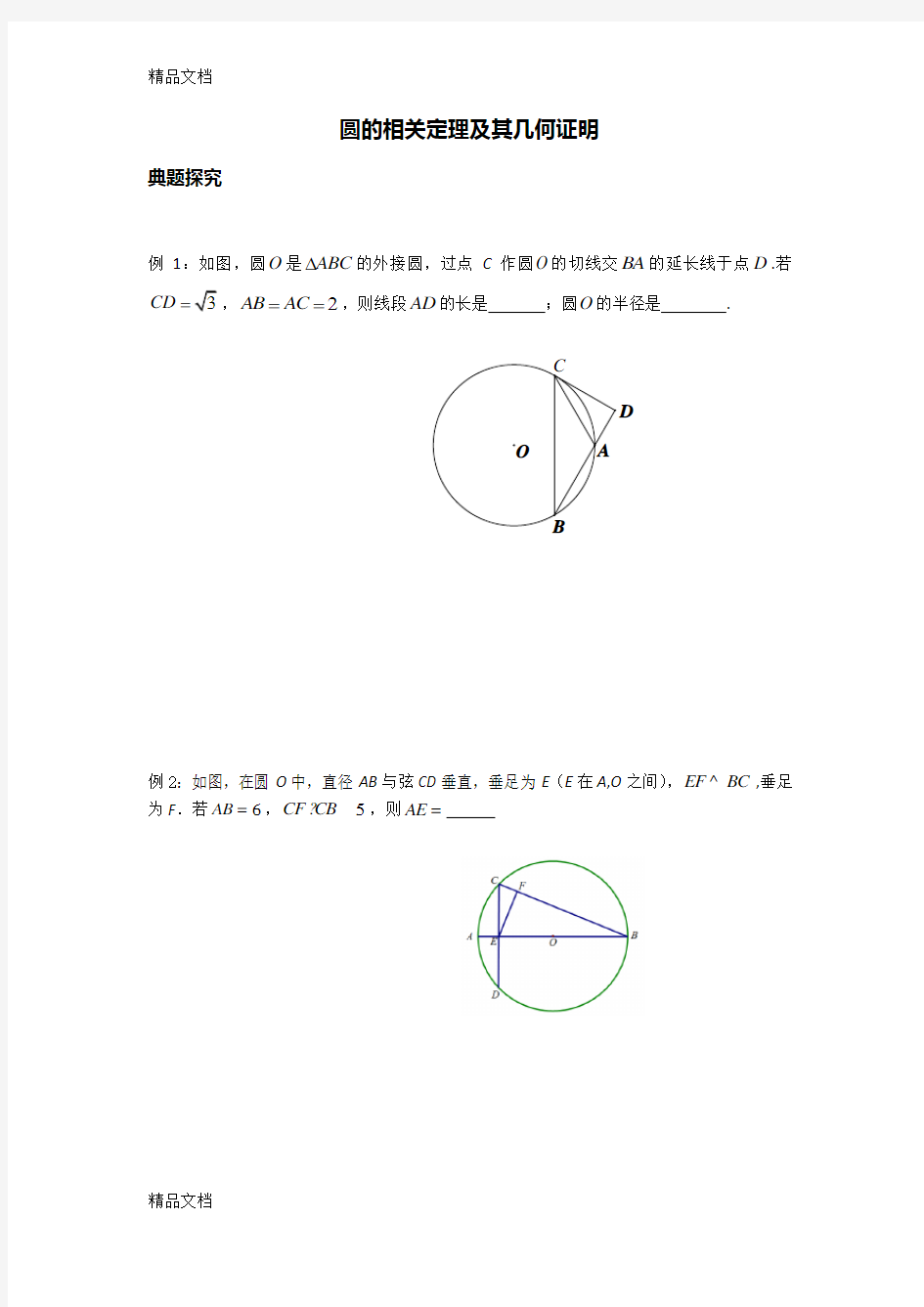
例1：如图，圆O是ABC

?的外接圆，过点C作圆O的切线交BA的延长线于点D.若3

CD=2

AB AC

==，则线段AD的长是；圆O的半径是.

例2：如图，在圆O中，直径AB与弦CD垂直，垂足为E（E在A,O之间），,垂足为F．若，，则

EF BC

AB=5

CF CB

?AE=

例3：如图已知PA 与圆O 相切于A ，半径OC OP ⊥，AC 交PO 于B ，

若1OC =,2OP =，则PA = ，=PB ．

例4：如图，从圆O 外一点P 引圆O 的切线PA 和割线PBC ，已知30BPA ∠=?，11BC =，

1PB =, 则PA = ,圆O 的半径等于

演练方阵

A 档（巩固专练）

1．如图，已知直线PD 切⊙O 于点D ，直线PO 交⊙O 于点E,F.

若21PF PD ==，则⊙O 的半径为；EFD ∠= .

B C

2. 如图，与切于点，交弦的延长线于点，过点作圆的切线交于点. 若，，则弦的长为_______.

3. 如图：圆O 的割线PAB 经过圆心O ，C 是圆上一点，PA ＝AC ＝1

AB ，则以下结论不正确．．．的是( )

A.CB CP =

B. PCAC PABC =

C. PC 是圆O 的切线

D. BC BABP =

4．如图，已知AB 是圆O 的直径，P 在AB 的延长线上，PC 切圆O 于点C ，CD OP ⊥于

D ．若6CD =，10CP =，则圆O 的半径长为______；BP =______．

AP O e A DB P B O AP C 90ACB ∠=?3,4BC CP ==DB

D C

B P

A O

E D C

5．如图所示，以直角三角形ABC 的直角边AC 为直径作⊙O ，交斜边AB 于点D ，过点D 作⊙O 的切线，交BC 边于点E .则

=BC

6．如图，直线AM 与圆相切于点M, ABC 与ADE 是圆的两条割线，且BD ⊥AD ，连接MD 、 EC 。则下面结论中，错误．．的结论是( ) A ．∠ECA = 90o

B ．∠CEM=∠DMA+∠DBA

C ．AM 2 = AD·AE

D ．AD·D

E = AB·BC

7．如图，AB 切圆于点A ,AC 为圆的直径，BC 交圆于点D ，E 为CD 的中点，且5,6,BD AC ==则CD =__________；AE =__________.

O O O

8．如图，PC切圆O于点C，割线PAB经过圆心O，4,8

PC PB

==，则tan COP

∠=，△OBC的面积是

9．如图，AB为⊙O的直径,AC切⊙O于点A,且过点C的割线,CMN交AB的延长线于点D,若CM MN ND

==,22

AC=CM=，AD=

10．如图，,,,

A B C D是⊙O上的四个点，过点B的切线与DC的延长线交于点E.若

110

BCD?

∠=，则DBE

∠=( )

A. 75?

B. 70?

C. 60?

D. 55?

D M

B 档（提升精练）

1．如图，已知⊙O 的弦AB 交半径OC 于点D,若AD=4,BD=3,OC=4,则CD 的长为______

2．如图,已知圆中两条弦AB 与CD 相交于点E F ,是AB 延长线上一点,且BF AF CF DF 2,2==

=,若CE 与圆相切,且2

CE ,则=BE E B F

D C

3．如图，AB 是半圆O 的直径，P 在AB 的延长线上，PD 与半圆O 相切于点C ，

AD PD ⊥．若4PC =，2PB =，则CD =______.

4．如图，AB 是⊙O 的直径，直线DE 切⊙O 于点D

，且与AB 延长线交于点C ，若CD =

，1CB =，则ADE ∠=

5．如图，AC 为⊙O 的直

径，OB AC ⊥，弦BN 交AC

于点

M ．若3OC =1OM =，则MN =_______

6．如图，PA 是圆O 的切线，切点为A ，PO 交圆O 于,B C 两点，3,1PA PB ==，则

ABC ∠=( )

A 70?

B 60?

C 45?

D 30?

7．如图所示，Rt △ABC 内接于圆，60ABC ∠=o

，PA 是圆的切线，A 为切点， PB 交AC 于E ，交圆于D ．若PA =AE ，PD 3BD =33AP = ，AC =

8. 如图，以ABC ?的边AB 为直径的半圆交AC 于点D ，交BC 于点E ，EF AB ^于点F ，

3AF BF =，22BE EC ==，那么CDE D= ，CD = .

9．如图，已知圆中两条弦AB 与CD 相交于点F ，CE 与圆相切交AB 延长线上于点E ，

若DF CF ==::4:2:1AF FB BE =，则线段CE 的长为

D P

C B

10.如图，直线与相切于点，割线经过圆心，弦⊥于点，

，，则

C档（跨越导练）

1.如图，△ABC是⊙O的内接三角形，PA是⊙O的切线，PB交AC于点E，交⊙O于点D．若PA PE

=，60

ABC?

∠=，1

PD=，9

PB=，则PA=_____；EC=_____ 2.如图，O

e的直径AB与弦CD交于点P，

,5,1

CP PD AP

===，则DCB

D＝___ ___

PC e O C PAB O CD AB E 4

PC=8

PB=CE=

3. 如图，AB 是圆O 的直径，CD AB ⊥于D ，且2AD BD =，E 为AD 的中点，连接CE 并延长交圆O 于F

．若CD =AB =_______， EF =_________

4. 如图所示，AB 是圆的直径，点C 在圆上，过点B ，C 的切线交于点P ，AP 交圆于D ，若AB =2，AC =1，则PC =______，PD =______

5. AB 是圆O 的直径，D 为圆O 上一点，过D 作圆O 的切线交AB 延长线于点C ，若DC P

圆幂定理

圆幂定理相交弦定理：圆内的两条相交弦，被交点分成的两条线段长的积相等。或：经过圆内一点引两条弦，各弦被这点所分成的两段的积相等。定理圆内的两条相交弦，被交点分成的两条线段长的积相等。（经过圆内一点引两条弦，各弦被这点所分成的两段的积相等）几何语言：若弦AB、CD交于点P则PA·PB=PC·PD（相交弦定理）概述相交弦定理为圆幂定理之一，其他两条定理为：切割线定理割线定理 2证明证明：连结AC，BD 由圆周角定理的推论，得∠A=∠D，∠C=∠B。（圆周角推论2: 同(等)弧所对圆周角相等.）∴△PAC∽△PDB ∴PA∶PD=PC∶PB，PA·PB=PC·PD 注：其逆定理可作为证明圆的内接四边形的方法. P点若选在圆内任意一点更具一般性。其逆定理也可用于证明四点共圆。 P 不是圆心 3比较

切割线定理切割线定理：从圆外一点引圆的切线和割线，切线长是这点到割线与圆交点的两条线段长的比例中项。是圆幂定理的一种。切割线定理示意图几何语言：∵PT切⊙O于点T，PBA是⊙O的割线∴PT2=PA·PB（切割线定理）推论：从圆外一点引圆的两条割线，这一点到每条割线与圆的交点的两条线段长的积相等几何语言： ∵PT是⊙O切线，PBA，PDC是⊙O的割线 ∴PD·PC=PA·PB（切割线定理推论）(割线定理）由上可知:PT2=PA·PB=PC·PD 2证明切割线定理证明: 设ABP是⊙O的一条割线，PT是⊙O的一条切线，切点为T，则PT2=PA·PB

证明：连接AT, BT ∵∠PTB=∠PAT(弦切角定理 ) 切割线定理的证明 ∠APT=∠APT(公共角) ∴△PBT∽△PTA(两角对应相等,两三角形相似) 则PB：PT=PT：AP 即：PT2=PB·PA 3比较相交弦定理、切割线定理及割线定理(切割线定理推论)以及他们的推论统称为圆幂定理。一般用于求直线段长度。割线定理：指的是从圆外一点引圆的两条割线，这一点到每条割线与圆交点的距离的积相等， 1定义文字表达：从圆外一点引圆的两条割线，这一点到每条割线与圆交点的距离的积相等。数学语言：从圆外一点L引两条割线与圆分别交于A.B.C.D 则有LA·LB=LC·LD=LT^2。如下图所示。(LT为切线）

《1.3.1圆幂定理》教学案3

《1.3.1圆幂定理》教学案【教学目标】 1.使学生理解相交弦定理、切割线定理及其推论间的相互关系，并能综合运用它们解决有关问题； 2.从运动的观点来统一认识圆幂定理.对学生进行事物之间是相互联系和运动变化的观点的教育. 【教学重难点】重点：相交弦定理、切割线定理及其推论之间的关系以及应用；难点：灵活运用圆幂定理解题. 【教学过程】相交弦定理：圆内的两条相交弦，被交点分成的两条线段长的积相等. 或：经过圆内一点引两条弦，各弦被这点所分成的两段的积相等. 定理圆内的两条相交弦，被交点分成的两条线段长的积相等.(经过圆内一点引两条弦，各弦被这点所分成的两段的积相等) 几何语言：若弦AB、CD交于点P则P A·PB=PC·P D(相交弦定理) 2证明证明：连结AC，BD 由圆周角定理的推论，得∠A=∠D，∠C=∠B.(圆周角推论2: 同(等)弧所对圆周角相等.) ∴△P AC∽△PDB ∴P A∶PD=PC∶PB，P A·PB=PC·PD 注：其逆定理可作为证明圆的内接四边形的方法. P点若选在圆内任意一点更具一般性.其逆定理也可用于证明四点共圆. 3比较相交弦定理、切割线定理以及他们的推论统称为圆幂定理.一般用于求线段长度. 4相交弦定理推论定理如果弦与直径垂直相交，那么弦的一半是它所分直径所成的两条线段的比例中项. 说明几何语言：若AB是直径，CD垂直AB于点P，则=P A·PB(相交弦定理推论)

切割线定理切割线定理：从圆外一点引圆的切线和割线，切线长是这点到割线与圆交点的两条线段长的比例中项.是圆幂定理的一种. 切割线定理示意图几何语言：∵PT切⊙O于点T，PBA是⊙O的割线∴PT2=P A·PB(切割线定理) 推论：从圆外一点引圆的两条割线，这一点到每条割线与圆的交点的两条线段长的积相等几何语言： ∵PT是⊙O切线，PBA，PDC是⊙O的割线 ∴PD·PC=P A·PB(切割线定理推论)(割线定理) 由上可知:PT2=P A·PB=PC·PD 2证明切割线定理证明: 设ABP是⊙O的一条割线，PT是⊙O的一条切线，切点为T，则PT2=P A·PB 证明：连接AT，BT ∵∠PTB=∠P AT(弦切角定理 ) 切割线定理的证明 ∠APT=∠APT(公共角) ∴△PBT∽△PTA(两角对应相等，两三角形相似) 则PB：PT=PT：AP 即：PT2=PB·P A

立体几何公理及定理

立体几何公理及定理一、空间点、线、面之间的关系 1、两条直线的位置关系有： 2、两个平面的位置关系有：公理1、如果一条直线上的两点在一个平面内，那么这条直线在此平面内。公理2、过不在一条直线上的三点，有且只有一个平面。推论1、一组平行直线确定唯一一个平面。推论2、一条直线及直线外一点确定唯一一个平面。公理3、如果有两个不重合的平面有一个公共点，那么它们有且只有一条过该点的公共直线。公理4（平行公理）、平行于同一直线的两直线平行。二、平行关系直线与平面平行的判定定理：平面外一条直线与此平面内的一条直线平行，则该直线与此平面平行。直线与平面平行的性质定理：一条直线与一个平面平行，则过这条直线的任意平面与此平面的交线与该直线平行。平面与平面平行的判定定理：一个平面内的两条相交直线与另一个平面平行，则这两个平面平行。平面与平面平行的性质定理： 1、如果两个平行平面同时和第三个平面相交，那么它们的交线平行。 2、两平面平行，其中一个平面内的任一直线平行于另一个平面。 3、夹在两个平行平面间的平行线段相等。 4、平行于同一平面的两个平面平行。三、垂直关系直线与平面垂直的判定定理：一条直线与一个平面内的两条相交直线都垂直，那么该直线与此平面垂直。直线与平面垂直的性质定理： 1、垂直于同一个平面的两条直线互相平行。 2、如果一条直线垂直一个平面，那么这条直线垂直于平面内的所有直线。平面与平面垂直的判定定理：如果一个平面过另一个平面的垂线，那么这两个平面垂直。平面与平面垂直的性质定理：如果两个平面垂直，则一个平面内垂直于交线的直线与另一个平面垂直。三角公式汇总一、任意角的三角函数 1. ①与α终边相同的角的集合（角α与角β的终边重合）：{} Z k k ∈+?=,360|αββ ②终边在x 轴上的角的集合： {} Z k k ∈?=,180| ββ

初中数学中被删掉的有用知识圆幂定理及其应用

圆幂定理及其应用教学目标 1.使学生理解相交弦定理、切割线定理及其推论间的相互关系，并能综合运用它们解决有关问题； 2.通过对例题的分析，提高学生分析问题和解决问题的能力，并领悟添加辅助线的方法； 3.从运动的观点来统一认识圆幂定理.对学生进行事物之间是相互联系和运动变化的观点的教育. 教学重点和难点相交弦定理、切割线定理及其推论之间的关系以及应用是重点；灵活运用圆幂定理解题是难点. 教学过程设计一、从学生原有的认知结构提出问题 1.根据图7-162(1)、(2)、(3)，让学生结合图形，说出相交弦定理、切割线定理、割线定理的内容. 2.然后提出问题.相交弦定理、切割线定理及其推论这三者之间是否有联系? 提出问题让学生思考，在学生回答的基础上，教师用电脑或投影演示图形的变化过程，从相交弦定理出发，用运动的观点来统一认识定理. (1)如图7-163，⊙O的两条弦AB，CD相交于点P，则PA·PB＝PC·PD.这便是我们学过的相交弦定理.对于这个定理有两个特例：一是如果圆内的两条弦交于圆心O，则有PA＝PB＝PC＝PD＝圆的半径R，此时AB，CD 是直径，相交弦定理当然成立.(如图7-164)

二是当P点逐渐远离圆心O，运动到圆上时，点P和B，D重合，这时PB＝PD＝O，仍然有PA·PB＝PC·PD＝O，相交弦定理仍然成立.(图7-165) (2)点P继续运动，运动到圆外时，两弦的延长线交于圆外一点P，成为两条割线，则有PA·PB＝PC·PD，这就是我们学过的切割线定理的推论(割线定理).(图7-166) (3)在图7-166中，如果将割线PDC按箭头所示方向绕P点旋转，使C，D两点在圆上逐渐靠近，以至合为一点C，割线PCD变成切线PC.这时有PA·PB＝PC·PD ＝PC2，这就是我们学过的切割线定理.(图7-167) (4)如果割线PAB也绕P点向外旋转的话，也会成为一条切线PA.这时应有PA2＝PB2，可得PA＝PB，这就是我们学过的切线长定理.(图7-168) 至此，通过点的运动及线的运动变化，我们发现，相交弦定理、切割线定理及其推论和切线长定理之间有着密切的联系. 3.启发学生理解定理的实质. 经过一定点P作圆的弦或割线或切线，如图7-169. 观察图7-169，可以得出：(设⊙O半径为R) 在图(1)中，PA·PB＝PC·PD＝PE·PF ＝(R-OP)(R+OP) ＝R2-OP2；在图(2)中，PA·PB＝PT2＝OP2-OT2 ＝OP2-R2 在图(3)中，PA·PB＝PC·PD＝PT2 ＝OP2-R2. 教师指出，由于PA·PB均等于｜OP2-R2｜，为一常数，叫做点P关于⊙O的幂，所以相交弦定理、切割线定理及其推论(割线定理)统称为圆幂定理. 二、例题分析(采用师生共同探索、讲练结合的方式进行) 例1 如图7-170，两个以O为圆心的同心圆，AB切大圆于B，AC切小圆于C，交大圆

初中数学所有几何证明定理

初中数学所有几何证明定理 TYYGROUP system office room 【TYYUA16H-TYY-TYYYUA8Q8-

初中数学所有几何证明定理证明题的思路很多几何证明题的思路往往是填加辅助线，分析已知、求证与图形，探索证明。对于证明题，有三种思考方式： (1)正向思维。对于一般简单的题目，我们正向思考，轻而易举可以做出，这里就不详细讲述了。 (2)逆向思维。顾名思义，就是从相反的方向思考问题。在初中数学中，逆向思维是非常重要的思维方式，在证明题中体现的更加明显。同学们认真读完一道题的题干后，不知道从何入手，建议你从结论出发。例如：可以有这样的思考过程：要证明某两条边相等，那么结合图形可以看出，只要证出某两个三角形相等即可；要证三角形全等，结合所给的条件，看还缺少什么条件需要证明，证明这个条件又需要怎样做辅助线，这样思考下去……这样我们就找到了解题的思路，然后把过程正着写出来就可以了。 (3)正逆结合。对于从结论很难分析出思路的题目，可以结合结论和已知条件认真的分析。初中数学中，一般所给的已知条件都是解题过程中要用到的，所以可以从已知条件中寻找思路，比如给我们三角形某边中点，我们就要想到是否要连出中位线，或者是否要用到中点倍长法。给我们梯形，我们就要想到是否要做高，或平移腰，或平移对角线，或补形等等。正逆结合，战无不胜。

证明题要用到哪些原理？要掌握初中数学几何证明题技巧，熟练运用和记忆如下原理是关键。下面归类一下，多做练习，熟能生巧，遇到几何证明题能想到采用哪一类型原理来解决问题。一、证明两线段相等 1.两全等三角形中对应边相等。 2.同一三角形中等角对等边。 3.等腰三角形顶角的平分线或底边的高平分底边。 4.平行四边形的对边或对角线被交点分成的两段相等。 5.直角三角形斜边的中点到三顶点距离相等。 6.线段垂直平分线上任意一点到线段两段距离相等。 7.角平分线上任一点到角的两边距离相等。 8.过三角形一边的中点且平行于第三边的直线分第二边所成的线段相等。 9.同圆（或等圆）中等弧所对的弦或与圆心等距的两弦或等圆心角、圆周角所对的弦相等。 10.圆外一点引圆的两条切线的切线长相等或圆内垂直于直径的弦被直径分成的两段相等。 11.两前项（或两后项）相等的比例式中的两后项（或两前项）相等。 12.两圆的内（外）公切线的长相等。 13.等于同一线段的两条线段相等。二、证明两个角相等 1.两全等三角形的对应角相等。 2.同一三角形中等边对等角。

圆幂定理及其应用

[文件] sxc3jja0008.doc [科目] 数学 [年级] 初三 [章节] [关键词] 圆/圆幂定理/应用 [标题] 圆幂定理及其应用 [内容] 教学目标 1.使学生理解相交弦定理、切割线定理及其推论间的相互关系，并能综合运用它们解决有关问题； 2.通过对例题的分析，提高学生分析问题和解决问题的能力，并领悟添加辅助线的方法； 3.从运动的观点来统一认识圆幂定理.对学生进行事物之间是相互联系和运动变化的观点的教育. 教学重点和难点相交弦定理、切割线定理及其推论之间的关系以及应用是重点；灵活运用圆幂定理解题是难点. 教学过程设计一、从学生原有的认知结构提出问题 1.根据图7-162(1)、(2)、(3)，让学生结合图形，说出相交弦定理、切割线定理、割线定理的内容. 2.然后提出问题.相交弦定理、切割线定理及其推论这三者之间是否有联系? 提出问题让学生思考，在学生回答的基础上，教师用电脑或投影演示图形的变化过程，从相交弦定理出发，用运动的观点来统一认识定理. (1)如图7-163，⊙O的两条弦AB，CD相交于点P，则PA·PB＝PC·PD.这便是我们学过的相交弦定理.对于这个定理有两个特例：一是如果圆内的两条弦交于圆心O，则有PA＝PB＝PC＝PD＝圆的半径R，此时AB，CD是直径，相交弦定理当然成立.(如图7-164)

高中立体几何八大定理

线面位置关系的八大定理、直线与平面平行的判定定理: 文字语言：如果平面外的一条直线与平面内的一条直线平行，则这条直线与平面平行图形语言：符号语言： a u a b u o alia a//b 作用：线线平行=线面平行二、直线与平面平行的性质定理：文字语言：如果一条直线和一个平面平行，经过这条直线的平面和这个平面相交，那么这条直线就和交线平行。图形语言： I//：符号语言：I u E l //m a o P = m 作用：线面平行=线线平行、平面与平面平行的判定定理文字语言：如果一个平面内有两条相交直线都平行于另一个平面，那么这两个平面平行. 图形语言：符号语言： a u a b u a aPlb = Au a//P a// P b/厂作用：线线平行=面面平行四、平面与平面平行的性质定理：文字语言：如果两个平行平面同时和第三个平面相交图形语言: ?// P 符号语言：「二a = a//b Y =b“ 作用：面面平行=线线平行,那么所得的两条交线平行

图形语言：符号语言： a 丄m a 丄n :a _ ： m 「n 二 A m 二二，n 二：作用：线线垂直=线面垂直 a / * 六、直线与平面垂直的性质定理: 文字语言：若两条直线垂直于同一个平面，则这两条直线平行图形语言：符号语言： a - :■ 匕 a//b b -:- 作用：线面垂直=线线平行七、平面与平面垂直的判定定理: 文字语言：如果一个平面经过另一个平面的一条垂线，则这两个平面互相垂直。图形语言：一 a 丄a 〕任符号表示： _ ■ a u Pj 注：线面垂直 =?面面垂直八、平面与平面垂直的性质定理: 文字语言：如果两个平面互相垂直，那么在一个平面内垂直与它们的交线的直线垂直于另个平面图形语言：符号语言: a 1 P l AB : AB _丨作用：面面垂直=线面垂直五、直线与平面垂直的判定定理：文字语言：如果一条直线和一个平面内的两条相交直线垂直,

牛顿几何三大定理及证明

精品文档 . 牛顿三大定理牛顿定理1：完全四边形两条对边的延长线的交点所连线段的中点和两条对角线的中点，三点共线。这条直线叫做这个四边形的牛顿线。证明：四边形ABCD,AB∩CD=E,AD∩BC=F,BD中点M,AC中点L,EF中点N。取BE中点P,BC 中点R,PN∩CE=Q R,L,Q共线，QL/LR=EA/AB，M,R,P共线。RM/MP=CD/DE，N,P,Q共线，PN/NQ=BF/FC 三式相乘得:QL/LR*RM/MP*PN/NQ=EA/AB*CD/DE*BF/FC 由梅涅劳斯定理 QL/LR*RM/MP*PN/NQ=1 由梅涅劳斯定理的逆定理知:L,M,N三点共线故牛顿定理1成立牛顿定理2圆外切四边形的两条对角线的中点，及该圆的圆心，三点共线。证明：设四边形ABCD是⊙I的外切四边形，E和F分别是它的对角线AC和BD的中点，连接EI只需证它过点F，即只需证△BEI与△DEI面积相等。显然，S△BEI=S△BIC+S△CEI-S△BCE，而S△DEI=S△ADE+S△AIE-S△AID。注意两个式子，由ABCD外切于⊙I，AB+CD=AD+BC，S△BIC+S△AID=1/2*S四边形ABCD，S△ADE+S △BCE=1/2*S△ACD+1/2*S△ABC=1/2*S四边形ABCD。即S△BIC+S△AID=S△ADE+S△BCE，移项得S△BIC-S△BCE=S△ADE-S△AID，由E是AC中点，S△CEI=S△AEI，故S△BIC-S △CEI-S△BCE=S△ADE-S△AIE-S△AID，即S△BEI=△DEI，而F是BD中点，由共边比例定理EI过点F即EF过点I，故结论成立。证毕。牛顿定理3圆的外切四边形的对角线的交点和以切点为顶点的四边形对角线交点重合。精品文档

圆幂定理及其证明#(优选.)

圆幂的定义假设平面上有一圆O，其半径为R，有一点P在圆O外，则OP^2-R^2即为P点到圆O的幂；若P点在圆内，则圆幂为R^2-OP^2；综上所述，圆幂为|OP^2-R^2|。圆幂恒大于或等于零。圆幂的由来过任意在圆O外的一点P引一条直线L1与一条过圆心的直线L2，L1与圆交于A、B（可重合，即切线），L2与圆交于C、D。则PA·PB=PC·PD。若圆半径为r，则PC·PD=(PO-r)·(PO+r)=PO^2-r^2=|PO^2-r^2| （要加绝对值，原因见下）为定值。这个值称为点P到圆O的幂。（事实上所有的过P点与圆相交的直线都满足这个值）若点P在圆内，类似可得定值为r^2-PO^2=|PO^2-r^2| 故平面上任意一点对于圆的幂为这个点到圆心的距离与圆的半径的平方差，而过这一点引任意直线交圆于A、B，那么PA·PB等于圆幂的绝对值。圆幂定理定理内容过任意不在圆上的一点P引两条直线L1、L2，L1与圆交于A、B（可重合，即切线），L2与圆交于C、D（可重合），则有。[1] 圆幂定理的所有情况考虑经过P点与圆心O的直线，设PO交⊙O与M、N，R为圆的半径，则有

圆幂定理的证明图Ⅰ：相交弦定理。如图，AB、CD为圆O的两条任意弦。相交于点P，连接AB、BD，由于∠B与∠D同为弧AC所对的圆周角，因此由圆周角定理知：∠B=∠D，同理∠A=∠C，所以。所以有：，即：图Ⅱ：割线定理。如图，连接AD、BC。可知∠B=∠D，又因为∠P为公共角，所以有，同上证得图Ⅲ：切割线定理。如图，连接AC、AD。∠PAC为切线PA与弦AC组成的弦切角，因此有∠PAC=∠D，又因为∠P为公共角，所以有易证

几何定理证明

几何定理证明 1、重心定理：三角形的三条中线交于一点，这点到顶点的距离是它到对边中点距离的2倍。该点叫做三角形的重心。先证明交于一点，如图一中线AD、BE交于G，延长CG 交AB于F，即证明F为AB中点即可，延长GD至H使 GD=DH，又BD=DC∴BDCG为平行四边形，∴BE∥CH， CF∥BH，又E为AC中点，EG为中位线，∴G为AH中点，又CF∥BH，∴FG为中位线，即F为AB中点，∴三条中线交于一点。再证明2倍问题证明1：如图：△ABC的中线AD、BE交于G（重心），求证：AG＝2GD 取CE的中点F，连接DF，则CE＝2EF＝AE ， ∴DF是△BCE的中位线， ∴GE∥DF ， AG／GD＝AE／EF＝2， ∴AG＝2GD 。证明2：面积法（三条中线将三角形分成6个面积相等的三角形） △ABC，AB、BC、CA中点分别为D、E、F，交于一点G。 ∵D、E、F为中点 ∴S△CAD=S△CDB=S△ABE=S△ACE=S△ABF=S△BCF =S△ABC／2 ∴S△ADG=S△CEG=S△BEG 同理S△BDG=S△BEG ∴S△ABG=2S△BEG ∴AG／GE=2即AG=2GE 证明3：相似三角形 △ABC，AB、BC、CA中点分别为D、E、F，交于一点G。 ∴DF//BC，DF=BC/2 ①（中位线定理）。 ∴△ADF∽△ABC, E为BC中点，∴H为DF中点（可证AH/AE=DH/BE=HF/EC, BE=EC, ∴DH=HF) ∴HF=DF/2 , BE=BC/2，又可由①知HF=BE/2 ∴HF//BE. 又∵∠BGE=∠FGH。 ∴△BGE∽△FGH ∴BG/GF=BE/HF=2。∴BG=（2/3）BF

《1.3.1圆幂定理》教学案1

《1.3.1圆幂定理》教学案教学目标 1．知识与技能：(1)理解相交弦定理及其推论，并初步会运用它们进行有关的简单证明和计算；(2)学会作两条已知线段的比例中项； 2．过程与方法：师生互动，生生互动，共同探究新知； 3．情感、态度、价值观：通过推论的推导，向学生渗透由一般到特殊的思想方法．教学重、难点重点：正确理解相交弦定理及其推论难点：相交弦定理及其推论的熟练运用教学过程前面讨论了与圆有关的角之间的关系.下面我们讨论与圆有关的线段的关系及其度量问题.下面沿用从特殊到一般地思路，讨论与圆的相交弦有关的问题. 探究1如图2-20，AB是⊙O的直径，CD⊥AB.AB与CD相交于P，线段P A、PB、PC、P D之间有什么关系？ ?=?(老师引导学生完成推导过程) . PA PB PC PD 探究2将图2-20中的AB向上(或向下)平移，使AB不再是直径(图2-21)，探究1的结论还成立吗？连接AD、BC，请同学们自己给出证明. 探究3如果CD与AB不垂直，如图2-22，CD、AB是圆内的任意两条相交弦，探究1的结论还成立吗？事实上，AB、CD是圆内的任意相交弦时，探究1仍然成立，而证方法不变.请同学们自己给出证明. 由上诉探究和论证，我们有 1.相交弦定理圆内的两条相交弦，被交点分成的两条线段长的积相等．探究4在图2-24中，使割线PB绕P运动到切线的位置(图2-25)，线段P A(或PB)、PC、P D之间有什么关系？ 2. =?(老师引导学生完成推导过程) PA PC PD

由上诉探究和论证，我们有 3.切割线定理：从圆外一点引圆的切线和割线，切线长是这点到割线与圆交点的两条线段长的比例中项．探究5下面对相交弦定理和切割弦定理作进一步分析：由切割线定理和相交弦定理不难看出，不论点P在圆内或圆外，通过圆的任一条割线交圆于A，B两点，只要点P的位置确定了，则P A? PB都是定值. 设定植为k，则：当点P在圆外时，如图，由切割线定理，可得 k = P A? PB = PT2= PO2- r2( r表示⊙O的半径 ) 当点P在圆内时，如图，过点P作AB垂直于OP，则： k = P A? PB = P A2= r2 - PO2( r表示⊙O的半径 ) 当点P在圆上时，显然k=0. 由上，我们可以得到：圆幂定理：已知⊙(O，r)，通过一定点的任意一条割线交圆于A，B两点，则：当点P在圆外时，k= PO2- r2；当点P在圆内时，k= r2- PO2；当点P在⊙O上时，k= 0. 我们称定值k为点P对⊙O的“幂” 【自主检测】 1. 圆内两弦相交，一弦长8cm且被交点平分，另一弦被交点分为1：4，则另一弦长为_ ____. 2. 已知：⊙O和不在⊙O上的一点P，过P的直线交⊙O于A、B两点，若P A·PB＝24，OP＝5，则⊙O的半径长为_______. 3 . 若P A为⊙O的切线，A为切点，PBC割线交⊙O于B、C，若BC＝20，P A=P C的长为_______. 4. AB、CD是⊙O切线，AB∥CD，⊙O的切线EF和AB、CD分别交于E、F，则∠EOF ＝______．

(完整版)高中立体几何八大定理

l m β α α b a 线面位置关系的八大定理一、直线与平面平行的判定定理：文字语言：如果平面外的一条直线与平面内的一条直线平行，则这条直线与平面平行图形语言：符号语言： //a b a b αα?? ? ???? ?//a α 作用：线线平行?线面平行二、直线与平面平行的性质定理：文字语言：如果一条直线和一个平面平行，经过这条直线的平面和这个平面相交，那么这条直线就和交线平行。图形语言：符号语言：//l l m α βαβ?? ????=? ?//l m 作用：线面平行?线线平行三、平面与平面平行的判定定理文字语言：如果一个平面内有两条相交直线都平行于另一个平面，那么这两个平面平行．图形语言：符号语言： //a b a b A a b α ααβββ ?????? =?????? I ∥∥ 作用：线线平行? 面面平行四、平面与平面平行的性质定理: 文字语言：如果两个平行平面同时和第三个平面相交,那么所得的两条交线平行图形语言: 符号语言:////a a b b αβαγβγ? ? ?=????=? 作用: 面面平行?线线平行

n m A α a α b a B A l β αa β α五、直线与平面垂直的判定定理：文字语言：如果一条直线和一个平面内的两条相交直线垂直，那么这条直线垂直于这个平面图形语言：符号语言： ,a m a n a m n A m n ααα⊥? ?⊥? ?⊥??=????? 作用：线线垂直?线面垂直六、直线与平面垂直的性质定理：文字语言：若两条直线垂直于同一个平面，则这两条直线平行图形语言：符号语言： //a a b b αα⊥? ??⊥? 作用：线面垂直?线线平行七、平面与平面垂直的判定定理：文字语言：如果一个平面经过另一个平面的一条垂线，则这两个平面互相垂直。图形语言：符号表示：a a ααββ⊥? ?⊥??? 注：线面垂直?面面垂直八、平面与平面垂直的性质定理：文字语言：如果两个平面互相垂直，那么在一个平面内垂直与它们的交线的直线垂直于另一个平面图形语言：符号语言：l AB AB AB l αβαββα⊥? ?=? ?⊥??? ?⊥? I 作用：面面垂直?线面垂直

初中数学所有几何证明定理

要掌握初中数学几何证明题技巧，熟练运用和记忆如下原理是关键。下面归类一下，多做练习，熟能生巧，遇到几何证明题能想到采用哪一类型原理来解决问题。一、证明两线段相等 1.两全等三角形中对应边相等。 2.同一三角形中等角对等边。 3.等腰三角形顶角的平分线或底边的高平分底边。 4.平行四边形的对边或对角线被交点分成的两段相等。 5.直角三角形斜边的中点到三顶点距离相等。 6.线段垂直平分线上任意一点到线段两段距离相等。 7.角平分线上任一点到角的两边距离相等。 8.过三角形一边的中点且平行于第三边的直线分第二边所成的线段相等。 9.同圆（或等圆）中等弧所对的弦或与圆心等距的两弦或等圆心角、圆周角所对的弦相等。 10.圆外一点引圆的两条切线的切线长相等或圆内垂直于直径的弦被直径分成的两段相等。 11.两前项（或两后项）相等的比例式中的两后项（或两前项）相等。 12.两圆的内（外）公切线的长相等。 13.等于同一线段的两条线段相等。二、证明两个角相等 1.两全等三角形的对应角相等。 2.同一三角形中等边对等角。 3.等腰三角形中，底边上的中线（或高）平分顶角。

专题13相似三角形定理与圆幂定理

专题十三相似三角形定理与圆幂定理本专题主要复习相似三角形的进一步认识、圆的进一步的认识．通过本专题的复习，了解平行线等分线段定理和平行截割定理；掌握相似三角形的判定定理及性质定理；理解直角三角形射影定理．理解圆周角定理及其推论；掌握圆的切线的判定定理及性质定理；理解弦切角定理及其推论．掌握相交弦定理、割线定理、切割线定理；理解圆内接四边形的性质定理与判定定理．【知识要点】 1．相似三角形概念相似三角形：对应角相等，对应边成比例的两个三角形是相似三角形．相似比：相似三角形对应边的比． 2．相似三角形的判定如果一个三角形的两个角与另一个三角形的两个角对应相等，那么这两个三角形相似(简叙为：两角对应相等两三角形相似)．如果一个三角形的两条边和另一个三角形的两条边对应成比例，并且夹角相等，那么这两个三角形相似(简叙为：两边对应成比例且夹角相等，两个三角形相似)．如果一个三角形的三条边与另一个三角形的三条边对应成比例，那么这两个三角形相似(简叙为：三边对应成比例，两个三角形相似)． 3．直角三角形相似的判定定理直角三角形被斜边上的高分成两个直角三角形和原三角形相似．如果一个直角三角形的斜边和一条直角边与另一个直角三角形的斜边和一条直角边对应成比例，那么这两个直角三角形相似． 4．相似三角形的性质相似三角形对应角相等，对应边成比例．相似三角形对应高的比，对应中线的比和对应角平分线的比都等于相似比．

相似三角形周长的比等于相似比．相似三角形的面积比等于相似比的平方． 5．相关结论平行于三角形一边的直线截其他两边，截得的三角形与原三角形的对应边成比例．三角形的内角平分线分对边成两段的长度比等于夹角两边长度的比．经过梯形一腰中点而平行于底边的直线平分另一腰．梯形的中位线平行于两底，并且等于两底和的一半．若一条直线截三角形的两边(或其延长线)所得对应线段成比例，则此直线与三角形的第三边平行． 6．弦切角定理弦切角定义：切线与弦所夹的角．弦切角的度数等于它所夹的弧的圆心角的度数的一半． 7．圆内接四边形的性质圆的内接四边形的对角互补，并且任意一个外角等于它的内对角． 8．圆幂定理相交弦定理：圆内的两条相交弦，被交点分成的两条线段长的积相等．切割线定理：从圆外一点引圆的切线和割线，切线长是这点到割线与圆交点的两条线段长的比例中项．割线定理：从圆外一点P引两条割线与圆分别交于A、B、C、D则有PA·PB＝PC·PD．【复习要求】 1．了解平行线等分线段定理和平行截割定理；掌握相似三角形的判定定理及性质定理；理解直角三角形射影定理． 2．理解圆周角定理及其推论；掌握圆的切线的判定定理及性质定理；理解弦切角定理及其推

立体几何证明定理及性质总结

一．直线和平面的三种位置关系： 1. 线面平行 2. 线面相交 l 符号表示：符号表示： 3. 线在面内符号表示：二．平行关系： 1.线线平行：方法一：用线面平行实现。方法二：用面面平行实现。 m l m l l // // ? ? ? ? ? ? = ? ? β α β α m l m l// // ? ? ? ? ? ? = ? = ? β γ α γ β α 方法三：用线面垂直实现。若α α⊥ ⊥m l,，则m l//。 2.线面平行：方法一：用线线平行实现。 α α α// // l l m m l ? ? ? ? ? ? ? ? 方法二：用面面平行实现。 α β β α // // l l ? ? ? ? ? 3.面面平行：方法一：用线线平行实现。方法二：用线面平行实现 l

βααβ//',',' //'//??? ?? ? ? ? ??且相交且相交m l m l m m l l 。βαβαα//,////??? ????且相交m l m l 三．垂直关系： 1. 线面垂直：方法一：用线线垂直实现。方法二：用面面垂直实现。 α α⊥??? ????? ?=?⊥⊥l AB AC A AB AC AB l AC l , αββαβα⊥???? ???⊥=?⊥l l m l m , 2. 面面垂直：方法一：用线面垂直实现。方法二：计算所成二面角为直角。 βαβα⊥?? ?? ?⊥l l 3. 线线垂直：方法一：用线面垂直实现。 m l m l ⊥?? ?? ?⊥αα 方法二：三垂线定理及其逆定理。 PO l OA l PA l αα⊥? ? ⊥?⊥????

圆幂定理(垂直弦定理)偏难

【例题求解】【例1】如图，PT 切⊙O 于点T ，PA 交⊙O 于A 、B 两点，且与直径CT 交于点D ，CD=2，AD=3，BD=6，则PB= ． (市中考题) 思路点拨综合运用圆幂定理、勾股定理求PB 长．注：比例线段是几之中一个重要问题，比例线段的学习是一个由一般到特殊、不断深化的过程，大致经历了四个阶段： (1)平行线分线段对应成比例； (2)相似三角形对应边成比例； (3)直角三角形中的比例线段可以用积的形式简捷地表示出来； (4)圆中的比例线段通过圆幂定理明快地反映出来．【例2】如图，在平行四边形ABCD 中，过A 、B 、C 三点的圆交AD 于点E ，且与CD 相切，若AB=4，BE=5，则DE 的长为( ) A ．3 B ．4 C ． 415 D ．5 16 (全国初中数学联赛题) 思路点拨连AC ，CE ，由条件可得多等线段，为切割线定理的运用创设条件．

注：圆中线段的算，常常需要综合相似三角形、直角三角形、圆幂定理等知识，通过代数化获解，加强对图形的分解，注重信息的重组与整合是解圆中线段计算问题的关键．【例3】如图，△ABC接于⊙O，AB是∠O的直径，PA是过A点的直线，∠PAC=∠B． (1)求证：PA是⊙O的切线； (2)如果弦CD交AB于E，CD的延长线交PA于F，AC=8，CE：ED=6：5，，AE：BE=2：3，求AB的长和∠ECB的正切值． (北京市海淀区中考题) 思路点拨直径、切线对应着与圆相关的丰富知识．(1)问的证明为切割线定理的运用创造了条件；引入参数x、k处理(2)问中的比例式，把相应线段用是的代数式表示，并寻找x与k的关系，建立x或k的程．【例4】如图，P是平行四边形AB的边AB的延长线上一点，DP与AC、BC分别交于点E、E，EG是过B、F、P三点圆的切线，G为切点，求证：EG=DE (省竞赛题) 思路点拨由切割线定理得EG2=EF·EP，要证明EG=D E，只需证明DE2=EF·EP，这样通过圆幂定理把线段相等问题的证明转化为线段等积式的证明．注：圆中的多问题，若图形中有适用圆幂定理的条件，则能化解问题的难度，而圆中线段等积式是转化问题的桥梁．需要注意的是，圆幂定理的运用不仅局限于计算及比例线段的证明，可拓展到平面几各种类型的问题

初中几何证明题要用到的一些定理

初中几何证明题要用到的一些定理证明两线段相等 1.两全等三角形中对应边相等。 2.同一三角形中等角对等边。 3.等腰三角形顶角的平分线或底边的高平分底边。 4.平行四边形的对边或对角线被交点分成的两段相等。 5.直角三角形斜边的中点到三顶点距离相等。 6.线段垂直平分线上任意一点到线段两段距离相等。 7.角平分线上任一点到角的两边距离相等。 8.过三角形一边的中点且平行于第三边的直线分第二边所成的线段相等。 *9.同圆（或等圆）中等弧所对的弦或与圆心等距的两弦或等圆心角、圆周角所对的弦相等。*10.圆外一点引圆的两条切线的切线长相等或圆内垂直于直径的弦被直径分成的两段相等。 11.两前项（或两后项）相等的比例式中的两后项（或两前项）相等。 *12.两圆的内（外）公切线的长相等。 13.等于同一线段的两条线段相等。证明两个角相等 1.两全等三角形的对应角相等。 2.同一三角形中等边对等角。 3.等腰三角形中，底边上的中线（或高）平分顶角。 4.两条平行线的同位角、内错角或平行四边形的对角相等。 5.同角（或等角）的余角（或补角）相等。 *6.同圆（或圆）中，等弦（或弧）所对的圆心角相等，圆周角相等，弦切角等于它所夹的

弧对的圆周角。 *7.圆外一点引圆的两条切线，圆心和这一点的连线平分两条切线的夹角。 8.相似三角形的对应角相等。 *9.圆的内接四边形的外角等于内对角。10.等于同一角的两个角相等证明两直线平行 1.垂直于同一直线的各直线平行。 2.同位角相等，内错角相等或同旁内角互补的两直线平行。 3.平行四边形的对边平行。 4.三角形的中位线平行于第三边。 5.梯形的中位线平行于两底。 6.平行于同一直线的两直线平行。 7.一条直线截三角形的两边（或延长线）所得的线段对应成比例，则这条直线平行于第三边。证明两条直线互相垂直 1.等腰三角形的顶角平分线或底边的中线垂直于底边。 2.三角形中一边的中线若等于这边一半，则这一边所对的角是直角。 3.在一个三角形中，若有两个角互余，则第三个角是直角。 4.邻补角的平分线互相垂直。 5.一条直线垂直于平行线中的一条，则必垂直于另一条。 6.两条直线相交成直角则两直线垂直。 7.利用到一线段两端的距离相等的点在线段的垂直平分线上。 8.利用勾股定理的逆定理。 9.利用菱形的对角线互相垂直。

【经典】圆的有关性质+知识点

圆的有关性质一、〖知识点〗圆、圆的对称性、点和圆的位置关系、不在同一直线上的三点确定一个圆、三角形的外接圆、垂径定理逆定理、圆心角、弧、弦、弦心距之间的关系、圆周角定理、圆内接四边形的性质〖大纲要求〗 1．正确理解和应用圆的点集定义，掌握点和圆的位置关系； 2．熟练地掌握确定一个圆的条件，即圆心、半径；直径；不在同一直线上三点。一个圆的圆心只确定圆的位置，而半径也只能确定圆的大小，两个条件确定一条直线，三个条件确定一个圆，过三角形的三个顶点的圆存在并且唯一； 3．熟练地掌握和灵活应用圆的有关性质：同（等）圆中半径相等、直径相等直径是半径的2倍；直径是最大的弦；圆是轴对称图形，经过圆心的任一条直线都是对称轴；圆是中心对称图形，圆心是对称中心；圆具有旋转不变性；垂径定理及其推论；圆心角、圆周角、弧、弦、弦心距之间的关系； 4．掌握和圆有关的角：圆心角、圆周角的定义及其度量；圆心角等于同（等）弧上的圆周角的2倍；同（等）弧上的圆周角相等；直径（半圆）上的圆周角是直角；90°的圆周角所对的弦是直径； 5．掌握圆内接四边形的性质定理：它沟通了圆内外图形的关系，并能应用它解决有关问题； 6．注意：（1）垂径定理及其推论是指：一条弦①在“过圆心”②“垂直于另一条弦”③“平分这另一条弦”④“平分这另一条弦所对的劣弧”⑤“ 平分这另一条弦所对的优弧”的五个条件中任意具有两个条件，则必具有另外三个结论（当①③为条件时要对另一条弦增加它不是直径的限制），条理性的记忆，不但简化了对它实际代表的10条定理的记忆且便于解题时的灵活应用，垂径定理提供了证明线段相等、角相等、垂直关系等的重要依据；（2）有弦可作弦心距组成垂径定理图形；见到直径要想到它所对的圆周角是直角，想垂径定理；想到过它的端点若有切线，则与它垂直，反之，若有垂线则是切线，想到它被圆心所平分；

平面几何中几个重要定理的证明

1 平面几何中几个重要定理及其证明一、塞瓦定理 1．塞瓦定理及其证明定理：在?ABC 内一点P ，该点与?ABC 的三个顶点相连所在的三条直线分别交?ABC 三边AB 、BC 、CA 于点D 、E 、F ，且D 、E 、F 三点均不是?ABC 的顶点，则有 1AD BE CF DB EC FA ??=．证明：运用面积比可得 ADC ADP BDP BDC S S AD DB S S ????==．根据等比定理有 ADC ADC ADP APC ADP BDP BDC BDC BDP BPC S S S S S S S S S S ??????????-=== -，所以 APC BPC S AD DB S ??=．同理可得 APB APC S BE EC S ??=， BPC APB S CF FA S ??=．三式相乘得 1AD BE CF DB EC FA ??=．注：在运用三角形的面积比时，要把握住两个三角形是“等高”还是“等底”，这样就可以产生出“边之比”． 2．塞瓦定理的逆定理及其证明定理：在?ABC 三边AB 、BC 、CA 上各有一点D 、E 、F ，且D 、E 、F 均不是?ABC 的顶点，若 1AD BE CF DB EC FA ??=，那么直线CD 、AE 、BF 三线共点．证明：设直线AE 与直线BF 交于点P ，直线CP 交AB 于点D /，则据塞瓦定理有 // 1AD BE CF D B EC FA ??=．因为 1AD BE CF DB EC FA ??=，所以有 A B C D F P A B C D E F P D /