知识讲解_圆的方程_基础

圆的方程
【学习目标】
1.掌握圆的标准方程的特点,能根据所给有关圆心、半径的具体条件准确地写出圆的标准方程,能运用圆的标准方程正确地求出其圆心和半径,解决一些简单的实际问题,并会推导圆的标准方程.
2.掌握圆的一般方程的特点,能将圆的一般方程化为圆的标准方程从而求出圆心的坐标和半径;能用待定系数法,由已知条件导出圆的方程.
【要点梳理】
【高清课堂:圆的方程370891 知识要点】 要点一:圆的标准方程
222()()x a y b r -+-=,其中()a b ,为圆心,r 为半径.
要点诠释:
(1)如果圆心在坐标原点,这时00a b ==,,圆的方程就是2
2
2
x y r +=.有关图形特征与方程的转化:如:圆心在x 轴上:b=0;圆与y 轴相切时:||a r =;圆与x 轴相切时:||b r =;与坐标轴相切时:
||||a b r ==;过原点:222a b r +=
(2)圆的标准方程2
2
2
()()x a y b r -+-=?圆心为()a b ,,半径为r ,它显现了圆的几何特点.
(3)标准方程的优点在于明确指出了圆心和半径.由圆的标准方程可知,确定一个圆的方程,只需要a 、b 、r 这三个独立参数,因此,求圆的标准方程常用定义法和待定系数法.
要点二:点和圆的位置关系 如果圆的标准方程为2
2
2
()()x a y b r -+-=,圆心为()C a b ,,半径为r ,则有
(1)若点()00M x y ,在圆上()()22
2
00||CM r x a y b r ?=?-+-=
(2)若点()00M x y ,在圆外()()22
2
00||CM r x a y b r ?>?-+->
(3)若点()00M x y ,在圆内()()22
2
00||CM r x a y b r ?
要点三:圆的一般方程
当22
40D E F +->时,方程2
2
0x y Dx Ey F ++++=叫做圆的一般方程.,22D E ??
-
- ??
?为圆心,
为半径. 要点诠释:
由方程2
2
0x y Dx Ey F ++++=得22
224224D E D E F x y +-?
???+++= ? ??
???
(1)当22
40D E F +-=时,方程只有实数解,22D E x y =-
=-.它表示一个点(,)22
D E
--. (2)当2
2
40D E F +-<时,方程没有实数解,因而它不表示任何图形.
(3)当22
40D E F +->时,可以看出方程表示以,2
2D E ??
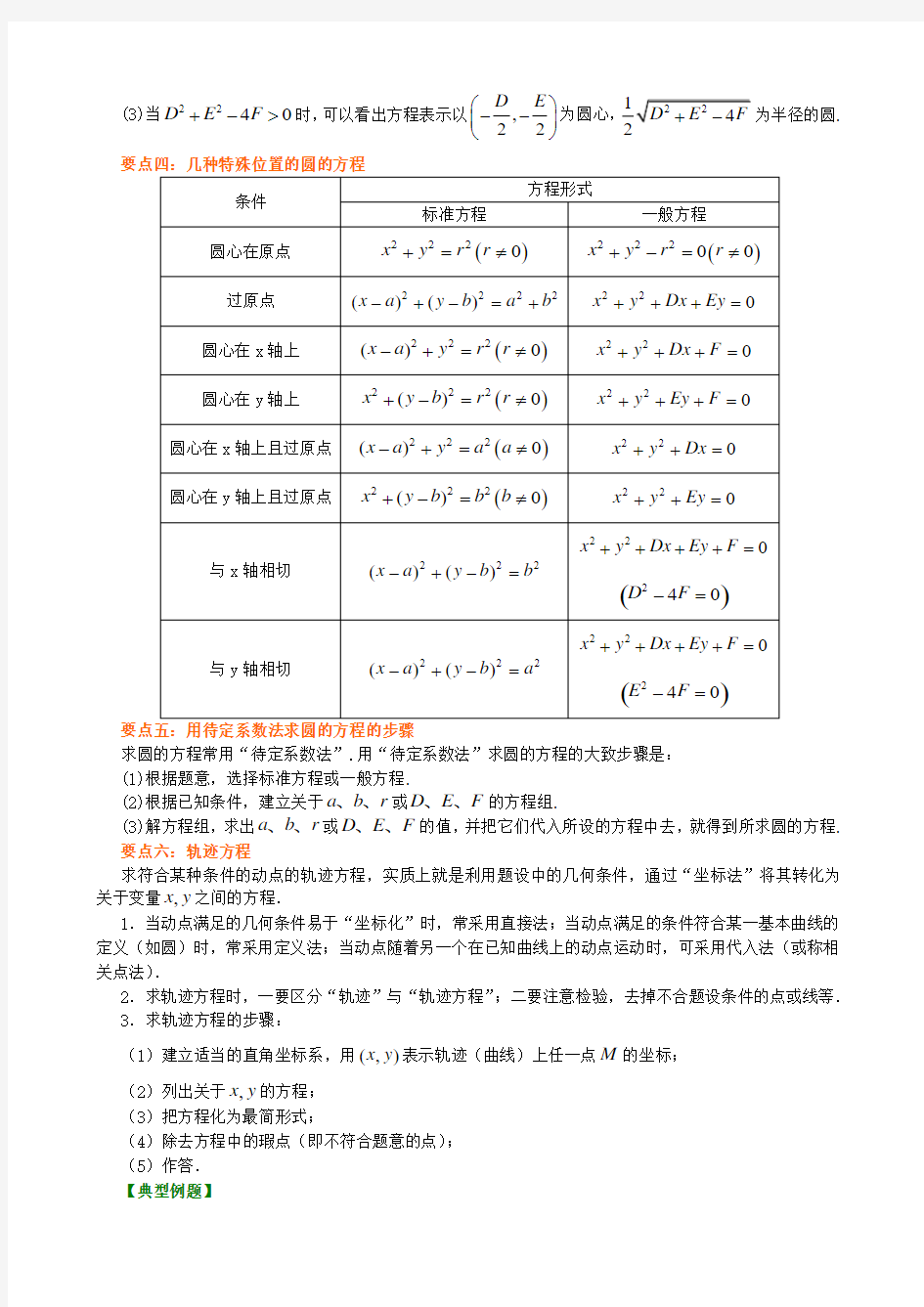
-- ???为半径的圆. 要点四:几种特殊位置的圆的方程
要点五:用待定系数法求圆的方程的步骤
求圆的方程常用“待定系数法”.用“待定系数法”求圆的方程的大致步骤是: (1)根据题意,选择标准方程或一般方程.
(2)根据已知条件,建立关于a b r 、、或D E F 、、的方程组. (3)解方程组,求出a b r 、、或D E F 、、的值,并把它们代入所设的方程中去,就得到所求圆的方程. 要点六:轨迹方程
求符合某种条件的动点的轨迹方程,实质上就是利用题设中的几何条件,通过“坐标法”将其转化为关于变量,x y 之间的方程.
1.当动点满足的几何条件易于“坐标化”时,常采用直接法;当动点满足的条件符合某一基本曲线的定义(如圆)时,常采用定义法;当动点随着另一个在已知曲线上的动点运动时,可采用代入法(或称相关点法).
2.求轨迹方程时,一要区分“轨迹”与“轨迹方程”;二要注意检验,去掉不合题设条件的点或线等. 3.求轨迹方程的步骤: (1)建立适当的直角坐标系,用(,)x y 表示轨迹(曲线)上任一点M 的坐标; (2)列出关于,x y 的方程;
(3)把方程化为最简形式;
(4)除去方程中的瑕点(即不符合题意的点); (5)作答. 【典型例题】
类型一:圆的标准方程
例1.求满足下列条件的各圆的方程: (1)圆心在原点,半径是3;
(2)圆心在点C (3,4
(3)经过点P (5,1),圆心在点C (8,―3)上.
【思路点拨】根据题设条件,可利用圆的标准方程解决. 【答案】(1)x 2+y 2=9 (2)(x ―3)2+(y ―4)2=5(3)(x ―8)2+(y+3)2=25 【解析】 (1)x 2+y 2=9;
(2)(x ―3)2+(y ―4)2=5;
(3)解法一:∵圆的半径||5r CP ===,圆心在点C (8,―3).
∴圆的方程是(x ―8)2+(y+3)2=25. 解法二:∵圆心为C (8,―3),故设圆的方程为(x ―8)2+(y+3)2=r 2. 又∵点P (5,1)在圆上,∴(5―8)2+(1+3)2=r 2,∴r 2=25, ∴所求圆的方程是(x ―8)2+(y+3)2=25.
【总结升华】 确定圆的标准方程只需确定圆心的坐标和圆的半径即可,因此圆心和半径被称为圆的两要素.
确定圆的方程的主要方法是待定系数法,即列出关于a 、b 、r 的方程组,求a 、b 、r 或直接求出圆心(a ,b )和半径r ,一般步骤为:
(1)根据题意,设所求的圆的标准方程为(x ―a)2+(y ―b)2=r 2; (2)根据已知条件,建立关于a 、b 、r 的方程组;
(3)解方程组,求出a 、b 、r 的值,并把它们代入所设的方程中去,就得到所求圆的方程. 举一反三:
【变式1】圆心是(4,―1),且过点(5,2)的圆的标准方程是( ) A .(x ―4)2+(y+1)2=10 B .(x+4)2+(y ―1)2=10
C .(x ―4)2+(y+1)2=100
D .22
(4)(1)x y -++=【答案】A
例2.写出下列方程表示的圆的圆心和半径. (1)x 2+y 2=2;
(2)(x ―3)2+y 2=a 2(a ≠0); (3)(x+2)2+(y+1)2=b 2(b ≠0).
【答案】(1)(0,0)(2)(3,0),|a|(3)(―2,―1),|b|
【解析】 (1)圆心(0,0)
(2)圆心(3,0),半径为|a|; (3)圆心(―2,―1),半径为|b|. 【总结升华】(2)、(3)两题中a 2、b 2仅为半径的平方,没有给定a >0,b >0,∴半径r=|a|、|b|. 例3.求经过A (0,―1)和直线x +y =1相切,且圆心在直线y =―2x 上的圆的方程.
【思路点拨】根据圆心在直线y =―2x 上,设出圆心坐标和半径,写出圆的标准方程,把点A 的坐标代入圆的方程得到一个关系式,由点到直线的距离公式表示圆心到直线x +y =1的距离,由距离等于圆的半径列出另一个关系式,两者联立即可求出圆心坐标和半径,把圆心坐标和半径代入即可写出圆的标准方程.
【答案】22
(1)(2)2x y -++=或22
1250()()9981
x y -++=
【解析】因为圆心在直线y =―2x 上,设圆心坐标为(a ,―2a ) 设圆的方程为 2
2
2
()(2)x a y a r -++= 圆经过点A (0,―1)和直线x +y =1相切,
所以有222(21)a a r r ?+-=?
=
解得r =
a =1或1
9
a =
所以圆的方程为 2
2
(1)(2)2x y -++=或22
1250()()9981
x y -++=
. 【总结升华】此题考查学生灵活运用点到直线的距离公式化简求值,掌握直线与圆相切时满足的条件,会利用待定系数法求圆的标准方程.
举一反三:
【变式1】求圆心在直线x ―2y ―3=0上,且过点A (2,―3),B (―2,―5)的圆的标准方程. 【答案】 (x+1)2+(y+2)2=10
【解析】设圆的标准方程为()2
2
2
()x a y b r -+-=,则
()()2222
222302(3)2(5)a b a b r a b r ?--=??-+--=??--+--=??
解得:2
1,2,10a b r =-=-= 所以所求圆的标准方程是:(x+1)2+(y+2)2=10. 类型二:圆的一般方程
例4.下列方程能否表示圆?若能表示圆,求出圆心和半径. (1)2x 2+y 2―7y+5=0; (2)x 2―xy+y 2+6x+7y=0; (3)x 2+y 2―2x ―4y+10=0; (4)2x 2+2y 2―5x=0.
【答案】(1)不能表示圆(2)不能表示圆(3)不能表示圆(4)表示圆 5
,04?? ???
5
4 【解析】 (1)∵方程2x 2+y 2―7y+5=0中x 2与y 2的系数不相同,∴它不能表示圆.
(2)∵方程x 2―xy+y 2+6x+7y=0中含有xy 这样的项,∴它不能表示圆. (3)方程x 2+y 2―2x ―4y+10=0化为(x ―1)2+(y ―2)2=―5,∴它不能表示圆.
(4)方程2x 2
+2y 2
-5x=0化为22
25544x y ????
-+= ? ?????
,∴它表示以5,04?? ???为圆心,54为半径长的圆.
【总结升华】(1)判断一个二元二次方程是否表示圆的方法:先看这个方程是否具备圆的一般方程的
特征,即:①x 2与y 2的系数相等;②不含xy 的项.当它具有圆的一般方程的特征时,再看它能否表示圆,此时有两种途径,一是看D 2+E 2―4F 是否大于零;二是直接配方变形,看右端是否为大于零的常数.
(2)圆的标准方程指出了圆心坐标与半径大小,几何特征明显;圆的一般方程表明圆的方程是一种
特殊的二元二次方程,代数特征明显.
举一反三: 【变式1】(1)下列方程各表示什么图形;
①x 2+y 2―4x ―2y+5=0;②x 2+y 2―2x+4y ―4=0;③22
0x y ax ++-=.
(2)圆C :x 2+y 2―2x ―4y+4=0的圆心到直线l :3x+4y+4=0的距离d=________. 【答案】
(1)①方程表示点(2,1);②方程表示以(1,―2)为圆心,3为半径长的圆;③当a=0时,该方程
表示的图形为一个点(0,0);当a ≠0时,该方程表示的图形为圆,圆心为,22a a ??
- ? ???
,半径长为|a|. (2)3 【解析】(1)略;
(2)圆的方程可化为:()()2
2
121x y -+-=,圆心坐标为(1,2),所以到直线l 的距离
15
35
d =
=
=. 例5.(2016春 辽宁大连庄河市期末)已知方程C :x 2+y 2―2x ―4y +m =0, (1)若方程C 表示圆,求实数m 的范围;
(2)在方程表示圆时,该圆与直线l :x +2y ―4=0相交于M 、N 两点,且||MN =
,求m 的值.
【思路点拨】(1)由圆的一般方程的定义知4+16―4m >0,由此能法语出实数m 的取值范围. (2)求出圆心到直线x +2y ―4=0的距离,由此利用已知条件能求出m 的值. 【答案】(1)(―∞,5);(2)m =4
【解析】(1)∵方程C :x 2+y 2―2x +4y +m =0表示圆, ∴D 2+E 2―4F >0,
即4+16―4m >0解得m <5, ∴实数m 的取值范围是(―∞,5). (2)∵方程C :x 2+y 2―2x ―4y +m =0, ∴(x ―2)2+(y ―2)2=5―m ,
圆心(1,2)到直线x +2y ―4=0的距离
d =
=
∵圆与直线l :x +2y ―4=0相交于M 、N 两点,且||MN =
, ∴22
(5)()
5m --=,
解得m =4.
【总结升华】本题考查圆的方事参数m 的取值范围,考查圆的方程中m 的值的求法,解题时要认真审题,注意点到直线的距离公式的合理运用.
举一反三:
【高清课堂:圆的方程370891 典型例题2】
【变式1】(1)求过(2,2),(5,3),(3,1)A B C -的圆的方程,及圆心坐标和半径; (2)求经过点(2,4)A --且与直线3260x y +-=相切于点(8,6)的圆的方程. 【答案】 【解析】
(1)法一:设圆的方程为:2
2
0x y Dx Ey F ++++=,则
8220345301030D E F D E F D E F +++=??+++=??+-+=?,解得:8212D E F =-??
=-??=?
所以所求圆的方程为:2
2
82120x y x y +--+=,即()2
2
4(1)5x y -+-=,所以圆心为(4,1),
法二:线段AB 的中点为为75,22??
???
,321523AB k -==-
线段AB 的中垂线为57322y x ?
?-
=-- ??
?,即3130x y --= 同理得线段BC 中垂线为260x y +-=
联立2603130x y x y +-=??
--=?,解得41
x y =??=?
所以所求圆的方程为(4,1)
,半径r ==所以()2
2
4(1)5x y -+-=.
(2)法一:设圆的方程为:22
0x y Dx Ey F ++++=,则
2024062382100860
D E F E
D D
E
F --+=??
?+?=??+
?
?+++=?,解得:11330D E F =-??=??=-? 所以圆的方程为2
2
113300x y x y +-+-=.
法二:过点B 与直线3260x y +-=垂直的直线是3180x y --=, 线段AB 的中垂线为40x y +-=,
由318040
x y x y --=??
+-=?得:圆心坐标为113,22??- ???,由两点间距离公式得半径2
1252r =,
所以圆的方程为2
2
113125222x y ???
?-++= ? ??
???.
【变式2】判断方程ax 2+ay 2―4(a ―1)x+4y=0(a ≠0)是否表示圆,若表示圆,写出圆心坐标和半径长.
【答案】2(1)2,a a
a -??
- ???,r =类型三:点与圆的位置关系
例6.判断点M (6,9),N (3,3),Q (5,3)与圆(x ―5)2+(y ―6)2=10的位置关系. 【答案】M 在圆上 N 在圆外 Q 在圆内
【解析】 ∵圆的方程为(x ―5)2+(y ―6)2=10, 分别将M (6,9),N (3,3),Q (5,3)代入得 (6―5)2+(9―6)2=10,∴M 在圆上; (3―5)2+(3―6)2=13>10,∴N 在圆外; (5―5)2+(3―6)2=9<10,∴Q 在圆内.
【总结升华】点与圆的位置关系,从形的角度来看,设圆心为O ,半径为r ,则点P 在圆内?|PQ|<r ;点P 在圆上?|PQ|=r ;点P 在点圆外?|PO|>r .从数的角度来看,设圆的标准方程为(x ―a)2+(y ―b)2=r 2,圆心为A (a ,b ),半径为r ,则点M (x 0,y 0)在圆上?(x 0―a)2+(y 0―b)2=r 2;点M (x 0,y 0)在圆外?(x 0―a)2+(y 0―b)2>r 2;点M (x 0,y 0)在圆内?(x 0―a)2+(y 0―b)2<r 2.
举一反三:
【变式1】已知点A (2,3)在圆2
2
240x y x y m +--+=外,则实数m 的取值范围为________. 【答案】(3,5)
【解析】∵圆2
2
240x y x y m +--+=即2
2
(1)(2)5x y m -+-=-, ∴5-m >0,则m <5.
∵点A (2,3)在圆2
2
240x y x y m +--+=外,∴4+9-4-12+m >0,∴m >3. 综上可得,3<m <5, 故答案为:(3,5). 类型四:轨迹问题
例7.已知一曲线是与两个定点O (0,0),A (3,0)距离的比为
1
2
的点的轨迹,求这条曲线的方程,并画出曲线.
【思路点拨】先设出要求点的坐标,然后列出点满足的几何条件,化简整理即可。 【答案】(x+1)2+y 2=4 曲线是圆心为C (―1,0),半径长为2的圆
【解析】 在给定的坐标系中,设M (x ,y )是曲线上的任意一点,点M 在曲线上的
条件是||1
||2
MO
MA
=.
1
2
=,两边平方并化简,得曲线方程x2+y2+2x―3=0,配方得
(x+1)2+y2=4.
所以所求曲线是圆心为C(―1,0),半径长为2的圆(如图).
【总结升华】本例求轨迹方程的方法是直接法.用直接法求曲线方程的步骤如下:
(1)建系设点:建立适当的直角坐标系,设曲线上任一点坐标为M(x,y);
(2)几何点集:写出满足题设的点M的集合P={M|P (M)};
(3)翻译列式:将几何条件P(M)用坐标x、y表示,写出方程f (x,y)=0;
(4)化简方程:通过同解变形化简方程;
(5)查漏除杂:验证方程表示的曲线是否为已知的曲线,重点检查方程表示的曲线是否有多余的点,曲线上是否有遗漏的点.
举一反三:
【变式1】如下图,过第一象限的定点C(a,b)作互相垂直的两直线CA、CB,分别交于x轴、y 轴的正半轴于A、B两点,试求线段AB的中点M的轨迹方程.
【答案】2ax+2by=a2+b2(x>0且y>0).
高三总复习直线与圆的方程知识点总结及典型例题.
直线与圆的方程 、直线的方程 已知 L 上两点 P 1( x 1,y 1) P 2( x 2,y 2 ) 当 x 1 = x 2 时, =900 , 不存在。当 0 时, =arctank , <0 时, = ②任何一个关于 x 、y 的二元一次方程都表示一条直线。 5、直线系:(1)共点直线系方程: p 0(x 0,y 0)为定值, k 为参数 y-y 0=k (x-x 0) 特别: y=kx+b ,表示过( 0、 b )的直线系(不含 y 轴) ( 2)平行直线系:① y=kx+b ,k 为定值, b 为参数。 ② AX+BY+ 入=0 表示与 Ax+By+C=0 平行的直线系 ③ BX-AY+ 入 =0 表示与 AX+BY+C 垂直的直线系 ( 3)过 L 1,L 2交点的直线系 A 1x+B 1y+C 1+入( A 2X+B 2Y+C 2)=0(不含 L2) 6、三点共线的判定:① AB BC AC ,②K AB =K BC , ③写出过其中两点的方程,再验证第三点在直线上。 、两直线的位置关系 k= y 2 y 1 x 2 x 1 20 2 已知 方程 说明 斜截式 K 、b Y=kx+b 不含 y 轴和行平 于 y 轴的直点斜式 P 1=(x 1,y 1) k y-y 1=k(x-x 1) 不含 y 轴和平 行 于 y 轴的直线 两点式 P 1(x 1,y 1) P 2(x 2,y 2) y y 1 x x 1 不含坐标辆和 平行于坐标轴 的直线 y 2 y 1 x 2 x 1 截距式 a 、b xy 1 ab 不含坐标轴、平 行于坐标轴和 过原点的直线 一般式 Ax+by+c=0 A 、 B 不同时为 0 3、截距(略)曲线过原点 横纵截距都为 0。 4、直线方程的几种形式 几种特殊位置的直 线 ①x 轴: y=0 ② y 轴: x=0 ③平行于 x 轴: y=b ④平行于 y 轴: x=a ⑤过原点: y=kx y 的二元一 次方程。 1、倾斜角: 0< < k 0 2 = 不存在 2 +arctank 2、斜
圆与方程知识点小结
圆与方程 2、1圆的标准方程:以点),(b a C 为圆心,r 为半径的圆的标准方程是222)()(r b y a x =-+-. 特例:圆心在坐标原点,半径为r 的圆的方程是:222r y x =+. 2、2点与圆的位置关系: 1. 设点到圆心的距离为d ,圆半径为r : (1)点在圆上 d=r ; (2)点在圆外 d >r ; (3)点在圆内 d <r . 2.给定点),(00y x M 及圆222)()(:r b y a x C =-+-. ①M 在圆C 内22020)()(r b y a x <-+-? ②M 在圆C 上22020)()r b y a x =-+-?( ③M 在圆C 外22020)()(r b y a x >-+-? 2、3 圆的一般方程:022=++++F Ey Dx y x . 当042 2 >-+F E D 时,方程表示一个圆,其中圆心? ?? ??--2,2 E D C ,半径2 42 2F E D r -+= . 当0422=-+F E D 时,方程表示一个点?? ? ? ?- - 2,2 E D . 当0422<-+ F E D 时,方程无图形(称虚圆). 注:(1)方程022=+++++F Ey Dx Cy Bxy Ax 表示圆的充要条件是:0 =B 且 ≠=C A 且 042 2 AF E D -+. 圆的直径或方程:已知0))(())((),(),(21212211=--+--?y y y y x x x x y x B y x A 2、4 直线与圆的位置关系: 直线0=++C By Ax 与圆222)()(r b y a x =-+-的位置关系有三种 (1)若2 2 B A C Bb Aa d +++= ,0相离r d ; (2)0=???=相切r d ; (3)0>???<相交r d 。 还可以利用直线方程与圆的方程联立方程组???=++++=++0 2 2 F Ey Dx y x C By Ax 求解,通过解 的个数来判断: (1)当方程组有2个公共解时(直线与圆有2个交点),直线与圆相交;
圆的方程_基础 知识讲解
圆的方程 编稿:丁会敏 审稿:王静伟 【学习目标】 1.掌握圆的标准方程的特点,能根据所给有关圆心、半径的具体条件准确地写出圆的标准方程,能运用圆的标准方程正确地求出其圆心和半径,解决一些简单的实际问题,并会推导圆的标准方程. 2.掌握圆的一般方程的特点,能将圆的一般方程化为圆的标准方程从而求出圆心的坐标和半径;能用待定系数法,由已知条件导出圆的方程. 【要点梳理】 【高清课堂:圆的方程370891 知识要点】 要点一:圆的标准方程 222()()x a y b r -+-=,其中()a b ,为圆心,r 为半径. 要点诠释: (1)如果圆心在坐标原点,这时00a b ==,,圆的方程就是2 2 2 x y r +=.有关图形特征与方程的转化:如:圆心在x 轴上:b=0;圆与y 轴相切时:||a r =;圆与x 轴相切时:||b r =;与坐标轴相切时: ||||a b r ==;过原点:222a b r += (2)圆的标准方程2 2 2 ()()x a y b r -+-=?圆心为()a b ,,半径为r ,它显现了圆的几何特点. (3)标准方程的优点在于明确指出了圆心和半径.由圆的标准方程可知,确定一个圆的方程,只需要a 、b 、r 这三个独立参数,因此,求圆的标准方程常用定义法和待定系数法. 要点二:点和圆的位置关系 如果圆的标准方程为2 2 2 ()()x a y b r -+-=,圆心为()C a b ,,半径为r ,则有 (1)若点()00M x y ,在圆上()()2 2 200||CM r x a y b r ?=?-+-= (2)若点()00M x y ,在圆外()()2 2 200||CM r x a y b r ?>?-+-> (3)若点()00M x y ,在圆内()()2 2 200||CM r x a y b r ?时,方程2 2 0x y Dx Ey F ++++=叫做圆的一般方程.,22D E ?? - - ?? ?为圆心, 为半径. 要点诠释: 由方程2 2 0x y Dx Ey F ++++=得22 224224D E D E F x y +-? ???+++= ? ?? ??? (1)当2240D E F +-=时,方程只有实数解,22D E x y =- =-.它表示一个点(,)22 D E --. (2)当2240D E F +-<时,方程没有实数解,因而它不表示任何图形.
高中数学直线与圆的方程知识点总结
高中数学直线与圆的方 程知识点总结 WTD standardization office【WTD 5AB- WTDK 08- WTD 2C】
高中数学之直线与圆的方程 一、概念理解: 1、倾斜角:①找α:直线向上方向、x 轴正方向; ②平行:α=0°; ③范围:0°≤α<180° 。 2、斜率:①找k :k=tan α (α≠90°); ②垂直:斜率k 不存在; ③范围: 斜率 k ∈ R 。 3、斜率与坐标:1 21 22121tan x x y y x x y y k --=--= =α ①构造直角三角形(数形结合); ②斜率k 值于两点先后顺序无关; ③注意下标的位置对应。 4、直线与直线的位置关系:222111:,:b x k y l b x k y l +=+= ①相交:斜率21k k ≠(前提是斜率都存在) 特例----垂直时:<1> 0211=⊥k k x l 不存在,则轴,即; <2> 斜率都存在时:121-=?k k 。 ②平行:<1> 斜率都存在时:2121,b b k k ≠=; <2> 斜率都不存在时:两直线都与x 轴垂直。 ③重合: 斜率都存在时:2121,b b k k ==; 二、方程与公式: 1、直线的五个方程:
①点斜式:)(00x x k y y -=- 将已知点k y x 与斜率),(00直接带入即可; ②斜截式:b kx y += 将已知截距k b 与斜率),0(直接带入即可; ③两点式:),(21211 21 121y y x x x x x x y y y y ≠≠--=--其中, 将已知两点),(),,(2211y x y x 直接带入即可; ④截距式: 1=+b y a x 将已知截距坐标),0(),0,( b a 直接带入即可; ⑤一般式:0=++C By Ax ,其中A 、B 不同时为0 用得比较多的是点斜式、斜截式与一般式。 2、求两条直线的交点坐标:直接将两直线方程联立,解方程组即可 3、距离公式: ①两点间距离:2 2122121)()(y y x x P P -+-= ②点到直线距离:2 2 00B A C By Ax d +++= ③平行直线间距离:2 2 21B A C C d +-= 4、中点、三分点坐标公式:已知两点),(),,(2211y x B y x A ①AB 中点),(00y x :)2 ,2( 2 121y y x x ++ ②AB 三分点),(),,(2211t s t s :)3 2,32(2 1 21y y x x ++ 靠近A 的三分点坐标 )3 2,32(2 121 y y x x ++ 靠近B 的三分点坐标 中点坐标公式,在求对称点、第四章圆与方程中,经常用到。 三分点坐标公式,用得较少,多见于大题难题。 5.直线的对称性问题
圆方程知识点总结典型例题
圆与方程 1. 圆的标准方程:以点),(b a C 为圆心,r 为半径的圆的标准方程是222)()(r b y a x =-+-. 特例:圆心在坐标原点,半径为r 的圆的方程是:222r y x =+. 2. 点与圆的位置关系: (1). 设点到圆心的距离为d ,圆半径为r : a.点在圆内 d <r ; b.点在圆上 d=r ; c.点在圆外 d >r (2). 给定点),(00y x M 及圆222)()(:r b y a x C =-+-. ①M 在圆C 内22020)()(r b y a x <-+-? ②M 在圆C 上22020)()r b y a x =-+-? ( ③M 在圆C 外22020)()(r b y a x >-+-? (3)涉及最值: ① 圆外一点B ,圆上一动点P ,讨论PB 的最值 min PB BN BC r ==- max PB BM BC r ==+ ② 圆内一点A ,圆上一动点P ,讨论PA 的最值 min PA AN r AC ==- max PA AM r AC ==+ 思考:过此A 点作最短的弦(此弦垂直AC ) 3. 圆的一般方程:022=++++F Ey Dx y x .
(1) 当042 2 >-+F E D 时,方程表示一个圆,其中圆心??? ??--2,2 E D C ,半径2 422F E D r -+= . (2) 当0422=-+F E D 时,方程表示一个点??? ??-- 2,2 E D . (3) 当0422<-+ F E D 时,方程不表示任何图形. 注:方程022=+++++F Ey Dx Cy Bxy Ax 表示圆的充要条件是:0=B 且0≠=C A 且 0422φAF E D -+. 4. 直线与圆的位置关系: 直线0=++C By Ax 与圆222)()(r b y a x =-+- 圆心到直线的距离2 2 B A C Bb Aa d +++= 1)无交点直线与圆相离??>r d ; 2)只有一个交点直线与圆相切??=r d ; 3)有两个交点直线与圆相交?? 2021届高考数学(理)考点复习 圆的方程 圆的定义与方程 定义 平面内到定点的距离等于定长的点的轨迹叫做圆 方 程 标准 式 (x -a )2+(y -b )2=r 2(r >0) 圆心为(a ,b ) 半径为r 一 般 式 x 2+y 2+Dx +Ey +F =0 充要条件:D 2+E 2-4F >0 圆心坐标:????-D 2,-E 2 半径r =1 2 D 2+ E 2-4F 概念方法微思考 1.二元二次方程Ax 2+Bxy +Cy 2+Dx +Ey +F =0表示圆的条件是什么? 提示 ???? ? A =C ≠0, B =0, D 2+ E 2-4A F >0. 2.点与圆的位置关系有几种?如何判断? 提示 点和圆的位置关系有三种. 已知圆的标准方程(x -a )2+(y -b )2=r 2,点M (x 0,y 0), (1)点在圆上:(x 0-a )2+(y 0-b )2=r 2; (2)点在圆外:(x 0-a )2+(y 0-b )2>r 2; (3)点在圆内:(x 0-a )2+(y 0-b )2 , 半径为1的圆经过点(3,4),可得该圆的圆心轨迹为(3,4)为圆心,1为半径的圆, 故当圆心到原点的距离的最小时, 连结OB ,A 在OB 上且1AB =,此时距离最小, 由5OB =,得4OA =, 即圆心到原点的距离的最小值是4, 故选A . 2.(2018?天津)在平面直角坐标系中,经过三点(0,0),(1,1),(2,0)的圆的方程为__________. 【答案】22(1)1x y -+=(或2220)x y x +-= 【解析】【方法一】根据题意画出图形如图所示, 结合图形知经过三点(0,0),(1,1),(2,0)的圆, 其圆心为(1,0),半径为1, 则该圆的方程为22(1)1x y -+=. 【方法二】设该圆的方程为220x y Dx Ey F ++++=, 则0 42020F D F D E F =?? ++=??+++=? , 解得2D =-,0E F ==; ∴所求圆的方程为2220x y x +-=. 故答案为:22(1)1x y -+=(或2220)x y x +-=. 直线与圆的方程 一、直线的方程 1、倾斜角: ,围0≤α<π, x l //轴或与x 轴重合时,α=00 。 2、斜率: k=tan α α与κ的关系:α=0?κ=0 已知L 上两点P 1(x 1,y 1) 0<α< 02 >?k π P 2(x 2,y 2) α= κπ ?2 不存在 ?k= 1 212x x y y -- 022 二、两直线的位置关系 (说明:当直线平行于坐标轴时,要单独考虑) 2、L 1 到L 2的角为0,则1 21 21tan k k k k ?+-= θ(121-≠k k ) 3、夹角:1 21 21tan k k k k +-= θ 4、点到直线距离:2 2 00B A c By Ax d +++= (已知点(p 0(x 0,y 0),L :AX+BY+C=0) ①两行平线间距离:L 1=AX+BY+C 1=0 L 2:AX+BY+C 2=0?2 221B A c c d +-= ②与AX+BY+C=0平行且距离为d 的直线方程为Ax+By+C ±022 =+B A d ③与AX+BY+C 1=0和AX+BY+C 2=0平行且距离相等的直线方程是 02 2 1=++ +C C BY AX 5、对称:(1)点关于点对称:p(x 1,y 1)关于M (x 0,y 0)的对称)2,2(1010Y Y X X P --' 第三章 直线与方程 (1)直线的倾斜角 定义:x 轴正向与直线向上方向之间所成的角叫直线的倾斜角。特别地,当直线与x 轴平行或重合时,我们规定它的倾斜角为0°.因此,倾斜角的取值范围是0180α?≤ 第四章圆与方程 4.1 圆得方程 4.1、1 圆得标准方程 1.以(3,-1)为圆心,4为半径得圆得方程为() A.(x+3)2+(y-1)2=4 B.(x-3)2+(y+1)2=4 C.(x-3)2+(y+1)2=16 D.(x+3)2+(y-1)2=16 2.一圆得标准方程为x2+(y+1)2=8,则此圆得圆心与半径分别为() A.(1,0),4 B.(-1,0),2 2 C.(0,1),4 D.(0,-1),2 2 3.圆(x+2)2+(y-2)2=m2得圆心为________,半径为________. 4.若点P(-3,4)在圆x2+y2=a2上,则a得值就是________. 5.以点(-2,1)为圆心且与直线x+y=1相切得圆得方程就是____________________. 6.圆心在y轴上,半径为1,且过点(1,2)得圆得方程为() A.x2+(y-2)2=1 B.x2+(y+2)2=1 C.(x-1)2+(y-3)2=1 D.x2+(y-3)2=1 7.一个圆经过点A(5,0)与B(-2,1),圆心在直线x-3y-10=0上,求此圆得方程. 8.点P(5a+1,12a)在圆(x-1)2+y2=1得内部,则a得取值范围就是() A.|a|<1 B.a<1 13 C.|a|<1 5 D.|a|<1 13 9.圆(x-1)2+y2=25上得点到点A(5,5)得最大距离就是__________. 10.设直线ax-y+3=0与圆(x-1)2+(y-2)2=4相交于A,B两点,且弦AB得长为 2 3,求a得值. 4、1、2 圆得一般方程 1.圆x2+y2-6x=0得圆心坐标就是________. 2.若方程x2+y2+Dx+Ey+F=0表示以(2,-4)为圆心,以4为半径得圆,则F=________、 3.若方程x2+y2-4x+2y+5k=0表示圆,则k得取值范围就是() A.k>1 B.k<1 C.k≥1 D.k≤1 4.已知圆得方程就是x2+y2-2x+4y+3=0,则下列直线中通过圆心得就是() A.3x+2y+1=0 B.3x+2y=0 C.3x-2y=0 D.3x-2y+1=0 5.圆x2+y2-6x+4y=0得周长就是________. 6.点(2a,2)在圆x2+y2-2y-4=0得内部,则a得取值范围就是() 高中数学之直线与圆的方程 一、概念理解: 1、倾斜角:①找α:直线向上方向、x 轴正方向; ②平行:α=0°; ③范围:0°≤α<180° 。 2、斜率:①找k :k=tan α (α≠90°); ②垂直:斜率k 不存在; ③范围: 斜率 k ∈ R 。 3、斜率与坐标:1 21 22121tan x x y y x x y y k --=--= =α ①构造直角三角形(数形结合); ②斜率k 值于两点先后顺序无关; ③注意下标的位置对应。 4、直线与直线的位置关系:222111:,:b x k y l b x k y l +=+= ①相交:斜率21k k ≠(前提是斜率都存在) 特例----垂直时:<1> 0211=⊥k k x l 不存在,则轴,即; <2> 斜率都存在时:121-=?k k 。 ②平行:<1> 斜率都存在时:2121,b b k k ≠=; <2> 斜率都不存在时:两直线都与x 轴垂直。 ③重合: 斜率都存在时:2121,b b k k ==; 二、方程与公式: 1、直线的五个方程: ①点斜式:)(00x x k y y -=- 将已知点k y x 与斜率),(00直接带入即可; ②斜截式:b kx y += 将已知截距k b 与斜率),0(直接带入即可; ③两点式:),(21211 21 121y y x x x x x x y y y y ≠≠--=--其中, 将已知两点),(),,(2211y x y x 直接 带入即可; ④截距式: 1=+b y a x 将已知截距坐标),0(),0,( b a 直接带入即可; ⑤一般式:0=++C By Ax ,其中A 、B 不同时为0 用得比较多的是点斜式、斜截式与一般式。 2、求两条直线的交点坐标:直接将两直线方程联立,解方程组即可 直线和圆的方程知识 点总结 一、直线方程. 1. 直线的倾斜角 2. 直线方程的几种形式:点斜式、截距式、两点式、斜切式. 3. ⑴两条直线平行: 1l 推论:如果两条直线21,l l 的倾斜角为21,αα则1l ∥212αα=?l . ⑵两条直线垂直: 两条直线垂直的条件:①设两条直线1l 和2l 的斜率分别为1k 和2k ,则有12121-=?⊥k k l l 4. 直线的交角: 5. 过两直线? ??=++=++0:0:22221111C y B x A l C y B x A l 的交点的直线系方程λλ(0)(222111=+++++C y B x A C y B x A 为参数,0222=++C y B x A 不包括在内) 6. 点到直线的距离: ⑴点到直线的距离公式:设点),(00y x P ,直线P C By Ax l ,0:=++到l 的距离为d ,则有2200B A C By Ax d +++= . 注: 1. 两点P 1(x 1,y 1)、P 2(x 2,y 2)的距离公式:21221221)()(||y y x x P P -+-=. 2. 定比分点坐标分式。若点P(x,y)分有向线段1212 PP PP PP λλ=u u u r u u u r 所成的比为即,其中P 1(x 1,y 1),P 2(x 2,y 2).则 λλλλ++=++=1,121 21y y y x x x 特例,中点坐标公式;重要结论,三角形重心坐标公式。 3. 直线的倾斜角(0°≤α<180°)、斜率:αtan =k 4. 过两点1212222111),(),,(x x y y k y x P y x P --=的直线的斜率公式:. 12()x x ≠ 数学基础知识与典型例题 直线和圆的方程 直线和 圆的方 程知识 关系 直线的方程一、直线的倾斜角和斜率 1.直线的倾斜角:一条直线向上的方向与x轴正方向所成的最小正角叫做这条直线的倾斜角,其中直线与x轴平行或重合时,其倾斜角为0o,故直线倾斜角α的范围是0180 α< o o ≤. 2.直线的斜率:倾斜角不是90o的直线其倾斜角α的正切叫这条直线的斜率k,即 tan kα =. 注:①每一条直线都有倾斜角,但不一定有斜率. ②当ο 90 = α时,直线l垂直于x轴,它的斜率k不存在. ③过两点 111 (,) P x y、 222 (,) P x y 12 () x x ≠的直线斜率公式21 21 tan y y k x x α - == - 二、直线方程的五种形式及适用条件 名称方程说明适用条件 斜截式y=kx+b k—斜率 b—纵截距 倾斜角为90°的直线 不能用此式 点斜式y-y0=k(x-x0) (x0,y0)—直线上已 知点, k ──斜率 倾斜角为90°的直线 不能用此式 两点式1 21 y y y y - - =1 21 x x x x - - (x1,y1),(x2,y2)是 直线上两个已知点 与两坐标轴平行的直 线不能用此式 截距式 x a + y b =1 a—直线的横截距 b—直线的纵截距 过(0,0)及与两坐标 轴平行的直线不能用 此式 一般式 A x+ B y+C=0 (A、B不全为零) A、B不能同时为零 两直线的位置关系⑵两条相交直线 1 l与 2 l的夹角: 两条相交直线 1 l与 2 l的夹角,是指由 1 l与 2 l相交所成的四 个角中最小的正角θ,又称为1l和2l所成的角,它的取值范围 是0, 2 π ?? ? ? ? ,当两直线的斜率k1,k2都存在且k1·k2≠-1时, 则有21 12 tan 1 k k k k θ - = + . 4.距离公式。 ⑴已知一点P(x0,y0)及一条直线l:A x+B y+C=0,则点P到直线l 的距离d=00 22 || Ax By C A B ++ + ; ⑵两平行直线l1:A x+B y+C1=0,l2:A x+B y+C2=0之间的距离 d=12 22 || C C A B - + 。 5.当直线位置不确定时,直线对应的方程中含有参数. 含参数方程中有两种特殊情形,它们的对应的直线是有规律的, 即旋转直线系和平行直线系. ⑴在点斜式方程y-y0=k(x-x0)中, ①当(x0,y0)确定,k变化时,该方程表示过定点(x0,y0)的 旋转直线系, ②当k确定,(x0,y0)变化时,该方程表示平行直线系. ⑵已知直线l:A x+B y+C=0, 则①方程A x+B y+m=0(m为参数)表示与l平行的直线系; ②方程-B x+A y+n=0(n为参数)表示与l垂直的直线系。 ⑶已知直线l1:A1x+B1y+C1=0, 直线l2:A2x+B2y+C2=0, 则方程A1x+B1y+C1+λ(A2x+B2y+C2)=0 表示过l1与l2交点的直线系(不含l2) 掌握含参数方程的几何意义是某种直线系,有时可以优化解题思 路. 例10. 经过两直线 11x-3y-9=0与 12x+y-19=0的交点,且过 点(3,-2)的直线方程为 _______. 例11. 已知△ABC中,A(2, -1),B(4,3), C(3,-2),求: ⑴BC边上的高所在直线方 程;⑵AB边中垂线方程;⑶ ∠A平分线所在直线方程. 例12. 已知定点 P(6,4)与定直线l1:y=4x, 过P点的直线l与l1交于第一 象限Q点,与x轴正半轴交 于点M,求使△OQM面积最 小的直线l方程. 简单的线性规划线性规划 ⑴当点P(x0,y0)在直线A x+B y+C=0上时,其坐标满足方程A x0+B y0+C=0; ⑵当P不在直线A x+B y+C=0上时,A x0+B y0+C≠0,即A x0+B y0+C>0或A x0+B y0+C<0。这就是二元一次不等式的几何意义:二元一次不等式A x+B y+C>0(或<0)表示直线A x+B y+C=0上方或下方区域,其具体位置的确定常用原点(0,0)代入检验。 利用此几何意义,可以解决一类二元函数的最值问题。这就是线性规划的内容。 高中数学圆与方程知识点分析 1. 圆的方程:(1)标准方程:2 22()()x a y b r -+-=(圆心为A(a,b),半径为r ) (2)圆的一般方程:022=++++F Ey Dx y x (0422>-+F E D ) 圆心(-2D ,-2 E )半径 F E D 421 22-+ 2. 点与圆的位置关系的判断方法:根据点与圆心的距离d 与r 在大小关系判断 3. 直线与圆的位置关系判断方法 (1)几何法:由圆心到直线的距离和圆的半径的大小关系来判断。 d=r 为相切,d>r 为相交,d 圆的方程 【考纲要求】 1.掌握圆的标准方程的特点,能根据所给有关圆心、半径的具体条件准确地写出圆的标准方程, 2.能运用圆的标准方程正确地求出其圆心和半径,解决一些简单的实际问题,并会推导圆的标准方程. 3.掌握圆的一般方程的特点,能将圆的一般方程化为圆的标准方程从而求出圆心的坐标和半径; 4.能用待定系数法,由已知条件导出圆的方程. 【知识网络】 【考点梳理】 【高清课堂:圆的方程405440 知识要点】 考点一:圆的标准方程 222()()x a y b r -+-=,其中()a b ,为圆心,r 为半径. 要点诠释:(1)如果圆心在坐标原点,这时00a b ==,,圆的方程就是222 x y r +=.有关图形特征与方程的转化:如:圆心在x 轴上:b=0;圆与y 轴相切时:||a r =;圆与x 轴相切时:||b r =;与坐标轴相切时:||||a b r ==;过原点:2 2 2 a b r +=. (2)圆的标准方程2 2 2 ()()x a y b r -+-=?圆心为()a b ,,半径为r ,它显现了圆的几何特点. (3)标准方程的优点在于明确指出了圆心和半径.由圆的标准方程可知,确定一个圆的方程,只需要a 、b 、r 这三个独立参数,因此,求圆的标准方程常用定义法和待定系数法. 考点二:圆的一般方程 当2 2 40D E F +->时,方程22 0x y Dx Ey F ++++=叫做圆的一般方程.,22D E ?? - - ?? ? 为圆心,. 圆的方程 圆的一般方程 简单应用 圆的标准方程 点与圆的关系 要点诠释:由方程2 2 0x y Dx Ey F ++++=得22 224224D E D E F x y +-? ???+++= ? ?? ??? (1)当22 40D E F +-=时,方程只有实数解,22D E x y =- =-.它表示一个点(,)22 D E --. (2)当2 2 40D E F +-<时,方程没有实数解,因而它不表示任何图形. (3)当22 40D E F +->时,可以看出方程表示以,2 2D E ?? -- ???. 考点三:点和圆的位置关系 如果圆的标准方程为222()()x a y b r -+-=,圆心为()C a b ,,半径为r ,则有 (1)若点()00M x y ,在圆上()()2 2 2 00||CM r x a y b r ?=?-+-= (2)若点()00M x y ,在圆外()()2 2 2 00||CM r x a y b r ?>?-+-> (3)若点()00M x y ,在圆内()()2 2 2 00||CM r x a y b r ? 圆的方程,直线、圆的位置关系 一·圆的方程 1. 圆的标准方程: 求标准方程的方法——关键是求出圆心(),a b 和半径r ①待定系数:往往已知圆上三点坐标,例如教材119P 例2 ②利用平面几何性质 往往涉及到直线与圆的位置关系,特别是:相切和相交 相切:利用到圆心与切点的连线垂直直线 相交:利用到点到直线的距离公式及垂径定理 2.圆的一般方程:02 2=++++F Ey Dx y x 22 40D E F +->表示圆,圆心C (,22D E -- 2240D E F +-=表示点(,22 D E --) 2240D E F +-<不表示任何图形 二·直线、圆的位置关系 1. 点与圆的位置关系: 点00(,)M x y 与圆的关系的判断方法: (1)圆方程为标准式222 ()()x a y b r -+-= 222()()x a y b r -+->?点在圆外 222()()x a y b r -+-=?点在圆上 222()()x a y b r -+-?点在圆外 022=++++F Ey Dx y x ?点在圆上 220x y Dx Ey F ++++?直线l 与圆C 相离?直线l 与圆C 无交点 r d =?直线l 与圆C 相切?直线l 与圆C 有一交点 r d V ?直线l 与圆C 相交?直线l 与圆C 有两交点 3. 圆与圆的位置关系: 圆与圆的位置关系判断方法 求出圆心距12C C ,两圆的半径12,r r 1212C C r r >+?圆1C 与圆2C 相离?有4条公切线 1212C C r r =+?圆1C 与圆2C 外切?有3条公切线 121212||r r C C r r -<<+?圆1C 与圆2C 相交?有2条公切线 1212||C C r r =-?圆1C 与圆2C 内切?有1条公切线 1212||C C r r <-?圆1C 与圆2C 内含?有0条公切线 补充:直径圆方程: (x-x 1)(x -x 2)-(y -y 1)(y -y 2)=0 圆系方程: 设圆C 1 : x 2+y 2+D 1x+E 1 y+F 1=0, C 2 : x 2+y 2+D 2x+E 2 y+F 2=0,则方 程C : x 2+y 2+D 1x+E 1 y+F 1 + m(x 2+y 2+D 2x+E 2 y+F 2)=0表示过两圆C 1、C 2的交点的圆系方程(m 不为-1,且不含圆C 2). 其中一圆可以退化成直线。 圆的参数方程: ()222cos 0sin x r x y r r y r θθ =?+=>??=?,θ为参数 ()()()222cos 0sin x a r x a y b r r y b r θθ=+?-+-=>??=+?,θ为参数 1 / 4 高一数学辅导资料 内容:圆与方程 本章考试要求 一、圆的方程 【知识要点】 1.圆心为),(b a C ,半径为r 的圆的标准方程为:)0()()(222>=-+-r r b y a x 0==b a 时,圆心在原点的圆的方程为:222r y x =+. 2.圆的一般方程02 2 =++++F Ey Dx y x ,圆心为点,2 2D E ?? -- ???,半径2 r = , 其中0422 >-+F E D . 3.圆系方程:过圆1C :221110x y D x E y F ++++=与圆2C :222220x y D x E y F ++++= 交点的圆系方程是()22221112220x y D x E y F x y D x E y F λ+++++++++=(不含圆2C ), 当1λ=-时圆系方程变为两圆公共弦所在直线方程. 【互动探究】 考点一 求圆的方程 问题1. 求满足下列各条件圆的方程: ()1以两点(3,1)A --,(5,5)B 为直径端点的圆的方程是 ()2求经过)2,5(A ,)2,3(-B 两点,圆心在直线32=-y x 上的圆的方程; ()3过点()4,1A 的圆C 与直线10x y --=相切于点()2,1B ,则圆C 的方程是? 考点二 圆的标准方程与一般方程 问题2.方程2222210x y ax ay a a +++++-=表示圆,则a 的取值范围是 考点三 轨迹问题 问题3.点()4,2P -与圆224x y +=上任一点连线的中点轨迹方程是 问题4.设两点()3,0A -,()3,0B ,动点P 到点A 的距离与到点B 的距离的比为2,求P 点的轨迹. 二、直线和圆、圆与圆的位置关系 【知识要点】 1.直线与圆的位置关系 将直线方程代入圆的方程得到一元二次方程,设它的判别式 为△,圆的半径为r ,圆心C 到直线l 的距离为d 则直线与 圆的位置关系满足以下关系: 2.直线截圆所得弦长的计算方法: 利用垂径定理和勾股定理:AB =r 为圆的半径,d 直线到圆心的距离). 0:111221=++++F y E x D y x C 0:222222=++++F y E x D y x C 则两圆的公共弦所在的直线方程是 4.相切问题的解法: ①利用圆心到切线的距离等于半径列方程求解 ②利用圆心、切点连线的斜率与切线的斜率的乘积为1-(或一条直线存在斜率,另一条不存在) ③利用直线与圆的方程联立的方程组的解只有一个,即0=?来求解. 特殊地,已知切点),(00y x P ,圆222r y x =+的切线方程为 . 圆222)()(r b y a x =-+-的切线方程为 【互动探究】 考点一 直线与圆的位置关系 问题1:()1已知圆22:40C x y x +-=,l 过点(3,0)P 的直线,则 .A l 与C 相交 .B l 与C 相切 .C l 与C 相离 .D 以上三个选项均有可能 ()2直线l :1mx y m -+-与圆C :() 2 211x y +-=的位置关系是 .A 相离 .B 相切 .C 相交 .D 无法确定,与m 的取值有关. ()3过点()1,3P 引圆2244100x y x y +---=的弦,则所作的弦中最短的弦长为 第四章圆与方程 4.1 圆的方程 4.1.1 圆的标准方程 1.以(3,-1)为圆心,4为半径的圆的方程为() A.(x+3)2+(y-1)2=4 B.(x-3)2+(y+1)2=4 C.(x-3)2+(y+1)2=16 D.(x+3)2+(y-1)2=16 2.一圆的标准方程为x2+(y+1)2=8,则此圆的圆心与半径分别为() A.(1,0),4 B.(-1,0),2 2 C.(0,1),4 D.(0,-1),2 2 3.圆(x+2)2+(y-2)2=m2的圆心为________,半径为________. 4.若点P(-3,4)在圆x2+y2=a2上,则a的值是________. 5.以点(-2,1)为圆心且与直线x+y=1相切的圆的方程是____________________.6.圆心在y轴上,半径为1,且过点(1,2)的圆的方程为() A.x2+(y-2)2=1 B.x2+(y+2)2=1 C.(x-1)2+(y-3)2=1 D.x2+(y-3)2=1 7.一个圆经过点A(5,0)与B(-2,1),圆心在直线x-3y-10=0上,求此圆的方程.8.点P(5a+1,12a)在圆(x-1)2+y2=1的内部,则a的取值范围是() A.|a|<1 B.a<1 13 C.|a|<1 5 D.|a|<1 13 9.圆(x-1)2+y2=25上的点到点A(5,5)的最大距离是__________. 10.设直线ax-y+3=0与圆(x-1)2+(y-2)2=4相交于A,B两点,且弦AB的长为2 3,求a的值. 4.1.2 圆的一般方程 1.圆x 2+y 2-6x =0的圆心坐标是________. 2.若方程x 2+y 2+Dx +Ey +F =0表示以(2,-4)为圆心,以4为半径的圆,则F =________. 3.若方程x 2+y 2-4x +2y +5k =0表示圆,则k 的取值范围是( ) A .k >1 B .k <1 C .k ≥1 D .k ≤1 4.已知圆的方程是x 2+y 2-2x +4y +3=0,则下列直线中通过圆心的是( ) A .3x +2y +1=0 B .3x +2y =0 C .3x -2y =0 D .3x -2y +1=0 5.圆x 2+y 2-6x +4y =0的周长是________. 6.点(2a,2)在圆x 2+y 2-2y -4=0的内部,则a 的取值范围是( ) A .-12021届高考数学(理)考点复习:圆的方程(含解析)
高三总复习直线与圆的方程知识点总结
最新直线与方程和圆与方程-知识点总结
人教版数学必修二第四章 圆与方程 知识点总结
高中数学直线与圆的方程知识点总结
直线和圆的方程知识点总结讲课稿
直线和圆的方程知识及典型例题
高中数学圆与方程知识点
知识梳理圆的方程(基础)
圆的方程-直线与圆的位置关系--知识点
高中数学圆的方程专题复习
最新人教版数学必修二第四章 圆与方程 知识点总结知识讲解
