概率论与数理统计复习资料

《概率论与数理统计》复习资料

一、填空题（15分）

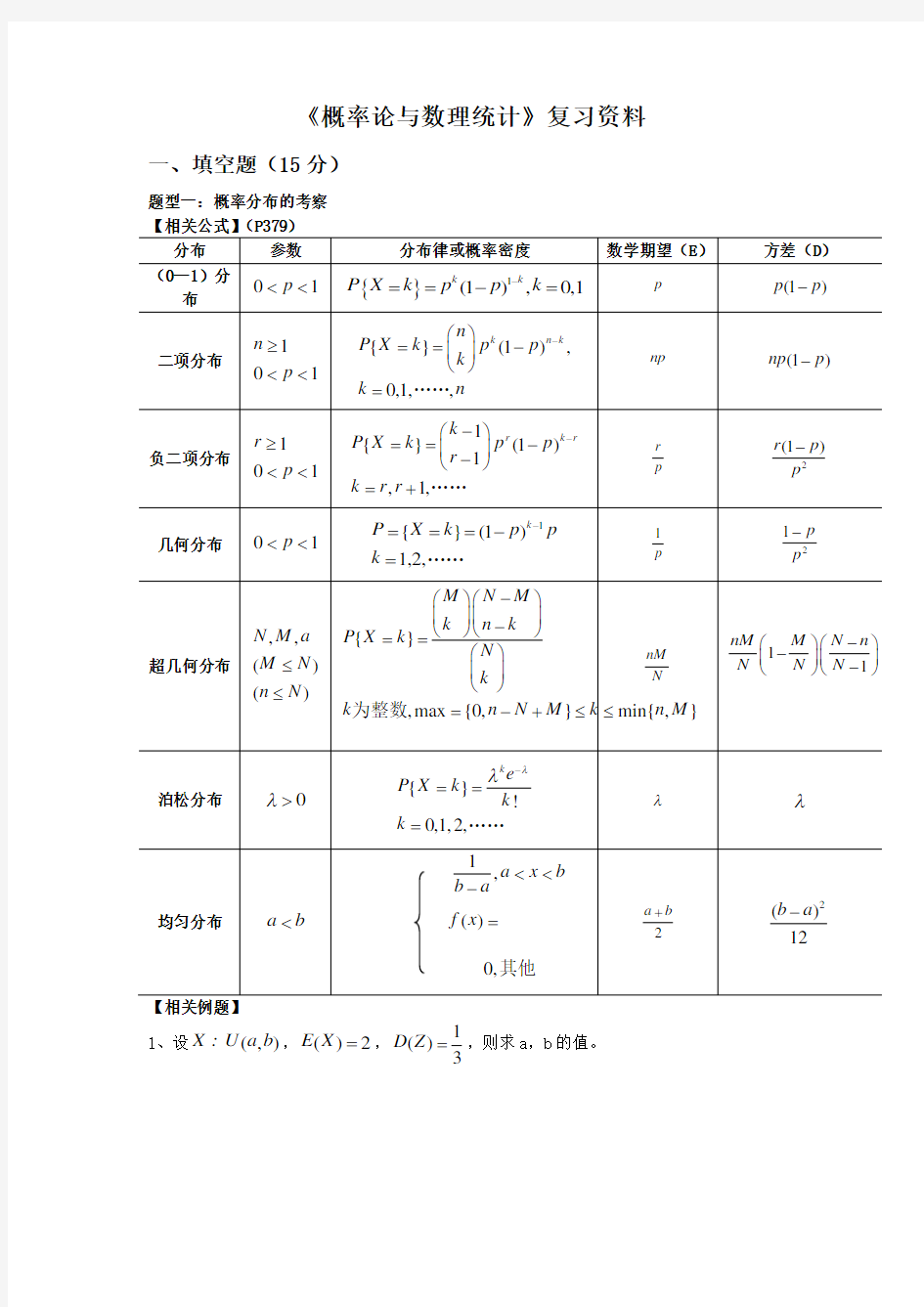
题型一：概率分布的考察 【相关公式】（P379）

【相关例题】

1、设(,)X U a b :，()2E X =，1

()3

D Z =

，则求a ，b 的值。

21

(,),()2,(),3

()1

2,,21231, 3.

X U a b E X D X a b b a a b

a b ==+-∴==<==Q :解：根据性质：

解得： 2、已知(,),()0.5,()0.45X b n p E X D X ==:,则求n ，p 的值。

0.5,(1)0.450.1.

np np p p =-==解：

由题意得：解得：

题型二：正态总体均值与方差的区间估计 【相关公式】（P163）

2/2,1-X X z ασμα??±

???

为已知的一个置信水平为的置信区间：

【相关例题】

1、（样本容量已知）

1225~(,0.81),,,,,5,0.99X N X X X X μμ=已知总体……为样本且则的置信度的置信区间为：

()()/20.0250.9550.18 1.96 4.6472,5.35285X z α????

+=±=±?= ? ?????解：代入公式得：

2、（样本容量未知）

()123(,1),,,,,,0.9510.88,18.92.

n X N X X X X μμ:已知为样本容量若关于的置信度的置信区间，

求样本容量2227.847.84 3.922 4.

X z X z z n ααα

????+-=?= ? ?????

=?=解：

由题意知：样本长度为，则有：

题型三：方差的性质 【相关公式】（P103）

()()()21()0,2()(),()()3,,()()()

D C C D CX C D X D X C D X C X Y D X Y D X D Y ==+=+=+为常数。

，为常数。

相互独立 【相关例题】 1、

12121212(2,4),(0,9),,,(2).X X X U X N X X D X X -::已知，两变量，且相互独立求

1221212~(2,4),(0,9)

()1

(2)()4()4936

123

X U X b a D X X D X D X -∴-=+=+?=Q :解：

题型四：

2

t χ分布、分布的定义 【相关公式】（P140、P138）

(

)()()()21232222

122221(0,1),(),,.

2,,,,(0,1),,.

n n X Y n X Y t n t t t n X X X X N X X X n n χχχχχ=

=+++:

:::设且相互独立，则称随机变量

服从自由度为的分布，记为设……是来自总体的样本则称统计量服从自由度为的分布记为

【相关例题】

1

、2

(0,1),(4),,X Y X Y χ:::若且相互独立？

(4)t : 2、()30

2

123301

,,,,0,1,?i

i X X X X N X

=∑:若变量……服从则

30

221

(30).i i X χ=∑:答：

题型五：互不相容问题 【相关公式】（P4）

,A B A B ?=?若则称事件与事件是互不相容的。

【相关例题】

1、()0.6,,,().P A A B P AB =若互不相容求

,()(())()()0.6

A B A B P AB P A S B P A AB P A ∴?=?

∴=-=-==Q 解：

互不相容

二、选择题（15分）

题型一：方差的性质 【相关公式】（见上，略） 【相关例题】（见上，略）

题型二：考察统计量定义（不能含有未知量） 题型三：考察概率密度函数的性质（见下，略）

题型四：和、乘、除以及条件概率密度（见下，略） 题型五：对区间估计的理解（P161） 题型六：正态分布和的分布 【相关公式】（P105） 【相关例题】

()~(0,2),~(3,9),~?X N Y N X Y +若则

(03,29)(3,11).N N ++=答：

题型七：概率密度函数的应用 【相关例题】

2,01x x << 设()X f x ==

0,其他

已知{}{},P X a P X a a >=<则求。

201{}{}

1

{}212|02022

a

P X a P X a P X a a xdx x a a -≤=<∴<=

==>∴=

?Q 解：由题意，得：即有：又

三、解答题（70分）

题型一：古典概型：全概率公式和贝叶斯公式的应用。

【相关公式】 全概率公式：

()()()()()()

n 1122S P()=|()||()()

(|)()

=()(|)()(|).

i n n E S A E B A P A B P B P A B P B P A B P B P AB P B A P A P A P A B P B P A B P B +++=

=+12设实验的样本空间为，为的事件，B ，B ，……，B 为的划分，且>0,则有：

P ?…其中有：。特别地：当n 2时，有：

贝叶斯公式：

()()i 1

00(1,2,,),()(|)()

(|)()(|)()

=()(|)()

(|)()(|)()(|)()

i i i i n

i i j E S A E A P B i n P B A P A B P B P B A P A P A B P B P AB P A B P B P B A P A P A B P B P A B P B =>>=====

+∑12n 设实验的样本空间为。为的事件,B ，B ，……，B 为S 的一个划分，且P ，……则有：特别地：

当n 2时，有：

【相关例题】

★1、P19 例5

元件制造厂

次品率 提供原件的份额

1 2 3

设这三家工厂的产品在仓库中是均匀混合的，且无区分标志。

问：

（1）在仓库中随机取一只元件，求它的次品率；

（2）在仓库中随机抽取一只元件，为分析此次品出自何厂，需求出此次品有三家工厂生产的概率分别是多少，试求这些概率。（见下）

(){}{}11223311121==(1,2,3).1()(|)()(|)()(|)()0.020.150.010.800.030.050.0125

(2)(|)()0.020.15

(|)0.24

()0.0125(|A B i i B P A P A B P B P A B P B P A B P B P A B P B P B A P A P B A ==++=?+?+?=?===解：设取到一只次品，在厂取到产品且、B2、B3是S 的一个划分。则由全概率公式有：

由贝叶斯公式有：

22333(|)()0.010.80

)0.64

()0.0125(|)()0.030.05

(|)0.12

()0.0125P A B P B P A P A B P B P B A P A ?===?===答：综上可得，次品出自二厂的可能性较大。

2、袋中装有m 枚正品硬币，n 枚次品硬币（次品硬币两面均有国徽），在袋中任意取一枚，

将他掷r 次，已知每次都得到国徽，问这枚硬币是正品的概率是多少？

()()()={}B={r }P |,1

=

,(),(|),(|) 1.2

1()(|)()2|.

1()(|)()(|)()2r r r A A B m n P A P A P B A P B A m n m n m

P AB P B A P A m n P A B m n

P B P B A P A P B A P A m n m n

===++?+===+?+++解：设所抛掷的硬币是正品，抛掷次都得到国徽，本题即求得：即有：3、设根据以往记录的数据分析，某船只运输的某种物品损坏的情况共有三种：损坏2%（这一事件记为A 1），损坏10%（这一事件记为A 2），损坏90%（这一事件记为A 3），且知P （A 1）=，P （A 2）=，P （A 3）=.现在从已经运输的物品中随机取3件，发现这三件都是好的（这一事件记为B ），

123(|),(|),(|)()P A B P A B P A B 试求这里物品件数很多，取出一件后不影响取后一件是否为好品的概率。

（见下）

333123123112233333111(|)0.98,(|)0.9,(|)0.1()0.8,()0.15,()0.05

()(|)()(|)()(|)()0.980.80.90.150.10.050.8624

(|)()0.9830.8

(|)0()0.8624

P B A P B A P B A P A P A P A P B P B A P A P B A P A P B A P A P B A P A P A B P B =======++=?+?+?=?===解：由题意可知：

23.8731

(|)0.1268(|)0.0001

P A B P A B ==

4、将A 、B 、C 三个字母之一输入信道，输出为原字母的概率为ɑ，而输出其他字母的概率都是（1-ɑ）/2.今将字母串AAAA 、BBBB 、CCCC 之一输入信道，输入AAAA 、BBBB 、CCCC 的概率分别为p1、p2、p3（p1+p2+p3=1），已知输出为ABCA 。问输入AAAA 的概率是多少？（设信道传输各字母的工作是相互独立的。）

{}()223333

123

22

1

2231={AAAA}={CCCC}={ABCA}|.

()(|)()(|)()(|)()

111()()()222

1(

)()(|)()2(|)11()()()()22A B BBBB C D P A D P D P D A P A P D B P B P D C P C p p p p P AD P D A P A P A D P D P D p αααααααααααα=++---=?+?+?-?===

--?+?解：设输入为，=输入为，输入为，输出为，依题意求323111

1123111()2

111(31)1()()(1)222p p p p p a p p p p p p ααααααααααα-+?===

----+-??+?+?+- ???

题型二：1、求概率密度、分布函数；2、正态分布

1、求概率密度

【相关公式】已知分布函数求概率密度在连续点求导；已知概率密度f(x)求分布函数抓住公

式

：

()1

f x dx +∞

=-∞?，且对于任意实数，有：

212211

{}()()()x P x X x F x F x f x dx x <<=-=?

。

【相关例题】

（1）设随机变量X 的分布函数为： 0,1x < F X （X ）= ln ,1x x e ≤<

1,x e ≥

① 5(2)(03)(2)2

P X P X P X <<≤<<求、、 ② ().x f x 求概率密度 （见下）

(1)(2)(2)ln 2

(03)(3)(0)101555

(2)()(2)ln

2241(2)()X X X X X P X P X P X F F P X F F d F X dx x

<=≤=<≤=-=-=<<=-==解：

1

,1x e x <<

()x f x ∴=

0,其他 （2）2

()()1A

f x x x =

-∞<<+∞+，是确定常数A 。 200+1

-1+([arctan ][arctan ]11

A

dx x A x x A π

+∞-∞∞=∞+==-

?解：由相关性质得：解得：

（3）

,036

x

x ≤< 设随机变量X 具有概率密度f(x)= 2,342

x

x -≤<，求X 的分布函数。

0,其他 解：

0，x<0

,0306x x dx x ≤

,0312

x x ?≤< 362

2,3403x x x x +-≤

x x x ?-+-≤< 1,4x ≥

()F x =

2、正态分布(高斯分布) 【相关公式】 （1

）公式22

()2()()x f x x μσ--

=

-∞<<+∞其中：

,,μσμσ为常数，则称X 服从参数为的正态分布。

（2）若()2

~=~(0,1).x X N

Z N μ

μσσ

-，，则 （3）相关概率运算公式：

122112{}{

}(

);

{}{}()();()1().

X x x P X x P x x x x X P x X x P x x μ

μ

μ

σ

σσ

μμμμ

μσσσσσ

---≤=≤

=Φ-----≤<=≤<=Φ-ΦΦ=-Φ-

【相关例题】

1、（P58 27）某地区18岁女青年的血压（收缩压：以mmHg 计）服从N~（110,122

），在该地任选一名18岁女青年，测量她的血压X ，求： （1）{105},{100120};P X P X ≤<≤ （2）确定最小的,{}0.05x P X x >≤使

2(1)~(110,12)

1101051105

{105}{}()1(0.42)10.66280.3372;

121212

100110110120110101010

{100120}{}()()2()10.5934

121212121212

110110(2){}1{}1{}1212X N X P X P X P X P X x P X x P X x P --∴<=<=Φ--Φ=-=---<≤=<≤=Φ-Φ-=Φ-=-->=-≤=-≤Q B 解：

min 110

1()0.05

12

110

()0.95(1.65)

12

110 1.65129.8

12

129.8

x x x x x -=-Φ≤-Φ≥Φ-?≥?≥∴=B 即有：

2、由某机器生产的螺栓的长度（cm ）服从参数10.05,0.06μσ==的正态分布，规定长度在范围10.050.12±内为合格品，求一螺栓为不合格的概率。 （见下）

()

{}.

9.9310.0510.0510.1710.0510.05

(){

}(22)2(2)10.9544

0.060.060.060.06

()1()10.95440.0456A P A X X P A P P P A P A =----=≤≤=-≤≤=Φ-=∴=-=-=解：设一螺栓合格，本题求

题型三：二维随机变量的题型

【相关公式】

++1(,)=(,)1-2(,)()()3(1):()()()()1(2):()()()(3):()X Y x y X Y X Y XY X Y Y X

f x y dxdy f x y dx dy f x y f x f y Z X Y f f f z y f y dy f x f z x dx

z

Z XY f z f x f dx

x x Y

Z f z X ∞∞∞∞??

=??∞∞∞-∞??=?+∞

+∞

=+*=-=--∞-∞∞==-∞=

???????、二维随机变量的求法：、联合概率密度求法:、随机变量的函数分布：

()()X Y x f x f xz dx

∞=-∞?【注意点】讨论x,y 取值范围。

【相关例题】

1、（P84 3）设随机变量（X,Y ）的概率密度为：

(6),02,24k

x y x y --<<<< (,)f x y =

0,其他

(1).(2){X<1,Y<3}.(3){X<1.5}.(4){4}.

k P P P X Y +≤确定常数求求求

（见下）

()()()()()()2

20

42441(6)6|1021202221

8

3113

2620884 1.5127(3)6208324412

(4)62083x k x y dx dy k x xy dy k y dy x y dx dy x y dx dy y x y dx dy ????--=--=-=??????????--=??????--=

????-??--=

????

??????????解：

解得:k=

由题意即求：由题意即求：由题意即求(如图)：

2、（P86 18）设X 和Y 是两个相互独立的随机变量，X 在区间（0,1）上服从均匀分布，Y

的概率密度为：

2

1,02

y e y ->

()Y f y =

0,其他

()()12{X Y}.

X Y P ≤求和的联合概率密度.

求

X 解：由题意的：的概率密度如下：

1,0

()2

22212

1(,),01,0

2

(,)0,(2)111112|00022221

y

y y y

x f x y e x y f x y y e dy dx e d dx e dx x x e

----∞-

∴=<<>=∞∞????

????=-?-=- ????? ?????????

=-?????其他

由题意,即求：

3、（P87 25）设随机变量X ，Y 相互独立，且具有相同的分布，它们的概率密度均为 1,1x

e x ->

()f x =

0，其他 求Z=X+Y 的概率密度。

1122(,)()()00

1(2).(2)1

x x z X Y X Y z

z f x y f x f z x dx e e dx z e dx e z x --++--∞∞

=-=?-==->???

解： 4、（P87 26）设随机变量X,Y 相互独立，它们的概率密度为 ,0x

e x -> ()

f x =

0，其他 求Z=Y/X 的概率密度。

()00(1)2000

0,0.

0()()()()()()1.10()0.

x zx x zx z x X Z x Y

f Z f x fX x fY zx dx x fX x fY zx dx

X

xe e dx xe e dx xe dx z x f Z Z ∞∞∞∞∞-----+>>>=======+≤=?????解：由题意知:当时，

当时,综上所述，的概率密度为：

()

2

1

,01z z >+

()Z f z =

0,0z ≤

题型四：最大似然估计的求解

【相关公式】

()()(1)()0ln ()0220ln 0(1,2,3,,)i i

d d L L d d i i L L i k θθθθθ

θθ==≥??===??当只有一个变量的时候，有：或；当未知变量有的时候，有：或……

【相关例题】

1、设概率密度为：

,01x

e x λλ-<<

()f x =

0,其他

λ求的最大似然估计.

()$111

1

()exp ln ()ln ()1()0=.n

n

x

n

i i i n

i

i n

i i n

L e

x l L n x d n l x d d l d x λλλλλλθλλλλλλλλ-====??

==- ?

??==-=-=∑∏∑∑解：令，即有：

2、（P174 8）

123,,,n X X X X 设,?… 是来自概率密度为：

1

,01x x θθ-<<

(;)f x θ=

0,其他 的总体的样本，θ未知，求θ的最大似然估计。

()$1

111111()()ln ()ln 1ln ln ()ln ln ()=0=

ln n

n

n i i i n i i n i i n i i L x x l L n x d n l x d d l d n x θθθθθθθθθθθθθθ

θ--=====??== ?

??

??

==+- ?

??

??=+ ???-??

???

∏∏∏∏∏令，得：

题型五：正态总体均值的假设检验、正态总体方差的假设检验

【相关公式】

(

)()()/20222

22

12

1(2)(1)(1)21(1)

1:(1)X Z X t t n X t t n H n S n n S n αασσχσχσ-=

=

-=

≥----≥-::1、正态总体均值的假设检验

标准差已知（Z 检验法）：

标准差未知（t 检验法）:

拒绝域为：、正态总体方差的假设检验

当为真时，有：

拒绝域为 【相关例题】

1、（P218 3）某批矿砂的5 个样品中的镍含量，经测定（%）

设测定值总体服从正态分布，但参数均未知，问在α=下能否接受假设，这批矿砂的镍含量的均值为.

()012

=0.013.25: 3.25

3.252=0.0130.3442:(1)0.005(4)

4.6061, 4.6061(4.6061,)0.3442 4.6061=0.01H x H x x S X t t t n t t H ααμα=≠===-==∈-∞-?+∞<∴∴B Q 0在显著性水平下检验问题：：检验统计量，，=3.25,n=5。代入数据，得观察值：拒绝域为即：接受在 3.2

5.

的情况下可以接受假设，这批矿砂的镍含量均值为

2、（P220 12）某种导线，要求电阻的标准差不得超过Ω，尽在一批导线中取样品9根，测得s=Ω，设总体为正态分布，参数值均未知，问在显著水平α=下能否认为这批导线的标准差显著偏大？

012

2

22

2210.050

=0.050.0050.005

0.007,9,0.005

(1)80.00715.68

0.005:(1)(8)15.50715.6815.507=0.05H H s n n S t n H αασσσσχχα-≤>===-?==≥-==>∴∴Q 解：

在显著水平下检验问题：：：检验统计量：代入数据，得观察值:拒绝域为拒绝在显著性水平下能认为这批导线的标准差显著性偏大。