增广最小二乘辨识白噪声和有色噪声的区别是什么

第一次作业

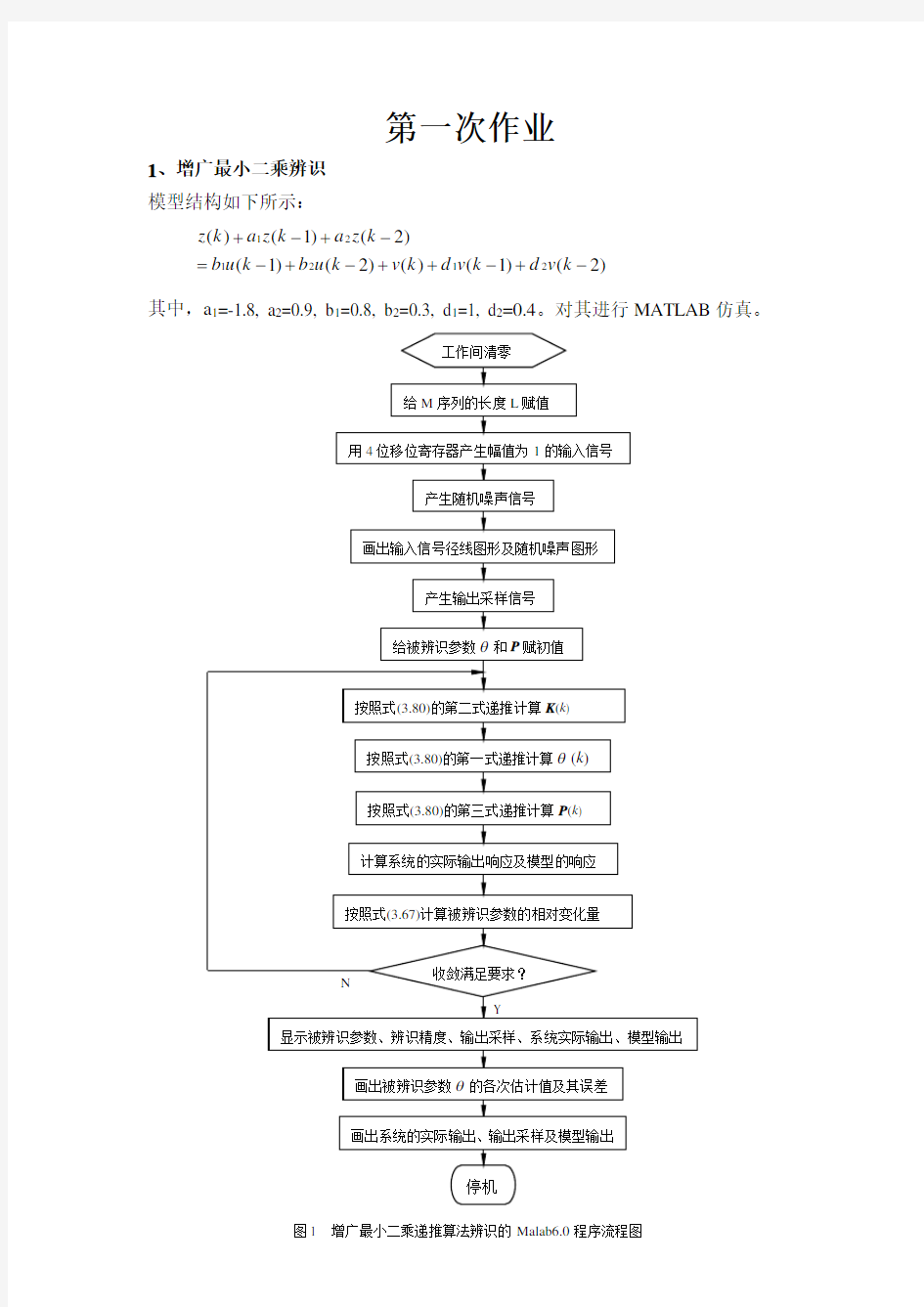
1、增广最小二乘辨识模型结构如下所示：

)

2()1()()2()1()

2()1()(212121-+-++-+-=-+-+k v d k v d k v k u b k u b k z a k z a k z

其中，a 1=-1.8, a 2=0.9, b 1=0.8, b 2=0.3, d 1=1, d 2=0.4。对其进行MATLAB 仿真。

停机

工作间清零

产生输出采样信号给被辨识参数θ和P 赋初值

按照式(3.80)的第三式递推计算P (k )

按照式(3.67)计算被辨识参数的相对变化量

收敛满足要求？

按照式(3.80)的第二式递推计算K (k )

按照式(3.80)的第一式递推计算θ(k )

用4位移位寄存器产生幅值为1的输入信号

计算系统的实际输出响应及模型的响应

给M 序列的长度L 赋值

画出被辨识参数θ的各次估计值及其误差

显示被辨识参数、辨识精度、输出采样、系统实际输出、模型输出

画出系统的实际输出、输出采样及模型输出

画出输入信号径线图形及随机噪声图形

产生随机噪声信号

图1 增广最小二乘递推算法辨识的Malab6.0程序流程图

解：

增广最小二乘辨识程序： >> clear L=60;

y1=1;y2=1;y3=1;y4=0; for i=1:L;

x1=xor(y3,y4); x2=y1; x3=y2; x4=y3; y(i)=y4; if y(i)>0.5,u(i)=-1; else u(i)=1; end

y1=x1;y2=x2;y3=x3;y4=x4; end figure(1); subplot(2,1,1); stem(u),grid on v=randn(1,60); subplot(2,1,2); plot(v),grid on;

u,v %显示输入信号和噪声信号

z=zeros(7,60);zs=zeros(7,60);zm=zeros(7,60);zmd=zeros(7,60);

z(2)=0; z(1)=0; zs(2)=0; zs(1)=0; zm(2)=0; zm(1)=0; zmd(2)=0; zmd(1)=0; c0=[0.1 0.1 0.1 0.1 0.1 0.1 0.1]';

y (k )

u (k )

e (k ) z (k )

+ v (k ) )

(1-z G )

(1-z N 图2 增广最小二乘法辨识实例结构图

p0=10^6*eye(7,7);

E=0.00000000005;

c=[c0,zeros(7,14)];

e=zeros(7,15);

for k=3:60;

z(k)=1.8*z(k-1)-0.9*z(k-2)+0.8*u(k-1)+0.3*u(k-2)+v(k)+v(k-1)+0.4*v(k-2);

h1=[-z(k-1),-z(k-2),u(k-1),u(k-2),v(k),v(k-1),v(k-2)]';

x=h1'*p0*h1+1; x1=inv(x); k1=p0*h1*x1;

d1=z(k)-h1'*c0; c1=c0+k1*d1;

zs(k)=-1.8*z(k-1)+0.9*z(k-2)+0.8*u(k-1)+0.3*u(k-2); %系统在M序列的输入下的输出响应

zm(k)=[-z(k-1),-z(k-2),u(k-1),u(k-2)]*[c1(1);c1(2);c1(3);c1(4)];

zmd(k)=h1'*c1;

e1=c1-c0; e2=e1./c0;

e(:,k)=e2;

c0=c1;

c(:,k)=c1;

p1=p0-k1*k1'*[h1'*p0*h1+1]; %find p(k)

p0=p1;

if e2<=E break;

end

c, e, %显示被辨识参数及参数收敛情况

z, zs, zm %显示输出采样值、系统实际输出值、模型输出值

%分离变量

a1=c(1,:); a2=c(2,:); b1=c(3,:); b2=c(4,:);

d1=c(5,:); d2=c(6,:); d3=c(7,:);

ea1=e(1,:); ea2=e(2,:); eb1=e(3,:); eb2=e(4,:);

ed1=e(5,:); ed2=e(6,:); ed3=e(7,:);

figure(2); %画第二个图形

i=1:60;plot(i,a1,'r',i,a2,'r:',i,b1,'b',i,b2,'b:',i,d1,'g',i,d2,'g:',i,d3,'g+') %画出各个被辨识

参数

title('Parameter Identification with Recursive Least Squares Method')

figure(3); i=1:60; %画出第三个图形

plot(i,ea1,'r',i,ea2,'r:',i,eb1,'b',i,eb2,'b:',i,ed1,'g',i,ed2,'g:',i,ed2,'r+')

title('Identification Precision')

figure(4); subplot(4,1,1); %画出第四个图形，第一个子图

i=1:60;plot(i,zs(i),'r')

subplot(4,1,2); i=1:60;plot(i,z(i),'g') %第二个子图，画出被辨识系统的采样输出响应

subplot(4,1,3); i=1:60;plot(i,zm(i),'b') %第三个子图，画出模型含有噪声的输出响应

subplot(4,1,4); i=1:60;plot(i,zs(i),'b') %第四个子图，画出模型去除噪声后的输出响应

（1）程序执行结果：

u =

Columns 1 through 17

1 -1 -1 -1 -1 1 1 1 -1 1 1 -1 -1 1 -1 1 -1 Columns 18 through 34

-1 -1 -1 1 1 1 -1 1 1 -1 -1 1 -1 1 -1 -1 -1 Columns 35 through 51

-1 1 1 1 -1 1 1 -1 -1 1 -1 1 -1 -1 -1 -1 1 Columns 52 through 60

1 1 -1 1 1 -1 -1 1 -1

v =

Columns 1 through 10

0.7254 -0.0631 0.7147 -0.2050 -0.1241 1.4897 1.4090 1.4172 0.6715 -1.2075 Columns 11 through 20

0.7172 1.6302 0.4889 1.0347 0.7269 -0.3034 0.2939 -0.7873 0.8884 -1.1471 Columns 21 through 30

-1.0689 -0.8095 -2.9443 1.4384 0.3252 -0.7549 1.3703 -1.7115 -0.1022 -0.2414

Columns 31 through 40

0.3192 0.3129 -0.8649 -0.0301 -0.1649 0.6277 1.0933 1.1093 -0.8637 0.0774 Columns 41 through 50

-1.2141 -1.1135 -0.0068 1.5326 -0.7697 0.3714 -0.2256 1.1174 -1.0891 0.0326 Columns 51 through 60

0.5525 1.1006 1.5442 0.0859 -1.4916 -0.7423 -1.0616 2.3505 -0.6156 0.7481

c =

Columns 1 through 10

0.1000 0 0.1000 0.0348 -0.0983 -0.6239 -0.4695 -1.6520 -1.8000 -1.8000 0.1000 0 0.1000 0.1000 0.5358 0.5292 0.7029 1.4373 0.9000 0.9000 0.1000 0 -0.0000 -0.1590 -0.0739 0.0055 0.1451 0.5864 0.8000 0.8000 0.1000 0 0.2000 0.0640 0.5459 0.8188 0.7485 0.2902 0.3000 0.3000 0.1000 0 0.1715 0.1495 0.2697 -0.2741 -0.2722 0.7596 1.0000 1.0000 0.1000 0 0.0937 0.1984 0.8904 0.9264 1.1464 0.7038 1.0000 1.0000 0.1000 0 0.1725 0.1716 -0.4338 -0.1614 0.1453 0.3301 0.4000 0.4000 Columns 11 through 20

-1.8000 -1.8000 -1.8000 -1.8000 -1.8000 -1.8000 -1.8000 -1.8000 -1.8000 -1.8000 0.9000 0.9000 0.9000 0.9000 0.9000 0.9000 0.9000 0.9000 0.9000 0.9000 0.8000 0.8000 0.8000 0.8000 0.8000 0.8000 0.8000 0.8000 0.8000 0.8000

0.3000 0.3000 0.3000 0.3000 0.3000 0.3000 0.3000 0.3000 0.3000 0.3000

1.0000 1.0000 1.0000 1.0000 1.0000 1.0000 1.0000 1.0000 1.0000 1.0000 1.0000 1.0000 1.0000 1.0000 1.0000 1.0000 1.0000 1.0000 1.0000 1.0000 0.4000 0.4000 0.4000 0.4000 0.4000 0.4000 0.4000 0.4000 0.4000 0.4000 Columns 21 through 30

0.3000 0.3000 0.3000 0.3000 0.3000 0.3000 0.3000 0.3000 0.3000 0.3000

e =

1.0e+004 *

Columns 1 through 10

0 0 0 -0.0001 -0.0004 0.0005 -0.0000 0.0003 0.0000 0.0000 0 0 0 0 0.0004 -0.0000 0.0000 0.0001 -0.0000 0.0000 0 0 -0.0001 1.3455 -0.0001 -0.0001 0.0025 0.0003 0.0000 -0.0000 0 0 0.0001 -0.0001 0.0008 0.0000 -0.0000 -0.0001 0.0000 -0.0000 0 0 0.0001 -0.0000 0.0001 -0.0002 -0.0000 -0.0004 0.0000 0.0000 0 0 -0.0000 0.0001 0.0003 0.0000 0.0000 -0.0000 0.0000 -0.0000 0 0 0.0001 -0.0000 -0.0004 -0.0001 -0.0002 0.0001 0.0000 -0.0000 Columns 11 through 20

0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 -0.0000 0.0000 -0.0000 -0.0000 -0.0000 -0.0000 -0.0000 0.0000 0.0000 0.0000 0.0000 -0.0000 -0.0000 0.0000 0.0000 -0.0000 0.0000 -0.0000 -0.0000 0.0000 -0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 -0.0000 0.0000 0.0000 -0.0000 -0.0000 -0.0000 -0.0000 0.0000 0.0000 -0.0000 0.0000 -0.0000 -0.0000 0.0000 -0.0000 -0.0000 -0.0000 -0.0000 -0.0000 0.0000 -0.0000 0.0000 Columns 21 through 30

0.0000 0.0000 0.0000 0.0000 -0.0000 -0.0000 0.0000 -0.0000 -0.0000 -0.0000 0.0000 0.0000 0.0000 0.0000 -0.0000 -0.0000 0.0000 -0.0000 -0.0000 -0.0000 -0.0000 -0.0000 -0.0000 -0.0000 -0.0000 0.0000 0.0000 0.0000 0.0000 -0.0000 -0.0000 -0.0000 -0.0000 -0.0000 0.0000 -0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 -0.0000 0.0000 -0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 -0.0000 0.0000 0.0000 0.0000 -0.0000 -0.0000 0.0000 0.0000 -0.0000 -0.0000 -0.0000 -0.0000 -0.0000 0.0000 0.0000 0.0000 -0.0000 0.0000

Columns 31 through 40

-0.0000 0.0000 -0.0000 -0.0000 -0.0000 0.0000 -0.0000 -0.0000 -0.0000 0.0000 -0.0000 0.0000 -0.0000 -0.0000 -0.0000 0.0000 -0.0000 -0.0000 -0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 -0.0000 -0.0000 -0.0000 0.0000 0.0000 0.0000 -0.0000 0.0000 0.0000 -0.0000 -0.0000 -0.0000 0.0000 0.0000 0.0000 -0.0000 0.0000 0.0000 -0.0000 -0.0000

0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 -0.0000 0.0000 0.0000 0.0000 0.0000 -0.0000 0.0000 0.0000 -0.0000 Columns 41 through 50

-0.0000 -0.0000 0.0000 -0.0000 -0.0000 0.0000 0.0000 -0.0000 -0.0000 -0.0000 -0.0000 0.0000 0.0000 -0.0000 -0.0000 0.0000 0.0000 -0.0000 -0.0000 -0.0000 -0.0000 -0.0000 0.0000 -0.0000 0.0000 0.0000 0.0000 -0.0000 0.0000 0.0000 0.0000 -0.0000 -0.0000 -0.0000 -0.0000 -0.0000 -0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 -0.0000 0.0000 -0.0000 -0.0000 -0.0000 0.0000 0.0000 -0.0000 -0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 -0.0000 -0.0000 0.0000 0.0000 0.0000 0.0000 -0.0000 0.0000 -0.0000 -0.0000 0.0000 -0.0000 -0.0000 Columns 51 through 60

-0.0000 -0.0000 -0.0000 0.0000 -0.0000 -0.0000 -0.0000 0.0000 -0.0000 -0.0000 -0.0000 0.0000 0.0000 0.0000 -0.0000 -0.0000 -0.0000 -0.0000 -0.0000 -0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 -0.0000 -0.0000 -0.0000 -0.0000 0.0000 0.0000 -0.0000 0.0000 0.0000 -0.0000 0.0000 -0.0000 0.0000 -0.0000 -0.0000 -0.0000 0.0000 0.0000 -0.0000 0.0000 0.0000 0.0000 0.0000 -0.0000 0.0000 -0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 -0.0000 0.0000 -0.0000 0.0000 0.0000 0.0000 0.0000 -0.0000 0.0000 0.0000 -0.0000 -0.0000 0.0000

z =

Columns 1 through 10

0 7.4465 30.7858 -28.7654 -10.2339 9.9215 -4.8162 -6.2668 17.9817 0 0 16.6698 27.1989 -38.6759 -1.2571 6.4731 -9.2722 -6.0145 14.8759 0 0.4418 22.8348 22.0320 -44.4573 6.4846 6.2759 -11.0952 -3.0199 10.8033 0 0.1799 26.3781 14.0638 -45.1291 13.8392 7.2537 -11.9115 3.9431 7.6303 0 -1.2171 29.8938 4.6047 -40.5751 18.1501 6.5658 -11.1172 12.9859 0 0 -2.1691 31.9745 -6.0426 -30.5736 18.3450 4.3079 -8.7503 18.5378 0 0 0.5401 31.7254 -17.9814 -19.6581 15.0451 0.6483 -6.9069 19.9813 0 0 Columns 11 through 20

0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0

0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 Columns 21 through 30

0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 Columns 31 through 40

0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 Columns 41 through 50

0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 Columns 51 through 60

0 0 0 0 0 0 0 0 0 0

0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0

zs =

Columns 1 through 10

0 -1.8244 -27.8287 27.4283 6.7683 -11.6707 2.2102 3.4572 -18.1822 0 0 -11.8175 -27.3616 36.6945 1.2288 -3.8181 8.1526 3.9640 -14.8840 0 -0.5000 -23.8039 -20.7508 44.8276 -7.4478 -1.6223 12.8554 5.6861 -11.6931 0 -1.8953 -25.5998 -15.6786 44.7149 -12.3037 -4.3708 11.1263 1.1227 -5.5576 0 -1.0261 -25.8293 -6.5860 41.7207 -19.5744 -7.9084 11.9551 -8.7155 0 0 1.2527 -30.5685 3.2690 33.5191 -21.3148 -4.7901 8.7906 -20.3258 0 0 3.3090 -31.7497 13.9208 18.0149 -17.7860 -0.7450 4.6450 -21.1808 0 0 Columns 11 through 20

0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 Columns 21 through 30

0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0

Columns 31 through 40

0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 Columns 41 through 50

0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 Columns 51 through 60

0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0

zm =

Columns 1 through 10

0 4.8865 28.8287 -26.4283 -8.9683 9.4707 -3.2102 -5.6572 20.3822 0 0 14.0175 26.3616 -34.4945 -0.2288 4.8181 -10.3526 -6.1640 13.8840 0 0.2000 22.8039 21.7508 -42.6276 6.4478 3.8223 -11.8554 -4.6861 9.4931 0

0.0796 26.5998 14.6786 -45.7149 13.3037 6.5708 -12.1263 1.0773 6.5576 0 -0.6911 28.0293 4.3860 -40.7207 18.5744 6.9084 -10.9551 10.9155 0 0 -1.6788 29.5685 -5.4690 -31.3191 19.1148 5.7901 -9.7906 19.3258 0 0 -0.7661 29.5497 -16.1208 -19.0149 15.5860 2.9450 -6.8450 22.1808 0 0 Columns 11 through 20

0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 Columns 21 through 30

0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 Columns 31 through 40

0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 Columns 41 through 50

0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0

0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 Columns 51 through 60

0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 （2）程序运行曲线：

Fig.1(1) Input Signal of M Series

(2) Stochastic Noises v

Fig.2 Parameter Identification With Recursive Least Squares Method

Fig.3 Identification Error

Fig.4 Responses

第二次作业

2、白噪声和有色噪声的区别是什么？

答：白噪声是指功率谱密度在整个频域内均匀分布的噪声，是所有频率具有相同能量的随机噪声。白噪声包含任何噪声。白噪声过程是均值为零，谱密度为非零常数的平稳随机过程，是由一系列不相关的随机变量组成的一种理想化随机过程，没有记忆性，t 时刻的数值与t 时刻以前的过去值无关，也不影响t 时刻以后的将来值。在数学上的描述为：如果随机过程ω(t)的自相关函数为

)()(2τδστω=R ，则称该随机过程为白噪声过程。白噪声过程ω(t)的谱密度为常数2σ，即∞<<-∞=ωσωω,)(2S 。

有色噪声是指任意一个具有非白色频谱的宽带噪声，噪声序列中每一时刻的噪声和另一时刻的噪声是相关的。其功率谱密度函数不平坦，即其功率谱密度函数不为常数，有色噪声并不具有上述白噪声所具有的性质。

3、极大似然参数估计与最小二乘估计主要区别是什么？答：（1）最小二乘估计是采用取极小值的方法。

系统输入输出的表达式为)()()(k e k k z T +=θh ，其中h 为样本集合，θ为被辨识的参数集合。

???????=-?---?--=T n n T

b a b a b b b a a a n k u k u n k z k z k ]

,,,,,,,[)](,),1(),(,),1([)(2121θh 取准则函数∑∑∞

=∞

=-==1

])()([)]([)(k T k k k z k e J θh θ，使min )(=θJ 的估计值记作

LS ^

θ，称作参数θ的最小二乘估计。

（2）极大似然估计是采用取极大值的方法。

其原理可表述成：

0])|([

^=??T L L M z L θθθ或0])|(ln [^

=??T

L L

M z L θθ

式中，)|(ln θL z L ML ^

θ称作极大似然参数估计值，使似然函数或对数似然函数达到最大值。

（3）数据长度L 充分大时，参数θ的极大似然估计等价于最小二乘估计。

4、极大似然法辨识方法

系统模型与图 5.5相类似，被辨识系统中参数的真值为:a1=-1.6, a2=1.0, b1=1.2, b2=0.9, d1=-0.6, d2=0.2, 试用DFP 变尺度法对系统的参数进行辨识，打印出辨识结果。

解：在程序中，)(?k θ用‘o ’和‘o1’表示；令)1,0(,)(==i Pi k P ；K k K =)(；

产生M 序列时，a(i)，b(i)，c(i)，d(i)表示四级移位寄存器的第1，2，3，4级寄存器的输出。程序如下：

clear

a(1)=1;b(1)=0;c(1)=1;d(1)=0;u(1)=d(1);z(1)=0;z(2)=0; for i=2:1200 a(i)=xor(c(i-1),d(i-1));

c(i)=b(i-1);

d(i)=c(i-1);

u(i)=d(i);

end

v=randn(1200,1);

V=0;

for i=1:1200

V=V+v(i)*v(i);

end

V1=V/1200;

for k=3:1200

z(k)=1.6*z(k-1)-1.0*z(k-2)+1.2*u(k-1)+0.9*u(k-2)+v(k)-0.6*v(k-1)+0.2*v(k-2); end

o1=0.001*ones(6,1);p0=eye(6,6);

zf(1)=0.1;zf(2)=0.1;vf(2)=0.1;vf(1)=0.1;uf(2)=0.1;uf(1)=0.1;

hf=[0.1;0.1;0;0;0.2;0.1];

for k=3:1200

h=[-z(k-1);-z(k-2);u(k-1);u(k-2);v(k-1);v(k-2)];

%hf=h;

K=p0*hf*inv(hf'*p0*hf+1);

p=[eye(6,6)-K*hf']*p0;

v(k)=z(k)-h'*o1;

o=o1+K*v(k) ;

p0=p;

o1=o;

a1(k)=o(1);

a2(k)=o(2);

b1(k)=o(3);

b2(k)=o(4);

d2(k)=o(6);

e1(k)=abs(a1(k)+1.2);

e2(k)=abs(a2(k)-0.6);

e3(k)=abs(b1(k)-1.0);

e4(k)=abs(b2(k)-0.5);

e5(k)=abs(d1(k)+1.0);

e6(k)=abs(d2(k)-0.2);

zf(k)=z(k)-d1(k)*zf(k-1)-d2(k)*zf(k-2);

uf(k)=u(k)-d1(k)*uf(k-1)-d2(k)*uf(k-2);

vf(k)=v(k)-d1(k)*vf(k-1)-d2(k)*vf(k-2);

hf=[-zf(k-1);-zf(k-2);uf(k-1);uf(k-2);vf(k-1);vf(k-2)]; end

%绘图

subplot(4,1,1)

k=1:1200;

plot(k,a1,'k:',k,a2,'b',k,b1,'r',k,b2,'m:',k,d1,'g',k,d2,'k');

xlabel('k')

ylabel('parameter')

legend('a1=-1.6,','a2=1.0','b1=1.2','b2=0.9','d1=-0.6','d2=0.2'); title('The parameter idendification of the RML');

end

subplot(4,1,2)

k=1:1200;

plot(k,e1,'k',k,e2,'b',k,e3,'r',k,e4,'m',k,e5,'g',k,e6,'k');

xlabel('k'); ylabel('error');

end

subplot(4,1,3)

k=1:1200;

plot(k,u);

xlabel('k'); ylabel('input');

end

subplot(4,1,4)

k=1:1200;

plot(k,v);

xlabel('k'); ylabel('random noise');

end

（1）程序运行结果：

o1 =

-1.6028

1.0041

2.7757

0.1792

-0.9612

0.6057

V1 =

0.9751

（2）程序运行曲线：

图3 RML辨识参数曲线

白噪声与高白区别

白噪声、高斯色噪声、高斯白噪声白噪声，就是说功率谱为一常数；也就是说，其协方差函数在delay=0时不为0，在delay不等于0时值为零；换句话说，样本点互不相关。（条件：零均值。）所以，“白”与“不白”是和分布没有关系的。当随机的从高斯分布中获取采样值时，采样点所组成的随机过程就是“高斯白噪声”；同理，当随机的从均匀分布中获取采样值时，采样点所组成的随机过程就是“均匀白噪声”。那么，是否有“非白的高斯”噪声呢？答案是肯定的，这就是”高斯色噪声“。这种噪声其分布是高斯的，但是它的频谱不是一个常数，或者说，对高斯信号采样的时候不是随机采样的，而是按照某种规律来采样的。仿真时经常采用高斯白噪声是因为实际系统（包括雷达和通信系统等大多数电子系统）中的主要噪声来源是热噪声，而热噪声是典型的高斯白噪声，高斯噪声下的理想系统都是线性系统。

相关讨论： 1、白噪声是指功率谱在整个频域内为常数的噪声，其付氏反变换是单位冲击函数的n倍（n取决于功率谱的大小），说明噪声自相关函数在t=0时不为零，其他时刻都为0，自相关性最强。高斯噪声是一种随机噪声，其幅度的统计规律服从高斯分布。高斯白噪声是幅度统计规律服从高斯分布而功率谱为常数的噪声如果在系统通带内功率谱为常数，成为带限白噪声“高斯”与“白”没有直接关系，有时人们还会提出高斯型噪声，这指的是噪声功率谱呈高斯分布函数的形状而已。 2、有一个问题我想提出来：连续白噪声和离散白噪声序列的关系是什么？它们之间不应该是简单的采样关系。因为连续白噪声的功率谱在整个频率轴上为常数，按照随机信号采样定理，对这样的信号采样，采样后的序列的功率谱必然发生混叠，而且混叠过后的功率谱是什么？应该是在整个频率轴上都为无穷大。这显然不满足离散白噪声序列的定义。那离散白噪声序列跟连续白噪声有何关系？我觉得是对带限的连续白噪声进行采样后得到的，这个带限的连续白噪声信号的带宽刚好满足Nyquist抽样定理。这样采样过后的信号的功率谱就能满足定义了。答：连续白噪声是离散白噪声在采样间隔趋近于零的极限。对带限的连续白噪声按照Nyquist采样定理进行采样就得到信息不损失的白噪声序列，当连续白噪声的带宽趋近于无穷大时，采样率也趋近于无穷大（采样间隔趋近于零），此时不会发生频谱混叠。用极限的概念理解二者的关系就很清楚了。需要说明的是，任何实际系统都是工作于一定频带范围内的，带宽为无穷大的信号仅仅存在于理论分析中，在实际系统中找不到。 3、对随机信号而言也有采样定理，这个采样定理是针对功率谱而言的。具体的证明可以参看陆大金老师的随机过程教材。（清华的博士入学考试指定的参考教材） 4、对于不限带的白噪声，已经分析的比较清楚了。而对于限带白噪声，我认为既然考虑采样定理，那么连续的限带白噪声可以利用采样函数作为正交基的系数来表示，这些系数就是对应的噪声采样值，这个过程

系统辨识最小二乘Matlab仿真

系统辨识和最小二乘参数估计Matlab仿真一、系统辨识在控制系统的分析中，首先要建立系统的数学模型，控制系统的数学模型是定量描述系统或过程内部物理量（或变量）之间关系的数学表达式。一般来说，建立控制系统数学模型有两种基本方法：（1）机理建模（白箱模型）：即根据系统内在运行机制、物料和能量守恒等物理学、化学规律建立系统的数学模型，一般步骤如下： Step1：根据系统工作原理及其在控制系统中的作用，确定输入和输出； Step2：根据物料和能量守恒等关系列写基本方程式； Step3：消去中间量； Step4：获得系统模型；（2）实验法建模（黑箱模型）：即对于机理尚不清楚或机理过于复杂的系统，可以人为的对其施加某种测试信号，并记录其输出响应，或者记录正常运行时的输入输出数据，然后利用这些输入输出数据确定系统模型结构和参数。多年来，系统辨识已经发展为一门独立学科分支，通过系统辨识建立一个对象的数学模型，通常包括两方面的工作：一是模型结构的确定（模型的类型、阶次），二是模型参数估计。根据时间是否连续，参数模型又可以分为连续时间系统模型和离散时间系统参数模型，这两类模型均可采用输入输出模型和状态空间模型描述，离散系统采用差分方程描述，以单输入单输出（SISO）离散系统参数模型为例。 1.确定性模型 SISO系统确定性模型可表示为： u(k)和y(k)分别为输入和输出，d为纯延时。 2.随机性模型如果受到随机扰动，则式子可写为：为系统随机扰动，其结构如图：

系统辨识的一般步骤如图：从图中可以看出，利用辨识的方法建立系统数学模型，从实验设计到模型获得，需要这些步骤。二、最小二乘参数估计 1.批处理最小二乘考虑以下CAR模型：

高斯白噪声与高斯噪声的相关概念

高斯噪声是一种随机噪声，在任选瞬时中任取n个，其值按n个变数的高斯概率定律分布。注： 1,高斯噪声完全由其时变平均值和两瞬时的协方差函数来确定，若噪声为平稳的，则平均值与时间无关，而协方差函数则变成仅和所考虑的两瞬时之差有关的相关函数，它在意义上等效于功率谱密度。 2,高斯噪声可以是大量独立的脉冲所产生的，从而在任何有限时间间隔内，这些脉冲中的每一个脉冲值与所有脉冲值的总和相比都可忽略不计。 3,实际上热噪声、散弹噪声及量子噪声都是高斯噪声。白噪声是一种功率频谱密度为常数的随机信号或随机过程。换句话说，此信号在各个频段上的功率是一样的，由于白光是由各种频率（颜色）的单色光混合而成，因而此信号的这种具有平坦功率谱的性质被称作是“白色的”，此信号也因此被称作白噪声。相对的，其他不具有这一性质的噪声信号被称为有色噪声（功率谱密度随频率变化）。理想的白噪声具有无限带宽，因而其能量是无限大，这在现实世界是不可能存在的。实际上，我们常常将有限带宽的平整讯号视为白噪音，因为这让我们在数学分析上更加方便。然而，白噪声在数学处理上比较方便，因此它是系统分析的有力工具。一般，只要一个噪声过程所具有的频谱宽度远远大于它所作用系统的带宽，并且在该带宽中其频谱密度基本上可以作为常数来考虑，就可以把它作为白噪声来处理。例如，热噪声和散弹噪声在很宽的频率范围内具有均匀的功率谱密度，通常可以认为它们是白噪声。白噪声的功率谱密度是一个常数。这是因为：白噪声的时域信号中任意两个不同时刻是不相关的，因此，白噪声的自相关函数为冲击函数，因此，白噪声的功率谱密度为常数。（自相关函数和功率谱密度是傅立叶变换对）。当随机的从高斯分布中获取采样值时，采样点所组成的随机过程就是“高斯白噪声”；同理，当随机的从均匀分布中获取采样值时，采样点所组成的随机过程就是“均匀白噪声”。 “非白的高斯”噪声——高斯色噪声。这种噪声其分布是高斯的，但是它的频谱不是一个常数，或者说，对高斯信号采样的时候不是随机采样的，而是按照某种规律来采样的。仿真时经常采用高斯白噪声是因为实际系统（包括雷达和通信系统等大多数电子系统）中的主要噪声来源是热噪声，而热噪声是典型的高斯白噪声，高斯噪声下的理想系统都是线性系统。高斯白噪声：如果一个噪声，它的幅度分布服从高斯分布，而它的功率谱密度又是均匀分布的，则称它为高斯白噪声。热噪声和散粒噪声是高斯白噪声。所谓高斯白噪声中的高斯是指概率分布是正态函数，而白噪声是指它的二阶矩不相关，一阶矩为常数，是指先后信号在时间上的相关性。这是考查一个信号的两个不同方面的问题。

系统辨识最小二乘参数估计matlab

最小二乘参数估计摘要：最小二乘的一次性完成辨识算法（也称批处理算法），他的特点是直接利用已经获得的所有（一批）观测数据进行运算处理。这种算法在使用时，占用内存大，离线辨识，观测被辨识对象获得的新数据往往是逐次补充到观测数据集合中去的。在应用一次完成算法时，如果要求在每次新增观测数据后，接着就估计出系统模型的参数，则需要每次新增数据后要重新求解矩阵方程()Z l T l l T l ΦΦΦ-∧=1θ。最小二乘辩识方法在系统辩识领域中先应用上已相当普及，方法上相当完善，可以有效的用于系统的状态估计，参数估计以及自适应控制及其他方面。关键词：最小二乘（Least-squares ），系统辨识（System Identification ）目录： 1.目的 (1) 2.设备 (1) 3引言 (1) 3.1 课题背景 (1) 4数学模型的结构辨识 (2) 5 程序 (3) 5.1 M 序列子函数 ................................................................................. 错误！未定义书签。 5.2主程序............................................................................................... 错误！未定义书签。 6实验结果： ................................................................................................................................... 3 7参考文献： ................................................................................................. 错误！未定义书签。 1.目的 1.1掌握系统辨识的理论、方法及应用 1.2熟练Matlab 下最小二乘法编程 1.3掌握M 序列产生方法 2.设备 PC 机1台（含Matlab 软件） 3引言 3.1 课题背景最小二乘理论是有高斯（K.F.Gauss ）在1795年提出：“未知量的最大可能值是这样一个数值，它使各次实际观测值和计算值之间的差值的平方乘以度量其精度的数值以后的和最小。”这就是最小二乘法的最早思想。最小二乘辨识方法提供一个估算方法，使之能得到一个在最小方差意义上与实验数据最

最小二乘法在系统辨识中的应用

最小二乘法在系统辨识中的应用王文进控制科学与控制工程学院控制理论与控制工程专业 2009010211 摘要：在实际的工程中，经常要对一个系统建立数学模型。很多时候，要面对一个未知的系统，对于这些未知系统，我们所知道的仅仅是它们的一些输入输出数据，我们要根据这些测量的输入输出数据，建立系统的数学模型。由此诞生了系统辨识这门科学，系统辨识就是研究怎样利用对未知系统的输入输出数据建立描述系统的数学模型的科学。系统辨识在工程中的应用非常广泛，系统辨识的方法有很多种，最小二乘法是一种应用及其广泛的系统辨识方法。本文主要讲述了最小二乘估计在系统辨识中的应用。首先，为了便于介绍，用一个最基本的单输入单输出模型来引入系统辨识中的最小二乘估计。例如：y = ax + （1）其中：y、x 可测，为不可测的干扰项，a未知参数。通过N 次实验，得到测量数据y k和x k ，其中k=1、2、3、…，我们所需要做的就是通过这N次实验得到的数据，来确定未知参数a 。在忽略不可测干扰项的前提下，基本的思想就是要使观测点y k和由式（1）确定的估计点y的差的平方和达到最小。用公式表达出来就是要使J最小：确定未知参数a的具体方法就是令： J a = 0 , 导出 a 通过上面最基本的单输入单输出模型，我们对系统辨识中的最小二乘法有了初步的了解，但在实际的工程中，系统一般为多输入系统，下面就用一个实际的例子来分析。在接下来的表述中，为了便于区分，向量均用带下划线的字母表示。水泥在凝固过程中，由于发生了一系列的化学反应，会释放出一定的热量。若水泥成分及其组成比例不同，释放的热量也会不同。水泥凝固放热量与水泥成分的关系模型如下： y = a0+ a1x1+…+ a n x n + 其中，y为水泥凝固时的放热量（卡/克）；x1~x2为水泥的几种成分。

高斯白噪声

一、概念英文名称：white Gaussian noise; WGN 定义：均匀分布于给定频带上的高斯噪声；所谓高斯白噪声中的高斯是指概率分布是正态函数，而白噪声是指它的二阶矩不相关，一阶矩为常数，是指先后信号在时间上的相关性。这是考察一个信号的两个不同方面的问题。高斯白噪声：如果一个噪声，它的幅度服从高斯分布，而它的功率谱密度又是均匀分布的，则称它为高斯白噪声。热噪声和散粒噪声是高斯白噪声。二、matlab举例 Matlab有两个函数可以产生高斯白噪声，wgn( )和awgn( )。 1. WGN：产生高斯白噪声 y = wgn(m,n,p) y = wgn(m,n,p) %产生一个m行n列的高斯白噪声的矩阵，p以dBW为单位指定输出噪声的强度。 y = wgn(m,n,p,imp) y = wgn(m,n,p,imp) %以欧姆(Ohm)为单位指定负载阻抗。 y = wgn(m,n,p,imp,state) y = wgn(m,n,p,imp,state) %重置RANDN的状态。 2. AWGN：在某一信号中加入高斯白噪声 y = awgn(x,SNR) y = awgn(x,SNR) %在信号x中加入高斯白噪声。信噪比SNR以dB为单位。x的强度假定为0dBW。如果x是复数，就加入复噪声。 clear,clc; N=0:1000; fs=1024; t=N./fs; y=3*sin(2*pi*t); x=wgn(1,1001,2); i=y+x; % i=awgn(y,2); subplot(3,1,1),plot(x); subplot(3,1,2),plot(y); subplot(3,1,3),plot(i);

用matlab实现最小二乘递推算法辨识系统参数

用matlab实现最小二乘递推算法辨识系统参数自动化系统仿真实验室指导教师：学生姓名班级计082-2 班学号撰写时间：全文结束》》-3-1 成绩评定：一．设计目的 1、学会用Matlab实现最小二乘法辨识系统参数。 2、进一步熟悉Matlab的界面及基本操作； 3、了解并掌握Matlab中一些函数的作用与使用；二．设计要求最小二乘递推算法辨识系统参数，利用matlab编程实现，设初始参数为零。z(k)-1、5*z(k-1)+0、7*z(k-2)=1*u(k-1)+0、5*u(k-2)+v(k); 选择如下形式的辨识模型：z(k)+a1*z(k- 1)+a2*z(k-2)=b1*u(k-1)+b2*u(k-2)+v(k);三．实验程序 m=3;N=100;uk=rand(1,N);for i=1:Nuk(i)=uk(i)*(-1)^(i-1);endyk=zeros(1,N); for k=3:N yk(k)=1、5*yk(k-1)-0、 7*yk(k-2)+uk(k-1)+0、5*uk(k-2); end%j=100;kn=0;%y=yk(m:j);%psi=[yk(m-1:j-1);yk(m-2:j-2);uk(m-1:j-1);uk(m-2:j- 2)];%pn=inv(psi*psi);%theta=(inv(psi*psi)*psi*y);theta=[0 ;0;0;0];pn=10^6*eye(4);for t=3:Nps=([yk(t-1);yk(t-

2);uk(t-1);uk(t-2)]);pn=pn- pn*ps*ps*pn*(inv(1+ps*pn*ps));theta=theta+pn*ps*(yk(t)-ps*theta);thet=theta;a1=thet(1);a2=thet(2);b1=thet(3);b2= thet(4); a1t(t)=a1;a2t(t)=a2;b1t(t)=b1;b2t(t)=b2;endt=1:N;plot(t,a 1t(t),t,a2t(t),t,b1t(t),t,b2t(t));text(20,1、 47,a1);text(20,-0、67,a2);text(20,0、97,b1);text(20,0、47,b2);四．设计实验结果及分析实验结果图：仿真结果表明，大约递推到第步时，参数辨识的结果基本到稳态状态，即a1=1、5999，b1=1，c1=0、5，d1=-0、7。五、设计感受这周的课程设计告一段落了，时间短暂，意义重大。通过这次次练习的机会，重新把matlab课本看了一遍，另外学习了系统辨识的有关内容，收获颇丰。对matlab的使用更加纯熟，也锻炼了自己在课本中搜索信息和知识的能力。在设计过程中虽然遇到了一些问题，但经过一次又一次的思考，一遍又一遍的检查终于找出了原因所在，也暴露出了前期我在这方面的知识欠缺和经验不足。同时我也进一步认识了matlab软件强大的功能。在以后的学习和工作中必定有很大的用处。

系统辨识-最小二乘法MATLAB仿真

《系统辨识》基于MATLAB的最小二乘法（一阶）的仿真 clc clear % ①白噪声的生成过程如下：e=randn(1,500); e=e/std(e); e=e-mean(e); A=0; %白噪声的均值为0 B=sqrt(0.1); %白噪声的方差为0.1 e=A+B*e; %绘制白噪声图 k=1:500; subplot(4,1,1) %画四行一列图形窗口中的第一个图形 plot(k,e,'r'); xlabel('k'), ylabel('e');title('(0,1)均匀分布的随机序列') % ②生成M序列的过程如下：X1=1;X2=0;X3=1;X4=0; %移位寄存器输入Xi初始状态（0101）， Yi寄存器的各级输出 m=500; %M序列的总长度 for i=1:m Y4=X4; Y3=X3; Y2=X2; Y1=X1; X4=Y3; X3=Y2; X2=Y1; X1=xor(Y3,Y4); %异或运算 if Y4==0 U(i)=-1; else U(i)=Y4; end end M=U; u=U; %绘制M序列图? i1=i k=1:1:i1; subplot(4,1,2) %画四行一列图形窗口中的第二个图形 plot(k,U,k,U,'rx') stem(M) xlabel('k') ylabel('M序列') title('移位寄存器产生的M序列') % ③参数估计的过程如下： %绘制参数估计的相关图形 z=zeros(1,500); %定义输出观测值的长度 for k=2:500 z(k)=0.9*z(k-1)+u(k-1)+e(k);%用理想输出值作为观测值 end subplot(4,1,3) %画四行一列图形窗口中的第三个图形 i=1:1:500; %横坐标的范围从1到500，步长为1 plot(i,z) %图形的横坐标是采样时刻i，纵坐标是输出观测值Z，图形格式为连续曲线

基于最小二乘法的系统参数辨识

基于最小二乘法的系统参数辨识吴令红，熊晓燕，张涛太原理工大学机械电子研究所，太原 (030024) E-mail lhwu0818@https://www.360docs.net/doc/7915081852.html, 摘要：系统辨识是自动控制学科的一个重要分支，由于其特殊作用，已经广泛应用于各种领域，尤其是复杂系统或参数不容易确定的系统的建模。过去，系统辨识主要用于线性系统的建模，经过多年的研究，已经形成成熟的理论。但随着社会、科学的发展，非线性系统越来越受到人们的关注，其控制与模型之间的矛盾越来越明显，因而非线性系统的辨识问题也越来越受到重视，其辨识理论不断发展和完善本。文重点介绍了系统参数辨识中最小二乘法的基本原理，并通过悬臂梁模型的辨识实例，具体说明了基于最小二乘法参数辨识在Matlab 中的实现方法。结果表明基于最小二乘法具有算法简单、精度较高等优点。关键词：系统辨识；参数辨识；滑动平均模型(ARX)；最小二乘法；Matlab 中图分类号：TH-9 1. 引言所谓辨识就是通过测取研究对象在人为输入作用下的输出响应，或正常运行时的输入输出数据记录，加以必要的数据处理和数学计算，估计出对象的数学模型。这是因为对象的动态特性被认为必然表现在它的变化着的输入输出数据之中，辨识只不过是利用数学的方法从数据序列中提炼出对象的数学模型而已[1]。最小二乘法是系统参数辨识中最基本最常用的方法。最小二乘法因其算法简单、理论成熟和通用性强而广泛应用于系统参数辨识中。本文基于悬臂梁的实测数据，介绍了最小二乘法的参数辨识在Matlab中的实现。 2. 系统辨识一般而言，建立系统的数学模型有两种方法：激励分析法和系统辨识法。前者是按照系统所遵循的物化（或社会、经济等）规律分析推导出模型。后者则是从实际系统运行和实验数据处理获得模型。如图1所示，系统辨识就是从系统的输入输出数据测算系统数学模型的理论和方法。更进一步的定义是L.A.Zadeh曾经与1962年给出的，即“系统辨识是在输入和输出的基础上，从系统的一类系统范围内，确立一个与所实验系统等价的系统”。另外，系统辨识还应该具有3个基本要素，即模型类、数据和准则[5]。被辨识系统模型根据模型形式可分为参数模型和非参数模型两大类。所谓参数模型是指微分方程、差分方程、状态方程等形式的数学模型；而非参数模型是指频率响应、脉冲响应、传递函数等隐含参数的数学模型。在辨识工程中，模型的确定主要根据经验对实际对象的特性进行一定程度上的假设，如对象的模型是线性的还是非线性的、是参数模型还是非参数模型等。在模型确定之后，就可以根据对象的输入输出数据，按照一定的辨识算法确定模型的参数[4]。 y 图1 被研究的动态系统

系统辨识之最小二乘法

方法一、最小二乘一次性算法：首先对最小二乘法的一次性辨识算法做简要介绍如下：过程的黑箱模型如图所示：其中u(k)和z(k)分别是过程的输入输出，)(1-z G 描述输入输出关系的模型，成为过程模型。过程的输入输出关系可以描述成以下最小二乘格式： )()()(k n k h k z T +=θ （1）其中z(k)为系统输出，θ是待辨识的参数，h(k)是观测数据向量，n(k) 是均值为0的随机噪声。利用数据序列{z （k ）}和{h （k ）}极小化下列准则函数： ∑=-=L k T k h k z J 12])()([)(θθ （2）使J 最小的θ的估计值^ θ，成为最小二乘估计值。具体的对于时不变SISO 动态过程的数学模型为 )()()()()(11k n k u z B k z z A +=-- （3）应该利用过程的输入、输出数据确定)(1-z A 和 )(1-Z B 的系数。对于求解θ的估计值^θ，一般对模型的阶次 a n ， b n 已定，且b a n n >；其次将（3）模型写成最小二乘格式 )()()(k n k h k z T +=θ （4）式中 ?????=------=T n n T b a b a b b b a a a n k u k u n k z k z k h ],,,,,,,[)](,),1(),(,),1([)(2121 θ （5）

L k ,,2,1 = 因此结合式（4）（5）可以得到一个线性方程组 L L L n H Z +=θ （6）其中 ???==T L T L L n n n n L z z z z )](),2(),1([)](),2(),1([ （7）对此可以分析得出，L H 矩阵的行数为),max(b a n n L -，列数b a n n +。在过程的输入为2n 阶次，噪声为方差为1，均值为0的随机序列，数据长度)(b a n n L +>的情况下，取加权矩阵L Λ为正定的单位矩阵I ，可以得出： L T L L T L z H H H 1^ )(-=θ （8）其次，利用在Matlab 中编写M 文件，实现上述算法。此次算法的实现，采用6阶M 序作为过程黑箱的输入；噪声采用方差为1，均值为0的随机数序列；黑箱模型假设为：y(k)-1.5y(k-1)+0.7y(k-2)=2u(k-1)+0.5u(k-2)，则系统输出为Z(k)-1.5Z(k-1)+0.7Z(k-2)=2U(k-1)+0.5U(k-2)+n （k ）；模型的阶次2,2==b a n n ；数据长度取L=200。程序清单如下见附录：最小二乘一次性算法Matlab 程序运行结果如下：图1 最小二乘一次性算法参数真值与估计值其中re 为真值，ans 为估计值^ θ 结果发现辨识出的参数与真值之间存在细微误差，这是由于系统噪声以及数据长度L 的限制引起的，最小二乘辨识法是一种无偏估计方法。方法二、最小二乘递推算法：最小二乘一次性算法计算量大，并且浪费存储空间，不利于在线应用，由此引出最小

基于最小二乘法的系统辨识的设计与开发(整理版)

---------------------------------------------------------------最新资料推荐------------------------------------------------------ 基于最小二乘法的系统辨识的设计与开发（整理版）课程（论文）题目：基于最小二乘法的系统辨识摘要：最小二乘法是一种经典的数据处理方法。最小二乘的一次性完成辨识算法（也称批处理算法），他的特点是直接利用已经获得的所有（一批）观测数据进行运算处理。在系统辨识领域中, 最小二乘法是一种得到广泛应用的估计方法, 可用于动态系统, 静态系统, 线性系统, 非线性系统。在随机的环境下，利用最小二乘法时，并不要求观测数据提供其概率统计方面的信息，而其估计结果，却有相当好的统计特性。关键词：最小二乘法；系统辨识；参数估计 1 引言最小二乘理论是有高斯（ K.F.Gauss）在 1795 年提出：未知量的最大可能值是这样一个数值，它使各次实际观测值和计算值之间的差值的平方乘以度量其精度的数值以后的和最小。这就是最小二乘法的最早思想。最小二乘辨识方法提供一个估算方法，使之能得到一个在最小方差意义上与实验数据最好拟合的数学模型。递推最小二乘法是在最小二乘法得到的观测数据的基础上，用新引入的数据对上一次估计的结果进行修正递推出下一个参数估计值，直到估计值达到满意的精确度为止。 1 / 10

对工程实践中测得的数据进行理论分析，用恰当的函数去模拟数据原型是一类十分重要的问题，最常用的逼近原则是让实测数据和估计数据之间的距离平方和最小，这即是最小二乘法。最小二乘法是一种经典的数据处理方法。在随机的环境下，利用最小二乘法时，并不要求观测数据提供其概率统计方面的信息，而其估计结果，却有相当好的统计特性。 2 最小二乘法的系统辨识设单输入单输出线性定常系统的差分方程为： 1),()()() 1()(01knkubkubnkxakxakxnn （ 1）上式中： )(ku为输入信号；)(kx为理论上的输出值。 )(kx只有通过观测才能得到，在观测过程中往往附加有随机干扰。 )(kx的观测值)(ky可表示为（ 2）将式（ 2）代入式（ 1）得 1()()() 1()(101kubkubnkyakyakyn (3) 我们可能不知道)(kn的统计特性，在这种情况下，往往把)(kn看做均值为 0 的白噪声。设（ 4）则式（ 3）可以写成 (5) 在测量)(ku时也有测量误差，系统内部也可能有噪声，应当

系统辨识最小二乘法大作业

系统辨识最小二乘法大作业系统辨识大作业最小二乘法及其相关估值方法应用学院:自动化学院专业:信息工程学号:2007302171 姓名:马志强日期:2010.11.14 基于最小二乘法的多种系统辨识方法研究 1. 最小二乘法的引出在系统辨识中用得最广泛的估计方法是最小二乘法(LS)。设单输入-单输出线性定长系统的差分方程为 (5.1.1) 式中:为随机干扰;为理论上的输出值。只有通过观测才能得到，在观测过程中往往附加有随机干扰。的观测值可表示为

(5.1.2) 式中:为随机干扰。由式(5.1.2)得 (5.1.3) 将式(5.1.3)带入式(5.1.1)得 (5.1.4) 我们可能不知道的统计特性，在这种情况下，往往把看做均值为0的白噪声。设 (5.1.5) 则式(5.1.4)可写成 (5.1.6) 在观测时也有测量误差，系统内部也可能有噪声，应当考虑它们的影响。因此假定不仅包含了的测量误差，而且包含了的测量误差和系统内部噪声。假定是不相关随机序列(实际上是相关随机序列)。现分别测出个随机输入值，则可写成个方程，即上述个方程可写成向量-矩阵形式 (5.1.7) 设则式(5.1.7)可写为 (5.1.8) 式中:为维输出向量;为维噪声向量;为维参数向量;为测量矩阵。因此式(5.1.8)是一个含有个未知参数，由个方程组成的联立方程组。如果，方程数少于未知数数目，则方程组的解是不定的，不能唯一地确定参数向量。如果，方程组正好与未知数数目相等，当噪声时，就能准确地解出 (5.1.9) 如果噪声，则

(5.1.10) 从上式可以看出噪声对参数估计是有影响的，为了尽量较小噪声对估值的影响。在给定输出向量和测量矩阵的条件下求系统参数的估值，这就是系统辨识问题。可用最小二乘法来求的估值，以下讨论最小二乘法估计。 2. 最小二乘法估计算法设表示的最优估值，表示的最优估值，则有 (5.1.11) 写出式(5.1.11)的某一行，则有 (5.1.12) 设表示与之差，即 - (5.1.13) 式中成为残差。把分别代入式(5.1.13)可得残差。设则有 (5.1.14) 最小二乘估计要求残差的平方和为最小，即按照指数函数 (5.1.15) 为最小来确定估值。求对的偏导数并令其等于0可得 (5.1.16) (5.1.17) 由式(5.1.17)可得的最小二乘估计 (5.1.18) 3.递推最小二乘法为了实现实时控制，必须采用递推算法，这种辨识方法主要用于在线辨识。设已获得的观测数据长度为，将式(5.1.8)中的和分别用来代替，即 (5.3.1) 用的最小二乘估计，则 (5.3.2)

最小二乘法

第3章线性动态模型参数辨识－最小二乘法 3.1 辨识方法分类根据不同的辨识原理，参数模型辨识方法可归纳成三类： ① 最小二乘类参数辨识方法，其基本思想是通过极小化如下准则函数来估计模型参数： min )()? (?== ∑=θ θL k k J 1 2ε 其中)(k ε代表模型输出与系统输出的偏差。典型的方法有最小二乘法、增广最小二乘法、辅助变量法、广义最小二乘法等。 ② 梯度校正参数辨识方法，其基本思想是沿着准则函数负梯度方向逐步修正模型参数，使准则函数达到最小，如随机逼近法。 ③ 概率密度逼近参数辨识方法，其基本思想是使输出z 的条件概率密度)|(θz p 最大限度地逼近条件0θ下的概率密度)|(0θz p ，即 )|()?|(0m a x θθz p z p ??→?。典型的方法是极大似然法。 3.2 最小二乘法的基本概念 ● 两种算法形式 ① 批处理算法：利用一批观测数据，一次计算或经反复迭代，以获得模型参数的估计值。 ② 递推算法：在上次模型参数估计值)(? 1-k θ的基础上，根据当前获得的数据提出修正，进而获得本次模型参数估计值)(? k θ，广泛采用的递推算法形式为 () ()()()~()θθk k k k d z k =-+-1K h 其中)(? k θ表示k 时刻的模型参数估计值，K (k )为算法的增益，h (k -d ) 是由观测数据组成的输入数据向量，d 为整数，)(~k z 表示新息。 ● 最小二乘原理

定义：设一个随机序列)},,,(),({L k k z 21∈的均值是参数θ 的线性函数 E{()}()T z k k θ=h 其中h (k )是可测的数据向量，那么利用随机序列的一个实现，使准则函数 21 ()[()()]L T k J z k k θθ==-∑h 达到极小的参数估计值θ? 称作θ的最小二乘估计。 ● 最小二乘原理表明，未知参数估计问题，就是求参数估计值θ? ，使序列的估计值尽可能地接近实际序列，两者的接近程度用实际序列与序列估计值之差的平方和来度量。 ● 如果系统的输入输出关系可以描述成如下的最小二乘格式 ()()()T z k k e k θ=+h 式中z (k )为模型输出变量，h (k )为输入数据向量，θ为模型参数向量，e (k )为零均值随机噪声。为了求此模型的参数估计值，可以利用上述最小二乘原理。根据观测到的已知数据序列)}({k z 和)}({k h ，极小化下列准则函数 21()[()()]L T k J z k k θθ==-∑h 即可求得模型参数的最小二乘估计值θ? 。 ● 最小二乘估计值应在观测值与估计值之累次误差的平方和达到最小值处，所得到的模型输出能最好地逼近实际系统的输出。 3.3 最小二乘问题的描述 (1) 考虑模型 )()()()()(11k e k u z B k z z A +=-- 式中u (k )和z (k ) 分别为过程的输入和输出变量，e (k )是均值为零、方差为2 n σ的随机噪声，)(1-z A 和)(1-z B 为迟延算子多项式，写成 A z a z a z a z B z b z b z b z n n n n a a b b ()()--------=++++=+++?????11122111221 (2) 假定模型阶次n a 和n b 为已知，且有b a n n ≥，也可设n n n b a ==, 并定义

(完整word版)多种最小二乘算法分析+算法特点总结

第一部分：程序设计思路、辨识结果分析和算法特点总结 (2) 一：RLS遗忘因子法 (2) RLS遗忘因子法仿真思路和辨识结果 (2) 遗忘因子法的特点： (3) 二：RFF遗忘因子递推算法 (4) 仿真思路和辨识结果 (4) 遗忘因子递推算法的特点： (5) 三：RFM限定记忆法 (5) 仿真思路和辨识结果 (5) RFM限定记忆法的特点： (7) 四：RCLS偏差补偿最小二乘法 (7) 仿真思路和辨识结果 (7) RCLS偏差补偿最小二乘递推算法的特点： (9) 五：增广最小二乘法 (9) 仿真思路和辨识结果 (9) RELS增广最小二乘递推算法的特点： (11) 六：RGLS广义最小二乘法 (12) 仿真思路和辨识结果 (12) RGLS广义最小二乘法的特点： (14) 七：RIV辅助变量法 (14) 仿真思路和辨识结果 (14) RIV辅助变量法的特点： (16) 八：Cor-ls相关最小二乘法（二步法） (17) 仿真思路和辨识结果 (17) Cor-ls相关最小二乘法（二步法）特点： (18) 九：MLS多级最小二乘法 (19) 仿真思路和辨识结果 (19) MLS多级最小二乘法的特点： (22) 十：yule_walker辨识算法 (23) 仿真思路和辨识结果 (23) yule_walker辨识算法的特点： (24) 第二部分：matlab程序 (24) 一：RLS遗忘因子算法程序 (24) 二：RFF遗忘因子递推算法 (26) 三：RFM限定记忆法 (28) 四：RCLS偏差补偿最小二乘递推算法 (31) 五：RELS增广最小二乘的递推算法 (33) 六;RGLS 广义最小二乘的递推算法 (36) 七：Tally辅助变量最小二乘的递推算法 (39) 八：Cor-ls相关最小二乘法（二步法） (42) 九：MLS多级最小二乘法 (45) 十yule_walker辨识算法 (49)

系统辨识最小二乘法大作业 (2)

系统辨识大作业最小二乘法及其相关估值方法应用学院：自动化学院学号：姓名：日期：

基于最小二乘法的多种系统辨识方法研究一、实验原理 1.最小二乘法在系统辨识中用得最广泛的估计方法是最小二乘法(LS)。设单输入-单输出线性定长系统的差分方程为 (5.1.1) 式中:为随机干扰；为理论上的输出值。只有通过观测才能得到，在观测过程中往往附加有随机干扰。的观测值可表示为 (5.1.2) 式中:为随机干扰。由式(5.1.2)得 (5.1.3) 将式(5.1.3)带入式(5.1.1)得 (5.1.4) 我们可能不知道的统计特性，在这种情况下，往往把看做均值为0的白噪声。设 (5.1.5) 则式(5.1.4)可写成 (5.1.6) 在观测时也有测量误差，系统内部也可能有噪声，应当考虑它们的影响。因此假定不仅包含了的测量误差，而且包含了的测量误差和系统内部噪声。假定是不相关随机序列(实际上是相关随机序列)。现分别测出个随机输入值，则可写成个方程，即上述个方程可写成向量-矩阵形式 (5.1.7) 设则式(5.1.7)可写为

(5.1.8) 式中：为维输出向量；为维噪声向量；为维参数向量；为测量矩阵。因此式(5.1.8)是一个含有个未知参数，由个方程组成的联立方程组。如果，方程数少于未知数数目，则方程组的解是不定的，不能唯一地确定参数向量。如果，方程组正好与未知数数目相等，当噪声时，就能准确地解出 (5.1.9) 如果噪声，则 (5.1.10) 从上式可以看出噪声对参数估计是有影响的，为了尽量较小噪声对估值的影响。在给定输出向量和测量矩阵的条件下求系统参数的估值，这就是系统辨识问题。可用最小二乘法来求的估值，以下讨论最小二乘法估计。 2.最小二乘法估计算法设表示的最优估值，表示的最优估值，则有 (5.1.11) 写出式(5.1.11)的某一行，则有 (5.1.12) 设表示与之差，即 - (5.1.13)式中成为残差。把分别代入式(5.1.13)可得残差。设则有 (5.1.14) 最小二乘估计要求残差的平方和为最小，即按照指数函数 (5.1.15) 为最小来确定估值。求对的偏导数并令其等于0可得 (5.1.16) (5.1.17)

增广最小二乘辨识白噪声和有色噪声的区别是什么

第一次作业 1、增广最小二乘辨识模型结构如下所示： ) 2()1()()2()1() 2()1()(212121-+-++-+-=-+-+k v d k v d k v k u b k u b k z a k z a k z 其中，a 1=-1.8, a 2=0.9, b 1=0.8, b 2=0.3, d 1=1, d 2=0.4。对其进行MATLAB 仿真。 N Y 停机工作间清零产生输出采样信号给被辨识参数θ和P 赋初值按照式(3.80)的第三式递推计算P (k ) 按照式(3.67)计算被辨识参数的相对变化量收敛满足要求？按照式(3.80)的第二式递推计算K (k ) 按照式(3.80)的第一式递推计算θ(k ) 用4位移位寄存器产生幅值为1的输入信号计算系统的实际输出响应及模型的响应给M 序列的长度L 赋值画出被辨识参数θ的各次估计值及其误差显示被辨识参数、辨识精度、输出采样、系统实际输出、模型输出画出系统的实际输出、输出采样及模型输出画出输入信号径线图形及随机噪声图形产生随机噪声信号图1 增广最小二乘递推算法辨识的Malab6.0程序流程图

解：增广最小二乘辨识程序： >> clear L=60; y1=1;y2=1;y3=1;y4=0; for i=1:L; x1=xor(y3,y4); x2=y1; x3=y2; x4=y3; y(i)=y4; if y(i)>0.5,u(i)=-1; else u(i)=1; end y1=x1;y2=x2;y3=x3;y4=x4; end figure(1); subplot(2,1,1); stem(u),grid on v=randn(1,60); subplot(2,1,2); plot(v),grid on; u,v %显示输入信号和噪声信号 z=zeros(7,60);zs=zeros(7,60);zm=zeros(7,60);zmd=zeros(7,60); z(2)=0; z(1)=0; zs(2)=0; zs(1)=0; zm(2)=0; zm(1)=0; zmd(2)=0; zmd(1)=0; c0=[0.1 0.1 0.1 0.1 0.1 0.1 0.1]'; + y (k ) u (k ) e (k ) z (k ) + v (k ) ) (1-z G ) (1-z N 图2 增广最小二乘法辨识实例结构图

系统辨识—最小二乘法

最小二乘法参数辨识 1 引言系统辨识是根据系统的输入输出时间函数来确定描述系统行为的数学模型。现代控制理论中的一个分支。通过辨识建立数学模型的目的是估计表征系统行为的重要参数，建立一个能模仿真实系统行为的模型，用当前可测量的系统的输入和输出预测系统输出的未来演变，以及设计控制器。对系统进行分析的主要问题是根据输入时间函数和系统的特性来确定输出信号。对系统进行控制的主要问题是根据系统的特性设计控制输入，使输出满足预先规定的要求。而系统辨识所研究的问题恰好是这些问题的逆问题。通常，预先给定一个模型类μ={M}（即给定一类已知结构的模型），一类输入信号u和等价准则J=L(y，yM)(一般情况下，J是误差函数，是过程输出y和模型输出yM的一个泛函)；然后选择使误差函数J达到最小的模型，作为辨识所要求的结果。系统辨识包括两个方面：结构辨识和参数估计。在实际的辨识过程中，随着使用的方法不同，结构辨识和参数估计这两个方面并不是截然分开的，而是可以交织在一起进行的。 2 系统辨识的目的在提出和解决一个辨识问题时，明确最终使用模型的目的是至关重要的。它对模型类（模型结构）、输入信号和等价准则的选择都有很大的影响。通过辨识建立数学模型通常有四个目的。 ①估计具有特定物理意义的参数有些表征系统行为的重要参数是难以直接测量的，例如在生理、生态、环境、经济等系统中就常有这种情况。这就需要通过能观测到的输入输出数据，用辨识的方法去估计那些参数。 ②仿真仿真的核心是要建立一个能模仿真实系统行为的模型。用于系统分析的仿真模型要求能真实反映系统的特性。用于系统设计的仿真，则强调设计参数能正确地符合它本身的物理意义。 ③预测这是辨识的一个重要应用方面，其目的是用迄今为止系统的可测量的输入和输出去预测系统输出的未来的演变。例如最常见的气象预报，洪水预报，其他如太阳黑子预报，市场价格的预测，河流污染物含量的预测等。预测模型辨识的等价准则主要是使预测误差平方和最小。只要预测误差小就是好的预测模型，对模型的结构及参数则很少再有其他要求。这时辨识的准则和模型应用的目的是一致的，因此可以得到较好的预测模型。 ④控制为了设计控制系统就需要知道描述系统动态特性的数学模型，建立这些模型的目的在于设计控制器。建立什么样的模型合适，取决于设计的方法和准备采用的控制策略。 3 系统辨识的方法经典方法：经典的系统辨识方法的发展已经比较成熟和完善，他包括阶跃响应法、脉冲

基于最小二乘法的系统参数辨识

基于最小二乘法的系统参数辨识研究生二队李英杰 082068 摘要：系统辨识是自动控制学科的一个重要分支，由于其特殊作用，已经广泛应用于各种领域，尤其是复杂系统或参数不容易确定的系统的建模。过去，系统辨识主要用于线性系统的建模，经过多年的研究，已经形成成熟的理论。但随着社会、科学的发展，非线性系统越来越受到人们的关注，其控制与模型之间的矛盾越来越明显，因而非线性系统的辨识问题也越来越受到重视，其辨识理论不断发展和完善本。文重点介绍了系统参数辨识中最小二乘法的基本原理，并通过热敏电阻阻值温度关系模型的辨识实例，具体说明了基于最小二乘法参数辨识在Matlab中的实现方法。结果表明基于最小二乘法具有算法简单、精度较高等优点。 1. 引言所谓辨识就是通过测取研究对象在人为输入作用下的输出响应，或正常运行时的输入输出数据记录，加以必要的数据处理和数学计算，估计出对象的数学模型。这是因为对象的动态特性被认为必然表现在它的变化着的输入输出数据之中，辨识只不过是利用数学的方法从数据序列中提炼出对象的数学模型而已[1]。最小二乘法是系统参数辨识中最基本最常用的方法。最小二乘法因其算法简单、理论成熟和通用性强而广泛应用于系统参数辨识中。本文基于热敏电阻阻值与温度关系数据，介绍了最小二乘法的参数辨识在Matlab中的实现。 2. 系统辨识一般而言，建立系统的数学模型有两种方法：激励分析法和系统辨识法。前者是按照系统所遵循的物化（或社会、经济等）规律分析推导出模型。后者则是从实际系统运行和实验数据处理获得模型。如图1 所示，系统辨识就是从系统的输入输出数据测算系统数学模型的理论和方法。更进一步的定义是L.A.Zadeh 曾经与1962 年给出的，即“系统辨识是在输入和输出的基础上，从系统的一类系统范围内，确立一个与所实验系统等价的系统”。另外，系统辨识还应该具有3 个基本要素，即模型类、数据和准则[5]。被辨识系统模型根据模型形式可分为参数模型和非参数模型两大类。所谓参数模型是指微分方程、差分方程、状态方程等形式的数学模型；而非参数模型是指频率响应、脉冲响应、传递函数等隐含参数的数学模型。在辨识工程中，模型的确定主要根据经验对实际对象的特性进行一定程度上的假设，如对象的模型是线性的还是非线性的、是参数模型还是非参数模型等。在模型确定之后，就可以根据对象的输入输出数据，按照一定的辨识算法确定模型的参数[4]。图1 被研究的动态系统 3. 最小二乘法（LS）参数估计方法对于参数模型辨识结构，系统辨识的任务是参数估计，即利用输入输出数据估计这些参数，建立系统的数学模型。在参数估计中最常用的是最小二乘法(LS)、