(完整版)相似三角形基本类型.doc
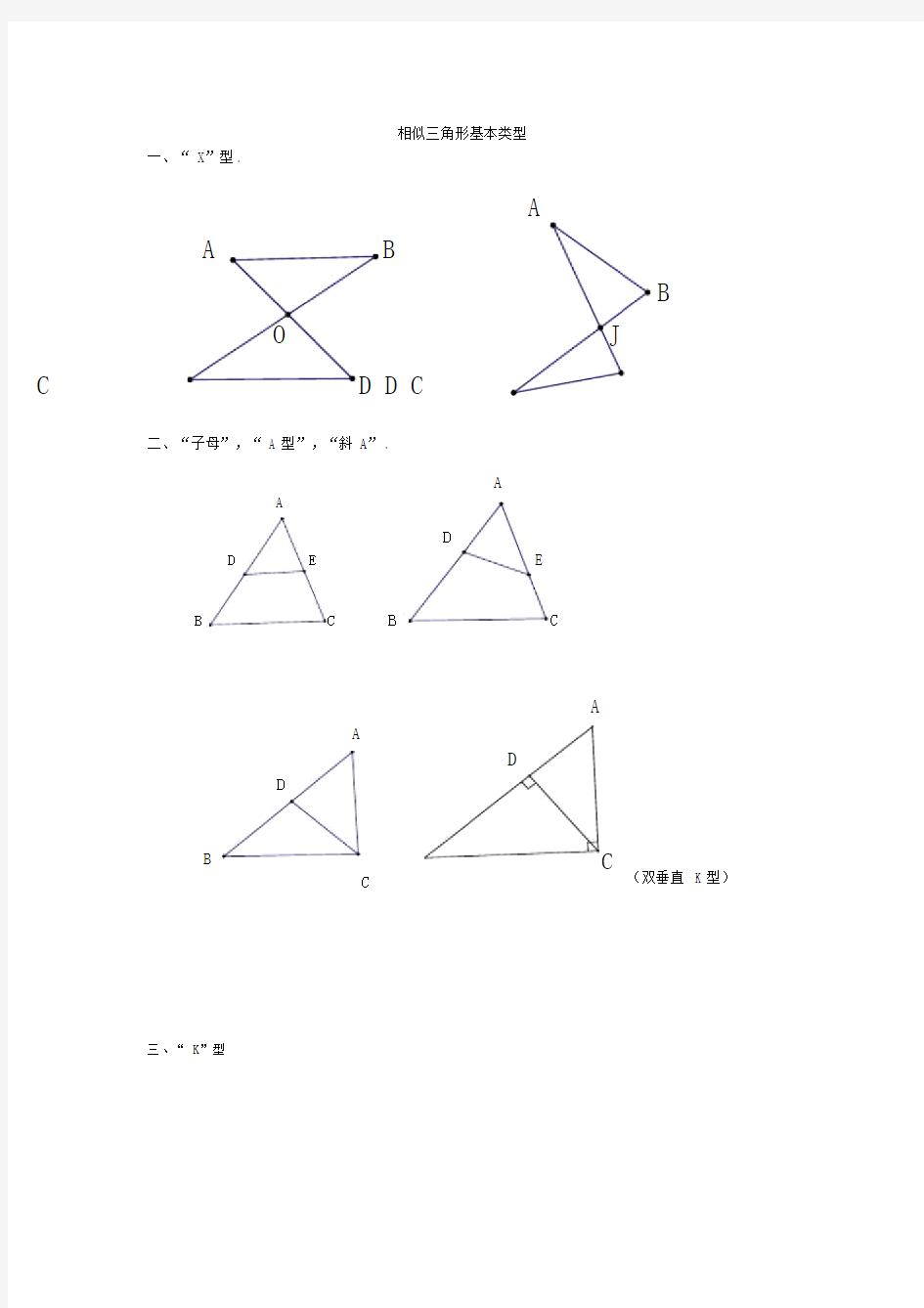
相似三角形基本类型
一、“ X”型 .
A
A B
B
O J
C D D C
二、“子母”,“ A 型”,“斜 A” .
A
A
D
D E E
B C B C
A
A
D
D
B
C C
(双垂直 K 型)
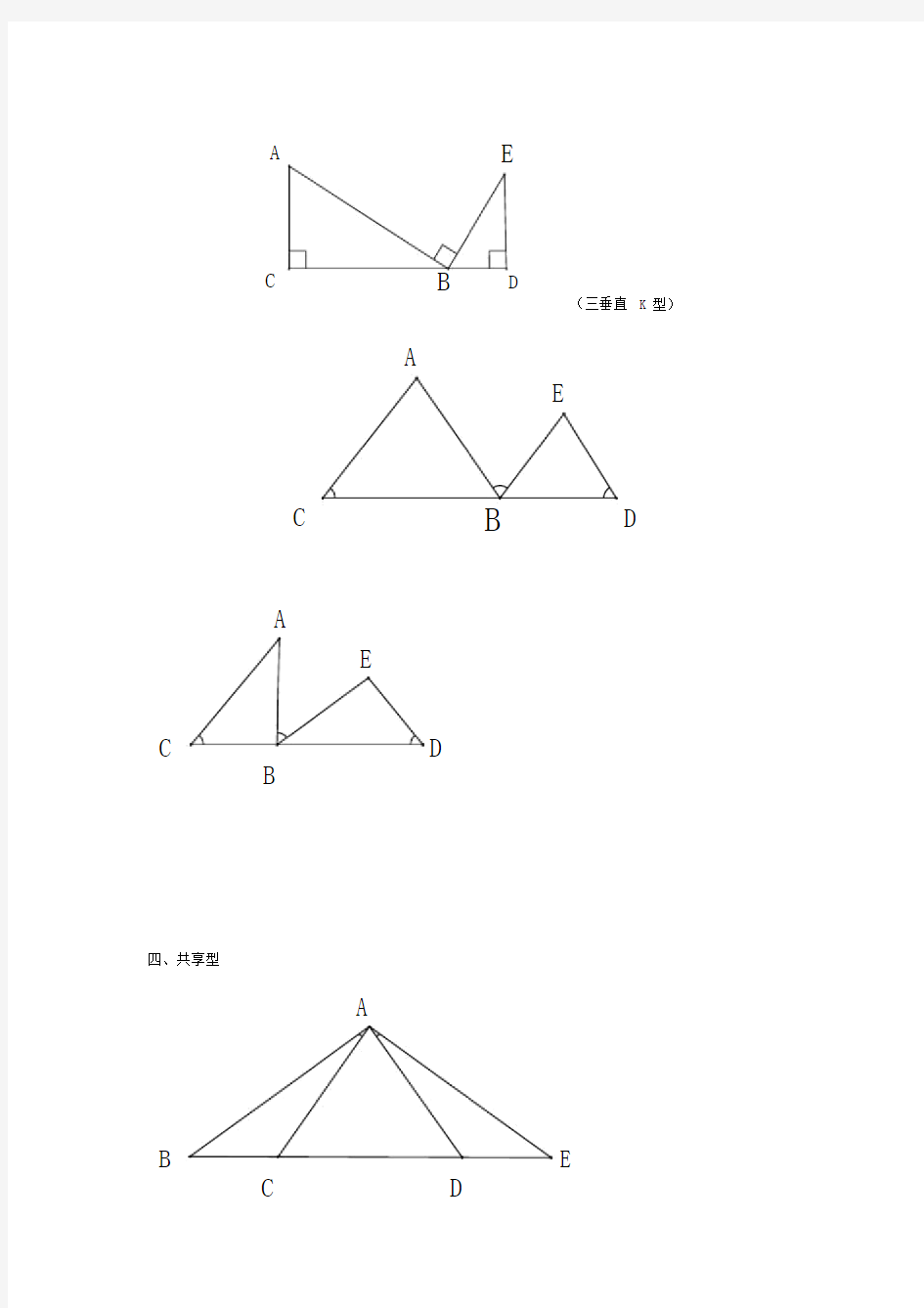
三、“ K”型
A E
C B D
(三垂直K 型)
A
E
C B D
A
E
C D
B
四、共享型
A
B E
C D
A
B C D
F E
A
E F
G
B C
A
E
D
B C
1.在△ ABC 和△ ADE中,∠ BAD=∠ CAE,∠ ABC=∠ ADE.
A
E
D
B C
1.如图,已知∠ 1=∠ 2,∠ 3=∠ 4,求证∠ ABE=∠ ACD.
A
1
2
E F 3
D B
2.
O
4
C
T E
G
F
A
B
P
3.如图,已知 C 是线段 AB 上的任意一点(端点除外),分别以AC、 BC 为斜边并且在AB 的
同一侧作等腰直角△ACD和△ BCE,连结 AE 交 CD于点 M ,连结 BD 交 CE于点 N,给出
以下三个结论:①MN ∥AB;②
1
=
1
+
1
;③ M N≤
1
AB,其中正确结论的个数MN AC BC 4
是()
A. 0B. 1C.2D.3
4.如图,Rt△AB C是由Rt△ABC绕点A顺时针旋转得到的,连结CC交斜边于点E,CC的延长线交 BB 于点 F.
(1)证明:△ACE∽△FBE;
( 2)设∠ABC= ,∠CAC = ,试探索、满足什么关系时,△ACE与△ FBE是全
等三角形,并说明理由.
B F
C'
B'
E
C A
5.
B
F
Q2
D E
C
A
6.在等边△ ABC中, D 为 BC边上一点, E 为 AC 边上一点,且∠ ADE=60°, BD=3,CE=2,则△ABC 的边长为 _________.
A
E
B D C
7. AE 900°, EDB 1 C .
2
(1)当 AB=AC时 ,①∠ EBF=_________.
②BE与 FD 数量关系 .
(2)当 AB=kAC,求BE
的值 .
FD
A A
E
E F
F
B D C
B D C
8. 如图,梯形ABCD中, AD∥BC, BC=20cm, AD= 10cm,现有两个动点P、 Q分别从 B、
D两点同时出发,点P 以每秒 2cm的速度沿BC向终点 C 移动,点Q以每秒 1cm的速度沿 DA ..
向终点 A 移动,线段 PQ与 BD相交于点 E,过 E 作 EF∥ BC交 CD于点 F,射线 QF交 BC的延长线于点 H,设动点 P、Q移动的时间为 t (单位:秒, 0 (1)当 t 为何值时,四边形 PCDQ为平行四边形? (2)在 P、 Q移动的过程中,线段 PH的长是否发生 改变?如果不变,求出线段PH的长;如果改变,请说明理由. 9.如图,在矩形ABCD中, AB=12cm ,BC= 8cm. 点 E、 F、 G 分别从点A、B、 C同时出发,沿矩形 的边按逆时针方向移动,点E、 G 的速度均为2cm/s , 点 F 的速度为 4cm/s ,当点 F 追上点 G( 即点 F 与点 G 重合 ) 时, 三个点随之停止移动.设移动开始后第ts 时,△ EFG的面积为Scm2. ( 1) 当 t=1s 时, S 的值是多少? ( 2) 写出 S 与 t 之间的函数解析式,并指出自变量t 的取值范围; C、( 3) 若点 F 在矩形的边BC上移动,当 t 为何值时,以点 B、E、F 为顶点的三角形与 以 F、 G 为顶点的三角形相似?请说明理由。 A D E G B F C 第一节:相似形与相似三角形 基本概念: 1.相似形:对应角相等,对应边成比例的两个多边形,我们称它们互为相似形。 2.相似三角形:对应角相等,对应边成比例的两个三角形,叫做相似三角形。 1.几个重要概念与性质(平行线分线段成比例定理) (1)平行线分线段成比例定理:三条平行线截两条直线,所得的对应线段成比例. 已知a ∥b ∥c, A D a B E b C F c 可得 EF BC DE AB DF EF AC BC DF EF AB BC DF DE AC AB EF DE BC AB =====或或或或 等. (2)推论:平行于三角形一边的直线截其它两边(或两边的延长线)所得的对应线段成比例. A D E B C 由DE ∥BC 可得:AC AE AB AD EA EC AD BD EC AE DB AD = ==或或.此推论较原定理应用更加广泛,条件是平行. (3)推论的逆定理:如果一条直线截三角形的两边(或两边的延长线)所得的对应线段成比例.那么这条直线平行于三角形的第三边. 此定理给出了一种证明两直线平行方法,即:利用比例式证平行线. (4)定理:平行于三角形的一边,并且和其它两边相交的直线,所截的三角形的三边与原三角形三边对应成比例. (5)①平行于三角形一边的直线和其他两边相交,所构成的三角形与原三角形相似。 ②比例线段:四条线段a ,b ,c ,d 中,如果a 与b 的比等于c 与d 的比,即b a =d c ,那么这四条线段a ,b ,c ,d 叫做成比例线段,简称比例线段。 2.比例的有关性质 ①比例的基本性质:如果 d c b a =,那么ad=b c 。如果ad=bc (a ,b ,c , d 都不等于0),那么 d c b a =。 ②合比性质:如果 d c b a =,那么d d c b b a ±=±。 (一)相似三角形 1、定义:对应角相等,对应边成比例的两个三角形,叫做相似三角形. ①当一个三角形的三个角与另一个(或几个)三角形的三个角对应相等,且三条对应边的比相等时,这两个(或几个)三角形叫做相似三角形,即定义中的两个条件,缺一不可; ②相似三角形的特征:形状一样,但大小不一定相等; ③相似三角形的定义,可得相似三角形的基本性质:对应角相等,对应边成比例. 2、相似三角形对应边的比叫做相似比. ①全等三角形一定是相似三角形,其相似比k=1.所以全等三角形是相似三角形的特例.其区别在于全等要求对应边相等,而相似要求对应边成比例. ②相似比具有顺序性.例如△ABC∽△A′B′C′的对应边的比,即相似比为k,则△A′B′C′∽ △ABC的相似比,当它们全等时,才有k=k′=1. ③相似比是一个重要概念,后继学习时出现的频率较高,其实质它是将一个图形放大或缩小的倍数,这一点借助相似三角形可观察得出. 3、如果两个边数相同的多边形的对应角相等,对应边成比例,那么这两个多边形叫做相似多边形. 4、相似三角形的预备定理:平行于三角形的一条边直线,截其它两边所在的直线,截得的三角形与原三角形相似. ①定理的基本图形有三种情况,如图其符号语言: ∵DE∥BC,∴△ABC∽△ADE; (双A型) ②这个定理是用相似三角形定义推导出来的三角形相似的判定定理.它不但本身有着广泛的应用,同时也是证明相似三角形三个判定定理的基础,故把它称为“预备定理”; ③有了预备定理后,在解题时不但要想到“见平行,想比例”,还要想到“见平行,想相似”. (二)相似三角形的判定 1、相似三角形的判定: 判定定理1:如果一个三角形的两个角与另一个三角形的两个角对应相等,那么这两个三角形相似。可简单说成:两角对应相等,两三角形相似。 例1、已知:如图,∠1=∠2=∠3,求证:△ABC∽△ADE. 发现、构造相似三角形的基本图形证题 支其韶 吴复 相似三角形主要有四种基本类型。 一、平行线型 如图1,若DE ∥BC ,则△ADE ∽△ABC 。 例1. 已知,如图2所示,AD 为△ABC 的中线,任一直线CF 交AD 、AB 于E 、F 。 求证:FB AF 2ED AE = 。 例2. 已知,如图3所示,BE 、CF 分别为△ABC 的两中线,交点为G 。 求证:2 GF GC GE GB ==。 例3. 已知,如图4所示,在△ABC 中,直线MN 交AB 、AC 和BC 的延长线于X 、Y 、Z 。 求证: AY CY CZ BZ BX AX ??=1。 二、相交线型 如图5,若∠1=∠B ,则可由公共角或对顶角得△ADE ∽△ABC 。 例4. 已知,如图6所示,△ABC 中,AB=AC ,D 为AB 上的点,E 为AB 延长线上的点, 且AE AD AB 2 ?=。 求证:BC 平分∠DCE 。 例5. 已知,如图7所示,CD 为Rt △ABC 的高,E 为CD 的中点,AE 的延长线交BC 于F ,FG ⊥AB 于G 。 求证:FB FC FG 2 ?=。 三、旋转型 如图8,若∠BAD=∠CAE ,则△ADE 绕点A 旋转一定角度后与△ABC 构成平行线型的相似三角形。 如图9,直角三角形中的相似三角形,若∠ACB=?90,AB ⊥CD ,则△ACD ∽△CBD ∽△ABC 。 例6. 已知,如图10所示,D 为△ABC 内的一点,E 为△ABC 外的一点,且∠EBC=∠DBA ,∠ECB=∠DAB 。 例7. 已知,如图11所示,F 为正方形ABCD 的边AB 的中点,E 为AD 上的一点,AE=41 AD , FG ⊥CE 于G 。 求证:CG EG FG 2 ?=。 例8. 已知,如图12所示,在平行四边形ABCD 中,O 为对角线BD 上的点,过O 作直线分别交DC 、AB 于M 、N ,交AD 的延长线于E ,交CB 的延长线于F 。 求证:OE ·ON=OM ·OF 。 相似三角形基本类型一、“X”型. B C B C 二、“子母”,“A型”,“斜A ”. B B B (双垂直K型)三、“K”型 C B (三垂直K 型) A C D B C A B D 四、共享型 A B E C D A B E B B 1.在△ABC 和△ADE 中,∠BAD=∠CAE ,∠ABC=∠ADE. A B E 1.如图,已知∠1=∠2,∠3=∠4,求证∠ABE=∠ACD. A B D 2. A B P 3.如图,已知C 是线段AB 上的任意一点(端点除外),分别以AC 、BC 为斜边并且在AB 的 同一侧作等腰直角△ACD 和△BCE ,连结AE 交CD 于点M ,连结BD 交CE 于点N ,给出以下三个结论:①MN ∥AB ;②1MN =1AC +1 BC ;③M N≤14AB ,其中正确结论的个数 是( ) A .0 B .1 C .2 D .3 F E C B B' C' 4.如图,Rt △AB 'C ' 是由Rt △ABC 绕点A 顺时针旋转得到的,连结CC ' 交斜边于点E , CC ' 的延长线交BB ' 于点F . (1)证明:△ACE ∽△FBE ; (2)设∠ABC =α,∠CAC ' =β,试探索α、β满足什么关系时,△ACE 与△FBE 是全 等三角形,并说明理由. 5. A D B 6.在等边△ABC 中,D 为BC 边上一点,E 为AC 边上一点,且∠ADE=60°,BD=3,CE=2,则△ABC 的边长为_________. A B C D 7. 0 90A E ∠=∠=°, 1 2 EDB C ∠= ∠. (1)当AB=AC 时,①∠EBF=_________. D C B A D C B A C B A C B A C B C P 《相似三角形中分类讨论思想的运用》 一、温故知新: 1. 已知△ABC 的三边长分别是4、6、8,△DEF 的一条边为24,如果△DEF 与△ABC 相似,则相似比为 2.两个相似三角形的面积之比是9:25,其中一个三角形一边上的高是6,那么另一个三角形对应边上的高为 3.已知线段AB=2,P 是线段AB 的黄金分割点,则AP 的长为 问题:什么是分类讨论?为什么要分类? 二、新知学习: 题组一: 1.例1.如图所示,在ABC ?中,AB=6,AC=4,P 是AC 的中点,过P 点的直线交AB 于点Q ,若使APQ ?与ABC ?相似,则AQ 的长为 2.变式一:如图所示, 在ABC ?中,P 是AC 上一点,过P 点的直线截ABC ?交AB 于点Q ,使截得的三角形与原三角形相似,则满足这样的直线有 条. 3. 变式二:如图所示,在ABC ?中,P 是AC 上一点,过P 点的直线截ABC ?,使截得的三角形与原三角形相似,则满足这样的直线最多有 条. 探究:如果ABC ?是直角三角形,点P 直角边上或点P 在斜边上上述结论还成立吗?等腰三角形呢? 题组二: 1.例2: 己知菱形ABCD 的边长是3,点E 在直线AD 上,DE =1,联结BE 与对角 线AC 相交于点M ,则MC AM = C B C B C B 2.变式一: 等腰ABC 中,AB=AC=10,BC=16,点P 在BC 边上,若PA 与腰垂直,则BP= . 3. 变式二: 在△ABC 中∠B=25°,AD 是BC 边上的高,并且AD 2=BD ·DC,则∠BCA= . 题组三 1.在矩形ABCD 中,AB=4,AD=5,P 是射线BC 上的一个动点,作PE ⊥AP ,PE 交射线DC 于点E ,射线AE 交射线BC 于点F ,设BP=x ,CE=y .求y 关于x 的函数解析式,并写出它的定义域;(点P 与点B 、C 都不重合), 2.已知AB=2,AD=4,∠DAB=90°,AD∥BC(如图).E 是射线BC 上的动点(点E 与点B 不重合),M 是线段DE 的中点.联结BD ,交线段AM 于点N ,如果以A 、N 、D 为顶点的三角形与△BME 相似,求线段BE 的长. 三、课后反思: 1. 相似三角形中有哪些几何情境需要分类讨论?分类的原则是什么? 2. 请积累你运用分类讨论思想解决的数学问题. A C D A C D 相似三角形综合题练习 类型一相似三角形中动点问题 例1:如图正方形ABCD的边长为2,AE=EB,线段MN的两端点分别在CB、CD上滑动,且MN=1,当CM为何值时△AED与以M、N、C为顶点的三角形相似? 变式:如图,在△ABC中,AB=8,BC=7,AC=6,有一动点P从A沿AB移动到B,移动速度为2单位/秒,有一动点Q从C沿CA移动到A,移动速度为1单位/秒,问两动点同时移动多少时间时,△PQA与△BCA相似. 例2:如图,已知△ABC是边长为6cm的等边三角形,动点P、Q同时从A、B两点出发,分别沿AB、BC匀速运动,其中点P运动的速度是1cm/s,点Q运动的速度是2cm/s,当点Q到达点C时,P、Q两点都停止运动,设运动时间为t(s),解答下列问题: (1)当t=2时,判断△BPQ的形状,并说明理由; (2)设△BPQ的面积为S(cm2),求S与t的函数关系式; (3)作QR//BA交AC于点R,连结PR,当t为何值时,△APR∽△PRQ? A B D C E N N C M B 变式:如图,在矩形ABC D中,AB=12cm,BC=8cm.点E 、F、G 分别从点A 、B 、C 三点同时出发,沿矩形的边按逆时针方向移动.点E 、G 的速度均为2c m/s ,点F 的速度为4cm/s,当点F 追上点G (即点F 与点G 重合)时,三个点随之停止移动.设移动开始后第t 秒时,△EFG 的面积为S(c m2) (1)当t =1秒时,S 的值是多少? (2)写出S 和t 之间的函数解析式,并指出自变量t 的取值范围. (3)若点F 在矩形的边B C上移动,当t 为何值时,以点E 、B 、F 为顶 点的三角形与以点F 、C 、G为顶点的三角形相似?请说明理由. 例3:如图,在梯形ABC D中,AD ∥BC,AD =3,DC=5,BC=10,梯形的高为4.动点M 从B点出发沿线段BC 以每秒2个单位长度的速度向终点C 运动;动N 同时从C 点出发沿线段C D以每秒1个单位长度的速度向终点D 运动.设运动的时间为t(秒). (1)当MN//AB 时,求t 的值; (2)试探究:t 为何值时,△MN C为直角三角形. 相似三角形基本模型与证明一、基本图形回顾 经典模型 构造相似辅助线——双垂直模型 1.在平面直角坐标系xOy中,点A的坐标为(2,1),正比例函数y=kx的图象与线段OA的夹角是45°,求这个正比例函数的表达式. 2.在△ABC中,AB=,AC=4,BC=2,以AB为边在C点的异侧作△ABD,使△ABD为等腰直角三角形,求线段CD的长. 3.在△ABC中,AC=BC,∠ACB=90°,点M是AC上的一点,点N是BC上的一点,沿着直线MN折叠,使得点C恰好落在边AB上的P点.求证:MC:NC=AP:PB. 4.如图,在直角坐标系中,矩形ABCO的边OA在x轴上,边OC在y轴上,点B的坐标为(1,3),将矩形沿对角线AC翻折B点落在D点的位置,且AD交y轴于点E.那么D点的坐标为 () A. B. C. D. 5.已知,如图,直线y=﹣2x+2与坐标轴交于A、B两点.以AB为短边在第一 象限做一个矩形ABCD,使得矩形的两边之比为1﹕2。 求C、D两点的坐标。 构造相似辅助线——A、X字型 6.如图:△ABC中,D是AB上一点,AD=AC,BC边上的中线AE交CD于F。 求证: 7.四边形ABCD中,AC为AB、AD的比例中项,且AC平分∠DAB。 求证: 8.已知:如图,在△ABC中,M是AC的中点,E、F是BC上的两点,且BE=EF=FC。求BN:NQ:QM. 9.(1)如图1,点在平行四边形ABCD的对角线BD上,一直线过点P分别交BA,BC的延长线于点Q,S,交于点.求证: (2)如图2,图3,当点在平行四边形ABCD的对角线或的延长线上时,是否仍然成立?若成立,试给出证明;若不成立,试说明理由(要求仅以图2为例进行证明或说明); 相似三角形基本模型 模型1X字型及其变形 (1)对顶角得对边平行;(2)对顶角得对边不平行,且∠OAB=∠OCD 例1(2016哈尔滨)如图,在△ABC中,D、E分别为AB、AC边上得点,DE∥B C,BE与CD相交于点F,则下列结论一定正确得就是( ) A。AD:AB=AE:ACB、DF:FC=AE:EC C。AD:DB=DE:BC D.DF:BF=EF:FC 1、(2016贵港)如图,?ABCD得对角线AC,BD交于点O,CE平分∠BCD交AB 于点E,交BD于点F,且∠ABC=60°,AB=2BC,连接OE.下列结论: ①∠ACD=30°;②S?ABCD=AC?BC;③OE:AC=√3:6;④S△OCF=2S△OEF 成立得个数有()A。 1个B。 2个C。 3个D、 4个 模型2A字型及其变形 例2、如图,已知△ABC中,CE⊥AB于E,BF⊥AC于F,求证:△AEF∽△ACB、2、如图,AD与BC相交于E,点F在BD上,且AB∥EF∥CD,求证:\f(1,AB)+ 1 CD=1 EF。 模型3子母型 例2、如图,在Rt△ABC中,CD⊥AB,D为垂足。 (1)若AD=3,AC=35,则斜边AB得长为; (2)若AD:DB=2:3,则AC:CB= 3、(2016云南)如图,D就是△ABC得边BC上一点,AB=4,AD=2,∠DAC=∠B。如果△ABD得面积为15,那么DC= 。 模型4一线三等角型 例4.如图,在正方形ABCD中,E为边AD得中点,点F在边CD上,且CF=3FD,∠BEF=90°. (1)求证:△ABE∽△DEF; (2)若AB=4,延长EF交BC得延长线于点G,求BG得长. 4、(2017潮阳)如图,在边长为9得等边△ABC中,BD=3,∠ADE=60°,则CE得长为___、 模型5旋转型 知识梳理 相似三角形的概念 对应角相等,对应边成比例的三角形,叫做相似三角形. 相似用符号“∽”表示,读作“相似于”. 相似三角形对应边的比叫做相似比(或相似系数). 相似三角形对应角相等,对应边成比例. 注意: ①对应性:即两个三角形相似时,通常把表示对应顶点的字母写在对应位置上,这样写比较容易 找到相似三角形的对应角和对应边. ②顺序性:相似三角形的相似比是有顺序的. ③两个三角形形状一样,但大小不一定一样. ④全等三角形是相似比为1的相似三角形.二者的区别在于全等要求对应边相等,而相似要求对 应边成比例. 相似三角形的基本定理 定理:平行于三角形一边的直线和其它两边(或两边延长线)相交,所构成的三角形与原 三角形相似. 定理的基本图形: 用数学语言表述是: BC DE // , ADE ∽ABC . 相似三角形的等价关系 (1)反身性:对于任一ABC 有ABC ∽ABC . (2)对称性:若ABC ∽'''C B A ,则'''C B A ∽ABC . (3)传递性:若ABC ∽C B A '',且C B A ''∽C B A ,则ABC ∽C B A . 三角形相似的判定方法 1、定义法:对应角相等,对应边成比例的两个三角形相似. 2、平行法:平行于三角形一边的直线和其它两边(或两边的延长线)相交,所构成的三角 形与原三角形相似. 3、判定定理1:如果一个三角形的两个角与另一个三角形的两个角对应相等,那么这两 个三角形相似.简述为:两角对应相等,两三角形相似. 4、判定定理2:如果一个三角形的两条边和另一个三角形的两条边对应成比例,并且夹 角相等,那么这两个三角形相似.简述为:两边对应成比例且夹角相等,两三角形相似. 5、判定定理3:如果一个三角形的三条边与另一个三角形的三条边对应成比例,那么这 两个三角形相似.简述为:三边对应成比例,两三角形相似.(在遇到两个三角形的三边都知道的情况优先考虑,把边长分别从小到大排列,然后分别计算他们的比值是否相等来判断是否相似) 6、判定直角三角形相似的方法: (1)以上各种判定均适用. (2)如果一个直角三角形的斜边和一条直角边与另一个直角三角形的斜边和一条直角边对应成比例,那么这两个直角三角形相似. (3)直角三角形被斜边上的高分成的两个直角三角形与原三角形相似. 直角三角形中,斜边上的高是两直角边在斜边上射影的比例中项。每一条直角边是这条直角边在斜边上的射影和斜边的比例中项。 公式 如图,Rt △ABC 中,∠BAC=90°,AD 是斜边BC 上的高,则有射影定理如下: (1)(AD )2=BD ·DC , (2)(AB )2=BD ·BC , (3)(AC )2=CD ·BC 。 证明:在 △BAD 与△ACD 中,∠B+∠C=90°,∠DAC+∠C=90°,∴∠B=∠DAC ,又∵∠ BDA=∠ADC=90°,∴△BAD ∽△ACD 相似,∴ AD/BD =CD/AD ,即 (AD )2=BD ·DC 。其余类似可证。 注:由上述射影定理还可以证明勾股定理。由公式(2)+(3)得: (AB )2+(AC )2=BD ·BC+CD ·BC =(BD+CD)·BC=(BC )2, 即 (AB )2+(AC )2=(BC )2。 这就是勾股定理的结论。 判断相似三角形的几条思路: 1 条件中若有平行线,可采用相似三角形的基本定理 2 条件中如果有一对等角,可再找一对等角(用判定1)或再找夹边成比例。(用判定2)3条件中若有两边对应成比例,可找夹角相等(直角可以直接得出相似)4条件中若有一对直角,可考虑在找一对等角或证明斜边,直角边对应成比例。5条件中若 相似三角形知识点大总结 知识点1 有关相似形的概念 (1)形状相同的图形叫相似图形,在相似多边形中,最简单的是相似三角形. (2)如果两个边数相同的多边形的对应角相等,对应边成比例,这两个多边形叫做相似多边形.相似多边形对应边长度的比叫做相似比(相似系数). 知识点2 比例线段的相关概念 (1)如果选用同一单位量得两条线段b a ,的长度分别为n m ,,那么就说这两条线段的比是 n m b a =,或写成n m b a ::=.注:在求线段比时,线段单位要统一。 (2)在四条线段d c b a ,,,中,如果b a 和的比等于d c 和的比,那么这四条线段d c b a ,,,叫做成比例线段,简称 比例线段. 注:①比例线段是有顺序的,如果说a 是d c b ,,的第四比例项,那么应得比例式为:a d c b =. ②()a c a b c d b d ==在比例式 ::中, a 、d 叫比例外项, b 、 c 叫比例内项, a 、c 叫比例前项,b 、 d 叫比例后项,d 叫第四比例项,如果b=c ,即 a b b d =::那么b 叫做a 、d 的比例中项, 此时有2 b ad =。 (3)黄金分割:把线段AB 分成两条线段)(,BC AC BC AC >,且使AC 是BC AB 和的比例中项,即2AC AB BC =?,叫做把线段AB 黄金分割,点C 叫做线段AB 的黄金分割点, (4)其中AB AC 215-=≈0.618AB .即AC BC AB AC == 简记为:1 2 长短==全长 注:黄金三角形:顶角是360 的等腰三角形。黄金矩形:宽与长的比等于黄金数的矩形 知识点3 比例的性质(注意性质立的条件:分母不能为0) (1) 基本性质: ①bc ad d c b a =?=::;②2 ::a b b c b a c =?=?. 注:由一个比例式只可化成一个等积式,而一个等积式共可化成八个比例式,如bc ad =,除 了可化为d c b a ::=,还可化为d b c a ::=,b a d c ::=,c a d b ::=,c d a b ::=,b d a c ::=,a b c d ::=,a c b d ::=. (2) 更比性质(交换比例的内项或外项): ()() ()a b c d a c d c b d b a d b c a ?=?? ?=?=?? ?=??, 交换内项,交换外项. 同时交换内外项 (3)反比性质(把比的前项、后项交换): a c b d b d a c =?=. (4)合、分比性质:a c a b c d b d b d ±±=?=. 注:实际上,比例的合比性质可扩展为:比例式中等号左右两个比的前项,后项之间 相似三角形知识点汇总 重点、难点分析: 1、相似三角形的判定性质是本节的重点也是难点. 2、利用相似三角形性质判定解决实际应用的问题是难点。 一、重要定理 (比例的有关性质): 二、有关知识点: 1.相似三角形定义: 对应角相等,对应边成比例的三角形,叫做相似三角形。 2.相似三角形的表示方法:用符号“∽”表示,读作“相似于”。 3.相似三角形的相似比: 相似三角形的对应边的比叫做相似比。 4.相似三角形的预备定理: 平行于三角形一边的直线和其他两边(或两边的延长线)相交,所截成的三角形与原三角形相似。 5.相似三角形的判定定理: 6.直角三角形相似: (1)直角三角形被斜边上的高分成两个直角三角形和原三角形相似。 (2)如果一个直角三角形的斜边和一条直角边与另一个直角三角形的斜边和一条直角边对应成比例,那么这两个直角三角形相似。 7.相似三角形的性质定理: (1)相似三角形的对应角相等。 (2)相似三角形的对应边成比例。 (3)相似三角形的对应高线的比,对应中线的比和对应角平分线的比都等于相似比。 (4)相似三角形的周长比等于相似比。 (5)相似三角形的面积比等于相似比的平方。 8. 相似三角形的传递性 如果△ABC ∽△A 1B 1C 1,△A 1B 1C 1∽△A 2B 2C 2,那么△ABC ∽A 2B 2C 2 反比性质:c d a b = 更比性质:d b c a a c b d ==或 合比性质:d d c b b a ±=± ?=?=bc ad d c b a (比例基本定理) 相似三角形判定的基本模型 A字型X字型反A字型反8字型 母子型旋转型双垂直三垂直相似三角形判定的变化模型 C B E D A 相似三角形分类整理 (超全) 第一节:相似形与相似三角形 基本概念: 1.相似形:对应角相等,对应边成比例的两个多边形,我们称它们互为相似形。 相似三角形:对应角相等,对应边成比例的两个三角形,叫做相似三角形。 1.几个重要概念与性质(平行线分线段成比例定理) (1)平行线分线段成比例定理:三条平行线截两条直线,所得的对应线段成比例. 已知a ∥b ∥c, A D a B E b C F c 可得EF BC DE AB DF EF AC BC DF EF AB BC DF DE AC AB EF DE BC AB = ====或或或或 等. (2)推论:平行于三角形一边的直线截其它两边(或两边的延长线)所得的对应线段成比例. A D E B C 由DE ∥BC 可得: AC AE AB AD EA EC AD BD EC AE DB AD ===或或.此推论较原定理应用更加广泛,条件是平行. (3)推论的逆定理:如果一条直线截三角形的两边(或两边的延长线)所得的对应线段成比例.那么这条直线平行于三角形的第三边. 此定理给出了一种证明两直线平行方法,即:利用比例式证平行线. (4)定理:平行于三角形的一边,并且和其它两边相交的直线,所截的三角形的三边与原三角形三边对应成比例. (5)①平行于三角形一边的直线和其他两边相交,所构成的三角形与原三角形相似。 ②比例线段:四条线段a ,b ,c ,d 中,如果a 与b 的比等于c 与d 的比,即b a =d c ,那么这四条线段a ,b ,c ,d 叫做成比例线段,简称比例线段。 2.比例的有关性质 ①比例的基本性质:如果 d c b a =,那么ad=b c 。如果ad=bc (a ,b ,c , d 都不等于0),那么 d c b a =。 1文档来源为:从网络收集整理.word 版本可编辑. A D B D A B C 相似中的基本图形练习 相似三角形是初中数学中重要的内容,应用广泛,可以证明线段的比例式;也可证明线段相等、平行、垂直等;还可计算线段的长、比值,图形面积及比值。 而识别(或构造)A 字型、X 字型、母子相似型、旋转型等基本图形是解证题的关键。 1.A 字型及变形 △ABC 中 , AD=2,BD=3,AE=1 (1)如图1,若DE ∥BC , 求CE 的长 (2)如图2,若∠ADE=∠ACB , 求CE 的长 2. X 字型及变形 (1)如图1,AB ∥CD ,求证:AO :DO=BO :CO (2)如图2,若∠A=∠C ,求证:AO ×DO=BO ×CO 3. 母子相似型及变形 (1)如右图,在△ABC 中, AD 把△ABC 分成两个三角形△BCD 和△CAD ,当∠ACD =∠B 时,说明△CAD 与△ABC 相似。 说明:由于小三角形寓于大三角形中,恰似子依母怀,故被称为“母子三角形” (2)如图, Rt △ABC 中 ,CD ⊥AB, 求证:AC 2=ADxAB,CD 2=ADxBD, 4. 旋转型 如图,若∠ADE=∠B ,∠BAD=∠CAE ,说明△ADE 与△ABC 相似 练习题 GED :S △ 1、如图1,在△ABC 中,中线BE 、CD 相交于点G ,则BC DE = ;S △ GBC = ; 2、如图2,在△ABC 中, ∠B=∠AED ,AB=5,AD=3,CE=6,则AE= ; 3、如图3,△ABC 中,M 是AB 的中点,N 在BC 上,BC=2AB ,∠BMN=∠C ,则△ ∽△ , 相似比为 ,NC BN = ; 4、如图4,在梯形ABCD 中,AD ∥BC ,S △ADE :S △BCE =4:9,则S △ABD :S △ABC = ; 5、如图5,在△ABC 中,BC=12cm ,点D 、F 是AB 的三等分点,点E 、G 是AC 的三等分点,则DE+FG+BC= ; 二、选择题 6、如图,在△ABC 中,高BD 、CE 交于点O ,下列结论错误的是( ) A 、CO ·CE=CD ·CA B 、OE ·OC=OD ·OB C 、A D ·AC=A E ·AB D 、CO ·DO=BO ·EO 7、如图,D 、E 分别是△ABC 的边AB 、AC 上的点, AD BD =CE AE =3, 且∠AED=∠B ,则△AED 与△ABC 的面积比是( ) A 、1:2 B 、1:3 C 、1:4 D 、4:9 8、已知,如图, 在△ABC 中,DE ∥BC ,AD=5,BD=3,求S △ADE :S △ABC 的值。 9、如图,已知在△ABC 中,CD=CE ,∠A=∠ECB ,试说明CD 2 =AD ·BE 。 一、运用新知,解决问题 1、已知两个三角形相似,请完成下列表格 2、如图,D 、E 分别是AC ,AB 上的点,∠ADE =∠B ,AG ⊥BC 于点G ,AF ⊥DE 于点 F.若AD =3,AB =5,求: (1)AG AF ; (2)△ADE 与△ABC 的周长之比; (3)△ADE 与△ABC 的面积之比. 二、加强训练,巩固新知 1.若两个相似三角形的相似比是2∶3,则它们的对应高线的比是 ,对应中线的比是 ,对应角平分线的比是 ,周长比是 ,面积比是 。 2.两个等边三角形的面积比是3∶4,则它们的边长比是 ,周长是 。 3.某城市规划图的比例尺为1∶4000,图中一个氯化区的周长为15cm ,面积为12cm 2 ,则这个氯化区的实际周长和面积分别为多少? 相似比 2 周长比 面积比 10000 A B C D E G 图1 A B C D E 图2 A B M N 图3 A B C D E 图4 A B C D F G E A E C D O A B C D E C A B D E A B C D E F A B C D E 1. 相似三角形的判定定理: 推论一一直角三角形相似: (1) 直角三角形被斜边上的高分成两个直角三角形和原三角形相似。 (2) 如果一个直角三角形的斜边和一条直角边与另一个直角三角形的斜边和一条直角边对应成比例, 那么这两个直角三角形相似。 2. 性质定理: (1) 对应角相等。 (2) 对应边成比例。 (3) 对应高线的比,对应中线的比和对应角平分线的比都等于相似比。 (4) 周长比等于相似比。 (5) 面积比等于相似比的平方。 3. 相似三角形的传递性 如果△ABC S ^I B I C I ,M I B I C I s 公2B 2C 2,那么△ ABC "A 2B 2C 2 精选文档 相似三角形考点 4、 比例的性质 a c (1) 比例的基本性质: =— b d a c a b (2) 合比性质: =- b d b (3) 等比性质:a =- = L =m b d n ad 二be (bd H 0) e d d a e L m a 八 b d L (b d L n u) n b 精选文档 如果两个多边形不仅相似,而且对应顶点的连线相交于一点,对应边互相平行,像这样的两个图形 叫做位似图形,这个点叫做位似中心。对应边的比叫做位似比,位似比等于相似比。 锐角三角函数知识点总结 1、勾股定理:直角三角形两直角边 a 、b 的平方和等于斜边 c 的平方。 a 2 b 2 c 2 2、如下图,在 Rt △ AB (中,/ C 为直角,则/ A 的锐角三角函数为(ZA 可换成/B ): 3、特殊角的三角函数值(重要) 三角函数 30 ° 45 ° 60 ° \ 疋 义 表达式 正 弦 sin A - A 的对边 斜边 a sin A — c 余 弦 cosA - A 的邻边 斜边 .b cos A - c 正 切 tan A - A 的对边 A 的邻边 tan A — b 相似三角形的基本类型总结 类型一 平行线型 相关定理 平行于三角形一边的直线,和其他两边(或两边的延长线)相交所构成的三角形与原三角形相似. 平行相似可分为“A”型平行相似和“X”型平行相似两种. 如图(1)(2)所示,由BC DE //可直接证得:△ADE ∽△ABC . E D C B A 图(1) E D C B A 图(2) 1. 如图(3)所示,已知BC DE //,8:1:=?DBCE ADE S S 四边形,则 =AC AE 【 】 (A )91 (B )31 (C )81 (D )2 1 2. 如图(4)所示,已知,//CD AB AD 与BC 相交于点O .若3 2 =OC BO ,10=AD ,则 =AO _________. 图(3) E D C B A 图(4) O D C B A F E D C B A 图(5) 3. 如图(5)所示,已知AC DF AB DE //,//. 求证:△DEF ∽△ABC . 类型二 相交型 如图(6)所示,由D B ∠=∠或 AE AC AD AB = ,可得△ABC ∽△ADE ; 如图(7)所示,由ADE B ∠=∠或AED C ∠=∠或AE AC AD AB = ,可得△ABC ∽△ADE ; 如图(8)所示,由D B ∠=∠或E C ∠=∠或AE AC AD AB = ,可得△ABC ∽△ADE . 像以上三种情况,若两个三角形有一个公共角,且公共角的对边相交,若另有一组对应角相等或夹公共角的两边对应成比例,则这两个三角形相似.这就是相交型相似. 图(6) E D C B A E D C B A 图(7) 图(8) E D C B A 4. 如图(9)所示,在△ABC 中,点D 、E 分别在边AB 、AC 上,B AED ∠=∠,射线AG 分别交线段DE 、BC 于点F 、G ,且CG DF AC AD = . (1)求证:△ADF ∽△ACG ; (2)若 21=AC AD ,求 FG AF 的值. G F E D C B A 图(9) 第一节 第二节 第九节:相似形与相似三角形基本概念: 1.相似形:对应角相等,对应边成比 例的两个多边形,我们称它们互为相似形。 2.相似三角形:对应角相等,对应边成比例的两个三角形,叫做相似三角形。 1.几个重要概念与性质(平行线分线段成比例定理) (1)平行线分线段成比例定理:三条平行线截两条直线,所得的对应线段成比例. 已知a ∥b ∥c, A D a B E b C F c 可得 EF BC DE AB DF EF AC BC DF EF AB BC DF DE AC AB EF DE BC AB =====或或或或 等. (2)推论:平行于三角形一边的直线截其它两边(或两边的延长线)所得的对应线段成比例. A D E B C 由DE ∥BC 可得: AC AE AB AD EA EC AD BD EC AE DB AD ===或或.此推论较原定理应用更加广泛,条件是平行. (3)推论的逆定理:如果一条直线截三角形的两边(或两边的延长线)所得的对应线段成比例.那么这条直线平行于三角形的第三边. 此定理给出了一种证明两直线平行方法,即:利用比例式证平行线. (4)定理:平行于三角形的一边,并且和其它两边相交的直线,所截的三角形的三边与原三角形三边对应成比例. (5)①平行于三角形一边的直线和其他两边相交,所构成的三角形与原三角形相似。 ②比例线段:四条线段a ,b ,c ,d 中,如果a 与b 的比等于c 与d 的比,即b a =d c ,那么这四条线段a ,b ,c ,d 叫做成比例线段,简称比例线段。 2.比例的有关性质 ①比例的基本性质:如果 d c b a =,那么ad=b c 。如果ad=bc (a ,b ,c , d 都不等于0), 相似三角形 1.如图,已知AB CD EF ∥∥,那么下列结论正确的是( ) A . AD BC DF CE = B . BC DF CE AD = C . CD BC EF BE = D . CD AD EF AF = 2.如图所示,给出下列条件: ①B ACD ∠=∠; ②ADC ACB ∠=∠; ③AC AB CD BC =; ④2AC AD AB = 其中单独能够判定ABC ACD △∽△的个数为( ) A .1 B .2 C .3 D .4 3.已知△ABC∽△DEF ,且AB :DE=1:2,则△ABC 的面积与△DEF 的面积之比为( ) A .1:2 B .1:4 C .2:1 D .4:14.如图,已知等边三角形ABC 的边长为2,D E 是它的中位线,则下面四个结论: (1)DE=1,(2)△CDE∽△CAB,(3)△CDE 的面积与△CAB 的面积之比为1:4. 其中正确的有:( ) A .0个 B .1个 C .2个 D .3个 A B D C E F 1题 A C D B (第2题图) 【参考答案】 1.A 2.C 3.B 4.D ◆考点聚焦 1.了解线段的比、成比例线段、黄金分割、相似图形有关概念及性质. 2.探索并掌握三角形相似的性质及条件,?并能利用相似三角形的性质解决简单的实际问题. 3.掌握图形位似的概念,能用位似的性质将一个图形放大或缩小. 4.掌握用坐标表示图形的位置与变换,在给定的坐标系中,?会根据坐标描出点的位置或由点的位置写出它的坐标,灵活运用不同方式确定物体的位置. ◆备考兵法 1.证明三角形相似的方法常用的有三个,到底用哪个要根据具体情况而定,要注意基本图形的应用,如“A型”“X型”“母子型”等. 2.用相似三角形的知识解决现实生活中实际问题,关键是要先把实际问题转化为数学问题,识别或作出相似三角形,再利用相似三角形的性质求解,并回答实际问题,注意题目的解一定要符合题意. 3.用直角坐标系中的点描述物体的位置,用坐标的方法来研究图形的运动变换,是较为常见的考法,要注意训练. ◆考点链接 一、相似三角形的定义 三边对应成_________,三个角对应________的两个三角形叫做相似三角形. 二、相似三角形的判定方法 1. 若DE∥BC(A型和X型)则______________. 2. 射影定理:若CD为Rt△ABC斜边上的高(双直角图形) 则Rt△ABC∽Rt△ACD∽Rt△CBD且AC2=________,CD2=_______,BC2=__ ____. 3. 两个角对应相等的两个三角形__________. 4. 两边对应成_________且夹角相等的两个三角形相似. 5. 三边对应成比例的两个三角形___________. WORD 格式可编辑 相似三角形经典模型总结 经典模型 平移旋转 180° ∽ 平行型 平行型 翻折 180° 翻折 180° 一般 特殊 翻折 180° 斜交型 斜交型 特殊一边平移 一般 平移 特殊 双垂直 斜交型 双垂直 一般 【精选例题】 “平行型” 【例 1】如图,EE1∥FF1∥MM1,若AE EF FM MB , 则S AEE : S四边形EE FF : S四边形FF M M : S四边形 MM C B _________ 1 1 1 1 1 1 A E E1 F F 1 M M1 B C WORD 格式可编辑 【例 2】如图,AD∥EF∥MN∥BC,若AD 9,BC 18 , AE:EM :MB 2:3:4,则EF _____ , MN _____ A D E F M N B C 【例 3】已知,P为平行四边形ABCD 对角线, AC 上一点,过点P 的直线与 AD , BC , CD 的延长线, AB 的延长线分别相交于点 E , F , G , H 求证: PE PH PF PG G D C E P F A B H 【例 4】已知:在ABC 中, D 为 AB 中点, E 为 AC 上一点,且 AE 2, BE、 CD相交于点 F , 求BF 的 值 EC EF A D F E B C 【例 5】已知:在ABC 中, AD 1 AB,延长 BC到F ,使CF 1 BC,连接 FD交 AC于点 E 2 3 求证:① DE EF ② AE 2CE A D E B 专业知识分享 【例 6】已知:D,E为三角形ABC 中 AB 、BC 边上的点,连接 DE 并延长交 AC 的延长线于点 F ,BD: DE AB: AC 求证:CEF 为等腰三角形 A C D E B F 【例7】如图,已知 AB / / EF / /CD ,若 AB a , CD b , EF c ,求证:1 1 1 . c a b A C E B F D 【例 8】如图,找出S ABD、 S BED、 S BCD之间的关系,并证明你的结论. C A E B F D 【例 9】如图,四边形ABCD 中, B D90M 是 AC 上一点, ME AD 于点 EMF BC ,, 于点 F 求证:MF ME 1 AB CD D E M A C F B 相似三角形 一、知识概述 1.平行线等分线段定理 如果一组平行线在一条直线上截得的线段相等,那么在其它直线上截得的线段也相等。 2.平行线分线段成比例定理 三条平行线截两条直线,所得的对应线段成比例。 3.相似三角形的定义 对应边成比例、对应角相等的两个三角形叫做相似三角形. 4.相似三角形的基本性质 ①相似三角形的对应边成比例、对应角相等. ②相似三角形的对应高线的比,对应中线的比和对应角平分线的比都等于相似比。 ③相似三角形的周长比等于相似比 ④面积比等于相似比的平方 温馨提示: ①全等三角形一定是相似三角形,其相似比k=1.所以全等三角形是相似三角形的特例.其区别在于全等要求对应边相等,而相似要求对应边成比例. ②相似比具有顺序性.例如△ABC∽△A′B′C′的对应边的比,即相似比为k,则△A′B′C′∽△ABC 的相似比,当且仅当它们全等时,才有k=k′=1. ③相似比是一个重要概念,后继学习时出现的频率较高,其实质它是将一个图形放大或缩小的倍数,这一点借助相似三角形可观察得出. 5. 相似三角形的判定定理 ①平行于三角形一边的直线和其他两边或其延长线相交,所得的三角形与原三角形相似; ②三边对应成比例的两个三角形相似; ③两角对应相等的两个三角形相似; ④两边对应成比例且夹角相等的两个三角形相似。 温馨提示: (1)判定三角形相似的几条思路: ①条件中若有平行,可采用判定定理1; ②条件中若有一对角相等(包括隐含的公共角或对顶角),可再找一对角相等或找夹边对应成比例; ③条件中若有两边对应成比例,可找夹角相等;但是,在选择利用判定定理2时,一对对应角相等必相似三角形分类整理超全
(完整版)相似三角形的判定方法
相似三角形基本类型证明题
相似三角形基本类型
(精心整理)相似三角形分类讨论
相似三角形综合题练习
相似三角形基本模型及证明
相似三角形基本类型
相似三角形详细讲义
相似三角形知识点梳理
(完整版)相似三角形知识点梳理
相似三角形分类整理(超全)上课讲义
相似三角形基本图形及练习题-绝对经典
相似三角形和三角函数
相似三角形的基本类型总结
相似三角形分类整理(超全)(汇编)
相似三角形中考题题型类
(完整版)相似三角形经典模型总结及例题分类.doc
相似三角形中考复习(知识点题型分类练习)38482
