典型相关性分析1

典型相关性分析
典型相关分析是借助主成分分析降维的思想,分别对两组变量提取主成分,且使得两组变量提取的主成分之间的相关程度达到最大,而从同一组内部提取的各主成分之间互不相关,用从两组之间分别提取的主成分的相关性来描述两组变量整体的线性相关关系。
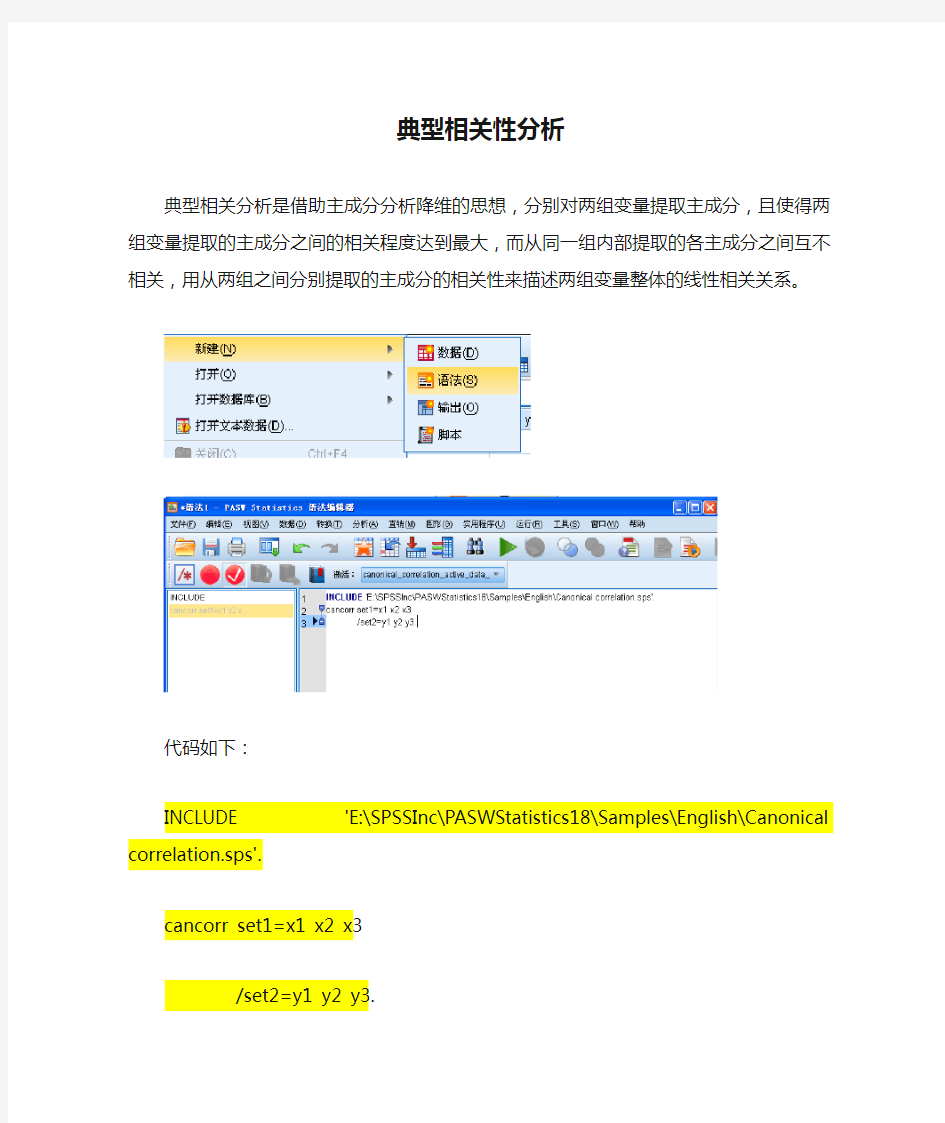
代码如下:
INCLUDE 'E:\SPSSInc\PASWStatistics18\Samples\English\Canonical correlation.sps'.
cancorr set1=x1 x2 x3
/set2=y1 y2 y3.
Run MATRIX procedure:
Correlations for Set-1
x1 x2 x3
x1 1.0000 .8702 -.3658
x2 .8702 1.0000 -.3529
x3 -.3658 -.3529 1.0000
数据集1中变量x1-x3的相关关系,有相关系数知,x1与x2有较强的相关性。
Correlations for Set-2
y1 y2 y3
y1 1.0000 .6957 .4958
y2 .6957 1.0000 .6692
y3 .4958 .6692 1.0000
数据集2中变量y1-y3的相关关系,有相关系数知,y1与y2有较强的相关性。
Correlations Between Set-1 and Set-2
y1 y2 y3
x1 -.3897 -.4931 -.2263
x2 -.5522 -.6456 -.1915
x3 .1506 .2250 .0349
x1-x3与y1-y3的相关关系,x1,x2与y1-y3是负相关关系,说明体重和腰围较大对运动能力具有负影响。
Canonical Correlations
1 .796
2 .201
3 .073
表示三个典型相关系数
Test that remaining correlations are zero:
Wilk's Chi-SQ DF Sig.
1 .350 16.255 9.000 .062
2 .955 .718 4.000 .949
3 .995 .082 1.000 .775
对三个典型相关系数的显著性检验,原假设是相关系数为0,在显著性水平为0.1上,第一个典型相关系数对应的Sig.为0.062<0.1,拒绝原假设,认为第一个典型相关系数不为0.第二和第三个典型相关系数对应的Sig.>0.1,认为二者均为0。
Standardized Canonical Coefficients for Set-1
1 2 3
x1 .775 -1.884 -.191
x2 -1.579 1.181 .506
x3 .059 -.231 1.051
数据集1标准化变量的典型相关变量函数表达式:U1=0.775x1*-1.579x2*+0.059x3*
U2=-1.884x1*+1.181x2*-0.231x3*,U3=-0.191x1*+0.506x2*+1.051x3*
Raw Canonical Coefficients for Set-1
1 2 3
x1 .031 -.076 -.008
x2 -.493 .369 .158
x3 .008 -.032 .146
数据集1原始变量的典型相关变量函数表达式:U1=0.031x1-0.493x2+0.008x3,U2...,U3…
Standardized Canonical Coefficients for Set-2
1 2 3
y1 .349 -.376 -1.297
y2 1.054 .123 1.237
y3 -.716 1.062 -.419
数据集2标准化变量的典型相关变量函数表达式:
V1=0.349y1*+1.054y2*-0.716y3*,V2…,V3…
Raw Canonical Coefficients for Set-2
1 2 3
y1 .066 -.071 -.245
y2 .017 .002 .020
y3 -.014 .021 -.008
数据集1原始变量的典型相关变量函数表达式:V1=0.066y1+0.017y2-0.014y3,V2…,V3…
Canonical Loadings for Set-1
1 2 3
x1 -.621 -.772 -.135
x2 -.925 -.378 -.031
x3 .333 .041 .942
典型载荷阵,-0.621表示变量x1(体重)与第一个典型相关变量U1的相关系数为-0.621,典型载荷阵相当于因子分析中的因子载荷阵,第一个典型相关变量U1与x2的相关系数绝对值最大,二者呈现负相关关系,说明这个典型变量U1主要反映人的体型不是肥胖(即健康)程度;
Cross Loadings for Set-1
1 2 3
x1 -.494 -.155 -.010
x2 -.736 -.076 -.002
x3 .265 .008 .068
典型交叉载荷,-0.494表示x1与数据集2的第一个典型相关变量V1的相关系数为-0.494.从x1-x3与V1的相关系数来看,x2与V1的相关系数绝对值最大,且二者负相关,所以x2(腰围)大的运动能力差。
Canonical Loadings for Set-2
1 2 3
y1 .728.237 -.644
y2 .818.573 .054
y3 .162 .959 -.234
典型载荷阵,第一典型变量V1与y1,y2的相关系数较大,V1表示人运动的程度。
Cross Loadings for Set-2
1 2 3
y1 .579 .048 -.047
y2 .651 .115 .004
y3 .129 .192 -.017
典型交叉载荷,y1,y2与数据集1的第一个典型相关变量U1的相关性较大,且为正相关,
U1表示人健康的程度,所以运动能力对人的健康具有正影响。
Redundancy Analysis:
冗余度分析
Proportion of Variance of Set-1 Explained by Its Own Can. Var.
Prop Var
CV1-1 .451
CV1-2 .247
CV1-3 .302
数据集1中的方差被同数据集中的典型相关变量所解释的方差比例,U1解释的方差比例是45.1%,U2解释的方差比例是24.7%,U3解释的比例是30.2%。
Proportion of Variance of Set-1 Explained by Opposite Can.Var.
Prop Var
CV2-1 .285
CV2-2 .010
CV2-3 .002
数据集1中的方差被对方数据集中的典型相关变量所解释的方差比例,V1解释的方差比例是28.5%,表示数据集1中典型变量(U1)解释原始变量(x1-x3)的方差被数据集2中V1重复解释的百分比。冗余测度体现了两组变量之间的相关程度。
Proportion of Variance of Set-2 Explained by Its Own Can. Var.
Prop Var
CV2-1 .408
CV2-2 .434
CV2-3 .157
Proportion of Variance of Set-2 Explained by Opposite Can. Var.
Prop Var
CV1-1 .258
CV1-2 .017
CV1-3 .001
------ END MA TRIX -----
典型相关分析SPSS例析
典型相关分析 典型相关分析(Canonical correlation )又称规则相关分析,用以分析两组变量间关系的一种方法;两个变量组均包含多个变量,所以简单相关和多元回归的解惑都是规则相关的特例。典型相关将各组变量作为整体对待,描述的是两个变量组之间整体的相关,而不是两个变量组个别变量之间的相关。 典型相关与主成分相关有类似,不过主成分考虑的是一组变量,而典型相关考虑的是两组变量间的关系,有学者将规则相关视为双管的主成分分析;因为它主要在寻找一组变量的成分使之与另一组的成分具有最大的线性关系。 典型相关模型的基本假设:两组变量间是线性关系,每对典型变量之间是线性关系,每个典型变量与本组变量之间也是线性关系;典型相关还要求各组内变量间不能有高度的复共线性。典型相关两组变量地位相等,如有隐含的因果关系,可令一组为自变量,另一组为因变量。 典型相关会找出一组变量的线性组合**=i i j j X a x Y b y =∑∑与 ,称 为典型变量;以使两个典型变量之间所能获得相关系数达到最大,这一相关系数称为典型相关系数。i a 和j b 称为典型系数。如果对变量进 行标准化后再进行上述操作,得到的是标准化的典型系数。 典型变量的性质 每个典型变量智慧与对应的另一组典型变量相关,而不与其他典型变量相关;原来所有变量的总方差通过典型变量而成为几个相互独立的维度。一个典型相关系数只是两个典型变量之间的相关,不能代
表两个变量组的相关;各对典型变量构成的多维典型相关,共同代表两组变量间的整体相关。 典型负荷系数和交叉负荷系数 典型负荷系数也称结构相关系数,指的是一个典型变量与本组所有变量的简单相关系数,交叉负荷系数指的是一个典型变量与另一组变量组各个变量的简单相关系数。典型系数隐含着偏相关的意思,而典型负荷系数代表的是典型变量与变量间的简单相关,两者有很大区别。 重叠指数 如果一组变量的部分方差可以又另一个变量的方差来解释和预测,就可以说这部分方差与另一个变量的方差之间相重叠,或可由另一变量所解释。将重叠应用到典型相关时,只要简单地将典型相关系数平方(2 CR),就得到这对典型变量方差的共同比例,代表一个典型变量的方差可有另一个典型变量解释的比例,如果将此比例再乘以典型变量所能解释的本组变量总方差的比例,得到的就是一组变量的方差所能够被另一组变量的典型变量所能解释的比例,即为重叠系数。 例1:CRM(Customer Relationship Management)即客户关系管理案例,有三组变量,分别是公司规模变量两个(资本额,销售额),六个CRM实施程度变量(WEB网站,电子邮件,客服中心,DM 快讯广告Direct mail缩写,无线上网,简讯服务),三个CRM绩效维度(行销绩效,销售绩效,服务绩效)。试对三组变量做典型相关分析。
典型相关分析及其应用实例
摘要 典型相关分析是多元统计分析的一个重要研究课题.它是研究两组变量之间相关的一种统计分析方法,能够有效地揭示两组变量之间的相互线性依赖关系.它借助主成分分析降维的思想,用少数几对综合变量来反映两组变量间的线性相关性质.目前它已经在众多领域的相关分析和预测分析中得到广泛应用. 本文首先描述了典型相关分析的统计思想,定义了总体典型相关变量及典型 相关系数,并简要概述了它们的求解思路,然后深入对样本典型相关分析的几种算法做了比较全面的论述.根据典型相关分析的推理,归纳总结了它的一些重要性质并给出了证明,接着推导了典型相关系数的显著性检验.最后通过理论与实例分析两个层面论证了典型相关分析的应用于实际生活中的可行性与优越性. 【关键词】典型相关分析,样本典型相关,性质,实际应用 ABSTRACT The Canonical Correlation Analysis is an important studying topic of the Multivariate Statistical Analysis. It is the statistical analysis method which studies the correlation between two sets of variables. It can work to reveal the mutual line dependence relation availably between two sets of variables. With the help of the thought about the Principal Components, we can use a few comprehensive variables to reflect the linear relationship between two sets of variables. Nowadays It has already been used widely in the correlation analysis and forecasted analysis. This text describes the statistical thought of the Canonical Correlation Analysis firstly, and then defines the total canonical correlation variables and canonical correlation coefficient, and sum up
如何在SPSS中实现典型相关分析
如何在SPSS中实现典型相关分析? SPSS 11.0 15.1 典型相关分析 15.1.1方法简介 在相关分析一章中,我们主要研究的是两个变量间的相关,顶多调整其他因素的作用而已;如果要研究一个变量和一组变量间的相关,则可以使用多元线性回归,方程的复相关系数就是我们要的东西,同时偏相关系数还可以描述固定其他因素时某个自变量和应变量间的关系。但如果要研究两组变量的相关关系时,这些统计方法就无能为力了。比如要研究居民生活环境与健康状况的关系,生活环境和健康状况都有一大堆变量,如何来做?难道说做出两两相关系数?显然并不现实,我们需要寻找到更加综合,更具有代表性的指标,典型相 关(CanonicalCorrelation)分析就可以解决这个问题。 典型相关分析方法由Hotelling提出,他的基本思想和主成分分析非常相似,也是降维。即根据变量间的相关关系,寻找一个或少数几个综合变量(实际观察变量的线性组合)对来替代原变量,从而将二组变量的关系集中到少数几对综合变量的关系上,提取时要求第一对综合变量间的相关性最大,第二对次之,依此类推。这些综合变量被称为典型变量,或典则变量,第1对典型变量间的相关系数则被称为第1典型相关系数。一般来说,只需要提取1~2对典型变量即可较为充分的概括样本信息。 可以证明,当两个变量组均只有一个变量时,典型相关系数即为简单相关系数;当一组变量只有一个变量时,典型相关系数即为复相关系数。故可以认为典型相关系数是简单相关系数、复相关系数的推广,或者说简单相关系数、复相关系数是典型相关系数的特例。 15.1.2引例及语法说明 在SPSS中可以有两种方法来拟合典型相关分析,第一种是采用Manova过程来拟合,第二种是采用专门提供的宏程序来拟合,第二种方法在使用上非常简单,而输出的结果又非常详细,因此这里只对它进行介绍。该程序名为Canonical correlation.sps,就放在SPSS的 安装路径之中,调用方式如下: INCLUDE 'SPSS所在路径\Canonical correlation.sps'. CANCORR SETl=第一组变量的列表 /SET2=第二组变量的列表. 在程序中首先应当使用include命令读入典型相关分析的宏程序,然后使用cancorr名称调用,注意最后的“.”表示整个语句结束, 不能遗漏。 这里的分析实例来自曹素华教授所著《实用医学多因素统计分析方法》第176页:为了研究兄长的头型与弟弟的头型间的关系,研究者随机抽查了25个家庭的两兄弟的头长和头宽,资料见文件canoncor.sav,希望求得两组变量的典型变量及典型相关系数。显然,代表兄长头形的变量为第一组变量,代表弟弟头形的变量为第二组变量,这里希望求得的是两组变量间的相关性,在语法窗口中键入的程 序如下: INCLUDE 'D:\SpssWin\Canonical correlation.sps'. 请使用时改为各自相应的安装目录 CANCORR SETl=longlwidthl 列出第一组变量 /SET2=long2width2. 列出第二组变量 选择菜单Run->All,运行上述程序,结果窗口中就会给出典型相关分析的结果。 15.1.3 结果解释 NOTE:ALL OUTPUT INCLUDING ERROR MESSAGES HAVE BEEN TEMPORARILY SUPPRESSED.IF YOU EXPERIENCE UNUSUAL BEHAVIOR THEN RERUN THIS
SPSS典型相关分析
SPSS数据统计分析与实践 第二十二章:典型相关分析 (Canonical Correlation) 主讲:周涛副教授 北京师范大学资源学院 教学网站:https://www.360docs.net/doc/9410109456.html,/Courses/SPSS
典型相关分析(Canonical Correlation)本章内容: 一、典型相关分析的基本思想 二、典型相关分析的数学描述 三、SPSS实例 四、小节
典型相关分析的基本思想 z典型相关分析是研究两组变量之间相关关系的一种多元统计方法。 z简单相关系数;复相关系数;典型相关系数 z典型相关分析首先在每组变量中找出变量的线性组合,使其具有最大相关性; z然后再在每组变量中找出第二对线性组合,使其与第一对线性组合不相关,而第二对本身具有最大相关性; z如此继续下去,直到两组变量之间的相关性被提取完毕为止; z这些综合变量被称为典型变量(canonical variates);第I对典型变量间的相关系数则被称为第I 典型相关系数(一般来说,只需提取1~2对典型变量即可较为充分的概括样本信息)。
典型相关分析的目的 T q T p Y Y Y Y X X X X ),,,() ,,,(2121K K ==设两组分别为p 与q 维 (p ≤q)的变量X ,Y :设p + q 维随机向量协方差阵,????????=Y X Z ??? ?????ΣΣΣΣ=Σ222112 11其中Σ11是X 的协方差阵,Σ22是Y 的协方差阵,Σ12=ΣT 21是X ,Y 的协方差阵 典型相关分析用X 和Y 的线性组合U =a T X , V =b T Y 之间的相关来研究X 和Y 之间的相关性。其目的就是希望找到向量a 和b ,使ρ(U ,V )最大,从而找到替代原始变量的典型变量U 和V 。
典型相关分析
武夷学院实验报告 课程名称:多元统计分析项目名称:典型相关分析 姓名:专业:14信计班级:1班学号:同组成员:无 -、实验目的 1.对典型相关分析问题的思路、理论和方法认识; 2.SPSS软件相应计算结果确认与应用; 3.SPSS软件相应过程命令。 二、实验内容 这里通过典型相关分析来反映我国财政收入与财政支出之间的关系。第一组反映财政收入的指标有国内增值税、营业税、企业所得税、个人所得税、专项收入及行政事业性收费收入等,分别用X1-X6来表示。第二 组反映财政支出的指标有一般公共服务、国防、公共安全、教育、科学技术、社会保障和就业、医疗卫生与计划生育及节能环保等,分别用Y1-Y8来表示。原始数据如下: jts 10^ ?96K! 1?痼8496.6641 H929? 129.06M.820H W234 8? 225.0B425.1 '2W.39tU.31 典型相关分析 在对经济问题的研究和管理研究中,不仅经常需要考察两个变量之间的相关程度,而且还经常需要考察多个变量与多个变量之间即两组变量之间的相关性。典型相关分析就是测度两组变量之间相关程度的一种多元统计方法。 典型相关分析计算步骤 (一)根据分析目的建立原始矩阵 原始数据矩阵 ?? ????????? ???nq n n np n n q p q p y y y x x x y y y x x x y y y x x x 2 1 2 1 222212221 1121111211 (二)对原始数据进行标准化变化并计算相关系数矩阵 R = ?? ? ? ??22211211 R R R R 其中11R ,22R 分别为第一组变量和第二组变量的相关系数阵,12R = 21 R '为第一组变量和第二组变量的相关系数 (三)求典型相关系数和典型变量 计算矩阵=A 111-R 12R 122-R 21R 以及矩阵=B 122-R 21R 1 11-R 12R 的特征值和特征向量,分 别得典型相关系数和典型变量。 (四)检验各典型相关系数的显著性 第五节 利用SPSS 进行典型相关分析 第一步,录入原始数据,如下表:X1 X2 X3 X4 X5 分别代表多孩率、综合节育率、初中及以上受教育程度的人口比例、人均国民收入和城镇人口比例。 1、点击“Files→New→Syntax”打开如下对话框。 2、输入调用命令程序及定义典型相关分析变量组的命令。如图 输入时要注意“Canonical correlation.sps”程序所在的根目录,注意变量组的格式和空格。 第三步,执行程序。用光标选择这些命令,使其图黑,再点击运行键,即可得到所有典型相关分析结果。 Correlations for Set-1 Y1Y2Y3 Y1 1.0000.9983.5012 Y2.9983 1.0000.5176 Y3.5012.5176 1.0000 第一组变量间的简单相关系数 Correlations for Set-2 X1X2X3X4X5X6X7X8X9X10X11X12X13 X1 1.0000-.3079-.7700-.7068-.6762-.7411-.7466-.5922-.1948-.1285-.2650-.9070-.6874 X2-.3079 1.0000-.0117.0103-.0613-.0283-.0140.3333.4161.3810.3831.1098-.0640 X3-.7700-.0117 1.0000.9905.9860.9973.9990.5892.0421-.0196.2492.9515.9903 X4-.7068.0103.9905 1.0000.9910.9935.9952.5634.0249-.0367.2476.9120.9953 X5-.6762-.0613.9860.9910 1.0000.9887.9912.5717.0363-.0277.2475.8972.9926 X6-.7411-.0283.9973.9935.9887 1.0000.9985.5563.0142-.0453.2210.9355.9950 X7-.7466-.0140.9990.9952.9912.9985 1.0000.5795.0319-.0298.2441.9390.9945 X8-.5922.3333.5892.5634.5717.5563.5795 1.0000.7097.6540.8990.6619.5138 X9-.1948.4161.0421.0249.0363.0142.0319.7097 1.0000.9922.8520.1350-.0228 X10-.1285.3810-.0196-.0367-.0277-.0453-.0298.6540.9922 1.0000.8184.0752-.0801 X11-.2650.3831.2492.2476.2475.2210.2441.8990.8520.8184 1.0000.3093.1840 X12-.9070.1098.9515.9120.8972.9355.9390.6619.1350.0752.3093 1.0000.9040 X13-.6874-.0640.9903.9953.9926.9950.9945.5138-.0228-.0801.1840.9040 1.0000 Correlations Between Set-1and Set-2 X1X2X3X4X5X6X7X8X9X10X11X12X13 Y1-.7542-.0147.9995.9940.9892.9989.9998.5788.0334-.0280.2426.9430.9937 Y2-.7280-.0234.9965.9958.9954.9977.9988.5859.0485-.0136.2573.9285.9949 Y3-.4485.2952.5096.4955.5230.4760.5048.9695.7610.7071.9073.5449.4500 Canonical Correlations 1 1.000 2 1.000 3 1.000 第一对典型变量的典型相关系数为CR1=1.....二三 Test that remaining correlations are zero:维度递减检验结果降维检验 Wilk's Chi-SQ DF Sig. 1.000.000.000.000 课时授课计划 课次序号:22 一、课题:实验九典型相关分析 二、课型:上机实验 三、目的要求:1.掌握典型相关分析的理论与方法、模型的建立与显著性检验; 2.掌握利用典型相关分析的SAS过程解决有关实际问题. 四、教学重点:典型相关分析的SAS过程. 教学难点:相关分析的理论与方法、模型的建立与显著性检验. 五、教学方法及手段:传统教学与上机实验相结合. 六、参考资料: 《应用多元统计分析》,高惠璇编,北京大学出版社,2005; 《使用统计方法与SAS系统》,高惠璇编,北京大学出版社,2001; 《多元统计分析》(二版),何晓群编,中国人民大学出版社,2008; 《应用回归分析》(二版),何晓群编,中国人民大学出版社,2007; 《统计建模与R软件》,薛毅编著,清华大学出版社,2007. 七、作业:4.9 4.10 八、授课记录: 九、授课效果分析: 实验九典型相关分析(Canonical Correlation Analysis) (2学时) 一、实验目的和要求 能利用原始数据与相关矩阵、协主差矩阵作相关分析,能根据SAS输出结果选出满足要求的几个典型变量. 二、实验内容 1.典型相关分析的SAS过程—PROC CANCORR过程 基本语句: PROC CANCORR 典型相关分析 摘要 利用典型相关分析的思想,提出了解决了当两组特征矢量构成的总体协方差矩阵奇异时,典型投影矢量集的求解问题,使之适合于高维小样本的情形,推广了典型相关分析的适用范围.首先,探讨了将典型分析用于模式识别的理论构架,给出了其合理的描述.即先抽取同一模式的两组特征矢量,建立描述两组特征矢量之间相关性的判据准则函数,然后依此准则求取两组典型投影矢量集,通过给定的特征融合策略抽取组合的典型相关特征并用于分类.最后,从理论上进一步剖析了该方法之所以能有效地用于识别的内在本质.该方法巧妙地将两组特征矢量之间的相关性特征作为有效判别信息,既达到了信息融合之目的,又消除了特征之间的信息冗余,为两组特征融合用于分类识别提出了新的思路. 一、典型相关分析发展的背景 随着计算机技术的发展,信息融合技术已成为一种新兴的数据处理技术,并已取得了可喜的进展.信息融合的3个层次像素级、特征级、决策级。 特征融合,对同一模式所抽取的不同特征矢量总是反映模式的不同特征的有效鉴别信息,抽取同一模式的两组特征矢量,这在一定程度上消除了由于主客观因素带来的冗余信息,对分类识别无疑具有重要的意义 典型相关分析(CanoniealComponentAnalysis:CCA)是一种处理两组随机变量之间相互关系的统计方法。它的意义在于:用典型相关变量之间的关系来刻画原来两组变量之间的关系!实现数据的融合和降维!降低计算复杂程度。 二、典型相关分析的基本思像 CCA 的目的是寻找两组投影方向,使两个随机向量投影后的相关性达到最大。具体讲,设有两组零均值随机变量 () T c ...c c p 21x ,,= 和 () T d ...d d q 21y ,,= CCA 首先要找到一对投影方向1 α和 1 β ,使得投影 y v 11T β= 和 x u 11T α=之间具有最大的相关性,1 u 和1v 为第一对典型变量;同 理,寻找第二对投影方向2 α和2 β,得到第二对典型变量2 u 和2 v ,使 第十章 典型相关分析 (Canonical Correlation Analysis ) §10.1 引言 一、何时采用典型相关分析 1.两个随机变量Y 与 X ?? ?→?相关关系 简单相关系数; 2.一个随机变量Y 与一组随机变量 p X X ,,1 ?→?多重相关(复相关系数); 3.一组随机变量q Y Y ,,1 与另一组随机变量p X X ,,1 ?→?典型(则)相关系数。 典型相关是简单相关、多重相关的推广;或者说简单相关系数、复相关系数是典型相关 系数的特例。 典型相关是研究两组变量之间相关性的一种统计分析方法,也是一种降维技术。 二、实例 由Hotelling (1935, 1936)最早提出,Cooley and Lohnes (1971)、 Kshirsagar (1972)和 Mardia, Kent, and Bibby (1979) 推动了它的应用。 实例(X 与Y 地位相同) 1985年中国28 省市城市男生(19~22岁)的调查数据。记形态指标身高(cm)、坐高、体重(kg)、胸围、肩宽、盆骨宽分别为621,,X X X ;机能指标脉搏(次/分)、收缩压(mmHg) 、舒张压(变音)、舒张压(消音)、肺活量(ml)分别为521,,Y Y Y 。现欲研究这两组变量之间的相关性。 简单相关系数矩阵 用简单相关系数描述两组变量的相关关系的缺点: 只是孤立考虑单个X 与单个Y 间的相关,没有考虑X 、Y 变量组内部各变量间的相关。 两组间有许多简单相关系数(实例为30个),使问题显得复杂,难以从整体描述。(复相关系数也如此)。 对于上例,要想研究两组变量间的相关关系,构造线性函数如下: 5 25222121616212111Y a Y a Y a V X a X a X a U +++=+++= 要求它们之间具有最大相关性,这就是典型相关分析问题。 §10.2 典型相关分析的统计思想 典型相关分析研究两组变量之间整体性的线性相关关系,它是将每一组变量作为一个整体来进行研究而不是分析每一组变量内部的各个变量。 典型相关分析是借助于主成分分析的思想,对每一组变量分别寻找线性组合,使生成的新的变量能代表原始变量大部分的信息,同时,与由另一组变量生成的新的综合变量的相关程度最大,这样一组新的综合变量称为第一对典型相关变量,同样的方法可以找到第二对、第三对…使得各对典型相关变量之间互不相关,典型相关变量之间的简单相关系数称为典型相关系数。典型相关分析就是用典型相关系数衡量两组变量之间的相关性。 一、典型相关分析的统计思想 采用主成分思想寻找第i 对典型(相关)变量: m q p i Y b Y b Y b Y b V X a X a X a X a U q iq i i i p ip i i i =='=+++='=+++=),min(,,2,1 ,22112211 典型相关系数),(i i i V U Corr CanR =典型变量系数或典型权重b a '',,此处X 、Y 是已经过标准化的变量。 记第一对典型相关变量间的典型相关系数为:),(111V U Corr CanR = 使1U 与1V 间最大相关;第二对典型相关变量间的典型相关系数为:),(222V U Corr CanR =使2U 与2V 间最大相关,且分别与11,V U 无关;……。第i 对典型相关变量间的典型相关系数为:),(i i i V U Corr CanR =,使i U 与i V 间最大相关,且分别与 ,,,,2211V U V U 无关;且 0121≥≥≥≥≥i CanR CanR CanR 。 二、典型相关分析的基本理论和方法 设有两组随机变量:()()' ='=q p Y Y Y Y X X X X ,,,,,,,2121 ,X 、Y 的协方差矩阵为:? ?? ? ??∑∑∑∑=∑22211211。设q p <,11∑是第一组变量的协方差阵,22∑是第二组变量的协方差 相关分析的类型 典型相关分析:用于探究一组解释变量与一组反应变量时间的关系。 典型相关分析函数:cancor(x,y,xcenter=T,ycenter=T) x为第一组变量数据矩阵 y为第二组变量数据矩阵 xcenter表示第一组变量是否中心化 ycenter表示第二组变量是否中心化 自编典型相关函数:cancor.test(x,y,plot=T) x为第一组变量数据矩阵 y为第二组变量数据矩阵 plot为是否绘制典型相关图 例1:d11.1 生理指标与训练指标之间的典型相关性。 生理指标:体重(x1)、腰围(x2)、脉搏(x3); 训练指标:引体向上次数(y1)、起坐次数(y2)、跳跃次数(y3)。> X<-read.table("clipboard",header=T) > R<-cor(X) > R x1 x2 x3 y1 y2 y3 x1 1.0000 0.8702 -0.36576 -0.3897 -0.4931 -0.22630 x2 0.8702 1.0000 -0.35289 -0.5522 -0.6456 -0.19150 x3 -0.3658 -0.3529 1.00000 0.1506 0.2250 0.03493 y1 -0.3897 -0.5522 0.15065 1.0000 0.6957 0.49576 y2 -0.4931 -0.6456 0.22504 0.6957 1.0000 0.66921 y3 -0.2263 -0.1915 0.03493 0.4958 0.6692 1.00000 > R11<-R[1:3,1:3];R12<-R[1:3,4:6];R21<-R[4:6,1:3];R22<-R [4:6,4:6] > A<-solve(R11)%*%R12%*%solve(R22)%*%R21 #A=(R11)-1 R12 (R22)-1 R21 > ev<-eigen(A)$values #特征值 > sqrt(ev) #典型相关系数 [1] 0.79561 0.20056 0.07257 以上过程是一步一步计算的,接下来我们使用R自带的典型相关函数: > xy<-scale(X) #数据标准化 > ca<-cancor(xy[,1:3],xy[,4:6]) #典型相关分析 > ca$cor #典型相关系数 [1] 0.79561 0.20056 0.07257 > ca$xcoef #x的典则载荷 [,1] [,2] [,3] x1 -0.17789 -0.43230 0.04381 x2 0.36233 0.27086 -0.11609 x3 -0.01356 -0.05302 -0.24107 > ca$ycoef #y的典则载荷 [,1] [,2] [,3] y1 -0.08018 -0.08616 0.29746 y2 -0.24181 0.02833 -0.28374 y3 0.16436 0.24368 0.09608 典型变量的系数载荷并不唯一,只要是它的任意倍数即可,所以每个软件得出的结果并不一样,而是相差一个倍数。 R自带的典型分析函数cancor()并不包括对典则相关系数的假设检验,为了方便,使用自编典型相关检验函数cancor.test()。 > cancor.test(xy[,1:3],xy[,4:6],plot=T) $cor [1] 0.79561 0.20056 0.07257 $xcoef [,1] [,2] [,3] 典型相关性分析 典型相关分析是借助主成分分析降维的思想,分别对两组变量提取主成分,且使得两组变量提取的主成分之间的相关程度达到最大,而从同一组内部提取的各主成分之间互不相关,用从两组之间分别提取的主成分的相关性来描述两组变量整体的线性相关关系。 代码如下: INCLUDE 'E:\SPSSInc\PASWStatistics18\Samples\English\Canonical correlation.sps'. cancorr set1=x1 x2 x3 /set2=y1 y2 y3. Run MATRIX procedure: Correlations for Set-1 x1 x2 x3 x1 1.0000 .8702 -.3658 x2 .8702 1.0000 -.3529 x3 -.3658 -.3529 1.0000 数据集1中变量x1-x3的相关关系,有相关系数知,x1与x2有较强的相关性。 Correlations for Set-2 y1 y2 y3 y1 1.0000 .6957 .4958 y2 .6957 1.0000 .6692 y3 .4958 .6692 1.0000 数据集2中变量y1-y3的相关关系,有相关系数知,y1与y2有较强的相关性。 Correlations Between Set-1 and Set-2 y1 y2 y3 x1 -.3897 -.4931 -.2263 x2 -.5522 -.6456 -.1915 x3 .1506 .2250 .0349 x1-x3与y1-y3的相关关系,x1,x2与y1-y3是负相关关系,说明体重和腰围较大对运动能力具有负影响。 Canonical Correlations 1 .796 2 .201 3 .073 表示三个典型相关系数 Test that remaining correlations are zero: Wilk's Chi-SQ DF Sig. 1 .350 16.255 9.000 .062 2 .955 .718 4.000 .949 3 .995 .082 1.000 .775 对三个典型相关系数的显著性检验,原假设是相关系数为0,在显著性水平为0.1上,第一个典型相关系数对应的Sig.为0.062<0.1,拒绝原假设,认为第一个典型相关系数不为0.第二和第三个典型相关系数对应的Sig.>0.1,认为二者均为0。 Standardized Canonical Coefficients for Set-1 1 2 3 x1 .775 -1.884 -.191 x2 -1.579 1.181 .506 x3 .059 -.231 1.051 数据集1标准化变量的典型相关变量函数表达式:U1=0.775x1*-1.579x2*+0.059x3* U2=-1.884x1*+1.181x2*-0.231x3*,U3=-0.191x1*+0.506x2*+1.051x3* Raw Canonical Coefficients for Set-1 1 2 3 x1 .031 -.076 -.008 x2 -.493 .369 .158 x3 .008 -.032 .146 数据集1原始变量的典型相关变量函数表达式:U1=0.031x1-0.493x2+0.008x3,U2...,U3… Standardized Canonical Coefficients for Set-2 1 2 3 y1 .349 -.376 -1.297 典型相关分析方法研究 摘要:典型相关分析是研究两组变量(或两个随机向量)之间的相关关系的一种统计方法。与仅研究二个变量间线性关系的简单相关分析相比,典型相关分析能揭示出两组变量之间的内在联系,且两组变量的数目可以改变,这确定了它的重要性。随着计算机技术的发展,典型相关分析在各个行业试验研究中应用日渐广泛。本文主要介绍典型相关分析的基本原理与步骤并举例说明其应用。 关键词:典型相关分析;基本原理;步骤;应用 Abstract:Canonical correlation analysis is the study of two groups of variables (or two random vectors) a statistical method the relationship between the. Compared with only the simple correlation analysis of linear relationship between two variables and canonical correlation analysis can reveal the internal relations between two sets of variables, and the number of two groups of variables can change, this determines the importance of it. With the development of computer technology, the canonical correlation analysis system has been widely used in various industries in experimental study. This paper mainly introduces the basic principle and procedure of canonical correlation analysis and examples of its application. Key words:Canonical correlation analysis; basic principle; step; application 一、引言 典型相关分析(Canonical Correlation Analysis 简称CCA)是处理两个随机矢量之间相关性的统计方法,在多元统计分析中占有非常重要的地位。典型相关分析可有效反映两组统计数据之间的关系,有着重要的应用背景[1]。 在实际分析问题中,当我们面临两组多变量数据,并希望研究两组变量之间的关系时,就要用到典型相关分析。例如,为了研究扩张性财政政策实施以后对宏观经济发展的影响,就需要考察有关财政政策的一系列指标如财政支出总额的增长率、财政赤字增长率、国债发行额的增长率、税率降低率等与经济发展的一系列指标如国内生产总值增长率、就业增长率、物价上涨率等两组变量之间的相关程度。 二、典型相关分析的国内外研究现状 典型相关分析及其改进算法已成功的应用到计算机视觉、模式识别、电子通信、生物医学、文本和图像检索和社会统计学等众多学科或领域。很多学者都在从事这方面的研究,并取得了良好的效果。孙权森[2]等将典型相关分析应用到特征融合中,利用典型相关分析达到了信息冗余的目的。陈拓[3]等利用典型相关分 一、典型相关分析的概念 典型相关分析(canonical correlation analysis )就是利用综合变量对之间的相关关系来反映两组指标之间的整体相关性的多元统计分析方法。它的基本原理是:为了从总体上把握两组指标之间的相关关系,分别在两组变量中提取有代表性的两个综合变量U1和V1(分别为两个变量组中各变量的线性组合),利用这两个综合变量之间的相关关系来反映两组指标之间的整体相关性。 二、条件: 典型相关分析有助于综合地描述两组变量之间的典型的相关关系。其条件是,两组变量都是连续变量,其资料都必须服从多元正态分布。 三、相关计算 如果我们记两组变量的第一对线性组合为: X u 11α'=Y v 1 1β'=),,,(121111'=p a a a α),,,(121111' =q ββββ 1)()(11111=∑'='=ααααX Var u Var 1 )()(1221111=∑'='=ββββY Var v Var 112111 11,),(),(11βαβαρ∑'='==Y X Cov v u Cov v u 典型相关分析就是求α1和β1,使二者的相关系数ρ达到最大。 典型相关分析希望寻求 a 和 b 使得 ρ 达到最大,但是由于随机变量乘以常数时不改变它们的相关系数,为了防止不必要的结果重复出现,最好的限制是令Var (U )=1 和Var (V )= 1。 A 关于的特征向量(a i1,a i2,…,a ip ),求 B 关于 的 特征向量(bi 1,b i2,…,bi p ) 5、计算Vi 和Wi ; i λ i λ() p X X X ,...,1=() q Y Y Y ,...,1=1.实测变量标准化; 2.求实测变量的相关阵R ; 3.求A 和B ; 4、求A 和B 的特征根及特征向量; 1111111 111111111()() p q p pp p pq xx xy yx yy p q q qp q qq p q p q r r r r r r r r R R XX XY R R R YX YY r r r r r r r r +?+?? ? ? ? ?? ?? ? === ? ? ? ????? ? ? ??? ∑∑∑∑ () ()()()∑∑∑∑∑∑∑∑----==XY XX YX YY B YX YY XY XX A 1 1 1 1 p λλλ≥≥≥...21p ip i i i X b X b X b V +++=...2211q iq i i i Y a Y a Y a W +++= (2211) 第 15 章 典型相关分析 典型相关分析(Canonical Correlation )是研究两组变量之间相关关系的一种多元统计方法。它能够揭示出两组变量之间的内在联系。 我们知道,在一元统计分析中,用相关系数来衡量两个随机变量之间的线性相关关系;用复相关系数研究一个随机变量和多个随机变量的线性相关关系。然而,这些统计方法在研究两组变量之间的相关关系时却无能为力。比如要研究生理指标与训练指标的关系,居民生活环境与健康状况的关系,人口统计变量(户主年龄、家庭年收入、户主受教育程度)与消费变量(每年去餐馆就餐的频率、每年出外看电影的频率)之间是否具有相关关系?阅读能力变量(阅读速度、阅读才能)与数学运算能力变量(数学运算速度、数学运算才能)是否相关?这些多变量间的相关性如何分析? 典型相关分析的目的是识别并量化两组变量之间的联系,将两组变量相关关系的分析,转化为一组变量的线性组合与另一组变量线性组合之间的相关关系分析。 目前,典型相关分析已被广泛应用于心理学、市场营销等领域,如用于研究个人性格与职业兴趣的关系,市场促销活动与消费者响应之间的关系等。 15.1 典型相关分析的理论与方法 15.1.1 典型相关分析的基本思想 典型相关分析的基本思想和主成分分析非常相似。首先在每组变量中找出变量的一个线性组合,使得两组的线性组合之间具有最大的相关系数。然后选取相关系数仅次于第一对线性组合并且与第一对线性组合不相关的第二对线性组合,如此继续下去,直到两组变量之间的相关性被提取完毕为止。被选出的线性组合配对称为典型变量,它们的相关系数称为典型相关系数。典型相关系数度量了这两组变量之间联系的强度。 一般情况,设、是两个相互关联的随机向量,分别在两组变量中选取若干有代表性的综合变量、,使得每一个综合变量是原变量的线性组合,即 (1)(1)(1)(1)12(,,,p X X X X =L ))P q (2)(2)(2)(2)12(,,,q X X X X =L i U i V ()(1)()(1)()(1)()(1)1122i i i i i P U a X a X a X a X ′=+++L ()(2)()(2)()(2)()(2)1122i i i i i q V b X b X b X b X ′=+++L 为了确保典型变量的唯一性,我们只考虑方差为1的(1)X 、(2)X 的线性函数与,求使得它们相关系数达到最大的这一组。若存在常向量,,在 的条件下,使得相关系数ρ到最大, 则()(1)i a X ′(1)b )()(2)i b X ′(1D a X (1)a (2)′达)(1)(1)(2)()()D b X ′′=1=(1)(1)(,a X ′(1)b X数学建模__SPSS_典型相关分析
SPSS典型相关分析结果解读
实验九典型相关分析报告
典型相关分析(CCA)附算法应用及程序
第十章典型相关分析
典型相关分析
典型相关性分析1
典型相关分析方法研究
典型相关分析
典型相关分析1
